Informational Complexity and Functional Activity of RNA Structures

Abstract

Very little is known about the distribution of functional DNA, RNA, and protein molecules in sequence space. The question of how the number and complexity of distinct solutions to a particular biochemical problem varies with activity is an important aspect of this general problem. Here we present a comparison of the structures and activities of eleven distinct GTP-binding RNAs (aptamers). By experimentally measuring the amount of information required to specify each optimal binding structure, we show that defining a structure capable of 10-fold tighter binding requires approximately 10 additional bits of information. This increase in information content is equivalent to specifying the identity of five additional nucleotide positions and corresponds to an ∼1000-fold decrease in abundance in a sample of random sequences. We observe a similar relationship between structural complexity and activity in a comparison of two catalytic RNAs (ribozyme ligases), raising the possibility of a general relationship between the complexity of RNA structures and their functional activity. Describing how information varies with activity in other heteropolymers, both biological and synthetic, may lead to an objective means of comparing their functional properties. This approach could be useful in predicting the functional utility of novel heteropolymers.

Introduction

Defined sequence heteropolymers may, under favorable conditions, fold into a restricted subset of all possible conformations^31504ab00001 with important functional properties such as specific ligand binding or catalytic activity. For such polymers, the relationship between sequence, conformation, and function is defined by the fitness landscape, in which each sequence is assigned a value corresponding to some functional property.^{31504ab00002,31504ab00003} Peaks in the fitness landscape correspond to macromolecular conformations specified by related sets of sequences. Fundamental properties of fitness landscapes, such as how many distinct solutions there are to a given functional problem, how this number might vary with activity, and how the complexity of the solutions might vary with activity, have received little experimental attention.^31504ab00004 In contrast, the statistical properties of molecular fitness landscapes have been the subject of considerable theoretical study since these properties determine the evolutionary response to selective pressure.^{31504ab00003,31504ab00005−31504ab00008} Other inquiry^{31504ab00009,31504ab00010} has focused on the ruggedness or smoothness of the fitness landscape, as this quality is important in determining the rate and extent to which optimization of a function is possible.

In part, the past emphasis on the ruggedness of fitness landcapes reflects the difficulties involved in experimentally surveying molecular sequence spaces.^{31504ab00004,31504ab00011} Sequence spaces tend to be rather large (e.g., there are ∼10⁶⁰ sequences of 100-nucleotide long RNA or DNA molecules and ∼10¹³⁰ sequences of 100-amino acid long proteins), so that conclusions must be extrapolated from relatively sparse samplings. Current methods allow for the identification of functional molecules from unbiased samples of at most 10¹⁶ RNA or DNA sequences and 10¹³ protein sequences.^31504ab00011 Nevertheless, for simple functions, it should now be possible to build up some understanding of the global properties of biological heteropolymer fitness landscapes. Methods currently under development will allow similar investigations of nonbiological heteropolymers.^{31504ab00012−31504ab00015} It is important to note that global relationships between sequence and function cannot be determined by the analysis of biological macromolecules, because they have evolved in response to complex and largely unknown historical constraints and selective pressures. Therefore, describing how sequence, structure, and function are related, considered over all of sequence space, is fundamentally a problem of chemistry.

Here we present an initial experimental investigation of the question of whether more difficult functional problems, such as higher-affinity binding to a target molecule, are likely to require more complex structural solutions that are less frequent in sequence space. It has been difficult in the past to address this issue experimentally^31504ab00016 due to the lack of a suitable comparison set of distinct structures that solve the same functional problem with varying degrees of effectiveness. We used a set of in vitro-evolved RNA aptamers that bind GTP to ask how the complexity of RNA structures varies with their affinity for a small-molecule ligand. We synthesized a mutagenized sequence library based on the functional region of each aptamer and then used in vitro selection to identify active sequence variants. Analysis of these sequences allowed us to construct optimized aptamers and to calculate the information content required to define each structure^31504ab00017 in the conditions used in the original selection. Our study reveals that more complex structures are required to bind a ligand with higher affinity and also suggests that the number of distinct structures with a given activity may increase sharply with complexity.

Experimental Section

Binding Assays. Apparent dissociation constants (K_ds) were determined using the ultrafiltration method^31504ab00018 as previously described^31504ab00019 with trace levels of ³²P-GTP and titration of the RNA concentration over the range where 50% of the GTP was bound. Binding buffer was 200 mM KCl, 10 mM potassium phosphate, 5 mM MgCl₂, 0.1 mM EDTA, pH 6.1.

In Vitro Selection. Degenerate oligodeoxynucleotide templates mutagenized at a rate of 21% per position (±3%, confirmed by sequencing) were chemically synthesized using phosphoramidite mixtures in all positions of the aptamers. New 5‘ and 3‘ constant regions were used to avoid amplifying contaminating sequences from the original selection. Selection conditions were the same as in the original selection¹⁹ except that no GTP pre-elution was performed. Approximately 0.2 mg of RNA derived from 10¹² DNA molecules was allowed to bind 100−200 μL of ∼0.5 mM GTP-γS immobilized on thiopropyl Sepharose 6-B (Pharmacia) for 15 min. On the basis of the extent of mutagenesis and pool sizes employed, we almost completely searched the sequence neighborhood surrounding each original isolate to a distance of about five mutations.^31504ab00020 The column was washed with 10−20 volumes of binding buffer before the RNA was eluted for 2 h (to ensure that molecules with slow off-rates were recovered) by the addition of 5 mM GTP. Three to seven rounds of selection for GTP binding were performed for each aptamer. Selections continued until either more than 20% of the RNA bound and eluted or when the same amount of binding was exhibited in three consecutive rounds; 30−80 clones were then sequenced and aligned.

Calculating Information Content. We computed complexity in terms of the information content required to define each functional RNA structure in its relevant environment. The Shannon uncertainty (H) was calculated for each loop position from the sequence alignments and subtracted from the maximum uncertainty possible, as described,^31504ab00021 to give information content (in bits). H = −ΣP_i log₂P_i summed over each of the four base types (i = A, U, G, C), where the observed frequency (F_i) of each base i is used to estimate P_i. The observed F_i s were normalized and adjusted for the distribution of nucleotides expected in the selections due to the 21% mutagenesis to calculate the information content required to specify a functional structure in random RNA sequence space (see Supporting Methods). The stem information content was calculated separately; the resulting loop and stem information contents were added to calculate the total aptamer information content.

A base in a simple stem is correlated to its pairing partner,^31504ab00017 which reduces the information content relative to an uncorrelated base in a loop position. There are sixteen possible two-nucleotide permutations (i.e., where A−U is different from U−A) giving a maximum uncertainty for the pair of 4 bits. Of the sixteen two-nucleotide permutations, four are Watson−Crick (W−C)base pairs (A−U, U−A, G−C, C−G). If a pair is W−C base-paired, the uncertainty is 2 bits; the information content is 4 bits − 2 bits = 2 bits. If G−U and A−C are considered stem-forming base-pairs, the uncertainty is reduced to 3 bits; the information content of this pairing is 4 bits − 3 bits = 1 bit.

Calculating Aptamer Abundance. The likelihood of a structure occurring in a pool is related to its information content and the length and number of different sequences in the library. The modularity, or number of separate pieces that comprise the aptamer, is also an important factor,^31504ab00022 as is origin from a fully random or partly designed library. We computed the expected abundance as the probability of making the R binary decisions necessary to specify the structure (2^-R, where R is information content) multiplied by the number of sequences in the library (2.5 × 10¹⁴ fully random and 2.5 × 10¹⁴ partly designed), with small corrections made for aptamer modularity and library composition.

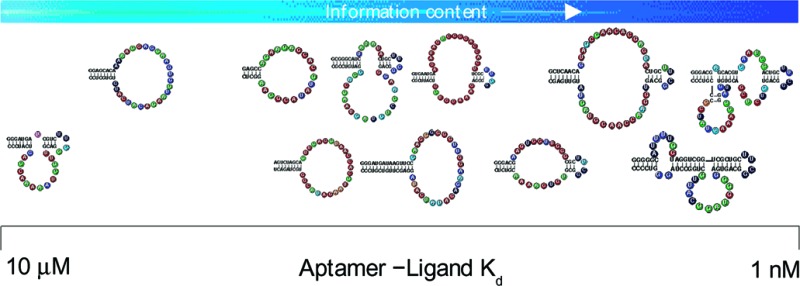
Seven of the aptamers (Figure 1, parts B and C) have secondary structures compatible with the internal stem-loop that was engineered into half of the initial library.^31504ab00019 Thus, the information content from the internal stem-loop was “free”; its contribution to the aptamer information content was subtracted before calculating the abundance. Aptamers with two binding loops can be constructed from sequence motifs in either of two orientations which increases their abundance by a factor of 2. The four stem-loop aptamers (Figure 1A) have structures incompatible with the engineered portion of the library. When sequences in a fully random pool are longer than the aptamer, the aptamer sequence can be present in different positions, or registers, within a molecule in the library. Thus, the abundance of an aptamer shorter than the pool molecules increases by a factor of (L−N), where L is the length of the pool and N is the length of the aptamer.

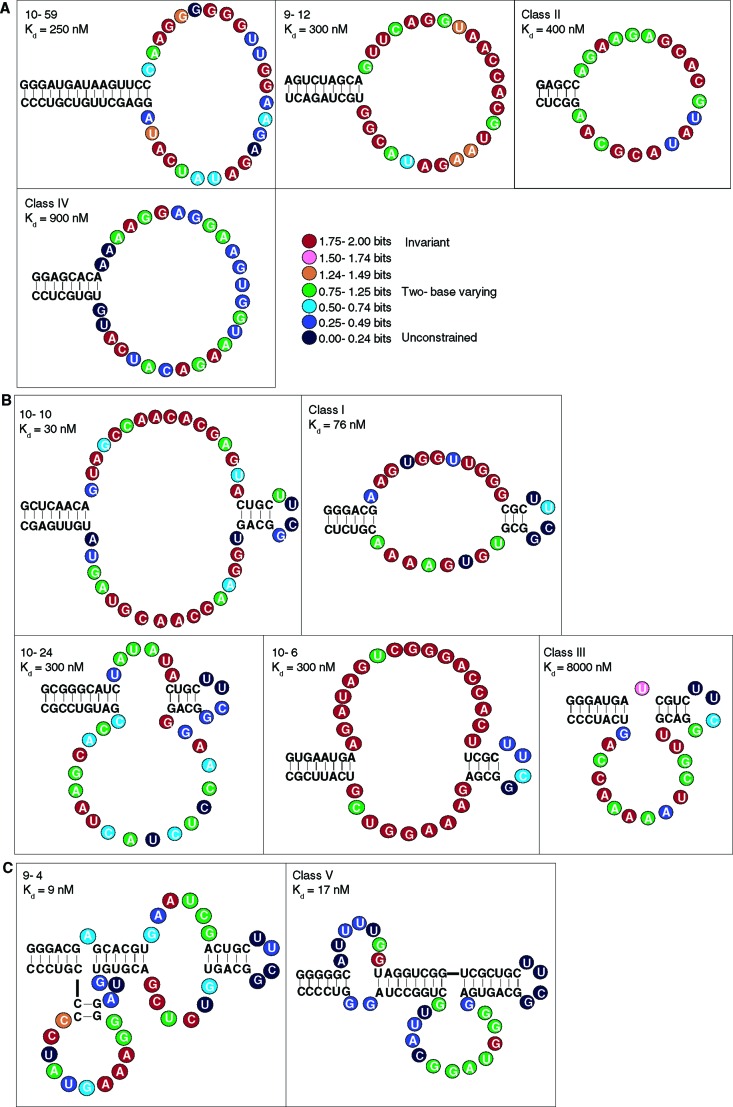
Figure 1.

Aptamer sequences and secondary structures. (A) aptamers with simple stem-loop structures, (B) aptamers with one internal bulge-loop, and (C) aptamers with two internal bulge-loops. The sequences shown have been optimized for GTP binding. Regions that showed W−C covariation are drawn as lines of plain text. The 5‘ end of each aptamer is at the top-left end of the structure. The information content of each position within the loops is color-coded as indicated.

Correlation Coefficients and Regression. We applied nonparametric tests of association and regression because they do not require specific assumptions about the underlying distribution of the data. In particular, nonparametric approaches are insensitive to deviations from the normal distribution.^31504ab00023 The Spearman rank correlation coefficient (r_s) is a nonparametric test of association appropriately used when there is some degree of uncertainty about the exact ordering of closely ranked data points.^31504ab00023 95% confidence intervals were used for all rankings. Ties were assigned the mean rank of those points. Significance was determined under the null hypothesis of no correlation with a one-tailed test, α = 0.05. P values were calculated from the test statistic as described.^31504ab00024 We used Kendall's robust line-fit method as described²³ to perform the nonparametric regression of aptamer information content onto activity expressed as log K_d. Unlike linear least-squares regression, Kendall's robust line-fit method does not rely upon the presence of independent and normally distributed values. Briefly, the slope is given by the median slope of all pairwise combinations of points. The intercept is the median intercept of all points computed with the median slope. The standard error of the slope was estimated from 10 000 bootstrap replicates with replacement^31504ab00025 using the bias-corrected percentile method as described in ref (31504ab00026).

Results

Aptamer Isolation and Optimization. To identify a set of structures with a wide range of abilities to perform the same function, we sequenced additional clones from the last four rounds of an in vitro selection experiment that had previously produced seven high-affinity GTP aptamers.^31504ab00021 We screened more than half of these (151 of 249) for solution binding to GTP, including all sequences that appeared in more than one round of selection, any found multiple times in a single round and an assortment of sequences that appeared only once. The screen yielded four new aptamers that, together with the seven already identified, provided a total of eleven for further study. Altogether, 124 of the assayed sequences exhibited a solution dissociation constant (K_d) for GTP of less than 35 μM, the approximate detection limit. Sequence comparison shows that 90 of the 124 binders (73%), representing 51 independent isolates, were members of one of the eleven identified aptamer classes. The remaining 34 sequences may represent additional distinct GTP aptamers. Some of the high-affinity aptamers (e.g., 10−6) were represented by a single sequence in the final round of selection, suggesting that other high-affinity aptamers may yet be identified. However, because the set of eleven aptamers represents more than half of all active selected sequences it is likely to contain the majority of the simplest solutions to the problem of moderate- to high-affinity GTP binding.

We began optimizing the activity of each aptamer by mapping the 5‘ and 3‘ ends of the functional region (Supporting Chart 1). We then used in vitro selection to search the sequence neighborhoods surrounding each minimal construct for functional variants by transcribing RNA from eleven different DNA pools of chemically synthesized mutants. We observed numerous W−C covariations in each of the 11 sets of selected and aligned sequences (Figure 2). These allowed us to predict base-paired regions and generate secondary structure models (Figure 1). In all cases, the models were corroborated by assaying engineered stem variants for solution or column binding. Lengthening the stems more than shown in Figure 1 did not improve the activity of any aptamer. Five of the aptamers had loop positions that exhibited selection to a particular base that appeared more often than expected by chance. We tested all positively selected mutations by analysis of RNA transcribed from synthetic DNA. The optimized aptamers have solution affinities for GTP that range from a K_d of 9 nM to 8 μM, a span of almost 3 orders of magnitude (Table 1). During the course of this optimization procedure, three aptamers showed no increase in binding affinity relative to the original isolate. Five showed increases of a factor of 2−3 in affinity. The class II, III, and V aptamers improved by a factor of 12, 14, and 235, respectively (Supporting Chart 1), demonstrating that their initial isolates were significantly sub-optimal and that the optimization procedure was essential for identifying their maximum activities.

Figure 2.

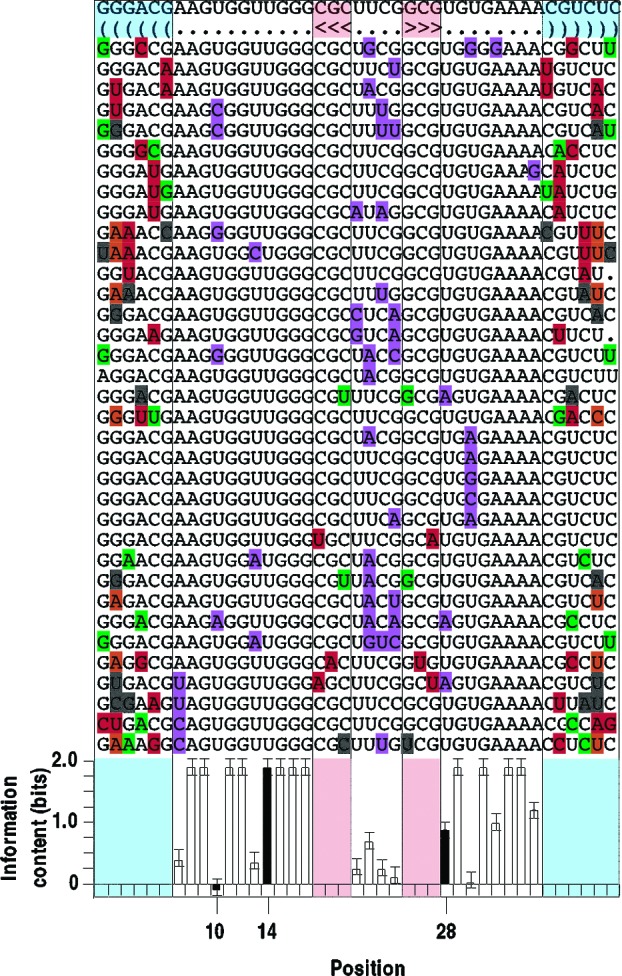
Example of selected sequence variants. The Class I-aptamer template was mutagenized 21% per position to search for functional sequence variants and is shown at the top. The secondary-structure model is shown in bracket form on the second line. Mutations in the stem regions are color-coded as follows:  red, W−C covariation; orange, new W−C pairings; green, Wobble-pairings; black, broken base pairs. Mutations in the loop regions are marked in purple. The graph shows the information content calculated for each loop position; positions referred to in the text are shaded. Error bars show ± SD See Supporting Figure 1 for all eleven sets of selected alignments and Supporting Chart 1 for all original, minimized, and optimized sequences.

Table 1.

Aptamer Attributes and Spearman Correlation Coefficients (r_s)

		size (bases)		information content (bits)
aptamer	kd (nM)a	total	loop	loopb	Apt (A)b	Apt (B)b	Apt (C)b
9−4	9 ± 1	69	27	27.0 ± 1.0	65.0	56.0	65.0
Class V	17 ± 4	68	22	12.5 ± 1.0	54.5	44.5	54.5
10−10	30 ± 6	60	32	45.0 ± 1.0	71.0	65.0	67.0
Class I	76 ± 3	41	19	26.0 ± 0.5	45.0	41.0	45.0
10−59	250 ± 20	50	26	30.5 ± 0.5	60.5	53.5	42.5
10−24	300 ± 50	55	25	23.5 ± 1.5	50.0	44.0	44.0
9−12	300 ± 50	43	25	40.5 ± 0.5	58.5	54.5	52.5
10−6	300 ± 100	54	26	45.5 ± 1.0	71.0	65.0	67.0
Class II	400 ± 200	30	20	28.0 ± 1.0	38.0	36.0	40.0
Class IV	900 ± 200	43	27	20.5 ± 1.0	36.5	32.5	32.5
Class III	8000 ± 1000	41	15	20.0 ± 1.0	43.5	38.5	41.5
Spearman correlation coefficients
rs of Kd and:		0.68	0.33	0.17	0.58	0.56	0.65
P value		<0.025	NS	NS	<0.050	<0.050	<0.025

^a K_d is the mean of three trials, SD is shown.^b These columns have the same SD. Three different methods for treating the stems were applied to calculate the aptamer information content. These are indicated as Apt (A), Apt (B), and Apt(C). NS indicates no statistical significance, α = 0.05.

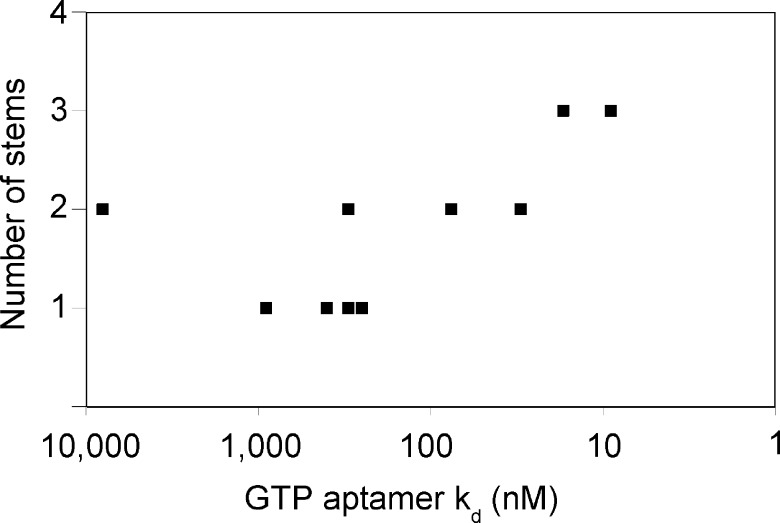
Aptamer Complexity. There is a remarkable correspondence between the affinities of the optimized aptamers, and the intricacy of their secondary structures (Figure 3). The four simple stem-loop aptamers (Figure 1A) are relatively weak binders (K_ds from 900 nM to 250 nM). The five internal bulge-loop aptamers (Figure 1B) have K_ds for GTP as low as 30 nM. The remaining two aptamers are more complex, with three stems and two internal bulge-loops (Figure 1C), and are the best binders, with K_ds of 17 and 9 nM. A reasonable expectation is that better binding requires, on average, longer recognition loops. However, there may be a physical limit to the length of a recognition loop beyond which folding into a unique structure becomes increasingly problematic. At that point, a transition occurs to a more elaborate secondary structure, in which a larger number of smaller recognition loops cooperate to form the binding structure.

Figure 3.

Good correspondence between binding affinity and the intricacy of aptamer secondary structures. The number of stems in each aptamer is plotted against logk_d.

To measure the amount of information required to describe these functional RNA structures in the experimental conditions, relative to completely random sequences, we must examine the length and degeneracy of their defining consensus sequences.^31504ab00017 The amount of information (in bits) required to specify an active structure can readily be obtained from an alignment of functional sequence variants.^31504ab00021 Two bits of information content are required to specify an invariant position in RNA; 1 bit specifies a position that can be either of two bases; no information content (0 bits) is needed to define an unconstrained position.^{31504ab00017,31504ab00021} The total information content of a structure is found by adding the information contents for every position in its sequence, after accounting for correlated bases such as those found in stems.^31504ab00017

We determined the information content of each of the eleven GTP aptamers from the aligned sequences obtained by in vitro selection as described above. Positions that did not exhibit W−C covariation in the selection alignments or evidence for base-pairing in site-directed mutagenesis experiments were considered to be loop bases. We calculated the information content of loop positions from the amount of sequence conservation exhibited.^31504ab00009 For example, within the alignment of Class I aptamer sequences shown in Figure 2, no variation was observed at position 14, which suggests (P < 0.02) that this base must be a U for the aptamer to function. At position 28, either A or U are accepted, while position 10 can be any nucleotide. With respect to these three positions, the information content required for function is therefore 2 + 1 + 0, or 3 bits. Small corrections to this simple calculation are made to account for the sampling error due to the use of a finite set of sequences²¹ (see Supporting Methods).

It is more difficult to determine the amount of information required to specify stems stable enough for optimal binding^31504ab00027 because stability is dependent upon both length and sequence.^31504ab00028 The information content of a base pair will likely be underestimated if the degree of conservation observed in the sequence alignments is used. For example, an aptamer might retain approximately optimal function with any five out of six potential base pairs in a stem. If each sequence in the alignment had one mismatch in a stem but these mismatches were at different positions in different sequences, the information content of all base pairs would appear low. Because of this ambiguity, we devised three distinct methods for determining the information content of stems required for optimal binding. In method A, we simply assigned 2 bits to each base pair. Method B allowed for multiple wobble-pairings by assigning 2 bits to half the base pairs and 1 bit to the others. The constructs used to determine optimal binding had outer stems that were stable enough that increasing their length did not improve activity. We also wanted to address the concern that slightly shorter stems may be sufficient for optimal binding, even though the sequence composition might then be more constrained. Therefore, in method C, we treated each outer stem as six W−C base pairs. It is difficult to calculate stem information content in a rigorous manner. However, the three methods we employed resulted in relatively small variations in calculated total information content, even though each involved different assumptions and approximations (Table 1).

Aptamer Abundance. There are a number of sources of uncertainty in the above calculations, including the finite number of sequences available for analysis, the likely presence of sub-optimal sequences in the dataset, and the difficulty of evaluating stem information content. To verify the accuracy of our complexity calculations, we used these computed values to predict which aptamers were simple enough to have been present multiple times in the original sequence pool.

The likelihood of a structure occurring in a pool of sequences depends on its information content, length and the number of modules into which it can be broken,^31504ab00022 as well as the composition of the library. When the modularity is low, the expected abundance is approximately the probability that a random sequence is an aptamer (2^-R, where R is information content in bits) multiplied by the number of sequences in the library (see Experimental Section).

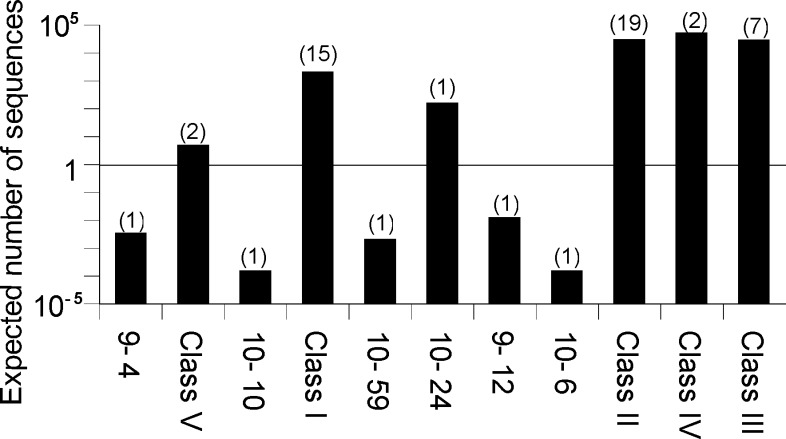
Aptamers with an expected abundance > 1 have a reasonable chance of being found in a pool with a composition similar to the one used in the original selection. We identified multiple isolates for five of the six aptamers estimated to be present in more than one copy in our original library (Figure 4). The agreement between the observed and expected subset of aptamers with multiple independent isolates suggests that our calculated complexities are approximately correct.

Figure 4.

Expected number of aptamer sequences in original pool. The expected number of sequences corresponding to each aptamer structure in a pool similar to the one used in the original selection¹⁹ is shown on a log scale. The number of independent sequence isolations we actually observed are indicated in parentheses.

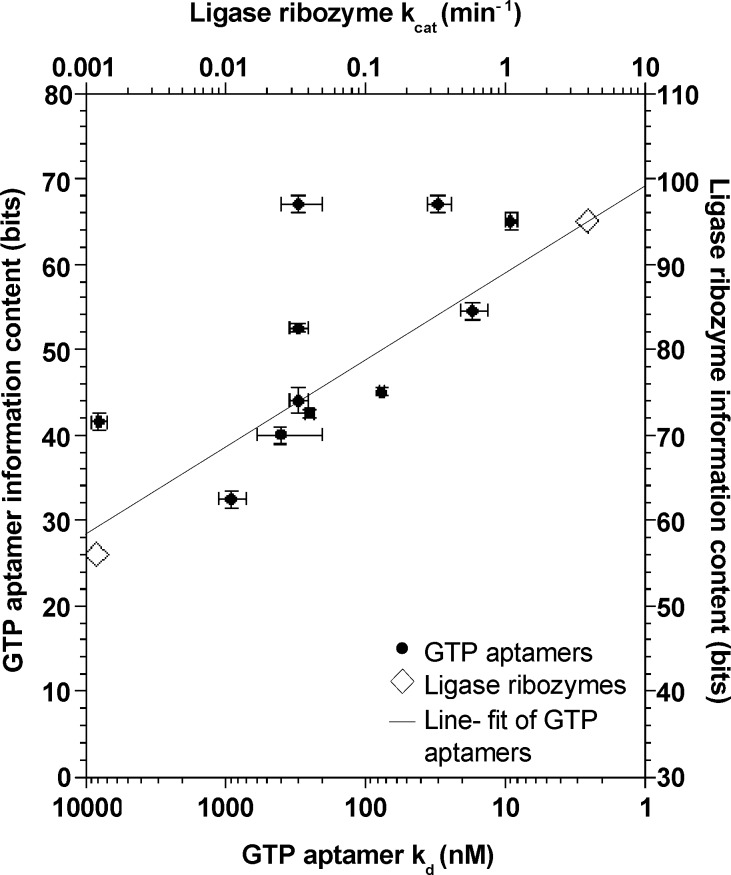
Activity and Complexity. Information content is correlated with binding affinity for the eleven aptamers we analyzed (P < 0.025), which strongly supports the hypothesis that greater complexity is required for greater activity (Table 1, Figure 5). The results are significant regardless of the method we used to compute stem information content. Aptamer size and K_d are also significantly correlated, which may in part reflect the fact that larger structures have more potential information content.

Figure 5.

More complex structures required for more activity. GTP aptamer information content (method C) is plotted against logk_d. Error bars show ± SD The line was generated by applying Kendall's robust line-fit method to the GTP aptamer data. Ligase ribozyme information content is plotted against log k_cat (vertically shifted for clarity).

The best-fit line for the GTP aptamer data over the available range of K_ds shows that, on average, an additional 10 ± 5 bits of information content are required to improve binding by a factor of 10. Because 2 bits of information content are needed to define an invariant position, this is equivalent to adding roughly 5 fixed positions (or 5 base pairs) to an RNA structure. To see if these values apply more broadly, we searched the literature for other examples where both optimal activity and data to estimate complexity were available for more than one RNA with the same biochemical function but significantly different levels of activity. We used published results^{31504ab00029,31504ab00030} from the one example we found to estimate the information content of two ribozymes that catalyze RNA−RNA ligation reactions. An optimized version of the Class I ligase (95 bits of information content) is 3250 times faster than an optimized Class III ligase (56 bits of information content). This suggests that each factor of 10 improvement in activity came at the cost of an additional 11 bits of information content, consistent with the 10 ± 5 bits observed in the case of GTP aptamers (Figure 5).

Discussion

We find that ∼ 10 bits of additional information are required to specify RNA structures with 10-fold better binding to GTP, over a range of 3 orders of magnitude in binding affinity. This observation is primarily of interest because of the possibility that some common underlying mechanism may govern the relationship between information content and molecular function. Our observation of a similar relationship between information content and catalytic activity in a comparison of two ribozyme ligases is highly encouraging in this regard. Many other examples will be required to see if there are such general rules.

We know, by comparing the results of different RNA selection experiments, that some molecular tasks are more difficult than others. For example, high affinity aptamers to flexible, hydrophobic ligands are less abundant than aptamers of equal affinity to planar, polar ligands.^31504ab00031 Expressing this in terms of information, structures that bind to a planar, polar target can be specified by less information than structures that bind with the same affinity to a flexible, nonpolar target in the same set of conditions. Nevertheless, a given improvement in binding could have the same informational cost in both cases if increased binding affinity results primarily from the specification of more stable aptamer structures. Similarly, better ribozymes might be attained by stabilizing the catalytically active conformation,^31504ab00032 leading to the same information/function relationship as for aptamers. Such considerations would lead to the relationship we observe if the kinds of changes that improve structural stability are scale-free, or similar over a broad range. Clearly, experimental data in a variety of systems, and over wider ranges of activity, will be required to test these conjectures.

Returning to our observations, why should a plot of the information content versus functional activity for a set of optimized aptamers and/or ribozymes form a line? The paucity of structures in the region below and to the right of the overall trend-line shows that greater complexity is required to achieve better function. On the other hand, one might expect to find structures anywhere above the line—it should always be possible to find solutions that are more complex than necessary to perform a given task. However, such “Rube Goldberg” structures would be less abundant in the initial sample of random sequences than simpler ones with similar activity. More complex structures may also suffer a bias in amplification. Both factors would tend to deplete the region above the line defined by the selected set. What accounts for the observed scatter of the points around the trend line? Our estimated errors in K_d measurements are relatively modest (<± 20%). The calculated information contents are based on several approximations, but these tend to introduce systematic biases; sampling errors in individual aptamer information contents are less than ± 5%. The actual variation is larger (Figure 5) and probably reflects the intrinsic noise in the relationship between sequence, structure, and activity.

A comparison of individual aptamers with similar affinities and secondary structures but different information contents reveals striking differences in tolerance to mutation. For example, aptamer 10−6, at 71 bits, is significantly more complex than aptamer 10−24, at 50 bits, even though both have K_ds for GTP of 300 nM. Furthermore, they have the same secondary structure organization and internal loop lengths of similar size. The difference is that 92% (24/26) of the loop positions of aptamer 10−6 are invariant, whereas only 28% (7/25) of the loop positions in aptamer 10−24 are invariant. Thus, in this case, low information content corresponds to decreased sensitivity to mutational change and tolerance of variation at a greater number of positions. The structural basis for these differences remains to be determined, as do the evolutionary implications. We suggest that aptamers that tolerate more variation might be more evolvable (i.e., better starting points for the evolution of related but distinct functions).^{31504ab00005,31504ab00033}

Two of the most complex aptamers that we recovered (9−4 and 10−10) have low estimated probabilities of occurrence in our initial RNA pool (P = 3.5 × 10^-3 and 1.5 × 10^-4, respectively, see Figure 4). Why were such complex, rare aptamers present in our limited pool of sequences? One possible interpretation is that the observed structures are representatives of a much larger number of possibilities. There may be thousands or millions of structures that would function as high-affinity GTP aptamers, any one of which is so rare that it is very difficult to find. However, the aggregate volume of sequence space occupied by these complex aptamers may be such that at least a few of them will be present in a real-world pool. The same argument has been used to rationalize the isolation of the very complex Class I ligase ribozyme.^31504ab00034 If correct, the existence of a large number of number of distinct structures with the ability to perform an arbitrarily chosen function could be an extremely important factor in allowing highly active molecular structures to be recovered by limited sampling of sequence space.

One of us (JWS) recently proposed a generalization of the relationship between information content and activity based on quantifying the amount of information necessary to specify a sequence whose activity exceeds a given threshold.^31504ab00035 The functional information required to perform a task is given by -log₂ of the fraction of all possible sequences that are active, irrespective of the number or type of distinct structural solutions employed. Functional information is dominated by the contributions of the simplest and therefore most abundant aptamers, which are the ones that we have characterized. If, as we have argued, the number of possible aptamer structures increases sharply with complexity, the number of functional sequences with high affinity would be greater than otherwise expected. We therefore suggest that the slope of the functional information versus activity plot will be less than that observed in the corresponding plot for individual aptamers.

The quest for structures with better binding or catalytic properties requires optimized pool design and selection methods.^{31504ab00019,31504ab00036} The original sequence library used to generate the aptamers we studied contained central variable regions 64-nucleotides long, with half of the library containing completely random sequences and half containing a stem-loop embedded within the random region.^31504ab00019 The four highest-affinity aptamers, out of 11 total, originated from the partly engineered portion of the library, providing further evidence that partially structured libraries sample regions of sequence space populated by highly active molecules.^31504ab00019 Our two highest-affinity aptamers (9−4 and Class V, Table 1) exceed the length of the random region of the original library; if structures with even higher affinity are significantly larger, they could only be present in longer pools. This result is consistent with the expectation that longer, more diverse sequence libraries are better starting points for the in vitro evolution of highly active structures.^31504ab00036 However, access to complex, highly active structures is limited by the propensity for the simplest, most abundant solutions to preferentially emerge unless stringent selection strategies are employed.^{31504ab00037,31504ab00038} Thus, to obtain more complex structures, whether for basic science or biotechnological applications,^31504ab00039 it will be important to develop enrichment procedures for in vitro evolution that are more stringent and more effective.

In summary, our results support the hypothesis that more complex RNA structures are required for greater GTP-binding or RNA-ligase activity. We are currently attempting to extend our initial observations to a greater range of RNA affinities for GTP, to the binding of other ligands, and to other ribozymes. We expect that future studies on information and activity will address the issue of whether DNA, polypeptide, and ultimately synthetic heteropolymers, are more or less efficient than RNA in forming functional structures.

Supporting Information Available

Supporting Information Available

Methods for determining errors in the information content calculations due to sampling and for calculating information content in terms of random RNA sequence space (Supporting methods). Selection sequence alignments for all eleven aptamers (Supporting Figure 1). DNA sequences corresponding original, minimized, and optimized aptamers (Supporting Chart 1). This material is available free of charge via the Internet at http://pubs.acs.org.

Funding Statement

National Institutes of Health, United States