Predicting Individual Renal Allograft Outcomes Using Risk Models with 1-Year Surveillance Biopsy and Alloantibody Data

Abstract

The ability to predict outcomes for individual patients would be a significant advance for not only counseling, but also identifying those for whom interventions may be needed. The goals of this study were to validate an existing risk prediction score that incorporates easily obtainable clinical factors and determine if histologic findings at 1-year surveillance biopsy and/or serum donor–specific alloantibody status could improve predictability of graft loss by 5 years. We retrospectively studied 1465 adults who received a solitary kidney transplant between January of 1999 and December of 2008 and had sufficiently detailed 5-year follow-up data for modeling. In this cohort, the Birmingham risk model (incorporating recipient factors at 1 year, including age, sex, ethnicity, renal function, proteinuria, and prior acute rejection) predicted death–censored and overall graft survival (c statistics =0.84 and 0.78, respectively). The presence of glomerulitis or chronic interstitial fibrosis (g and ci scores by Banff, respectively) on 1-year biopsy specimens independently correlated with graft loss by 5 years. Adding these variables to the model for death–censored graft loss increased predictability (c statistic =0.90), improved calibration (ability to stratify risk from high to low), and reclassified risk of failure in 29% of patients. Adding the presence of donor-specific alloantibody at 1 year did not improve predictability or reclassification but did improve calibration marginally. We conclude that, at 1 year after kidney transplant, a risk model of graft survival that incorporates clinical factors and histologic findings at surveillance biopsy is highly predictive of individual risk and well calibrated.

Predicting outcomes of kidney transplantation is a core component of clinical care, informing patients and clinicians alike. However, although many factors have been shown to be associated with renal allograft loss, few have been found to have high predictive value for individual patients. For example, eGFR is a strong risk factor for graft failure within a population, but it is poorly predictive for individual patients.^1–3

Our group has previously developed and validated a six–variable risk score for death–censored graft failure and a seven–variable risk score for overall graft failure (including death with graft function) on the basis of easily collectable clinical and biochemical data collected 12 months post-transplantation. Detailed evaluation in three independent validation cohorts showed good performance of the scores for the key measures of predictive utility for individual patients.⁴ However, potentially important prognostic information was lacking, in particular transplant histology and anti-HLA antibodies.⁵

Therefore, the primary goal of this study was to evaluate whether risk models incorporating histology and/or antibody evaluation offer improved prediction of renal allograft loss compared with our risk models. In a population of kidney transplant recipients at the Mayo Clinic (Rochester, MN) who were followed closely with both surveillance biopsies at 1 year and donor–specific alloantibody (DSA) data, we performed a stepwise analysis that aimed to (1) confirm the existing model, (2) identify which aspects of histology at 1 year correlated with 5-year graft loss, and (3) incorporate histology and DSA into a new model. Our improved scoring system has implications for the clinical surveillance strategies in kidney transplantation and suggests future approaches to refining our understanding of transplantation biology and risk prediction.

Results

Patients and Outcomes

At 1 year, 93.2% (1476 of 1584) were alive with a functioning graft. Of these, 1465 had sufficient data at 1 year for modeling and 5-year follow-up. The demographics of this group are presented in Table 1. In this study cohort (all had functioning grafts at 1 year), overall 5-year graft survival was 86.7% (195 losses), and death–censored graft survival was 93.7% (93 losses).

Table 1.

Characteristics of the validation cohort of standard–risk kidney transplants

Variable	Whole Cohort of Transplant Recipients, n=1465	Cohort with Histology Data, n=981	Cohort with Antibody Data, n=622	Cohort with Histology and Antibody Data, n=556
Age, yr	52 (41–62)	53 (42–62)	54 (43–62)	54 (43–63)
Men	60.2% (883)	59.0% (579)	62.5% (389)	61.5% (340)
Race
Black	2.9% (43)	2.8% (27)	2.4% (15)	2.5% (14)
White	91.5% (1340)	93.2% (908)	93.4% (578)	93.7% (518)
Diabetes	30.8% (451)	30.8% (273)	30.8% (188)	30.8% (162)
Median dialysis time, mo (IQR)	13 (6–32)	13 (6–31)	14 (6–33)	14 (6–32)
Preemptive	41.8% (613)	44.8% (439)	44.7% (278)	45.5% (253)
Previous transplant	14.5% (213)	13.5% (132)	14.3% (89)	14.0% (78)
Total HLA mismatch (ABDR), mean±SD	3.0±1.8	3.0±1.8	3.2±1.8	3.2±1.9
Living donor	78.6% (1151)	78.5% (770)	77.7% (483)	77.9% (433)
Deceased donor	21.4% (314)	21.5% (211)	22.3% (139)	22.1% (123)
Hepatitis B	1.1% (16)	1.2% (12)	1.1% (7)	1.1% (6)
Hepatitis C	0.9% (13)	0.9% (9)	1.1% (7)	1.3% (7)
Antibody data at 1 yr	42.5% (622)	56.7% (556)	100% (622)	100% (556)
Class 1 DSA	3.9% (24)	4.0% (22)	3.9% (24)	3.9% (24)
Class 1 DSA PEAK	529 (323–1090)	529 (297–1053)	529 (323–1090)	529 (297–1053)
Class 1 NDSA	31.0% (193)	17.6% (173)	31.0% (193)	31.1% (173)
Class 1 NDSA PEAK	1095 (666–3308)	1053 (637–3150)	1095 (666–3308)	1053 (637–3150)
Class 2 DSA	10.0% (62)	13.0% (56)	10.0% (62)	10.7% (56)
Class 2 DSA PEAK	602 (432–1376)	602 (438–1389)	602 (423–1376)	602 (438–1389)
Class 2 NDSA	22.5% (140)	13.0% (128)	22.5% (140)	23.0% (128)
Class 2 NDSA PEAK	1037 (583–1857)	1037 (554–1792)	1037 (583–1857)	1037 (554–1792)
Biopsy data at 1 yr	67.0% (981)	100% (981)	89.4% (556)	100% (556)
Rejection in first year	10.7% (158)	10.7% (154)	10.7% (78)	10.7% (69)
Serum albumin	42 (39–44)	42 (40–44)	41 (41–45)	43 (41–45)
eGFR	51.8 (42.6–61.0)	51.7 (43.1–60.9)	53.1 (44.6–63.2)	53.0 (44.6–63.0)
Proteinuria (estimated UACR)	10.3 (7.2–35.0)	18.0 (12.0–37)	18.0 (11.0–37.0)	18.0 (11.0–37.0)
BK nephropathy in 1 yr	4.5% (66)	5.4% (53)	4.0% (25)	4.1% (23)
Recurrent GN	21.2% (310)	22.7% (223)	26.4% (164)	27.2% (151)
Age at 1 yr	53 (42–63)	54 (43–63)	55 (44–63)	55 (44–64)
No. of deaths at 5 yr	102 (7.0%)	50 (5.1%)	20 (3.2%)	17 (3.1%)
No. of allograft failures at 5 yr	93 (6.3%)	45 (4.6%)	20 (3.2%)	15 (2.7%)

Total cohort data and data for each different modeling group are shown, with overlap within each cohort. Data are expressed as means±SDs or medians (interquartile ranges) if not normally distributed. IQR, interquartile range; ABDR, HLA A, B, DR loci; PEAK, maximum MFI of single highest antibody; NDSA, nondonor-specific alloantibody; BK, polyoma virus.

At 1 year, 67.6% (981 of 1465) had histology data, and 42.5% (622 of 1465) had anti–HLA single–antigen bead. Detailed data for surveillance biopsies Banff scores are shown in Supplemental Table 1 and have been described in previous publications.^6,7

Predictive Performance of the Existing Birmingham Risk Score on the Mayo Clinic Cohort

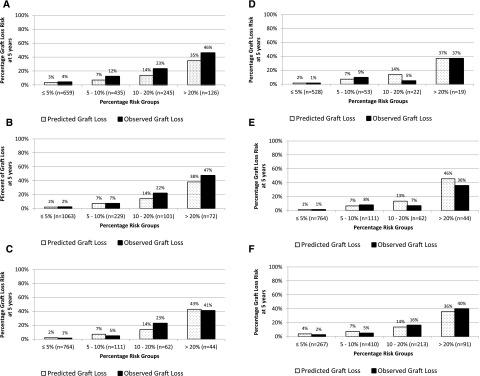
The existing Birmingham risk score performed well with good discrimination for patients with and without graft failure 5 years post-transplantation for both overall and death–censored graft failure (c statistics =0.78 and 0.84, respectively). Actual and predicted rates of graft failure are shown in Figure 1, A and B, showing overall good calibration, albeit underestimation of risk at higher-risk strata. Use of the risk score resulted in significant risk reclassification of death–censored graft failure compared with eGFR (net reclassification improvement [NRI] =17.4%; 95% confidence interval [95% CI], 15.4% to 19.4%; P<0.001) or urinary albumin-to-creatinine ratio (UACR; NRI=2.7%; 95% CI, 0.5% to 4.8%; P=0.02) in isolation.⁸ This was also the case for overall graft failure, with an NRI of 30.9% (95% CI, 24.0% to 37.8%; P<0.001) compared with eGFR and an NRI of 25.7% (95% CI, 18.8% to 32.6%; P<0.001) compared with UACR.

Figure 1.

Improved prediction rates are achieved by including histology data in the risk model. Actual and predicted rates of death–censored and overall transplant failure. (A) Transplant cohort using the existing Birmingham model for overall graft failure. (B) Transplant cohort using the existing Birmingham model for death–censored graft failure. (C) Transplant cohort using the new model with histology for death–censored graft failure. (D) Transplant cohort using the new model with DSA class 2 for death–censored graft failure standard risk. (E) Transplant cohort using the new model with histology and DSA class 2 for death–censored graft failure standard risk. (F) Transplant cohort using the new model with histology for overall graft failure.

Independent Predictors of Transplant Failure

Models were constructed with backward stepwise procedures using binary outcome of survival or failure at 5 years incorporating histology and antibody data alongside the existing clinical variables of the Birmingham risk scores. In these analyses, three groups were used for modeling on the basis of the available dataset: clinical plus histology (n=981), clinical plus HLA antibody (n=622), or clinical combined with both histology and antibody data (n=556). These overlapping groups are described in Table 1.

The final multivariate models for death–censored graft failure are shown in Table 2. Glomerulitis (g) score, chronic interstitial fibrosis (ci) score, and anti-class 2 DSA levels (modeled as a categorical variable with a cutoff mean fluorescence intensity (MFI) of 800, representing the median value in those who did display such an antibody) all correlated with an increased risk of failure (P≤0.003 for all analyses). The histologic scores showed the greatest effect sizes compared with the other variables, because the hazard ratio is incremental per unit of Banff score. The univariate analyses for each are shown in Supplemental Table 2. In the analysis of overall graft failure, no univariate association between any of the antibody measures and outcome was evident. A univariate association between g score and outcome was found on the analyses of the groups where histology was available. Therefore, multivariate analysis of overall graft failure was only undertaken in this group. The final multivariate model for this analysis is shown in Table 2, and it shows an independent association between g score and risk of overall graft failure (P<0.001).

Table 2.

Risk model variable outcomes

Model and Variable	Hazard Ratio (95% CI)	P Value
Death–censored graft loss
1, n=981
UACRa,b	1.65 (1.44 to 2.31)	<0.001
eGFRc	0.66 (0.58 to 0.76)	<0.001
eGFR2c	1.07 (1.03 to 1.11)
Black race	2.15 (0.96 to 0.48)	0.06
Recipient, men	1.25 (0.86 to 1.82)	0.25
Rejectiond	1.34 (0.86 to 2.04)	0.19
Rejection × UACR	1.68 (0.89 to 3.13)	0.11
Recipient agec	0.78 (0.69 to 0.90)	<0.001
g Scoree	2.53 (1.87 to 3.42)	<0.001
ci Scoree	1.66 (1.35 to 2.06)	<0.001
2, n=622
UACRa,b	2.15 (1.24 to 3.71)	<0.01
eGFRc	0.57 (0.46 to 0.70)	<0.001
eGFR2c	1.06 (0.99 to 1.14)
Black race	2.00 (0.46 to 8.73)	0.04
Recipient, men	1.14 (0.63 to 2.05)	0.66
Rejectiond	2.16 (1.06 to 4.43)	0.04
Rejection × UACR	1.28 (0.46 to 3.55)	0.64
Recipient agec	0.69 (0.34 to 3.97)	<0.001
C2 DSA cum
≤800	1.17 (0.34 to 3.97)	0.001
>800	4.34 (1.98 to 9.52)
3, n=556
UACRa,b	1.65 (0.89 to 3.09)	0.11
eGFRc	0.64 (0.48 to 0.85)	<0.01
eGFR2c	0.94 (0.82 to 1.09)
Black race	1.18 (0.25 to 5.52)	0.84
Recipient, men	1.07 (0.56 to 2.07)	0.83
Rejectiond	1.03 (0.43. 2.42)	0.95
Rejection × UACR	2.73 (0.86 to 8.69)	0.09
Recipient agec	0.64 (0.51 to 0.80)	<0.001
g Scoree	2.74 (1.77 to 4.25)	<0.001
ci Scoree	1.90 (1.27 to 2.85)	0.002
C2 DSA cum
≤800	0.72 (0.16 to 3.35)	0.003
>800	4.57 (1.89 to 11.1)
Overall graft loss
1, n=981
UACRa	1.41 (1.12 to 1.77)	0.004
Albuminc	0.66 (0.55 to 0.79)	<0.001
eGFR	0.78 (0.71 to 0.85)	<0.001
eGFR2	1.07 (1.04 to 1.10)
Rejection	1.63 (1.23 to 2.16)	0.001
Black race	1.53 (0.83 to 2.81)	0.17
Recipient, men	1.19 (0.93 to 1.53)	0.18
Recipient agec	1.12 (1.00 (1.25)	<0.001
Recipient age2c	1.09 (1.03 to 1.16)
g Scoree	1.83 (1.44 to 2.31)	<0.001

Death–censored graft loss shows the final multivariate models for death–censored graft failure after analysis of the univariate factors (seen in Supplemental Table 2). These factors are analyzed in addition to the existing Birmingham model risk factors; thus, although not significant with the additional data, they still performed well in outcome prediction. There are three models for each of the cohorts with available data. Overall graft loss shows the final multivariate model for overall graft failure, which only was performed in the histology group, because it was the only risk factor for failure in univariate analysis. The histologic score hazard ratio is incremental per unit of Banff score. C2 DSA cum, cumulative mean fluorescence intensity of class 2 donor–specific alloantibody.

^aVariable was analyzed on log scale (base 10).

^bEffect of UACR varies depending on rejection. Results are reported when there was no rejection.

^cHazard ratios are reported for a 10-U increase in variable.

^dEffects of rejection vary depending on UACR. Reported results are for UACR=2.9.

^eHazard ratio is per unit of histologic Banff score.

Predictive Performance of the Birmingham–Mayo Risk Scores

Risk models in regard to 5-year graft failure were then developed and evaluated for predictive performance on the basis of the weighted effect sizes in these multivariate analyses (see Concise Methods). For this evaluation, events 5 years post-transplantation were considered categorical (yes or no), because this was considered most clinically relevant and allows evaluation of actual rather than actuarial data.

To ensure that the development of a new model was a true representation of the addition of new factors, recalibration of the Birmingham risk scores to the Mayo Clinic cohort was undertaken. After recalibration, the Birmingham scores displayed the following performance characteristics: death–censored allograft failure calibration improved (chi squared =5.3; P=0.07) compared with the previous values (chi squared =11.0; P=0.004), and for overall graft failure, the calibration improved (chi squared =20.2; P<0.001) compared with the previous values (chi squared =46.5; P<0.001).

Death–Censored Graft Failure.

For 5-year death–censored graft failure, compared with the recalibrated Birmingham risk score, the histology–based Birmingham–Mayo model improved the c statistic to 0.90 (95% CI, 0.85 to 0.95) from 0.84 (95% CI, 0.78 to 0.90). Results were similar after bootstrapping the dataset (c statistics =0.90 and 0.84, respectively; P=0.05). The histology-based model also improved calibration, despite having previously recalibrated the Birmingham risk score to this cohort (chi squared =8.9; P=0.01 versus chi squared =12.4; P=0.002) (Figure 1C). The histology-based model resulted in significant and clinically relevant risk reclassification compared with the original (recalibrated) Birmingham score (NRI=29.0%; 95% CI, 21.2% to 36.8%; P<0.001).

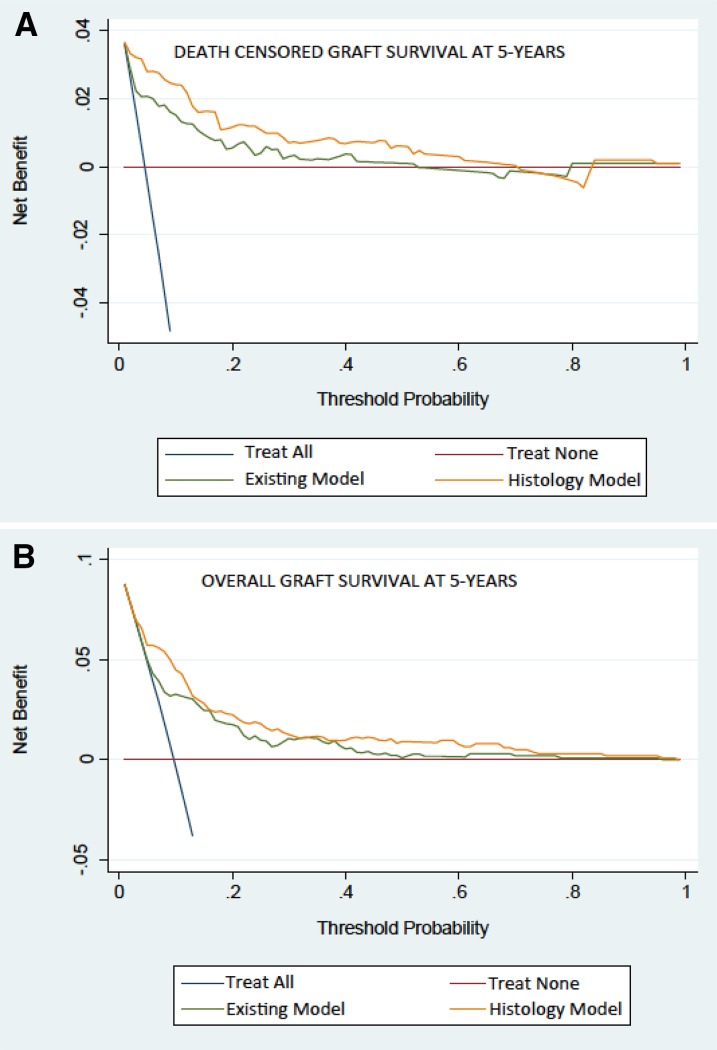
Decision curve analysis shows a threshold of risk at which treatment will cause greater benefit for true positives and treatment of false positives will be reduced. Figure 2A shows that the new histology model, including g and ci scores, results in consistently better risk prediction than the original model across clinically relevant thresholds for potential intervention.

Figure 2.

Decision Curve Analysis is improved with histology added into the risk model. Decision curve analysis comparing the Birmingham risk model and the Birmingham–Mayo model with histology for improvement in clinical utility. The net benefit on the basis of the model including histology showed benefit over the existing clinical variables in both (A) death–censored graft survival and (B) overall graft survival.

Despite the statistical association between class 2 DSA MFI and outcome, no clear benefit in regard to predictive performance of the antibody-based model was evident. Specifically, discrimination was similar to the original Birmingham risk score (c statistic =0.83 [0.72–0.92] versus 0.82 [0.72–0.94]), and no improvement in risk reclassification was seen (NRI=1.2%; 95% CI, −18.5% to 20.5%; P=0.90), although there was some suggestion that calibration was improved (chi squared =2.2; P=0.32 versus chi squared =12.8; P=0.002) (Figure 1D).

The final model combining both histology and DSA data showed improved discrimination compared with the original Birmingham model (c statistic =0.83 [0.64–0.89] versus 0.76 [0.69–0.96]), and there was also some suggestion that calibration was improved (chi squared =1.3; P=0.53 versus chi squared =14.9; P<0.001) (Figure 1E). However, application of this model did not result in statistically significant risk reclassification, which was also numerically lower than that afforded by the model on the basis of histology alone as described above (NRI=14.4%; 95% CI, −3.2% to 32.0%; P=0.11). The NRIs in the three models compared with the Birmingham model are shown in Table 3, showing significant improvement in risk classification for the histology-based model.

Table 3.

Performance of the histology–based (Birmingham–Mayo) risk score compared with the original clinical (Birmingham) risk score in risk reclassification improvement for events, nonevents, and the combination (NRI)

Standard Immune Risk	Overall Graft Failure (Histology Alone)	Death–Censored Graft Failure
		Histology Alone	DSA Alone	Histology and DSA Combined
NRI	30.8%a	29.0%a	1.2%b	14.4%c
Improvement in reclassifying events	−25.3% (6–30)/95	6.7% (14–11)/45	−25.0% (2–7)/20	−13.3% (5–7)/15
Improvement in reclassifying nonevents	56.1% (519–19)/886	22.3% (271–62)/936	26.2% (179–21)/602	27.7% (171–21)/541

Improvement in reclassifying events signifies increasing the risk category for the patients who subsequently had an event. Improvement for reclassifying nonevents signifies reduction of the risk category for patients who did not have an event. Thus, for all patients within the event/nonevent group, the number moving up risk category minus the number moving down risk category is divided by the number in the event/nonevent group.

^aP<0.01.

^bP=0.90.

^cP=0.11.

Overall Graft Failure.

The performance of the separate model predicting 5-year overall graft failure and containing the clinical variables and g scores, which were significantly associated with overall failure rates as described above, was next tested. This Birmingham–Mayo histology–based model showed improvement in discrimination (0.81 versus 0.78) and calibration (chi squared =7.2; P=0.03 versus chi squared =20.2; P<0.001) (Figure 1F) compared with the original (recalibrated) Birmingham risk score. The bootstrapping process confirmed the improvement in discrimination using the model (c statistics =0.81 and 0.77; P=0.05). Significant and clinically relevant risk reclassification was evident with an NRI value of 30.8% (95% CI, 21.5% to 40.2%; P<0.001) compared with the Birmingham risk score for overall graft failure. Finally, the decision curve analysis for overall graft failure (Figure 2B) shows improved histology–based model performance, particularly at relevant thresholds of potential intervention.

Sources of Misclassification.

Although as described above, the histology–based risk model offered improved risk reclassification compared with the original score on the basis of clinical data only, additional evaluation of the individual components of the NRI is informative (Table 3). Incorrect reclassification of patients with events (whose grafts failed by 5 years but in whom the model predicted no graft failure) was seen. The underlying reason for this was, in large part, because of patients dying with graft function, which comprised 70% (21 of 30) of the misclassified patients. This is supported by a recent report describing histology in patients dying with a functioning graft.⁹

Discussion

The results of this study confirm that the Birmingham risk score can accurately predict 5-year graft loss on the basis of 1-year variables. The fact that the Mayo Clinic population consists of mostly white recipients of living donor kidney transplants suggests that the model is robust across a wide variety of patient populations with different induction agents. However, of interest and relevance, the addition of histologic findings on 1-year surveillance biopsies (specifically, the presence of glomerulitis or chronic interstitial fibrosis) improved predictive utility, even compared with the original model specifically recalibrated to the Mayo Clinic cohort. Indeed, this Birmingham–Mayo model correctly reclassified a highly significant and clinically relevant 29% of the grafts in patients with death–censored graft failure and 31% of the grafts in patients with overall graft failure and performed well in a decision curve analysis. The c statistic of 0.9 seen for death–censored graft survival also testifies to the very good/excellent performance of the new Birmingham–Mayo clinicopathologic risk model. The addition of DSA data at 1 year did not improve predictability but did seem to have some role in improving calibration.

The fact that g and ci scores at 1 year were found to be factors associated with subsequent graft loss is consistent with previous work from the cohort showing that 68% of allograft losses were attributed to glomerular or fibrotic pathology in the allograft.¹⁰ However, these data further illustrate how a risk score on the basis of a combination of factors tends to predict graft failure better than individual factors, such as histology, alone. It is also worth mentioning that biopsy–proven polyoma virus nephropathy and recurrent disease were not predictive of outcome when variables, such as renal function and proteinuria, were taken into consideration. Of relevance, the decision curve analysis suggests the utility of the score(s) in regard to clinical management across a range of thresholds for potential intervention as defined by clinician judgement and patient preference, which takes into account the penalty of a false-positive diagnosis (or in this case, prognosis).

DSA was found to have a relatively small effect on our risk prediction model. This may be because of several reasons. In this group of conventional patients, the number of patients who lose their grafts to antibody-mediated rejection between 1 and 5 years is small.¹⁰ Thus, attributing any outcome to this cause will require the assessment of many more events. Even the use of more detailed antibody characteristics, such as C1q or antibody subclass, would be unlikely to change the findings. The inclusion of the g score (glomerular inflammation) was significant in the model. However, this lesion is not specific for chronic antibody-mediated rejection, because it also includes recurrent and de novo glomerular diseases. It is possible that the inclusion of larger numbers of patients or the development of a risk score for patients with DSA (either de novo or those with DSA at the time of transplant) would yield a model in which DSA (either total IgG or subclasses) might be shown to play a very important role. However, in this study, the presence of DSA with an MFI>800 did not improve the risk model, and the use of different cutoff values for DSA did not perform as well as MFI>800 in univariate analyses. Indeed, the presence of glomerulitis does correlate with graft loss and thus, may substitute for DSA in identifying antibody–mediated grafts losses.^11,12 Furthermore, not all patients with circulating DSAs experience detrimental sequelae, which may reflect the characteristics of the antibodies and also, the interplay between cellular and humoral arms of the immune system; greater understanding of these relationships may improve both the prognostic utility of antibody evaluation and the understanding of the biology of the alloimmune response,^13,14 but this was beyond the scope of this study. Similarly, subclinical inflammation (interstitial inflammation (i) and tubulitis (t) scores) has been associated with graft loss but did not improve the risk model. Low eGFR and interstitial fibrosis (almost always present at least in mild form when inflammation occurs) may substitute more effectively than the inflammation scores.¹⁵

The original Birmingham model displayed good predictive performance in the independent Mayo Clinic cohort, suggesting robustness across different transplant populations. Thus, the broader application of this model across transplant centers and national programs is possible and offers clinicians validated risk scores for evaluating graft failure risk at the level of individual patients. This will not only aid management of patients but also, recruitment into studies and increase awareness of higher-risk patients to ensure that maximize medical therapy is achieved to prevent allograft failure.

In the process of refining the score(s), a balance between generalizability and robustness of modeling was required. Specifically, we were conscious to avoid creating an overfitted model, which might fit the investigated cohort very well but at the detriment of generalizability. To that end, we used only the variables contained within the original Birmingham score alongside novel histologic and antibody data rather than incorporating a wider variety of predictor variables. In doing so, the resulting histology–based scores show not only good to excellent predictive performance but also, the potential for useful generalization. It should also be noted that, for the comparison between the original Birmingham score and the new histology–based score, the original score was recalibrated to robustly show the benefit of including histology in the model. It should be noted that, although the calibration of the model may be assessed statistically using the Hosmer–Lemeshow statistic, there are pitfalls to the use of this, particularly in large samples, where acceptable calibration may nevertheless be associated with a significant difference between expected and observed event rates.^16–19 More relevant and clinically intuitive is the description of these event rates (as shown in the figures) alongside results for discrimination (the standard tool to evaluate risk models), risk reclassification, and decision analysis.

Although complete histologic and immunologic data were not available for the entirety of the studied cohort, this study represents the largest study synthesizing clinical information with protocolized histologic and immunologic data and the first to address patient–level risk prediction using these readouts. Nevertheless, we should acknowledge that a stronger influence of DSA might be identified if studied in even larger cohorts with greater numbers of graft failures. A particular strength of the study is the duration of follow-up, whereby actual rates of graft failure 5 years after transplantation (rather than actuarial rates) are evaluated with the knowledge of events at (or before) 12 months post-transplantation. This underpinned the use of graft failure as a categorical variable in the performance analyses. It is, of course, possible that additional refinement is possible. Other variables not studied here include gene expression profiles in the graft, peripheral blood or urine, more detailed DSA characterization as described above, and/or more detailed histologic studies, including immunohistochemistry for specific cell types of the infiltrates.

How should such a risk score be incorporated into clinical practice? These models can inform patients and physicians regarding the probability of graft loss in the medium term and help with counseling. It seems that the original Birmingham risk score performs well in identifying grafts with a low risk of failure destined to fail, whereas the addition of allograft histology helps to stratify the risk in grafts with risk factors for failure. Thus, at 1 year, allograft biopsies might only be indicated in grafts deemed to be at higher risk of graft failure, identifying specific pathology that might be modifiable with changes in immunosuppression or other management,^16–18 while obviating the need for biopsy in every patient. Furthermore, this study shows that, in patients deemed at higher risk of graft failure, the inclusion of biopsy data allows additional risk reclassification improvement, specifically by reclassifying into lower-risk categories.²⁰ This has a twofold benefit. First, it has more accurate prognostication and also, reassurance for both patient and clinician. Second and more importantly, interventional studies into at-risk grafts are best targeted to those who do, indeed, remain at higher risk, and therefore, understanding this more accurately for individual patients should potentially improve the effect of intervention in such patients. Finally, evaluation of transplant practice can be on the basis of risk scores as surrogate markers of allograft failure, which may be earlier and more sensitive measures of practice patterns than evaluation of failure rates over a longer observation period.

In conclusion, this study shows the incremental predictive utility of surveillance biopsy data in standard–risk kidney transplant recipients. We believe that the histology–based risk score as derived in this study has the potential to inform patients and clinicians and improve patient care, while also confirming the original clinical risk score to have generalizable prognostic utility. We suggest how this might most effectively and safely be incorporated into clinical programs and highlight potentially fruitful avenues of research into the fields of risk prediction and transplant biology.

Concise Methods

Patient Population

All adults who received a solitary kidney transplant between January of 1999 and December of 2008 and signed consent for inclusion in clinical studies under protocols approved by the Institutional Review Board of the Mayo Foundation and Clinic (n=1584) were included in this study. All patients had a negative T cell anti-human globulin crossmatch and/or B cell flow cytometric crossmatch at the time of transplantation. Surveillance renal allograft biopsies and serum DSA measurements (determined by LABscreen using MFI) were determined retrospectively for patients before 2006.^21,22 DSA results were modeled as follows: (1) presence versus absence, (2) number, (3) highest MFI for an individual antibody in the category, and (4) cumulative MFI for all antibodies in the category.

Study End Points and Exposures

Death–censored (dialysis therapy or retransplantation) and overall (including death with graft function) graft failures at 5 years post-transplantation were the primary outcome measures of interest. Clinical variables collected at 12 months post-transplantation included eGFR, acute rejection (any grade and any severity), proteinuria, age, sex, race, and serum albumin. eGFR was estimated using the Modification of Diet in Renal Disease equation.⁸

In addition to these data, available histologic scores according to Banff criteria were recorded according to Banff classification at the time of biopsy.^21,22 In addition, recurrent disease and polyoma virus detected in the biopsy report were recorded and included in the analyses for risk.

All patients studied had 24-hour urine protein collections available. However, because the UACR is the proteinuria measure within the existing risk score, the following adjustments were made. First, daily urine creatinine excretion was estimated according to the formula derived by Ix et al.²³ Second, albumin excretion was estimated from protein excretion using the conversion factor proposed by Halimi et al.²⁴ In this way, the UACR was evaluated as a component of the prognostic score.

Statistical Analyses

The existing Birmingham risk score was calculated using the existing online calculator (http://www.renalmed.co.uk/risk-calculator). Its prognostic utility in predicting outcomes at 5 years post-transplantation in the Mayo Clinic cohorts was evaluated as follows. Receiver–operating characteristic curve analysis assessed the ability of the scores to discriminate patients with and without transplant failure and is reported as the associated c statistic (area under the receiver–operating characteristic curve); calibration of the prediction models (Hosmer–Lemeshow test), representing the accuracy of the scores in predicting the probability of subsequent events (that is, whether observed and predicted event rates were comparable), is shown graphically on the basis of risk strata, with model chi–squared statistics reported. Finally, risk reclassification assessed whether the score was better able to predict the observed outcome compared with eGFR or proteinuria (both accepted risk factors for transplant loss in a population) in isolation.²⁵ Reclassification was on the basis of the following clinically relevant and applicable risk categories: ≤5%, 6%–10%, 11%–20%, and >20%. The NRI represents the summed percentage of patients in whom the new model correctly assigned a higher-risk category for graft failures and correctly assigned a lower-risk category for grafts continuing to function.²⁰ Because the aim of this part of the study was to evaluate the generalizability of the existing scores, recalibration of the existing scores was not undertaken, because this leads to improved statistical outcomes without improving the widespread model applicability.²⁶

Next, new risk models (for death–censored and overall graft failures) were developed from data available 12 months post-transplantation from the study cohort at the Mayo Clinic. To achieve broad consistency and avoid overfitted models, the clinical variables tested were those previously shown to associate with graft failure that are included in the Birmingham risk scores, namely eGFR, acute rejection, proteinuria, age, sex, race, and serum albumin. Furthermore, on the basis of biologic relevance, statistical interactions between UACR and rejection, between UACR and eGFR, and between UACR and serum albumin level were investigated. In addition to these variables, we evaluated histologic qualifiers on 1-year protocol biopsies and anti–HLA antibody characteristics at the same time as predictor variables. Analysis of risk was calculated for each incremental score in the Banff histologic score in analyses. Similarly, histologic evidence of polyoma virus nephropathy or recurrent disease (on 12-month protocol biopsy or indication biopsy with the first 12 months post-transplantation) was also considered as an additional predictor variable. The incidence of hepatitis was too low to allow robust evaluation.

Skewed data underwent logarithmic transformation before analysis, and polynomial terms were added as required to improve model fit. Time to event analyses were performed using Cox models. The assumption of proportionality was met for all analyses. Variables showing univariate associations (P<0.15) were entered into multiple regression models, with final models constructed by means of a backward conditional stepwise selection processes. Variables remaining in the final model with P<0.05 comprised the final models. Risk scores then were generated on the basis of calculation of weighted coefficients from the regression analyses as described, and estimates of transplant failure risk at 5 years post-transplantation were developed.

For each predictor variable, the coefficient was multiplied by the value of the variable and then summed. Categorical variables were considered to take the value of zero if the characteristic was absent and the value of one if the characteristic was present. The weighted coefficients for the new clinical and histology–based model are shown in Table 4, and on the basis of these weighted coefficients, the probability of transplant loss was calculated as follows:

Table 4.

Weighted coefficients for variables associated with death–censored and overall transplant failure at 5 years in both the original Birmingham model and the Birmingham–Mayo model

Variable	Original Birmingham Model			New Birmingham–Mayo Histology–Based Model
	Transformation	Death-Censored Failure	Overall Transplant Failure	Transformation	Death-Censored Failure	Overall Transplant Failure
UACR, mg/mmol	Log scale	—	0.666	Log10 value	—	0.3712
UACR, mg/mmol	Log scale −0.46	1.107	—	Log10 value −46	0.5053	—
Serum albumin, g/L	(Value −40)/5	—	−0.217	(Value −40)/5	—	0.4000
eGFR, ml/min per 1.73 m2	(Value −47)/10	−0.297	−0.206	(Value −47)/10	−0.3969	−0.2367
eGFR2, (ml/min per 1.73 m2)2	[(Value −47)/10]2	0.0711	0.0669	[(Value −47)/10]2	0.0677	0.06613
Rejection		1.038	0.550	—	0.2806	0.4988
Black ethnicity		1.324	1.095	—	0.7582	—
Asian ethnicity	—	1.039	0.653
Recipient age, yr	(Value −46)/10	0.138	0.00149	(Value −46)/10	−0.2366	0.1202
Recipient age, yr2	[(Value −46)/10]2	0.204	0.187	[(Value −46)/10]2	—	0.0858
UACR with rejection interaction	Log(UACR)2 −0.46 for rejection	−0.543	—	Log10(UACR value) −0.46 for rejection	0.5579	—
g Score				Value	0.917	0.5985
ci Score				Value	0.5074	—

Urinary albumin-creatinine ratio values <0.1 amended to 0.1 before logarithmic transformation. —, no value.

1. Assume that the sum of the regression model equals x.

2. Calculate y=exp(x); then, the probability of death–censored transplant failure =1−0.97913574_y and the probability of overall transplant failure =1−0.94957466_y.

These scores were then evaluated for discrimination, calibration, and risk reclassification (by means of NRI compared with the existing Birmingham scores) as described above. In addition, bootstrapping was performed within the study population where 100 bootstrap samples were created, the differences in c statistics were calculated for each method, and the observed mean difference was reported. Furthermore, decision curve analysis was performed as described by Vickers et al.²⁷ Briefly, this clinical evaluation extends the aforementioned mathematic evaluation of the model by taking into account clinician (and patient) –defined risk thresholds at which potential interventions might be initiated, while applying a penalty for false-positive results. The net benefit displayed on the decision curve represents the number of (weighted) false-positive results subtracted from the number of true positives and normalized to the study size.

For these analyses, to avoid inflating the utility of the newly derived scores, the existing Birmingham risk scores were recalibrated to the Mayo Clinic cohort, such that the true incremental predictive utility of histology and/or antibody status could be more robustly evaluated.

The Stata software package, version 12.0 (StataCorp., College Station, TX) was used for data analysis and modeling. Data are shown as means±SDs, unless otherwise indicated. The excel calculator is online as Supplementary Material.

Disclosures

M.D.S. has research contracts with Alexion Pharmaceuticals Cheshire, Connecticut and Millennium Pharmaceuticals Cambridge, Massachusetts.