Charting Moment-to-Moment Brain Signal Variability From Early to Late Childhood

Abstract

Large-scale brain signals exhibit rich intermittent patterning, reflecting the fact that the cortex actively eschews fixed points in favor of itinerant wandering with frequent state transitions. Fluctuations in endogenous cortical activity occur at multiple time scales and index a dynamic repertoire of network states that are continuously explored, even in the absence of external sensory inputs. Here, we quantified such moment-to-moment brain signal variability at rest in a large, cross-sectional sample of children ranging in age from seven to eleven years. Our findings revealed a monotonic rise in the complexity of electroencephalogram (EEG) signals as measured by sample entropy, from the youngest to the oldest age cohort, across a range of time scales and spatial regions. From year to year, the greatest changes in intraindividual brain signal variability were recorded at electrodes covering the anterior cortical zones. These results provide converging evidence concerning the age-dependent expansion of functional cortical network states during a critical developmental period ranging from early to late childhood.

At the population level detectable by non-invasive surface recordings, groups of neurons sustain multiple oscillations that are implicated in functional communication between different neuronal assemblies (Voytek & Knight, 2015). Brain electrical activity exhibits a coherent frequency architecture, consisting of a number of bandwidth classes that are marked by oscillatory peaks with characteristic spectral centroids (Buzsáki & Draguhn, 2004; Klimesch, 2012). These frequency peaks are approximately arranged in a geometric series (i.e., the ratio between two successive bandwidth centroids is constant) possessing an irrational number, with the physiological consequence that perfect synchronization between bands is impossible and any observed periodic regularity is necessarily unstable and short-lived (Buzsáki, 2006; Pletzer et al., 2010). The presence of this mathematical ratio corresponds to the readily observable intermittent spatio-temporal fluctuations of electroencephalogram (EEG) and magnetoencephalogram (MEG) time series signals.

A defining feature of endogenous brain signals during the so-called default or resting mode is the absence of a fixed equilibrium state (Cabral et al., 2014; Friston, 1997; Tognoli & Kelso, 2014). Instead, the electrical and hemodynamic output of the cerebrum exhibits itinerant dynamics during which a repertoire of functional networks are explored in successive transient sequences (Britz et al., 2010; Deco et al., 2011, 2013; Hansen et al., 2015; Khana et al., 2015). In common with many other adaptive dynamical systems, the cerebral cortex is poised precariously between transient epochs of stability and noisy perturbations and this “meta-stable” regime is evident across multiple spatio-temporal scales (Faisal et al., 2008; Kelso, 2012; Rabinovich et al., 2008; Tognoli & Kelso, 2014; Werner, 2007). The complex nature of neuronal activity, in which transient periods of synchronizability are spontaneously punctuated by rapid state transitions is an emergent product of the myriad numbers and kinds of structural interactions supported by the underlying connectome (Deco et al., 2013; Honey et al., 2007; Nakagawa et al., 2013; Shen et al., 2015). In particular, the meta-stability of functional brain activity seems to arise as a consequence of two competing constraints that have shaped cortical architecture – namely, local segregation and global integration (Sporns, 2011). The cerebral cortex combines high modularity with short characteristic path lengths (Muldoon, Bridgeford, & Bassett, 2016), enabling canonical computations in regional circuits as well as the distributed dissemination of local computations in spatio-temporally specific ways.

The potentially beneficial effects of variability (often called “noise”) in physiology (Buchman, 2002) and in nervous systems more specifically have long been recognized (McDonnell & Ward, 2011; Pinneo, 1966). Similarly, theoretical models that view development as an emergent property of numerous decentralized and local interactions of the growing brain treat variability as functionally useful rather than as a nuisance factor (Smith & Thelen, 2003). A specific example of this in the developmental context is the acquisition of skilled motor actions in children, where the increased task proficiency that comes with age is sub-served by exploiting variability at a microstructural level (Manoel & Connolly, 1995). Within cortex, the benefits of meta-stability include optimizing circuits for information processing (Beggs, 2008; Friston et al., 2012; Garrett et al., 2010; Shew & Plenz, 2012), using the strategy of “liquid state” computing (Rabinovich et al., 2008), and enhancing the likelihood of adaptive responses in external environments that are noisy, uncertain and constantly changing (Garrett et al., 2013; Ward, 2009). The number of functional cortical network configurations (or the repertoire size) is a fluid feature that is capable of expansion with learning and maturation (Deco et al., 2013). In particular, increased synchronous coordination of neuronal assemblies across the cortex widens the space of potential functional architectures (Deco & Kringelbach, 2016; Fries, 2005). In the context of brain maturation and development, there is a wealth of evidence to suggest that ontogenetic sculpting of synaptic connectivity (including changes in pruning and axonal myelination of long-distance fascicular pathways) produces refinements in the functional integration of distant cortical regions (Luna & Sweeney, 2004; Stevens, 2009). The resulting synaptic retuning and network integration from infancy to adulthood manifests in functional cortical activity that becomes smaller in overall amplitude but more precisely coordinated (Liu, Woltering, & Lewis, 2014; Mathes et al., 2016; Papenberg et al., 2013; Uhlhaas et al., 2009) and globally integrated (Fair et al., 2009; Supekar et al., 2009). Although largely overlooked in the past, the amount of information integrated across cortical networks (i.e., greater information transmission) increases the unpredictability of signals recorded at the population level (McDonough & Nishira, 2014; Misic et al., 2011; Vakorin et al., 2011). The irregularity of large-scale neuronal signals, in this case, simultaneously reflects and promotes the exploration of a diversified network repertoire, thereby extending the brain’s representational capacity (Deco & Kringelbach, 2016; Ghosh et al., 2008). Within dynamic system perspectives, variability/noise (when properly tuned) provides the “kinetic energy” required for the brain to visit a richer state space (Golos, Jirsa, & Daucé, 2015). In principle then, developmental increases in the informational complexity of brain signals ought to be reflected in mathematical indices that are sufficiently sensitive to pattern regularity at multiple temporal scales (McIntosh et al., 2010).

Intraindividual Brain Signal Variability

On the basis of the evidence reviewed above, there has been a rapidly growing interest in treating intraindividual brain signal variability as a new frontier for studies examining neural development, learning, and nervous system pathology (Garrett et al., 2013; McIntosh et al., 2010; Takahashi, 2013; Vakorin et al., 2013). Although there exist numerous ways of quantifying brain signal variability, one prominent class of computational methods that exhibit superior performance (as compared to conventional estimates based on simple mean and variance) involves computing regularity statistics that capture the degree of unpredictability inherent in time series recordings (Garrett et al., 2013; Takahashi, 2013; Vakorin & McIntosh, 2012). Although there are several families of statistics for computing temporal irregularity, sample entropy is an information theoretic measure that was introduced specifically for the analysis of non-stationary, physiological signals (Richman & Moorman, 2000). In brief, sample entropy captures the amount of self-similarity that is contained within a time series – a signal with high self-similarity is assigned low sample entropy values while a signal that is highly unpredictable or irregular results in high sample entropy.

A specific measure derived from this family of methods that is particularly suitable for the analysis of neuronal time series data (Vakorin & McIntosh, 2012) is known as multiscale entropy (MSE). An important advantage of the MSE technique over conventional sample entropy estimates is that it evaluates irregularity at multiple time scales, which increases its sensitivity for differentiating the non-stationary dynamical complexity of physiological signals (which is fractal-like and expressed across many temporal scales) from uncorrelated time series data (e.g., white noise) that exhibit no temporal structure (Costa et al., 2005, Goldberger et al., 2002). By virtue of its sensitivity to signal content at multiple time scales, the MSE method assigns low values to both completely deterministic and stochastic signals, but tends to be high for signals that straddle the middle ground between these extremes. By contrast, when sample entropy is computed at a single time scale, it assigns high values to processes generated entirely by random sampling, ignoring the fact that at longer time scales these signals carry very little information (Costa et al., 2005). The temporal sensitivity of the MSE method is an important consideration insofar as it accurately captures one of the hallmark features of complexity that exists in biological systems – namely, that it is a proportional mixture of system order and disorder (Tononi et al., 1998)¹.

Several studies have established that the amount of signal complexity or “brain noise”, as measured by MSE, increases with cortical maturation (McIntosh et al., 2010; Misic et al., 2010) and subsequently begins to decline during senescence (Garrett et al., 2011; Grady & Garrett, 2014; Manor & Lipsitz, 2013; Yang et al., 2014). The amount of MSE present in surface recorded event-related EEG signals has been reported to increase parametrically from 8–9 years of age to young adulthood (20–33 years of age) and the increased brain noise predicts reduced within-subject behavioral variability on a simple decision task (McIntosh et al., 2008). The developmental trajectory of task-specific EEG signal complexity from infancy to 5 years of age corresponds to the differential structural maturation of distinct cortical lobes, such that MSE peaks first in those regions that exhibit earlier development of dendritic arborization and axonal myelination (Lippé et al., 2009). Consistent with the idea that network-wide information integration leads to increased temporal irregularity of signals recorded from large neuronal populations, increases in the amount of brain signal variability during normal development are related to the maturation of long-range functional connections between distal cortical regions (Vakorin et al., 2011).

The Present Study

Here we undertook what is, to our knowledge, the largest cross-sectional study investigating ongoing neuroelectrical signal variability from early to late childhood in the course of normal human brain development. Moreover, in contrast to previous developmental studies of EEG sample entropy reviewed above, which involved neurophysiological time series signals recorded in response to sensory stimulation and/or task performance, the present study focuses on ongoing, resting-state cortical signals unstructured by experimental demands.

We have recently documented extensive reorganization of spontaneous functional cortical networks during the transition from early to late childhood, resulting in increasingly dense and spatially variable functional connectivity networks as age increased from 7 to 11 years (Miskovic et al., 2015). Given that the complexity of neural signals is positively related to the degree of functional connectivity (McDonough & Nashiro, 2014; Misic et al., 2011), specifically between distal brain areas (Vakorin et al., 2011), we expected to observe a parametric increase in MSE values of EEG signals from early to late childhood at multiple time scales, perhaps with a stronger magnitude of differences at the coarser scales. Moreover, we hypothesized that these developmental trends would honor well-known spatial gradients of electrocortical maturation, with posterior cortical areas developing prior to more anterior zones (Matousek & Petersen, 1973). This particular topographic pattern is also generally consistent with evidence from structural imaging (Colby et al., 2011; Gogtay et al., 2004) and other sources (Guillery, 2005), indicating that cortical regions lower in the processing hierarchy develop earlier in time than higher-order “association” zones.

Method

Participants

Participants were a subset drawn from an ongoing study of children recruited from a rural community in northeast USA. Although the sample contains some children included in our earlier report (Miskovic et al., 2015), it has been substantially expanded with subsequently collected data. Moreover, the analytic methods used here provide unique information about cortical development as described in more detail below. The inclusion criterion was being between 7 and 11 years of age. Exclusionary criteria were the presence of severe developmental or learning disabilities (e.g., autism) in children per parent report. Other factors that would be expected to impact EEG signals, such as medication status, were not exclusion criteria and are addressed by a control analysis discussed below. Resting EEG data were available from a total of 464 children. The final number of participants included across all five age groups was as follows: 109 seven year olds, 100 eight year olds, 93 nine year olds, 88 ten year olds, and 74 eleven year olds. Of the children included in our sample, 47% were female, 86% were Caucasian (13% African American) and the median family income was $35,000 to $40,000.

Procedure

Potential participants were recruited from the community through a variety of means (e.g., television, newspaper and bus ads, flyers). Parents responding to the recruitment advertisements were initially screened over the phone to determine potential eligibility. Upon arrival, parents were asked to provide informed consent and children were asked to provide assent to be in the study. Next, participants were seated quietly in the experimental room and instructed to remain still with their eyes closed for a full minute. The eyes closed condition is considered to provide the most valid method for capturing spontaneous brain function (Logothetis et al., 2009). The eyes closed resting condition was collected at the beginning of a larger EEG/ERP experimental protocol, examining emotional processing in this population. However, here we focus only on the resting component since we were specifically interested in endogenous cortical activity, unstructured by experimental demands and stimulus onsets.

EEG Recording

Continuous EEG was recorded using a custom cap and the BioSemi ActiveTwo system. EEG was digitized at 24-bit resolution with a sampling rate of 512 Hz. Recordings were taken from 36 sintered Ag/AgCl active electrodes based on the International 10/20 system and evenly distributed across the scalp, and left and right mastoids. Two additional scalp electrodes were used in the study: an active Common Mode Sense (CMS) and a passive Driven Right Leg (DRL) electrode, located at the mid-line between C3 and CZ, and CZ and C4, respectively. Raw EEG were recorded relative to CMS. The CMS/DRL electrodes formed a loop that principally served as the ground for recordings through a feedback that subtracted the average potential of the subject (i.e. the Common Mode voltage) to drive EEG recordings as close as possible to the “zero” ADC reference voltage in the AD-box (please see http://www.biosemi.com/faq/cms&drl.htm for further details). The electrooculogram was recorded from four facial electrodes to capture vertical and horizontal eye movements that were subsequently used to aid visual inspection of the EEG time series.

EEG Analysis and Data Reduction

Offline processing of EEG data was accomplished using a combination of EEGLAB (Makeig et al., 2000) functions and in-house MATLAB routines. After re-referencing the EEG data to average mastoids, a two-way least squares finite impulse response (FIR) filter was used to bandpass the time domain signal (high pass cut-off: 0.01 Hz, low pass cut-off: 80 Hz). Since the preprocessing of neuronal time series data is especially important for analyses of brain signal variability (Garrett et al., 2013) and given that we wished to avoid sharp transients that might be introduced as a result of manually rejected data segments and data splicing, we implemented denoising procedures by independent components analysis (ICA), using the runica function in the EEGLAB toolbox (Makeig et al., 1996). Default settings of the runica function were used, based on the logistic infomax ICA algorithm of Bell and Sejnowski (1995), with the natural gradient feature of Amari, Cichocki, and Yang (1996) to speed computations. Generally, the runica ICA algorithm separates input data recorded at N electrodes × time into an equivalent number of temporally independent component time courses spatially filtered from the data of each electrode. ICA was applied to each participants’ full data (including ~ 1,203,200 sample points concatenated across the entire experimental session of each participant). Artifact correction consisted of manual inspection of EEG data by a trained observer for stereotypical ocular EEG artifacts (e.g. blink activity: brief, large, deflections at frontal electrode sites and deflections of opposite polarity at the vertical EOG) that were then matched with that of simultaneous ICA time courses. Potential artifactual ICA components were then verified by plotting their scalp topography and removed if maps provided further evidence that the component was artifact activity (e.g. ICA blink activity projects most strongly to far frontal sites). The flagged ICA components were then removed prior to back projection to the electrode level.

Multiscale Entropy

The ICA-denoised time domain EEG data were used for estimating MSE as originally implemented in Costa et al. (2005). Briefly, this procedure involves quantifying the sample entropy (Richman & Moorman, 2000) of EEG signals at multiple time scales. The first step involves temporal coarse graining where for a given time scale (τ) the corresponding time series is calculated by averaging neighboring data points within non-overlapping windows of length τ from the original time series signal. Subsequent to this coarse graining procedure, sample entropy is quantified separately at each of the time scale factors (from 1 to 20 in our case, where 1 represents the original signal and 20 indicates a window size of 20 sample points). Sample entropy represents the conditional probability that any two consecutive data sequences of pattern length (m + 1) will match each other given a match for the first m points across the duration of a time series at a given scale factor. Subsequent patterns are considered to recur if the absolute amplitude difference falls within a particular criterion or tolerance range, r. Sample entropy is calculated using the following equation:

$$S_E(m,r,N)=-\text{ln}\frac{{\sum }_{i=1}^{N-M}{n}_i^{\prime m}}{{\sum }_{i=1}^{N-M}{n}_i^{\prime m+1}}$$

where $n_i^{\prime m}$ is the number of matches and N is the length of the original time series.

S_E thus captures the regularity of a signal: low values indicate high self-similarity (low complexity) and high values denote irregularity (high complexity). On the basis of recommendations provided elsewhere (Richman & Moorman, 2000), as well as precedents established in previous EEG and MEG studies (Heisz et al., 2012, 2015; McIntosh et al., 2008; Misic et al., 2010, 2011), we set m = 2 and r = 0.5 (data amplitudes matched if the absolute amplitude difference between them was ≤50% of the time series standard deviation). An attractive feature of sample entropy (in contrast to related measures, such as approximate entropy) is that the estimated values remain stable around many different choices of m and r in addition to being less dependent on signal length (Richman & Moorman, 2000). We confirmed the essential stability of MSE estimates during preliminary analyses examining an extended range of criterion threshold values. Since MSE values can be biased by the presence of artifacts, we decided to omit electrodes that are most susceptible to residual ocular (e.g., eye rolling) and muscular activity: Fp1, Fp2, AF3, AF4, M1 and M2. We calculated MSE for all of the remaining (30) cephalic electrodes.

Although MSE is partially related to spectral power analyses, which were the focus of a previous report from our group (Miskovic et al., 2015), these two approaches are differentially sensitive to the non-linear brain dynamics reflected in the interactions of frequency components (Vakorin & McIntosh, 2012). The unique sensitivity of MSE, relative to spectral power analysis, to temporal dependencies embedded within brain signals is highlighted in Figure 1.

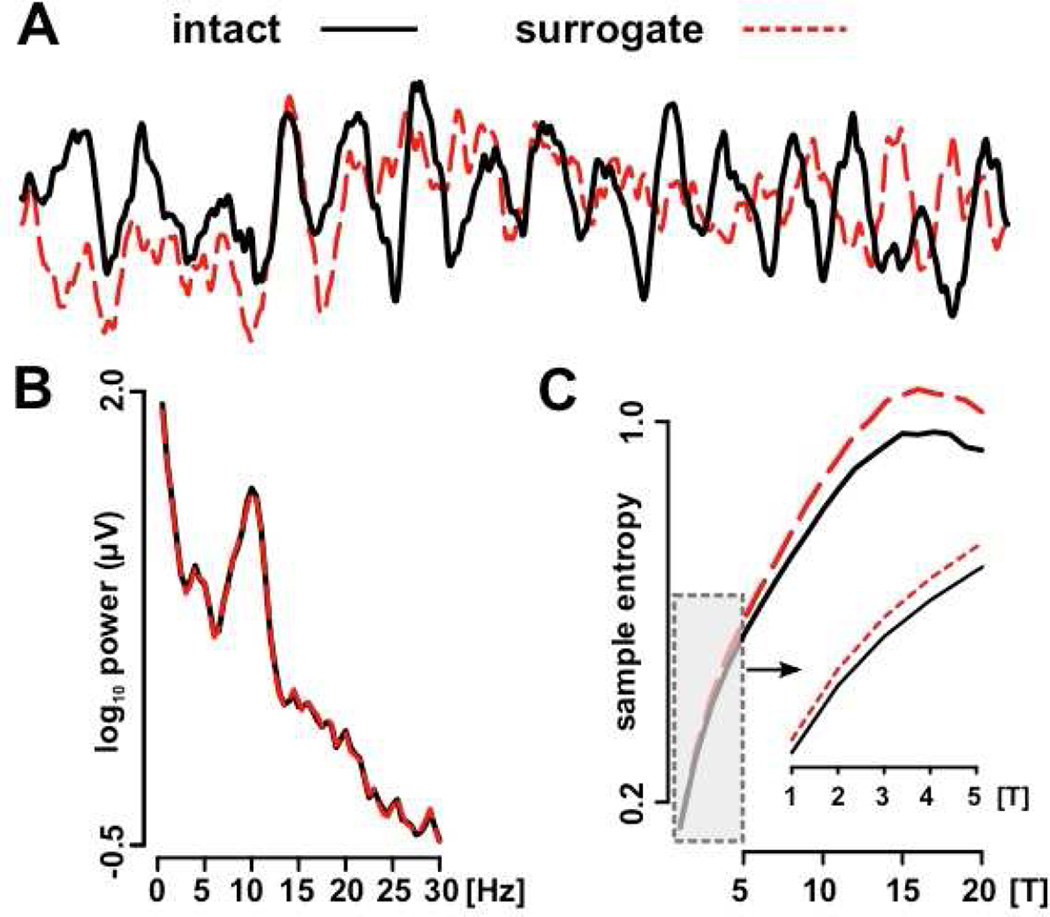
Figure 1.

Spectral power and mutli-scale entropy analyses are differentially sensitive to irregularities in the time series EEG data. Panel (A) depicts a short segment of a continuous eyes-closed EEG signal from a representative participant (11 year old child, Oz electrode). The intact time series is the original EEG recording. The surrogate time series was generated by (i) performing a Fourier transform on the EEG, (ii) randomly scrambling the phase content of the Fourier components, followed by (iii) an inverse Fourier transform back to the time domain. The power spectrum (B) was identical for the intact and surrogate time series, since this analysis is only sensitive to the signal’s frequency characteristics. By comparison, multi-scale entropy analysis (C), which is sensitive to temporal dependence within the signal, discriminated between the two signals, being higher for the surrogate where the phase randomization process introduced more irregularity/unpredictability. Sample entropy for the surrogate signal was increased particularly at coarse time scales, but it was also evident at the fine time scales (1 to 5) depicted in the inset (scale magnified for illustrative purposes).

For illustrative purposes and to further demonstrate that our measure of signal complexity captured the crucial aspects of complexity in physiological systems, Figure 2 depicts sample MSE curves for the empirical EEG time series as well as for two simulated types of colored noise fluctuations with distinct 1/f^α spectral properties. Similar to previous findings obtained using EEG, MEG and fMRI data (Garrett et al., 2013), the sample entropy of brain signals was relatively low (i.e., highly regular) at the fine timescales, but steadily increased at the more coarse timescales. Importantly, and in contrast to conventional single scale estimates of sample entropy, a completely uncorrelated stochastic data sequence (i.e., white noise), exhibited vanishing S_E at longer timescales. Pink (1/f⁻¹) noise exhibited high and stable entropy values, due to the fact that this form of noise contains information at both short and long timescales. Neurophysiological activity approximated pink noise at the longer timescales, indicative of long range temporal correlations consistent with “history” effects in this particular signal type (Costa et al., 2005).

Figure 2.

Multi-scale entropy for three representative time series signals: empirical EEG (averaged across all electrodes and participants in our sample) and two types of synthetic colored noise (white and pink), generated to have the same length as the EEG signal. A white noise sequence (1/f⁰) exhibits high S_E values at the fine time scales, but vanishing S_E at the long time scales (where a random data fluctuation approaches a flat line around zero). By comparison, pink noise (1/f⁻¹) has stable S_E values indicative of complex structure at multiple time scales. Note that, consistent with previous findings from multiple recording modalities, brain signals approximate pink noise at coarse time scales (scale factors > 10).

Statistical Analyses

To examine the spatial distribution of MSE values, we averaged data across distinct regional and hemispheric clusters of electrodes (see Figure 4 topographic map), and then performed a repeated-measures ANOVA using the within-subject factors of Region (frontal, central and parieto-occipital) and Laterality (left and right hemisphere). The ANOVA model was evaluated using Type III Sums of Squares and Greenhouse-Geisser corrections were applied in cases where Mauchly’s test revealed violations of the sphericity assumption. The generalized eta squared is reported as a measure of effect size for these analysis on the basis of recommendations for repeated-measures designs (Bakeman, 2005).

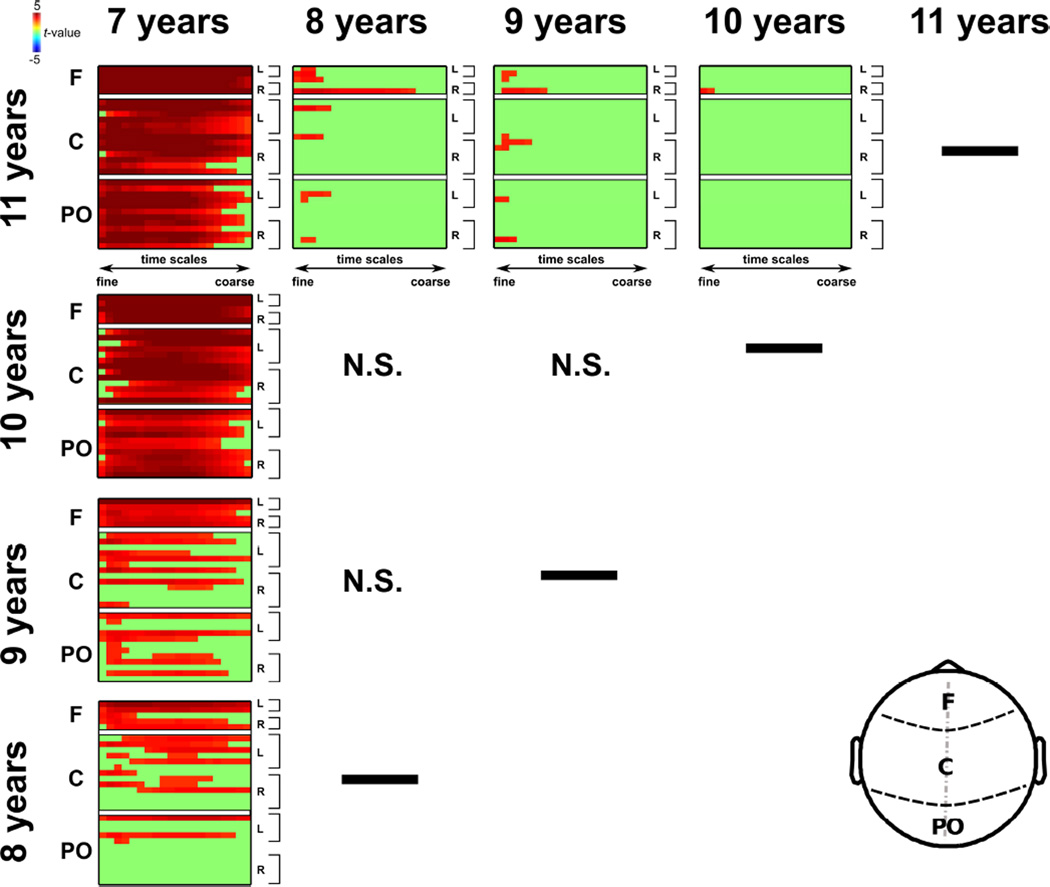
Figure 4.

Pairwise age group contrasts at each electrode and time scale factor. Color represents t-test values (hot colors indicate greater S_E for the older group in a given contrast), masked by significance as determined using the t_max Monte Carlo method (with 1000 random between-subject data permutations). Green areas depict contrasts that did not survive statistical thresholding (p_perm < 0.05). Note: F – frontal; C – central; PO – parieto-occipital. L – left hemisphere; R – right hemisphere. N.S. – no significant contrasts.

To test for differences in EEG signal complexity as a function of chronological age, we submitted the sample entropy data to an independent samples, two-tailed permutation test based on the t_max statistic (Groppe et al., 2011) using a family-wise alpha level of 0.05, effectively controlling for the inflation of Type I error rates. All 30 cephalic electrodes and all 20 time scale factors were entered into these analyses, without averaging. Adopting a Monte Carlo approach, we used 1000 random between-participant permutations of the data to empirically approximate the distribution of the null hypothesis (i.e., no difference between age groups) for the contrasts of interest. The number of random permutations was based on previous suggestions in the literature (Manly, 1997). Based on this estimate, critical t-scores were derived and any between-group differences in the original data that exceeded the t_max statistic were deemed reliable. All statistical analyses were performed using MATLAB and R (R Development Core Team, 2008).

Results

Topographic distribution of brain signal variability

We first examined the spatial distribution of average MSE values (integrated over all time scales) across the scalp surface, ignoring chronological age. As illustrated in Figure 3, there was a clear posterior-to-anterior gradient, with sample entropy gradually decreasing over the frontal regions. This visual impression was confirmed by a main effect of Region (frontal, central, parieto-occipital; F_2,926 = 503.59, Greenhouse-Geisser corrected p < 0.001, η²_G = 0.04). Parieto-occipital regions exhibited enhanced MSE compared to the central and frontal regions, while the central electrodes exhibited increased MSE compared to the frontal channels (all ps < 0.001). Additionally, MSE values were greater for electrodes positioned over the right, compared to the left, cerebral hemisphere as indicated by a main effect of Laterality (left and right; F_1,463 = 48.18, p < 0.001, η²_G = 0.003).²

Figure 3.

Electroencephalographic multi-scale entropy (collapsed across chronological age), shown separately for the major scalp regions and the left/right hemispheres (N = 464). Note the presence of a clear posterior-to-anterior gradient and the increase in MSE levels for electrodes covering the right cerebral hemisphere. The inset depicts the topographic distribution of average_MSE (integrated across time scales).

As is evident from examining the full sweep of MSE values (see Figure 2), both the regional and hemispheric differences increased in magnitude from fine to coarse scales. A set of paired permutation controlled t-test contrasts confirmed significant regional and hemispheric differences at virtually all time scales (all p_perm < 0.05, from scales 2 to 20), except for the parieto-occipital region where the right hemispheric bias was only evident at the coarse time scales (scale factors from 10 to 20).

Age-related changes in moment-to-moment brain signal variability

To perform a detailed examination of differences in EEG signal variability as a function of chronological age, we conducted a series of mass univariate tests for each electrode and time scale factor. The results of these analyses are depicted in Figure 3. As can been seen from inspecting the t-test maps, eleven-year olds exhibited greater EEG sample entropy at nearly all electrode sites and time scales than seven-year olds. However, as the age gap diminished, the differences in sample entropy were most evident for the more anterior regions (e.g., the nine versus seven and eight versus seven-year-old contrasts). The seven to eight year age transition seems to mark a major stage in the development of EEG complexity, as the differences between eleven year olds and the older age groups grew increasingly sparse, circumscribed to the fine time scales and weakly lateralized over the right hemisphere. There were no observable instances of statistically reliable age-related reductions in sample entropy for the age ranges and time scales investigated here. To exclude the possibility that the children’s medication status influenced these findings, we performed an additional set of control analyses where we adopted a conservative approach excluding all children reported to be on a medication of any sort (including, for example, allergy medications). Although this set of exclusionary criteria led to a considerably reduced sample size relative to the original (seven year-olds N=84; eight year-olds N=71; nine year-olds N=70; ten year-olds N=66; eleven year-olds N=47), the mass univariate contrasts were almost identical to those shown in Figure 4.

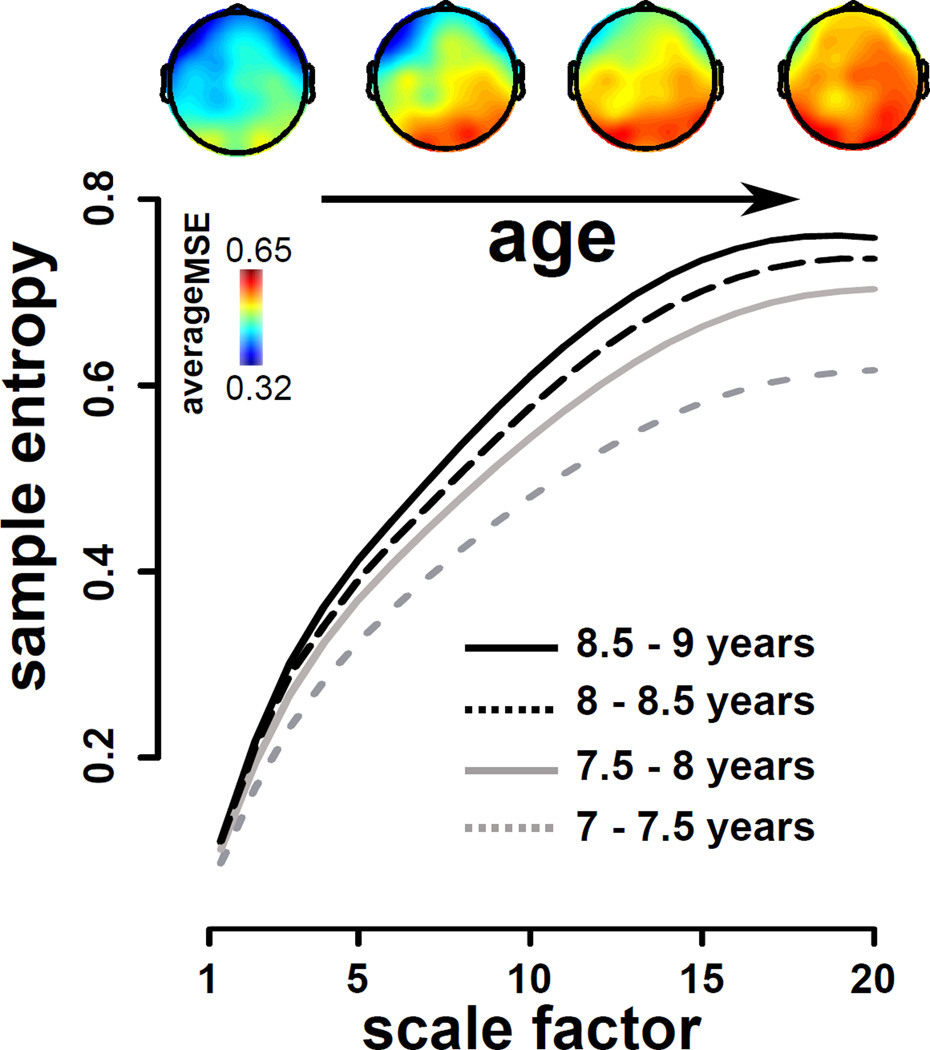
Given that the most drastic age gains appeared to occur roughly during the seven to eight year transitional window, we next examined finer stratification solely within this age range. Figure 5 illustrates the grand mean MSE values amongst the two youngest cohorts, with sub-groups split into 6-month brackets. Although there were no sub-group differences that survived permutation-controlled correction for multiple testing between the youngest and oldest seven year olds, or the youngest and oldest eight year olds, there was nevertheless a linear progression in EEG MSE levels with increasing chronological age. Although not pictured, inter-cohort gaps grew progressively smaller beyond this particular range. The topographic maps highlight that the most salient sequential changes were roughly located within the anterior (fronto-central) zones.

Figure 5.

Electroencephalogram multi-scale entropy, averaged across region and hemisphere, in the two youngest cohorts, with stratification into 6-month brackets. Top row depicts the topographic distribution of average_MSE (integrated across time scales) from the youngest (left) to the oldest (right) cohort sub-groups.

Discussion

We investigated changes in endogenous (resting state) cortical fluctuations from early to late childhood in a large, cross-sectional community sample. Our main findings revealed that brain signal variability (an indicator of neuronal complexity) was greater in older children, with the largest changes seemingly occurring somewhere between the seven to eight year transition. Relative to seven year olds, the older age groups exhibited increased brain signal variability across a wide range of time scales. However, the spatial topography of these chronological effects varied as a function of cohort separation in years, with a widespread spatial distribution for the largest age difference (e.g., eleven year olds compared to seven year olds) and a primarily fronto-central distribution with a diminishing age gap (e.g., eight year olds compared to seven year olds). The eleven year olds continued to exhibit increased brain signal variability compared to eight, nine and ten year old cohorts; however, these effects were considerably weaker in magnitude and encompassed only the local time scales with a slight bias toward the more anterior zones. The increasingly anterior distribution of between-group differences with shrinking age gaps was, in some ways, a mirror image of the posterior-to-anterior gradient observed for the distribution of MSE values in the sample as a whole.

Our results extend previous work on the ontogenetic development of cortical fluctuations (see McIntosh et al., 2010, for a review) to the brain in a resting state. Unconstrained by sensory input or the execution of motor routines, ongoing large-scale neuronal activity is characterized by itinerant wandering along a set of linked, heteroclinic channels (Cabral et al., 2014; Deco et al., 2011, 2013). This meta-stability of neurophysiological time series signals is an emergent property of the underlying cortical architecture and neurochemistry and it reflects the fact that the brain is a loosely coupled system whose functional networks reflect both deterministic and stochastic processes (Buzsáki, 2006; Sporns, 2011). The age-dependent increase of moment-to-moment brain signal variability is a quantitative marker that reflects exploration of a growing dynamic repertoire of the cerebral cortex from early to late childhood. From a neural systems perceptive, the increased variability in the patterns of brain electrical activity likely emerges as a consequence of greater functional integration that gradually emerges in the developing cerebral cortex (Luna & Sweeney, 2004). An increased emphasis on network-level functional coordination can enrich neural constructivist theories of development, by accounting for age-dependent changes in cognitive function as arising from the increased information integration between hierarchically ‘lower’ and ‘higher’ cortical networks (Stevens, 2009). A corollary of this increase in the information content of neurophysiological signals, across multiple time scales, is the growing cognitive sophistication of the child brain – for example, the greater multi-scale entropy evident in EEG signals has been directly linked to age-dependent reductions in behavioral variability on simple decision tasks (McIntosh et al., 2008). Deviations from the normative pattern of increased EEG signal variability may be indicators of developmental risk. Reduced multi-scale entropy of brain signals has been successfully used to classify infants who are at high risk for neurodevelopmental disorders, such autism spectrum, compared to their typically developing counterparts (Bosl et al., 2011). An intriguing suggestion in the literature is that meta-stability of large-scale neuronal systems can serve as a proxy measure of cognitive potential (Deco et al., 2013). To further test these suggestions it will be important for future research to combine non-invasively obtained measures of brain signal variability in development with batteries of cognitive tests to probe putative brain-behavior links that are hypothesized to exist. Although we have emphasized the functional, adaptive aspects of brain signal variability, there is good reason to expect that this is scale-dependent and that the amount of noise has to be maintained within a particular range, outside of which impairments may arise (McDonnell & Ward, 2011). Excessive neuronal noise, or noise at specific spatio-temporal scales, is likely to impair functional communication and may be expected to underlie particular kinds of neuropsychiatric pathology (Takahashi et al., 2013, 2016).

Our observation that the topographic variation in MSE values is distributed along a general posterior-to-anterior gradient is reassuring insofar as it agrees with long established findings pertaining to a similar spatial structure in the development of EEG spectral power (Matousek & Petersen, 1973). To the extent that the dynamic range of neural activity is shaped by the underlying cortical architecture, it might reasonably be expected that MSE levels also follow a rostro-caudal arc, with the highest values in those regions that are most fully developed earlier in time (Colby et al., 2011; Gogtay et al., 2004; Guillery, 2005). The fact that between-group differences were increasingly confined to electrodes covering the more anterior zones as the age disparity between cohorts diminished is an interesting observation then, since it suggests that the most salient differences were roughly situated in those cortical regions that might have been the site of most active neuronal development. Converging evidence for this proposal comes from a previous study employing a distinct measure of neural complexity, which likewise reported the greatest age-related gains during childhood for electrodes covering the frontal associative cortices (Anokhin et al., 1996).

Although we had no a priori hypotheses concerning hemispheric differences, electrodes covering the right cerebral hemisphere tended to exhibit greater signal variability relative to those over the left hemisphere – especially at longer time scales that primarily reflect the contribution of slow cortical oscillations. Although this finding was unexpected, its regularity across all of the major anatomical clusters suggests that it is very likely not a fluke. Importantly, enhanced multi-scale entropy for electrodes covering the right cerebral hemisphere did not seem to differ as a function of handedness in our exploratory analysis. A potentially related finding is the observation of generally increased EEG coherence within the right compared to the left hemisphere of adults (Tucker et al., 1986), which was originally attributed to the greater white-to-gray matter ratio of the right hemisphere (Gur et al., 1980). Given evidence that increased functional connectivity is positively correlated with the variability of signals recorded using multiple imaging modalities (McDonough & Nashiro, 2014; Misic et al., 2011), this may provide a partial explanation for our findings. We remain skeptical of this interpretation, however, given that Barry and colleagues (2012) discovered enhanced left hemisphere EEG coherence in a sample of children that was similar in age to our community sample, and we are unaware of any systematic factors that would explain the apparent discrepancy.

Conclusion

Relative to the youngest cohort of children, the older groups exhibited uniformly increased brain signal variability across nearly all of the time scales investigated here. The results of our study stand to inform existing theories of development, especially those motivated by a dynamic systems perspective, which have emphasized the functional aspects of variability (Smith & Thelen, 2003). Notwithstanding the limitations of cross-sectional study designs when it comes to making inferences about intraindividual maturational trajectories, we believe that our large sample size represents a substantial contribution to the literature on the evolution of neuronal complexity during this sensitive developmental window. Our findings are also in close correspondence with previous studies that have investigated task-related EEG recordings (see McIntosh et al., 2010) as well as those that have used different mathematical estimates of signal complexity (Anokhin et al., 1996; Lindenberger, 1996; Müller & Lindenberger, 2012; Pierce et al., 2000). The spatial distribution of our effects suggests that MSE levels generally exhibited good correspondence with known spatial gradients of neural development. One promising avenue for future research will involve linking the neural dynamics documented here to a wider range of spatio-temporal scales as well as comprehensive cognitive batteries in order to explore the putative functional consequences of increased neuronal signal variability.