Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2017 Sep 1.
Published in final edited form as: J Pharmacol Toxicol Methods. 2016 May 11;81:233–239. doi: 10.1016/j.vascn.2016.05.005

A Temperature-dependent In Silico Model of the Human ether-à-go-go-related (hERG) Gene Channel

Zhihua Li 1, Sara Dutta 1, Jiansong Sheng 1, Phu N Tran 1, Wendy Wu 1, Thomas Colatsky 1
PMCID: PMC5042861  NIHMSID: NIHMS810789  PMID: 27178106

Abstract

Introduction

Current regulatory guidelines for assessing the risk of QT prolongation include in vitro assays assessing drug effects on the human ether-à-go-go-related (hERG; also known as Kv11.1) channel expressed in cell lines. These assays are typically conducted at room temperature to promote the ease and stability of recording hERG currents. However, the new Comprehensive in Vitro Proarrhythmia Assay (CiPA) paradigm proposes to use an in silico model of the human ventricular myocyte to assess risk, requiring as input hERG channel pharmacology data obtained at physiological temperatures. To accommodate current industry safety pharmacology practices for measuring hERG channel activity, an in silico model of hERG channel that allows for the extrapolation of hERG assay data across different temperatures is desired. Because temperature may have an effect on both channel gating and drug binding rate, such models may need to have two components: a base model dealing with temperature-dependent gating changes without drug, and a pharmacodynamic component simulating temperature-dependent drug binding kinetics. As a first step, a base mode that can capture temperature effects on hERG channel gating without drug is needed.

Methods and Results

To meet this need for a temperature-dependent base model, a Markov model of the hERG channel with state transition rates explicitly dependent on temperature was developed and calibrated using data from a variety of published experiments conducted over a range of temperatures. The model was able to reproduce observed temperature-dependent changes in key channel gating properties and also to predict the results obtained in independent sets of new experiments.

Discussion

This new temperature-sensitive model of hERG gating represents an attempt to improve the predictivity of safety pharmacology testing by enabling the translation of room temperature hERG assay data to more physiological conditions. With further development, this model can be incorporated into the CiPA paradigm and also be used as a tool for developing insights into the thermodynamics of hERG channel gating mechanisms and the temperature-dependence of hERG channel block by drugs.

Key terms: CiPA, hERG, Kv11.1, Markov model, Methods, Temperature

1. Introduction

The human ether-à-go-go-related gene (hERG, also known as Kv11.1) encodes the alpha pore-forming subunit of the rapidly activating component of the cardiac delayed rectifier current (IKr) (Sanguinetti, Jiang, Curran, & Keating, 1995). IKr is critical for cardiac action potential (AP) repolarization(Jurkiewicz & Sanguinetti, 1993) and suppressing IKr by drugs can be associated with electrocardiographic QT prolongation and an elevated risk of serious proarrhythmia, specifically Torsade de Pointes (TdP) (Malik & Camm, 2001). Because of this, current regulatory guidelines consider hERG channel block a potential safety concern and recommend the evaluation of drug effects on hERG channel as part of the preclinical development program (“ICH S7B: Note for Guidance on the Nonclinical Evaluation of the potential for Delayed Ventricular Repolarization (QT Interval Prolongation) by Human Pharmaceuticals.,”). The evaluation of hERG channel block is typically carried out early in drug discovery to determine the concentration at which hERG channel activity is reduced by 50% (IC50) (Redfern, et al., 2003). The methodology used to conduct hERG assays varies widely across laboratories, as do the results obtained, with voltage protocol and temperature being among the top sources of variability (Kirsch, et al., 2004).

Some effort has been made to address this issue of methodological differences. For example, computational models have been developed to extract kinetic information from dynamic drug-hERG channel interaction data that are intrinsic to the drug/channel interaction and less dependent a priori on the protocol used (Di Veroli, Davies, Zhang, Abi-Gerges, & Boyett, 2013, 2014). However, unless explicitly introducing temperature-dependent parameters, these models cannot account for temperature-dependent hERG channel activity changes and therefore are limited in their ability to permit an extrapolation of the results across temperatures.

Because temperature may have an effect on both channel gating and drug binding rate, such models may need to have two components: a base model dealing with temperature-dependent gating changes without drug, and a pharmacodynamic component simulating temperature-dependent drug binding kinetics. Despite extensive studies on temperature effects on hERG channel gating (Vandenberg, et al., 2006; Zhou, et al., 1998) and early attempts to build a temperature-dependent hERG channel model (Fink, Noble, Virag, Varro, & Giles, 2008), a base model that can quantitatively reproduce these effects across different labs and independently predict new experimental data across different temperatures is currently unavailable.

Here we developed a Markov model that can recapitulate macroscopic hERG channel gating behavior for a temperature range of 20°C to 37°C. Based on literature data, this model was calibrated using extensive experimental results obtained at different temperatures, and was validated using independent sets of experiments. Such a model would improve on existing hERG models by yielding more insight into the molecular basis of temperature-dependent channel activities, and also could be used as the base model to study temperature-dependent drug binding kinetics.

2. Methods

2.1 Model development

Several Markov models for hERG channel have been described in the literature with varying structure and number of states (Clancy & Rudy, 2001; Di Veroli, et al., 2013; Fink, et al., 2008; Kiehn, Lacerda, & Brown, 1999). We based our model on the Di Veroli et al (Di Veroli, et al., 2013) model because this is the only model designed to study drug binding kinetics. The Markov model uses distinct states to represent different hERG channel conformations and the states transitions are modeled as ordinary differential equations. All state transition rates are defined as:

R=A∗eB∗V∗q(T-20)/10

where R is the state transition rate, V is membrane potential (electrical field across the channel), A and B reflect the energy barrier height in the absence and presence of electrical field respectively (Balser, Roden, & Bennett, 1990), T is temperature, and q is the commonly used temperature extrapolating Q10 value defined as the change in rate for each 10°C change in temperature (Hille, 2001). We chose Q10 over more complex thermodynamic formulations (Fink, et al., 2008; Irvine, Jafri, & Winslow, 1999) to represent temperature sensitivity because it simplifies model parameterization and interpretation. A similar strategy was used by others in modeling cardiac sodium channel gating (Clancy & Rudy, 1999). Microscopic reversibility was ensured by fixing the products of forward and reverse transition rates of closed loops (Hille, 2001). The model was implemented in R (http://www.r-project.org), and the equations are numerically solved by the R package deSolve (http://desolve.r-forge.r-project.org). Model fitting was done on a computer cluster hosted by High Performance Computing Lab of FDA using GAPSM (Genetic Algorithm-based Parameterization for Systems Modeling), a genetic algorithm-based fitting method we developed in the process of building other large scale systems biology/pharmacology models (Li, Zhou, Lu, & Colatsky, 2014). The differential equations and parameter values are described in the Online Supplement.

2.2 Model Simulations

A series of voltage protocols were applied to the model in order to calibrate and validate it against hERG biophysical data (Di Veroli, et al., 2013; Vandenberg, et al., 2006; Zhou, et al., 1998). The current value can be approximated using the model’s open state as follows: I = G * O * (V − EK), where I is the current, G is the conductance, O is the open state of the model, V is the voltage and EK is the potassium reversal potential. For normalized current and conductance this equation can be simplified to O/Omax, where Omax is the maximum open state value.

2.2.1 Fitting the model to hERG channel biophysical data at 20°C from Di Veroli et al study (Di Veroli, et al., 2013)

Deactivation time course protocol

Membrane potential was held at −80 mV for 2 s and then a step to +60 mV was applied for 4 s before stepping to Vtest (−30, −45, −60, −75 and −90 mV) for 3 s. The first 1000 ms upon stepping to Vtest were plotted normalized to the peak current value.

Activation time course protocol

An envelope of tails protocol was used to elucidate activation kinetics. Membrane potential was held at −100 mV for 3 s and then a step to Vtest (+60, +40, +20, +10, +0 mV) for t1 was applied. Another step to −100 mV for 3 s was applied followed by another step to Vtest for t2 > t1. The process was repeated eight times for different durations. The activation time course was obtained by taking peak values upon each repolarization to −100 mV and normalizing to the value obtained for Vtest = +60 mV.

Activation current voltage protocol

Membrane potential was held at −80 mV for 2 s and then a step to Vtest was applied for 4 s before stepping to −80 mV for 2 s. The protocol was applied 10 times with Vtest ranging from −70 mV to +70 mV. Peak values upon repolarization to −80 mV were used to build the activation curve by normalizing to the value obtained with Vtest=+70 mV.

Inactivation curve protocol

Membrane potential was held at −80 mV for 2 s and then a step to +60 mV was applied for 4 s. Another step to a voltage of Vtest (9 values between −100 mV and +60 mV) was applied for 3 s afterwards. Peak values during Vtest were used to build the inactivation curve by normalizing to the value obtained with Vtest = −100 mV.

Inactivation rates protocol

For Vtest ranging from −100 mV to −40 mV, the same protocol as the inactivation curve protocol (defined above) was used. The initial current shape (until it reaches its maximum) upon repolarization to Vtest was used to generate reactivation rates by fitting a single exponential function and extracting the time constant (the exponential recovery equation is described below). For Vtest ranging from −30 mV to +50 mV, membrane potential was held at −80 mV for 2 s and then a step to +60 mV was applied for 5 s. Then a brief step to −100 mV lasting 6 ms was applied before stepping to Vtest for 4s. Finally, another step to −80 mV for 4 s was added afterward. The initial part of the current shape obtained upon depolarization to Vtest (the first 100 ms) was used to derive inactivation rates by fitting a single exponential function and extracting the time constant (the exponential decay equation is described below).

2.2.2 Fitting the model to hERG channel biophysical data at various temperatures from Vandenberg et al study (Vandenberg, et al., 2006)

Activation curve protocol

Membrane potential was initially set at −80 mV, and then it was stepped up to Vtest (ranging from −80 mV to +40 mV) for 30 s before stepping down to −120 mV. Peak values during Vtest were used to build the inactivation curve by normalizing to the value obtained with Vtest = +40 mV.

Inactivation curve protocol

Membrane potential was initially set at −80 mV, and then it was stepped up to +40 mV for 1 s to fully activate and inactivate the channels, before stepping to Vtest (ranging from −150 mV to +60 mV). The peak amplitude of the tail current at each potential, after recovery from inactivation, was calculated and corrected for channel deactivation (Smith, Baukrowitz, & Yellen, 1996). For Vtest < −20 mV, an exponential curve was fitted to the decay part and extrapolated the peak value. Data was then normalized to Vtest = −150 mV.

Activation time course protocol

Membrane potential was depolarized to 0 mV for various durations (between 100 and 3500 ms) before stepping down to −50 mV. Peak values upon repolarizing to −50 mV were normalized to the step with maximum duration 3500 ms.

Protocol to calculate time constants of inactivation, deactivation and recovery

A triple pulse protocol was applied, consisting of a depolarization step to +40 mV for 1 s, a repolarization step to −80 mV for 20 ms, followed by a voltage step to +40 mV for 100 ms and finally a step to −120 mV. To calculate the recovery constant, a single exponential (as described below) was fitted to the first part of the rising phase after stepping to −120 mV. The deactivation time constant was calculated by fitting the decay part after the maximum is reached when stepping to −120 mV with a single exponential. For the inactivation time constant, we fit a single exponential function to the second +40 mV step.

2.2.3 Predicting independent hERG biophysical data at 35°C from Zhou et al (Zhou, et al., 1998)

Activation current voltage protocol

Membrane potential was held at −80 mV and then a depolarization step to Vtest (ranging from −60 mV to +50 mV) was applied for 4 s, after which the membrane potential was held at −50 mV for 5 s. The peak tail current upon stepping to −50 mV was normalized to Vtest=+50 mV.

Activation time course protocol

Membrane potential was held at −80 mV, followed by a depolarizing step to 0 mV for different times (between 10 and 450 ms) and a repolarizing step to −60 mV. Peak tail current upon repolarization to −60 mV was normalized to the longest step time.

Deactivation time course protocol

From −80 mV, the potential was stepped to +60 mV and then to −70 mV. The decay of the current upon stepping to −70 mV was recorded and normalized to the maximum value reached.

Protocol to calculate recovery from inactivation time constants

Membrane potential was held at −80 mV, before stepping to +60 mV for 200 ms and then to Vtest (ranging from −100 mV to −20 mV) for 100 ms. Recovery time constants were calculated by fitting a single exponential function (as defined below) upon stepping to Vtest.

Protocol to calculate inactivation time constants

Membrane potential was held at −80 mV, followed by a depolarizing step to +60 mV for 200 ms, then to −100 mV for 2 ms and finally to Vtest (ranging between −20 mV and +60 mV). The inactivation time constant was calculated by fitting a single exponential function upon stepping to Vtest.

2.2.4 Predicting the three-step protocol at room temperature

Membrane potential was held at −80 mV, followed by a depolarizing step to +20 mV for 1 s. The membrane potential was then stepped down to −40 mV for 500 ms and finally to −120 mV for 500 ms before stepping back to −80 mV. The current was approximated using the equation described in 2.2 (I = G * O * (V − EK)) and normalized to the absolute maximum value reached. The potassium reversal potential (Ek) was calculated as (RTF)∗log(KoKi), where R is the gas constant (8314.0 J/kmol/K), T is the absolute temperature, F is the Faraday constant (96485.0 coul/mol), Ko is the extracellular potassium concentration (5 mM), and Ki is the intracellular potassium concentration (140 mM).

2.2.5 Equations

The equations described here were used to calculate recovery, inactivation and deactivation time constants, as well as voltage dependence (Vhalf) of I–V relationship as in Milnes et al (Milnes, Witchel, Leaney, Leishman, & Hancox, 2010). Recovery time constants were calculated by fitting to the following equation:

O=Span∗(1-e-k∗t)+Omin,

where O is the open state, t is time, Span is the difference between the minimum fraction of open channels, Omin, and the extrapolated plateau value, k is the rate-constant of the exponential recovery and the time constant can be calculated as 1/k. Inactivation and deactivation time constants were calculated by fitting to the following equation:

O=A∗(e-tτ)+C,

where A is the total fraction of open channels, t is time, τ is the time constant of decay and C is the residual fraction of open channels. The inactivation I–V relationship curves were fitted by a modified Boltzmann equation as follows:

IImax=1-1/(1+e(Vhalf-Vm)/S)

Where I is the current corresponding to membrane potential Vm, Imax is the maximal current observed, Vhalf is the half inactivation voltage, and S is the slope factor describing the I–V relationship.

2.3 Electrophysiology

For hERG current recording, a HEK293 cell line stably expressing hERG1a protein (Generously supplied by Dr. Gail Roberton, University of Wisconsin-Madison) was cultured in MEM supplemented with non-essential amino acids solution, 10% FBS and 10 μM G418 (GIBCO, Grand Island, NY). During electrophysiological recording, cells were constantly perfused with extracellular solution containing (in mM): 130 NaCl, 5 KCl, 10 HEPES, 1 MgCl2, 1 CaCl2, 12.5 Dextrose (pH 7.4, adjusted with NaOH). The internal pipette solution contains (in mM): 120 K-Gluconate, 20 KCl, 10 HEPES, 5 EGTA, 1.5 MgATP (pH 7.3, adjusted with KOH). MultiClamp 700B, Axon Digidata 1550A and pClamp software (Molecular Devices, Sunnyvale, CA) were used for whole-cell recording and data acquisition. All voltage commands were corrected with a −15 mV liquid junction potential resulting from using the above internal solution.

3. Results

As shown in Figure 1, the hERG model has six states corresponding to open, closed, or inactivated channel conformations, with each state transition governed by membrane voltage and temperature. Each transition is governed by a different set of free parameters, in contrast to the original Di Veroli hERG model in which many state transitions were assumed to have the same parameters. By forcing some state transition parameters to be identical, the number of free parameters is reduced but the model becomes less flexible and robust. We loosened the constraints on the state transition parameters by allowing them to be independent from each other in order to build a robust model that accounts for the breadth of published data across different temperatures and studies.

Figure 1. Structure of the hERG model.

Figure 1

Open in a new tab

C1 and C2 are closed states, O is open state, and the corresponding inactivated states are IC1, IC2, and IO. The transition between adjacent states is a first order reaction dependent on membrane voltage, temperature, with three free parameters A, B, and q (see Methods). Each state transition has a different set of free parameters, which are distinguished between each other by numeric suffixes.

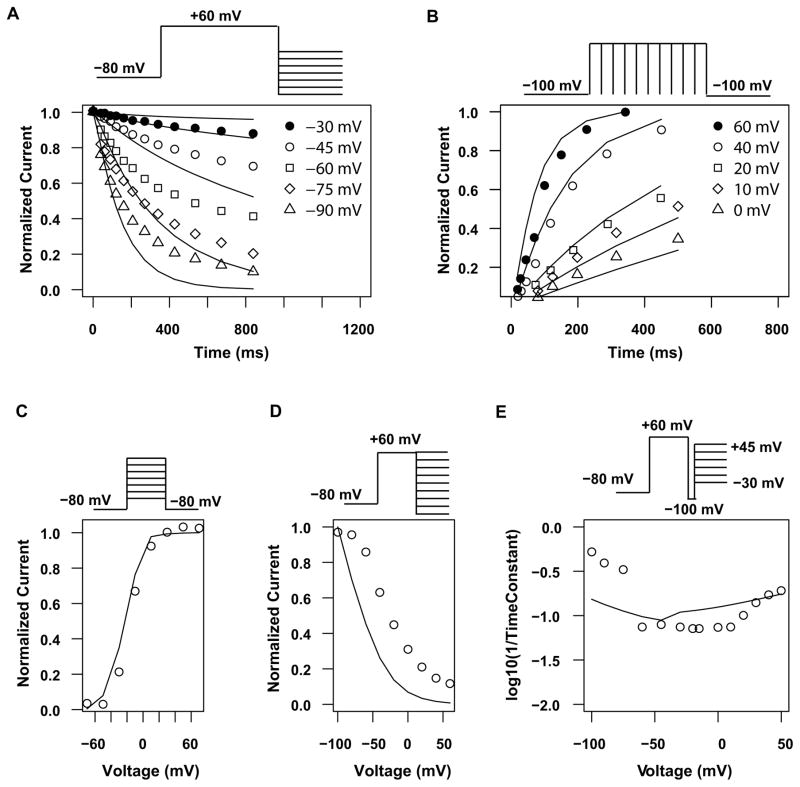
The new hERG model was fitted simultaneously to experimental data from two comprehensive studies to estimate free parameters. The Di Veroli study used CHO cells to study the biophysical properties of hERG channel at 20°C on an automated patch clamp system (Di Veroli, et al., 2013), while the Vandenberg study used the same cell line and a different set of protocols to probe channel gating processes at various temperatures using a manual patch clamp system (Vandenberg, et al., 2006). The fitting of our model to the Di Veroli dataset at 20°C and the Vandenberg study at multiple temperatures are shown in Figures 2 and 3 respectively. As shown in Figure 2, while some data points were fitted well, others show less good a fit compared to the original Di Veroli model (Di Veroli, et al., 2013), especially the inactivation I–V curve (Figure 2D) and recovery time constants (first half of Figure 2E). Careful examination suggests that this is due to the variability between the room temperature data from Di Veroli and Vandenberg studies. For instance, the Di Veroli inactivation I–V curve (circles in Figure 2D) would result in a half inactivation voltage (Vhalf) of −20 mV, while the room temperature inactivation I–V curve in Vandenberg study (non-filled circles in Figure 3B) gave a Vhalf of −88 mV. Because the inactivation curve in Figure 3B was corrected for deactivation (Vandenberg, et al., 2006) while Figure 2D was not, we also calculated a Vhalf using non-corrected inactivation I–V curve based on Figure 5C of the original Vandenberg paper (Vandenberg, et al., 2006) to make it more comparable to Di Veroli’s value in Figure 2D. This resulted in an inactivation Vhalf of −73 mV, still much more negative than Di Veroli’s value (−20 mV). This discrepancy is probably due to lab-to-lab and system-to-system (manual vs automated) variability. Trying to fit values from both data set, the model computed an inactivation I–V relationship (solid line in Figure 2D) with a Vhalf of −56 mV to achieve an overall best fit to all the data, which also leads to a seemingly bad fitting on Figure 2D. Interestingly, this calculated Vhalf is close to at least two other studies reporting room temperature inactivation Vhalf values (Lu, Mahaut-Smith, Huang, & Vandenberg, 2003; B. D. Walker, et al., 2000), suggesting our model was able to “average out” the occasional biased values found in any particular study. A similar pattern was found for the room temperature recovery data. Di Veroli data (circles in Figure 2E) suggested a time constant (τ) of ~1.9 ms at −100 mV. In contrast, Vandenberg study reported a room temperature recovery τ of 3.8 ms at −120 mV (Figure 3D), and judging by the voltage dependency of recovery speed, one would expect an even larger τ at −100 mV. Even though Di Veroli study temperature (20°C) is lower than that of Vandenberg study (24°C), this small temperature difference cannot explain the > 2 fold difference in recovery speed at the same voltage (−100 mv). Again, the model found a middle ground solution (5.8 ms at −100 mV) that minimized the overall error, but at the same time created a seemingly bad fitting (Figure 2E). In terms of fitting to multiple temperature data from Vandenberg study, our model correctly reproduced the left shift of the activation curve and the right shift of the inactivation curve as temperature increases (Figure 3A and B). The significant increase in activation speed after temperature increases was quantitatively captured by the model (Figure 3C), and so were the temperature sensitivities of deactivation, inactivation, and recovery from inactivation (Figure 3D). Even though a few data points were not fitted perfectly, the overall fitting to the Vandenberg study in Figure 3 is reasonable, suggesting our model can reproduce temperature-dependent changes in various hERG channel gating processes.

Figure 2. Fitting to hERG biophysical data at 20°C.

Figure 2

Open in a new tab

Experimental data, taken from Di Veroli et al (Di Veroli, et al., 2013), are shown as symbols, and simulated data are shown as solid lines. A, fraction of open channels over time during deactivation. B, fraction of open channels over time during activation. C, activation curve. D, inactivation curve. E, recovery and inactivation rate. The top panels show the voltage protocols used. Note that points in panel E were calculated using two separate protocols: recovery time constants (−100 to −40 mV) using the protocol 2D while inactivation time constants (−30 to +50 mV) using the protocol in 2E.

Figure 3. Fitting to hERG channel experiments at various temperatures.

Figure 3

Open in a new tab

Experimental data, taken from Vandenberg et al (Vandenberg, et al., 2006), are shown as symbols and simulated data are shown as solid lines. A, activation curve. B, inactivation curve. C, activation time course. D, time constants of various processes at room or physiological temperatures; Measured are experimentally determined data from Vandenberg paper while Fitted are simulated using our model. The insets show the voltage command protocol used. Note that for A and B, the original Vandenberg study contains 14°C data, which are not used for model fitting here because the main purpose is to extrapolate between room temperature and physiological temperature.

The data presented above were used to parameterize the model (the fitted parameters can be found in the Online Supplement). While it is encouraging to see that a single set of parameters can reproduce the results of an ensemble of different voltage protocols across different temperatures and labs, it is more important to determine whether this same parameter set can predict the results of an independent set of experimental data not used in the fitting process. For the purpose of validation, we chose a third set of data using hERG-transfected HEK cells recorded at near physiological temperature (Zhou, et al., 1998). As shown in Figure 4, the current model is able to predict quantitatively most of the experimental results in this independent data set, including the activation I–V relationship (Figure 4A), activation/deactivation time course (Figure 4B and C), as well as time constants for recovery (Figure 4D) and inactivation (Figure 4E). In addition, to test if our model can also independently predict new experimental results from room temperature, we challenged the model with a new three-step protocol (Figure 5) and then compared the predicted traces to those experimentally obtained using HEK cells at room temperature in our laboratories. As shown in Figure 5, the model was able to predict the amplitude and shape of the currents across the three steps. Both the outward (−40 mV step) and the inward (−120 mV step) tail currents were predicted very well. The computed pre-pulse currents (+20 mV step) are a little low compared to experimental values, but are within the standard deviation of the data. Taken together, this suggests that the hERG model is able to predict the experimental results from protocols and cell lines not used in the fitting process. This feature is very useful if the model were to be used to study drug-channel interactions, where new voltage protocols will be designed to study different aspects of drug binding/unbinding kinetics.

Figure 4. Prediction of independent experiments at 35°C in HEK cells.

Figure 4

Open in a new tab

The hERG model was used to predict the outcome of experiments from an independent study (Zhou, et al., 1998). Solid lines are model prediction while symbols are experimental data. A. Activation I–V relationship. B. Activation time course. C. Deactivation time course. D. Recovery from inactivation time constants. E. Inactivation time constants. The insets show the voltage command protocol used.

Figure 5. Prediction of independent experiments at room temperature in HEK cells.

Figure 5

Open in a new tab

A new three-step voltage protocol was applied to HEK cells at room temperature (24°C) and the results (symbols) are compared to independent prediction of the model (lines). Error bars indicating standard deviation are also shown (N=3). The inset shows the voltage command protocol used. The three sections of symbols correspond to the pre-pulse (+20 mV), the first test pulse (−40 mV), and the second test pulse (−120 mV) respectively.

4. Discussion

Here we presented a computational hERG model for which the channel gating parameters are explicitly dependent on temperature. To our best knowledge this is the first hERG model that can quantitatively reproduce and independently predict the temperature sensitivities of hERG channel gating properties. Incorporating temperature into the model allows it to predict how temperature changes affect gating processes under various voltage protocols. After supplementing the base model with a pharmacodynamics component describing temperature-dependent drug binding kinetics, the full model can potentially allow for the extrapolation of hERG assay data obtained at room temperature to models of the human cardiac ventricular myocyte at 37°C. The Markovian nature of this model makes it straightforward to simulate state-dependent blocking and dissociation, an important feature of many hERG-blocking drugs (Stork, et al., 2007; B.D. Walker, et al., 1999). Thus the current model provides an initial framework for studying temperature-dependent hERG channel gating changes and the kinetics of drug block.

As with any computational approach to simulate the real world behaviors, it is critical to bear in mind the strength and weakness of the current hERG model. First of all, because the goal is to build a “generic” hERG model that can reproduce the widest range of data possible, the model was calibrated and validated using data across different laboratories, different recording systems (manual and automated patch system), and different cell lines (CHO and HEK cells). While this strategy allows for broader application of the model, it also introduces significant potential inter-laboratory and inter-platform variability into the data. As can be seen from Figures 2 and 3, sometimes the fitting to a particular dataset was not optimal because the best fit to that dataset was sacrificed to achieve a better overall fitting to the whole set. Thus applications in a particular experimental setting may require further adjustment of the parameters. Secondly, for a model with such complexity and a training data set with such variability, inevitably some parameters are not well constrained (Irvine, et al., 1999). As a result, the set of parameters presented here is not the only possible solution during the parameterization process. However, the fact that this parameter set can predict the results of independent experiments suggests that this model captures some underlying biological mechanisms from the training data rather than “memorizes” or overfits the data. Lastly, this is a base model with only channel gating processes, and drug binding/unbinding processes will need to be added later for each specific drug. Currently for most compounds it is unknown how much an effect temperature has on drug binding kinetics. It has been suggested that the drug binding processes might be less temperature sensitive (Di Veroli, et al., 2013) and modeling the temperature effects on gating processes, but not drug binding processes, may be enough to explain the drug-channel interactions at different temperatures (Vandenberg, et al., 2006). However, some drugs/toxins do show temperature sensitivity in their binding/unbinding rates (Hill, Sunde, Campbell, & Vandenberg, 2007) and in those cases, drug-specific temperature parameters (Q10s) will have to be introduced into the drug binding component and estimated by doing channel blocking experiments at multiple temperatures. Currently a series of compounds are being tested at both room and physiological temperatures to add a pharmacodynamic component to the base model and to evaluate the necessity of modeling the drug binding processes in a temperature-dependent manner.

In summary, here we presented a computational hERG model that can quantitatively reproduce and predict temperature-induced changes in major gating processes. This model improves on existing hERG Markov models by incorporating temperature dependence of state transitions, and could be used to probe dynamic drug-channel interactions in a temperature dependent manner. Currently the model is being further developed (e.g. to make its gating behavior more closely resemble human native IKr currents in vivo) and integrated into the consensus human ventricular cardiomyocyte model (O’Hara Rudy, or ORd) (O’Hara, Virag, Varro, & Rudy, 2011) to extract dynamic drug-channel interaction for the compounds on the CiPA training list (Fermini, et al., 2016)

Supplementary Material

Supplemental

Acknowledgments

Sources of Funding

This project was funded by FDA Critical Path Award. The study sponsor(s) played no role in the study design; in the collection, analysis, and interpretation of data; in the writing of the report; and in the decision to submit the paper for publication.

Footnotes

Conflict of Interest Statement

The authors declared no conflict of interest.

Disclaimer

This report is not an official U.S. Food and Drug Administration guidance or policy statement. No official support or endorsement by the U.S. Food and Drug Administration is intended or should be inferred.

Reference List

  1. Balser JR, Roden DM, Bennett PB. Global parameter optimization for cardiac potassium channel gating models. Biophysical Journal. 1990;57:433–444. doi: 10.1016/S0006-3495(90)82560-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Clancy CE, Rudy Y. Linking a genetic defect to its cellular phenotype in a cardiac arrhythmia. Nature. 1999;400:566–569. doi: 10.1038/23034. [DOI] [PubMed] [Google Scholar]
  3. Clancy CE, Rudy Y. Cellular consequences of HERG mutations in the long QT syndrome: precursors to sudden cardiac death. Cardiovascular Research. 2001;50:301–313. doi: 10.1016/s0008-6363(00)00293-5. [DOI] [PubMed] [Google Scholar]
  4. Di Veroli GY, Davies MR, Zhang H, Abi-Gerges N, Boyett MR. High-throughput screening of drug-binding dynamics to HERG improves early drug safety assessment. American Journal of Physiology - Heart and Circulatory Physiology. 2013;304:H104–H117. doi: 10.1152/ajpheart.00511.2012. [DOI] [PubMed] [Google Scholar]
  5. Di Veroli GY, Davies MR, Zhang H, Abi-Gerges N, Boyett MR. hERG inhibitors with similar potency but different binding kinetics do not pose the same proarrhythmic risk: implications for drug safety assessment. Journal of Cardiovascular Electrophysiology. 2014;25:197–207. doi: 10.1111/jce.12289. [DOI] [PubMed] [Google Scholar]
  6. Fermini B, Hancox JC, Abi-Gerges N, Bridgland-Taylor M, Chaudhary KW, Colatsky T, Correll K, Crumb W, Damiano B, Erdemli G, Gintant G, Imredy J, Koerner J, Kramer J, Levesque P, Li Z, Lindqvist A, Obejero-Paz CA, Rampe D, Sawada K, Strauss DG, Vandenberg JI. A New Perspective in the Field of Cardiac Safety Testing through the Comprehensive In Vitro Proarrhythmia Assay Paradigm. Journal of Biomolecular Screening. 2016;21:1–11. doi: 10.1177/1087057115594589. [DOI] [PubMed] [Google Scholar]
  7. Fink M, Noble D, Virag L, Varro A, Giles WR. Contributions of HERG K+ current to repolarization of the human ventricular action potential. Progress in Biophysics & Molecular Biology. 2008;96:357–376. doi: 10.1016/j.pbiomolbio.2007.07.011. [DOI] [PubMed] [Google Scholar]
  8. Hill AP, Sunde M, Campbell TJ, Vandenberg JI. Mechanism of block of the hERG K+ channel by the scorpion toxin CnErg1. Biophysical Journal. 2007;92:3915–3929. doi: 10.1529/biophysj.106.101956. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Hille B. Ion Channels of Excitable Membranes. 3 2001. [Google Scholar]
  10. ICH S7B. Note for Guidance on the Nonclinical Evaluation of the potential for Delayed Ventricular Repolarization (QT Interval Prolongation) by Human Pharmaceuticals. Lodon: The International Conference on Harmonisation of Technical Requirements for Registration of Pharmaceuticals for Human Use; pp. 3–9. [Google Scholar]
  11. Irvine LA, Jafri MS, Winslow RL. Cardiac sodium channel Markov model with temperature dependence and recovery from inactivation. Biophysical Journal. 1999;76:1868–1885. doi: 10.1016/s0006-3495(99)77346-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Jurkiewicz NK, Sanguinetti MC. Rate-dependent prolongation of cardiac action potentials by a methanesulfonanilide class III antiarrhythmic agent. Specific block of rapidly activating delayed rectifier K+ current by dofetilide. Circulation Research. 1993;72:75–83. doi: 10.1161/01.res.72.1.75. [DOI] [PubMed] [Google Scholar]
  13. Kiehn J, Lacerda AE, Brown AM. Pathways of HERG inactivation. American Journal of Physiology. 1999;277:H199–H210. doi: 10.1152/ajpheart.1999.277.1.H199. [DOI] [PubMed] [Google Scholar]
  14. Kirsch GE, Trepakova ES, Brimecombe JC, Sidach SS, Erickson HD, Kochan MC, Shyjka LM, Lacerda AE, Brown AM. Variability in the measurement of hERG potassium channel inhibition: effects of temperature and stimulus pattern. Journal of Pharmacological and Toxicological Methods. 2004;50:93–101. doi: 10.1016/j.vascn.2004.06.003. [DOI] [PubMed] [Google Scholar]
  15. Li Z, Zhou H, Lu Y, Colatsky T. A Critical Role for Immune System Response in Mediating Anti-influenza Drug Synergies Assessed by Mechanistic Modeling. CPT: Pharmacometrics & Systems Pharmacology. 2014;3:e135. doi: 10.1038/psp.2014.32. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Lu Y, Mahaut-Smith MP, Huang CL, Vandenberg JI. Mutant MiRP1 subunits modulate HERG K+ channel gating: a mechanism for pro-arrhythmia in long QT syndrome type 6. Journal of Physiology. 2003;551:253–262. doi: 10.1113/jphysiol.2003.046045. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Malik M, Camm AJ. Evaluation of drug-induced QT interval prolongation: implications for drug approval and labelling. Drug Safety. 2001;24:323–351. doi: 10.2165/00002018-200124050-00001. [DOI] [PubMed] [Google Scholar]
  18. Milnes JT, Witchel HJ, Leaney JL, Leishman DJ, Hancox JC. Investigating dynamic protocol-dependence of hERG potassium channel inhibition at 37 degrees C: Cisapride versus dofetilide. Journal of Pharmacological and Toxicological Methods. 2010;61:178–191. doi: 10.1016/j.vascn.2010.02.007. [DOI] [PubMed] [Google Scholar]
  19. O’Hara T, Virag L, Varro A, Rudy Y. Simulation of the undiseased human cardiac ventricular action potential: model formulation and experimental validation. PLoS Computational Biology. 2011;7:e1002061. doi: 10.1371/journal.pcbi.1002061. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Redfern WS, Carlsson L, Davis AS, Lynch WG, MacKenzie I, Palethorpe S, Siegl PK, Strang I, Sullivan AT, Wallis R, Camm AJ, Hammond TG. Relationships between preclinical cardiac electrophysiology, clinical QT interval prolongation and torsade de pointes for a broad range of drugs: evidence for a provisional safety margin in drug development. Cardiovascular Research. 2003;58:32–45. doi: 10.1016/s0008-6363(02)00846-5. [DOI] [PubMed] [Google Scholar]
  21. Sanguinetti MC, Jiang C, Curran ME, Keating MT. A mechanistic link between an inherited and an acquired cardiac arrhythmia: HERG encodes the IKr potassium channel. Cell. 1995;81:299–307. doi: 10.1016/0092-8674(95)90340-2. [DOI] [PubMed] [Google Scholar]
  22. Stork D, Timin EN, Berjukow S, Huber C, Hohaus A, Auer M, Hering S. State dependent dissociation of HERG channel inhibitors. British Journal of Pharmacology. 2007;151:1368–1376. doi: 10.1038/sj.bjp.0707356. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Vandenberg JI, Varghese A, Lu Y, Bursill JA, Mahaut-Smith MP, Huang CL. Temperature dependence of human ether-a-go-go-related gene K+ currents. American Journal of Physiology - Cell Physiology. 2006;291:C165–C175. doi: 10.1152/ajpcell.00596.2005. [DOI] [PubMed] [Google Scholar]
  24. Walker BD, Singleton CB, Bursill JA, Wyse KR, Valenzuela SM, Qiu MR, Breit SN, Campbell TJ. Inhibition of the human ether-a-go-go-related gene (HERG) potassium channel by cisapride: affinity for open and inactivated states. British Journal of Pharmacology. 1999;128:444–450. doi: 10.1038/sj.bjp.0702774. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Walker BD, Singleton CB, Tie H, Bursill JA, Wyse KR, Valenzuela SM, Breit SN, Campbell TJ. Comparative effects of azimilide and ambasilide on the human ether-a-go-go-related gene (HERG) potassium channel. Cardiovascular Research. 2000;48:44–58. doi: 10.1016/s0008-6363(00)00155-3. [DOI] [PubMed] [Google Scholar]
  26. Zhou Z, Gong Q, Ye B, Fan Z, Makielski JC, Robertson GA, January CT. Properties of HERG channels stably expressed in HEK 293 cells studied at physiological temperature. Biophysical Journal. 1998;74:230–241. doi: 10.1016/S0006-3495(98)77782-3. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplemental
NIHMS810789-supplement-Supplemental.docx (22.4KB, docx)

RESOURCES