A hybrid continuous-discrete method for stochastic reaction–diffusion processes

Abstract

Stochastic fluctuations in reaction–diffusion processes often have substantial effect on spatial and temporal dynamics of signal transductions in complex biological systems. One popular approach for simulating these processes is to divide the system into small spatial compartments assuming that molecules react only within the same compartment and jump between adjacent compartments driven by the diffusion. While the approach is convenient in terms of its implementation, its computational cost may become prohibitive when diffusive jumps occur significantly more frequently than reactions, as in the case of rapid diffusion. Here, we present a hybrid continuous-discrete method in which diffusion is simulated using continuous approximation while reactions are based on the Gillespie algorithm. Specifically, the diffusive jumps are approximated as continuous Gaussian random vectors with time-dependent means and covariances, allowing use of a large time step, even for rapid diffusion. By considering the correlation among diffusive jumps, the approximation is accurate for the second moment of the diffusion process. In addition, a criterion is obtained for identifying the region in which such diffusion approximation is required to enable adaptive calculations for better accuracy. Applications to a linear diffusion system and two nonlinear systems of morphogens demonstrate the effectiveness and benefits of the new hybrid method.

1. Introduction

Many biological systems are subject to stochastic fluctuations when the copy number of the molecules is relatively small [1,2]. For spatially inhomogeneous systems that involve both reactions and diffusions, the spatial distributions of the molecules are important because local copy number fluctuations may result in phenotypic differences, though the total number of molecules of the relevant species may be high [3].

For a spatially homogeneous system, the Gillespie stochastic simulation algorithm (SSA) tracks each reaction event and updates the state of the system after each occurrence of reactions [4]. Numerous methods have been developed to improve the efficiency of this method for cases involving large sizes for certain species or frequent reactions; examples of such methods include the next reaction method [5], τ-leaping [6–8], the hybrid methods for simulating fast and slow reactions [9–11] and the adaptive multi-level simulation algorithm [12].

For a spatially inhomogeneous system, the SSA can be applied by first partitioning the spatial domain into many compartments. In each compartment, reactions are treated as in the homogeneous case; however, molecules may jump between adjacent compartments through diffusion [13]. In this approach, the size of each compartment must be sufficiently small that diffusive jumps occur more rapidly than reactions and the inhomogeneity inside each compartment can be ignored [14,15]. Also, the time scale for the molecule to diffuse throughout a compartment should be much faster than the time scale for the fastest bimolecular chemical reaction [14,16,17].

In the case of frequent diffusive jumps, the spatial SSA may become computationally inefficient. Consequently, modifications have been made to accelerate the SSA, as in the next sub-volume method [18] and the null process [19], or to develop a new computational algorithm that optimizes the search process in the SSA [20], or to approximate diffusion, as in the multinomial simulation algorithm [21], the diffusive finite state projection method [22] and adaptive algorithms [23,24]. These approximation methods share a common feature: reaction and diffusion processes are simulated independently, and the diffusive jumps occur at predetermined time intervals, between which the reactions are simulated. As a result, the time step depends on the fastest diffusion rate, leading to excessive computational cost, in particular, for the case of fast diffusion.

Several hybrid methods were developed for solving stochastic reaction–diffusion systems [25–28]. The most common approach is a spatially hybrid method between the SSA and deterministic approach. Noise effect in high concentration region is relativity small so deterministic approach such as using partial differential equations is sufficient to ensure the accuracy of simulations. However, small noise effect in high concentration region may still result in large fluctuations in low concentration region because of communication between the regions, so the development of a hybrid method which combines two or more stochastic approaches without involving any deterministic approach becomes an important and effective approach.

Here, we introduce a hybrid continuous-discrete method to simulate spatially inhomogeneous systems with better efficiency and accuracy. As in the Central Limit Theorem, a continuous Gaussian random variable can be used to approximate the change in the number of molecules introduced by a large number of independent diffusive jumps. A brief overview of the algorithm is listed below:

1. Calculating the time of the next occurring reaction based on the SSA.

2. Approximating the numbers of diffusive jumps using Gaussian random vectors with time-dependent means and covariances by assuming no reactions during the period of time.

3. If the approximated number of diffusive jumps at some compartments is large enough, the approximation is then applied at that locations; otherwise the SSA is applied. Since the number of diffusive jumps may be different at each time period between reactions, so the locations at which the approximation is applied are set adaptively over time.

As a result, the updating takes place only when a reaction occurs, and the time step is then determined by the reaction rates. Because the correlation among diffusive jumps is considered in our method, the approximation of the diffusion is reliable, and its effect on the reactions is small.

The method is applied to 3 one-dimensional reaction–diffusion systems for morphogen gradients in addition to a two-dimensional morphogen system. The efficiency of the method improves as the diffusion coefficients increase or the number of diffusing molecules increases, yielding more than 60% savings in computational cost compared with the standard spatial SSA. In addition, because of the new time-adaptive criterion for identifying the region for the diffusion approximation, our hybrid method allows for zero initial conditions (i.e. an initial state without any molecules) in the simulations, unlike many other existing stochastic methods, which need to start with a certain level of molecules in order to obtain good approximations.

2. Material and methods

2.1. Chemical master equations for spatially inhomogeneous systems

Consider a system along a one-dimensional domain with length L, where N molecular species {S₁,S₂,…,S_N} are involved in the following M reactions {R₁,R₂,…,R_M}:

$$R_j:s_{j1}^{\mathrm{r}}{S}_1+\cdots +s_{jN}^{\mathrm{r}}{S}_{\mathrm{N}}\stackrel{{\gamma }_j}{\to }{s}_{j1}^{\mathrm{p}}{S}_1+\cdots +s_{jN}^{\mathrm{p}}{S}_{\mathrm{N}}.$$

Here, $s_{ji}^{\mathrm{r}}$ and $s_{ji}^{\mathrm{p}}$ are the stoichoimetric coefficients of the reactant and product species, respectively, and γ_j is the macroscopic rate constant of R_j. Although we describe the method on a one-dimensional domain, it is worth noting that it is easy to extend this method in a higher dimensional domain. The examples in one- and two-dimensional domains will be discussed in the Simulation results section.

If the system is spatially inhomogeneous, then the domain is partitioned into K identical compartments with uniform length h, where h=L/K. The subsystem in each compartment is assumed to be homogeneous. Molecules in different compartments are treated as different species, denoted by {S₁₁,S₁₂,…,S_ki,…,S_KN}, where S_ki is the ith species in the kth compartment. The system state is denoted by

$$X(t)=(X_{11}(t),X_{12}(t),\dots ,X_{ki}(t),\dots ,X_{KN}(t)),$$

where X_ki is the number of molecules of S_ki.

Only molecules in the same compartment can react. The jth reaction in the kth compartment R_kj is as follows:

$$R_{kj}:s_{j1}^{\mathrm{r}}{S}_{k1}+\cdots +s_{jN}^{\mathrm{r}}{S}_{kN}\stackrel{{\gamma }_{kj}}{\to }{s}_{j1}^{\mathrm{p}}{S}_{k1}+\cdots +s_{jN}^{\mathrm{p}}{S}_{kN},$$

where γ_kj is the reaction rate constant of reaction R_kj.

Diffusion is treated as a reaction in which a molecule in one compartment jumps to one of its neighbouring compartments at a constant rate. Without loss of generality, we assume that only species S₁ diffuses in the algorithm description. Assume that species S₁ diffuses with the coefficient D₁ with reflective boundary conditions on the boundary of the domain. Then, the diffusive jumps obey the following chain reactions:

$$S_{11}\underset{D_1/h^2}{\overset{D_1/h^2}{\rightleftharpoons }}{S}_{21}\underset{D_1/h^2}{\overset{D_1/h^2}{\rightleftharpoons }}{S}_{31}\cdots \underset{D_1/h^2}{\overset{D_1/h^2}{\rightleftharpoons }}{S}_{N1}.$$

Multiple diffusive species can be easily treated using the same approach, and an example of such a case is presented in the Simulation results section.

Consider X(t) as a variable x, the probability that the reaction R_kj will fire in the next time interval [t,t+dt) is a_kj(x) dt, where a_kj is called the propensity function of R_kj. The state of the system transfers from one state to another through reaction firing. The net change of the state of the system caused by one occurrence of reaction R_kj is denoted as ν_kj and so

$${\nu }_{kj}=(0,\dots ,0,\underset{\mathrm{from}\hspace{0.17em}((k-1)N+1)\mathrm{th}\hspace{0.17em}\mathrm{to}\hspace{0.17em}kN\mathrm{th}}{\underbrace{s_{j1}^{\mathrm{p}}-s_{j1}^{\mathrm{r}},\dots ,s_{jN}^{\mathrm{p}}-s_{jN}^{\mathrm{r}}}},0,\dots ,0).$$

In addition, denote as a_kL(x) and a_kR(x) the propensity functions of diffusion jumps $J_{kL}:S_{k1}\to S_{(k-1)1}$ and $J_{kR}:S_{k1}\to S_{(k+1)1}$, respectively. Denote as ν_kL and ν_kR the net change of the state of the system caused by J_kR and J_kL, respectively. As diffusion is treated as mono-molecular reactions, we have

$$a_{kL}(x)=\frac{D_1}{h^2}{X}_{k1},\hspace{0.17em}\text{for }2<k\le K,\text{and}{a}_{kR}(x)=\frac{D_1}{h^2}{X}_{k1},\hspace{0.17em}\text{for }1\le k<K-1$$

and the elements of ν_iL and ν_iR equal 1, −1 or 0.

The chemical master equation (CME) that governs the temporal evolution of the probability density function p(x,t) that the state of the system is x at time t is as follows:

$$\begin{array}{rl}\frac{\mathrm{\partial }}{\mathrm{\partial }t}p(x,t)& =\underset{\mathrm{Left}\hspace{0.17em}\mathrm{jump}}{\underbrace{-\sum _{k=2}^K{a}_{kL}(x)p(x,t)+\sum _{k=2}^K{a}_{kL}(x-{\nu }_{kL})p(x-{\nu }_{kL},t)}}\\ & \underset{\mathrm{Right}\hspace{0.17em}\mathrm{jump}}{\underbrace{-\sum _{k=1}^{K-1}{a}_{kR}(x)p(x,t)+\sum _{k=1}^{K-1}{a}_{kR}(x-{\nu }_{kR})p(x-{\nu }_{kR},t)}}\\ & \underset{\mathrm{Reaction}}{\underbrace{-\sum _{k=1}^K\sum _{j=1}^M{a}_{kj}(x)p(x,t)+\sum _{k=1}^K\sum _{j=1}^M{a}_{kj}(x-{\nu }_{kj})p(x-{\nu }_{kj},t)}}.\end{array}$$ 2.1

2.2. Diffusion approximation

For most biological systems, the state space and the dimension of the CME are large or infinite, rendering the CME impossible to solve. The stochastic process underlying the CME can be simulated by the spatial SSA (details can be found in appendix A). Similar to the existing methods [14–17], the compartment size is first appropriately chosen such that diffusive jumps are usually more frequent than reactions because of the assumption of the homogeneity of reactions in each compartment. In the case of frequent diffusive jumps, the spatial SSA may become computationally inefficient. Here we shall approximate the diffusion processes using Gaussian random vectors with time-dependent means and covariances.

Given X(t₀)=x₀=(x₀₁₁,x₀₁₂,…,x_0ki,…,x_0KN), let n_kL(t) and n_kR(t) denote the numbers of leftward and rightward diffusive jumps of molecules from the kth compartment between time t₀ and time t. Under the assumption that a large number of diffusive jumps occurs between reactions in each compartment, we can approximate the numbers of diffusive jumps as follows:

$$\frac{n_{kL}(t)}{\mathit{\Lambda }}={\varphi }_{kL}(t)+\frac{{\xi }_{kL}}{\sqrt{\mathit{\Lambda }}}+O\left(\frac{1}{\mathit{\Lambda }}\right)$$ 2.2

and

$$\frac{n_{(k-1)R}(t)}{\mathit{\Lambda }}={\varphi }_{(k-1)R}(t)+\frac{{\xi }_{(k-1)R}}{\sqrt{\mathit{\Lambda }}}+O\left(\frac{1}{\mathit{\Lambda }}\right),$$ 2.3

for k=2,3,…,K. The functions ϕ_kL(t) and ϕ_kR(t) characterize the macroscopic features of the diffusive jumps. When the copy number of molecules is large enough, the system of the average of molecule concentration will approach a deterministic diffusion system. The macroscopic features of the diffusive jumps are determined by the solution of the deterministic system. The second terms ξ_kL and ξ_kR are real random numbers, measuring the fluctuations around ϕ_kL(t) and ϕ_kR(t). The means of these random numbers are zero and the covariances can be determined by the formula presented later in this section. The constant Λ is the number of molecules per unit concentration in a compartment. For example, if the concentration 1 μM corresponds to 600 molecules in each compartment, then Λ=600 μM⁻¹. When Λ≫1, ϕ_kL(t) and ϕ_kR(t) are considered to be continuous functions of t.

Let Π(ξ_1L,ξ_2L,ξ_2R,…,ξ_nL,t) be the probability density function of ξ_1L, ξ_2L, ξ_2R,…,ξ_nL at time t. The function Π for molecule concentrations can be obtained from a rescaling of the probability density function p, which is for the number of molecules. The formula for Π is as follows:

$$\mathit{\Pi }({\xi }_{1L},{\xi }_{2L},{\xi }_{2R},\dots ,{\xi }_{nL},t)=\frac{1}{{\mathit{\Lambda }}^{2n-2}}p(x_0+\sum _{k=1}^{K-1}{n}_{kR}{\nu }_{kR}+\sum _{k=2}^K{n}_{kL}{\nu }_{kL},t|x_0,t_0),$$

where p(x,t | x₀,t₀) is the probability density function that the state of the system is x at time t with the condition X(t₀)=x₀.

By performing the standard systematic expansion of the master equation equation (2.1) [29], we obtain the following equation:

$$\begin{array}{rl}& \frac{\mathrm{\partial }\mathit{\Pi }}{\mathrm{\partial }t}-\sqrt{\mathit{\Lambda }}(\frac{\mathrm{\partial }\mathit{\Pi }}{\mathrm{\partial }{\xi }_{1R}},\frac{\mathrm{\partial }\mathit{\Pi }}{\mathrm{\partial }{\xi }_{2L}},\dots ,\frac{\mathrm{\partial }\mathit{\Pi }}{\mathrm{\partial }{\xi }_{KL}})\cdot (\frac{\mathrm{\partial }{\varphi }_{1R}(t)}{\mathrm{\partial }t},\frac{\mathrm{\partial }{\varphi }_{2L}(t)}{\mathrm{\partial }t},\dots ,\frac{\mathrm{\partial }{\varphi }_{KL}(t)}{\mathrm{\partial }t})\\ & =\sqrt{\mathit{\Lambda }}[-\frac{D_1}{h^2}(c_{0_{11}}-{\varphi }_{1R}+{\varphi }_{2L})\frac{\mathrm{\partial }\mathit{\Pi }}{\mathrm{\partial }{\xi }_{1R}}-\frac{D_1}{h^2}(c_{0_{K1}}-{\varphi }_{KL}+{\varphi }_{(K-1)R})\frac{\mathrm{\partial }\mathit{\Pi }}{\mathrm{\partial }{\xi }_{KL}}\\ & -\frac{D_1}{h^2}\sum _{k=2}^{K-1}(c_{0_{k1}}-{\varphi }_{kR}-{\varphi }_{kL}+{\varphi }_{(k+1)L}+{\varphi }_{(k-1)R})\frac{\mathrm{\partial }\mathit{\Pi }}{\mathrm{\partial }{\xi }_{kR}}\\ & -\frac{D_1}{h^2}\sum _{k=2}^{K-1}(c_{0_{k1}}-{\varphi }_{kR}-{\varphi }_{kL}+{\varphi }_{(k+1)L}+{\varphi }_{(k-1)R})\frac{\mathrm{\partial }\mathit{\Pi }}{\mathrm{\partial }{\xi }_{kL}}]\\ & +\frac{D_1}{h^2}\sum _{k=1}^{K-1}\frac{\mathrm{\partial }}{\mathrm{\partial }{\xi }_{kR}}({\xi }_{kR}\mathit{\Pi }-{\xi }_{(k+1)L}\mathit{\Pi })+\frac{D_1}{h^2}\sum _{k=2}^{K-1}\frac{\mathrm{\partial }}{\mathrm{\partial }{\xi }_{kR}}({\xi }_{kL}\mathit{\Pi }-{\xi }_{(k-1)R}\mathit{\Pi })\\ & +\frac{D_1}{h^2}\sum _{k=2}^K\frac{\mathrm{\partial }}{\mathrm{\partial }{\xi }_{kL}}({\xi }_{kL}\mathit{\Pi }-{\xi }_{(k-1)R}\mathit{\Pi })+\frac{D_1}{h^2}\sum _{k=2}^{K-1}\frac{\mathrm{\partial }}{\mathrm{\partial }{\xi }_{kL}}({\xi }_{kR}\mathit{\Pi }-{\xi }_{(k+1)L}\mathit{\Pi })\\ & +\frac{D_1}{2h^2}\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{\xi }_{1R}^2}\left((c_{0_{11}}-{\varphi }_{1R}+{\varphi }_{2L})\mathit{\Pi }\right)+\frac{D_1}{2h^2}\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{\xi }_{KL}^2}((c_{0_{K1}}-{\varphi }_{KL}+{\varphi }_{(K-1)R})\mathit{\Pi })\\ & +\frac{D_1}{2h^2}\sum _{k=2}^{K-1}\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{\xi }_{kR}^2}((c_{0_{k1}}-{\varphi }_{kR}-{\varphi }_{kL}+{\varphi }_{(k+1)L}+{\varphi }_{(k-1)R})\mathit{\Pi })\\ & +\frac{D_1}{2h^2}\sum _{k=2}^{K-1}\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{\xi }_{kL}^2}((c_{0_{k1}}-{\varphi }_{kR}-{\varphi }_{kL}+{\varphi }_{(k+1)L}+{\varphi }_{(k-1)R})\mathit{\Pi })\\ & -\sum _{l=1}^K\sum _{j=1}^M{a}_{lj}\left(\mathit{\Lambda }(c_0+\sum _{k=1}^{K-1}{\varphi }_{kR}{\nu }_{kR}+\sum _{k=2}^K{\varphi }_{kL}{\nu }_{kL})\right)\mathit{\Pi }+O\left(\frac{1}{\sqrt{\mathit{\Lambda }}}\right),\end{array}$$

where c₀=(c₀₁₁,c₀₁₂,…,c_0KN)=x₀/Λ. Assuming

$$\mathit{\Lambda }\gg 1\text{and}\underset{1\le j\le M,1\le k\le K}{max}{a}_{kj}\ll \frac{D_1}{h^2}\underset{1\le k\le K-1}{min}\{\frac{\mathrm{\partial }\mathit{\Pi }}{\mathrm{\partial }{\xi }_{kR}},\frac{\mathrm{\partial }\mathit{\Pi }}{\mathrm{\partial }{\xi }_{(k+1)L}}\},$$ 2.4

and comparing the order term $\sqrt{\mathit{\Lambda }}$, we have

$$\begin{array}{rl}& \frac{\mathrm{\partial }}{\mathrm{\partial }t}\left(\begin{array}{c}{\varphi }_{1R}\\ {\varphi }_{2L}\\ {\varphi }_{2R}\\ ⋮\\ {\varphi }_{KL}\end{array}\right)=\frac{D_1}{h^2}\left(\begin{array}{c}{c}_{0_{11}}-{\varphi }_{1R}+{\varphi }_{2L}\\ c_{0_{21}}-{\varphi }_{2R}-{\varphi }_{2L}+{\varphi }_{3L}+{\varphi }_{1R}\\ c_{0_{21}}-{\varphi }_{2R}-{\varphi }_{2L}+{\varphi }_{3L}+{\varphi }_{1R}\\ ⋮\\ c_{0_{K1}}-{\varphi }_{KL}+{\varphi }_{(K-1)R}\end{array}\right),\\ & {({\varphi }_{1R},{\varphi }_{2L},{\varphi }_{2R},\dots ,{\varphi }_{KL})}^{\prime }=0\text{at }t=t_0.\end{array}$$

Letting

$${\mathit{\Pi }}_s=\mathit{\Pi }\exp (-{\int }_{t_0}^t\sum _{l=1}^K\sum _{j=1}^M{a}_{lj}\left(\mathit{\Lambda }(c_0+\sum _{k=1}^{K-1}{\varphi }_{kR}(\tau ){\nu }_{kR}+\sum _{k=2}^K{\varphi }_{kL}(\tau ){\nu }_{kL})\right)\mathrm{d}\tau )$$ 2.5

and defining the vector variable (y₁,y₂,y₃,…,y_2K−2)′=(ξ_1R,ξ_2L,ξ_2R,…,ξ_KR)′, we obtain the following Fokker–Planck equation:

$$\frac{\mathrm{\partial }{\mathit{\Pi }}_s}{\mathrm{\partial }t}=-\sum _{i,j}{A}_{ij}\frac{\mathrm{\partial }}{\mathrm{\partial }{y}_i}(y_j{\mathit{\Pi }}_s)+\frac{1}{2}\sum _{i,j}{B}_{ij}(t)\frac{{\mathrm{\partial }}^2{\mathit{\Pi }}_s}{\mathrm{\partial }{y}_i\mathrm{\partial }{y}_j}+O\left(\frac{1}{\mathit{\Lambda }}\right),$$

where

$$A=\frac{D_1}{h^2}\left(\begin{array}{ccc}-1& 1& \\ 1& -1& -1& 1& \\ 1& -1& -1& 1& \\ & & 1& -1& -1& 1& \\ & & 1& -1& -1& 1& & \\ & & & \ddots & \ddots & \ddots & \ddots & \\ & & & & 1& -1& -1& 1\\ & & & & 1& -1& -1& 1\\ & & & & & & 1& -1\end{array}\right)$$

and

$$B(t)=\frac{D_1}{h^2}\left(\begin{array}{ccccc}{c}_{0_{11}}-{\varphi }_{1R}+{\varphi }_{2L}& & & & \\ & c_{0_{21}}-{\varphi }_{2R}-{\varphi }_{2L}+{\varphi }_{1R}+{\varphi }_{3L}& & & \\ & & c_{0_{21}}-{\varphi }_{2R}-{\varphi }_{2L}+{\varphi }_{1R}+{\varphi }_{3L}& & \\ & & & \ddots & \\ & & & & c_{0_{K1}}-{\varphi }_{KL}+{\varphi }_{(K-1)R}\end{array}\right).$$

So the corresponding covariance matrix is

$$\rho ={\int }_0^{t}Y(t)Y^{-1}(\tau )B(\tau ){(Y^{-1}(\tau ))}^{\prime }Y{(t)}^{\prime }\hspace{0.17em}\mathrm{d}\tau ,$$

where $Y(t)=\exp (At)$.

This approximation is valid under the assumption (2.4), which is true when the number of diffusive molecules and the value of diffusion coefficient are large. Overall, we approximate the numbers of diffusive jumps by obtaining (i) the macroscopic features of the diffusive jumps, Φ:=(ϕ_1R,ϕ_2L,ϕ_2R,…,ϕ_KL)′; (ii) the distributions of the fluctuations, Ξ:=(ξ_1L,ξ_2L,ξ_2R,…,ξ_KL)′ and (iii) the probability, P_R(t), that no reaction will occur until time t. These three components can be solved as follows:

1. Φ satisfies the following equations:

   $$\begin{array}{rl}& \frac{\mathrm{d}\mathit{\Phi }}{\mathrm{d}t}=A\mathit{\Omega }+\left(\frac{D_1}{h^2}\right)C\\ \text{and}& \mathit{\Omega }=0\text{at }t=t_0,\end{array}\}$$ 2.6

   where C=(x₀₁₁,x₀₂₁,…,x_0k1,…,x_0K1)′/Λ. Based on the study of Othmer & Scriven [30], the eigenvalues and eigenvectors of A can be obtained analytically and used to solve the system directly.
2. Ξ is a Gaussian random vector with a mean of zero and a covariance of

   $$\rho ={\int }_0^{t}Y(t)Y^{-1}(\tau )B(\tau ){(Y^{-1}(\tau ))}^{\prime }Y{(t)}^{\prime }\hspace{0.17em}\mathrm{d}\tau ,$$ 2.7

   where $Y(t)=\exp (At)$ and B(t)=diag(∂Φ/∂t) is a diagonal matrix with the diagonal elements equal to ∂Φ/∂t.
3. P_R(t) takes the form

   $$P_{\mathrm{R}}(t)=\exp (-{\int }_{t_0}^t\sum _{l=1}^K\sum _{j=1}^M{a}_{lj}(x_0+\mathit{\Lambda }\sum _{k=1}^{K-1}{\varphi }_{kR}(\tau )v_{kR}+\mathit{\Lambda }\sum _{k=2}^K{\varphi }_{kL}(\tau ){\nu }_{kL})\mathrm{d}\tau ),$$

   where a_lj is the propensity function of reaction R_lj for l=1,2,…,K and j=1,2,…,M.

2.3. Adaptivity of the time step and the spatial partitioning of the compartments

To determine the next time step after time t₀, we generate a random number r that is uniformly distributed in [0,1] and find t such that P_R(t)=r. To update the numbers of diffusive jumps at time t, we calculate Φ and generate Ξ, a random vector that has a multivariate normal distribution with a mean of zero and a covariance of ρ. However, because t is chosen as a random number, the interval between t and t₀ might be short; this would allow only a small number of diffusive jumps to occur among compartments with a low copy number of molecules, leading to poor accuracy of the Gaussian approximation. In such compartments where the Gaussian approximation fails due to a low copy number of molecules, we simulate the diffusive jumps using the SSA method. To determine which compartments fit this criterion, we compare the Poisson distribution with mean μ to the Gaussian distribution with mean μ and variance μ. It is known that as μ increases, the difference between the two distributions decreases. For example, when μ is larger than 10, we have

$$\underset{n\ge 0}{max}|\frac{1}{\sqrt{2\pi \mu }}\exp [-\frac{{(n-\mu )}^2}{2\mu }]-\frac{\exp (-\mu ){\mu }^n}{n!}|\le \mathrm{0.01.}$$ 2.8

Therefore, we apply the SSA method for diffusion in those compartments where the mean number of diffusive jumps is small (e.g. fewer than 10). For the case in which the amount of species S₁ decreases monotonically towards the Kth compartment in the deterministic model, we use the SSA method in all compartments with an index larger than or equal to k_g(t), which is the smallest integer such that

$$\mathit{\Lambda }{\varphi }_{k_g(t)L}(t)\le T_A\text{or}\mathit{\Lambda }{\varphi }_{k_g(t)R}(t)\le T_A,$$ 2.9

where Λϕ approximates the mean value of diffusive jump and T_A is the cut-off threshold for determining the region for the Gaussian approximation. We set T_A=10 to ensure that the absolute difference between the Poisson and Gaussian distributions is less than 0.01, as seen in (2.8). When T_A increases, the SSA is applied in more compartments and it may increase the CPU time cost in our hybrid method. For two or more types of diffusive molecules, we can still apply (2.9) as long as the diffusion process of each type of molecules is independent of each other. As a result, different types of diffusive molecules have different k_g values.

2.4. Algorithm overview

Given x(t₀)=x₀, we perform the following steps:

1. Generate two independent random numbers r₁ and r₂ that are uniformly distributed in [0,1].

2. Find t such that P_R(t)=r₁

   and let

   $${\overline{\alpha }}_{lj}={\int }_{t_0}^t{a}_{lj}(x_0+\mathit{\Lambda }\sum _{k=1}^{K-1}{\varphi }_{kR}(\tau )v_{kR}+\mathit{\Lambda }\sum _{k=2}^K{\varphi }_{kL}(\tau ){\nu }_{kL})\mathrm{d}\tau .$$
3. Evaluate k_g using equation (2.9) to determine the compartments for which the SSA method will be used. If k_g=1, simulate diffusion in all compartments using the SSA method; if k_g>1, perform the following steps:

   • (a) simulate diffusion between the k_gth compartment and the Kth compartment using the SSA method, and treat the k_gth compartment as a reflective boundary;
   • (b) calculate Φ and ρ in equation (2.6) and equation (2.7) at time t; remove rows 2k_g−2,2k_g−1,…,2K−2 and columns 2k_g−2,2k_g−1,…,2K−2 in the matrix ρ, and let ρ_s be the remaining submatrix;
   • (c) generate a (2k_g−3)-variate Gaussian random vector Ξ with a mean of zero and a covariance of ρ_s;
   • (d) evaluate n_kL and n_kR in equations (2.2) and (2.3) at time t, and update x_k1 using n_kL and n_kR for 1≤k≤k_g−2;
   • (e) add n_(kg−2)R−n_(kg−1)L−n_(kg−1)R+Λϕ_kgL to x_(kg−1)1, and add n_(kg−1)R−Λϕ_kgL to x_kg1; and
   • (f) round the x_k1 values to their nearest non-negative integers.
4. Find the smallest values of m and q such that

   $$\sum _{l=1}^{q-1}\sum _{j=1}^M{\overline{\alpha }}_{lj}+\sum _{j=1}^m{\overline{\alpha }}_{qj}\ge r_2\sum _{l=1}^K\sum _{j=1}^M{\overline{\alpha }}_{lj}.$$

   Then, let the mth reaction occur in the qth compartment, and update x in accordance with reaction R_qm.

5. Advance the time to t. Then, go back to step 1 until the simulation time reaches the stop criterion.

In this algorithm, the calculations of ${\overline{\alpha }}_{lj}$ in step 2 and ρ in step 3(b) are the most computationally expensive steps among all steps. ${\overline{\alpha }}_{lj}$ and ρ can be estimated using simple numerical integration quadratures such as the trapezoidal rule, which we use in the test cases presented below. In step 3(b), Φ can be solved directly and efficiently using the eigenvalues and eigenvectors of A. Negative values and non-integers may appear in the Gaussian approximation so we round the values to their nearest non-negative integers in step 3(f). This step may lead to loss of mass. However, the error introduced by this rounding can be reduced by increasing the number of molecules.

3. Simulation results

In this section, we will compare the performance of the hybrid method and the SSA using different morphogen models. First a one-dimensional simple morphogen system with different values of diffusion coefficients is considered. Next, we extend our study to a morphogen–receptor system, a morphogen system containing two types of diffusive molecules, a two-dimensional morphogen system and a Turing system to show that the results are consistent with the one-dimensional simple morphogen system we consider in the first part. All the numerical tests are implemented in Matlab.

3.1. Example I: morphogen system with linear degradation

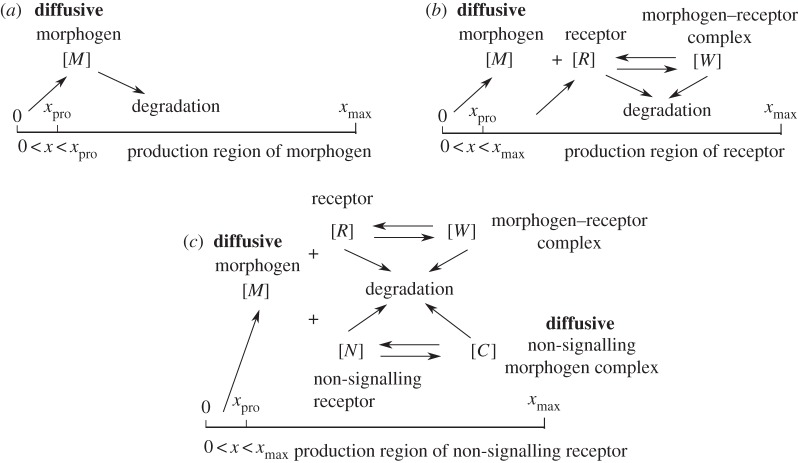
First, we consider a one-dimensional morphogen system in which morphogens diffuse out from a local production region and undergo degradation throughout the entire domain (figure 1a). This model was used to study the stochastic effect on patterning of the Drosophila wing disc [31,32]. The deterministic dynamics of morphogen concentration [M] can be described by the following PDE system with no-flux boundary conditions:

$$\frac{\mathrm{\partial }[M]}{\mathrm{\partial }t}=D_{\mathrm{M}}\frac{{\mathrm{\partial }}^2[M]}{\mathrm{\partial }{x}^2}-d_{\mathrm{M}}[M]+V(x),$$

where D_M is the diffusion coefficient, d_M is the degradation rate coefficient and V (x) is the production rate of morphogen. We define the production rate as

$$V(x)=v_{\mathrm{M}}\hspace{0.17em}\text{if }0\le x\le x_{\mathrm{pro}};V(x)=0\hspace{0.17em}\text{if }{x}_{\mathrm{pro}}<x\le x_{max}.$$

The one-dimensional domain $[0,x_{max}]$ is divided into 100 compartments with 2 μm width which is based on the cell size of the Drosophila wing disc, so that the domain size we consider is $x_{max}=200\hspace{0.17em}\text{μ}\mathrm{m}$. The initial condition for simulations is [M](0,x)=V (x)/d_M. The parameters are listed in table 1.

Figure 1.

Morphogen models used for numerical tests in examples I–IV. (a) Examples I and IV: morphogen system with linear degradation. (b) Example II: morphogen–receptor system. (c) Example III: morphogen system with two types of diffusive molecules.

Table 1.

List of parameter values used in examples I–IV. The values are based on [32].

parameters	definitions	values
DM	diffusion coefficient of free morphogens	5 μm2 s−1−40 μm2 s−1
DC	diffusion coefficient of morphogen–receptor complexes	5 μm2 s−1−10 μm2 s−1
vM	production rate of morphogens	10−4 μM s−1
vR	production rate of receptors	10−4 μM s−1
vN	production rate of non-signalling receptors	2×10−4 μM s−1
dM	degradation rate coefficient of morphogens	10−2 s−1
dR	degradation rate coefficient of receptors	10−4 s−1
dN	degradation rate coefficient of non-signalling receptors	10−4 s−1
dW	degradation rate coefficient of receptors	10−4 s−1
dC	degradation rate coefficient of non-signalling receptors	10−4 s−1
α1	binding rate coefficient for morphogen–receptor complexes	5×10−2 μM s−1
β1	dissociation rate coefficient for morphogen–receptor complexes	5×10−4 μM s−1
α2	binding rate coefficient for morphogen–non-receptor complexes	5×10−2 μM s−1
β2	dissociation rate coefficient for morphogen–non-receptor complexes	5×10−4 μM s−1
ΛM	number of morphogens per unit concentration in a compartment	1.8×104 μM−1
ΛR (ΛN)	number of receptors (non-receptors) per unit concentration in a compartment	2×102 μM−1
xpro	size of morphogen production region	14 μm

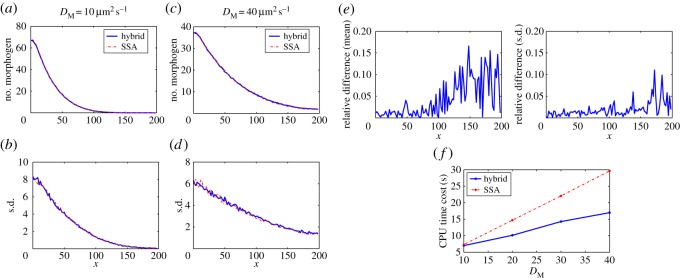
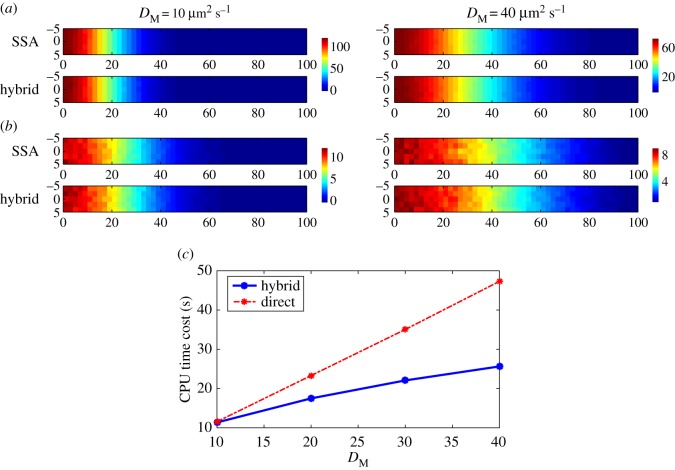
Figure 2a–d displays the means and standard deviations of the number of morphogens in each compartment at simulation time 100 s, based on both the SSA and the hybrid method with different diffusion coefficients D_M=10 μm² s⁻¹ and D_M=40 μm² s⁻¹. In the results, 500 simulations were used to calculate the statistical quantities for each case.

Figure 2.

Simulation results for example I with different values of D_M. In the results, 500 simulations were used to calculate the statistical quantities for each case. The parameters are listed in table 1. (a,b) Model with diffusion coefficient 10 μm² s⁻¹: (a) means of the number of morphogens and (b) standard deviations of the number of morphogens. (c–d) Model with diffusion coefficient 40 μm² s⁻¹: (c) means of the number of morphogens and (d) standard deviations of the number of morphogens. (e) Relative differences of means and standard deviations for the simulations with diffusion coefficient 40 μm² s⁻¹. (f) CPU time costs for two stochastic methods with different values of diffusion coefficients.

As observed in figure 2a–d, there is good agreement between the results of the two methods throughout the simulations. For systematic comparison, we calculate the relative differences between the simulations by the SSA and the hybrid method, (M_SSA−M_Hybrid)/M_SSA. Figure 2e shows that the relative differences of means and standard deviations are less than 0.15 when D_M=40 μm² s⁻¹. Then we calculate the averages of CPU time costs in the 500 simulations of each case. Figure 2f shows that the CPU time cost of the SSA is linearly increasing with the value of D_M, and is much higher than the cost of the hybrid method when D_M=40 μm² s⁻¹. Although the CPU time cost of the hybrid method is also increasing with the value of D_M, the increasing rate is much lower than the SSA. When the diffusion coefficient D_M increases, the morphogen system becomes a diffusion-dominant system that highlights the advantage of the diffusion approximation which allows a larger time step for each time iteration in our hybrid method.

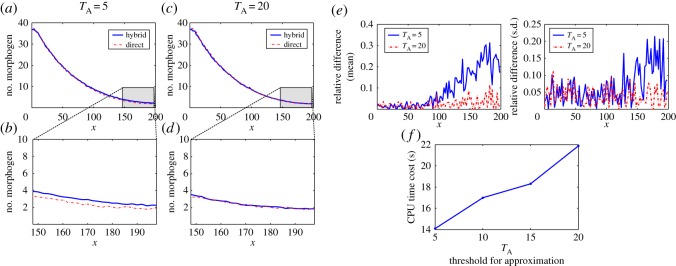
Other than changing the value of the diffusion coefficient D_M, we test how the value of T_A in (2.9) affects the CPU time cost and the performance of the hybrid method. For the simulations in figure 3, we apply the setting used in figure 2, but with different values of T_A. The simulations in figure 3a–d show that the accuracy of the hybrid method improves when T_A increases. Figure 3e displays that the relative differences of means and standard deviations between the simulations by the hybrid method and the SSA decrease significantly in the region of low copy number of molecules when T_A increases from 5 to 20. By contrast, figure 3f shows a trade-off in which the CPU time cost is increasing with the value of T_A.

Figure 3.

Simulation results for example I with different values of T_A in (2.9). In the results, 500 simulations were used to calculate the statistical quantities for each case. The parameters are listed in table 1 and D_M= 40 μm² s⁻¹. (a–b) Model with T_A=5: (a) means of the number of morphogens and (b) means of the number of morphogens in the region of lower copy number of morphogens. (c–d) Model with T_A=20: (c) means of the number of morphogens and (d) means of the number of morphogens in the region of lower copy number of morphogens. (e) Relative differences of means and standard deviations for the simulations with T_A=5 and T_A=20. (f) CPU time costs for the hybrid methods with different values of T_A.

3.2. Example II: morphogen–receptor system

Here we consider a one-dimensional morphogen–receptor system in which receptors are produced in the entire region and bind with morphogen to induce morphogen degradation (figure 1b). This model involves the stochastic effect in a binding process between two kinds of molecules [32,33]. The deterministic dynamics of three kinds of molecule concentrations (morphogen [M], receptor [R] and morphogen–receptor complex [W]) can be described by the following PDE system with no-flux boundary conditions:

$$\begin{array}{rl}\frac{\mathrm{\partial }[M]}{\mathrm{\partial }t}& =D_{\mathrm{M}}\frac{{\mathrm{\partial }}^2[M]}{\mathrm{\partial }{x}^2}-{\alpha }_1[M][R]+{\beta }_1[W]+V(x),\\ \frac{\mathrm{\partial }[R]}{\mathrm{\partial }t}& =-{\alpha }_1[M][R]+{\beta }_1[W]-d_{\mathrm{R}}[R]+v_{\mathrm{R}},\\ \mathrm{and}\frac{\mathrm{\partial }[W]}{\mathrm{\partial }t}& ={\alpha }_1[M][R]-{\beta }_1[W]-d_{\mathrm{W}}[W].\end{array}$$

The morphogen production function V (x), the domain and its discretization are defined as in example I. The initial conditions for simulations are [M](0,x)=V (x)/d_M, [R](0,x)=V _R/d_R and [W](0,x)=0. The parameters are listed in table 1.

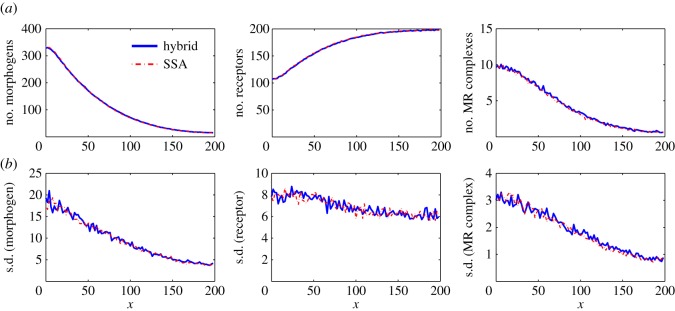
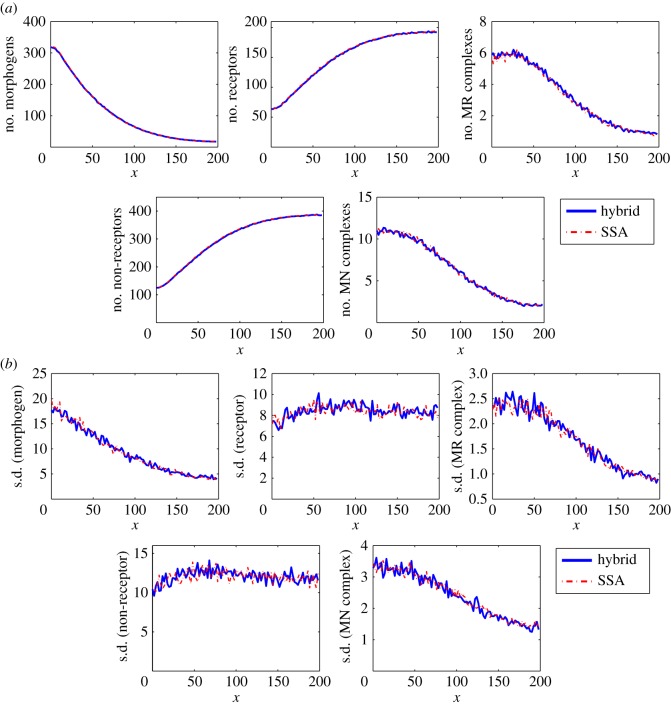
Figure 4 displays the means and standard deviations of the numbers of morphogens, receptors and morphogen–receptor complexes in each compartment at simulation time 1000 s, based on both the SSA and the hybrid method with D_M=5 μm² s⁻¹. In this case, 200 simulations were used to calculate the statistical quantities. The means calculated using both stochastic methods agree well with each other, and the standard deviations are consistent between the two stochastic methods. The simulation results with D_M=10 μm² s⁻¹ and D_M=20 μm² s⁻¹ also have good agreement between the SSA and the hybrid method. For studying time cost, we calculate the averages of CPU time costs in the 200 simulations of each case. Table 2 shows that the CPU time cost of the SSA is much higher than the cost of the hybrid method when D_M=5 μm² s⁻¹, 10 μm² s⁻¹ or 20 μm² s⁻¹. In particular, the CPU time cost of the hybrid method is around 20% of that of the SSA when D_M=20 μm² s⁻¹.

Figure 4.

Simulation results for example II. (a) Means of the numbers of morphogens, receptors and morphogen–receptor complexes. (b) The corresponding standard deviations. In the results, 200 simulations were used to calculate the statistical quantities for each case. In this simulation, we take D_M= 5 μm² s⁻¹ and the remaining parameters are listed in table 1.

Table 2.

CPU time cost of SSA and hybrid methods for examples II–III.

	example II			example III
DM(μm2 s−1)	5	10	20	5	10	20
DC(μm2 s−1)	—	—	—	5	10	20
CPU time (SSA)	251.6 s	495.5 s	949.8 s	757.0 s	1481.2 s	2868.4 s
CPU time (hybrid)	126.3 s	177.7 s	187.6 s	457.8 s	703.6 s	926.7 s

3.3. Example III: morphogen system with two types of diffusive molecules

In this example, we want to study the performance of the hybrid method for the system with two types of diffusive molecules. Many studies on morphogen system were based on reaction–diffusion models with only one diffusion term in either free or non-signalling bound-morphogens [31–33]. However, this type of one-diffusion model is not biologically complete because it is possible to have more than one type of diffusion transport. Morphogen models with two types of diffusive molecules have been proposed and studied in [34–36]. Here we consider a morphogen model with both diffusion of free morphogens and movement of non-signalling morphogen complexes through a ‘bucket brigade’ process [35] (figure 1c). The deterministic dynamics of five kinds of molecule concentrations (morphogen [M], receptor [R], non-signalling receptor [N], morphogen–receptor complex [W] and diffusive non-signalling morphogen complex [C]) can be described by the following PDE system with no-flux boundary conditions:

$$\begin{array}{rl}\frac{\mathrm{\partial }[M]}{\mathrm{\partial }t}& =D_{\mathrm{M}}\frac{{\mathrm{\partial }}^2[M]}{\mathrm{\partial }{x}^2}-{\alpha }_1[M][R]+{\beta }_1[W]-{\alpha }_2[M][N]+{\beta }_2[C]+V(x),\\ \frac{\mathrm{\partial }[R]}{\mathrm{\partial }t}& =-{\alpha }_1[M][R]+{\beta }_1[W]-d_{\mathrm{R}}[R]+v_{\mathrm{R}},\\ \frac{\mathrm{\partial }[W]}{\mathrm{\partial }t}& ={\alpha }_1[M][R]-{\beta }_1[W]-d_W[W],\\ \frac{\mathrm{\partial }[N]}{\mathrm{\partial }t}& =-{\alpha }_2[M][N]+{\beta }_2[C]-d_{\mathrm{N}}[N]+v_{\mathrm{N}},\\ \text{and}\frac{\mathrm{\partial }[C]}{\mathrm{\partial }t}& =D_{\mathrm{C}}\frac{{\mathrm{\partial }}^2[C]}{\mathrm{\partial }{x}^2}+{\alpha }_2[M][N]-{\beta }_2[C]-d_{\mathrm{C}}[C].\end{array}$$

Similar to the previous examples, the morphogen production function V (x), the domain and its discretization are defined as in example I. The initial conditions for simulations are [M](0,x)=V (x)/d_M, [R](0,x)=V _R/d_R, [W](0,x)=0, [N](0,x)=V _N/d_N and [C](0,x)=0. The parameters are listed in table 1.

Figure 5 reveals that the statistical quantities obtained using the hybrid method agree well with those obtained using the SSA with diffusion coefficients D_M=D_C=5 μm² s⁻¹ at simulation time 2000 s. Table 2 displays the CPU cost of the hybrid method is only 60%, 48% and 32% of that of the SSA when the diffusion coefficients are $D_{\mathrm{M}}=D_{\mathrm{C}}=5\hspace{0.17em}\text{μ}{\mathrm{m}}^2\hspace{0.17em}{\mathrm{s}}^{-1}$, $D_{\mathrm{M}}=D_{\mathrm{C}}=10\hspace{0.17em}\text{μ}{\mathrm{m}}^2\hspace{0.17em}{\mathrm{s}}^{-1}$ and $D_{\mathrm{M}}=D_{\mathrm{C}}=20\hspace{0.17em}\text{μ}{\mathrm{m}}^2\hspace{0.17em}{\mathrm{s}}^{-1}$, respectively. Our hybrid method works very well for such systems with more than one type of diffusive molecules.

Figure 5.

Simulation results for example III. (a) Means of the numbers of morphogens, receptors, morphogen–receptor complexes, non-signalling receptors and diffusive non-signalling morphogen complexes. (b) The corresponding standard deviations. In the results, 200 simulations were used to calculate the statistical quantities. In this simulation, we take $D_{\mathrm{M}}=D_{\mathrm{C}}=5\hspace{0.17em}\text{μ}{\mathrm{m}}^2\hspace{0.17em}{\mathrm{s}}^{-1}$ and the remaining parameters are listed in table 1.

3.4. Example IV: two-dimensional morphogen system

Here, we study the performance of hybrid method for a two-dimensional morphogen system which is based on example I (figure 1a). The two-dimensional domain $[0,x_{max}]\times [-y_{max},y_{max}]$ is divided into 250 compartments with uniform dimension 2×2 μm, which is based on the cell size of Drosophila wing disc. The domain size we consider is $x_{max}=100\hspace{0.17em}\text{μ}\mathrm{m}$ and $y_{max}=5\hspace{0.17em}\text{μ}\mathrm{m}$. We define the morphogen production function as

$$V(x,y)=v_{\mathrm{M}}\hspace{0.17em}\text{if }0\le x\le x_{\mathrm{pro}};V(x)=0\hspace{0.17em}\text{if }{x}_{\mathrm{pro}}<x\le x_{max}.$$ 3.1

The initial condition for simulations is [M](0,x,y)=V (x,y)/d_M. The parameters for this example are equal to the set we used in example I. Five hundred simulations were used to calculate the statistical quantities. In this case, the number of morphogens decreases monotonically along the x-axis in the deterministic model, so the condition (2.9) is applied on x-direction.

Figure 6a,b displays the means and standard deviations of the number of molecules in each 2 μm×2 μm compartment at simulation time 10 s, based on both the SSA and the hybrid method with different diffusion coefficients D_M=10 μm² s⁻¹ and D_M=40 μm² s⁻¹. The figures support that the two stochastic methods have good agreement in two-dimensional simulations. This result is consistent with the one-dimensional simulations shown in figure 2. The CPU time cost of the SSA is linearly increasing with the value of D_M, and the cost of the hybrid method is around 50% of the SSA when D_M=40 μm² s⁻¹ (figure 6c).

Figure 6.

Simulation results for example IV. (a) Means of the numbers of morphogens for the system with D_M=5 μm² s⁻¹ and D_M= 40 μm² s⁻¹. (b) The corresponding standard deviations. (c) CPU time costs for different methods and different values of diffusion coefficients. In the results, 200 simulations were used to calculate the statistical quantities for each case. Other than the diffusion coefficient, the remaining parameters are listed in table 1.

3.5. Example V: non-monotone pattern

In general, the adaptive method can be applied for some types of non-monotone pattern. Similar to example I, when the morphogen production region is considered at the centre of the domain as

$$V(x)=v_{\mathrm{M}}\hspace{0.17em}\text{if }94\le x\le 106;V(x)=0\text{ otherwise},$$

in the one-dimensional domain [0,200], the same setting used in example I can generate a single-peak solution as in figure 7a. We reformulate the condition (2.9) by considering the largest region [k_g1,k_g2] near the peak such that for all j∈[k_g1,k_g2], we have

$$\mathit{\Lambda }{\varphi }_{jL}(t)>T_A\text{or}\mathit{\Lambda }{\varphi }_{jR}(t)>T_A.$$ 3.2

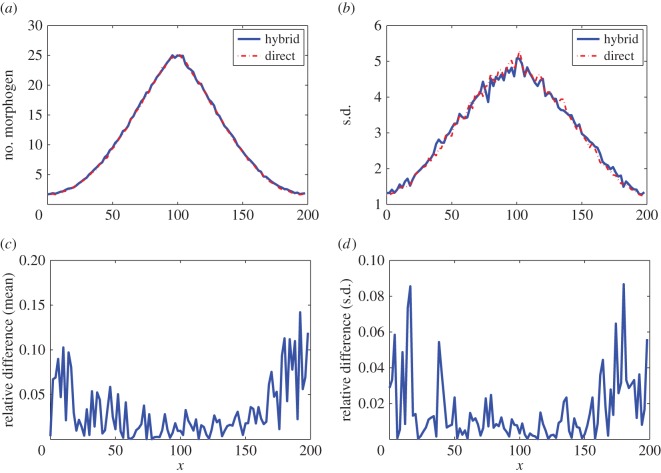
This condition ensures the accuracy of the Gaussian approximation in the region at the centre. Figure 7a,b displays the means and standard deviations of the number of molecules in each compartment at simulation time 20 s with D=40 μm² s⁻¹. In the results, 500 simulations were used to calculate the statistical quantities for each case. Figure 7c,d shows that the relative differences of means and standard deviations between the simulations by the hybrid method and the SSA are less than 0.15. For efficiency, the CPU time cost of the hybrid method is around 57% of that of the SSA. The adaptive method can be extended to patterns consisting of multiple peaks if the peaks can be determined by the deterministic system.

Figure 7.

Simulation results for example V in which the morphogen production region is located at the centre of the domain. In the results, 500 simulations were used to calculate the statistical quantities for each case. The parameters are listed in table 1 and D_M=40 μm² s⁻¹. (a) Means of the number of morphogens. (b) Standard deviations of the number of morphogens. (c) Relative differences of means for the simulations by the SSA and the hybrid method. (d) Relative differences of standard deviations for the simulations by the SSA and the hybrid method.

3.6. Example VI: Turing system

In the last example, we consider an activator-substrate Turing system consisting of a short-range diffusion for the activator and a long-range diffusion for the substrate. The normalized one-dimensional activator-substrate Turing system [37] can be described by the following two-equation system with the no-flux boundary conditions:

$$\begin{array}{rl}\frac{\mathrm{\partial }[A]}{\mathrm{\partial }t}& =D_{\mathrm{A}}\frac{{\mathrm{\partial }}^2[A]}{\mathrm{\partial }{x}^2}+\alpha [S]{[A]}^2-\beta [A]+{\rho }_{\mathrm{A}},\\ \frac{\mathrm{\partial }[S]}{\mathrm{\partial }t}& =D_{\mathrm{S}}\frac{{\mathrm{\partial }}^2[S]}{\mathrm{\partial }{x}^2}-\alpha [S]{[A]}^2+{\rho }_{\mathrm{S}},\end{array}$$

in 0≤x≤10. The constants D_A and D_S measure the diffusion coefficients of activators and substrates, respectively. In order to generate a spatial inhomogeneous steady-state solution, the diffusion coefficient D_A needs to be much less than D_S. Here we use D_S=50 and D_A=0.1. For other parameters, we take α=β=ρ_S=1 and ρ_A=0.01. The one-dimensional domain [0,10] is divided into 50 compartments. The number of molecules per unit concentration in a compartment is Λ_A=Λ_S=500. The initial condition for simulations is the homogeneous steady-state solution [A](0,x)=1.01 and [S](0,x)=(1.01)⁻².

The Gaussian approximation is used only for the fast diffusion in substrates. Since the chemical gradients may not be monotonic in space, the time-adaptive criterion (2.9) is not used in this example, and instead, the Gaussian approximation for the diffusion process of substrates is applied everywhere in space. Since the number of substrates is large enough in each compartment, the approximation has a good accuracy in the entire space.

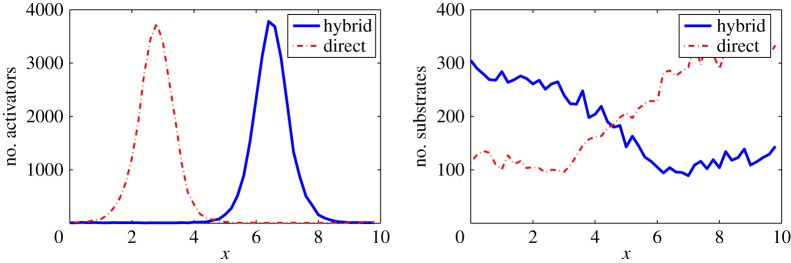
The study using different methods (figure 8) indicates that two stochastic methods show a similar pattern for A at t=10. The averages of CPU time costs in the 500 simulations for different methods indicate that the SSA costs 5.61×10³ s for each simulation and the hybrid method costs 2.16×10³ s, suggesting a 50% speed-up of the hybrid method.

Figure 8.

Example simulations obtained by the SSA (dashed line)and the hybrid method (solid line) for the one-dimensional activator-substrate Turing system in example VI. In the hybrid method, the Gaussian approximation is applied for simulating the diffusion processes of substrates which have rapid diffusion processes.

4. Discussion

We have introduced a new algorithm to accelerate the stochastic simulation of reaction–diffusion systems. In this hybrid approach, the numbers of diffusive jumps in regions with a high level of molecules are calculated using Gaussian vectors, whereas the diffusive jumps in regions with a low level of molecules, along with the reaction events, are simulated using the SSA. Because of the diffusion approximation, the size of the time step, which predominantly depends on rate of reactions, can be significantly larger than that allowed by the existing approaches. Thus, the hybrid method is particularly effective for diffusion-dominant systems. Moreover, the diffusion approximations for different diffusing species are performed independently, which makes the method particularly advantageous for application to systems with multiple diffusing species.

To determine the compartments for which the diffusion approximation is applied, we use a macroscopic quantity that can be easily calculated. In addition, the approximation region can be adaptively specified in both space and time with a good control of approximation errors. Thus, the hybrid method is effective in dealing with spatial distributions of molecules that may vary significantly over time or may not be monotonic in space.

The Gaussian random vector is directly related to the matrix whose non-zero location is determined by the communication among compartments. The partitioning of a domain with an irregular geometry may be achieved using existing software (COMSOL or URDME [38]) to enable application to complex domains. To extend our method for the system incorporating rapid and slow reactions, we can accelerate the simulation of rapid reactions by coupling our method with the hybrid SSA/τ-Leaping strategy [6] to create a hybrid diffusion approximation + SSA/τ-Leaping strategy. The overall approach introduced in this work will be an efficient and accurate algorithm for simulating biological and physical systems in which number of molecular copies has a large range within the spatial domain and diffusion is dominant comparing with other types of reactions.

Appendix A

A.1. Spatial stochastic simulation algorithm

The stochastic process underlying the CME can be simulated by the SSA. In SSA, two random numbers r₁ and r₂, that are uniformly distributed in [0, 1], are generated for determining the time and the index of the next reaction, respectively. The time for the next reaction is t+τ, with

$$\tau =-\frac{\ln r_1}{a_0(x)},$$

where a₀(x) is the sum of all propensity functions:

$$a_0(x)=\sum _{k=1}^K\sum _{j=1}^M{a}_{kj}(x)+\sum _{k=2}^K{a}_{kL}(x)+\sum _{k=1}^{K-1}{a}_{kR}(x).$$

The index of the next reaction is obtained by finding the smallest m and q such that

$$\begin{array}{rl}& \sum _{k=1}^{q-1}\sum _{j=1}^M{a}_{kj}+\sum _{j=1}^m{a}_{qj}\ge r_2{a}_0\end{array}$$ A 1

$$\begin{array}{rl}\text{or}& \sum _{k=1}^K\sum _{j=1}^M{a}_{kj}+\sum _{k=2}^q{a}_{kL}\ge r_2{a}_0\end{array}$$ A 2

$$\begin{array}{rl}\text{or}& \sum _{k=1}^K\sum _{j=1}^M{a}_{kj}+\sum _{k=2}^K{a}_{kL}+\sum _{k=1}^q{a}_{kR}\ge r_2{a}_0.\end{array}$$ A 3

If the condition (A 1) is satisfied, then the reaction R_qm happens and the state of the system is updated as X(t+τ)=X(t)+ν_qm; or if the condition (A 2) is satisfied, then the diffusion jump J_qL happens and the state of the system is updated as X(t+τ)=X(t)+ν_qL; or if the condition (A 3) is satisfied, then the diffusion jump J_qR happens and the state of the system is updated as X(t+τ)=X(t)+ν_qR.

The simulation repeats the above process until it reaches the stop criterion.

Authors' contributions

W.-C.L., L.Z. and Q.N. contributed to the method design and wrote the manuscript. W.-C.L. and L.Z. performed the numerical tests and Q.N. supervised the project.

Competing interests

The authors declare no competing interests.

Funding

This study was partially supported by the NSF grant nos DMS1161621 and DMS1562176 and by the NIH grant nos P50GM76516 and R01GM107264. W.-C.L. was partially supported by a grant from the Research Grants Council of the Hong Kong Special Administrative Region, China (Project No. 9048043) and a CityU StUp Grant (Project No. 7200437).