Hierarchical Self-Assembly of Cellulose Nanocrystals in a Confined Geometry

Abstract

Complex hierarchical architectures are ubiquitous in nature. By designing and controlling the interaction between elementary building blocks, nature is able to optimize a large variety of materials with multiple functionalities. Such control is, however, extremely challenging in man-made materials, due to the difficulties in controlling their interaction at different length scales simultaneously. Here, hierarchical cholesteric architectures are obtained by the self-assembly of cellulose nanocrystals within shrinking, micron-sized aqueous droplets. This confined, spherical geometry drastically affects the colloidal self-assembly process, resulting in concentric ordering within the droplet, as confirmed by simulation. This provides a quantitative tool to study the interactions of cellulose nanocrystals beyond what has been achieved in a planar geometry. Our developed methodology allows us to fabricate truly hierarchical solid-state architectures from the nanometer to the macroscopic scale using a renewable and sustainable biopolymer.

Designing and controlling the interaction of elementary building blocks into complex hierarchical architectures enables nature to optimize a large variety of materials with multiple functionalities.¹⁻³ Within the fascinating variety of designs and materials, helicoidal architectures are a recurring motif in nature,⁴⁻⁸ yet little is known about the natural assembly process.⁹ Consequently, the ability to fabricate biomimetic replicas is fundamentally important not only to elucidate the design principles that underlie the evolution of complex hierarchical structures in nature but also to inspire the development of materials where their functionalities are encoded in the building blocks that compose them.¹⁰⁻¹² However, control across a diversity of length scales ranging from nanometers to several hundreds of microns is extremely challenging in man-made materials.¹³

Here, inspired by the helicoidal architectures found in the plant cell wall,¹⁴ we study the assembly of cholesteric architectures of cellulose nanocrystals (CNCs) confined within monodisperse micron-sized droplets, generated via droplet-based microfluidics.^15,16 The self-assembly process is monitored with polarized optical microscopy, and the effect of the initial aqueous CNC concentration on the resultant self-assembled architecture is studied. This system not only allows for the localized, quantitative investigation of the complex dynamic interaction of CNCs in suspension but also offers a pathway to obtain highly hierarchical structures in a confined geometry from the nanometer to the macroscopic scale, using a renewable and sustainable polymer.

Exploitation of cellulose has existed since the beginning of civilization, from clothes and paper to use as a construction material,¹⁷ yet over the last two decades, it has attracted a growing interest due to its abundance and versatility when processed on the nanoscale in the form of cellulose nanocrystals.¹⁸ By strong acid hydrolysis, CNC can be extracted from a variety of natural sources, producing stable aqueous suspensions that exhibit cholesteric liquid-crystalline behavior at higher concentrations.¹⁹ The evaporation of CNC suspensions on a flat substrate can result in the formation of a solid film with a periodic chiral structure that can reflect visible light.²⁰ Traditionally, the self-assembly of such colloidal liquid-crystal systems has been studied in planar geometries,²¹⁻²³ offering a large variety of applications, for example, in pressure or temperature sensors.^24,25 However, more recently, there has been increasing study into the effects of topological constraints.²⁶ Of particular interest is the spherical geometry, where the curvature imposed, for example, by the interface of an emulsified droplet leads to frustrated liquid-crystalline self-organization.²⁷ This spherical topology, either as a droplet or as a thin shell of liquid, has been shown to give rise to peculiar phenomena, with potential applications in actuators or lasers.^16,28,29

The study of the self-assembly of CNCs in a microdroplet enables (i) the reproducible measurement of the cholesteric pitch at concentrations that are inaccessible with traditional pitch diagrams due to kinetic arrest, and (ii) monitoring of the self-assembly process over a few hours, instead of several days or weeks,³⁰ thereby reducing errors induced by desulfation of the CNC.³¹

Results and Discussion

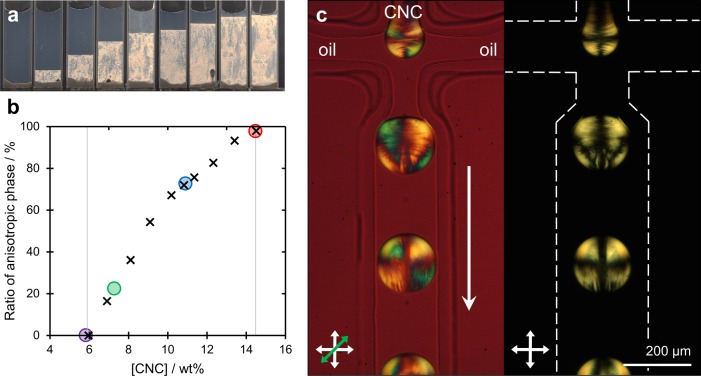
An aqueous suspension of cellulose nanocrystals (Figure S1, Supporting Information) was prepared as described in the Experimental Methods. To characterize the lyotropic properties of this suspension, it was diluted to give a series of CNC concentrations from 14.5 to 4.7 wt %, and the proportion of anisotropic phase was evaluated at each concentration (Figure 1a). This enabled the construction of a traditional phase diagram, as shown in Figure 1b. This phase diagram allows for determination of the critical values of CNC concentration for this specific suspension at which the transition from the isotropic to the anisotropic phase occurs.

Figure 1.

(a) Phase behavior of CNC suspensions of increasing concentration, as imaged under cross-polarizers, where a clear transition from pure isotropic to anisotropic phase is observed from left to right. (b) Calculated ratio of anisotropic phase present for each concentration investigated in (a) was used to compile the phase diagram (crosses). The specific concentrations investigated within microdroplets are indicated by the colored circles. (c) Polarization micrograph of the generation of microfluidic water-in-oil droplets from a 14.5 wt % suspension of CNCs, as imaged under cross-polarizers (right) and with a first-order tint plate (left), illustrating the initial radial assembly.

In order to understand the impact of geometrical confinement, it was necessary to study how the initial concentration of the CNC suspension affected self-assembly within a micron-scale droplet. Microdroplets were generated in a single step as an aqueous emulsion in hexadecane oil within a polydimethylsiloxane (PDMS) flow-focusing microfluidic device, as described in the Experimental Methods. At the flow-focusing junction, the aqueous CNC suspension intersected perpendicularly with flows of hexadecane oil, resulting in segmentation into monodisperse microdroplets (coefficient of variation <2%), with a diameter defined by the geometry of the flow focus, and the relative flow rates and viscosities of the immiscible solutions. Once formed, the droplets were collected via microbore tubing onto a fluorophilic substrate for further study. It should be noted that the aqueous droplets are denser than the surrounding oil and, as such, settle onto the surface of the fluorophilic substrate rather than at the air–oil interface (Figure S2, Supporting Information). The presence of this oil layer slows the loss of water from the droplets, allowing them to be studied over time scales from hours to days.

Microdroplets with a typical diameter of 140 μm were prepared from a series of CNC concentrations across the phase transition, as indicated by the colored circles in Figure 1b. In all cases, the optical anisotropy of the suspension allowed for the ordering of CNC domains to be visualized during droplet formation by polarized optical microscopy, as described in the Experimental Methods. This is exemplified with a 14.5 wt % CNC suspension, as denoted by the red circle in the phase diagram (Figure 1b). Here, the generation of an interface between the two fluids at the neck of the flow focus resulted in an immediate radial ordering of the CNCs within the microdroplet, giving rise to a pronounced Maltese cross-like pattern when imaged under crossed polarizers (Figure 1c; see Video S1 and Video S2). However, this arrangement is rapidly disrupted by chaotic advection induced within the microdroplet by shearing interactions with its surroundings as it travels along the microfluidic channel. At such a high concentration, the suspension is highly viscous and is almost entirely in a liquid-crystalline phase. For this reason, the shear experienced by the cholesteric phase inside the droplet induces many topological defects. This droplet consequentially remains trapped in this disordered anisotropic state without any particular reordering of the structure. Upon subsequent removal of water (by diffusion into the oil) and corresponding concentration of the confined suspension, this arrangement is preserved (Figure S3, Supporting Information). A similar trend is observed for a lower concentration of 10.9 wt % (blue circle on Figure 1b). Here, despite microdroplets containing both isotropic and anisotropic phases, the relaxation toward a radial geometry was again not significantly observed after initial droplet formation (Figure S4, Supporting Information).

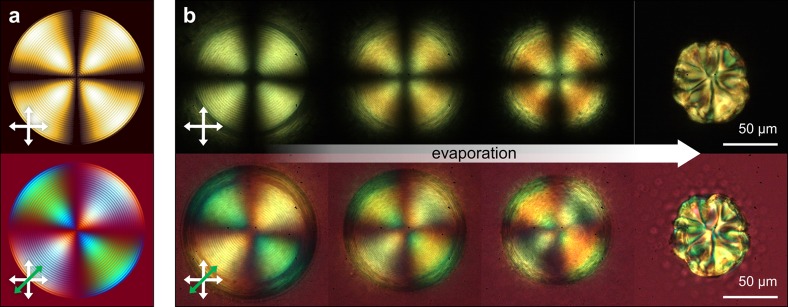
A markedly different assembly process is observed when the isotropic phase is dominant within the microdroplet, as is the case for 7.3 wt % suspension of CNCs (green circle in Figure 1b). As before, radial ordering of the liquid-crystalline structure is observed upon generation of the microfluidic droplets; however, mixing within the droplet as it flows along the channel results in microdroplets in a predominantly isotropic phase, containing clearly defined tactoids (Figure S5, Supporting Information). Upon the loss of water from the droplet the tactoids rearrange, resulting in the formation of an ordered chiral nematic shell, growing inward from the water–oil interface (Figure 2). Depending on the number and dimensions of the tactoids (which is influenced by the individual composition of each microdroplet), either a chiral nematic shell containing free tactoids or a radial order throughout the entire diameter of the droplet is obtained (Figure S6, Supporting Information). In the latter case, such ordering can be preserved until the onset of buckling during the final stages of water loss from the droplet (Figure S7, Supporting Information). We attribute buckling to the interplay between increasing Laplace pressure at lower radius of curvature and the resistance to isotropic compression of the solidified CNC shell of the microdroplet, which allows for loss of the remaining water content without laterally compressing the rigidified surface. The presence of the chiral nematic organization throughout the entire diameter of the droplet is confirmed by the numerically simulated pattern shown in Figure 2a (see Supporting Information for simulation details). In particular, the observation of concentric dark and bright circles corresponds to the fingerprint pattern of the cholesteric structure. The superimposed Maltese cross pattern is due to the isoclines of the radial cholesteric helix axis aligned with the axes of the crossed polarizers, in agreement with a planar anchoring of the CNC local director with the droplet interface.

Figure 2.

Comparison between (a) theoretical and (b) experimental images obtained from the confinement of a cholesteric CNC suspension within a spherical geometry, when viewed through cross-polarizers (top row) and upon addition of a first-order tint plate (bottom row). Upon loss of water, the Maltese cross is retained until the onset of buckling upon final drying.

Low viscosity and a homogeneous composition are expected to increase the proportion of droplets retaining the radial chiral nematic order, with the in situ formation of a chiral nematic phase expected to reduce the generation of shear-induced topological defects. This was confirmed with droplets solely containing an isotropic suspension of CNC (5.8 wt %, purple circle in Figure 1b), where the formation of independent tactoids within the volume of the droplet was no longer observed upon droplet shrinkage, with the isotropic–anisotropic phase transition instead initiated exclusively at the water–oil interface (Figure S8, Supporting Information). Furthermore, lower concentrations have been tested. However, for values lower than 4 wt %, the loss of water in ambient conditions leads only to a thin shell with transient cholesteric order. This shell is subsequently disrupted by buckling³² prior to the droplet core becoming sufficiently concentrated.

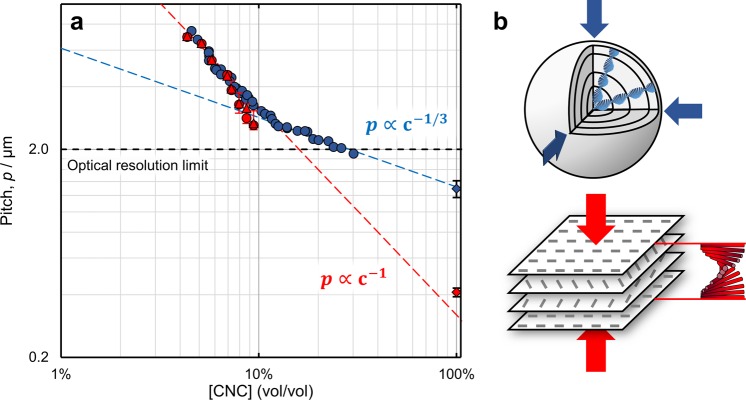
The observation of the microdroplet shrinkage process by polarized optical microscopy allowed for monitoring of the pitch evolution as a function of the water content. This particular configuration enables the construction of an “evolution pitch diagram” which depicts the behavior of the cholesteric phase from low concentration at the equilibrium toward the final dry state. The pitch (p) is measured as twice the periodicity of the fingerprint pattern observed between crossed polarizers, while the suspension concentration is calculated from the droplet diameter. Variation in the pitch measured across a single droplet was within experimental error, indicating that the CNC concentration was uniform throughout the shrinking droplet. Similarly, droplets with comparable CNC concentration displayed the same cholesteric pitch. The values of the pitch measured during the loss of water from the microdroplets are reported in Figure 3 and compared to the values of the pitch independently obtained from measurement in a glass capillary (see Experimental Methods). It is worth noting here that, for a given initial value of CNC concentration, the same trend in pitch is measured irrespective of the dimensions of the initial droplets (Figure S9, Supporting Information).

Figure 3.

(a) Evolution pitch diagram. The cholesteric pitch measured in the droplets (blue circles) is compared against a macroscale capillary measured by laser diffraction (red circles) and microscopy (red triangles). The pitch below 2 μm was not measured due to the optical resolution limit. Upon increasing CNC concentration, the measured cholesteric pitch in the droplets is initially consistent with the pitch measured in the capillary; however, for the case of confined suspensions, a transition at c_g = 12% v/v (∼19 wt %) is observed. Extrapolation of the c^–1 and c^–1/3 trend lines correlates with the pitch measured by scanning electron microscopy for a dry film and microparticle, respectively (diamonds). The capillary error bars correspond to the gradient in pitch observed as a function of position within the anisotropic phase, as shown in Figure S16, Supporting Information. (b) Schematics illustrating the effect on the helicoidal cholesteric structure upon three-dimensional contraction when confined within a sphere, as occurs after c_g (p ∝ c^–1/3, top), compared to unidirectional contraction in a planar geometry (p ∝ c^–1, bottom).

The essence of the self-assembly process of CNC in suspension is illustrated by Figure 3. At a low concentration of CNC in suspension, the cholesteric pitch observed both in the droplets and in the capillaries overlaps and appears to be inversely proportional to concentration, p ∝ c^–1, as expected from Straley modeling of chiral nonflexible rods.³³ The small discrepancy between the two pitch measurements above 9.7 wt % is attributed to the cholesteric monodomain within the droplets, as commented upon in the Supporting Information. In contrast, droplets prepared from [CNC] = 10.9 wt % remain trapped in a polydomain structure and, as such, more closely follow the capillary data (Figure S10).

Significantly, above a critical concentration denoted here as c_g, a transition after which the pitch scales as p ∝ c^–1/3 is observed. This transition is attributed to the manifestation of the kinetic arrest, where the sample cannot relax. Indeed, such kinetic arrest is expected to take place at some point during shrinkage toward a fully dried sphere of self-assembled CNCs. The value of c_g for this specific suspension (12% v/v ≈ 19 wt % in Figure 3) was found to be comparable between individual radially ordered cholesteric droplets, irrespective of the initial size, CNC concentration, or rate of water removal. The concentration at which this transition occurs has been discussed and addressed in the literature as a key factor in the understanding of the self-assembly of CNCs but remains challenging to assess.³⁴ As the suspension gets kinetically trapped, the cholesteric structure cannot relax over time, but it still can be affected by the local shear experienced upon drying, and therefore, it is sensitive to any geometrical constraints. In this system, the spherical geometry leads to a three-dimensional contraction of the cholesteric structure, in agreement with the observed power law. This contrasts with the usual configuration where a film is cast onto a planar substrate, which leads to a unidirectional, vertical straining of the cholesteric structure and consequentially to a similar power law of p ∝ c^–1. For this reason, the spherical geometry allows for a clear discrimination of the transition upon kinetic arrest.

Finally, Figure 4 shows the morphology of CNC microparticles after the complete loss of water. For this experiment, smaller microdroplets (50 μm in diameter) are employed to minimize the effects of buckling on the particle structure.³⁵ Similarly, to the case of planar CNC films,²⁰ the chiral nematic nature can be maintained, evidenced by the clear helicoidal structure observed in the scanning electron microscopy (SEM) image reported in Figure 4d. Moreover, the value of the pitch measured directly from such images, closely matches the extrapolated confined pitch for a CNC concentration near 100%, as indicated by the dashed blue line in Figure 3. In contrast, casting a planar film via slow evaporation using the same suspension (Figure S11, Supporting Information) results in a cholesteric pitch consistent with the standard power law behavior (dashed red line).

Figure 4.

(a) Image of a dried CNC microparticle, as imaged in transmission (left) and under cross-polarizers with a first-order tint plate (right). (b–d) SEM images of a dry, buckled CNC microparticle, showing (c) the clear ordering of cellulose nanocrystals on the surface and (d) the helicoidal assembly of CNC with a defined pitch, p, within the particle.

Conclusions

In conclusion, we have fabricated bioinspired hierarchical cellulose structures over multiple length scales by controlling the self-assembly process of cellulose nanocrystals in micron-sized droplets. The obtained droplets are sufficiently monodisperse to allow for local study of the self-assembly of the CNC water suspension. It is further demonstrated that this geometrical confinement leads to a drastic effect on the self-assembly of cellulose nanocrystals. This allows for the construction of an “evolution pitch diagram” that provides a tool to investigate the suspension behavior for a large range of concentrations. To our knowledge, this has not been reported so far, due to the fact that kinetic arrest usually leads to unreliable pitch values for high concentration.³⁰

Experimental Methods

Materials

Hexadecane (99%) and Span 80 were purchase from Sigma-Aldrich and Fluka, respectively, and were used without further purification. The initial suspension of 14.5 wt % cellulose nanocrystals was prepared from filter paper, as described below, with subsequent formulations diluted with deionized water (Millipore Milli-Q gradient A10, resistivity >18 MΩ·cm^–1).

Instrumentation

Microdroplets were imaged in transmission using a Vision Research Phantom Miro ex4-M fast camera, attached to an Olympus IX-71 inverted microscope (10–64× objectives). Polarized optical microscopy was performed in transmission with crossed polarizers. In order to indicate CNC orientation, a sensitive tint plate (Olympus U-TP530) was additionally inserted between the crossed polarizers. SEM images were acquired using a Zeiss Leo Gemini 1530VP system, working at 90° with respect to the electron beam. SEM samples were mounted on aluminum stubs using conductive carbon tape and, to minimize surface charging, sputtered with a 5–10 nm layer of Au/Pd (Emitech K550; I = 55 mA for 10 s). The acceleration voltage used was 2.0 kV, and the working distance was 1–2 mm. Atomic force microscopy (AFM) images were acquired with an Agilent 5500, collected in tapping mode (OTESPA-R3 tip) and at room temperature over a 25 μm² area. AFM samples were prepared by drop-casting 10 μL of a diluted CNC suspension on to poly(l-lysine)-functionalized mica. After deposition, the samples were rinsed with deionized water and dried under nitrogen flow.

Cellulose Nanocrystal Suspension

Cellulose nanocrystals were obtained from the hydrolysis of Whatman No. 1 cellulose filter paper (30 g) with sulfuric acid (64 wt %, 420 mL) at 64 °C for 30 min, before being quenched using Milli-Q ice and water. Soluble cellulose residues and acid were removed by centrifugation (three steps at 20 000g for 20 min) and dialysis against deionized water (MWCO 12–14 kDa membrane), and a stable suspension of [CNC] = 2.2 wt % was obtained. Conductivity titration against sodium hydroxide indicated [SO₄^2–] = 205 mmol·kg^–1 of CNC.³⁶ The suspension was tip-sonicated in an ice bath (Fisherbrand Ultrasonic disintegrator 500 W, amplitude 30% max 8200 J·g^–1 of CNC) and vacuum-filtered (8.0 μm then 0.8 μm nitrocellulose, Sigma-Aldrich).

The suspension was concentrated by heating at 60 °C in a water bath for 12 h, resulting in a 14.5 wt % (∼9.4% v/v) suspension of CNC. The ionic content of this concentrated suspension was deduced from conductometric titration against sodium hydroxide, complemented by pH measurements before and after potassium chloride addition, and corresponds to the following: 36% surface charge loss by CNC partial desulfation ([SO₄^2–] = 131 mmol·kg^–1 of CNC) [CNC^–] = 19 mM, the release of [SO₄^2–]_free = 10.7 mM, [H⁺]_free = 18.7 mM and [H⁺]_total = 40.4 mM. Planar films of CNC were prepared by casting 1.0 mL of a 2.0 wt % CNC suspension in a 3.5 cm diameter polystyrene petri dish, before being allowed to evaporate under ambient conditions.

Phase Diagram and Pitch Measurement in Capillaries

The initial 14.5 wt % CNC suspension was diluted with deionized water using a high precision scale, vortexed, and transferred to a flat capillary of sufficiently large inner dimensions to eliminate any confinement effects (1.00 × 10.00 × 50 mm) and sealed with glass plates and nail polish. The self-assembly was observed after 4 days and later after 95 days with no noticeable change of the critical concentrations (Figure S12). The cholesteric pitch in the glass capillaries was then determined using (i) polarized optical microscopy (TPlan Nikon, 20× (NA = 0.30, WD = 30 mm) and 50× (NA = 0.40, WD = 22 mm) objectives, Figure S13, Supporting Information); the pitch was measured as twice the period of the fingerprint pattern, taking either an average over 10 pitch distances or using a fast Fourier transform of the image processed with ImageJ; (ii) laser diffraction performed using a laser (λ = 531.8 nm) and observing the diffraction pattern in transmission (as exemplified in Figures S14 and S15, Supporting Information). The pitch was derived using Bragg’s law, as adapted by Kahn to include Snell law correction.³⁷ In order to account for possible sample inhomogeneity in the vertical dimension, the pitch was measured at regular intervals throughout the anisotropic phase and is reported in Figure S16 in the Supporting Information.

Droplet-Based Microfluidics

Monodisperse water-in-oil microdroplets were generated within a hydrophobic flow-focusing microfluidic device. These were manufactured from PDMS via soft lithography, whereby the microchannel network was (i) designed in silico (AutoCAD), (ii) printed as a negative photomask, and (iii) transferred onto a silicon wafer spin-coated with SU-8 photoresist via UV-photolithography to form a mold. PDMS and the cross-linker (Sylgard 184 elastomer kit, Dow Corning) in a 10:1 ratio were poured onto this mold and allowed to stand overnight at 70 °C. The PDMS layer, imprinted with the microfluidic channel design, was removed, and using a biopsy punch (1.0 mm), inlets and an outlet were formed. The imprinted PDMS and a glass substrate were exposed to oxygen plasma for 8 s and then pressed together to seal the microfluidic channels.

To study the self-assembly of the CNC suspension within the microdroplet, a 200 μm wide flow-focusing junction (A) was employed with a channel depth of 80 μm. For structural analysis of solid microparticles a smaller flow-focusing junction (43 × 43 μm, B) was employed to generate the templating microdroplets. To render the channels fluorophilic, they were immediately flushed with a 0.5% v/v solution of trichloro(1H,1H,2H,2H-perfluorooctyl)silane in Fluorinert FC-40 (3M) and subsequently cured at 120 °C overnight. This hydrophobic surface modification was also applied to glass slides that were used in “shrinking droplet” studies, ensuring low wetting of the surface by the aqueous microdroplets.

To generate microdroplets, the continuous oil phase and the discrete aqueous phase were injected into the microfluidic device via two syringe pumps (PHD 2000, Harvard Apparatus) with controlled flow rates of 200 and 80 μL·h^–1, respectively. At the intersection, the shear forces caused the formation of aqueous droplets in oil (typically for a 7.3 wt % CNC suspension: Ø_A = 139.5 ± 2.5 μm and Ø_B = 50.1 ± 0.6 μm; Figure S17, Supporting Information). The continuous phase comprised the organic oil, hexadecane, with 2.0 wt % Span 80 surfactant. The dispersed phase consisted of an aqueous suspension of cellulose nanocrystals; this was diluted as appropriate with deionized water from an initial 14.5 wt % CNC suspension and vortexed to homogenize the sample prior to injection into the microfluidic device. Once the microemulsion was generated, it exited the microfluidic device through microbore polythene tubing (Ø_I = 380 μm, l ≈ 10 cm) and was collected onto a microscope slide.

The aqueous phase was allowed to slowly diffuse into the oil at RTP until solid microparticles were formed. During droplet shrinkage, a linear decrease in the droplet diameter was observed (Figure S18, Supporting Information). This was typically in the range of 10–20 μm·h^–1 for the large droplets (Ø_A) and increased to 25 μm·h^–1 for the smaller droplets (Ø_B) reported in Figure 4 (see Supporting Information).

Microparticle Analysis

Residual surfactant was removed from the dry microparticles by washing with n-hexane prior to imaging by SEM. To image the interior of a droplet, it was fractured using the following protocol: the particles (on a substrate) were first placed in a nitrogen atmosphere, cooled in liquid nitrogen, and finally mechanically crushed. The low temperature made the droplets more brittle, while the low humidity inhibited condensation of water.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsnano.6b03355.

• AFM of CNC rods, additional images of cholesteric droplets, evolution pitch diagrams, comparative SEM of cross sections of films and microdroplets prepared from the same suspension, comparison of pitch measurements by laser diffraction and optical microscopy, droplet size distribution and their drying rate; with supplementary discussions on the evaporation process, phase diagram, pitch diagram, and modeling of the optical behavior of cholesteric droplets (PDF)

• Video S1 (AVI)

• Video S2 (AVI)

Author Contributions

^† R.M.P. and B.F.-P. contributed equally to this work.

The authors declare no competing financial interest.

Notes

Additional data related to this publication is available at the University of Cambridge data repository (http://dx.doi.org/10.17863/CAM.1233).