Abstract
Nucleosomes form the basic unit of compaction within eukaryotic genomes, and their locations represent an important, yet poorly understood, mechanism of genetic regulation. Quantifying the strength of interactions within the nucleosome is a central problem in biophysics and is critical to understanding how nucleosome positions influence gene expression. By comparing to single-molecule experiments, we demonstrate that a coarse-grained molecular model of the nucleosome can reproduce key aspects of nucleosome unwrapping. Using detailed simulations of DNA and histone proteins, we calculate the tension-dependent free energy surface corresponding to the unwrapping process. The model reproduces quantitatively the forces required to unwrap the nucleosome and reveals the role played by electrostatic interactions during this process. We then demonstrate that histone modifications and DNA sequence can have significant effects on the energies of nucleosome formation. Most notably, we show that histone tails contribute asymmetrically to the stability of the outer and inner turn of nucleosomal DNA and that depending on which histone tails are modified, the tension-dependent response is modulated differently.
Short abstract
A detailed model of the DNA−histone complex, validated against available experimental data, is used to explain at a molecular level the tension-dependent free energy of nucleosome unwrapping.
Introduction
Eukaryotic genomes are packaged into a compact, yet dynamic, structure known as chromatin. The basic building block of chromatin is the nucleosome, a disk-like structure consisting of 147 base pairs of DNA wrapped into 1.7 superhelical turns around proteins known as histones.1,2 These histone proteins form what is known as the histone octamer, a protein complex consisting of two copies of histone proteins H2A, H2B, H3, and H4. The surface of the histone octamer is highly positive, which interacts favorably with the negative backbone of DNA. As a result, at sufficiently low ionic conditions, nucleosomes are stable and spontaneously form.
The locations of nucleosomes along the genome play a central role in eukaryotic regulation. DNA segments incorporated into nucleosomes are inaccessible to other DNA binding proteins, including transcription factors and polymerases, and thus nucleosomes must be disrupted in order for the cellular machinery to access nucleosomal DNA. As such, the positions occupied by nucleosomes provide an additional, important mechanism by which eukaryotic genomes are regulated. Indeed, past work has demonstrated that deregulation of these processes is implicated in numerous diseases, including cancer.3−5 Quantifying the strength of interactions within the nucleosome structure and the forces required to disrupt them is of fundamental importance to understanding the delicate dynamics of chromatin compaction.
Optical-trapping single-molecule techniques have been particularly effective at probing the many interactions within the nucleosome. In these experiments, chromatin fibers6−9 or single nucleosomes10−15 are subjected to pico-newton scale forces, thereby providing the ability to precisely perturb the native nucleosome structure. By analyzing the deformations that result from these forces, one can infer the underlying strength of binding energies within the nucleosome. Following the initial work by Mihardja et al.,10 a consensus is emerging11,13,15 in which a single nucleosome is disrupted in two stages. In the first, at 3 pN, the outer wrap of DNA is removed from the histone surface. This first wrap is removed gradually and is considered to be an equilibrium process, where spontaneous unwrapping and rewrapping events can be observed under a constant force. The second transition occurs at forces 8–9 pN and occurs rapidly via so-called “rips”, where the remaining wrap of DNA is suddenly released.10 More recently, these transitions have been shown to depend on torque (i.e., DNA supercoiling via twist),13 and to occur asymmetrically due to variability in the bound DNA sequence.15
Several theoretical and computational studies have sought to help interpret these experimental results. Following the initial work of Kulić and Schiessel,16 most current treatments represent the nucleosome as an oriented spool, and the unbound DNA as a semiflexible worm-like chain.17,18 While earlier studies were only able to detect a single distinct unwrapping transition,16,19 consistent with the first experiments,6 more recent work17,18 has been able to reproduce the two transitions observed by Mihardja et al.10 By relying on simple, primarily analytic models, these studies have provided significant insights into the fundamental physics that govern interactions within the nucleosome. Such approaches, however, have necessarily had to invoke assumptions and introduce adjustable parameters in order to describe experiments17,18 (e.g., the DNA–histone binding energy). This limits their ability to predict nucleosomal behavior under different conditions, such as variations in DNA sequence or ionic environment, without resorting to additional experimental data. Additionally, these models cannot explicitly account for histone modifications, which are central to nucleosome positioning and higher-order chromatin structure.9,20−23
A complementary approach, which should in principle enable prediction of nucleosomal interactions under a wide array of situations, could rely on molecular models where the nucleosome can be assembled or disassembled explicitly. Though these approaches are particularly promising, their success has been frustrated by the inability to access the experimentally relevant time scales of stretching, typically rates of 100 nm/s. Clearly, these time scales are inaccessible to atomistic simulations, yet even a highly coarse-grained spool-like model of the nucleosome still employed stretching rates several orders of magnitude too fast.19 There is therefore a need to develop models and methodologies to facilitate more direct comparisons between optical-trapping experiments and molecular-level calculations. If successful, such models could reveal the subtle, yet incredibly important effects of DNA-sequence and histone modifications on nucleosome stability.
In this work, we build on a recently proposed coarse-grained model of the nucleosome24−26 to examine its response to external perturbations. A computational framework is proposed in which the tension-dependent response of the nucleosome is examined at equilibrium, thereby providing access to the free energy of nucleosome unwrapping under tension. Our results are found to be in agreement with experimental measurements by Mihardja et al.10 and Brower-Toland et al.,9 and serve to demonstrate that it is indeed possible to reproduce the absolute binding free energies of nucleosome formation in terms of purely molecular-level information, without resorting to additional parameters. Importantly, that model is then used to predict the impact of DNA sequence and histone modifications on the relative free energies of binding within the nucleosome.
Results
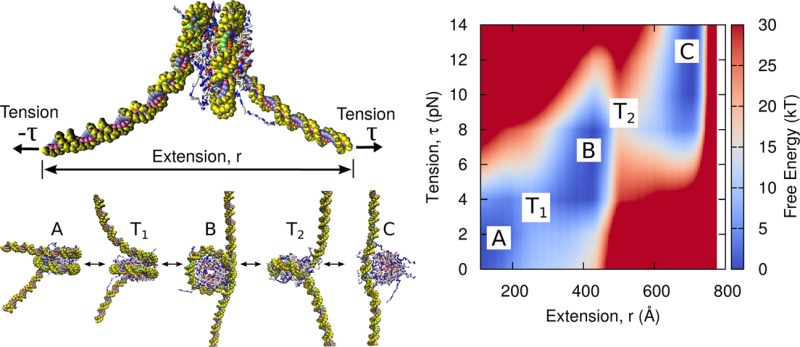
A schematic representation of our simulation setup is shown in Figure 1a. As with optical-trapping experiments, the “state” of the nucleosome is represented by two parameters: the tension (or force) exerted on the DNA molecule, τ, and the extension of the DNA ends, r. To facilitate comparison with experiments,10 the ends of the DNA are not torsionally constrained. Figure 1b shows instantaneous configurations of the nucleosome model for five different values of extension, r. Consistent with previous observations, the outer wrap of the nucleosome is first removed (A → T1 → B), followed by the inner wrap (B → T2 → C).
Figure 1.
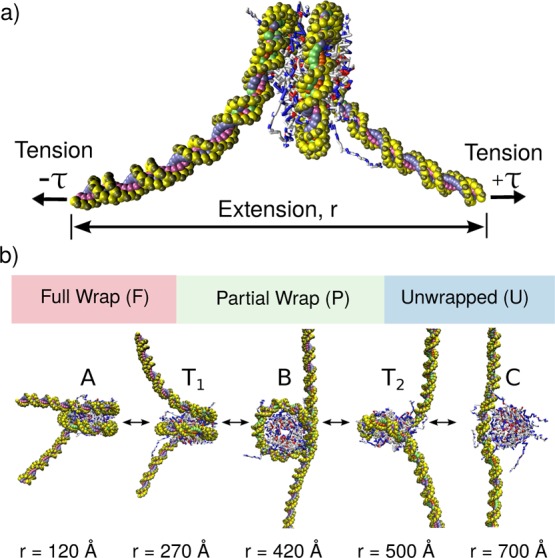
Model of nucleosome unwrapping. (a) Coarse-grained topology of nucleosome. DNA is represented by 3SPN2.C,24 and the histone proteins by AICG.26 Both the end-to-end extension, r, and tension, τ, are constrained during a simulation. (b) Unwrapping process. During extension, the wraps of DNA around histone proteins are removed one by one. T1 and T2 denote the transition states separating the first (A ↔ B) and second (B ↔ C) unwrapping events. Figures were generated using VMD.27
In order to quantify these transitions, we examine the tension-dependent free energy of nucleosome unwrapping. By calculating the tension-dependent free energy instead of a simple force–extension curve, as done previously,19,28 we can determine the true equilibrium behavior of the unwrapping process. Additionally, by performing simulations at equilibrium, we circumvent the issue of time scales that frustrate comparisons of traditional nonequilibrium molecular simulations to optical pulling experiments.
A representative two-dimensional tension-extension free energy surface for the 601 positioning sequence29 is shown in Figure 2. Rather than increasing linearly with tension, the extension is quantized into three well-defined vertical bands, located at ∼120, 420, and 700, corresponding to states “A”, “B”, and “C” in Figure 1. At low tension (τ < 3 pN), a low extension (r < 200) is preferred. As tension is increased (τ ≈ 4–8 pN), the minimum free energy shifts to intermediate values of extension (r ≈ 420). At higher tension (τ > 8 pN), the minimum free energy shifts to larger values of extension (r ≈ 700). The free energy penalty of low tension and high extension (e.g., τ = 3, r = 700) or high tension with low extension (e.g., τ = 12, r = 200) results in large energy barriers >40 kT.
Figure 2.
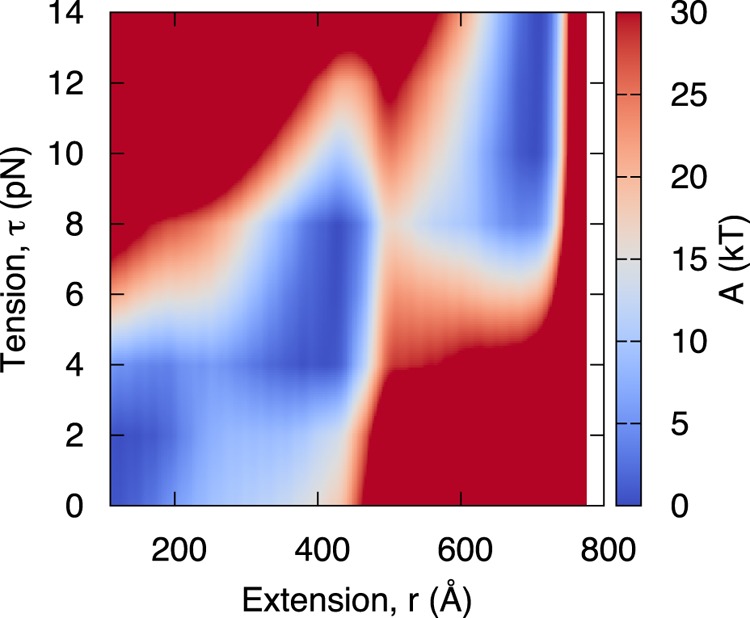
Tension-dependent free energy surface of nucleosome unwrapping for 601 positioning sequence. The free energy surface demonstrates minima at extensions of r ≈ 120, 420, 700, depending on tension. As tension increases, the minimum-energy extension shifts to larger values. Consistent with Mihardja et al.,10 two transitions are observed.
The tension-dependent transition can also be visualized by plotting one-dimensional “slices” of the free energy surface at different values of tension (Figure 3a). Visualizing the data in this way clearly demonstrates that there are three basins of nucleosome extension: “fully wrapped”, “partially wrapped” and “unwrapped”. The basin that is favored depends on the tension applied to the DNA ends. As tension increases, the free energy minima shifts first from the “fully wrapped” to the “partially wrapped” basin, and then to the “unwrapped” basin. The boundaries of these basins are defined by the locations of the transition states (i.e., local maximum in the free energy) that separate neighboring basins. The transition states separating the A → B transition, T1, and the B → C transition, T2, are shown in Figure 1b.
Figure 3.
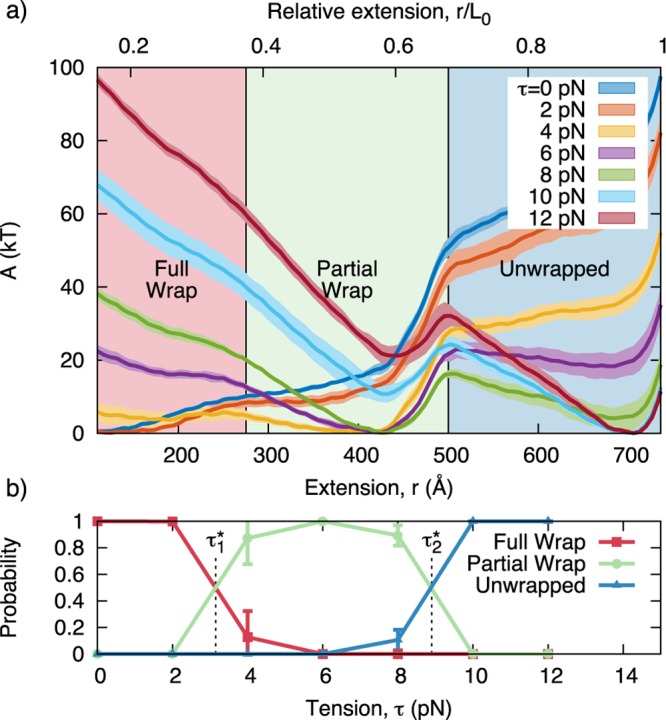
(a) Free energy versus extension for different values of tension with the 601 positioning sequence. The locations of the transition states, T1 and T2, are used to define three basins: “fully wrapped”, “partially wrapped”, and “unwrapped”. L0 represents the contour length of the DNA molecule. (b) Probability of observing the nucleosome in each free energy basin for different tensions. The “fully” and “partially” wrapped states are at equilibrium (i.e., equal probability) when τ1* = 3.2 pN. The “partially” and “unwrapped” states are at equilibrium when τ2 = 8.9 pN. Error bars represent standard deviation across four independent simulations.
Once these three basins are defined, we can determine the precise tension at which the outer and inner DNA turns unwrap from the nucleosome. This is obtained by converting the tension-dependent free energy into probabilities and then integrating these probabilities to determine the total probability of finding the system in each basin (see Methods). The corresponding results are shown in Figure 3b; it can be appreciated that the probability of finding the system in the “fully wrapped” or “partially wrapped” basin is equivalent when τ ≈ 3.2 pN. Thus, when τ ≈ 3.2 pN the outer turn of nucleosomal DNA is in equilibrium (in a statistical mechanics sense) with its unbound state. We define this tension as τ1*. Similarly, the probability of the nucleosome in the “partially wrapped” and “unwrapped” basins is the same (i.e., the inner wrap is in equilibrium) when τ ≈ 8.9 pN, defined as τ2). These values are in quantitative agreement with those measured by Mihardja et al.,10 who observed that the outer and inner DNA loops were removed at 3 pN and 8–9 pN, respectively.
A complementary approach to estimate τ1* and τ2 is to determine the tension at which the free energy barriers of the forward and reverse reactions are equal.17Figure 4 shows the corresponding tension-dependent free energy barriers of the outer (A ↔ T1 ↔ B) and inner unwrapping (B ↔ T2 ↔ C) events. At low tension, the energy barriers for the forward reactions, A → B and B → C, dominate, and the forward (i.e., unwrapping) reaction rate is low. As tension increases, the energy barriers for the forward reactions decrease, while those for the reverse increase, thereby causing the unwrapping reaction to proceed at a higher rate. When the energy barriers of the forward and reverse reactions are equal, the two basins are at equilibrium (in a transition state theory sense), and τ1* and τ2 can be determined. These unwrapping tensions are estimated to be 3.3 pN and 8.5 pN, in excellent agreement with the probability-based analysis of Figure 3b.
Figure 4.
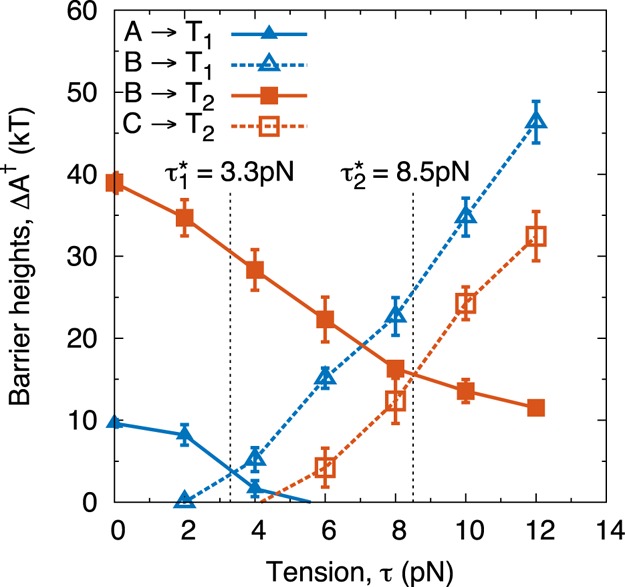
Free energy barrier heights of nucleosome unwrapping for 601 positioning sequence. Solid lines represent the unwrapping (forward) reactions, dotted lines represent wrapping (reverse) reactions. When the unwrapping and wrapping barriers are equal, the two basins are at equilibrium with one another. This is found when τ1* = 3.3 pN for the outer wrap, and τ2 = 8.5 pN for the inner wrap. ΔA†(τ1*) = 4 kT and ΔA†(τ2) = 16 kT. Error bars represent standard deviation across four independent simulations.
The magnitude of the free energy barrier also helps explain the observation by Mihardja et al.10 that the outer turn of DNA can be removed reversibly, while the inner turn cannot. Since the energy barrier separating the “Fully” and “Partially” wrapped states is only ≈5 kT, the system can quickly transition between states when held at τ = τ1*. In contrast, the “partial wrap” and “unwrapped” states are separated by an energy barrier of ∼18 kT, indicating that even at equilibrium the P ↔ U transition occurs slowly. Thus, removal of the outer wrap may appear to be reversible on the time scales of a typical optical trapping experiment, while the inner wrap may not. Further, because force–extension curves are usually obtained via optical trapping by pulling a nucleosome at a fixed velocity, the experiments may not observe a P → U transition until τ > τ2. This would cause the experiments to overestimate the value of τ2* and lead to a sudden, irreversible “ripping” event. We also note that the barrier estimates in this work (ΔA1 = 4 kT, ΔA2† = 16 kT) are in excellent agreement with those predicted by Sudhanshu et al.17 (ΔA1 ≈ 6 kT, ΔA2† ≈ 15 kT).
Electrostatics, Sequence Dependence, Histone Modifications
Having validated the proposed model against experimental data,10 we now examine the influence of ionic environment, DNA sequence, and histone modifications on the stability of the nucleosome. Such variations can have a significant impact on nucleosome formation, and the precise molecular origins of their impact is still poorly understood.
We first investigate the origins of the tension-dependent response by exploring the role of DNA–DNA electrostatic repulsion on the stability of the nucleosome structure. Past theoretical work16,18 has suggested that DNA–DNA repulsion within the nucleosome is central to its tension-dependent response. Other studies, however, have observed that DNA–DNA electrostatic repulsion is unimportant and that the correct response can be achieved by accounting for the tension-dependent orientation of the free DNA ends.17 Since our proposed model explicitly includes both contributions, we can directly evaluate the importance of DNA–DNA repulsion on nucleosome unwrapping. To examine this effect, we disable DNA–DNA electrostatic repulsion in our model between base pairs separated by more than 20 base pairs. Only disabling electrostatics between distant regions of DNA was necessary to avoid implicitly lowering the persistence length of DNA by neglecting Coulombic interactions between neighboring base pairs. All electrostatics responsible for DNA-histone affinity, however, remain intact.
Our results are summarized in Figure 5a,b. As anticipated,16 removal of DNA–DNA repulsive interactions has a greater impact on the outer DNA loop (Δτ1* = +1.7pN) than on the inner DNA loop (Δτ2 = +1.1pN). However, in the absence of DNA–DNA repulsions, the qualitative features of the tension-dependent response remain unchanged. These results indicate that while DNA–DNA repulsions play a role in nucleosome disassembly, they are not primarily responsible for the two unwrapping steps observed in experiments. Our results are also consistent with prior experimental measurements, where the role of DNA–DNA repulsion on the stability of the outer turn was observed to be small.30
Figure 5.
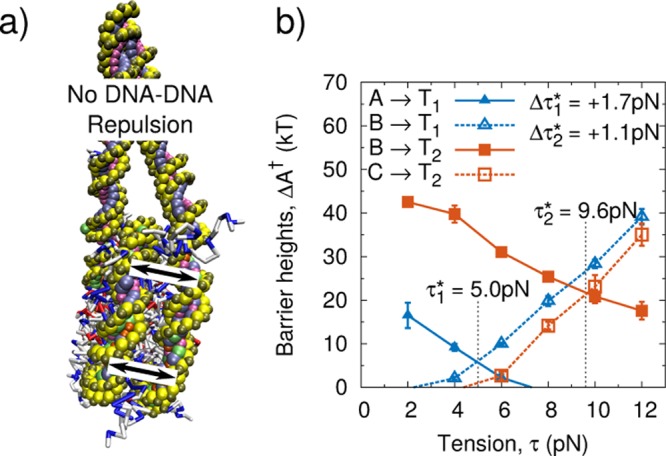
(a) Schematic representation of proposed model with DNA–DNA repulsion removed. (b) Tension-dependent free energy barriers for 601 positioning sequence with DNA-DNA repulsion removed. Δτ1* and Δτ2 represent change relative to complete model. Error bars represent standard deviation across three independent simulations.
We next examine the impact of DNA sequence on the relative binding free energies of nucleosome formation. Optical trapping experiments could in principle be used to probe the sequence-dependent energies within the nucleosome, but recent literature studies have been limited to the 601 positioning sequence10,11,13 and slight variations.15 Instead, competitive reconstitution assays are the dominant experimental technique for characterization of sequence-dependent relative binding free energies.31,32 To compare model predictions to these experiments, we use the technique employed by Freeman et al.,25 where the relative binding free energies of different DNA sequences are assessed computationally using alchemical transformations and thermodynamic integration (see Methods). A comparison of predicted and experimental free energies, shown in Figure 6, indicates that, as with previous work,25 the model adopted here accurately reproduces the binding free energies of many different sequences. In general, the key predictor of binding free energy is the sequence-dependent shape of the DNA molecule (i.e., minor groove widths and intrinsic curvature). Sequences that bind strongly (low ΔΔA) possess periodic sequence motifs (e.g., TA base steps) that impart a shape that favorably “fits” underlying histone structure.32 In contrast, weakly binding sequences (large ΔΔA) do not possess these periodic motifs.
Figure 6.
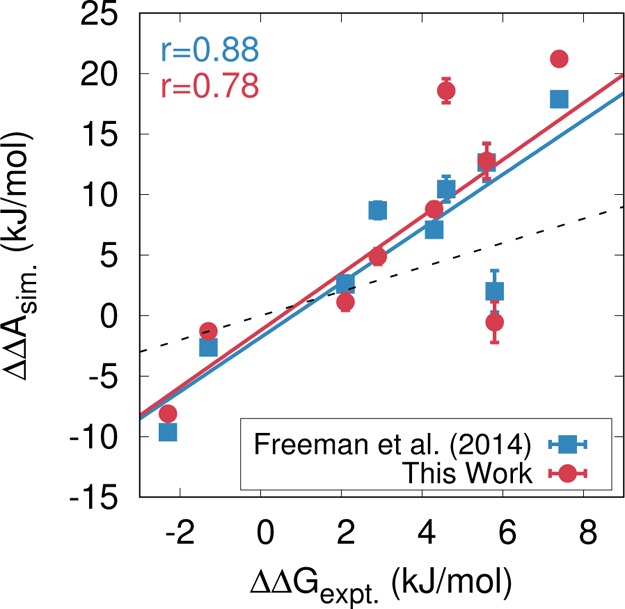
Sequence-dependent binding free energies. Squares denote model proposed by Freeman et al.25 (obtained at 300 K and 150 mM ionic strength). Circles denote model proposed in this work, obtained at 277 K and vanishing ionic strength (for consistency with ref (31)). Despite differing solution conditions and DNA–protein interactions, both models reproduce the relative binding free energies of nucleosome formation. The DNA sequences used here are given in ref (25). The dotted line corresponds to quantitative agreement.
In addition to DNA sequence, the modification of histone tails is widely considered to be the single most important determinant of chromatin structure.20 Methylated and acetylated histones are enriched at promoters of highly expressed genes and are thought to play a role in the strong positioning of certain nucleosomes.21,22 Histone tails are central to nucleosome–nucleosome interactions, and their modification has important implications on chromatin’s three-dimensional structure.23 Experiments9 have also established that removal of histone tails has a significant impact on the stability of the nucleosome.
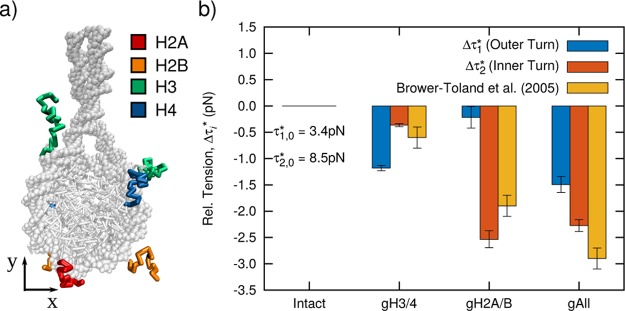
To examine the role of histone tails on nucleosome stability at a molecular level, we return to our earlier analysis and calculate the tension-dependent free energy of nucleosome unwrapping. Our results can be compared to the optical trapping experiments of Brower-Toland et al.,9 where arrays of 17 nucleosomes were disassembled for different histone tail modifications, including the complete removal via trypsin digest or post-translationally via acetylation. In the model, we perform this trypsin digest in silico to each histone (see Figure 7a) and calculate the resulting tension-dependent response. Figure 7b shows the change in the equilibrium tension of the outer, Δτ1*, and inner, Δτ2, turn of DNA due to the removal of different histone tails. The experimental measurements are also included and correspond to the impact of histone modifications on the stability of the inner turn of DNA (i.e., Δτ2*). Our results are in excellent agreement with experimental measurements and predict the effect of each histone modification to within ±0.5 pN. Yet our results provide additional insight into these experiments, whose limited spatial resolution prevented the observation of the individual release of the outer DNA turn. Most importantly, we observe that tails of different histones contribute asymmetrically to the stability of each turn of nucleosomal DNA. The H3/4 tails dominate the stability of the outer DNA turn, Δτ1 = −1.2 pN, but contribute weakly to the stability of the inner turn, Δτ2* = −0.2 pN. In contrast, H2A/B tails have a small effect on the outer turn, Δτ1 = 0.4 pN, but a significant effect on the inner DNA turn, Δτ2* = 2.5 pN. Therefore, depending on whether histone modifications occur on H2A/B or H3/4, the stability of the nucleosome will be modulated differently. This observation suggests a potent mechanism by which each turn of nucleosomal DNA can be independently regulated and could help to explain the importance and role of H3/4 modifications relative to those of H2A/B.
Figure 7.
(a) Molecular configuration highlighting histone tails removed by in silico trypsin digest. The exact residues removed are given in the original work by Brower-Toland et al.9 (b) Change in equilibrium tension of outer, Δτ1*, and inner DNA turn, Δτ2, resulting from removal of H3/4 tails (gH3/4), H2A/B tails (gH2A/B), and all histone tails (gAll). Tensions are reported relative to Δτ1,0* and Δτ2,0, the values reported previously in Figure 4 for the 601 positioning sequence. Experimental data correspond to removal of the inner turn of DNA (i.e., Δτ2*). Error bars represent standard deviation across three independent simulations or reported in ref (9).
Conclusion
In this work we have demonstrated that a molecular-model of the nucleosome, composed of two coarse-grained models of DNA and proteins,24−26 can be combined parameter-free to accurately reproduce the tension-dependent response of nucleosome unwrapping. This model quantitatively reproduces the unwrapping forces observed in experiments9,10 and the barrier heights predicted by prior theoretical studies.17 We then demonstrated that this model can be used to examine, without adjustment, the role of subtle phenomena in nucleosome formation such as DNA–DNA Coulombic repulsion, DNA-sequence, and histone tail modifications.
Our proposed approach opens up a new avenue for theoretical examinations of nucleosome stability. As a first step, this model can aid the interpretation of recent optical pulling experiments where the nucleosome is subjected to torque13 and is suitable for examining subtle features within the nucleosome such as sequence-dependent asymmetric unwrapping.15 Further, analysis of experimental measurements can become increasingly sophisticated, because our model provides a tool for interrogating raw data, including the fluctuations, from FRET and optical pulling experiments. This combination of experiment and simulation could help to resolve nanometer-scale phenomena such as dynamic DNA–protein contacts and could effectively increase the spatial resolution of experimental measurements to the base-pair level. Yet the potential of our approach extends beyond single nucleosome experiments and can begin to elucidate many unsolved questions within chromatin biophysics. How does the methylation of specific histone tails (and not others) enhance the positioning of certain nucleosomes? What are the free energies of different folded chromatin structures, and how do histone modifications effect this energy landscape? What is the role of DNA sequence on these processes, and do certain DNA sequences dispose chromatin to different “folds”? The approach presented in this work represents an important step toward answering these questions.
Methods
The model adopted in this work relies on a coarse-grained model of DNA24,25 and proteins,26 which are combined to represent the nucleosome. Both models were developed independently, but they are implemented at the same level of description, thereby facilitating their concerted use. Specifically, for DNA we use the 3SPN coarse-grained representation, where each nucleotide is described by three force sites located at the phosphate, sugar and base.24,33−35 For the histone proteins, we use the “atomistic-interaction based coarse-grained model” (AICG), where the protein is represented by one site per amino acid located at the center of mass of the side chain.26
Interactions between the 3SPN2.C and AICG models included electrostatic and excluded volume effects. Phosphate sites with 3SPN were assigned a charge of −0.6 as described previously.35 Each protein site was given the net charge of that residue at physiological pH (i.e., +1 for Arg, His, and Lys; −1 for Asp and Glu, 0 for others). As with prior work,25 the effective charge of interactions between DNA and protein sites was scaled by a factor of 1.67 to bring the local charge of the phosphates back to −1. We note that DNA–protein interactions in this work differ slightly from those employed by Freeman et al.,25 where, in addition to electrostatics, a small Lennard–Jones attraction was added between all DNA and protein sites. The strength of this attraction was very weak (ϵPro–DNA = 0.25 kJ/mol) and was originally included to reduce fluctuations within the nucleosome structure. Here we demonstrate that this weak interaction is unnecessary; by omitting it, both the relative and absolute formation free energies of the nucleosome can be reproduced. The combined model is effectively parameter-free: both the model of DNA and protein are included as originally proposed without any additional terms. Electrostatic forces are approximated by Debye–Hückel theory. Debye–Hückel theory invokes many assumptions about the electrostatic environment, and is not strictly valid for the highly charged association of the histone proteins and DNA. Nonetheless, Debye–Hückel theory provides a useful first-order approximation of Coulombic forces and is employed here, without resorting to higher-order techniques. All simulations were performed in the canonical ensemble using a Langevin thermostat and 150 mM ionic strength.
As an initial condition, we combine the 1KX5 crystal structure2 of the nucleosome core particle with a proposed configuration of exiting DNA36,37 to form a 223 base-pair structure, with 147 base pairs bound to the histone proteins and 38 flanking bases on each side. When using the 601 positioning sequence,29 the flanking bases were chosen as polyA. This configuration was only used as the initial configuration, and no information from either structure was directly encoded into the nucleosome model.
To extract the tension-dependent free energy surface, two constraints were applied to the nucleosomal model. First, a constant force (i.e., tension) was applied to each end of DNA in order to mimic the experimental setup of optical-trapping experiments. Then, harmonic constraints were applied to the end-to-end extension of the DNA molecule, and umbrella sampling was performed to determine the free-energy as a function of DNA extension. In umbrella sampling, many independent simulations are performed at specified locations in phase space, and molecular fluctuations are used to estimate the local free energy surface at that location. These many local estimates are then systematically combined to obtain the total free energy surface.38,39 Because tension is held at a constant value during a simulation, the resulting free energy “surfaces” are not truly continuous functions of tension. They are instead a compilation of two-dimensional “curves” that are plotted cocurrently to construct the “surface” presented in Figure 2.
The relative free energy of binding for different DNA sequences (ΔΔA) was calculated as described in detail previously.25 Briefly, a thermodynamic cycle was defined that represents the relative sequence-dependent free energy of nucleosome formation, ΔΔA, as the difference between the free energy difference of two DNA sequences in the bulk, ΔAbulk, and bound to the histone proteins, ΔAbound (i.e., ΔΔA = ΔAbulk – ΔAbound); ΔAbulk and ΔAbound are determined by thermodynamic integration. The DNA sequences analyzed are given explicitly in ref (25).
Acknowledgments
This work was performed under the following financial assistance Award 70NANB14H012 from U.S. Department of Commerce, National Institute of Standards and Technology, as part of the Center for Hierarchical Materials Design (CHiMaD). The development of the 3SPN.2C model was supported by NSF CBET-1264021, and the development of advanced sampling codes required for free energy calculations was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division through the Midwest Integrated Center for Computational Materials (MICCoM). D.C.S. acknowledges support from the National Human Genome Research Institute (NIH R01-HG-000225). Computational resources were provided by the Midway computing cluster at the University of Chicago and the University of Wisconsin-Madison Center for High Throughput Computing. The authors gratefully acknowledge Professor Andrew Spakowitz and Dr. Gordon Freeman for helpful discussions and Professor Ralf Everaers and Sam Meyer for providing the configuration of the 223 base-pair nucleosome.
The authors declare no competing financial interest.
References
- Luger K.; Mader A. W.; Richmond R. K.; Sargent D. F.; Richmond T. J. Crystal structure of the nucleosome resolution core particle at 2.8 Å. Nature 1997, 389, 251–260. 10.1038/38444. [DOI] [PubMed] [Google Scholar]
- Davey C. A.; Sargent D. F.; Luger K.; Maeder A. W.; Richmond T. J. Solvent mediated interactions in the structure of the nucleosome core particle at 1.9 a resolution. J. Mol. Biol. 2002, 319, 1097–1113. 10.1016/S0022-2836(02)00386-8. [DOI] [PubMed] [Google Scholar]
- Hendrich B.; Bickmore W. Human diseases with underlying defects in chromatin structure and modification. Hum. Mol. Genet. 2001, 10, 2233–2242. 10.1093/hmg/10.20.2233. [DOI] [PubMed] [Google Scholar]
- Bhaumik S. R.; Smith E.; Shilatifard A. Covalent modifications of histones during development and disease pathogenesis. Nat. Struct. Mol. Biol. 2007, 14, 1008–1016. 10.1038/nsmb1337. [DOI] [PubMed] [Google Scholar]
- Sadri-Vakili G.; Bouzou B.; Benn C. L.; Kim M.-O.; Chawla P.; Overland R. P.; Glajch K. E.; Xia E.; Qiu Z.; Hersch S. M.; Clark T. W.; Yohrling G. J.; Cha J.-H. J. Histones associated with downregulated genes are hypo-acetylated in Huntington’s disease models. Hum. Mol. Genet. 2007, 16, 1293–1306. 10.1093/hmg/ddm078. [DOI] [PubMed] [Google Scholar]
- Brower-Toland B. D.; Smith C. L.; Yeh R. C.; Lis J. T.; Peterson C. L.; Wang M. D. {M}echanical disruption of individual nucleosomes reveals a reversible multistage release of {DNA}. Proc. Natl. Acad. Sci. U. S. A. 2002, 99, 1960–1965. 10.1073/pnas.022638399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cui Y.; Bustamante C. Pulling a single chromatin fiber reveals the forces that maintain its higher-order structure. Proc. Natl. Acad. Sci. U. S. A. 2000, 97, 127–132. 10.1073/pnas.97.1.127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gemmen G. J.; Sim R.; Haushalter K. a.; Ke P. C.; Kadonaga J. T.; Smith D. E. Forced unraveling of nucleosomes assembled on heterogeneous DNA using core histones, NAP-1, and ACF. J. Mol. Biol. 2005, 351, 89–99. 10.1016/j.jmb.2005.05.058. [DOI] [PubMed] [Google Scholar]
- Brower-Toland B.; Wacker D. A.; Fulbright R. M.; Lis J. T.; Kraus W. L.; Wang M. D. Specific Contributions of Histone Tails and their Acetylation to the Mechanical Stability of Nucleosomes. J. Mol. Biol. 2005, 346, 135–146. 10.1016/j.jmb.2004.11.056. [DOI] [PubMed] [Google Scholar]
- Mihardja S.; Spakowitz A. J.; Zhang Y.; Bustamante C. Effect of force on mononucleosomal dynamics. Proc. Natl. Acad. Sci. U. S. A. 2006, 103, 15871–15876. 10.1073/pnas.0607526103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kruithof M.; van Noort J. Hidden Markov Analysis of Nucleosome Unwrapping Under Force. Biophys. J. 2009, 96, 3708–3715. 10.1016/j.bpj.2009.01.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall M. A.; Shundrovsky A.; Bai L.; Fulbright R. M.; Lis J. T.; Wang M. D. High-resolution dynamic mapping of histone-DNA interactions in a nucleosome. Nat. Struct. Mol. Biol. 2009, 16, 124–129. 10.1038/nsmb.1526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheinin M. Y.; Li M.; Soltani M.; Luger K.; Wang M. D. Torque modulates nucleosome stability and facilitates H2A/H2B dimer loss. Nat. Commun. 2013, 4, 2579. 10.1038/ncomms3579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mack A. H.; Schlingman D. J.; Ilagan R. P.; Regan L.; Mochrie S. G. Kinetics and Thermodynamics of Phenotype: Unwinding and Rewinding the Nucleosome. J. Mol. Biol. 2012, 423, 687–701. 10.1016/j.jmb.2012.08.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ngo T. T. M.; Zhang Q.; Zhou R.; Yodh J. G.; Ha T. Asymmetric Unwrapping of Nucleosomes under Tension Directed by DNA Local Flexibility. Cell 2015, 160, 1135–1144. 10.1016/j.cell.2015.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kulić I. M.; Schiessel H. DNA Spools under Tension. Phys. Rev. Lett. 2004, 92, 228101. 10.1103/PhysRevLett.92.228101. [DOI] [PubMed] [Google Scholar]
- Sudhanshu B.; Mihardja S.; Koslover E. F.; Mehraeen S.; Bustamante C.; Spakowitz A. J. Tension-dependent structural deformation alters single-molecule transition kinetics. Proc. Natl. Acad. Sci. U. S. A. 2011, 108, 1885–1890. 10.1073/pnas.1010047108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mollazadeh-Beidokhti L.; Mohammad-Rafiee F.; Schiessel H. Nucleosome dynamics between tension-induced states. Biophys. J. 2012, 102, 2235–2240. 10.1016/j.bpj.2012.04.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wocjan T.; Klenin K.; Langowski J. Brownian dynamics simulation of DNA unrolling from the nucleosome. J. Phys. Chem. B 2009, 113, 2639–2646. 10.1021/jp806137e. [DOI] [PubMed] [Google Scholar]
- Jenuwein T.; Allis C. D. Translating the histone code. Science 2001, 293, 1074–1080. 10.1126/science.1063127. [DOI] [PubMed] [Google Scholar]
- Kurdistani S. K.; Tavazoie S.; Grunstein M. Mapping Global Histone Acetylation Patterns to Gene Expression. Cell 2004, 117, 721–733. 10.1016/j.cell.2004.05.023. [DOI] [PubMed] [Google Scholar]
- Barski A.; Cuddapah S.; Cui K.; Roh T. Y.; Schones D. E.; Wang Z.; Wei G.; Chepelev I.; Zhao K. High-Resolution Profiling of Histone Methylations in the Human Genome. Cell 2007, 129, 823–837. 10.1016/j.cell.2007.05.009. [DOI] [PubMed] [Google Scholar]
- Zhou V. W.; Goren A.; Bernstein B. E. Charting histone modifications and the functional organization of mammalian genomes. Nat. Rev. Genet. 2011, 12, 7–18. 10.1038/nrg2905. [DOI] [PubMed] [Google Scholar]
- Freeman G. S.; Hinckley D. M.; Lequieu J. P.; Whitmer J. K.; de Pablo J. J. Coarse-grained modeling of DNA curvature. J. Chem. Phys. 2014, 141, 165103. 10.1063/1.4897649. [DOI] [PubMed] [Google Scholar]
- Freeman G. S.; Lequieu J. P.; Hinckley D. M.; Whitmer J. K.; de Pablo J. J. DNA Shape Dominates Sequence Affinity in Nucleosome Formation. Phys. Rev. Lett. 2014, 113, 168101. 10.1103/PhysRevLett.113.168101. [DOI] [PubMed] [Google Scholar]
- Li W.; Wolynes P. G.; Takada S. Frustration, specific sequence dependence, and nonlinearity in large-amplitude fluctuations of allosteric proteins. Proc. Natl. Acad. Sci. U. S. A. 2011, 108, 3504–3509. 10.1073/pnas.1018983108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Humphrey W.; Dalke A.; Schulten K. VMD: Visual Molecular Dynamics. J. Mol. Graphics 1996, 14, 33–38. 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- Kenzaki H.; Takada S. Partial Unwrapping and Histone Tail Dynamics in Nucleosome Revealed by Coarse-Grained Molecular Simulations. PLoS Comput. Biol. 2015, 11, e1004443. 10.1371/journal.pcbi.1004443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lowary P. T.; Widom J. New DNA sequence rules for high affinity binding to histone octamer and sequence-directed nucleosome positioning. J. Mol. Biol. 1998, 276, 19–42. 10.1006/jmbi.1997.1494. [DOI] [PubMed] [Google Scholar]
- Moyle-Heyrman G.; Tims H. S.; Widom J. Structural Constraints in Collaborative Competition of Transcription Factors Against the Nucleosome. J. Mol. Biol. 2011, 412, 634–646. 10.1016/j.jmb.2011.07.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thåström A.; Lowary P. T.; Widom J. Measurement of histone-DNA interaction free energy in nucleosomes. Methods 2004, 33, 33–44. 10.1016/j.ymeth.2003.10.018. [DOI] [PubMed] [Google Scholar]
- Segal E.; Fondufe-Mittendorf Y.; Chen L.; Thåström A.; Field Y.; Moore I. K.; Wang J.-P. Z.; Widom J. A genomic code for nucleosome positioning. Nature 2006, 442, 772–778. 10.1038/nature04979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knotts T. A.; Rathore N.; Schwartz D. C.; de Pablo J. J. A coarse grain model for DNA. J. Chem. Phys. 2007, 126, 084901. 10.1063/1.2431804. [DOI] [PubMed] [Google Scholar]
- Sambriski E. J.; Schwartz D. C.; de Pablo J. J. A mesoscale model of DNA and its renaturation. Biophys. J. 2009, 96, 1675–1690. 10.1016/j.bpj.2008.09.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hinckley D. M.; Freeman G. S.; Whitmer J. K.; de Pablo J. J. An experimentally-informed coarse-grained 3-site-per-nucleotide model of DNA: Structure, thermodynamics, and dynamics of hybridization. J. Chem. Phys. 2013, 139, 144903. 10.1063/1.4822042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Syed S. H.; Goutte-Gattat D.; Becker N.; Meyer S.; Shukla M. S.; Hayes J. J.; Everaers R.; Angelov D.; Bednar J.; Dimitrov S. Single-base resolution mapping of H1-nucleosome interactions and 3D organization of the nucleosome. Proc. Natl. Acad. Sci. U. S. A. 2010, 107, 9620–9625. 10.1073/pnas.1000309107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer S.; Becker N. B.; Syed S. H.; Goutte-Gattat D.; Shukla M. S.; Hayes J. J.; Angelov D.; Bednar J.; Dimitrov S.; Everaers R. From crystal and NMR structures, footprints and cryo-electron-micrographs to large and soft structures: nanoscale modeling of the nucleosomal stem. Nucleic Acids Res. 2011, 39, 9139–9154. 10.1093/nar/gkr573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar S.; Rosenberg J. M.; Bouzida D.; Swendsen R. H.; Kollman P. A. Multidimensional free-energy calculations using the weighted histogram analysis method. J. Comput. Chem. 1995, 16, 1339–1350. 10.1002/jcc.540161104. [DOI] [Google Scholar]
- Kästner J. Umbrella sampling. Wiley Interdiscip Rev. Comput. Mol. Sci. 2011, 1, 932–942. 10.1002/wcms.66. [DOI] [Google Scholar]