Skip to main content
PMC home page
ACS Central Science logoLink to ACS Central Science
. 2016 Aug 23;2(9):608–613. doi: 10.1021/acscentsci.6b00168

Diffusion-Controlled Rotation of Triptycene in a Metal–Organic Framework (MOF) Sheds Light on the Viscosity of MOF-Confined Solvent

Xing Jiang †, Hai-Bao Duan ‡,†,*, Saeed I Khan †, Miguel A Garcia-Garibay †,*
PMCID: PMC5043434  PMID: 27725958

Abstract

graphic file with name oc-2016-001687_0006.jpg

Artificial molecular machines are expected to operate under conditions of very low Reynolds numbers with inertial forces orders of magnitude smaller than viscous forces. While these conditions are relatively well understood in bulk fluids, opportunities to assess the role of viscous forces in confined crystalline media are rare. Here we report one such example of diffusion-controlled rotation in crystals and its application as a probe for viscosity of MOF-confined solvent. We describe the preparation and characterization of three pillared paddlewheel MOFs, with 9,10-bis(4-pyridylethynyl)triptycene 3 as a pillar and molecular rotator, and three axially substituted dicarboxylate linkers with different lengths and steric bulk. The noncatenated structure with a bulky dicarboxylate linker (UCLA-R3) features a cavity filled by 10 molecules of N,N-dimethylformamide (DMF). Solid-state 2H NMR analysis performed between 293 and 343 K revealed a fast 3-fold rotation of the pillar triptycene group with the temperature dependence consistent with a site exchange process determined by rotator-solvent interactions. The dynamic viscosity of the MOF-confined solvent was estimated to be 13.3 N·s/m2 (or Pa·s), which is 4 orders of magnitude greater than that of bulk DMF (8.2 × 10–4 N·s/m2), and comparable to that of honey.

Short abstract

Operating at the diffusion-controlled limit, and measured by solid state 2H NMR, a barrierless molecular rotor in a metal organic framework (MOF) can be used to determine the dynamic viscosity of the nanoconfined solvent.

The design of usable artificial molecular machines will require the input of a broad range of physical and material scientists; however, it will be up to chemists to develop the structural platforms needed to realize their functions.1−11 Early work on artificial molecular machinery was guided by the structural and dynamic analogies between macroscopic objects and small molecules in solution.12 In recent years, alternative approaches have been inspired by the structural design and function of biomolecular machines1,3 such as ATP synthase, bacterial flagellum, and skeletal muscle.13 Their mechanisms of function highlight the importance of biased Brownian motion under conditions where inertial forces are orders of magnitude smaller than viscous forces,3 and suggest the advantage of using nanometer size units as building blocks for assemblies of higher complexities.

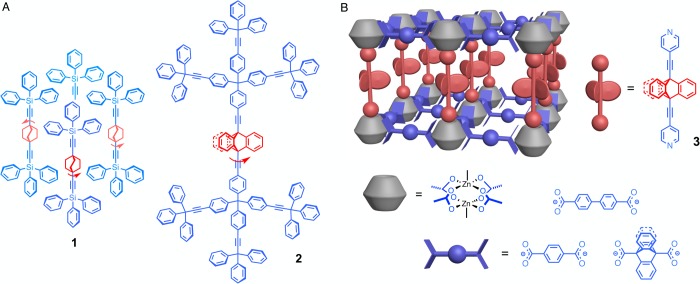
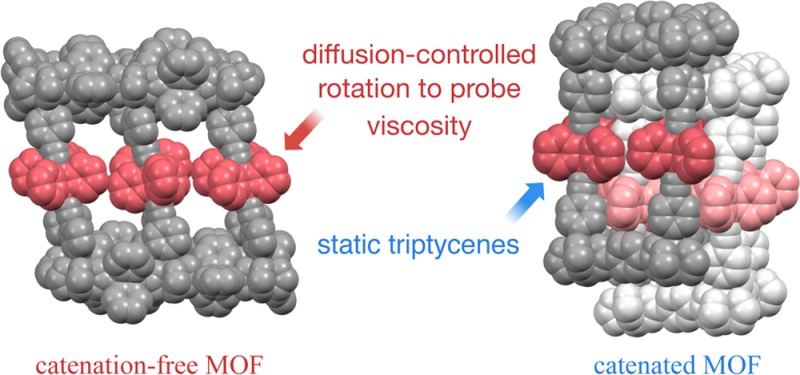
With the objective of exploring structures that display those characteristics, we suggested the design of artificial molecular machinery based on molecules capable of performing dynamic processes in the crystalline state, such that their molecular level operation can be determined by external control in the macroscopic world.14 The number of “amphidynamic” crystals built with static and dynamic elements has increased over the past few years,15−25 including several examples of porous structures where the dynamics of rotators in the host have been explored both in empty form and in the presence of added guest molecules.18,20,21 In addition, motion in solids has been reliably engineered using molecules with conformationally flexible bulky groups acting as a stator, which are covalently linked to a central group that acts as the rotator, such as bicyclo[2.2.2]octane in 1(26) (Figure 1A). It has been shown that low packing densities and conformational degrees of freedom allow for volume fluctuations16,25 that play a role analogous to that of viscous forces in liquids and can be used in simple scaling strategies to support the dynamics of significantly larger rotators. For example, line shape analysis of solid-state 2H NMR (SS 2H NMR) spectra showed that the deuterium-labeled triptycenes in 2-d8 have 3-fold site exchanges with a frequency of 4.6 kHz at 300 K.27 While these have been important steps forward to expand the dimensions of crystalline molecular rotors and to explore the role of random forces in the dynamics of condensed phase media, one can appreciate that a simple scaling strategy drastically reduces the density of rotators in the lattice and increases the distance between them, rendering it unfeasible to take advantage of dipole–dipole interactions or mechanical gearing in the design of molecular machines. A promising strategy for the construction of a dense array of larger molecular rotators with the absence of close contacts in the crystal lattice is given by the use of metal–organic frameworks (MOFs).28−34 By taking advantage of different carboxylate and amine linkers, it is possible to fine-tune pillared paddlewheel MOF structures to provide an optimized spatial arrangement of molecular rotators and functional groups.35−38 Herein, we report the preparation of three pillared paddlewheel MOFs, UCLA-R1, UCLA-R2, and UCLA-R3, and the remarkable rotational dynamics of triptycene groups in MOF UCLA-R3. As shown in Figure 1B, ligand 3 with a triptycene rotator covalently linked by triple bonds to two pyridine moieties makes up a pillar, which connects the 2D layers formed by dinuclear zinc nodes and dicarboxylate linkers. Three different dicaboxylates (terephthalate, biphenyl-4,4′-dicarboxylate, and triptycene-9,10-dicaboxylate) were used to adjust the distance between the neighboring triptycene rotators as well as the degree of catenation, defined as the interpenetration of two or more identical and independent frameworks.35 With the pillar triptycenes of the frameworks selectively labeled, we performed SS 2H NMR experiments and found that rotation of triptycenes is only possible in the catenation-free UCLA-R3, which displays 3-fold jumps with frequencies in the MHz (106 s–1) regime near ambient temperatures. Notably, the temperature dependence of the rotational frequencies revealed a dynamic behavior that results from interactions between the rotator and solvent molecules confined in the crystal. With no steric or intrinsic barriers in the structure, the rotation of the triptycene group in UCLA-R3 constitutes a diffusion-controlled process.

Figure 1.

Figure 1

Open in a new tab

(A) Chemical structures of the molecular rotor 1 illustrating a packing structure that supports the rotation of a compact bicyclo[2.2.2]octane rotator and molecular rotor 2 with a larger triptycene rotator. (B) A schematic representation of the designed MOFs with the pillar ligand 9,10-bis(4-pyridylethynyl)triptycene 3 connecting the 2D layers formed by the dinuclear zinc nodes and dicarboxylates, including terephthalate (UCLA-R1), biphenyl-4,4′-dicaboxylate (UCLA-R2), and triptycene-9,10-dicarboxylate (UCLA-R3).

Results and Discussion

Samples of ligand 9,10-bis(4-pyridylethynyl)triptycene 3 and its isotopologue 3-d8 were prepared by Sonagashira reactions between 4-bromopyridine and 9,10-diethynyltriptycene and 9,10-diethynyltriptycene-d8, respectively.27 MOFs UCLA-R1–R3 were prepared by solvothermal synthesis from a mixture of zinc nitrate hexahydrate, the carboxylic acids, and pillaring ligand 3 in DMF. Single crystals were picked up from the vials in the presence of DMF and used for X-ray diffraction immediately as irreversible phase transitions and structure collapse were shown to occur when the samples were exposed to air and the solvent escaped. As a result, all characterizations were performed on solvent-saturated samples.

The single crystal structures of MOFs UCLA-R1–R3 obtained at 100 K are illustrated in Figure 2. The paddlewheel architectures with dinuclear zinc nodes connected to dicaboxylates and ligand 3 were obtained as expected for all three frameworks. Samples of UCLA-R1 crystallized in the space group P1̅ with an asymmetric unit consisting of two zinc units, four terephthalates, and two molecules of 3. The 2-fold catenated structure observed for UCLA-R1 with the pillar distorted to accommodate the catenation is shown in Figure 2A, and the constituting lattices are shown in gray and blue in Figure 2B. A structural feature resulting from the interpenetration was a close π–π stacking between the triptycene rotators in one pillar and the pyridine groups of the adjacent networks, as shown in the space-filling model. This close contact, together with the relatively short distance between triptycenes within the same network (ca. 8.1 Å, between bridge head carbons), makes it difficult for triptycenes to rotate. A higher degree of catenation was observed in the crystal structure of UCLA-R2, which was solved in the space group P21/c. Since the voids in the 2D grids formed by zinc nodes and biphenyl-4,4′-dicarboxylates are larger than those in UCLA-R1, a 4-fold interdigitated structure was observed. Two pyridines from the neighboring networks are consequently placed in between the blades of each triptycene in the pillar, leaving little room for any motion of those groups. The crystal structure of UCLA-R3 was solved in the monoclinic space group C2/c. In this case, the presence of sterically demanding triptycene-9,10-dicarboxylate linkers led to the formation of densely packed layer structures and prevented catenation. While the triptycene groups in the layer structure are expected to be static as all of their blades are meshed with each other, the ones in the pillar structures have contacts only with the DMF molecules and might be able to undergo fast dynamics. A close inspection of neighboring triptycene groups (Figure 3) reveals a distance of 10.3 Å between their rotational axes, which is almost twice the radius of their volume of revolution.27,39 The closest distance of approach between hydrogen atoms in adjacent rotators occurs away from their crystallographic positions, at which they are 2.9 Å away from each other, suggesting the lack of significant rotator–rotator interactions. In fact, as shown in Figure 3B, only solvent molecules could be observed in the proximity of the triptycene rotator in the crystal structure.

Figure 2.

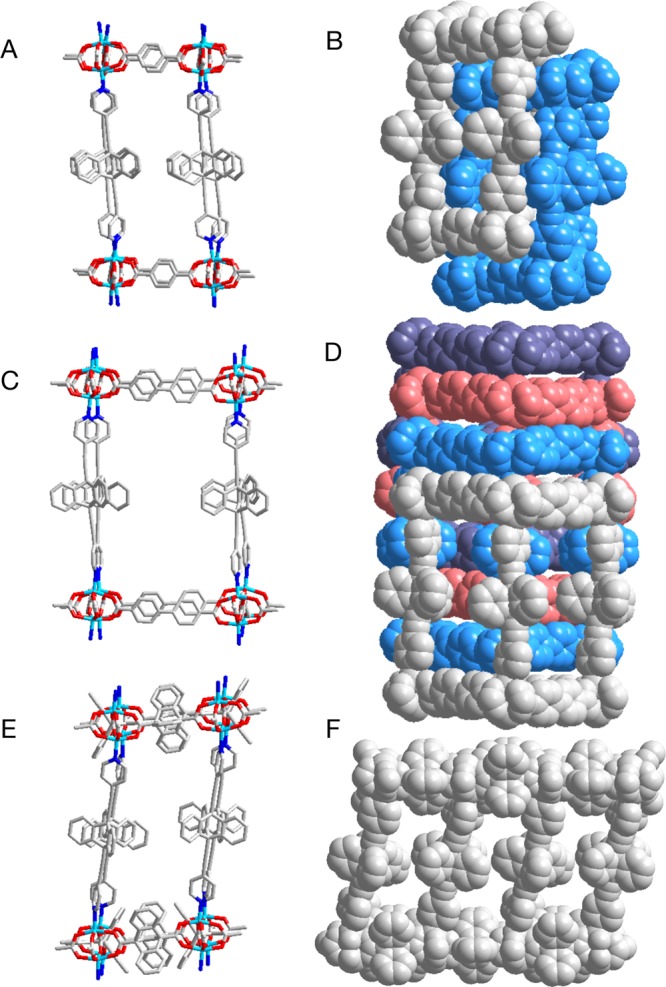
Figure 2

Open in a new tab

Crystal structures of UCLA-R1 (A,B), UCLA-R2 (C,D), and UCLA-R3 (E,F) showing cubelike cages after a partial expansion. Solvent molecules (DMF) and hydrogen atoms are omitted for clarity. The space-filling representations are colored to show the 2-fold (B) and the 4-fold catenated (D) structures. For the capped stick models (A, C, E), the color code is designated as follows: Zn, cyan; N, blue; O, red; C, silver.

Figure 3.

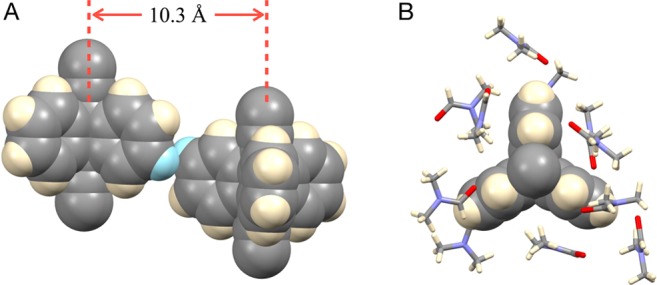
Figure 3

Open in a new tab

(A) The distance between the rotational axes of neighboring triptycene rotators are 10.3 Å, which is close to twice the radius of the volume of revolution of a triptycene rotator. Only two hydrogen atoms highlighted in cyan are relatively close to each other at a distance of 2.9 Å, which is longer than the sum of their van der Waals radii (2.4 Å). (B) DMF molecules are the only ones making van der Waals contacts with the triptycene rotator in the crystal.

The rotational dynamics of triptycene rotators in the pillars were analyzed by solid-state 2H NMR spin echo experiments (SS 2H NMR) using solvent-containing polycrystalline (powder) samples of UCLA-R1-d8, UCLA-R2-d8, and UCLA-R3-d8 with partially deuterated triptycene rotators. Qualitatively, this method takes advantage of changes in the line shape of the spectrum resulting from the dynamic modulation of the C–D bond vectors with respect to the direction of the external magnetic field.40 The line shape is sensitive to motions of frequencies ranging from a few kilohertz to tens of megahertz (ca. 103–107 Hz). Samples with groups bearing static C–D bonds are characterized by a very broad, symmetric spectrum with two shoulders and two peaks, known as a Pake, or powder pattern, which extends for ca. 260 kHz. Similarly, C–D bond vectors aligned with the rotational axis (cone angle 0°) do not change their orientation with the external field as a function of rotation and give rise to the same Pake pattern, as shown by the purple spectra assigned to the α-deuterons in Figure 4B. By contrast, the C–D vector of the β-deuterons (shown in red in Figure 4A) makes a 60° degree angle with the rotational axis and changes its orientation with respect to the external magnetic field. With this difference in mind, we were able to simulate the experimental spectra by assuming that the triptycene rotator undergoes a degenerate 3-fold rotation about the alkyne axis, and that the overall spectrum is a weighted sum of two profiles.41 As shown by spectral simulations in Figure 4B, when the simulated frequency of rotation is low (10 kHz), the β-deuteron spectrum is almost identical to the static pattern; however, its relative intensity is lower than that of α-deuterons because of a reduction factor of 0.17, reflecting a frequency dependent echo-damping effect in two-pulse solid-state echo experiments.42 As the rotation gets faster (500 kHz), the spectrum of the β-deuterons features a set of peaks at the center of the spectrum. Because of an even smaller reduction factor (0.05), the central peaks only account for a small fraction of the overall simulated spectrum. Lastly, when the simulated rate of rotation reaches 10 MHz, the central peaks coalesce into two peaks separated by about 13 kHz. With a relatively large reduction factor of 0.68 and narrow spectrum width, the central peaks become the dominant feature of the overall spectrum.

Figure 4.

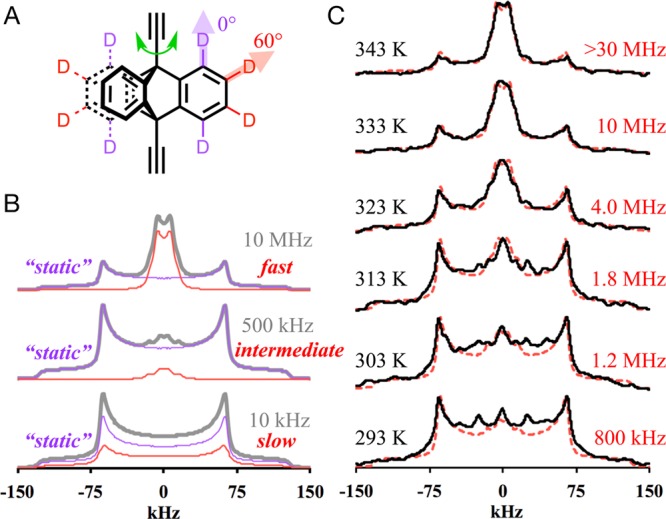
Figure 4

Open in a new tab

(A) Chemical structure of the partially deuterated triptycene rotator highlighting α- and β-deuterons. (B) Simulated 2H NMR spectra (shown in gray) with various rotational frequencies are composed of spectra reflecting “static” α-deuterons (purple) and dynamic β-deuterons (red). (C) Experimental (black solid curves) and simulated (red dashed curves) 2H NMR spectra of UCLA-R3-d8.

Both samples of UCLA-R1-d8 and UCLA-R2-d8 showed spectra with line shape of static rotators at 303 K, and the spectra remained the same when the samples were heated to 373 K, which was close to the upper limit of temperature we could apply before significant solvent evaporation and decomposition (see Supporting Information). These results indicated that the triptycene groups of UCLA-R1-d8 and UCLA-R2-d8 are static, as suggested by their crystal structures. The solvated sample of UCLA-R3-d8, to our delight, displayed a spectrum with some features at the center at 293 K (Figure 4C). As the sample was gradually heated to 343 K, the intensity of the central peaks increased while the intensity of the side peaks decreased. The observed spectra could be reproduced with the simple 3-fold site exchange model previously discussed. The rate of exchange obtained from the best simulation of the experimental data at 293, 303, 313, 323, 333, and 343 K was 1.0, 1.4, 1.9, 4.5, 11, and 30 MHz, with the latter being an estimate, as indicated by the large error bar in Figure 5. Additional SS 2H NMR spin echo experiments performed on partially and completely desolvated samples of UCLA-R3-d8 (see Supporting Information) revealed slower rotational dynamics in agreement with the structural collapse observed before.

Figure 5.

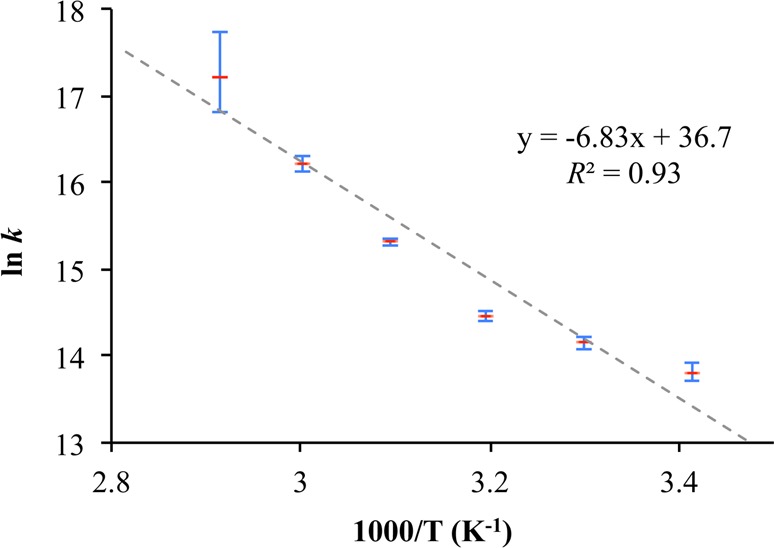
Figure 5

Open in a new tab

An Arrhenius plot shown by the dashed line highlights the large deviation of the data points from the expected linearity.

An Arrhenius plot of the variable temperature data shown in Figure 5 is strongly nonlinear with an upward curvature in the range of temperatures we explored. The best linear fit suggests an activation energy of ca. 13.5 kcal/mol and a pre-exponential factor of 8.7 × 1015 s–1. Considering the large deviation from linearity and the fact that the expected pre-exponential factor for a triptycene rotator should be ca. 4 orders of magnitude smaller (ca. 5 × 1011 s–1),43 one would come to the conclusion that the temperature dependence of the rotational frequency does not reflect a static energy potential from permanent structural features in the crystal.16,44 Knowing that gas phase rotation of the triptycene rotator about the two triple bond axle should be essentially free,45 hindrance must arise from interactions between triptycene and the solvent molecules in the crystal. Interestingly, spin–lattice relaxation studies carried out at ambient temperature in liquid CHCl3 have shown that the correlation time for the rotation of triptycene about its 3-fold axis (50 ps) is about three times longer than the one for rotation about the perpendicular 2-fold axes (16 ps), while the difference between their moments of inertia is relatively small.46−48 This suggests that solvent molecules fill the space between the three blades and slow down the rotation along the 3-fold axis, which is also suggested by the solid-state structural features shown in Figure 3B. Assuming that hydrodynamic theory can describe the behavior of a pinned molecular rotor in a strictly confined liquid, using a calculated molecular volume for triptycene of Vmol = 2.3 × 10–28 m3, and considering that it has a rotational correlation time of ca. τrot = 714 ns at 303 K (from τrot = 1/krot = 1/(1.4 × 106 s–1), Figure 4), we can estimate the dynamic viscosity η of the MOF-confined DMF to be

graphic file with name oc-2016-001687_m001.jpg

which is about 4 orders of magnitude greater than the dynamic viscosity of bulk DMF at the same temperature, ηliq-DMF = 8.2 × 10–4 N s/m2, and is similar to the viscosity of honey.49

A diffusion-controlled mechanism implies that the large activation energy and pre-exponential factor in the case of UCLA-R3 reflect changes in the viscosity of the local environment as a function of temperature where the effect of solvent confinement is manifested in terms of an apparent activation energy that changes from 1.79 kcal/mol in the bulk liquid49 to 13.5 kcal/mol in the MOF cavity.50 The fact that the observed triptycene rotation depends solely on the confined solvents also provides an opportunity to investigate the hydrodynamic properties of such systems with high effective viscosity, to which fluorescence anisotropy decay measurements cannot be applied.43,51,52

Conclusion

We have shown that a simple modular approach leads to the successful preparation of a homologous set of pillared paddlewheel MOFs with a relatively large 9,10-bis(pyridylethynyl)triptycene acting as a pillar and molecular rotator, complemented by dicarboxylate linkers of varying lengths and steric bulk. Single crystals obtained from DMF by changing the linker from terephthalate (UCLA-R1) to biphenyl-4,4′-dicarboxylate (UCLA-R2) and triptycene-9,10-dicarboxylate (UCLA-R3) display 2-fold, 4-fold, and no catenation, respectively, reflecting the amount of space available in their corresponding 2D frames. While the two catenated structures display a tight packing environment with interlattice contacts, the noncatenated crystals of UCLA-R3 have no contacts between pillars and linkers in lattice. Rotation by a Brownian 3-fold jumping mechanism was determined by line shape analysis of SS 2H NMR spectra obtained with tritptycene-d8 labeled samples. Having a barrierless alkyne linkage and no steric interactions, it was suggested that the rotation of the triptycene group in UCLA-R3 is determined by the confined DMF molecules in the lattice. Assuming a hydrodynamic model, we estimate the viscosity of MOF-confined DMF to be about 4 orders of magnitude greater than that of the bulk liquid. The abnormal temperature dependence of the rotational motion with very high apparent activation energy and pre-exponential factor is interpreted in terms of viscosity changes, which suggests an opportunity to analyze the dynamics of fluids under tight confinement at variable temperatures. The results reported here prove the robust nature of molecular and crystal design and reveal new strategies to engineer the dynamics of crystalline rotators.

Acknowledgments

This work is supported by National Science Foundation Grant DMR140268 (M.A.G.-G.) and National Natural Science Foundation of China Grant 21171097 (H.-B.D.).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscentsci.6b00168.

  • Synthesis and characterization of materials, spectroscopic data, and supporting experiments (PDF)

The authors declare no competing financial interest.

Notes

The crystal structures have been deposited at CCDC (1479422–1479424).

Supplementary Material

oc6b00168_si_001.pdf (5.2MB, pdf)

References

  1. Erbas-Cakmak S.; Leigh D. A.; McTernan C. T.; Nussbaumer A. L. Artificial molecular machines. Chem. Rev. 2015, 115, 10081–10206. 10.1021/acs.chemrev.5b00146. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Abendroth J. M.; Bushuyev O. S.; Weiss P. S.; Barrett C. J. Controlling motion at the nanoscale: rise of the molecular machines. ACS Nano 2015, 9, 7746–7768. 10.1021/acsnano.5b03367. [DOI] [PubMed] [Google Scholar]
  3. Coskun A.; Banaszak M.; Astumian R. D.; Stoddart J. F.; Grzybowski B. A. Great expectations: can artificial molecular machines deliver on their promise?. Chem. Soc. Rev. 2012, 41, 19–30. 10.1039/C1CS15262A. [DOI] [PubMed] [Google Scholar]
  4. Kottas G. S.; Clarke L. I.; Horinek D.; Michl J. Artificial molecular rotors. Chem. Rev. 2005, 105, 1281–1376. 10.1021/cr0300993. [DOI] [PubMed] [Google Scholar]
  5. Franchi P.; Bleve V.; Mezzina E.; Schäfer C.; Ragazzon G.; Albertini M.; Carbonera D.; Credi A.; Di Valentin M.; Lucarini M. Structural changes of a doubly spin-labeled chemically driven molecular shuttle probed by PELDOR spectroscopy. Chem. - Eur. J. 2016, 22, 8745–8750. 10.1002/chem.201601407. [DOI] [PubMed] [Google Scholar]
  6. Zheng Z.-G.; Li Y.; Bisoyi H. K.; Wang L.; Bunning T. J.; Li Q. Three-dimensional control of the helical axis of a chiral nematic liquid crystal by light. Nature 2016, 531, 352–356. 10.1038/nature17141. [DOI] [PubMed] [Google Scholar]
  7. Manna D.; Udayabhaskararao T.; Zhao H.; Klajn R. Orthogonal light-induced self-assembly of nanoparticles using differently substituted azobenzenes. Angew. Chem., Int. Ed. 2015, 54, 12394–12397. 10.1002/anie.201502419. [DOI] [PubMed] [Google Scholar]
  8. Zhang L.; Naumov P. Light- and humidity-induced motion of an acidochromic film. Angew. Chem., Int. Ed. 2015, 54, 8642–8647. 10.1002/anie.201504153. [DOI] [PubMed] [Google Scholar]
  9. Cheng C.; McGonigal P. R.; Schneebeli S. T.; Li H.; Vermeulen N. A.; Ke C.; Stoddart J. F. An artificial molecular pump. Nat. Nanotechnol. 2015, 10, 547–553. 10.1038/nnano.2015.96. [DOI] [PubMed] [Google Scholar]
  10. May R.; Jester S.-S.; Höger S. A giant molecular spoked wheel. J. Am. Chem. Soc. 2014, 136, 16732–16735. 10.1021/ja5096705. [DOI] [PubMed] [Google Scholar]
  11. Venkataramani S.; Jana U.; Dommaschk M.; Sönnichsen F. D.; Tuczek F.; Herges R. Magnetic bistability of molecules in homogeneous solution at room temperature. Science 2011, 331, 445–448. 10.1126/science.1201180. [DOI] [PubMed] [Google Scholar]
  12. Iwamura H.; Mislow K. Stereochemical consequences of dynamic gearing. Acc. Chem. Res. 1988, 21, 175–182. 10.1021/ar00148a007. [DOI] [Google Scholar]
  13. Goodsell D. S.The Machinery of Life, 2nd ed.; Springer: New York, 2009. [Google Scholar]
  14. Vogelsberg C. S.; Garcia-Garibay M. A. Crystalline molecular machines: function, phase order, dimensionality, and composition. Chem. Soc. Rev. 2012, 41, 1892–1910. 10.1039/C1CS15197E. [DOI] [PubMed] [Google Scholar]
  15. Lang G. M.; Shima T.; Wang L.; Cluff K. J.; Skopek K.; Hampel F.; Blümel J.; Gladysz J. A. Gyroscope-like complexes based on dibridgehead diphosphine cages that are accessed by three-fold intramolecular ring closing metatheses and encase Fe(CO)3, Fe(CO)2(NO)+, and Fe(CO)3(H)+ rotators. J. Am. Chem. Soc. 2016, 138, 7649–7663. 10.1021/jacs.6b03178. [DOI] [PubMed] [Google Scholar]
  16. Jiang X.; O’Brien Z. J.; Yang S.; Lai L. H.; Buenaflor J.; Tan C.; Khan S.; Houk K. N.; Garcia-Garibay M. A. Crystal fluidity reflected by fast rotational motion at the core, branches, and peripheral aromatic groups of a dendrimeric molecular rotor. J. Am. Chem. Soc. 2016, 138, 4650–4656. 10.1021/jacs.6b01398. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Ichikawa J.; Hoshino N.; Takeda T.; Akutagawa T. Collective in-plane molecular rotator based on dibromoiodomesitylene π-stacks. J. Am. Chem. Soc. 2015, 137, 13155–13160. 10.1021/jacs.5b08215. [DOI] [PubMed] [Google Scholar]
  18. Kaleta J.; Dron P. I.; Zhao K.; Shen Y.; Císařová I.; Rogers C. T.; Michl J. Arrays of molecular rotors with triptycene stoppers: surface inclusion in hexagonal tris(o-phenylenedioxy)cyclotriphosphazene. J. Org. Chem. 2015, 80, 6173–6192. 10.1021/acs.joc.5b00661. [DOI] [PubMed] [Google Scholar]
  19. Harada J.; Ohtani M.; Takahashi Y.; Inabe T. Molecular motion, dielectric response, and phase transition of charge-transfer crystals: acquired dynamic and dielectric properties of polar molecules in crystals. J. Am. Chem. Soc. 2015, 137, 4477–4486. 10.1021/jacs.5b00412. [DOI] [PubMed] [Google Scholar]
  20. Comotti A.; Bracco S.; Ben T.; Qiu S.; Sozzani P. Molecular rotors in porous organic frameworks. Angew. Chem., Int. Ed. 2014, 53, 1043–1047. 10.1002/anie.201309362. [DOI] [PubMed] [Google Scholar]
  21. Comotti A.; Bracco S.; Yamamoto A.; Beretta M.; Hirukawa T.; Tohnai N.; Miyata M.; Sozzani P. Engineering switchable rotors in molecular crystals with open porosity. J. Am. Chem. Soc. 2014, 136, 618–621. 10.1021/ja411233p. [DOI] [PubMed] [Google Scholar]
  22. Setaka W.; Yamaguchi K. Order–disorder transition of dipolar rotor in a crystalline molecular gyrotop and its optical change. J. Am. Chem. Soc. 2013, 135, 14560–14563. 10.1021/ja408405f. [DOI] [PubMed] [Google Scholar]
  23. Lemouchi C.; Iliopoulos K.; Zorina L.; Simonov S.; Wzietek P.; Cauchy T.; Rodríguez-Fortea A.; Canadell E.; Kaleta J.; Michl J.; Gindre D.; Chrysos M.; Batail P. Crystalline arrays of pairs of molecular rotors: correlated motion, rotational barriers, and space-inversion symmetry breaking due to conformational mutations. J. Am. Chem. Soc. 2013, 135, 9366–9376. 10.1021/ja4044517. [DOI] [PubMed] [Google Scholar]
  24. Zhang W.; Ye H.-Y.; Graf R.; Spiess H. W.; Yao Y.-F.; Zhu R.-Q.; Xiong R.-G. Tunable and switchable dielectric constant in an amphidynamic crystal. J. Am. Chem. Soc. 2013, 135, 5230–5233. 10.1021/ja3110335. [DOI] [PubMed] [Google Scholar]
  25. Jarowski P. D.; Houk K. N.; Garcia-Garibay M. A. Importance of correlated motions on the low barrier rotational potentials of crystalline molecular gyroscopes. J. Am. Chem. Soc. 2007, 129, 3110–3117. 10.1021/ja0637907. [DOI] [PubMed] [Google Scholar]
  26. Karlen S. D.; Reyes H.; Taylor R. E.; Khan S. I.; Hawthorne M. F.; Garcia-Garibay M. A. Symmetry and dynamics of molecular rotors in amphidynamic molecular crystals. Proc. Natl. Acad. Sci. U. S. A. 2010, 107, 14973–14977. 10.1073/pnas.1008213107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Jiang X.; Rodríguez-Molina B.; Nazarian N.; Garcia-Garibay M. A. Rotation of a bulky triptycene in the solid state: toward engineered nanoscale artificial molecular machines. J. Am. Chem. Soc. 2014, 136, 8871–8874. 10.1021/ja503467e. [DOI] [PubMed] [Google Scholar]
  28. Inukai M.; Fukushima T.; Hijikata Y.; Ogiwara N.; Horike S.; Kitagawa S. Control of molecular rotor rotational frequencies in porous coordination polymers using a solid-solution approach. J. Am. Chem. Soc. 2015, 137, 12183–12186. 10.1021/jacs.5b05413. [DOI] [PubMed] [Google Scholar]
  29. Vukotic V. N.; O’Keefe C. A.; Zhu K.; Harris K. J.; To C.; Schurko R. W.; Loeb S. J. Mechanically interlocked linkers inside metal–organic frameworks: effect of ring size on rotational dynamics. J. Am. Chem. Soc. 2015, 137, 9643–9651. 10.1021/jacs.5b04674. [DOI] [PubMed] [Google Scholar]
  30. Zhu K.; O’Keefe C. A.; Vukotic V. N.; Schurko R. W.; Loeb S. J. A molecular shuttle that operates inside a metal-organic framework. Nat. Chem. 2015, 7, 514–519. 10.1038/nchem.2258. [DOI] [PubMed] [Google Scholar]
  31. Zhu K.; Vukotic V. N.; O’Keefe C. A.; Schurko R. W.; Loeb S. J. Metal-organic frameworks with mechanically interlocked pillars: controlling ring dynamics in the solid-state via a reversible phase change. J. Am. Chem. Soc. 2014, 136, 7403–7409. 10.1021/ja502238a. [DOI] [PubMed] [Google Scholar]
  32. Murdock C. R.; McNutt N. W.; Keffer D. J.; Jenkins D. M. Rotating phenyl rings as a guest-dependent switch in two-dimensional metal-organic frameworks. J. Am. Chem. Soc. 2014, 136, 671–678. 10.1021/ja4088709. [DOI] [PubMed] [Google Scholar]
  33. Shustova N. B.; Ong T.-C.; Cozzolino A. F.; Michaelis V. K.; Griffin R. G.; Dincă M. Phenyl ring dynamics in a tetraphenylethylene-bridged metal-organic framework: implications for the mechanism of aggregation-induced emission. J. Am. Chem. Soc. 2012, 134, 15061–15070. 10.1021/ja306042w. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Gould S. L.; Tranchemontagne D.; Yaghi O. M.; Garcia-Garibay M. A. Amphidynamic character of crystalline MOF-5: rotational dynamics of terephthalate phenylenes in a free-volume, sterically unhindered environment. J. Am. Chem. Soc. 2008, 130, 3246–3247. 10.1021/ja077122c. [DOI] [PubMed] [Google Scholar]
  35. Farha O. K.; Malliakas C. D.; Kanatzidis M. G.; Hupp J. T. Control over catenation in metal–organic frameworks via rational design of the organic building block. J. Am. Chem. Soc. 2010, 132, 950–952. 10.1021/ja909519e. [DOI] [PubMed] [Google Scholar]
  36. Vagin S. I.; Ott A. K.; Hoffmann S. D.; Lanzinger D.; Rieger B. Synthesis and properties of (triptycenedicarboxylatio)zinc coordination networks. Chem. - Eur. J. 2009, 15, 5845–5853. 10.1002/chem.200802691. [DOI] [PubMed] [Google Scholar]
  37. Shekhah O.; Wang H.; Paradinas M.; Ocal C.; Schüpbach B.; Terfort A.; Zacher D.; Fischer R. A.; Wöll C. Controlling interpenetration in metal-organic frameworks by liquid-phase epitaxy. Nat. Mater. 2009, 8, 481–484. 10.1038/nmat2445. [DOI] [PubMed] [Google Scholar]
  38. Dybtsev D. N.; Chun H.; Kim K. Rigid and flexible: a highly porous metal–organic framework with unusual guest-dependent dynamic behavior. Angew. Chem., Int. Ed. 2004, 43, 5033–5036. 10.1002/anie.200460712. [DOI] [PubMed] [Google Scholar]
  39. Frantz D. K.; Linden A.; Baldridge K. K.; Siegel J. S. Molecular spur gears comprising triptycene rotators and bibenzimidazole-based stators. J. Am. Chem. Soc. 2012, 134, 1528–1535. 10.1021/ja2063346. [DOI] [PubMed] [Google Scholar]
  40. Hansen M. R.; Graf R.; Spiess H. W. Solid-state NMR in macromolecular systems: insights on how molecular entities move. Acc. Chem. Res. 2013, 46, 1996–2007. 10.1021/ar300338b. [DOI] [PubMed] [Google Scholar]
  41. Macho V.; Brombacher L.; Spiess H. W. The NMR-WEBLAB: an internet approach to NMR lineshape analysis. Appl. Magn. Reson. 2001, 20, 405–432. 10.1007/BF03162288. [DOI] [Google Scholar]
  42. Wittebort R. J.; Olejniczak E. T.; Griffin R. G. Analysis of deuterium nuclear magnetic resonance line shapes in anisotropic media. J. Chem. Phys. 1987, 86, 5411–5420. 10.1063/1.452565. [DOI] [Google Scholar]
  43. Inertial rotation of triptycene was obatined from a calculated moment of inertia, I = 1838 g·mol–1·Å2, as indicated in:Kawski A. Fluorescence anisotropy: theory and applications of rotational depolarization. Crit. Rev. Anal. Chem. 1993, 23, 459–529. 10.1080/10408349308051654. [DOI] [Google Scholar]
  44. Vogelsberg C. S.; Bracco S.; Beretta M.; Comotti A.; Sozzani P.; Garcia-Garibay M. A. Dynamics of molecular rotors confined in two dimensions: transition from a 2D rotational glass to a 2D rotational fluid in a periodic mesoporous organosilica. J. Phys. Chem. B 2012, 116, 1623–1632. 10.1021/jp2119263. [DOI] [PubMed] [Google Scholar]
  45. Harris R. K.; Newman R. H. Anisotropic molecular rotation in solution: the interpretation of carbon-13 T1 data for triptycene and 9H-fluorene. Mol. Phys. 1979, 38, 1315–1327. 10.1080/00268977900102451. [DOI] [Google Scholar]
  46. Sipachev V. A.; Khaikin L. S.; Grikina O. E.; Nikitin V. S.; Trætteberg M. Structure, spectra and internal rotation of bis(trimethylsilyl) acetylene: spectral analysis by scaling quantum-chemical force fields and two methods for calculating vibrational effects. J. Mol. Struct. 2000, 523, 1–22. 10.1016/S0022-2860(99)00387-7. [DOI] [Google Scholar]
  47. Saebø S.; Almlöf J.; Boggs J. E.; Stark J. G. Two approaches to the computational determination of molecular structure: the torsional angle in tolane and the effect of fluorination on the structure of oxirane. J. Mol. Struct.: THEOCHEM 1989, 200, 361–373. 10.1016/0166-1280(89)85066-3. [DOI] [Google Scholar]
  48. Abramenkov A. V.; Almenningen A.; Cyvin B. N.; Cyvin S. J.; Jonvik T.; Khaikin L. S.; Rømming C.; Vilkov L. V. Internal rotation in tolane: molecular structure in gas and crystal phases. Acta Chem. Scand. 1988, 42A, 674–684. 10.3891/acta.chem.scand.42a-0674. [DOI] [Google Scholar]
  49. Bernal-García J. M.; Guzmán-López A.; Cabrales-Torres A.; Estrada-Baltazar A.; Iglesias-Silva G. A. Densities and viscosities of (N,N-dimethylformamide + water) at atmospheric pressure from (283.15 to 353.15) K. J. Chem. Eng. Data 2008, 53, 1024–1027. 10.1021/je700671t. [DOI] [Google Scholar]
  50. It is well known that confined liquids have greatly enhanced viscosities, e.g.:Bell R. C.; Wang H. F.; Iedema M. J.; Cowin J. P. Nanometer-resolved interfacial fluidity. J. Am. Chem. Soc. 2003, 125, 5176–5185. 10.1021/ja0291437. [DOI] [PubMed] [Google Scholar]
  51. Lakowicz J. R.Principles of Fluorescence Spectroscopy, 2nd ed.; Kluwer Academic/Plenum Publishers: New York, 1999. [Google Scholar]
  52. Haidekker M. A.; Theodorakis E. A. Molecular rotors–fluorescent biosensors for viscosity and flow. Org. Biomol. Chem. 2007, 5, 1669–1678. 10.1039/B618415D. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

oc6b00168_si_001.pdf (5.2MB, pdf)

Articles from ACS Central Science are provided here courtesy of American Chemical Society

RESOURCES