Computerized triplet beam orientation optimization for MRI-guided Co-60 radiotherapy

Abstract

Purpose:

Magnetic resonance imaging (MRI)-guided Co-60 provides daily and intrafractional MRI soft tissue imaging for improved target and critical organ tracking. To increase delivery efficiency, the system uses three Co-60 sources at 120° apart, allowing up to 600 cGy combined dose rate at isocenter. Despite the potential tripling in output, creating a delivery plan that uses all three sources is considerably unintuitive. Here, the authors computerize the triplet orientation optimization using column generation, an approach that was demonstrated effective in integrated beam orientation and fluence optimization for noncoplanar therapies. To achieve a better plan quality without increasing the treatment time, the authors then solve a fluence map optimization (FMO) problem while regularizing the fluence maps to reduce the number of deliverable MLC segments.

Methods:

Three patients—one prostate, one lung, and one head and neck boost plan (H&N_Boost)—were evaluated in this study. For each patient, the beamlet doses were calculated using Monte Carlo, under a 0.35 T magnetic field, for 180 equally spaced coplanar beams grouped into 60 triplets. The beamlet size is 1.05 × 0.5 cm determined by the MLC leaf thickness and step size. The triplets were selected using the column generation algorithm. The FMO problem was formulated using an L2-norm dose fidelity term and an L1-norm anisotropic total variation regularization term, which allows controlling the number of MLC segments, and hence the treatment time, with minimal degradation to the dose. The authors’ Fluence Regularization and Optimized Selection of Triplets (FROST) plans were compared against the clinical treatment plans (CLNs) produced by an experienced dosimetrist. PTV homogeneity, max dose, mean dose, D95, D98, and D99 were evaluated. OAR max and mean doses, as well as R50, defined as the ratio of the 50% isodose volume over the planning target volume were investigated.

Results:

The mean PTV D95, D98, and D99 differ by +0.04%, +0.07%, and +0.25% of the prescription dose between planning methods. The mean PTV homogeneity was virtually same with values at 0.8788 (FROST) and 0.8812 (CLN). R50 decreased by 0.67 comparing FROST to CLN. On average, FROST reduced D_max and D_mean of OARs by 7.30% and 6.08% of the prescription dose, respectively. The manual CLN planning processes required numerous trial and error runs. The FROST plans on the other hand required minimal human intervention.

Conclusions:

Efficient delivery of MRI-guided Co-60 therapy needs the output of multiple sources yet suffers from unintuitive and laborious manual beam selection processes. Computerized triplet orientation optimization improves both planning efficiency and plan dosimetry. The novel fluence map regularization provides additional controls over the number of MLC segments and treatment time.

1. INTRODUCTION

A newly developed magnetic resonance imaging (MRI)-guided intensity modulated radiation therapy (IMRT) system combines a 0.35 T magnetic resonance imaging scanner with therapeutic gamma-rays from Co-60 sources. The combination provides daily and intrafractional MRI soft tissue and functional imaging for improved target tracking and adaptive radiotherapy.¹ However, the use of cobalt sources instead of x-ray linac has significant implications including low output from a single source and subsequently long treatment time that worsens with Co-60 decay.² To compensate the low output, the system uses three Co-60 sources equidistantly spaced 120° apart to triple the output. However, this source arrangement complicates beam selection. In conventional treatment planning, a dosimetrist would intuitively select beams that better avoid the critical organs. The experience, however, does not apply to the triple source Co-60 platform (tri-Co-60). As shown in Fig. 1, beam 1 is ideally selected to avoid central organs that are sensitive to radiation but the other two beams in the triplet group would penetrate the spinal cord and the heart. The dosimetrist is often compelled to make an undesired trade-off between the plan quality and delivery time. Understandably, the human beam selection becomes increasingly difficult with increasing number of beams. Therefore, there is a strong motivation to computerize beam orientation selection. Previously, we showed in noncoplanar treatment planning that computerized beam orientation optimization is a compelling solution in situation where the manual beam selection is no longer feasible.^3–6 Similarly, a computerized beam orientation optimization method may significantly improve the planning efficiency and quality for the tri-Co-60 platform.

FIG. 1.

Example geometry for a lung tumor (outlined in blue) and critical structures (various colors). A triplet of Co-60 beams is shown to target the tumor. Beam 1 is ideal to treat the tumor and avoid central critical organs but the other two beams in the triplet are suboptimal.

A second important consideration for the study is that the deliverability of the computerized beam selection plans has to be equal to or better than the original clinical plan (CLN). Different from a linac that the x-ray can be switched on and off almost instantaneously, the tri-Co-60 sources need to be retracted into the safe between beam segments in the step-and-shoot IMRT delivery and slow down the treatment. In other words, the tri-Co-60 treatment plans need to be more “frugal” in the number of MLC segments. In the commercial MRI-guided tri-Co-60 planning system, a plan efficiency parameter was implemented to reduce the number of MLC segments. The parameter is effective in attaining plans with a few segments but often at a cost of plan quality. In this study, to compare plans on a fair ground, the number of MLC segments needs to be part of the calculation. In the computerized beam orientation optimization approach, to avoid dose degradation typically seen in conventional fluences map simplification and MLC segmentation,^7–11 we introduce a second dose domain regularization (DDR) problem to reduce the number of MLC segments while maintaining the dosimetric quality. The DDR formulation is convex and can be efficiently solved with the Chambolle–Pock algorithm, a first-order primal–dual algorithm.^12,13 The motivation of the study can thus be summarized as a Fluence Regularization and Optimized Selection of Triplets (FROST) method for tri-Co-60 beam orientation and the fluence optimization.

2. MATERIALS AND METHODS

As explained in the Introduction, FROST planning is divided into three main sequential steps: (1) the computerized triplet angle optimization, (2) the dose domain regularization of the fluence map, and (3) stratification and MLC segmentation. The details are described as follows.

2.A. Step 1: Computerized triplet angle and fluence map optimization (FMO)

The triplet angle selection and fluence map optimization is based on a column generation algorithm, whose variables are tabulated in Table I.

TABLE I.

List and description of variables involved with the column generation algorithm.

Variable	Type	Description
Tall	Set	Set of all available triplets
Tselect	Set	Set of selected triplets
t	Index	Index for triplet
s	Index	Index for OAR
r	Index	Index for PTV
m	Index m ∈ s, r	Index for structure. Includes both OAR and PTV structures
αm	Scalar	Weight for mth structure
$G_m\left(\cdot \right)$	Function	Cost function for mth structure
ft	Vector	Fluence of tth triplet. Single element of ft is referred to as “beamlet”
At	Matrix	Fluence-to-dose transformation matrix for tth triplet
d	Vector	Dose array containing all voxels in dose domain
dm	Vector	Dose array containing only voxels for mth structure
γs	Scalar 0 ≤ γs ≤ 1	Trade-off factor between mean dose and max dose for the sth OAR
pr	Vector	Prescription dose for rth PTV. Entire vector typically set to one value
u	Vector	Lagrange multiplier corresponding to the constraint d = ∑t∈TallAtft
v	Vector	Lagrange multiplier corresponding to the constraint d ≤ q
wt	Vector	Lagrange multiplier corresponding to the constraint ft ≥ 0 for t ∈ Tall

To solve the integrated triplet selection and fluence map optimization problem, we consider the following master problem:

$${\displaystyle \begin{array}{l}\begin{array}{c}\hfill argmin\hfill \\ \hfill d,{\left\{f_t\right\}}_{t\in T_{\text{all}}}\hfill \\ \hfill \hfill \end{array}\sum _{m\in s,r}{\alpha }_m{G}_m\left(d_m\right),\hfill \\ \text{subject}\text{to}d=\sum _{t\in T_{\text{all}}}{A}_t{f}_t,\hfill \\ d\le q\hfill \\ f_t\ge 0\text{for}t\in T_{\text{all}},\hfill \end{array}}$$ (1)

where

$${\displaystyle G_s\left(d\right)={\gamma }_s\text{mean}\left(d_s\right)+\left(1-{\gamma }_s\right)max\left(d_s\right)\text{for}\text{the}s\text{th}\text{OAR},G_r\left(d\right)=\text{mean}\left({\left(p_r-d_r\right)}_{+}\right)\text{for}\text{the}r\text{th}\text{PTV}.}$$ (2)

The optimization variables are the triplet fluence, f_t, and the projected dose, d. The fluence-to-dose transformation matrix, A_t, maps fluence f_t to dose d based on precomputed beamlets. The OAR objective function, G_s, penalizes the mean and max dose for the sth OAR. The weighting factor, γ_s ∈ (0, 1) is determined by the radiobiological seriality of the organ. For parallel and serial organs, γ_s approaches one and zero to weigh more heavily on the mean and max doses, respectively. In this study, γ_s was set to 0.75 for highly parallel structures, such as the lung (LNG), 0.25 for highly serial structures, such as the spinal cord, and 0.5 for organs with seriality in between.

The PTV objective function, G_r penalizes underdosing to the PTV from the prescription dose, p_r. The non-negative operator, ${\left(\cdot \right)}_{+}$, projects the argument onto the non-negative orthant. The structure weight, α_m, determines the importance of individual structures. The upper bound constraint, q, limits the maximum dose to any voxel. In this study, q was set to be 110% of the prescription dose to hard-constrain the maximum dose.

With t ∈ T_all, the master problem is formulated to optimize the fluence of all candidate triplets. However, it is not of our interest to solve the master problem. Other than being computationally expensive, the solution is not practical to deliver. Instead, our goal is to select a small subset of triplets, T_select, that are most important to the master problem. We define a subproblem similar to the master problem,

$${\displaystyle \begin{array}{l}\begin{array}{c}\hfill argmin\hfill \\ \hfill d,{\left\{f_t\right\}}_{t\in T_{\text{select}}}\hfill \\ \hfill \hfill \end{array}\sum _{m\in s,r}{\alpha }_m{G}_m\left(d\right),\hfill \\ \text{subject}\text{to}d=\sum _{t\in T_{\text{select}}}{A}_t{f}_t,\hfill \\ d\le q,\hfill \\ f_t\ge 0\text{for}t\in T_{\text{select}}.\hfill \end{array}}$$ (3)

The only difference here is that the subproblem is solving over t ∈ T_select instead of t ∈ T_all.

The goal of treatment planning is to find a suitable T_select and optimize the fluence using (3). To add a triplet from T_all/T_select to T_select, we evaluate the Karush–Kuhn–Tucker (KKT) conditions¹⁴ of the master problem.

The KKT conditions of the master problem are divided into four condition categories including the primal feasibility, dual feasibility, stationarity, and complementary slackness, of which the dual feasibility and stationarity conditions are used to select the triplets,

$${\displaystyle \left.\begin{array}{l}v\ge 0\hfill \\ w_t\ge 0\text{for}t\in T_{\text{all}}\hfill \end{array}\right\}\text{dual}\text{feasibility}\left.\begin{array}{l}{w}_t=A_t^{T}u\text{for}t\in T_{\text{all}}\hfill \\ u\in \sum _{m\in s,r}\left({\alpha }_m\partial G_m\left(d_m\right)\right)+v_m\hfill \end{array}\right\}\text{stationarity}}$$ (4)

The variables u, v, and w_t are Lagrange multipliers associated to the subject to constraints of the master problem (see Table I). To determine the most valuable triplet that is not currently in the selected set, we are particularly interested in evaluating the Lagrange multiplier, w_t, which is the multiplier corresponding to the constraint f_t ≥ 0. All w_t where t ∈ T_all/T_select are calculated using the first stationarity condition, $w_t=A_t^{T}u$. The Lagrange multiplier u is directly obtained as one of the dual variables from the primal–dual solution of subproblem (3) for a given T_select. Note that this applies to the initialization of optimization when T_select is an empty set. While w_t meets the non-negativity dual feasibility condition for t ∈ T_select, the variable can be negative where t ∈ T_all/T_select. Since w_t is a vector, all the negative values in w_t for a triplet are summed to produce a single value for that triplet. The triplet with the most negative value is responsible for the worst KKT violation and thus will have the highest contribution in reducing the objective value of the master problem. This triplet is added to T_select, and the subproblem (3) is minimized again with the updated T_select. The iteration solves what is known as the pricing problem.¹⁵ The pseudo code of the column generation algorithm for triplet selection and fluence optimization is as follows.

• •Initialize empty selection set T_select
• •Repeat until desired number of triplets is achieved

  {

• •Solve subproblem in Eq. (3)
• •Directly obtain Lagrangian multiplier u
• •Calculate $w_t=A_t^{T}u$ for t ∈ T_all/T_select
• •Find $t^{*}=\begin{array}{c}\hfill argmin\hfill \\ \hfill t\in T_{\text{all}}/T_{\text{select}}\hfill \\ \hfill \hfill \end{array}\text{sum}\left({\left(w_t\right)}_{-}\right)$
• •Add t^* to T_select

  }

The non positive projection operator, ${\left(\cdot \right)}_{-}$, projects the argument onto the nonpositive orthant. The formulation is solved using CPLEX (IBM, Academic Research Edition 12.2).

2.B. Step 2: Dose domain fluence map regularization formulation

For tri-Co-60 planning, it is equally important to minimize the number of MLC segments via simplification of the fluence maps. We introduced fluence map regularization in the dose domain optimization problem to control the number of MLC segments while maintaining the optimization results.¹⁶ This dose domain regularization method is shown superior to other fluence map simplification methods that relied on smoothing the map while minimizing the difference between the original and simplified map,^7–11 due to the fact that the fidelity term minimized error in the dose domain, rather than the fluence domain. The DDR method was applied to the problem at hand following the cost function:

$${\displaystyle \arg \hspace{0.17em}\min {\left\{f_t\right\}}_{t\in T_{\text{select}}}\frac{1}{2}{∥W\left(\sum _{t\in T_{\text{select}}}\left(A_t{f}_t\right)-d_0\right)∥}_2^2+\lambda \sum _{t\in T_{\text{select}}}\left(D_1{f{}_t}_1+\lambda D_2{f{}_t}_1\right)\text{subject}\text{to}{f}_t\ge 0\text{for}t\in T_{\text{select}}}$$ (5)

W is a diagonal weighting matrix that weights the structures of interest. D₁ and D₂ take the derivatives of the fluence parallel and perpendicular to the MLC leaf movement direction. The weighting matrix W is initially selected based from the α_m in the triplet selection processes, and minor adjustments are made if the dosimetry is not acceptable. The weight λ controls how much influence the total variation (TV) term has on the cost function and was set as λ = 1/100 ∥ [A_t=1…A_t=n]∥₁. For some vector, x, the pth norm is defined as ${∥x∥}_p=\sqrt[p]{{\sum }_i{\left(x_i\right)}^p}$.

The optimization formulation, Eq. (5), was solved utilizing the Chambolle–Pock algorithm, a proximal-class primal–dual algorithm.^12,13 This optimization formulation, with an L2-norm fidelity and an anisotropic total variation regularization, matches the formulation presented previously for dose domain regularization,¹⁶ which the only exception being the added weighting term, W. With the same base formulation, the operations performed for using the Chambolle–Pock algorithm are identical to the one presented previously, which was already described in great detail. The Chambolle–Pock algorithm efficiently handles problems of this form, since it does not need to solve a system of linear equations at each iteration. The majority of its computational expense comes from the straightforward multiplication of A_t, D₁, and D₂ on to the fluence and its corresponding dual variable at each iteration.

It is noted that the FROST approach is heuristic and does not guarantee global optimality. This algorithm for triplet selection is greedy in nature, and the dose domain regularization is a separate optimization with a different cost function, performed after the triplet selection process is entirely finished.

2.C. Step 3: Stratification and MLC segmentation

In order to convert the optimized fluence maps into MLC deliverable fluence maps, an MLC segmentation algorithm, based on the reducing level method by Xia and Verhey,¹¹ is implemented. This algorithm stratifies the fluences into a discrete equal step sizes, and then, using the reducing level method, breaks down the binned fluence to segments that are deliverable along the leaf direction. Further details on the algorithm were presented previously.¹⁶ A bisection algorithm that adjusts the stratification step size is utilized to find a specified number of deliverable segments.

2.D. Evaluation

Three patients, which include one prostate (PRT), one lung, and one head and neck boost plan (H&N_Boost), were evaluated in this study. Patient data are shown in Table II, including the initial plan for the head and neck case (H&N_Initial), which was also planned and treated with the MRI-guided tri-Co-60 platform. The beamlet dose was calculated using a Monte Carlo dose calculation engine derived from the well-verified dose planning method (DPM)¹⁷ with various improvements in efficiency, step size artifact, and variance reduction techniques. This implementation considers all electrons set free from interaction sites with a high weighting (i.e., considers them to be “fat”), which leads to an increased degree of uncertainty when a low number of statistics are used, especially in the out-of-field region where contaminant electron statistics are poor. The engine utilizes the patient electron density for dose calculation and also accounts for the attenuation of the patient couch during simulation. The number of histories per beamlet was set to 10⁶, as compared to the 2.5 × 10⁶ particle histories used clinically. The magnetic field was included in the simulation to accurately account for its effect on secondary electron scatter. The beamlet size is 1.05 × 0.5 cm, as defined by the MLC leaf width and the step size. For each beam, MLC positions were conformed to the PTV structure +1 cm margin from beam’s eye view to create a set of conformal fields. In order to reduce out-of-field dose that is primarily caused by Monte Carlo calculation noise in each beamlet, the beamlet dose outside the 9 cm diameter cylinder along the beamlet axis was set to zero. Figure 2 shows a comparison of the beamlet dose with and without the cutoff applied. For each patient, the beamlet dose was calculated for 180 coplanar beams, spaced 2° apart, and the beams were grouped into 60 triplets. After dose calculation, the dose information is stored into the dose matrix A_t for each triplet, to allow for conversion from the beamlet intensity to the dose.

TABLE II.

Prescription dose and PTV volume for each patient case.

	Prescription dose (Gy)	PTV volume (cm3)
PRT	40	68.909
LNG	50	8.094
H&NBoost	14	4.363
H&NInitial	66	28.190

FIG. 2.

Beamlet dose comparison between the raw Monte Carlo dose without cropping (left) and the dose after cropping was applied (right). Cropping allows for the removal of the extra noise outside of the beamlet-line to reduce computational expense without affecting the beamlet’s dose contribution.

For evaluation, the FROST plans were compared against the clinical plans (CLNs), which were produced by an experienced dosimetrist. The H&N_Boost plan was compared standalone, as well as a comparison as a plan sum with the initial H&N plan (H&N_PlanSum). The plan sums for the FROST and CLN methods both use the same H&N_Initial plan, and the only differing aspect is the FROST or CLN boost plan. PTV homogeneity, max dose, mean dose, D95, D98, and D99 were evaluated. OAR max and mean doses were also evaluated and compared. PTV homogeneity is defined as D95/D5. The maximum dose, following the recommendations of ICRU-83,¹⁸ is defined as the dose to 2% of the structure volume, D2. R50, a measure of high dose spillage and defined as the ratio of the 50% isodose volume over the planning target volume, was also determined.

3. RESULTS

The Monte Carlo beamlet dose calculation took an average of 5 h per patient for all 180 coplanar beams using a CPU. This is an additional one time cost compared to the commercial planning system using a proprietary analytical model to calculate beamlets only for the few manually selected beams. However, the time is expected to reduce with GPU parallelization and adopting a similar analytical beamlet model. The dose matrix size ranged from 20 to 40 MB per beam—approximately 100 MB per triplet. The beam angle selection process took 20–30 min to complete, and the dose domain fluence map regularization process took approximately 5 min. The process was repeated if OAR and PTV weighting parameters needed to be retuned. On average, the weighting parameters were retuned two to three times for an acceptable dose distribution. It should be noted that no interaction is needed with the optimizers while it is running, so the time needed for active user intervention is minimal. In comparison, the laborious manual planning by the dosimetrists took several hours or longer to complete a plan.

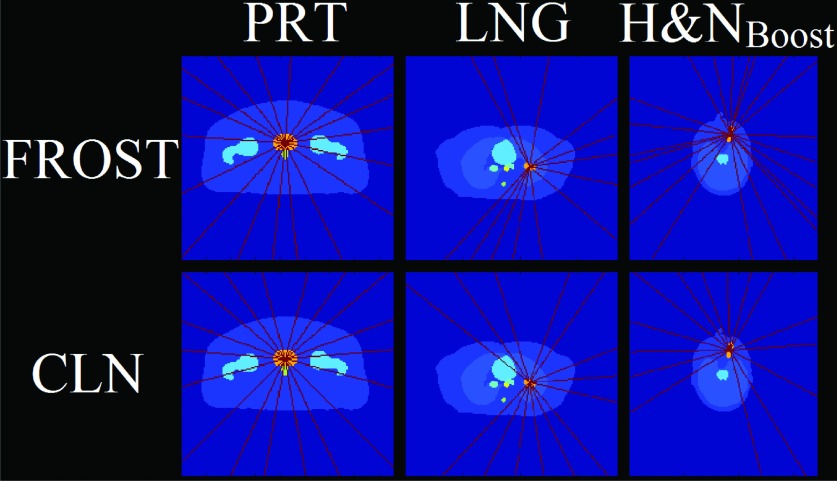
The FROST plans either resulted in same or fewer beam groups than the CLN cases. Because of the capability of simultaneous delivery of the grouped beams, the delivery time is heavily influenced by the number of triplets rather than the number of on beams. The number of beam groups and its breakdown into triplets, doublets, and singlets is shown in Table III. The PRT case used similar beam groups and arrangements between both FROST and CLN plans. However the LNG and H&N_Boost cases used markedly different beam orientations in FROST than in CLN, shown in the schematic in Fig. 3. Although the total number of beams is the same in FROST and CLN for the LNG case, there are fewer beam groups in FROST than that in CLN and all beam groups are triplets in FROST vs two triplets and three doublets in CLN. The H&N_Boost case used the same number of beam groups in both FROST and CLN, but the selected FROST beam groups are all triplets, in contrast to the CLN plan that used two triplets, four doublets, and one singlet.

TABLE III.

Beam triplet and number of segments per beam data for each case.

		Number of
Patient case		Beam groups	Triplets	Doublets	Singlets	“On” beams	Average number of segments per beam
PRT	FROST	6	6	0	0	18	8.77
	CLN	6	6	0	0	18	8.77
LNG	FROST	6	1	5	0	13	2.31
	CLN	6	3	2	1	14	2.29
H&NBoost	FROST	7	7	0	0	21	3.00
	CLN	7	2	4	1	15	2.73

FIG. 3.

Schematic of the beam angle arrangements for the on beams for each case. The beam angles are indicated in red and the PTV in orange. All other OARs are displayed in various colors.

Figure 4 shows a FROST fluence map that is subject to stratification and MLC segmentation. The total variation regularization term in the FROST formulation encourages piecewise smoothness in the fluence maps, giving the fluences a blocky pattern that is robust to the MLC segmentation step. As shown in Fig. 4, the fluence map was minimally changed with stratification and the MLC segmentation to preserve the optimized plan quality.

FIG. 4.

Schematic of a PRT beam fluence optimized with FROST, and then undergoing postprocessing steps, described previously (Ref. 16) to make it deliverable.

Figure 5 shows the DVHs for the three patients and the plan sum of the H&N case. Qualitatively, the FROST plans better spared the OARs while maintaining a comparable PTV dosimetry. For PRT, all OAR doses and the PTV dose homogeneity were improved with FROST. The H&N_Boost case shows essentially the same PTV dose with markedly improved dose sparing in the critical structures, including a 4 Gy reduction to the left optical nerve using the FROST plan.

FIG. 5.

DVHs of all the patient cases, including the plan sum.

On average, D95, D98, and D99 between FROST and CLN methods differed by +0.04%, +0.07%, and +0.25% of the prescription dose, showing that dose coverage is virtually the same for all of the cases. The mean PTV homogeneity, between all the cases, also showed to be nearly identical with values at 0.8788 (FROST) and 0.8812 (CLN). R50, on average, decreased by 0.67 with FROST over CLN. The largest increase in max dose was the oral cavity by 0.55 Gy in the H&N_Boost case, but this was still a minor change compared to the 4.38 Gy that the FROST plan was able to spare the eyes. On average, FROST was able to spare D_max and D_mean from the OARs by 7.30% and 6.08%, respectively. More detailed statistics for the PTV and R50 are shown in Table IV and for the OARs are shown in Table V.

TABLE IV.

Statistics for R50, PTV homogeneity, dose coverage (D95, D98, and D99), and D_max.

		PTV statistics
		Homogeneity		D95	D98	D99	Dmax	R50
Patient case		FROST	CLN	DFROST − DCLN (Gy)				FROST	CLN
PRT		0.945	0.938	+0.02	+0.02	−0.07	−0.34	5.954	7.909
LNG		0.840	0.834	+0.04	−0.02	+0.10	−0.01	11.467	10.587
H&NBoost		0.894	0.906	+0.00	+0.03	+0.16	+0.20	17.551	18.500
H&NPlanSum	PTV	0.779	0.794	−1.48	−1.36	−1.30	−0.03	8.829	8.631
	Boost PTV	0.936	0.934	+0.28	+0.43	+0.43	+0.18

TABLE V.

Largest, smallest, and average values found for (FROST-CLN) dose differences for D_max and D_mean.

	Dmax			Dmean
Dose difference DFROST − DCLN (Gy)	Largest value	Smallest value	Average value	Largest value	Smallest value	Average value
PRT	+0.13	−3.96	−1.42	−1.98	−5.88	−4.01
	Bladder	Penile bulb		L Femur	Penile bulb
LNG	−0.29	−5.61	−2.27	−0.23	−3.30	−1.00
	Cord	Bronchus		Cord	Bronchus
H&NBoost	+0.55	−4.38	−1.41	+0.14	−4.37	−0.90
	Oral cavity	Eyes		Oral cavity	L Opt Nrv
H&NPlanSum	+0.52	−4.48	−1.36	+0.13	−4.38	−0.90
	Mandible	Eyes		Oral cavity	L Opt Nrv

The H&N_PlanSum case saw similar dose sparing to the H&N_Boost plan. The FROST plan had better boost PTV coverage in the plan sum. Although the original PTV had a lower D95, D98, and D99 in FROST, it should be noted that the H&N_Boost plan did not have the original PTV in their objectives and that the initial plan had met all of the dose coverage criteria.

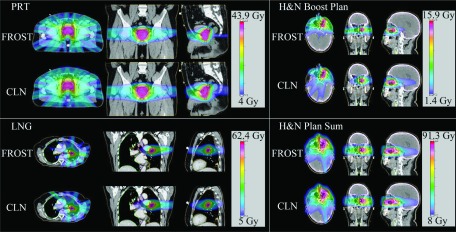
Figure 6 shows the dose color wash for all of the patients. The dose distributions produced by FROST are visually different from those produced by CLN, particularly in the LNG and H&N_Boost cases. The LNG FROST plan spared the right lung volume from 5 Gy or greater doses, as opposed to the large dosing the anterior tip of the right lung volume in the CLN plan. Likewise, the H&N_Boost FROST plan clearly better spared the brain than the CLN plan. The PRT case has fairly similar dosimetry between both the FROST and CLN plans, but improved dose conformity can be appreciated for doses above 20 Gy showing in green. The dose conformity improvement was also confirmed by the lower R50 for the FROST plan in Table IV.

FIG. 6.

Dose washes of the three cases as well as the H&N_PlanSum. Dose cutoff for viewing is 10% of the prescription dose.

4. DISCUSSION

Because of the superior soft tissue contrast, MRI-guided radiotherapy has the promise of improving image guided radiation therapy. It may also pave the path to longitudinal monitoring of the tumor and normal tissue response to radiotherapy using multiparametric imaging such as the diffusion MRI for cellularity measurement.¹ However, it is a significant engineering challenge to combine the therapy and imaging modalities in the same platform. The MRI-guided tri-Co-60 system uses a simpler radiation source and was able to gain early clinical access that is extremely valuable for accumulating knowledge about MRI-guided RT.^19–28 There are several known limitations with Co-60 sources, including lower energy and penetration, compared to the 6 MV and above x-ray energies used by a conventional linac and large source size (2 cm) compared to the linac source (∼2 mm). Relevant to the current study, in addition to these known limitations in using the Co-60 sources, treatment planning on the tri-Co-60 system is counterintuitive due to the triplet source arrangement designed to increase the dose rate, making approaching a clinically acceptable plan difficult even after tedious manual searching of beam orientations.

Another difficulty in tri-Co-60 planning is to balance the plan quality against the number of MLC segments, which substantially influence the plan delivery time due to the mechanical motion needed to shield the source between MLC segments. Conventional methods to smooth the fluence map inevitably degrade the plan quality but the degradation is not as obvious when the number of MLC segments is not as restrictive.

The contribution of the current study is to show that the last two issues are manageable. The computerized beam triplet selection chose the optimal triplets via column generation, and FMO formulation utilized a L2-norm fidelity term to minimize the dose distribution of the prescription dose, and an anisotropic total variation regularization to encourage piecewise smoothness in the fluence maps. The column generation algorithm was inspired by the column generation method for direct aperture optimization outlined by Romeijn et al.¹⁵ While being applied to a different problem, both algorithms use the KKT information to determine the next action to perform. The column generation approach was successfully retooled for noncoplanar beam angle selection.^3–6,29,30 The advantage of column generation, besides being efficient to solve large scale optimization problems, is to be able to integrate fluence optimization into the triplet selection. Instead of relying on human operators to select the triplet orientations, the computerized beam orientation identified optimal triplets that may seem unintuitive to human operators. The tri-Co-60 planning problem further benefits from the dose domain optimization with fluence map regularization that is able to control the dose degradation while minimizing the number of MLC segments.

Our method can be applied to other planning problems involving multiple sources at fixed geometry, such as the GammaKnife³¹ and the GammaPod.³² Although these devices are not equipped with MLC but inverse optimization utilizing available cones can be performed. The demonstrated beam orientation optimization method can be used to improve the delivery efficiency by using as many sources as possible at the same time.

5. CONCLUSION

A Fluence Regularization and Optimized Selection of Triplets (FROST) method for tri-Co-60 beam orientation and the fluence optimization was developed to overcome the planning challenges imposed by the multiple source geometry. Although the process is heuristic and does not guarantee optimality, the results showed that the more efficient FROST plans also yielded universally superior quality plans than manually created plans.

CONFLICT OF INTEREST DISCLOSURE

The authors have no COI to report.