Abstract
Purpose
Parallel imaging and partial Fourier acquisition are two classical approaches for accelerated MRI. Methods that combine these approaches often rely on prior knowledge of the image phase, but the need to obtain this prior information can place practical restrictions on the data acquisition strategy. In this work, we propose and evaluate SENSE-LORAKS, which enables combined parallel imaging and partial Fourier reconstruction without requiring prior phase information.
Theory and Methods
The proposed formulation is based on combining the classical SENSE model for parallel imaging data with the more recent LORAKS framework for MR image reconstruction using low-rank matrix modeling. Previous LORAKS-based methods have successfully enabled calibrationless partial Fourier parallel MRI reconstruction, but have been most successful with nonuniform sampling strategies that may be hard to implement for certain applications. By combining LORAKS with SENSE, we enable highly-accelerated partial Fourier MRI reconstruction for a broader range of sampling trajectories, including widely-used calibrationless uniformly-undersampled trajectories.
Results
Our empirical results with retrospectively undersampled datasets indicate that when SENSE-LORAKS reconstruction is combined with an appropriate k-space sampling trajectory, it can provide substantially better image quality at high-acceleration rates relative to existing state-of-the-art reconstruction approaches.
Conclusion
The SENSE-LORAKS framework provides promising new opportunities for highly-accelerated MRI.
Keywords: Parallel MRI, Partial Fourier Reconstruction, Constrained Reconstruction, Low-Rank Matrix Recovery
Introduction
Slow data acquisition speed has always been a major limitation of MRI. While many speed improvements have been achieved over the past 40+ years of MRI technology development, relatively long data acquisition times are still a barrier in many important clinical and research scenarios.
Existing strategies for making MRI experiments faster include:
The use of specialized pulse sequences that rapidly sample k-space like echo-planar imaging (EPI) (1), spiral imaging (2), and steady-state free precession (SSFP) imaging (3,4).
The use of novel non-Fourier encoding mechanisms like the spatially-varying sensitivity profiles of an array of receiver coils (5–12) and tailored spatially-selective radiofrequency pulses (13–18).
The use of powerful constrained reconstruction approaches that use prior knowledge about the image characteristics (e.g., phase constraints (19–23), support constraints (22, 24, 25), sparsity constraints (26–31), and rank constraints (32–34)) to enable data sampling below the conventional Nyquist rate.
These different fast imaging strategies can be combined in some scenarios to enable even higher acceleration rates. However, it's often the case that the ideal sampling strategy is different for different fast imaging methods. For example, fast EPI and balanced SSFP pulse sequences can be more prone to artifacts when used with nonuniform phase encoding step sizes (35, 36), and are most easily used with uniform k-space sampling. In contrast, advanced reconstruction methods based on sparsity or rank constraints often advocate the use of sub-Nyquist random or nonuniform k-space sampling (26–29, 31–34), while phase-constrained partial Fourier methods often require a sizeable region from the center of k-space (a “calibration region”) to be sampled at the Nyquist rate in order to estimate the image phase (20–22). These different sampling considerations are nontrivial to reconcile, and practical trade-offs are often made when these fast imaging methods are combined that end up limiting the potential acceleration rates.
In this work, we propose a new method called SENSE-LORAKS that combines parallel imaging with constrained image reconstruction based on phase and support constraints, in a manner that enables simple combination of partial Fourier acquisition with arbitrary sampling trajectories, including the uniform undersampling strategies used by fast EPI and balanced SSFP pulse sequences. Unlike existing methods for using these constraints, this is achieved using a flexible regularization constraint, without any need for the k-space trajectory to include a phase calibration region, nonuniform sampling, prior information about the image phase or support, or specialized processing to account for the features of the sampling pattern.
As the name would suggest, one component of SENSE-LORAKS is based on our original LORAKS (Low-RAnk modeling of local K-Space neighborhoods) framework (37,38), which has recently been generalized in a number of ways (39–44). LORAKS is a novel constrained image reconstruction framework that is based on the fact that many MRI images have limited spatial support (i.e., there are empty regions within the field of view) and smoothly varying phase. These are the same constraints used in classical support-constrained and phase-constrained image reconstruction methods (19–22, 24, 25). However, a key difference from previous methods is that LORAKS does not require a prior estimate of the image phase or image support and does not require calibration data. This gives additional flexibility in the design of k-space sampling patterns, which can be leveraged to achieve higher experimental efficiency. However, a potential limitation of the LORAKS framework is that it often has substantially lower performance with uniform sampling relative to nonuniform sampling and/or sampling with a calibration region. To address this limitation, SENSE-LORAKS combines the LORAKS framework with the SENSE (SENSitivity Encoding) model for parallel imaging data acquisition (6, 7). SENSE modeling is powerful in this setting because it can use prior knowledge of the coil sensitivity maps (derived from a prescan) to resolve the structured aliasing ambiguities associated with uniform undersampling, while also providing benefits when used with arbitrary trajectories.
It should be noted that SENSE has already been combined with phase and support constraints in a number of different ways (45–50). However, unlike SENSE-LORAKS, these techniques all require a good prior estimate of the image phase and support, which is derived using a calibration region and/or specialized trajectory-specific data processing.
It should also be noted that SENSE-LORAKS is not the first generalization of LORAKS to parallel imaging. The LORAKS framework was previously extended to parallel imaging in a framework known as P-LORAKS (39), which leverages similar parallel imaging constraints to earlier methods like GRAPPA (8), PRUNO (11), ESPIRiT (12), and especially SAKÉ (34), but also enforces additional phase constraints. Compared to SENSE-LORAKS, P-LORAKS is fully calibrationless and does not require prior information about the coil sensitivity maps. P-LORAKS and SENSE-LORAKS both utilize the same regularization penalty, allowing both approaches to enforce the same kinds of calibrationless support and phase constraints. However, for cases where coil sensitivities are available, SENSE-LORAKS can take advantage of this additional information to produce improved reconstructions. This leads to substantial advantages for SENSE-LORAKS over P-LORAKS, particularly for widely-available uniform undersampling trajectories.
Theory
Review of SENSE and Phase-Constrained SENSE
The SENSE framework models parallel MRI data acquisition as (6,7)
| [1] |
for m = 1, 2,…, M and ℓ = 1, 2,…, L, where ρ(x) is the unknown image to be estimated (which varies as a function of the spatial position x), dℓ(km) is the data measured from the ℓth coil at the mth k-space location km, sℓ(x) is the sensitivity map for the ℓth channel, and nℓ(km) is the measurement noise from the ℓth coil at the mth k-space location. We use M to denote the number of k-space sampling locations and L to denote the number of channels.
Discretizing ρ(x) in terms of Q different voxels leads to
| [2] |
for m = 1, 2,…, M and ℓ = 1, 2,…, L, which can be written compactly as the matrix equation
| [3] |
where d is the length-LM vector of data samples from each coil dℓ(km), E is the LM × Q matrix containing entries e−i2πkm⋅xqsℓ(xq), ρ is the length-Q vector of unknown voxel coefficients ρ(xq), and n is the length-LM vector of noise samples nℓ(km).
Assuming Gaussian noise and that the inter-channel noise covariance has been whitened, the SENSE approach finds the statistically-optimal maximum likelihood estimate for ρ (when E has full column rank) by solving the simple least squares problem (6,7)
| [4] |
The matrices E, EH, and EHE are generally too big to fit within the memory limits of modern computers, so are neither stored in memory nor directly inverted. Instead, the solution to Eq. [4] can be found iteratively, using diagonal matrices, fast Fourier transforms (FFTs), and gridding (if non-Cartesian trajectories are used) to efficiently compute matrix-vector multiplications with E and it's adjoint EH (7).
When k-space data is aggressively undersampled, Eq. [4] is frequently ill-posed, and it is necessary to impose additional constraints to avoid severe noise amplification. The most common approach is to use Tikhonov regularization (51,52)
| [5] |
which prefers reconstructions with smaller ℓ2-norms. The regularization parameter λT can be chosen to adjust the relative contributions of the data fidelity term and the regularization term to the final reconstruction.
Phase-constrained partial Fourier methods are based on the well-known fact that real-valued images will have conjugate-symmetric Fourier transforms (19–22). As a result, it is unnecessary to measure data from both sides of k-space for such images, leading to substantial accelerations in data acquisition. In practice, MRI images are never real-valued, and instead will typically have slowly-varying phase. However, if the image phase is known, it is still possible to predict one side of k-space from the other (20–22), which still enables acceleration by almost a factor of two.
Phase-constrained approaches have been previously combined with SENSE reconstruction (45–50), and a typical approach is to use regularization to enforce the phase constraints (46–49). Let ϕ̂(xq) denote the estimated phase for the gth image voxel ρ(xq), and let P be a Q × Q diagonal matrix of eiϕ̂(xq) values. Phase-constrained SENSE approaches generally solve
| [6] |
where Imag{PH ρ} is the imaginary part of PH ρ and λP is another regularization parameter that controls the strength of the phase constraint. Notice that if ϕ̂(xq) is estimated accurately, then PH ρ should be real-valued and Imag{PHρ} ≈ 0. This phase constraint is enforced by the third term of the cost function, which is the only difference between phase-constrained SENSE and Eq. [5].
Typically, the phase information needed for phase-constrained SENSE is estimated by acquiring additional phase calibration data from the low-frequency region of k-space. Measurement of this calibration information usually requires additional scan time, which limits achievable acceleration rates. In addition, measuring a Nyquist-sampled calibration region is not easily compatible with uniformly-undersampled accelerated EPI or balanced SSFP acquisitions.
Review of LORAKS and P-LORAKS
Our previous LORAKS work (37,38,40) was based on the observation that the linear k-space dependencies used for phase-constrained (19–22) and support-constrained (22,24,25) MRI reconstruction could be mapped into the nullspace vectors of specially-constructed structured matrices formed from Nyquist-sampled k-space data. As a result, powerful recent low-rank matrix recovery techniques (53) could be used to reconstruct MRI images from noisy and/or undersampled k-space data. Importantly, this approach could be used with both calibration-based and calibrationless partial Fourier k-space trajectories, and could be used without any prior information of the image support or phase. In addition, the support and smooth-phase constraints could be imposed as generic low-rank regularization penalties that can be combined with arbitrary k-space sampling trajectories and arbitrary additional regularization constraints. LORAKS has been demonstrated to offer unique capabilities, and enables the use of promising novel k-space sampling trajectories that are not very compatible with existing reconstruction approaches.
The early LORAKS literature describes three different ways of constructing low-rank matrices from k-space data (37,38). All three of these low-rank matrix constructions could be used simultaneously within the LORAKS framework. However, to simplify the description, we focus in this work on one specific low-rank matrix construction (called the “S matrix” in previous literature) that has been empirically observed to be the most powerful of the low-rank matrix constructions across a range of applications (37–40,43,44). Using the S matrix alone instead of using all three matrices together has the effect of reducing computational complexity and simplifying the selection of regularization parameters, with only minor performance degradations observed in previous empirical studies (37). Due to space limitations, we only present a high-level description of the S matrix, and refer interested readers to (37) for further detail.
For simplicity, we will assume for this description that ρ(x) is a 2D image and that the discretization ρ(xq), q = 1, 2,…, Q is defined on a rectilinear grid of sampling locations. Let F be the Q × Q unitary FFT matrix such that f = Fρ is the length-Q vector of Nyquist-grid samples of the Fourier transform of ρ. We will use the notation f[p] to denote the value of f at the grid point specified by the integer vector p ∈ ℤ2. The S matrix can be constructed from the vector f according to a linear operator 𝒫S(⋅) : ℂQ → ℝ2T× 2NR defined by
| [7] |
where the matrices Sr+, Sr−, Si+, Si− ∈ ℝT×NR have elements,
| [8] |
| [9] |
| [10] |
| [11] |
In this expression, the vectors mq, q = 1, 2,…, NR are the full set of integer vectors within a radius of R from the origin (i.e., ), and the vectors pt ∈ ℤ2, t = 1,2,…,T are the full set of integer vectors from a rectilinear Nyquist-sampled k-space grid. It should be observed that the matrices Sr+, Sr−, Si+, Si− are all convolution matrices, and that each row from these matrices is constructed from a local neighborhood of NR points in k-space. The neighborhood radius R is a user-selected parameter that plays a similar role to the kernel size in GRAPPA and related parallel imaging methods (8,11,12,34). It should also be noted that Sr+ and Si+ are formed using data from the opposite side of k-space relative to Sr− and Si−, as would be expected since the S matrix captures linear dependence relationships between opposite sides of k-space. It has been shown that the S matrix will have low rank if the continuous image ρ(x) has limited spatial support or slowly-varying phase (37,40).
P-LORAKS (39) extends LORAKS to parallel imaging data, leveraging the same inter-channel linear dependence relationships used in previous Fourier-domain parallel imaging methods (8, 11,12,34). Specifically, if f1, f2,…, fL are the Nyquist-sampled k-space data from L different channels in a parallel imaging experiment and fP denotes the length-LQ vector concatenating them, then P-LORAKS constructs a modified S matrix using the linear operator 𝒫PS(⋅) : ℂLQ → ℝ2T×2LNRdefined by
| [12] |
i.e., the concatenation of the single-channel S matrices. The single-channel S matrices will have low rank if the image has limited support or slowly-varying phase, and the concatenation will have even better low-rank characteristics because of correlations between different channels. Importantly, this enables parallel imaging reconstruction without requiring knowledge of the sensitivity maps and without requiring a fully-sampled k-space calibration region.
The P-LORAKS matrix reduces to the LORAKS matrix when the number of channels L = 1, so we will use P-LORAKS notation without loss of generality. In much of our previous work (37–40,44), LORAKS/P-LORAKS image reconstruction was performed by minimizing
| [13] |
where U ∈ ℂLM×LQ is a block diagonal matrix representing the k-space subsampling operation for each channel, and ‖ ⋅ ‖F denotes the Frobenius norm. The first term in this expression is a standard maximum likelihood data fidelity term, while the second term is a nonconvex regularization penalty that encourages the S matrix to have low rank. The regularization parameter λS controls the tradeoff between these two terms. The operator ℒr : ℝ2T×2LNR → ℝ2T×2LNR computes the optimal rank-r approximation of its argument (using truncation of the singular value decomposition (54)), where r is a user-selected rank parameter.
The optimization problem in Eq. [13] is a nonconvex approach to imposing rank constraints that incorporates prior knowledge of the matrix rank. We have previously shown (55) that this kind of formulation can offer substantial performance advantages over alternative convex relaxation approaches that are popular for imposing rank constraints (53). This type of formulation is not only found in previous LORAKS work (37–40, 44), but has also proven successful for other structured (34,41) and unstructured (32) low-rank matrix completion problems in MRI.
The Proposed SENSE-LORAKS Approach
The reconstruction approach proposed in this paper is a fusion of the SENSE and P-LORAKS approaches, and takes advantage of their complementary advantages. Using the SENSE data model is beneficial, because it allows use of prior information about the coil sensitivity maps that wouldn't normally be taken into account by P-LORAKS. Specifically, the SENSE model can be interpreted as imposing inter-coil linear dependence relationships in k-space (12) in a similar way to P-LORAKS. However, P-LORAKS solves the much harder problem of estimating these linear dependence relationships from undersampled data, while SENSE derives these inter-coil relationships in a much simpler way by using prescan data. Although P-LORAKS can successfully estimate the inter-coil relationships when data is sampled appropriately, there are certain common structured k-space trajectories for which it is very challenging for P-LORAKS to learn the inter-coil relationships successfully. For example, with uniform undersampling (i.e., the most common undersampling trajectory provided by modern commercial MRI scanners), no two adjacent lines of k-space are ever sampled simultaneously, which makes it nearly impossible to learn the inter-coil k-space relationships between adjacent lines. Using SENSE modeling in combination with P-LORAKS removes this ambiguity. Using the P-LORAKS model is also beneficial to SENSE, because it can incorporate support and phase constraints into SENSE reconstruction without requiring prior information about the image support or phase, without requiring support or phase calibration data, and without making any assumptions about the k-space sampling pattern.
Our proposed SENSE-LORAKS image reconstruction is obtained by solving the following optimization problem
| [14] |
where the matrix G ∈ ℂLQ×Q is constructed as
| [15] |
and the matrices Bℓ, ℓ = 1, 2,…, L are Q × Q diagonal matrices containing the samples of the sensitivity profiles sℓ(xq) for each channel. Intuitively, the matrix-vector multiplication Gρ uses the image ρ and the sensitivity maps to generate a simulated set of Nyquist-sampled multi-channel k-space data, as required by P-LORAKS to construct the S matrix.
Similar to our previous LORAKS work (37–40), we solve the nonlinear optimization problem in Eq. [14] using an iterative majorize-minimize algorithm that is guaranteed to monotonically decrease the cost function. Convergence to the global optimum is not guaranteed because of the nonconvexity of the cost function, though our previous empirical experience suggests that the algorithm frequently converges to good local optima (37–40) without requiring a sophisticated initialization. The detailed steps of our algorithm are described below.
Set iteration number i = 0, and initialize ρ̂(0). For all results shown in this paper, we initialize with the simple (and likely sub-optimal) SENSE reconstruction obtained by solving Eq. [5].
Compute S(i) = 𝒫PS(Gρ̂(i)), and its rank-r approximation L(i) = ℒr(S(i)).
-
Solve the least squares problem
In this expression, I is the Q × Q identity matrix, is the adjoint of the 𝒫PS(⋅) operator, and PPS is the LQ × LQ matrix representation of the operator . As described in (37,38,40), PPS is a simple diagonal matrix that is easy to calculate based on the structure of the S matrix.[16] Similar to SENSE (7), Eq. [16] can be solved iteratively using the conjugate gradient algorithm, using diagonal matrices, FFTs, and gridding to compute fast matrix-vector multiplications without directly constructing or inverting large matrices.
Set i = i + 1. Iterate steps 2 - 4 until convergence.
Methods
SENSE-LORAKS was implemented as described in the previous section, using a k-space neighborhood radius of R = 3. As will be discussed later, reconstruction performance was not very sensitive to the choice of the rank parameter r or the regulation parameters λS and λT. As a result, we used coarsely-tuned sampling-independent (suboptimal) parameters for SENSE-LORAKS, though performed much more thorough parameter tuning for the alternative reconstruction methods we compare against.
The proposed SENSE-LORAKS reconstruction was compared against four alternative reconstruction techniques:
SENSE (6,7,51,52). Image reconstruction was performed using Eq. [5], with the Tikhonov regularization parameter λT optimized for each sampling configuration to achieve the smallest possible normalized root-mean-squared error (NRMSE).
Phase-Constrained SENSE (46–49). Image reconstruction was performed using Eq. [6]. The phase regularization parameter λP and the Tikhonov regularization parameter λT were optimized for each dataset and sampling configuration to achieve the smallest possible NRMSE.
- SENSE+TV (28,30). Image reconstruction was performed using
where the total variation (TV) norm ‖ ⋅ ‖TV computes the ℓ1-norm of the image gradient (as estimated using finite differences). The TV regularization parameter λTV was optimized for each dataset and sampling configuration to achieve the smallest possible NRMSE.[17] P-LORAKS (39). Image reconstruction was performed using Eq. [13]. The rank parameter r and the LORAKS regularization parameter λS were optimized for each dataset and sampling configuration to achieve the smallest possible NRMSE.
Performance of these methods was evaluated on three different retrospectively undersampled datasets. To highlight the generality and flexibility of SENSE-LORAKS, we have chosen a diverse set of datasets, with variations in the number of receiver channels, acquisition matrix size, image contrast, and pulse sequences:
-
T2-Weighted Turbo Spin Echo (TSE) Data
Fully sampled data was acquired from a healthy subject using a 2D multislice T2-weighted TSE sequence on a 3T Siemens Tim Trio scanner with a 12 channel headcoil. Imaging parameters included a 256 mm × 187 mm FOV, 256 × 187 Cartesian acquisition grid, 1 mm slice thickness, TE/TR = 89 ms/13500 ms. For simplicity, we perform subsampling and reconstruction on a single slice from this dataset. The gold standard SENSE reconstruction (obtained using fully-sampled data) is shown in Fig. 1(a,b). For SENSE-LORAKS reconstruction with this dataset, we used the coarsely-tuned parameters λS = 1.9 × 10−3, λT = 10−3, and r = 40 for all acceleration rates and all undersampling patterns.
-
T1-Weighted MPRAGE Data
Fully sampled data was acquired from a stroke patient using a 3D MPRAGE sequence on a 3T Siemens Tim Trio scanner with a 12 channel headcoil. The headcoil was operated in combined mode, producing 4 channels of output k-space data. Imaging parameters included a 256 mm × 256 mm × 208 mm FOV, 256×256×208 Cartesian acquisition grid, flip angle = 10◦, TI/TE/TR = 800 ms/3.09 ms/2530 ms. A 1D inverse Fourier transform was applied along the frequency encoding dimension (superior-inferior) to decouple the reconstructions of the individual 2D slices. For simplicity, we perform subsampling and reconstruction on a single slice from this dataset. The gold standard SENSE reconstruction (obtained using fully-sampled data) is shown in Fig. 1(c,d). For SENSE-LORAKS reconstruction with this dataset, we used the coarsely-tuned parameters λS = 3.4 × 10−3, λT = 10−2, and r = 55 for all acceleration rates and all undersampling patterns.
For this dataset, while subsampling along both phase encoding dimensions would be feasible and improve reconstruction results for all methods (9), we only show results with common forms of 1D acceleration.
-
T2-Weighted EPI data
Fully sampled data was acquired from a healthy subject using a single-shot 2D spin-echo EPI sequence on the Siemens 3T Connectom scanner with a 64 channel headcoil. Imaging parameters included a 200 mm × 200 mm FOV, 100×100 Cartesian acquisition grid, 2 mm slice thickness, TE/TR = 80 ms/7400 ms. Discrepancies between even and odd lines were compensated using zero- and first-order phase corrections, and ramp sampled data was resampled onto the Nyquist grid prior to reconstruction. For simplicity, we perform subsampling and reconstruction on a single slice from this dataset. The gold standard SENSE reconstruction (obtained using fully-sampled data) is shown in Fig. 1(e,f). For SENSE-LORAKS reconstruction with this dataset, we used the coarsely-tuned parameters λS = 4.8 × 10−3, λT = 10−3, and r = 50 for all acceleration rates and all undersampling patterns. To preserve the characteristics of this EPI dataset, this dataset was only retrospectively under-sampled using uniform undersampling strategies. In addition, retrospective undersampling was restricted such that the readout gradient polarities alternate between adjacent lines.
Figure 1.
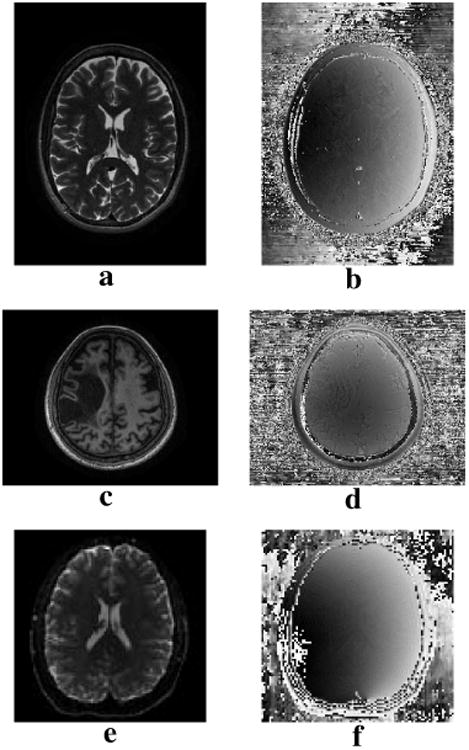
Gold standard (a,c,e) magnitude and (b,d,f) phase images used for evaluation. Images correspond to the (a,b) TSE, (c,d) MPRAGE, and (e,f) EPI datasets.
Sensitivity maps were computed for each dataset by applying ESPIRiT (12) to a 32 × 32 Nyquist-sampled grid of calibration data.
Our retrospective undersampling experiments explored several sampling schemes that are representative of modern sampling design strategies. Specifically, we considered the following four k-space sampling patterns for a range of different acceleration factors:
-
Uniform sampling (Uniform)
This standard sampling scheme uses evenly-spaced phase encoding lines that are spread across both sides of k-space. This is the sampling scheme used by standard Cartesian SENSE (6), and is associated with coherent aliasing.
-
Uniformly undersampled partial Fourier (Uniform PF)
Like Uniform sampling, this sampling scheme uses evenly spaced phase encoding lines. However, instead of sampling both sides of k-space, Uniform PF sampling spreads the phase encoding lines over 5/8ths of the relevant portion of k-space (encompassing one full half of k-space plus the low-frequency region from the other side). Measuring 5/8ths of k-space is a typical strategy for partial Fourier methods (20–22). For the same total number of phase encoding lines, Uniform sampling PF will have a smaller sampling interval (higher sampling density) than Uniform sampling within the measurement region.
-
Randomly undersampled partial Fourier (Random PF)
This sampling scheme is identical to Uniform PF, except that the phase encoding lines are randomly spaced according to a 1D Poisson disk distribution (56). This sampling pattern has less coherence than the previous sampling patterns, and as a result, may be better suited to sparsity-based and low-rank based methods like SENSE+TV and P-LORAKS.
-
Autocalibrated partial Fourier (AC PF)
This sampling scheme is similar to Uniform PF, except that the sampling density is adjusted so that the center of k-space is sampled uniformly and densely, while high-frequency k-space is sampled uniformly but less densely. This is a conventional sampling approach for phase-constrained SENSE (46–49), since the highly-sampled center of k-space can be used to generate a high-quality phase estimate. For our implementation, we used the central 32 phase encoding lines as the calibration region. Rather than fully sampling this region (which would lead to extreme undersampling of the high-frequency content), we uniformly under-sampled the calibration region by a factor of 2 (i.e., a total of 16 phase encoding lines were measured). The full calibration region was recovered using standard SENSE reconstruction with minimal loss of accuracy.
For all reconstructions, performance was quantified by computing the NRMSE with respect to the gold standard fully-sampled reconstruction. We also visualized the reconstructed images and associated error maps to provide insight into the spatial distribution of error.
Results
Performance Comparisons using TSE and MPRAGE Data
Figures 2-4 and Supporting Figs. S1-S4 show comparisons of the proposed SENSE-LORAKS method against various other reconstruction methods for the TSE data and the MPRAGE data. Using these results to compare SENSE-LORAKS with conventional SENSE reconstruction, we observe, as expected (6), that conventional SENSE reconstruction with conventional Uniform sampling performs well at low acceleration factors, though performance degrades rapidly as the acceleration factor increases. As similarly expected, it is also observed that P-LORAKS does not work very effectively with Uniform sampling. In comparison, applying SENSE-LORAKS to the same Uniform data yields improved reconstruction performance. We believe that this improvement should be expected, since SENSE-LORAKS is able to incorporate additional phase and support constraints that are not modeled by SENSE.
Figure 2.
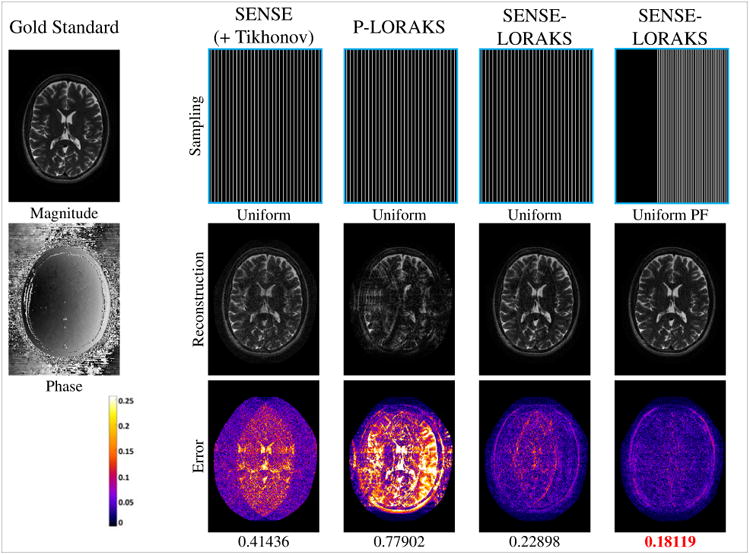
Comparison between (a) SENSE with conventional Uniform sampling, (b) P-LORAKS with conventional Uniform sampling, (c) SENSE-LORAKS with conventional Uniform sampling, and (d) SENSE-LORAKS with Uniform PF sampling for the TSE data with 5.1× acceleration. Images for other acceleration factors are shown in Supporting Figs. S1 and S2, while NRMSE values are plotted in Fig. 4(a). Reconstructed images are shown using a linear grayscale (normalized so that image intensities are in the range from 0 to 1), while error images are shown using the indicated colorscale (which ranges from 0 to 0.25 to highlight small errors). NRMSE values are shown underneath each reconstruction, with the best NRMSE values highlighted with red.
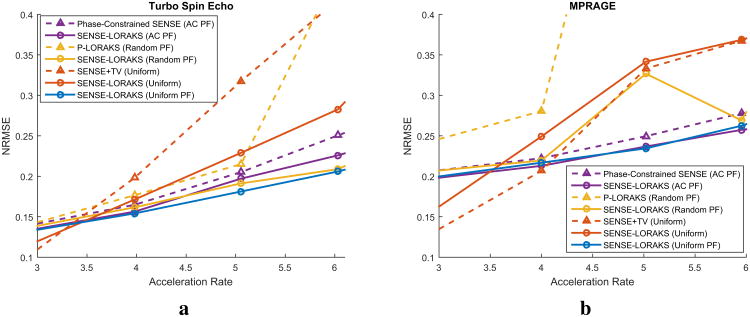
Figure 4.
Plots of the reconstruction NRMSE as a function of the acceleration rate for the (a) TSE data (corresponding images were shown in Fig. 2 and Supporting Figs. S1 and S2) and (b) MPRAGE data (corresponding images were shown in Fig. 3 and Supporting Figs. S3 and S4).
Using these same figures to compare SENSE-LORAKS with conventional Uniform sampling against SENSE-LORAKS with Uniform PF sampling, we observe that conventional Uniform sampling can slightly outperform Uniform PF sampling at low acceleration factors, while Uniform PF sampling is substantially better than conventional Uniform sampling at high acceleration factors. We believe that this result should also be expected. Specificially, at low acceleration factors, SENSE with Uniform sampling is a well-conditioned inverse problem, while partial Fourier sampling has the potential to incorrectly estimate any high resolution information that does not completely satisfy the k-space symmetry constraints. On the other hand, we know that the reconstruction errors are dominated by the ill-posedness of the problem at high acceleration rates. In these settings, we expect that the lower sampling density obtained with conventional Uniform sampling will make the SENSE problem more ill-posed than it is for Uniform PF sampling with the same acceleration rate.
Figures 5-7 and Supporting Figs. S5-S8 present a comparison between SENSE-LORAKS against phase-constrained SENSE, SENSE+TV, and P-LORAKS for the TSE and MPRAGE data. For each comparison, sampling patterns were chosen that were most applicable to the method being compared against. For the TSE data (Figs. 5 and 7(a) and Supporting Figs. S5 and S6), we observe that when SENSE-LORAKS is compared against the other methods using the same sampling pattern, SENSE-LORAKS consistently outperformed phase-constrained SENSE and P-LORAKS, and outperformed SENSE+TV at all but the lowest acceleration factor. Among different SENSE-LORAKS sampling schemes, Uniform PF sampling always produced the best performance at high acceleration factors. Consistent with our previous results, conventional Uniform sampling yielded the best performance at low acceleration factors, which we again hypothesize is related to differences in the relatively well-posed nature of the SENSE problem for conventional Uniform sampling at low acceleration factors.
Figure 5.
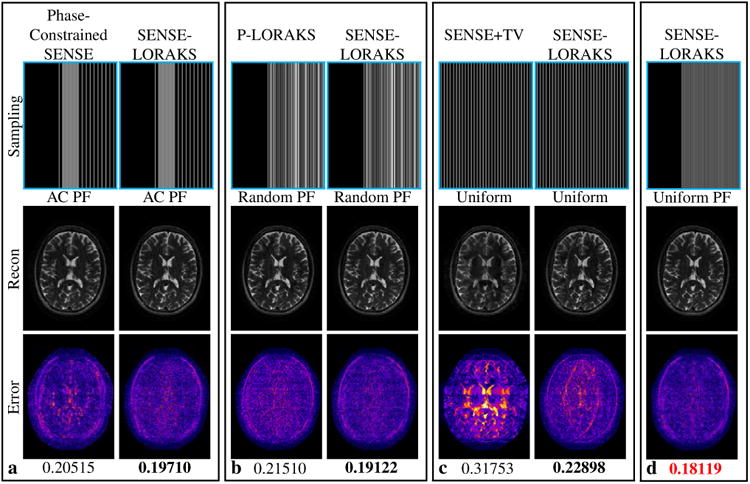
Comparison of SENSE-LORAKS against (a) phase-constrained SENSE with AC PF sampling, (b) P-LORAKS with Random PF sampling, and (c) SENSE+TV with conventional Uniform sampling for the TSE dataset with 5.1× acceleration. Reconstructions obtained using SENSE-LORAKS with Uniform PF sampling are shown in (d). Images for other acceleration factors are shown in Supporting Figs. S5 and S6, while NRMSE values are plotted in Fig. 7(a). The reconstructed images are displayed using a linear grayscale (normalized so that image intensities are in the range from 0 to 1). The error images are displayed using the indicated colorscale (which ranges from 0 to 0.25 to highlight small errors). NRMSE values are shown underneath each reconstruction, with the best NRMSE values highlighted with bold text in each sampling pattern. The smallest NRMSE values for a given acceleration rate are indicated in red.
Figure 7.
Plots of the reconstruction NRMSE as a function of the acceleration rate for the (a) TSE data (corresponding images were shown in Fig. 5 and Supporting Figs. S5 and S6) and (b) MPRAGE data (corresponding images were shown in Fig. 6 and Supporting Figs. S7 and S8).
For the MPRAGE data (Figs. 6 and 7(b) and Supporting Figs. S7 and S8), SENSE-LORAKS again consistently outperformed phase-constrained SENSE and P-LORAKS. However, different from the TSE case, SENSE-LORAKS was consistently outperformed by SENSE+TV when applied to conventional Uniform data. Despite this small difference, the MPRAGE results are largely consistent with the TSE results from the TSE data. Specifically, the best overall performance was still achieved by SENSE-LORAKS with Uniform PF or AC PF sampling at the higher acceleration factors, while SENSE+TV combined with Uniform sampling had the best performance at the lower acceleration factors. It should be noted that, while SENSE-LORAKS with AC PF sampling very slightly outperforms SENSE-LORAKS with Uniform PF sampling at an acceleration factor of 6×, the Uniform PF sampling scheme may still be preferred in practical applications because it yields smaller errors within the brain.
Figure 6.
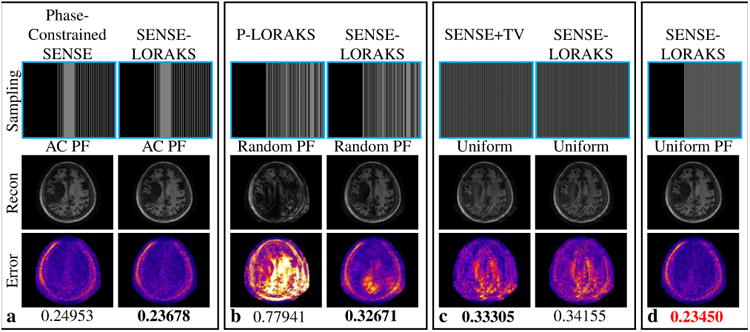
Comparison of SENSE-LORAKS against (a) phase-constrained SENSE with AC PF sampling, (b) P-LORAKS with Random PF sampling, and (c) SENSE+TV with conventional Uniform sampling for the MPRAGE dataset with 5.0× acceleration. Reconstructions obtained using SENSE-LORAKS with Uniform PF sampling are shown in (d). Images for other acceleration factors are shown in Supporting Figs. S7 and S8, while NRMSE values are plotted in Fig. 7(b). The reconstructed images are displayed using a linear grayscale (normalized so that image intensities are in the range from 0 to 1). The error images are displayed using the indicated colorscale (which ranges from 0 to 0.25 to highlight small errors). NRMSE values are shown underneath each reconstruction, with the best NRMSE values highlighted with bold text in each sampling pattern. The smallest NRMSE values for a given acceleration rate are indicated in red.
Comparing the error images shown in Figs. 2, 3, 5, and 6 and Supporting Figs. S2, S4, S6, and S8, it can also be observed that the majority of SENSE-LORAKS errors are spatially-localized near the skull in these reconstructions, while errors within the brain parenchyma are generally much smaller in magnitude. We believe that these errors are related to the relatively fast phase variations associated with extracranial lipid signal, which violate the smooth phase assumptions used by SENSE-LORAKS and other phase constrained methods.
Figure 3.
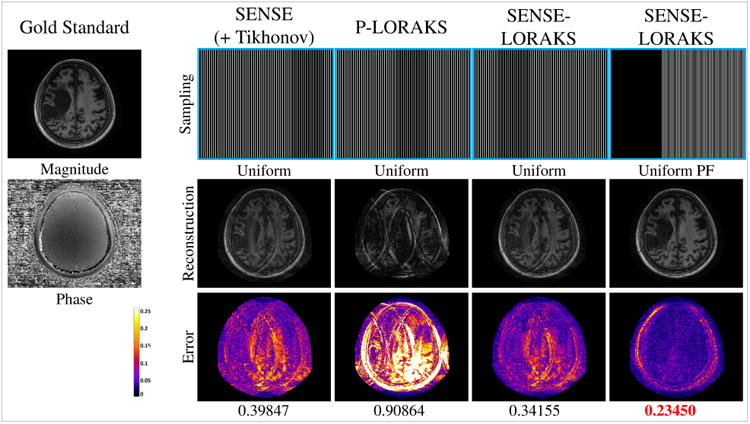
Comparison between (a) SENSE with conventional Uniform sampling, (b) P-LORAKS with conventional Uniform sampling, (c) SENSE-LORAKS with conventional Uniform sampling, and (d) SENSE-LORAKS with Uniform PF sampling for the MPRAGE data with 5.0× acceleration. Images for other acceleration factors are shown in Supporting Figs. S3 and S4, while NRMSE values are plotted in Fig. 4(b). Reconstructed images are shown using a linear grayscale (normalized so that image intensities are in the range from 0 to 1), while error images are shown using the indicated colorscale (which ranges from 0 to 0.25 to highlight small errors). NRMSE values are shown underneath each reconstruction, with the best NRMSE values highlighted with red.
Performance Comparisons using EPI Data
One benefit of the Uniform PF and conventional Uniform sampling strategies is that they have uniformly spaced phase encoding lines, and are therefore easily used with EPI and balanced SSFP acquisitions. Figure 8 shows results based on undersampled EPI data using these sampling patterns. The results in this case are consistent with the previous TSE and MPRAGE results. Specifically, SENSE-LORAKS outperforms conventional SENSE when both methods are applied to conventional Uniform sampling data. In addition, Uniform PF sampling can have substantially better performance than conventional Uniform sampling, particularly at high acceleration factors. Notably, SENSE-LORAKS with 7.7×-accelerated Uniform PF sampling is able to achieve similar reconstruction performance to conventional SENSE with 5×-accelerated conventional Uniform sampling.
Figure 8.
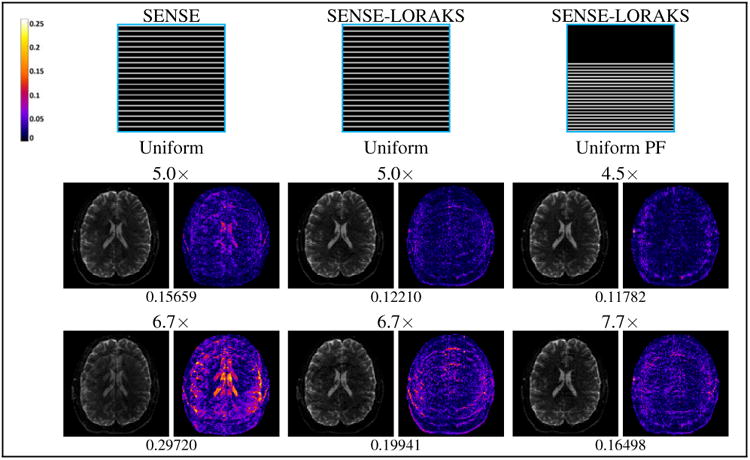
Comparison between (left) SENSE with conventional Uniform sampling, (middle) SENSE-LORAKS with conventional Uniform sampling, and (right) SENSE-LORAKS with Uniform PF sampling for the EPI data. The left columns show reconstructed images using a linear grayscale (normalized so that image intensities are in the range from 0 to 1), while the right columns show error images using the indicated colorscale (which ranges from 0 to 0.25 to highlight small errors). NRMSE values are shown underneath each reconstruction.
Parameter Selection
Using SENSE-LORAKS requires the selection of three different reconstruction parameters: the low-rank regularization parameter λS, the rank constraint r, and the Tikhonov regularization parameter λT. Many strategies have been previously proposed for automatically selecting regularization parameters for general regularized reconstruction problems (52,57,58), and while these are applicable to SENSE-LORAKS, they are often computation-intensive. For practical applications, it is important to know how much fine-tuning of the parameters is necessary to achieve good performance.
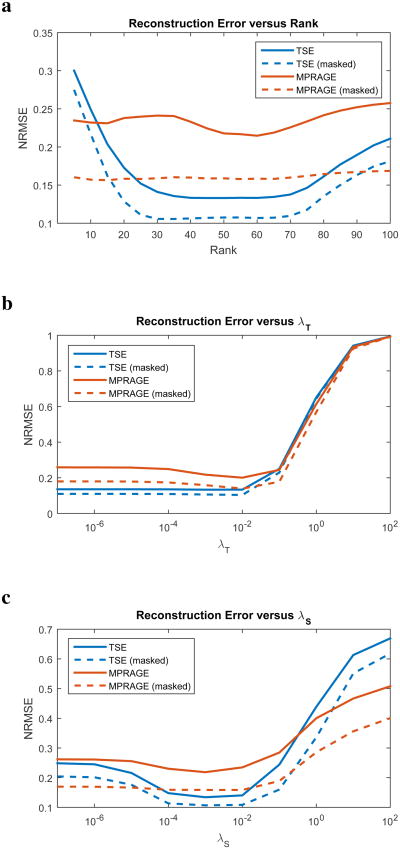
Figure 9 provides an analysis of reconstruction performance as the parameters λS, r, and λT are systematically varied. This evaluation was conducted using the TSE and MPRAGE datasets with Uniform PF sampling and 3× acceleration. Performance was quantified using NRMSE. In addition, we also computed NRMSE after applying a spatial mask that preserves the brain parenchyma while excluding the extracranial regions. The extracranial regions are typically less interesting for MRI brain studies, and as described previously, are also the spatial locations where SENSE-LORAKS tends to have the largest errors.
Figure 9.
SENSE-LORAKS reconstruction performance as a function of (a) rank r, (b) Tikhonov regularization parameter λT, and (c) LORAKS regularization parameter λS. Except where parameter values are being explicitly changed, the r, λT, and λS parameters were set to their default values as described in the Methods section.
As seen from Fig. 9, reconstruction errors are relatively stable across a wide range of λS, r, and λT values. Rank parameters between 45–60 and λT and λS parameters between 10−3 and 10−2 all produced similar NRMSE values in all cases. Therefore, fine-tuning of the reconstruction parameters may not be very important. This is also consistent with our previous observation that SENSE-LORAKS is very effective compared to other reconstruction methods across a range of different sampling patterns and acceleration rates, even though the SENSE-LORAKS reconstruction parameters were not individually tailored to each sampling configuration.
While our proposed formulation includes both Tikhonov regularization and LORAKS-based regularization, it is worth noting that the LORAKS constraint is primarily responsible for the improvements in image quality. The effect of Tikhonov regularization is to slightly improve the stability of the SENSE-LORAKS solution by reducing noise sensitivity, which is similar to its use in conventional SENSE (51, 52). A comparison of different regularization strategies can be seen in Supporting Fig. S9. While the impact of Tikhonov regularization on SENSE-LORAKS reconstruction is not very dramatic, we have chosen to include it because it does lead to a small improvement in image quality, while not having a major negative impact on parameter tuning or computational complexity.
Discussion
Our results confirmed that SENSE-LORAKS with Uniform PF sampling can have substantial advantages over previous sampling and reconstruction methods, especially at high acceleration factors where the reconstruction error becomes dominated by the ill-posedness of the SENSE problem. For simplicity, our results were based on simple 2D k-space datasets with 1D Cartesian undersampling. However, it should be noted that the SENSE-LORAKS constraints are easily applied to other experiment types (including experiments with non-Cartesian sampling (7), experiments with non-negligible field inhomogeneity (59), 3D imaging with 2D or 3D undersampling (9), simultaneus multi-slice imaging (14–18), etc.) by making the appropriate modifications to the data acquisition model matrix E.
The LORAKS regularization constraint is also flexible, and is easily adapted to dynamic imaging (37, 42), simultaneous multi-slice imaging (44), or scenarios where the image has limited support or smoothly-varying phase in a known transform domain (40–42). In addition, one of the benefits of the LORAKS framework is that the constraints are applied using regularization techniques. As a result, it is easy to combine LORAKS constraints with other forms of regularization to achieve even higher reconstruction performance (37,39). As an example of this, it is possible to combine SENSE-LORAKS with TV regularization by solving
| [18] |
Figure 10 and Supporting Fig. S10 compare reconstruction performance for SENSE-LORAKS with TV against SENSE-LORAKS and SENSE+TV for Uniform PF sampling. Results indicate that the combination of SENSE-LORAKS with the TV constraint improves performance, as would be expected because the different constraints use different and synergistic prior information about the structure of typical MRI images.
Figure 10.
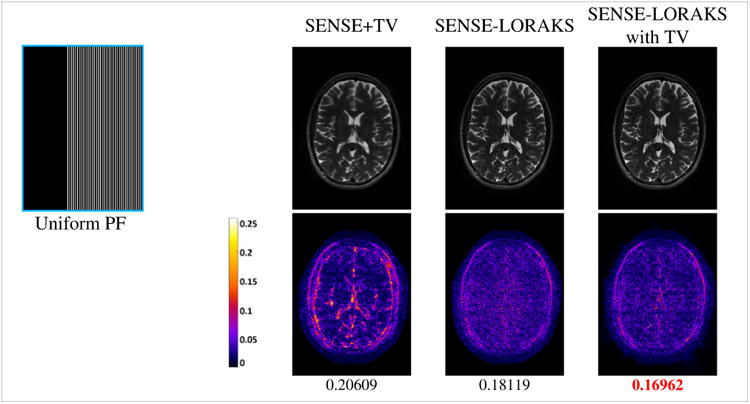
Comparison between SENSE+TV, SENSE-LORAKS, and SENSE-LORAKS with TV sampling for TSE data with Uniform PF sampling and 5.1× acceleration. Other acceleration factors are shown in Supporting Fig. S10. The top row shows reconstructed images using a linear grayscale (normalized so that image intensities are in the range from 0 to 1), while the bottom row shows error images using the indicated colorscale (which ranges from 0 to 0.25 to highlight small errors). NRMSE values are shown underneath each reconstruction, with the best NRMSE value highlighted in red.
It is important to keep in mind that, similar to previous LORAKS work (37–40,43,44), the successful application of SENSE-LORAKS will depend on the phase, support, and parallel imaging characteristics of the measured data. Images with looser fields of view, slowly varying phase, and well-designed array coils will be easier to accelerate than images with tighter fields of view, rapidly varying phase, or array coils with suboptimal configurations. These different factors influence the matrix rank in predictable ways (37,40), and are important to keep in mind when designing an accelerated MRI experiment for use with SENSE-LORAKS reconstruction.
It is also worth mentioning that, while our quantitative evaluation of SENSE-LORAKS was based on NRMSE, NRMSE is a coarse measure of image quality that hides information about the spatially-varying nature of the reconstruction errors and does not necessarily correlate with the context-specific tasks that reconstructed images are often used to perform (60) (e.g., pathology detection, parameter quantification, image registration, tissue segmentation/parcellation, morphometry, etc.). Showing the reconstructed images and error maps, as we have done, helps address a portion of these issues. Nevertheless, as we have previously described (31,37,39,60), we strongly believe that nonlinear reconstruction methods like SENSE-LORAKS should be tested thoroughly on context-specific tasks before they are deployed for routine use in practical applications.
As with all advanced constrained reconstruction methods, computation is an important practical issue for SENSE-LORAKS. In this work, we were primarily interested in investigating the potential usefulness of SENSE-LORAKS, and have not yet put any effort into optimizing computation speed. As a result, our preliminary Matlab-based implementation is relatively slow, especially when run on a simple desktop computer (Intel Xeon E5-1620 3.7 GHz quad core CPU processor and 16 GB memory). We have observed that reconstruction times depend on various factors, including convergence criteria, the number of channels L, the number of samples M, the size of the neighborhood size R used by LORAKS, the matrix rank constraint r, and the acceleration factor. For example, using our current implementation, it took 10-15 minutes to reconstruct the 12-channel TSE data at low acceleration rates (i.e., 2× or 3×), while it could take up to 30 minutes to reconstruct the same image with highly-accelerated data (i.e., 6× or 7×). The computation time also increases with the number of coils. For example, it took around 4 hours to reconstruct the 64-channel EPI data with 7.7× acceleration. There are many opportunities to improve computation speed dramatically, since the optimization algorithm has not been designed for fast convergence speed and the computing hardware has not been optimized. In addition, the use of coil compression techniques (61) could also lead to substantially faster reconstructions. We believe that exploring faster implementations is a promising area for future development.
One of the key features of the proposed SENSE-LORAKS approach is that it is flexible enough to enable the use of phase-constrained reconstruction with highly accelerated calibrationless partial Fourier EPI trajectories. While the partial Fourier acquisition is useful for enhancing reconstruction performance because it enables increased sampling density relative to conventional uniform sampling, partial Fourier acquisitions also have other benefits in the context of EPI. For example, for fixed resolution and bandwidth, the use of partial Fourier acquisition can also be used to decrease the minimum echo time and mitigate the effects of relaxation during the readout (62). We believe that such features make SENSE-LORAKS even more attractive for this context.
Conclusion
This work proposed and investigated the SENSE-LORAKS approach for constrained MRI reconstruction. Compared to existing methods, SENSE-LORAKS enables partial Fourier reconstruction without prior phase information, and is very flexible with respect to the data sampling scheme. Specifically, SENSE-LORAKS can be used with both calibration-based and calibrationless sampling patterns, with both uniform and nonuniform sampling patterns, and with both partial Fourier and full Fourier sampling patterns. This flexibility provides new opportunities for sampling trajectory optimization, and also means that SENSE-LORAKS can be more compatibile with classical fast imaging methods that use partial Fourier EPI and balanced SSFP pulse sequences. In addition, due to the simple regularization-based nature of the SENSE-LORAKS formulation, the approach is easily combined with other useful constraints like image sparsity. Our results suggest that SENSE-LORAKS can provide state-of-the-art reconstruction performance, particularly at high acceleration rates, and we believe that this new approach has the potential to enhance data acquisition and image reconstruction performance across a wide spectrum of practical application scenarios.
Supplementary Material
Figure S1. Reconstructed TSE images for a range of acceleration factors, presenting a detailed view of the results summarized in Figs. 2 and 4(a). Comparison between (a) SENSE with conventional Uniform sampling, (b) P-LORAKS with conventional Uniform sampling, (c) SENSE-LORAKS with conventional Uniform sampling, and (d) SENSE-LORAKS with Uniform PF sampling. Reconstructed images are shown using a linear grayscale (normalized so that image intensities are in the range from 0 to 1). NRMSE values are shown underneath each reconstruction, with the best NRMSE values highlighted with red. Corresponding error images are shown in Supporting Fig. S2.
Figure S2. Error images corresponding to Supporting Fig. S1. Error images are shown using the indicated colorscale (which ranges from 0 to 0.25 to highlight small errors). NRMSE values are shown underneath each image where the smallest NRMSE values for a given acceleration rate are indicated in red.
Figure S3. Reconstructed MPRAGE images for a range of acceleration factors, presenting a detailed view of the results summarized in Figs. 3 and 4(b). Comparison between (a) SENSE with conventional Uniform sampling, (b) P-LORAKS with conventional Uniform sampling, (c) SENSE-LORAKS with conventional Uniform sampling, and (d) SENSE-LORAKS with Uniform PF sampling. Reconstructed images are shown using a linear grayscale (normalized so that image intensities are in the range from 0 to 1). NRMSE values are shown underneath each reconstruction, with the best NRMSE values highlighted with red. Corresponding error images are shown in Supporting Fig. S4.
Figure S4. Error images corresponding to Supporting Fig. S3. Error images are shown using the indicated colorscale (which ranges from 0 to 0.25 to highlight small errors). NRMSE values are shown underneath each image where the smallest NRMSE values for a given acceleration rate are indicated in red.
Figure S5. Reconstructed TSE images for a range of acceleration factors, presenting a detailed view of the results summarized in Figs. 5 and 7(a). Comparison of images reconstructed using SENSE-LORAKS against (a) phase-constrained SENSE with AC PF sampling, (b) P-LORAKS with Random PF sampling, (c) SENSE+TV with conventional Uniform sampling. Reconstructions obtained using SENSE-LORAKS with Uniform PF sampling are shown in (d). Reconstructed images are shown using a linear grayscale (normalized so that image intensities are in the range from 0 to 1). NRMSE values are shown underneath each reconstruction, with the best NRMSE values highlighted with red. Corresponding error images are shown in Supporting Fig. S6.
Figure S6. Error images corresponding to Supporting Fig. S6. Error images are shown using the indicated colorscale (which ranges from 0 to 0.25 to highlight small errors). NRMSE values are shown underneath each image where the smallest NRMSE values for a given acceleration rate are indicated in red.
Figure S7. Reconstructed MPRAGE images for a range of acceleration factors, presenting a detailed view of the results summarized in Figs. 6 and 7(b). Comparison of images reconstructed using SENSE-LORAKS against (a) phase-constrained SENSE with AC PF sampling, (b) P-LORAKS with Random PF sampling, (c) SENSE+TV with conventional Uniform sampling. Reconstructions obtained using SENSE-LORAKS with Uniform PF sampling are shown in (d). Reconstructed images are shown using a linear grayscale (normalized so that image intensities are in the range from 0 to 1). NRMSE values are shown underneath each reconstruction, with the best NRMSE values highlighted with red. Corresponding error images are shown in Supporting Fig. S8.
Figure S8. Error images corresponding to Supporting Fig. S7. Error images are shown using the indicated colorscale (which ranges from 0 to 0.25 to highlight small errors). NRMSE values are shown underneath each image where the smallest NRMSE values for a given acceleration rate are indicated in red.
Figure S9. Illustration of the effects of Tikhonov regularization on (a) SENSE and (b) SENSE-LORAKS.
Figure S10. Comparison between SENSE+TV, SENSE-LORAKS, and SENSE-LORAKS with TV for TSE data with Uniform PF sampling. A subset of these results was shown in Fig. 10. The top rows show reconstructed images using a linear grayscale (normalized so that image intensities are in the range from 0 to 1), while the bottom rows show error images using the indicated colorscale (which ranges from 0 to 0.25 to highlight small errors). NRMSE values are shown underneath each reconstruction, with the best NRMSE values highlighted in red.
Acknowledgments
This work was supported in part by NSF CAREER award CCF-1350563 and NIH grants R01-NS089212, R24-MH106096, and R01-EB019437.
References
- 1.Mansfield P. Multiplanar image formation using NMR spin echoes. J Phys C: Solid State Phys. 1977;10:L55–L58. [Google Scholar]
- 2.Ahn CB, Kim JH, Cho ZH. High-speed spiral-scan echo planar NMR imaging–I. IEEE Trans Med Imag. 1986;MI-5:2–7. doi: 10.1109/TMI.1986.4307732. [DOI] [PubMed] [Google Scholar]
- 3.Carr HY. Steady-state free precession in nuclear magnetic resonance. Phys Rev. 1958;112:1693–1701. [Google Scholar]
- 4.Oppelt A, Graumann R, Barfuss H, Fischer H, Hartl W, Schajor W. FISP – a new fast MRI sequence. Electromedica. 1986;54:15–18. [Google Scholar]
- 5.Sodickson DK, Manning WJ. Simultaneous acquisition of spatial harmonics (SMASH): fast imaging with radiofrequency coil arrays. Magn Reson Med. 1997;38:591–603. doi: 10.1002/mrm.1910380414. [DOI] [PubMed] [Google Scholar]
- 6.Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med. 1999;42:952–962. [PubMed] [Google Scholar]
- 7.Pruessmann KP, Weiger M, Börnert P, Boesiger P. Advances in sensitivity encoding with arbitrary k-space trajectories. Magn Reson Med. 2001;46:638–651. doi: 10.1002/mrm.1241. [DOI] [PubMed] [Google Scholar]
- 8.Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Generalized autocalibrating partially parallel acquisitions (GRAPPA) Magn Reson Med. 2002;47:1202–1210. doi: 10.1002/mrm.10171. [DOI] [PubMed] [Google Scholar]
- 9.Breuer FA, Blaimer M, Mueller MF, Seiberlich N, Heidemann RM, Griswold MA, Jakob PM. Controlled aliasing in volumetric parallel imaging (2D CAIPIRINHA) Magn Reson Med. 2006;55:549–556. doi: 10.1002/mrm.20787. [DOI] [PubMed] [Google Scholar]
- 10.Lin FH, Wald LL, Ahlfors SP, Hamalainen MS, Kwong KK, Belliveau JW. Dynamic magnetic resonance inverse imaging of human brain function. Magn Reson Med. 2006;56:787–802. doi: 10.1002/mrm.20997. [DOI] [PubMed] [Google Scholar]
- 11.Zhang J, Liu C, Moseley ME. Parallel reconstruction using null operations. Magn Reson Med. 2011;66:1241–1253. doi: 10.1002/mrm.22899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, Vasanawala SS, Lustig M. ESPIRiT–an eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magn Reson Med. 2014;71:990–1001. doi: 10.1002/mrm.24751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Maudsley AA. Multiple-line-scanning spin density imaging. J Magn Reson. 1980;41:112–126. [Google Scholar]
- 14.Larkman DJ, Hajnal JV, Herlihy AH, Coutts GA, Young IR, Ehnholm G. Use of multicoil arrays for separation of signal from multiple slices simultaneously excited. J Magn Reson Imag. 2001;13:313–317. doi: 10.1002/1522-2586(200102)13:2<313::aid-jmri1045>3.0.co;2-w. [DOI] [PubMed] [Google Scholar]
- 15.Breuer FA, Blaimer M, Heidemann RM, Mueller MF, Griswold MA, Jakob PM. Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) for multi-slice imaging. Magn Reson Med. 2005;53:684–691. doi: 10.1002/mrm.20401. [DOI] [PubMed] [Google Scholar]
- 16.Moeller S, Yacoub E, Olman CA, Auerbach E, Strupp J, Harel N, Ugurbil K. Multiband multislice GE-EPI at 7 Tesla, with 16-fold acceleration using partial parallel imaging with application to high spatial and temporal whole-brain fMRI. Magn Reson Med. 2010;63:1144–1153. doi: 10.1002/mrm.22361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Feinberg DA, Moeller S, Smith SM, Auerbach E, Ramanna S, Glasser MF, Miller KL, Ugurbil K, Yacoub E. Multiplexed echo planar imaging for sub-second whole brain fMRI and fast diffusion imaging. PLoS One. 2010;5:1–11. doi: 10.1371/journal.pone.0015710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Setsompop K, Gagoski BA, Polimeni JR, Witzel T, Wedeen VJ, Wald LL. Blipped-controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty. Magn Reson Med. 2012;67:1210–1224. doi: 10.1002/mrm.23097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Margosian P, Schmitt F, Purdy D. Faster MR imaging: imaging with half the data. Health Care Instrum. 1986;1:195–197. [Google Scholar]
- 20.Noll DC, Nishimura DG, Macovski A. Homodyne detection in magnetic resonance imaging. IEEE Trans Med Imag. 1991;10:154–163. doi: 10.1109/42.79473. [DOI] [PubMed] [Google Scholar]
- 21.Huang F, Lin W, Li Y. Partial Fourier reconstruction through data fitting and convolution in k-space. Magn Reson Med. 2009;62:1261–1269. doi: 10.1002/mrm.22128. [DOI] [PubMed] [Google Scholar]
- 22.Liang ZP, Boada F, Constable T, Haacke EM, Lauterbur PC, Smith MR. Constrained reconstruction methods in MR imaging. Magn Reson Med. 1992;4:67–185. [Google Scholar]
- 23.Zhao F, Noll DC, Nielsen JF, Fessler JA. Separate magnitude and phase regularization via compressed sensing. IEEE Trans Med Imag. 2012;31:1713–1723. doi: 10.1109/TMI.2012.2196707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Cheung KF, Marks RJ., II Imaging sampling below the Nyquist density without aliasing. J Opt Soc Am A. 1990;7:92–105. [Google Scholar]
- 25.Plevritis SK, Macovski A. Spectral extrapolation of spatially bounded images. IEEE Trans Med Imag. 1995;14:487–497. doi: 10.1109/42.414614. [DOI] [PubMed] [Google Scholar]
- 26.Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007;58:1182–1195. doi: 10.1002/mrm.21391. [DOI] [PubMed] [Google Scholar]
- 27.Ye JC, Tak S, Han Y, Park HW. Projection reconstruction MR imaging using FOCUSS. Magn Reson Med. 2007;57:764–775. doi: 10.1002/mrm.21202. [DOI] [PubMed] [Google Scholar]
- 28.Block KT, Uecker M, Frahm J. Undersampled radial MRI with multiple coils iterative image reconstruction using a total variation constraint. Magn Reson Med. 2007;57:1086–1098. doi: 10.1002/mrm.21236. [DOI] [PubMed] [Google Scholar]
- 29.Trzasko J, Manduca A. Highly undersampled magnetic resonance image reconstruction via homotopic ℓ0-minimization. IEEE Trans Med Imag. 2009;28:106–121. doi: 10.1109/TMI.2008.927346. [DOI] [PubMed] [Google Scholar]
- 30.Liang D, Liu B, Wang JJ, Ying L. Accelerating SENSE using compressed sensing. Magn Reson Med. 2009;62:1574–1584. doi: 10.1002/mrm.22161. [DOI] [PubMed] [Google Scholar]
- 31.Haldar JP, Hernando D, Liang ZP. Compressed-sensing MRI with random encoding. IEEE Trans Med Imag. 2011;31:893–903. doi: 10.1109/TMI.2010.2085084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Haldar JP, Liang ZP. Spatiotemporal imaging with partially separable functions: A matrix recovery approach. Proc IEEE Int Symp Biomed Imag. 2010:716–719. [Google Scholar]
- 33.Lingala SG, Hu Y, DiBella E, Jacob M. Accelerated dynamic MRI exploiting sparsity and low-rank structure: k-t SLR. IEEE Trans Med Imag. 2011;30:1042–1054. doi: 10.1109/TMI.2010.2100850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Shin PJ, Larson PEZ, Ohliger MA, Elad M, Pauly JM, Vigneron DB, Lustig M. Calibrationless parallel imaging reconstruction based on structured low-rank matrix completion. Magn Reson Med. 2014;72:959–970. doi: 10.1002/mrm.24997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Bernstein MA, King KF, Zhou XJ. Handbook of MRI Pulse Sequences. Burlington: Elsevier Academic Press; 2004. [Google Scholar]
- 36.Bieri O, Markl M, Scheffler K. Analysis and compensation of eddy currents in balanced SSFP. Magn Reson Med. 2005;54:129–137. doi: 10.1002/mrm.20527. [DOI] [PubMed] [Google Scholar]
- 37.Haldar JP. Low-rank modeling of local k-space neighborhoods (LORAKS) for constrained MRI. IEEE Trans Med Imag. 2014;33:668–681. doi: 10.1109/TMI.2013.2293974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Haldar JP. Low-rank modeling of local k-space neighborhoods (LORAKS): Implementation and examples for reproducible research Technical Report USC-SIPI-414. University of Southern California; Los Angeles, CA: 2014. [Google Scholar]
- 39.Haldar JP, Zhuo J. P-LORAKS: Low-rank modeling of local k-space neighborhoods with parallel imaging data. Magn Reson Med. 2015 doi: 10.1002/mrm.25717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Haldar JP. Low-rank modeling of local k-space neighborhoods: from phase and support constraints to structured sparsity. Proc SPIE. 2015;9597:959710. [Google Scholar]
- 41.Ongie G, Jacob M. Off-the-grid recovery of piecewise constant images from few Fourier samples. arXiv Preprint. 2015 doi: 10.1137/15M1042280. http://arxiv.org/abs/1510.00384. [DOI] [PMC free article] [PubMed]
- 42.Jin KH, Lee D, Ye JC. A novel k-space annihilating filter method for unification between compressed sensing and parallel MRI. Proc IEEE Int Symp Biomed Imag. 2015:327–330. [Google Scholar]
- 43.Haldar JP. Autocalibrated LORAKS for fast constrained MRI reconstruction. Proc IEEE Int Symp Biomed Imag. 2015:910–913. [Google Scholar]
- 44.Kim TH, Haldar JP. SMS-LORAKS: Calibrationless simultaneous multislice MRI using low-rank matrix modeling. Proc IEEE Int Symp Biomed Imag. 2015:323–326. [Google Scholar]
- 45.Samsonov A, Kholmovski EG, Parker DL, Johnson CR. POCSENSE: POCS-based reconstruction for sensitivity encoded magnetic resonance imaging. Magn Reson Med. 2004;52:1397–1406. doi: 10.1002/mrm.20285. [DOI] [PubMed] [Google Scholar]
- 46.Willig-Onwuachi JD, Yeh EN, Grant AK, Ohliger MA, McKenzie CA, Sodickson DK. Phase-constrained parallel MR image reconstruction. J Magn Reson. 2005;176:187–198. doi: 10.1016/j.jmr.2005.06.004. [DOI] [PubMed] [Google Scholar]
- 47.Bydder M, Robson MD. Partial Fourier partially parallel imaging. Magn Reson Med. 2005;53:1393–1401. doi: 10.1002/mrm.20492. [DOI] [PubMed] [Google Scholar]
- 48.Lew C, Pineda AR, Clayton D, Spielman D, Chan F, Bammer R. SENSE phase-constrained magnitude reconstruction with iterative phase refinement. Magn Reson Med. 2007;58:910–921. doi: 10.1002/mrm.21284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Blaimer M, Heim M, Neumann D, Jakob PM, Kannengiesser S, Breuer F. Comparison of phase-constrained parallel MRI approaches: Analogies and differences. Magn Reson Med. 2015 doi: 10.1002/mrm.25685.. [DOI] [PubMed] [Google Scholar]
- 50.Chang HC, Guhaniyogi S, Chen NK. Interleaved diffusion-weighted EPI improved by adaptive partial-Fourier and multiband multiplexed sensitivity-encoding reconstruction. Magn Reson Med. 2015;73:1872–1884. doi: 10.1002/mrm.25318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Liang ZP, Bammer R, Ji J, Pelc NJ, Glover GH. Making better SENSE: Wavelet denoising, Tikhonov regularization, and total least squares. Proc Int Soc Magn Reson Med. 2002:2388. [Google Scholar]
- 52.Lin FH, Kwong KK, Belliveau JW, Wald LL. Parallel imaging reconstruction using automatic regularization. Magn Reson Med. 2004;51:559–567. doi: 10.1002/mrm.10718. [DOI] [PubMed] [Google Scholar]
- 53.Recht B, Fazel M, Parrilo PA. Guaranteed minimum-rank solutions of linear matrix equations via nuclear norm minimization. SIAM Rev. 2010;52:471–501. [Google Scholar]
- 54.Golub G, van Loan C. Matrix Computations. third. London: The Johns Hopkins University Press; 1996. [Google Scholar]
- 55.Haldar JP, Hernando D. Rank-constrained solutions to linear matrix equations using power-factorization. IEEE Signal Processing Letters. 2009;16:584–587. doi: 10.1109/LSP.2009.2018223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Nayak KS, Nishimura DG. Randomized trajectories for reduced aliasing artifact. Proc Int Soc Magn Reson Med. 1998:670. [Google Scholar]
- 57.Ramani S, Liu Z, Rosen J, Nielsen JF, Fessler JA. Regularization parameter selection for nonlinear iterative image restoration and MRI reconstruction using GCV and SURE-based methods. IEEE Trans Image Process. 2012;21:3659–3672. doi: 10.1109/TIP.2012.2195015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Candes EJ, Sing-Long CA, Trzasko JD. Unbiased risk estimates for singular value thresholding and spectral estimators. IEEE Trans Signal Process. 2013;61:4643–4657. [Google Scholar]
- 59.Sutton BP, Noll DC, Fessler JA. Fast, iterative image reconstruction for MRI in the presence of field inhomogeneities. IEEE Trans Med Imag. 2003;22:178–188. doi: 10.1109/tmi.2002.808360. [DOI] [PubMed] [Google Scholar]
- 60.Kim JH, Song SK, Haldar JP. Signal-to-noise ratio-enhancing joint reconstruction for improved diffusion imaging of mouse spinal cord white matter injury. Magn Reson Med. 2015 doi: 10.1002/mrm.25691.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Huang F, Vijayakumar S, Li Y, Hertel S, Duensing GR. A software channel compression technique for faster reconstruction with many channels. Magn Reson Imag. 2008;26:133–141. doi: 10.1016/j.mri.2007.04.010. [DOI] [PubMed] [Google Scholar]
- 62.Hyde JS, Biswal BB, Jesmanowicz A. High-resolution fMRI using multislice partial k-space GR-EPI with cubic voxels. Magn Reson Med. 2001;46:114–125. doi: 10.1002/mrm.1166. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S1. Reconstructed TSE images for a range of acceleration factors, presenting a detailed view of the results summarized in Figs. 2 and 4(a). Comparison between (a) SENSE with conventional Uniform sampling, (b) P-LORAKS with conventional Uniform sampling, (c) SENSE-LORAKS with conventional Uniform sampling, and (d) SENSE-LORAKS with Uniform PF sampling. Reconstructed images are shown using a linear grayscale (normalized so that image intensities are in the range from 0 to 1). NRMSE values are shown underneath each reconstruction, with the best NRMSE values highlighted with red. Corresponding error images are shown in Supporting Fig. S2.
Figure S2. Error images corresponding to Supporting Fig. S1. Error images are shown using the indicated colorscale (which ranges from 0 to 0.25 to highlight small errors). NRMSE values are shown underneath each image where the smallest NRMSE values for a given acceleration rate are indicated in red.
Figure S3. Reconstructed MPRAGE images for a range of acceleration factors, presenting a detailed view of the results summarized in Figs. 3 and 4(b). Comparison between (a) SENSE with conventional Uniform sampling, (b) P-LORAKS with conventional Uniform sampling, (c) SENSE-LORAKS with conventional Uniform sampling, and (d) SENSE-LORAKS with Uniform PF sampling. Reconstructed images are shown using a linear grayscale (normalized so that image intensities are in the range from 0 to 1). NRMSE values are shown underneath each reconstruction, with the best NRMSE values highlighted with red. Corresponding error images are shown in Supporting Fig. S4.
Figure S4. Error images corresponding to Supporting Fig. S3. Error images are shown using the indicated colorscale (which ranges from 0 to 0.25 to highlight small errors). NRMSE values are shown underneath each image where the smallest NRMSE values for a given acceleration rate are indicated in red.
Figure S5. Reconstructed TSE images for a range of acceleration factors, presenting a detailed view of the results summarized in Figs. 5 and 7(a). Comparison of images reconstructed using SENSE-LORAKS against (a) phase-constrained SENSE with AC PF sampling, (b) P-LORAKS with Random PF sampling, (c) SENSE+TV with conventional Uniform sampling. Reconstructions obtained using SENSE-LORAKS with Uniform PF sampling are shown in (d). Reconstructed images are shown using a linear grayscale (normalized so that image intensities are in the range from 0 to 1). NRMSE values are shown underneath each reconstruction, with the best NRMSE values highlighted with red. Corresponding error images are shown in Supporting Fig. S6.
Figure S6. Error images corresponding to Supporting Fig. S6. Error images are shown using the indicated colorscale (which ranges from 0 to 0.25 to highlight small errors). NRMSE values are shown underneath each image where the smallest NRMSE values for a given acceleration rate are indicated in red.
Figure S7. Reconstructed MPRAGE images for a range of acceleration factors, presenting a detailed view of the results summarized in Figs. 6 and 7(b). Comparison of images reconstructed using SENSE-LORAKS against (a) phase-constrained SENSE with AC PF sampling, (b) P-LORAKS with Random PF sampling, (c) SENSE+TV with conventional Uniform sampling. Reconstructions obtained using SENSE-LORAKS with Uniform PF sampling are shown in (d). Reconstructed images are shown using a linear grayscale (normalized so that image intensities are in the range from 0 to 1). NRMSE values are shown underneath each reconstruction, with the best NRMSE values highlighted with red. Corresponding error images are shown in Supporting Fig. S8.
Figure S8. Error images corresponding to Supporting Fig. S7. Error images are shown using the indicated colorscale (which ranges from 0 to 0.25 to highlight small errors). NRMSE values are shown underneath each image where the smallest NRMSE values for a given acceleration rate are indicated in red.
Figure S9. Illustration of the effects of Tikhonov regularization on (a) SENSE and (b) SENSE-LORAKS.
Figure S10. Comparison between SENSE+TV, SENSE-LORAKS, and SENSE-LORAKS with TV for TSE data with Uniform PF sampling. A subset of these results was shown in Fig. 10. The top rows show reconstructed images using a linear grayscale (normalized so that image intensities are in the range from 0 to 1), while the bottom rows show error images using the indicated colorscale (which ranges from 0 to 0.25 to highlight small errors). NRMSE values are shown underneath each reconstruction, with the best NRMSE values highlighted in red.