Incorporating Dixon Multi-Echo Fat Water Separation for Novel Quantitative Magnetization Transfer of the Human Optic Nerve in vivo

Abstract

Purpose

The optic nerve (ON) represents the sole pathway between the eyes and brain; consequently, diseases of the ON can have dramatic effects on vision. However, qMT applications in the ON have been limited to ex vivo studies, in part due to the fatty connective tissue, which surrounds the ON, confounding the MT experiment. Therefore, the aim of this study was to implement a multi-echo Dixon fat-water separation approach to remove the fat component from MT images.

Methods

MT measurements were taken in a single slice of the ON and frontal lobe using a three-echo Dixon readout, and the water and out-of-phase images were applied to a two-pool model in ON tissue and brain white matter to evaluate the effectiveness of using Dixon fat-water separation to remove fatty tissue from MT images.

Results

White matter data showed no significant differences between image types, however, there was a significant increase (p < 0.05) in variation in the out-of-phase images in the ON relative to the water images.

Conclusions

The results of this study demonstrate that Dixon fat-water separation can be robustly utilized for accurate MT quantification of anatomies susceptible to partial volume effects due to fat.

Introduction

The optic nerve (ON) is responsible for mediating visual information from the eyes to the optic chiasm and represents the sole pathway between the eyes and brain. The integrity of these nerves is imperative in maintaining visual function; consequently, diseases of the ON can have dramatic effects on daily function. One significant challenge in the management of patients with optic neuropathies (such as glaucoma, optic neuritis) has been the lack of robust, quantitative tools capable of characterizing the underlying pathophysiology. For example, conventional MRI scan contrasts, e.g. spin-density, T₁- and T₂-weighted, currently do not provide significant diagnostic (3) or prognostic value over conventional ophthalmologic exams in optic neuropathies.

Magnetization transfer (MT) imaging has emerged as an MRI technique capable of quantifying myelin density changes (4-6) brought about by neurodegenerative diseases affecting the brain, spinal cord, and peripheral nerves (7-16); it may therefore provide similar quantitative information in ON diseases. MT MRI exploits the fact that there are protons residing on immobile macromolecules in tissue in addition to the free water protons observed with conventional MRI (17). Conventional MRI cannot image these protons directly because their T₂ relaxation times are too short (≈10 μs) to be captured by typical readout schemes. However, these macromolecular protons communicate with the surrounding water and can be indirectly imaged by exploiting this exchange, which is referred to as the MT effect.

The contrast in an MT experiment is generated via application of a radiofrequency (RF) irradiation pulse at an offset frequency with respect to water (Δω) to selectively saturate the spectrally broad macromolecular proton resonance. This saturation is transferred to the free water pool via MT, resulting in an observed signal attenuation. The MT effect is semi-quantitatively characterized via the magnetization transfer ratio (MTR), which has been shown to correlate with myelin content (6). Unfortunately, the MTR is also sensitive to pulse sequence design, RF transmit field (B₁), and magnetic static field (B₀) inhomogeneity (18), as well as by tissue relaxation times and other non-MT-specific NMR parameters (19,20), limiting researchers and clinicians from creating a standard MTR metric to define pathology. To overcome some of these limitations and derive indices that are directly reflective of MT phenomena, quantitative MT (qMT) has been developed and implemented in the brain and spinal cord (20-24). qMT typically requires images to be acquired at multiple RF irradiation powers and/or frequency offsets, generating a so-called MT z-spectrum for each voxel (25). The resulting z-spectrum can be fit to a two (or more)-pool model to estimate quantitative indices, such as the pool size ratio (PSR), defined as the macromolecular pool size divided by the free pool size, the MT exchange rate from the macromolecular pool to the free pool (k_mf), and the transverse and longitudinal relaxation times for each pool (20,26). Often, the focus is on the PSR, as it has been shown to correlate well with white matter (WM) myelin density (6,27-29), and may offer a biomarker of demyelination and axonal loss in WM pathologies.

MT imaging of the ON, therefore, has the potential to report on microstructural changes preceding atrophy, potentially offering greater insight into changes that may persist after transient inflammation has subsided. Despite this promise, qMT applications in the ON have been limited to ex vivo studies (20,30), largely due to the technical challenges associated with quantitative imaging of the ON. First, qMT methods often require long scan times for accurate data fitting (31). The ON is approximately 3 mm in diameter (32), necessitating longer, higher-resolution scans for whole-nerve quantification. Short scan times are, however, often required for quantitative ON imaging, as eye fixation is advisable to reduce to impact of constant eye motion. Secondly, fatty connective tissue surrounds the ON and exhibits markedly different MT properties than nerve, requiring fat suppression techniques to accurately separate the nerve from the surrounding anatomy. For conventional MRI, spectral fat suppression techniques, such as spectral presaturation with inversion recovery (SPIR) (33) or spectral attenuated inversion recovery (SPAIR) (34), are typically employed. Unfortunately, these approaches are often incompatible with qMT imaging because they are performed with an off-resonance pulse that can affect MT quantification. Short TI inversion recovery (STIR) methods have also been proposed (35), however, STIR results in significant water signal attenuation and a reduction in SNR. Lastly on-resonant fat suppression techniques such as binomial spatial-spectral excitation pulses can be applied, however, they require a large, 3-D field of view and increased gradient demands, which may not always be achievable in vivo.

We, therefore, propose a multi-echo Dixon fat-water separation approach (36-39) to remove the fat component from the MT images. The Dixon method takes advantage of the differences in precession rates between water and fat by acquiring data at multiple echo times to separate the fat and water components of the signal (40). While whole-brain fat and water images have been successfully implemented in slice locations that cover the ON (41), to the authors’ knowledge, Dixon-separated qMT has not been studied. The importance of the work presented here is to evaluate the stability of qMT under multi-echo signal combinations and utilize this information to derive qMT indices reflective of myelination at resolutions that are typically prohibitive for qMT methods. Toward this end, we performed in vivo qMT in the brain and ON of healthy volunteers using a three-echo Dixon method, and evaluated this technique against traditional single-echo out-of-phase imaging data.

Methods

All numerical simulations and data analyses were performed with scripts written in MATLAB 2014a & 2015a (The MathWorks, Inc; Natick, MA).

Simulations

To predict the effect from fitting a two-pool (water + MT) qMT model to a tissue that contains three effective pools (water + MT + fat), data were numerically generated from a three-pool model based on the equations from Portnoy and Stanisz (42). A set of typical parameters for WM and fat (WM: R_1obs = 0.9 s⁻¹, T_2f = 30 ms, T_2m = 11 μs, k_mf = 10 s⁻¹, PSR = 0.15; Fat: R_1obs,fat = 0.365 s⁻¹, T_2,fat = 133 ms) (43) were used to model the tissue, and the sampling scheme included two saturation powers at nominal flip angles (α_MT) of 900° and 1200°, with frequency offsets (Δω) of 1, 1.5, 2, 2.5, 8, 16, 32, and 100 kHz. The fat fractions were varied between 0.0 and 0.95, stepped by 0.05. Gaussian noise was added to the data to simulate an SNR of 100 at thermal equilibrium (to match experimental parameters), and the two-pool model described by Yarnykh and Yuan (44) & Yarnykh (31), which does not account for the effect of fat on the observed signal fraction, was used to fit the noisy signal data at each fat fraction over 10,000 noise realizations per fat fraction. The mean and standard deviation of the fitted qMT parameters were plotted as a function of fat fraction and used to predict the effect of an un-modeled fat component on the qMT analysis.

Experimental Data

Subjects

Eight healthy controls were recruited and imaged for this study (mean age 29.4 ± 5.4, 4 female). The local Institutional Review Board approved this study, and signed informed consent was obtained prior to the examination.

Data Acquisition

All data was acquired on a 3.0 tesla Philips Achieva scanner (Philips Healthcare, Best, The Netherlands). A 2-channel, multi-transmit body coil was used for excitation and an 8-channel head coil was used for signal reception. The MT acquisition consisted of a single-slice with the field-of-view (FOV) centered along the ethmoid bone (using high-resolution T₂ images (32)), perpendicular to both ONs, and spanned, at minimum, the width of the head in all subjects. Parallel imaging with sensitivity encoding (SENSE) and second-order shimming over both ONs was used to minimize image artifacts arising from susceptibility differences between bone, tissue, and air. All images had an FOV of 150 × 150 mm², a slice thickness of 3 mm, and included both the ON and the brain (see Fig. 1a,b). MT-weighted images were acquired using a 2D MT-prepared, three-echo spoiled gradient echo sequence (SPGR) (22). Nominal in-plane resolution was 1 × 1 mm², (reconstructed to 0.3 × 0.3 mm²) with 2 signal averages, and a SENSE factor of 2. MT weighting was achieved using a 20 ms, single-lobed sinc-Gauss pulse, and the parameters listed in Table 1. The water (W), in-phase, out-of-phase (OP), and fat images were reconstructed using the seven peak fat spectrum, multi-echo mDixon option in the Philips scanner software (37,38). Optic nerve motion artifacts were minimized by employing fixation every other dynamic using the Psychophysics Toolbox MATLAB extensions (45-48), resulting in 32 dynamics with two full sets of (fixated and non-fixated) qMT data. This consisted of an “on” dynamic, where subjects were asked to fixate on a white cross against a black background, and an “off” dynamic, where there was a black screen. To help address eye fatigue, the subjects were encouraged to not focus during the “off” dynamics.

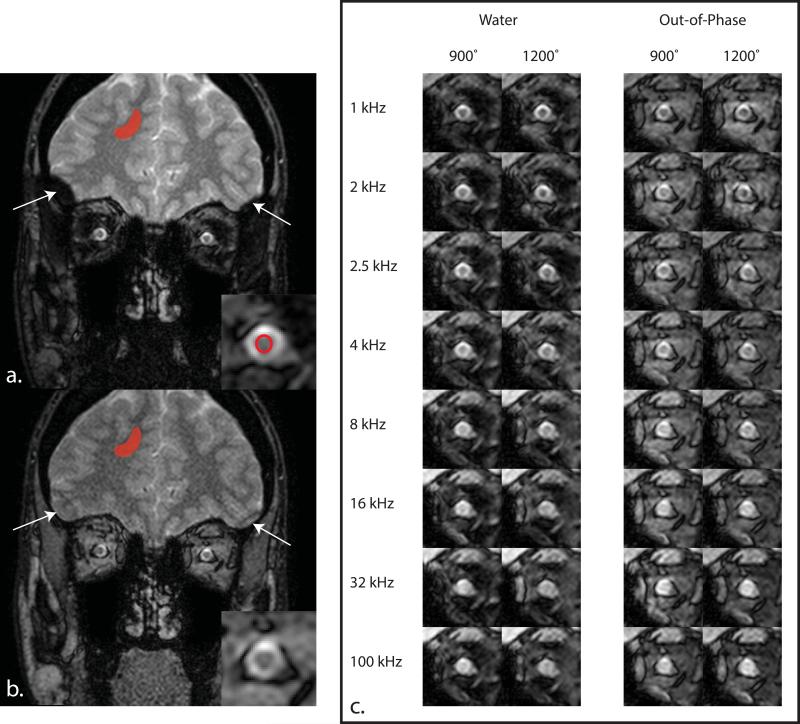
Figure 1.

Panels (a.) and (b.) illustrate the MT effect at 1000 kHz with a saturation power of 900° for the (a.) water and (b.) out-of-phase images for a slice immediately posterior to the globe (proximal retrobulbar). The cutoff area of the brain on the outer edges of the volume in the water image is indicative of poor shimming in these regions, and thus, a mislabeling effect of the Dixon method (see arrows). The ROIs in (a.) and (b.) display the area used to compare the water and out-of-phase qMT parameters in the brain and optic nerve. The optic nerve ROI in (a.) is propagated to (b.) for analysis in the out-of-phase images. (c) Example MT-weighted data in the optic nerve for the water and out-of-phase images. Notice the increased conspicuity of the optic nerve against the surrounding tissue in the water images compared to the out-of-phase images.

Table 1.

Scan parameters and MT prepulse parameters for the MT, B₁, B₀, and T₁ scans.

Scan:	Scan Parameters:	MT Prepulse Parameters:		Scan Time (m:ss)
		Δω (kHz)	Powers
MT	TR/TE1/ΔTE/α: 78/5.8/3.1 ms/10°	1, 2, 2.5, 4, 8, 16, 32, 100	900°, 1200°	6:32
B1	TR1/TR2/TE/α: 30/130/5.7 ms/60°	—	—	0:21
B0	TR/TE1/TE2/α: 50/5.8/8.1 ms/25°	—	—	0:34
T1	TR/TE: 20/5.7 ms α: 5, 15, 20, 25, 30°	—	—	2:00
			Total Time:	9:27

To correct for B₁ and B₀ inhomogeneities present in the imaging volume, B₁ (using the dual-TR actual flip angle GRE method (49)) and B₀ (using dual-TE GRE) maps were acquired using fast 3D techniques over 3 slices, centered on the MT acquisition. T₁ mapping was performed using a multiple flip angle (MFA) acquisition over 3 slices, centered on the MT acquisition. Fixation was not employed for the B₁, and B₀ acquisitions because it was assumed that B₁ and B₀ inhomogeneities will be slowly varying over the volume, while the T₁ acquisition did not utilize fixation in order to save time on the acquisition due to eye fatigue. Detailed scan parameters and acquisition times are listed in Table 1.

Data Postprocessing

Brain Data

To determine the effects of the Dixon method on MT data, we first considered the W and OP data in the brain regions for all subjects. Using the Brain Extraction Tool (BET (50,51)) and FLIRT (52,53) packages from FSL (54), the skull and ONs were removed, and the data was co-registered to the first MT offset for each image type, respectively. Large ROIs were drawn in the WM of the right hemisphere of the brain using the Δω = 1000 kHz offset (see Figure 1a,b), and these were propagated to the MT-weighted, T₁, B₁, and B₀ images. OP data was used to approximate a normal out-of-phase acquisition, and to ensure user error during ROI selection did not contribute to differences in parameter values.

Optic Nerve Data

ROIs were drawn in the W only images for each offset of the MT-weighted data of the ON (see Figure 1a) in each eye, as well as for the T₁, B₁, and B₀ data. As the W and OP images were taken from the same acquisition, the ROIs in the W images were also propagated to the OP images. Following the ROI selection, W and OP qMT parameters were generated in both ONs for each volunteer using the methods described above.

Parameter Generation

The resulting data was used to generate qMT parameters for each volunteer using the qMT model described in Yarnykh (24) & Yarnykh and Yuan (44). This model contains six independent parameters: R_1m, R_1f, T_2m, T_2f, PSR = M_0m/M_0f, and k_mf = k_fm/PSR. The R_1obs (1/T_1obs) maps were independently reconstructed by regressing MFA data to the SPGR signal equation in the steady-state (55); these maps were used during MT parameter estimation (below) to estimate the parameter R_1f (24,44). Henkelman, et al. (19) & Morrison and Henkelman (30) showed that the signal dependence on R_1m is weak; therefore, it was set equal to the R_1f as well (31). The remaining MT parameters (PSR, k_mf, T_2f, and T_2m) were estimated for the W and OP brain data by fitting the qMT data to the two-pool model (24,44). For all fitting, the nominal offset frequency and RF amplitudes were corrected using B₀ and B₁ maps, respectively (21).

Statistical Analysis

The mean and standard deviation for each image type (W and OP) were calculated for each qMT-derived index in the brain and ONs. Statistical variations between the left and right ON (for both W and OP image types) and between the W and OP brain data were evaluated using the non-parametric Wilcoxon signed rank test, with a threshold for significance of p < 0.05, for each qMT parameter (PSR, k_mf, T_2f, and T_2m).

MAD Analysis

While the statistical analysis above is straightforward in the brain, due to the relatively homogeneous ROIs taken in each image type, the Wilcoxon signed rank test in the ON is more complicated (see Results), because this approach does not capture the potential for nested variance structures or an asymmetric number of voxels between eyes, and thus may potentially underestimate the true variance between each image type. Therefore, we also computed the mean absolute difference (MAD) of all possible left and right ON voxel pairs drawn from an empirically determined distribution (below). If there are n voxels in the right and m voxels in the left ON for a single subject, then the MAD is given by

$$MAD=\left(\frac{1}{mn}\right)\sum _{k=1}^m\sum _{l=1}^n\mid h_k\left(Left\right)-h_l\left(Right\right)\mid$$ [1]

where h_k(Left) denotes a measure (e.g., PSR) on the k^th voxel in the left ON, and similarly, h_l(Right) denotes the same measure (e.g., PSR) on the l^th voxel of the right ON. The distribution of data for each qMT parameter was empirically constructed via the bootstrap method with 3000 iterations (56). For each iteration, the subject-level MT data were resampled with replacement to generate a Z-spectrum, and qMT parameter maps were determined from this sampled MT data. The ROI-derived values for the T₁, B₁, and B₀ data from each subject was used in each case to avoid biases due to the variance that could occur from these parameters. The data for each subject was then combined, and a total MAD score was calculated. The empirical 95% confidence interval of the MAD for each parameter of interest was computed and examined for statistical significance.

We assumed no differences would exist in healthy subjects for each qMT parameter between the left and right ON, and that a low MAD indicates a greater symmetry between the right and left ON for a given qMT parameter and image type. Comparing across image types, we calculated the ΔMAD% as the difference in MAD values for each technique relative to the MAD for the OP acquisition as summarized in the following equation:

$$\Delta MAD\%=\frac{MAD\left(W\right)-MAD\left(OP\right)}{MAD\left(OP\right)}\times 100$$ [2]

A negative ΔMAD% indicates a lower W MAD score compared with the OP MAD, and the ΔMAD% is an estimate of the relative improvement (or worsening) when using the Dixon method relative to using an OP image.

Results

Simulations

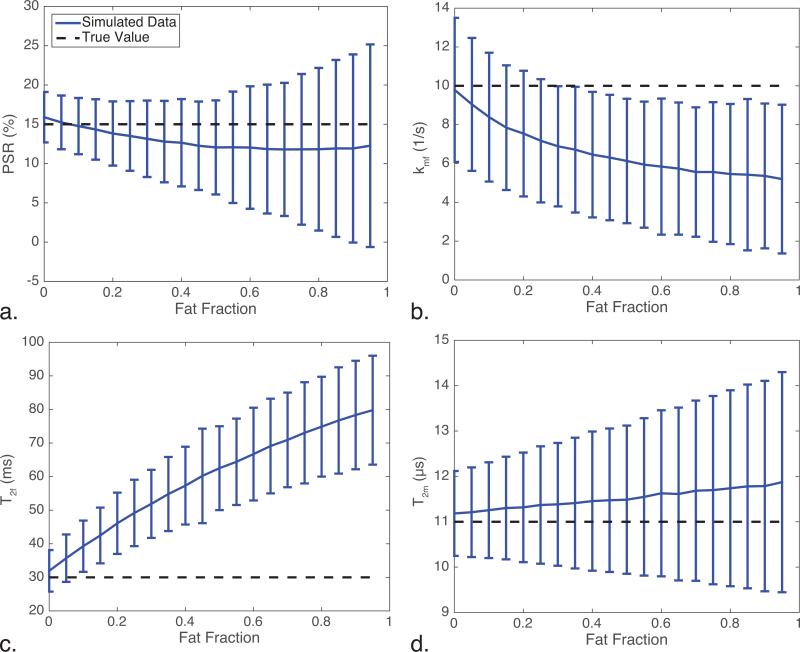
Figure 2 illustrates the effect of fat on the qMT parameters where the qMT-derived indices (from simulation) are shown against the fat fraction. Note the dotted black line is the true, expected value and the blue line shows the fit results for each parameter, with the error bars representing one standard deviation over 10,000 noise iterations at each point. The PSR never significantly diverges from the true PSR value (larger than one standard deviation from the true value); however, the k_mf and T_2f parameters significantly diverge from the true value for fat fractions greater than 0.3 and 0.1, respectively. Furthermore, the variance in the PSR and T_2m increase as a function of fat fraction, which can generally be assumed as instability in the fitting algorithm at higher fat fractions.

Figure 2.

Results of the numerical simulations of the qMT parameters as a function of fat fraction, focusing on (a.) PSR, (b.) k_mf, (c.) T_2f, and (d.) T_2m. Notice that (a.), (b.), and (d.) all show increased variance with increasing fat fraction, while (b.) and (c.) show significantly different deviations from the true value at relatively low fat fractions (20% and 30% fat, respectively).

Experimental Data

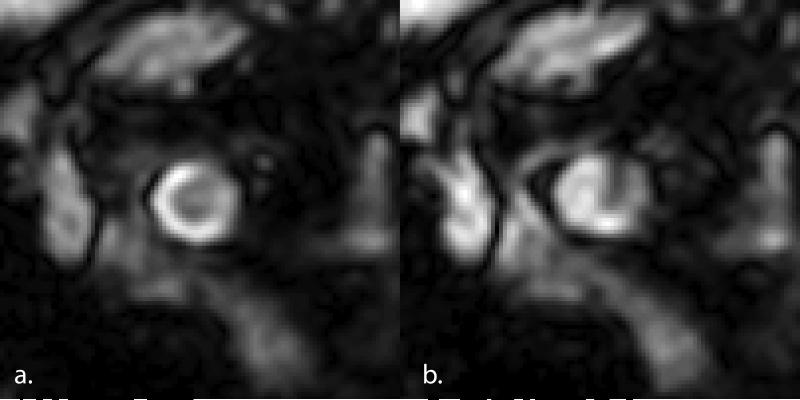
Representative MT data for the W and OP image types are displayed in Fig. 1. The conspicuity between the ON and surrounding tissue increases dramatically in the W images compared to the OP images (Fig. 1c). Furthermore, fixation provides a marked increase in ON visualization, as can be seen in Fig. 3a.

Figure 3.

Example MT data with (a.) and without (b.) fixation. The nerve is much more clearly delineated when using fixation. An example ROI is also presented in (a.) to illustrate the area used to quantify the MT data.

Brain Data

The results comparing the qMT-derived indices between the W and OP image types in the brain are shown in Table 2. The mean values across methods are indistinguishable indicating no effect from combining multiple echoes for all qMT-derived indices. Further, all parameter p-values are well above the threshold for significance (p-values: PSR = 0.64, k_mf = 0.95, T_2f = 0.38, T_2m = 0.25), indicating there is no statistical significance between the W and OP images when no fat is expected to be present. Therefore, the Dixon method does not alter the MT-weighted observations and resulting fits during the multi-echo reconstruction.

Table 2.

Mean and Standard Deviation of qMT Parameters in the Brain.

	PSR (%)	kmf (1/s)	T2f (10−2)	T2m (μs)	R1obs (1/s)
Water	17.0±1.7	17.2±5.2	1.8±0.2	11.1±0.8	1.15±0.17
Out-of-Phase	17.6±3.7	17.6±7.1	1.9±0.3	11.3±1.3

Optic Nerve: W vs OP Data

qMT-derived indices for the ON are presented in Table 3, with an example of the fits displayed in Fig. 4. Compared to the brain, the qMT-derived indices from the W ON data are different in the ON (lower for PSR, k_mf, and T_2m, higher for T_2f), which may be driven by differences in the neurological tissue between the brain and ON (as is seen in the spinal cord (23)), or minor partial volume effects from cerebrospinal fluid (CSF).

Table 3.

Mean and Standard Deviation of qMT Parameters for Left and Right Optic Nerves.

	PSR (%)		kmf (1/s)		T2f (10−2)		T2m (μs)		R1obs (1/s)
	Left	Right	Left	Right	Left	Right	Left	Right	Left	Right
Water	15.8±4.4	14.7±2.7	11.1±3.6	10.2±3.2	2.9±1.8	2.3±1.0	8.5±2.7	8.3±1.1	0.94±0.19	0.82±0.12
Out-of-Phase	34.0±31.6	18.2±11.2	28.5±44.3	41.5±41.6	2.9±1.8	2.0±0.6	9.9±2.8	7.9±3.4

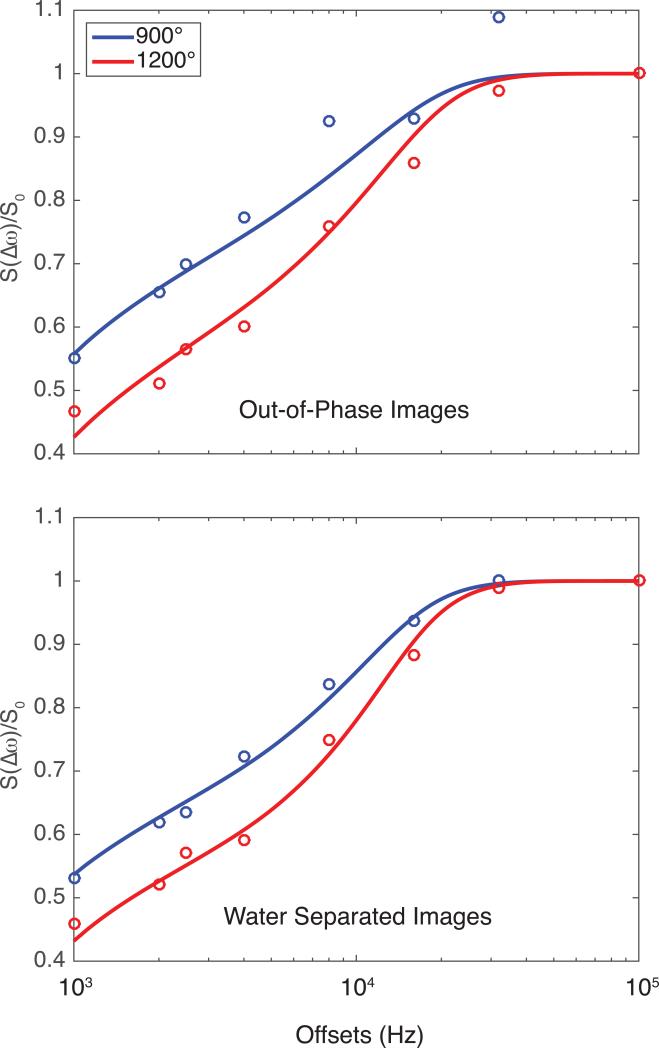
Figure 4.

Example optic nerve Z-spectra for the out-of-phase and water images for a single subject. The water images (normalized residual = 0.0035) show better goodness of fit, and visually performed better compared to the out-of-phase images (normalized residual = 0.0228).

However, the k_mf in the OP data has a much higher mean and standard deviation than the W data (Table 3). Although the OP images have approximately $\sqrt{2}$ more noise than the W images, this does not fully account for the larger standard deviation seen in the OP images relative to the W images, as can be seen in Fig. 5, which displays a box plot of the qMT parameters. This is important, as the PSR, T_2f, and T_2m seem to be relatively consistent across image types, indicating that the k_mf may be sensitive to the unmodeled fat components in the tissue. When considering the MT-weighted data and the resulting fits (Figs. 4 and 5), the fits for the OP data were worse than those for the water separated data, indicating that some fat may be influencing the OP image data (see Fig. 4 for representative residual values).

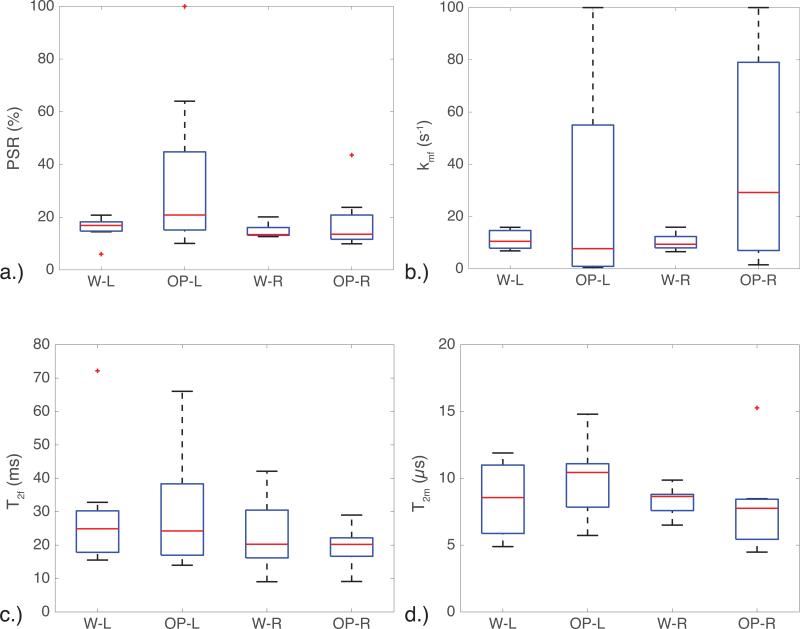
Figure 5.

Box plots illustrating the variance in the a.) PSR, b.) k_mf, c.) T_2f, and d.) T_2m for the left (L) and right (R) optic nerves in both the water (W) and out-of-phase (OP) images. The k_mf shows a large amount of variation in the OP images, and small variation in the W images. A similar trend is seen in the PSR, indicating that the two-pool qMT model used here did not fit the OP data well.

Optic Nerve: Left vs. Right Data

Comparing the left and right ON data for each method, no significant differences can be seen for either method (p-values range from 0.11-0.95). This is expected, as the ONs in healthy subjects should not be significantly different from one another. We used this result to increase the power of the statistical test between image types (W versus OP) by combining the left and right ON data. Evaluating the mean qMT-derived indices in the W and OP data, there were no significant differences between any of the qMT parameters when employing the Wilcoxon signed rank test (p-values: PSR = 0.13, k_mf = 0.44, T_2f = 0.64, T_2m = 0.92). However, this is most likely due to the large variances found in the OP parameters (as seen in Fig. 5), which ensures a high likelihood that each image type will be determined to be from the same distribution. The k_mf in particular displayed a large variance in the fitting derived from the OP images (L/R = 28.5±44.3/41.5±41.6 s⁻¹), implying that the OP images did not always yield high-quality fits to the data (see Table 3).

MAD Analysis

Table 4 provides the results of the MAD calculation (mean absolute difference between the left and right ONs drawn from an empirically determined distribution). We report the initial MAD value, the 95% CI for MAD from 3000 bootstrap iterations, and the ΔMAD%, which is the relative difference between the W and OP parameter values (note a negative value indicates improved MAD in the W images relative to the OP images). Recall that the MAD is a reflection of the variation across eyes rather than a variation of the mean qMT-derived index of interest. The variation across eyes for each qMT parameter are approximately the same between image types, and indeed, most of the 95% CI overlap one another (PSR, T_2f, T_2m). However, the k_mf 95% CI for each image type (W and OP) do not overlap, indicating that they may be drawn from separate distributions, and thus, these image types may show significantly different fits.

Table 4.

MAD Between Left and Right Optic Nerves at the Initial Point and 95% CI (MAD) and relative improvement (−) or Worsening (+) of Dixon Water Images Versus Out-of-Phase Images.

	PSR (%)			kmf (s−1)			T2f (ms)			T2m (μs)
	MAD	95% CI	ΔMAD%	MAD	95% CI	ΔMAD%	MAD	95% CI	ΔMAD%	MAD	95% CI	ΔMAD%
Water	7.69	[7.11, 7.83]	−4.46	9.16	[8.92, 9.57]	−6.76	6.50	[5.99, 7.08]	−5.63	1.24	[1.13, 1.27]	−11.32
Out-of-Phase	8.05	[7.40, 8.04]		9.83	[9.80, 10.19]		6.88	[6.24, 7.35]		1.40	[1.22, 1.40]

We next assessed the ΔMAD%, which is a reflection of the relative improvement (a negative ΔMAD%) or worsening (a positive ΔMAD%) of the variability across ONs (assumed to be small) when considering two different techniques. The ΔMAD% is negative for each qMT-derived index, indicating a general reduction in the variation across eyes derived from the W images compared to the OP images. Therefore, the W imaging data from which we derive our qMT-indices outperform the same data considered from only OP images.

Discussion

The goal of this study was to demonstrate that qMT techniques will not be adversely affected by the use of the Dixon method. Furthermore, when considering regions, like the ON, where fat may influence the image, Dixon qMT imaging may derive higher fidelity fits and more accurate quantitatively derived indices. We compared the impact of fat on qMT-derived PSR, k_mf, T_2f, and T_2m via simulations (indicating the importance of accurate fat removal), and across healthy volunteers in the brain, where there is no fat, and in the ON, which is surrounded by a fatty sheath. Lastly, we evaluated the statistical impact of removing fat contamination from qMT data in difficult anatomies. We show that the OP images do not provide robust estimations of qMT-derived indices in the presence of fat, and that the Dixon method can be employed to reliably separate fat and water without altering the ability to characterize the MT effect using a two-pool qMT model. The ability to generate accurate qMT parameter maps while utilizing the Dixon method may increase the clinical applicability of qMT, as it provides a method to apply MT saturation in anatomies where fat may be in abundance, such as in the muscle (60), breast (61), or even the peripheral nervous system where fat is interlaced within the nerves (8).

Strength of Dixon Method

While on-resonant fat separation methods exist, they do not have the same advantages as the Dixon method. Binomial pulses may be used for fat suppression, however, clinically available gradient strengths/slew rates require implementation of large 3D volumes, which may not be suitable in anatomies prone to significant amounts of motion, such as the ON or abdomen, and may also significantly increase scan time. While echo planar imaging trains can be used to reduce scan time, employing these sequences in anatomies with large B₀ inhomogeneities, such as the ON and parts of the abdomen, may cause undesirable image distortion artifacts (62). The Dixon method, however, can be employed over any chosen (i.e. smaller) volume, reducing scan time, to accurately separate fat and water images. It should also be noted that the Dixon method is relatively robust to B₀ inhomogeneities, which can be problematic across different anatomies (36).

Statistical Implications

While the Wilcoxon signed rank test failed to statistically quantify the differences between the W and OP images in the ON, several conclusions can be drawn from the data itself. The k_mf parameter has a much higher variance in the OP images compared with the W images (Fig. 5), suggesting that k_mf is sensitive to the underlying distribution. Therefore, if there are tissue components in a voxel that are not accounted for in the model, k_mf will be difficult to characterize, thus producing inaccuracies in the other qMT parameters. This is further confirmed utilizing the MAD data (Table 4). The ΔMAD% illustrates an improvement in the consistency of each qMT-derived index between eyes when the W only images are considered relative to the OP images. Furthermore, although there is a factor of $\sqrt{2}$ difference in SNR between the OP and W images, the MAD utilizes empirical data, which reduces the influence of nested variance and differences in noise between image types. Particularly important to this argument is the fact that our results from the brain indicate these differences are not due to variations driven by the different reconstruction methods (Dixon vs. non-Dixon) (see Table 2), suggesting the k_mf in tissues where voxels have a combination of tissue types is poorly characterized.

Simulations

Considering the simulations further (Fig. 2), T_2f and k_mf deviate significantly as the fat fraction increases. Additionally, the PSR and T_2m show larger variance in their fit as the fat fraction increases, indicating greater instability in the fitting algorithm due to the presence of fat. This indicates that the errors from the k_mf and T_2f may be influencing the stability of the PSR and T_2m. This may also be the case in the OP ON images: although the PSR, T_2f, and T_2m are not significantly different from the W images, the k_mf is significantly different, indicating there may be errors present within the other OP qMT parameters as well. Therefore, ensuring all parameters in the qMT model are well determined is important to accurately model the MT effect, particularly in tissues where there may be significant partial volume effects present.

Data Reduction Strategies

While this study utilized a single slice acquisition to explore the Dixon method for fat suppression, an expanded 3D volume may be considered. However, scan time cannot be disregarded with any qMT method due to the number of powers and/or offsets that are required for appropriate fitting. A single-point qMT model (1 MT-weighted volume with the addition of T₁, B₁, and B₀ maps) has been introduced to reduce the scan time to a clinically appropriate length, and has been applied to the brain (31), spinal cord (23) and muscle (63). However, the assumption for single-point qMT is that the parameters k_mf, T_2f, and T_2m are well-determined from prior scans utilizing a full qMT acquisition. Therefore, without adequate fat suppression, variance in the assumed model parameters may result in a poorly constrained model and will be hampered in tissues where fat cannot be excluded such as the ON, peripheral nerves, and muscle. Importantly, these experiments utilized out-of-phase images to perform the T₁ mapping. However, this may introduce fat signal into the T₁ data, confounding the results. While the observed T₁ does not seem to be adversely affected by the presence of fat here, this will potentially limit the scan if appropriate fat suppression techniques are not employed.

This study used a fixation cross to help minimize motion across dynamics, due to the large saturation and readout times for each MT dynamic (approximately 10 seconds), which resulted in large amounts of motion blur (Fig. 3). To minimize tiring during fixation, we utilized a 1-on and 1-off acquisition scheme (one dynamic under fixation and the next dynamic without), which effectively doubles the scan time. Requiring fewer dynamics would significantly alleviate these challenges.

Limitations

While fat was the target of this study, the CSF surrounding the ON may also influence the signal from nerve tissue due to partial volume effects. CSF will reduce the MT effect within the nerve and thus partial volume effects will result in an underestimation of the PSR, k_mf, and T_2m and overestimation of T_2f (Tables 2 and 3). Researchers have investigated the use of inversion recovery pulses in diffusion imaging for CSF suppression (65,66) however, this would add significantly to the scan time and may introduce extraneous off-resonance effects for nearby slices. Additionally, while techniques such as DANTE (67) may provide advantages over inversion recovery methods, they would still introduce extra off-resonance saturation effects, which would alter the observed MT effect and would need to be incorporated into the model.

Therefore, to preserve the fidelity of the observed MT effect in tissue, alternative techniques can be considered to accurately suppress CSF. A three-pool model (2 MT pools, and 1 non-exchanging pool) was recently introduced by Mossahebi, et al. (68) to fit the CSF pool (non-exchanging) in the brain. Their results suggest that the PSR can be accurately quantified even in the presence of significant amounts of CSF contamination. Research has also been performed to separate the CSF sheath from the ON using a model derived using T₂-weighted 3-D spin echo sequences with a turbo spin echo readout (32). These sequences have similar contrast to the small offset MT scans, and thus may be applicable to the MT-weighted data. Thus, further research is warranted to address the removal of the CSF sheath from the ON.

Conclusions

The results of this study demonstrate the ability to successfully remove the fat component from MT images using the Dixon fat-water separation method. The development of this technique provides a method to perform qMT while in the presence of significant B₀ inhomogeneities, and over small imaging volumes. Future work includes further investigation of this technique in the presence of disease, and application of this method in other anatomies with large fat components.