Using the diffusion model to explain cognitive deficits in Attention Deficit Hyperactivity Disorder

Abstract

Slow, variable, and error-prone performance on speeded reaction time (RT) tasks has been well documented in childhood ADHD, but equally well documented is the context-dependent nature of those deficits, particularly with respect to event rate. As event rates increase (or, as the interstimulus intervals become shorter), RTs decrease, a pattern of performance that has long been interpreted as evidence that cognitive deficits in ADHD are a downstream consequence of a fundamental difficulty in the regulation of arousal to meet task demands. We test the extent to which this is a misinterpretation of the data that occurs when RT and accuracy are considered separately, as is common in neurocognitive research. In two samples of children aged 8–10 with (N = 97; 33 girls) and without (N = 39; 26 girls) ADHD, we used the diffusion model, an influential computational model of RT, to examine the effect of event rate on inhibitory control in a go-no-go task. Contrary to longstanding belief, we found that fast event rates slowed the rate at which children with ADHD accumulated evidence to make a decision to “no-go”, as indexed by drift rate. This in turn resulted in a higher proportion of failed inhibits, and occurred despite increased task engagement, as reflected by changes in the starting point of the decision process. Thus, although faster event rates increased task engagement among children with ADHD, the increased engagement was unable to counteract the concurrent slowing of processing speed to “no-go” decisions. Implications for theoretical models of ADHD and treatments are discussed.

Response disinhibition is arguably one of the most well studied aspects of cognitive control in Attention Deficit Hyperactivity Disorder (ADHD), and much of this work has utilized the well-known stop signal paradigm (Barkley, 1997; Logan & Cowan, 1984; Nigg, 2001). In the most standard version of this paradigm, children view a sequence of X’s and O’s that appear onscreen (“go” signal), and are asked to indicate whether the stimulus is an X or an O. On a minority of trials (e.g., 25%), an auditory tone is presented at some delay from the onset of the “go” signal which indicates that they should not respond to that trial. Results from several meta-analyses have reported that to be as successful as their non-ADHD peers in stopping an ongoing behavior, children with ADHD require a longer delay between the onset of a “go” and the onset of a “stop” signal because the speed of their inhibitory process (i.e. the stop signal reaction time, or SSRT) is slower (Alderson, Rapport, & Kofler, 2007; Lijffijt, Kenemans, Verbaten, & van Engeland, 2005; Metin, Roeyers, Wiersema, van der Meere, & Sonuga-Barke, 2012; Willcutt, Doyle, Nigg, Faraone, & Pennington, 2005). The slow speed of the inhibitory process is believed to contribute to the frequent impulsive behaviors that are so emblematic of the disorder.

However, the most common method of calculating SSRT (i.e. mean reaction time - mean stop signal delay), leads to estimates of SSRT that are strongly influenced by the shape of the reaction time (RT) distribution, and are highly correlated with mean RT (Verbruggen, Chambers, & Logan, 2013). This has prompted some to speculate whether a specific deficit in inhibitory control is present, or whether slow SSRT among children with ADHD instead reflects a more general deficit in processing speed (Alderson et al., 2007; Karalunas & Huang-Pollock, 2013; Lijffijt et al., 2005; Verbruggen et al., 2013). In fact, the most frequently used indices of performance on the most common measures of executive function (EF) (e.g. go-no-go, continuous performance tasks, flanker tasks, stroop, etc.), are RT and error rate. Thus, in comparison to the complex EF construct, a more tractable description of ADHD-related cognitive deficits may be that they tend to be slow, variable, and error prone on RT tasks.

Why might this be? The neuroenergetic theory (NeT) of ADHD (Killeen, 2013; Killeen, Russell, & Sergeant, 2013) proposes that responding to rapid and externally paced stimuli requires access to lactate, which the neuron uses for fuel. NeT posits that this supply chain is compromised in ADHD, possibly through a breakdown of the astrocyte-lactate-neuron-shuttle (Brown & Ransom, 2007) responsible for meeting the local metabolic demands of firing neurons. According to NeT, the ultimate result of an insufficient neuronal energy supply is neuronal fatigue, which in turn causes the slow, variable, and error-prone performance that is characteristic of ADHD. In this way, NeT is similar to other biologically-based limited-resource/depletion models of self-control (e.g. Masicampo & Baumeister, 2008). What NeT would therefore predict is that as event rates increase (or, as the interstimulus intervals become shorter), and assuming explicit periods of rest are not provided between trials, longer and more variable response times should be seen among affected children in tasks requiring effortful control. This is because the rapid pace would be expected to exacerbate neuronal fatigue.

However, this prediction is in direct opposition with what is commonly observed: RTs tend to speed up with faster event rates (Andreou et al., 2007; Epstein et al., 2011; Sanders, 1970; Sergeant, 2000; Wiersema, van der Meere, Roeyers, Van Coster, & Baeyens, 2006). In fact, this relationship is one of the hallmark pieces of evidence used to support the well-known and influential cognitive energetic theory of ADHD, which was among the first theories to suggest that cognitive deficits in ADHD were context-dependent (Sergeant, 2000, 2005; Sonuga-Barke, Wiersema, van der Meere, & Roeyers, 2010). Specifically, the cognitive energetic theory argues that manipulations which increase arousal (e.g. faster event rates) will improve performance as observed through RT speed-up.

That being said, how performance is affected by event rate depends in large part on which outcome variable is examined. A recent meta-analysis of event rate effects on go-no-go performance in ADHD reported larger ADHD deficits for slow event rates when RT was the dependent variable (effect size d_RT=0.56 vs. 0.33), but larger ADHD deficits for fast event rates when commission errors (i.e. failed inhibits) were the dependent variable (effect size d_Com=0.57 vs. 0.37) (Metin et al., 2012). How should such contradictory results be interpreted? The cognitive energetic theory has suggested that the relationship between event rate and performance takes the shape of an inverted U. That is, slow event rates are under-arousing (leading to slow and variable RTs), but fast event rates are over-activating (leading to fast RTs and frequent failed inhibits).

What is often ignored, however, is that RT and accuracy are produced simultaneously; they are two descriptors of a single response, and are not generated by independent processes. Thus, considering RT and accuracy separately provides at best an incomplete understanding of performance, and at worse, erroneous interpretations of data. The most accurate description of performance would require a theory capable of accounting for both RT and accuracy simultaneously.

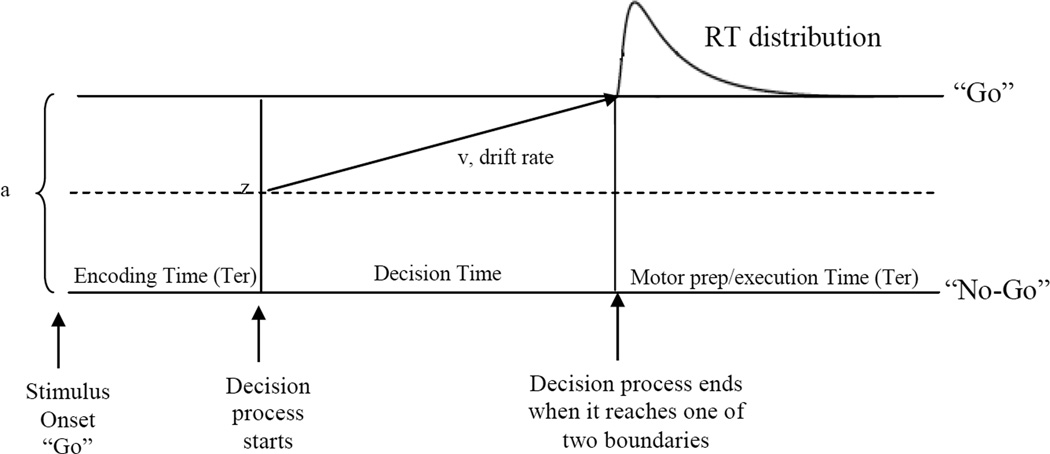
One way forward is to consider inhibitory control as part of a broader decision making process: a decision to go vs. not to go (Figure 1). The diffusion model is a stochastic accumulator model of simple (i.e. <2s) one and two-choice decisions that produces parameters which incorporate both RT and accuracy data in a single set of performance indicators (Ratcliff & McKoon, 2008). The model assumes that after a stimulus is encoded, a decision process (e.g. Is it a word or non-word? Do I go or not go?) begins from a start point, denoted as z, in the direction of one of the two decisional boundaries (0, “no-go” and a, “go”), until one of the boundaries is reached. At that point, depending on which boundary is crossed, the appropriate response is initiated (in the case of a “no-go” decision, the response would be to not press). The rate at which an individual accumulates information to reach one of the decision boundaries is called drift rate, and is denoted as v. Drift rate is influenced by individual and developmental differences where younger and atypically developing children have slower drift rates than typically developing children, adolescents, and adults (Cohen-Gilbert et al., 2014; Huang-Pollock, Karalunas, Tam, & Moore, 2012; Ratcliff, Love, Thompson, & Opfer, 2012). It is also influenced by states of arousal where low arousal leads to slower drift rates (Ratcliff & Van Dongen, 2011). Boundary separation, denoted as a, represents how much information an individual requires to make a decision, and is determined by an individual’s default speed-accuracy-trade-off setting, or by an explicit strategy (i.e. tending or being instructed to emphasize speed over accuracy). A larger boundary separation indicates a greater emphasis on accuracy, or more conservative responding. Start point, denoted as z, is influenced by the expectation of events or rewards (e.g. a decision will start closer to the “go” boundary if “go” signals are presented more often than “no-go” signals). Ter refers to the time it takes to complete all non-decision based processes (primarily, the time it takes to encode a stimulus and motor preparation), and can be influenced by the complexity or difficulty of the required motor response.

Figure 1.

Anatomy of a reaction time. After a stimulus is encoded, the decision process starts at z, and moves in the direction of one of two boundaries (is the stimulus a word or non-word? Should I go or not go?). Drift rate (v) is the rate at which information accumulates towards a decision. Once the decision process has reached one of the boundaries, the corresponding motor response is initiated. How far apart the boundaries are (i.e. the boundary separation, or a) is an indication of the conservativeness of the response criterion. Wider separations indicate more conservative responding (i.e. more information is needed before a decision can be reached). Non-decision time (Ter) represents the time it takes to complete all non-decision processes, such as stimulus encoding and motor preparation. Reaction time = Decision Time + Non-decision Time. Trial-to-trial variability in drift produces RT distributions.

Broadly speaking, these parameter values are obtained by simultaneously fitting the observed RT distributions for correct and error responses, by the RT distributions that are predicted by the diffusion model. Using an initial set of parameter values, predictions are derived and then the values of the parameters are adjusted using an automatic function minimization routine (SIMPLEX; see Ratcliff & Tuerlinckx, 2002). The routine generates parameter values near the starting values, computes the goodness of fit, and then replaces the parameter values that had the worst fit with new ones. By this method, it iterates to the parameter values that produce the best fit. Once the best fitting set of parameters is obtained, the values of those parameters are then used as indices of the latent psychological processes that each parameter represents (i.e. cognitive processing efficiency, speed-accuracy trade off settings, response bias, and the time to encode/prepare a motor response). Because the model is able to separate cognitive processing efficiency (i.e. drift rate), which typically represents the construct of interest, from other processes, including the speed of encoding and motor preparation/ execution, as well as speed-accuracy settings, it is a significant improvement over the individual use of RT or accuracy alone in the analysis and interpretation of cognitive performance data.

The model has been well-validated and used to understand cognitive performance in both healthy (Cohen-Gilbert et al., 2014; Ratcliff et al., 2012; Ratcliff, Thapar, & McKoon, 2006) and atypical (Huang-Pollock et al., 2012; Karalunas, Huang-Pollock, & Nigg, 2012; Pe, Vandekerckhove, & Kuppens, 2013; Weigard & Huang-Pollock, 2014, in press; White, Ratcliff, Vasey, & McKoon, 2010) populations across the lifespan. Recent studies have also linked these parameters to neural network functionality (Bogacz, Wagenmakers, Forstmann, & Nieuwenhuis, 2010; Philiastides & Sajda, 2007; White, Mumford, & Poldrack, 2012), demonstrating its utility and promise to move the field’s understanding of psychopathology from stagnant behavioral manifestations to specifying the neurocognitive processes that are unique and shared across disorders (White et al., 2010; Wiecki, Poland, & Frank, 2015).

Here, we examine the impact of event rate on inhibitory control using a go-no-go diffusion model applied to a go-no-go task (Gomez, Perea, & Ratcliff, 2007; Ratcliff, Huang-Pollock, & McKoon, in press). Like the two-choice model, the go-no-go diffusion model assumes that there are two decision boundaries. Termination at one boundary (i.e. decision to “go”) leads to a motor response, whereas termination at the other (i.e. decision to “no-go”) leads the participant to not make a button press and to wait out the trial. Because there is no RT measure for a no-go decision, the go-no-go model differs from the standard two-choice model in that no-go decisions are fit to the model using choice probabilities for no-go choices (Ratcliff & Tuerlinckx, 2002). Go-decisions are fit using RT distributions, as with the standard two choice model.

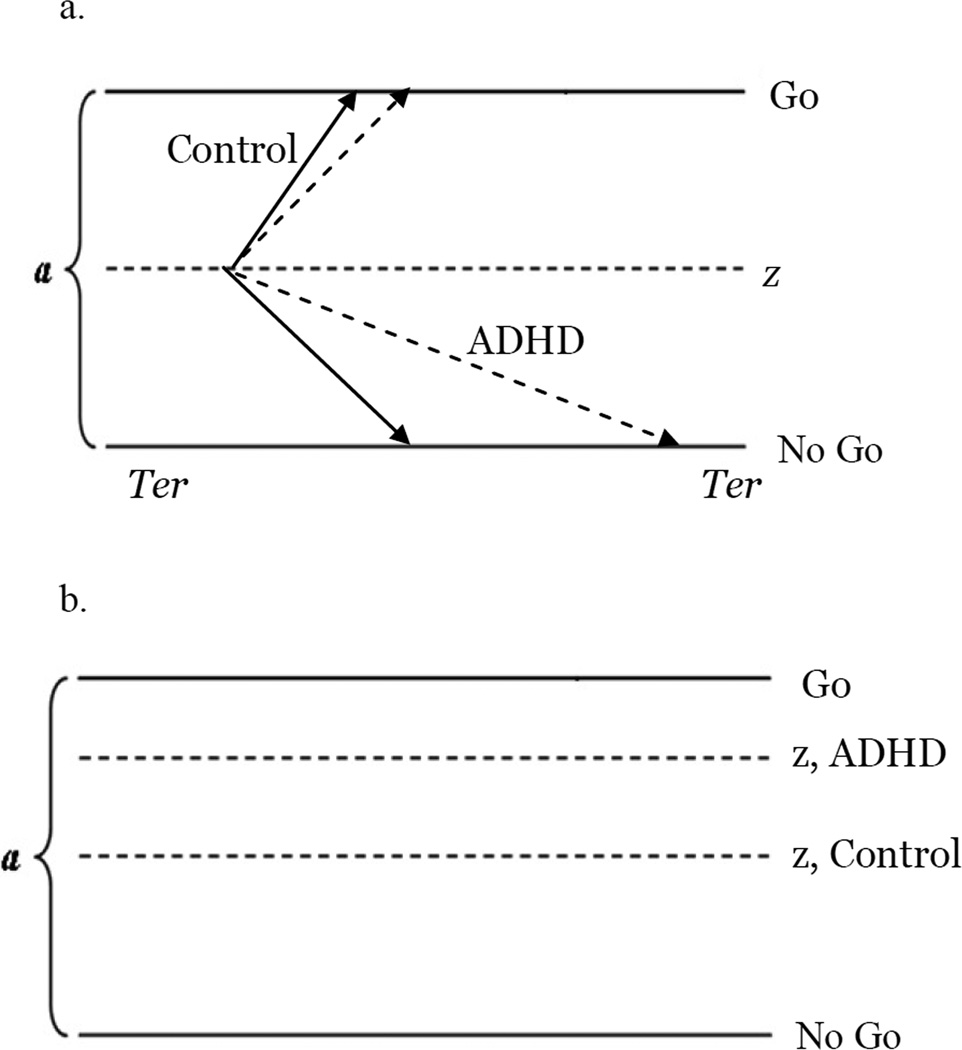
Our aim is to use the analyses provided by the diffusion model to evaluate the predictions the cognitive energetic and neuroenergetic theories of ADHD make with respect to event rate manipulations. From a decision process perspective, poor inhibitory control can be viewed as a bias in decision making that might occur in one of three ways. First, it may be that ADHD drift rates are slower to the no-go vs. go boundary (i.e. there is a bias in drift; Figure 2a). Slower drift to no-go decisions would mean that the time required to make a decision to “no-go” is longer. In this way, drift to no-go is conceptually similar, but not equivalent, to SSRT. However, drift to no-go represents a purer measure of processing efficiency because the variance associated with non-decision time and speed-accuracy trade-off settings has been removed. Second, it may be that children with ADHD set their start points closer to “go,” making it more difficult to inhibit when necessary (Figure 2b). Or, it could be a combination of those factors.

Figure 2.

Hypothetical causes of inhibitory deficits in ADHD.

a. Bias in drift where drift to no-go is slower than drift to go. ADHD dashed lines.

b. ADHD start point biased to “go”

In summary, NeT predicts that fast event rates, in the absence of explicit between-trial periods of rest, will exacerbate neuronal fatigue. The inhibition of a prepotent response requires more effortful control than the more automatic process of allowing an ongoing action to proceed (Muraven & Baumeister, 2000). Because fatigue would affect processes that are more effortful, in the context of a go-no-go task, this should result in the preferential slowing of drift to the no-go decision relative to the go decision. In contrast, cognitive energetic theory predicts that fast event rates raise arousal levels, which would preferentially speed up drift rate. In line with this reasoning, our primary predictions are therefore as follows: results finding that drift to no-go is slower under fast event rates would be consistent with NeT, but results finding drift to no-go is faster under fast event rates would be consistent with the cognitive energetic theory. Children with ADHD may also show greater start point bias to “go,” (contributing to a greater proportion of failed inhibits), but we would not expect this to be altered by event rate in either theory. Ter and a are similarly not expected to vary by event rate.

Methods

Participants

Children aged 8–12 were community recruited from radio, magazine, and internet ads, as well as public flyers posted in the community and provided to local schools in the Central and Dauphin counties of Pennsylvania. Exclusion criteria included: (1) current non-stimulant medication treatment (e.g., neuroleptics or antidepressants), (2) diagnosis of pervasive developmental disorder, intellectual disability, sensorimotor disability, psychosis, or other parent-reported neurological disorder, and (3) estimated Full Scale IQ (FSIQ)<80.

Children with ADHD

Children with ADHD met DSM-IV criteria for ADHD including age of onset, duration, cross situational severity, and impairment as determined by parent report on the Diagnostic Interview Schedule for Children-IV (DISC-IV: Shaffer, Fisher, & Lucas, 1997). At least one parent and one teacher report of behavior on the Attention, Hyperactivity, or ADHD subscales of the Behavioral Assessment Scale for Children-2 (BASC-2: Reynolds & Kamphaus, 1992) or the Conner’s Rating Scale (Conners, 1997) was required to exceed the 85^th percentile (T-score>61). Both measures are commonly used and well-validated for the evaluation and diagnosis of ADHD. Following DSM-IV field trials (Lahey et al., 1994), an “or” algorithm integrating parent report on the DISC-IV and teacher report on the ADHD Rating-Scale (DuPaul, Power, Anastopoulos, & Reid, 1998) was used to determine final symptom count and subtype (Table 1). Children prescribed stimulant medication were asked to discontinue medication use for 24–48 hours.

Table 1.

Sample demographics.

	Slow event rate			Fast event rate			Slow vs Fast
	ADHD	Control	F (1,65)=	ADHD	Control	F (1,67)=	ADHD t(95)=
	(n=46)	(n=21)		(n=51)	(n=18)
Male:Female	31:15	6:15		33:18	7:11
Age	10.35 (2.26)	10.12 (1.28)	0.47,p=.50	9.95 (1.34)	9.64 (1.29)	0.74,p=.39	1.57,p=.12
IQ	103.87 (11.01)	107.19 (9.01)	1.46,p=.23	101.45 (13.93)	108.11 (9.55)	3.51,p=.07	1.13,p=.26
#Attention symptoms	8.13 (0.83)	0.29 (0.46)	1624.44,p<.001	7.90 (1.89)	0.28 (0.57)	281.42,p<.001	0.88,p=.38
#Hyper/Impulsive symptoms	5.54 (2.65)	0.38 (0.59)	77.48,p<.001	5.69 (2.74)	0.17 (0.51)	71.56,p <.001	−0.13,p=.90
ADHD Subtype (C:I:H)	25:21	−	--	27:22:2	−	--
# ODD, CD	22, 7	1, 0		19, 3	1, 0
# GAD, MDD, DD	6, 2, 2	0, 0, 0		3, 2, 1	0, 0, 0

Note: C=Combined subtype, I=Primarily inattentive subtype, H=Primarily hyperactive/impulsive subtype, ODD=Oppositional Defiant Disorder, CD=Conduct Disorder, GAD=Generalized Anxiety Disorder, MDD=Major Depressive Disorder, DD=Dysthymic Disorder

Controls

Controls did not meet ADHD criteria on DISC-IV, had T-scores below the 80^th percentile (T-score<58) on all ADHD-related parent and teacher rating scales, and had never been previously diagnosed or treated for ADHD. All had ≤4 total symptoms and ≤3 symptoms per ADHD dimension according to the “or” algorithm. The presence of anxiety, depression, oppositional defiant, and conduct disorders were not exclusionary. To control for the potential confounding effects of IQ on the high end of the spectrum, controls were required to have estimated IQs <115. No upper IQ limit was set for children with ADHD.

Validation and comparison of samples in each condition

Children completed either the slow or fast event rate condition, with recruitment for the slow event rate condition occurring prior to the fast event rate condition. In the slow event rate condition, there were n=46 children with ADHD and n=21 non-ADHD controls. Sample ethnicity reflected regional demographics: 85% Caucasian, 7.5% African American, 1.5% Asian, and 6% mixed. Seventeen (37%) children with ADHD were prescribed a stimulant medication, and the median medication washout period was 74 hours.

In the fast event rate condition, there were n=51 children with ADHD and n=18 non-ADHD controls. Sample ethnicity was 78% Caucasian, 8.8% African American, 3% Hispanic, 3% Asian, and 7% mixed ethnicity. Fifteen (29%) children with ADHD were prescribed a stimulant medication, and the median medication washout period was 68 hours.

As expected, in both conditions, parent and teacher ratings of ADHD symptomology for the ADHD group exceeded controls (all p <.001). There were no diagnostic differences in age or IQ (obtained using a 2-subtest short form (vocabulary and matrix reasoning) of the Wechsler Intelligence Scale for Children-IV (Wechsler, 2003) (all p >.07). Children with ADHD who were recruited for the slow vs. fast event rate condition did not vary in ADHD severity, age, or estimated FSIQ (all p>. 12).

Procedures

Informed written consent from parents and verbal assent from children were obtained prior to participation. Parents were given $100 and relevant clinical feedback. Children were given a small prize. Participants completed the below paradigms as part of a battery of tasks associated with a larger study examining neurocognitive deficits in childhood ADHD.

Go-no-go paradigm

The GNG paradigm used stimuli from a numerosity discrimination task (Gomez et al., 2007 Exp 5; Ratcliff et al., 2012). Ten blocks of 80 trials were administered with optional rest periods in between. At the start of each trial, a number of white asterisks filled random positions in a 10 × 10 array at the center of a black screen. Children were told “We’re going to play a game called the Candy Factory now. Some of the boxes of candy that the factory makes have a lot of candy in them, and some only have a little. But, the sorter is broken! We need your help! Every time you see a box that has ‘a lot’ of candy, press the spacebar. Don’t press anything if the box has “a little” bit of candy. This is a hard game, but try to work as quickly as you can without making mistakes. Let’s try some for practice.” Four practice trials were then given.

75% of the stimuli (selected at random without replacement) were “go” trials and contained 61–70 asterisks. The remaining “no-go” trials contained 31–40 asterisks. Children were not informed of the sorting strategy, but were provided a brief tone on errors. In the slow event rate condition, stimuli remained onscreen for 1500ms, even if a response had already been made. This was followed by a 300ms blank screen before the next trial started. Time to completion was ~30 minutes. In the fast event rate condition, the next trial began 300ms after a response and took on average 20 minutes to complete.

Fitting the diffusion model

The first block of trials and RTs <300ms were removed from the data (Ratcliff et al., 2012). This is to ensure that atypical and outlier responses that are generated as participants are “getting used to” the paradigm are eliminated. The values of all parameters were estimated simultaneously for all the data for each participant individually (see Ratcliff & Tuerlinckx, 2002 for full details). To fit the model to the data, RT distributions for all “go” responses (i.e. correct “go” as well as failed inhibits) were represented by nine quantiles, the .1, .2, .3, …, .9 quantiles. The quantiles and the response proportions were entered into a chi-square minimization routine (Ratcliff & Tuerlinckx, 2002), and the diffusion model was used to generate the predicted cumulative probability of a response occurring by that quantile RT. Subtracting the cumulative probabilities for each successive quantile from the next higher quantile gives the proportion of responses between adjacent quantiles. For a chi-square computation, these are the expected proportions, to be compared to the observed proportions of responses between the quantiles (i.e., the proportions between 0, .1, .2, …, .9, and 1.0, which are .1, .1, .1, …, and .1). The proportions are multiplied by the number of observations in the condition (this produces values of the proportions weighted by accuracy) to give observed (O) and expected (E) frequencies. Summing over (O-E)2/E for all conditions gives a single chi-square value to be minimized. The number of degrees of freedom in the data are the 20 proportions between and outside the quantiles (10 each for correct and error responses) minus 1 (because the sum must equal 1) multiplied by the number of conditions in the data.

For all "no-go" responses (i.e. correct "no-go" responses and errors of omission, where the child did not go when a go response should have been made), a single bin was used for the contribution to chi-square, namely, (O-E)2/E, where O is the observed frequency of "no-go" responses and E is the expected frequency of "no-go" responses. Thus, the number of degrees of freedom was 10-1 for the RT bins for the "go" responses plus 1 for the "no-go" responses.

We note that the within trial variance of the diffusion process for any given trial is usually treated as a scaling parameter. This means that if the parameter is set to a particular value (by convention, it is typically set to 0.1, see: Wagenmakers, van der Maas, & Grasman, 2007). If this were doubled, then other parameters in the model would also be doubled, but the predicted values would be identical. Although the choice of the scaling parameter has no impact on significance testing, the arbitrary nature of the scaling parameter means that there are no “units” for the absolute value of drift rate (v), boundary separation (a), or start point (z), and the interpretation of these values is dependent on the relative values. Larger absolute values of drift rate indicate faster drift. Larger values of boundary separation indicate more conservative responding, and z represents the distance between the start point and no-go boundary. Ter is reported in seconds.

Results

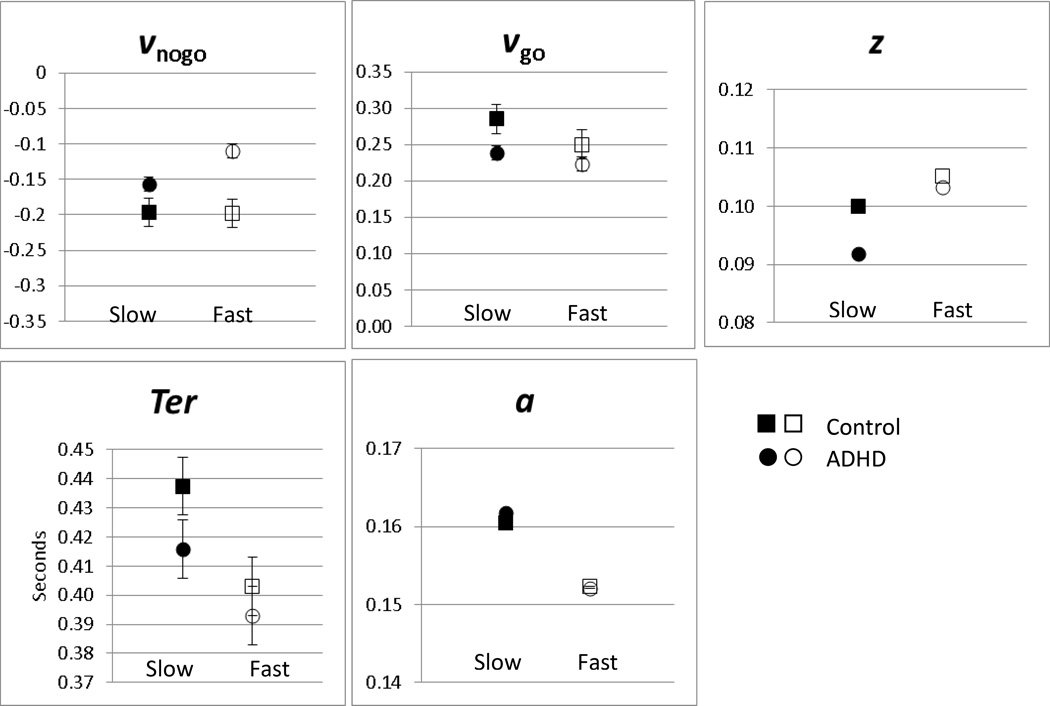
Table 2 contains performance (RT and accuracy values) as well as the diffusion model parameters. Figure 3 shows the behavior of diffusion model parameters graphically.

Table 2.

Go-no-go task performance by diagnostic group and by sample. Means and standard deviations in parentheses.

	Slow event rate			Fast event rate			Slow vs. Fast
	ADHD	Control	F (1,65)=	ADHD	Control	F (1,67)=	ADHD	Control
	(n=46)	(n=21)		(n=51)	(n=18)		t(95)=	t(37)=
Accuracy	0.88 (0.09)	0.93 (0.04)	5.05p=.03, η2 =0.07*	0.86 (0.05)	0.91 (0.04)	13.69, p=001, η2 =0.17***	1.72,p=.09	1.50,p=.14
%omissions	0.07 (0.08)	0.03 (0.02)	5.54p=.02, η2 =0.08*	0.04 (0.04)	0.02 (0.04)	1.80p=.18, η2 =0.03	2.20,p=.03*	0.18,p=.86
%failed inhibits	0.25 (0.16)	0.20 (0.10)	1.53p=.22, η2 =0.02	0.44 (0.15)	0.29 (0.12)	14.44p<.001, η2 =0.18***	−5.96,p<.001***	−2.32,p=.03*
RT (ms)	681.82 (83.59)	644.53 (64.42)	3.28p=.08, η2 =0.05	588.56 (88.34)	585.48 (67.80)	0.02p=.89, η2 <.001	5.32,p< .001***	2.78,p=.01**
SDRT (ms)	234.47 (47.64)	197.08 (39.13)	9.87p=.003, η2 =0.13**	219.14 (38.11)	188.16 (33.27)	9.35p=.003, η2 =0.12**	1.76,p=.08	0.76,p=.45
Ter (seconds)	0.415 (0.06)	0.437 (0.05)	1.97p=.16, η2 =0.03	0.393 (0.05)	0.403 (0.05)	0.58,p=.45, η2=0.009	2.00,p=.05*	2.28,p=.03*
a	0.162 (0.02)	0.160 (0.02)	0.06p=.80, η2 =.001	0.152 (0.01)	0.152 (0.02)	<.00p=.99, η2 <.001	2.69,p=.008**	1.33,p=.19
z	0.092 (0.01)	0.100 (0.02)	4.33p=.04, η2 =0.06*	0.103 (0.02)	0.105 (0.02)	0.15,p=.70, η 2 =0.002	−3.95,p<.001***	0.03,p=.42
v to “go”	0.238 (0.08)	0.285 (0.08)	5.06p=.03, η2 =0.07*	0.223 (0.05)	0.250 (0.06)	3.77p=.06, η2 =0.05	1.26,p=.21	1.53,p=.14
v to “no-go”	−0.157 (0.11)	−0.197 (0.07)	2.2, p=14, η2 =0.03	−.109 (0.08)	−.198 (0.10)	15.13p<.001, η2 =0.18**	−2.48,p=.02**	−0.82,p=.98

Note.

^*p<.05

^**p<.01

^***p<.001

RT = reaction time. SDRT = standard deviation of RT. Ter = non-decision time. a = boundary separation, where larger values indicate more conservative responding. z = the distance between the start point and no-go boundary. v = drift rate. Larger absolute values of drift (v) indicate faster drift.

Figure 3.

DDM parameters. SE bars displayed.

Slow event rate

Compared to controls, children with ADHD made more errors of omission, F(1,65)=5.54,p=. 02, η² =0.08, had significantly larger standard deviation of RT (SDRT), F(1,65)=9.87, p=.003, η²=0.13, and non-significantly slower RTs, F(1,65)=3.28, p=. 08, η² =0.05. There were no group differences in the number of failed inhibits, F(1,65)=1.53, p=.22,η²=0.02.

With respect to diffusion model parameters, drift rate to “go” was slower, F(1,65)=5.06,p=. 03, η²=0.07, and start point (z) was closer to the no-go boundary, F(1,65)=4.33,p=.04, η²=0.06, among children with ADHD, but there were no group differences in drift rate to “no-go,” a, or Ter (all p>. 14, all η²<03).

Fast event rate

Compared to controls, children with ADHD made more failed inhibits, F(1,67)=14.44, p <.001, η²=0.18, and had larger SDRTs, F(1,67)=9.35, p=.003, η²=0.12. There were no group differences in RT or errors of omission (both p>. 18, both η²<03).

With respect to diffusion model parameters, there were no group differences in start point (z), F(1,67)=0.15, p=.70,η² =0.002. Drift to “go”, F(1,67)=3.77,p=.06,η² =0.05, and drift to “no-go,” F(1,67)=15.13,p <001,η² =0.18, were slower among children with ADHD, although drift to “go” was not significantly slower. There were no group differences in a or Ter (both p>.45, both η²<01).

Comparing event rate effects within groups

NeT predicts that fast event rates will exacerbate neuronal fatigue among children with ADHD. Therefore, evidence in favor of NeT would be observed if drift to no-go slowed (relative to go) in the fast event rate condition. Slowing of drift to no-go relative to go is expected because the inhibitory process in a go-no-go task is the process that requires effort. In contrast, the cognitive energetic theory predicts that faster event rates would lead to increases arousal, which would be reflected in faster drift rates to no-go decisions (relative to go).

We found that among children with ADHD, RTs were faster, t(95)=5.32,p <.001, there were fewer errors of omission, t(37)=2.26,p<.03, and more failed inhibits, t(37)=−5.92,p <.001 in the fast vs. slow event rate condition. There were no effects of event rate for drift to “go” or SDRT (both t <1.76, both p>.08). However, consistent with NeT, drift to “no-go” was slower under fast event rates, t(96)=−2.42,p=.02. Start point, z, also shifted further away from the no-go boundary, t(96)=−3.98,p <.001 under fast event rates. Finally, a was smaller, t(96)=2.77,p=.007, and Ter was faster, t(96)=1.97,p=.05.

Among controls, event rate did not alter the number of omissions, SDRT, a, z, drift to “go,” or drift to “no-go” (all t <1.53, all p>.14). However, RTs, t(37)=2.78,p=.01, and Ter, t(37)= 2.28,p=.03 were faster in the fast event rate condition, and there were more failed inhibits, t(37)=−2.32,p=.03.

In summary, diffusion model analyses found that among children with ADHD, fast event rates slowed drift to “no-go” decisions, and shifted ADHD start points closer to the go boundary, compared to the slow event rate condition. In contrast, performance for controls was not as strongly influenced by event rate as that of children with ADHD.

Discussion

We examined the effect of event rate on inhibitory control in children with ADHD to evaluate the neuroenergetic (NeT) and cognitive energetic theories of ADHD. We did so using the diffusion model which, in its simultaneous consideration of both RT and accuracy data, allows it to isolate the multiple cognitive subprocesses that interact with and contribute to speeded decision making. Primary components of the model include information processing efficiency (drift rate, or v), start point (z), speed-accuracy trade off settings (boundary separation, or a), and the time it takes to encode a stimulus and plan a motor response (non-decision time, or Ter).

Consistent with NeT, compared to slow event rates, fast event rates were associated with slower drift to the “no-go” decision, and a higher proportion of failed inhibits. This was despite the fact that (a) RTs for both groups were faster in the fast vs. slow event rate condition, and that (b) there were no group differences in RT in the fast event rate condition. Until now, this main effect of RT speedup under fast event rates, representing a hallmark piece of evidence in favor of the cognitive energetic theory, has historically been interpreted as evidence of improved performance secondary to increased arousal (Metin et al., 2012; Sergeant, 2000, 2005).

The cognitive energetic theory predicts that the relationship between event rate and arousal is an inverted U-shaped function, with the worst performance seen under both very slow and very fast event rates. It therefore remains possible that our fast event rate condition overshot the optimal state of arousal. Though such a possibility should of course be considered in the design of future studies, the need to invoke an inverted U only occurs when RT and accuracy data are believed to be independent indicators of performance. When drift rate, a better index of processing speed, because it is isolated from non-decision time (captured in Ter) and speed-accuracy trade off strategies (captured in a), is used as the primary index of performance, the interpretation is more parsimonious. That is, faster event rates were associated with slower/less efficient processing among children with ADHD.

Beyond the implications of our results to understanding the neurocognitive mechanisms that may be involved in the development of childhood ADHD, our findings highlight how easy it is to misinterpret cognitive data when standard indices of performance are used. For example, within our ADHD sample, had we based our analyses on RT alone, we would have concluded that faster event rates improved performance. But, had we based our analyses on the number of failed inhibits, we would have concluded that faster event rates lead to worse performance. And, had we based our analyses on RT variance (i.e. standard deviation of RT), we would have concluded that event rates do not affect performance at all. It is only through the simultaneous consideration of the shape of the RT distributions for correct and incorrect responses that we are able to obtain the most accurate and complete description of performance.

Furthermore, continuing to depend on unidimensional performance indices hinders the development of strong etiologic theory and the evaluation of therapeutic effects. For example, what would we make of a medication or psychotherapy if it showed evidence of improving reaction times at the expense of increases in error rate? Even in the absence of speed-accuracy-trade-off effects, consider the implications of a treatment that reduces RTs by improving central cognitive processing efficiency vs. one that reduces RTs through improvements in the speed of stimulus encoding. ADHD is the prototypical childhood psychiatric disorder associated with cognitive performance deficits, and in particular, with failed inhibitory control, and the go-no-go task is widely used in both research and clinical settings to document deficits in inhibition. It is therefore of utmost importance that the field recognize the limitations inherent in the use of standard indices of performance (RT and accuracy) on this and all simple RT tasks.

Go:No-go signal ratio was 75% in both event rates. Because the majority of trials required a go response, typically developing children, like adults (Leite & Ratcliff, 2011; Mulder, Wagenmakers, Ratcliff, Boekel, & Forstmann, 2012), tended to respond (or were biased to respond) “go” (i.e. their start points were closer to the go than to the no-go boundary) regardless of condition. Curiously, however, children with ADHD set their start points not on the absolute proportion of go signals, but on the rate at which go signals appeared. In the slow condition, a new stimulus appeared every 1800 ms (i.e. the total ISI) vs. in the fast condition, a new stimulus appeared twice as rapidly, about 1 every 900 ms (300 ms ISI + the average RT in that condition, ~600 ms). At slow event rates, ADHD start points were closer to the no-go boundary (because the majority of the time, they were not “going,” even though the majority of the stimuli were “go” stimuli). But, under fast event rates, ADHD start points were similar to that of controls, and were set closer to the go boundary.

Increased sensitivity to the passage of time among children with ADHD has previously been noted (Castellanos & Tannock, 2002; Noreika, Falter, & Rubia, 2013; Rubia, Halari, Christakou, & Taylor, 2009), though the cause of such sensitivity is not well understood. However, competition for attentional resources results in the experience of temporal shortening (i.e. “time flies when you’re having fun”) (Block, Hancock, & Zakay, 2010; Brown, 1997; Droit-Volet & Gautier, 2000; Gautier & Droit-Volet, 2002a, 2002b). So, consistent with the cognitive energetic theory, one could still argue that fast event rates are associated with increased arousal, which results in greater task/attentional engagement thereby correcting children’s experience of the proportion of Go:No-go signals (as reflected in changing start points). All of this could ultimately lead to a greater preparedness to respond. That being said, these changes should have improved performance. But that was not the case.

Indeed, reward and response cost manipulations designed to increase task engagement/motivation have been inconsistent in their ability to normalize cognitive performance across a range of laboratory tasks (Luman, Oosterlaan, & Sergeant, 2005). Standard explanations for these inconsistencies have included variations in the type, frequency, and schedule of the rewards, individual differences in the valuation of those rewards, and variation in the outcome variables being monitored (e.g. RT, accuracy, or SSRT). All of that is likely true. However, interpreted in the context of NeT, it could also be that increased motivation/ engagement leads to improved overall performance only to the extent that the neuronal energy supply is not simultaneously being depleted by that increased engagement.

The potential implications of these findings to ADHD specifically (assuming additional validations of NeT) are that the consistent application of behavioral incentives and rewards, which represents an important mechanism of action in evidence-based psychosocial treatments for ADHD (Fabiano et al., 2009; Pelham & Fabiano, 2008; Sagvolden, Johansen, Aase, & Russell, 2005), may simultaneously, by virtue of increasing cognitive engagement and response preparedness, more rapidly deplete the neuronal energy supply. This could help explain both the short-term effects of psychosocial treatments and the moderately larger effect sizes that amphetamine products have over methylphenidate products (Faraone & Buitelaar, 2010). That is, deficits in dopamine-related reward systems have long been proposed for ADHD, and though the exact mechanism of action of stimulant drugs is not known, such deficits are generally believed to be mitigated by the increase in tonic dopamine made available through the administration of a stimulant-based medication (Sagvolden et al., 2005). However, amphetamines block both dopamine, as well as the re-uptake of norepinephrine, which directly influences lactate availability. In comparison, methylphenidate’s mechanism of action is presumed to act primarily on the dopamine system (Faraone & Buitelaar, 2010).

It bears mentioning that motivation and reward-based models of self-control (Botvinick & Braver, 2015; Inzlicht, Schmeichel, & Macrae, 2014; Westbrook & Braver, 2015) have taken issue with depletion theories, of which NeT is one. These models posit that organisms weigh the benefits of task engagement and the execution of cognitive control (i.e., good performance or an explicit reward) against the anticipated costs of that control (i.e., loss of leisure or opportunity costs). When benefits outweigh the costs, then cognitive exertion is expended in the service of acquiring those benefits. The invocation of a biologically-based limited-resource is seen as an unnecessary construct. Under this rubric, the utility for maintaining preparedness for a target that appears more frequently in time would be greater than that for a target that appears less frequently in time. Thus, similar to predictions of cognitive energetic theory (but for different reasons), these models would predict faster drift rates with faster event rates. This of course was not observed.

Faster event rates were associated with faster Ter and smaller a, but there were no diagnostic group differences in either condition. How the diffusion model parameters change in response to event rate has not been specifically examined, but a decreases when speed is emphasized over accuracy, or when a time pressure to respond is experienced (as might be the case in the fast event rate condition when the next trial begins immediately after a response). In these situations, motor responses must also be more rapidly executed so that a shortening of Ter, reflecting a potential motor priming effect, would not necessarily be unexpected.

One of the many strengths of the design were that go and no-go stimuli were distinguished by degree rather than kind, which allowed the paradigm to index a more effortful (vs. automatic) form of inhibitory control (Verbruggen & Logan, 2008). It also circumvented the need to have a clear, unambiguous external stop signal that is commonly used in standard laboratory tasks of inhibitory control, but seldom experienced in the real world (Aron, 2011). Limitations of the study include the use of a between subjects design, and two event rates (rather than 3 or more) to better estimate the shape of the performance function. Clearly, replication using a within-subjects multiple-event rate design is needed. However, it is also worthwhile to consider future paradigms that titrate event rate to optimal performance, which might better quantify the degree of cognitive heterogeneity in the population. Finally, with respect to motivation and reward-based models of self-control, it remains possible that children with ADHD found the fast event rate condition less motivating/engaging than the slow event rate condition because the no-go trials arrive more frequently in time alongside the go trials. If this were the case, then slower drift in the fast event rate condition could still be consistent with a reward/motivation account of disinhibitory control. However, given well documented evidence of delay aversion in ADHD (Patros et al., 2015; Pauli-Pott & Becker, 2011; Sonuga-Barke, Sergeant, Nigg, & Willcutt, 2008), finding a reversed preference for slower vs faster event rates seems unlikely. Regardless, the design of the current study is unable to rule out this possibility. One way to examine this in future studies, however, would be to directly measure preference for task engagement (Westbrook & Braver, 2015; Westbrook, Kester, & Braver, 2013).

Summary and Conclusions

In summary, we found that consistent with the neuroenergetic theory of ADHD, faster event rates were associated with slower drift to no-go decisions, which was in turn responsible for a higher proportion of failed inhibits in that condition. Earlier models and data were hampered in their interpretation by using methods that restricted analyses to either RT or accuracy alone, and were unable to isolate/separate variance associated with non-decision components (encoding time, motor preparation, speed-accuracy trade-off effects). Intriguingly, we also found that the start point of the decision process in children with ADHD was similar to controls under fast event rates, suggesting increased motivation or preparedness to respond. However, this increase in preparedness under fast event rates was ultimately unable to counteract the effects of slowed processing speed in that condition, which may have important implications for understanding the long term effects of psychosocial and medical treatments for ADHD.

The promise of computational approaches is that it allows psychological research to move away from dependence on unidimensional variables, to one that is more sensitive and better suited to identifying the neurocognitive basis of behavior (White et al., 2010; Wiecki et al., 2015). The strength and nuance of our findings is only possible because the diffusion model was able to capture the independent cognitive processes that would otherwise be hidden and thus misinterpreted.