Changing Cycle Lengths in State-Transition Models: Challenges and Solutions

Abstract

The choice of a cycle length in state-transition models should be determined by the frequency of clinical events and interventions. Sometimes there is need to decrease the cycle length of an existing state-transition model to reduce error in outcomes resulting from discretization of the underlying continuous-time phenomena or to increase the cycle length to gain computational efficiency. Cycle length conversion is also frequently required if a new state-transition model is built using observational data that have a different measurement interval than the model’s cycle length. We show that a commonly used method of converting transition probabilities to different cycle lengths is incorrect and can provide imprecise estimates of model outcomes. We present an accurate approach that is based on finding the root of a transition probability matrix using eigendecomposition. We present underlying mathematical challenges of converting cycle length in state-transition models, and provide numerical approximation methods when the eigendecomposition method fails. Several examples and analytical proofs show that our approach is more general and leads to more accurate estimates of model outcomes than the commonly used approach. MATLAB codes and a user-friendly online toolkit are made available for the implementation of the proposed methods.

INTRODUCTION

State-transition models (STMs) are frequently used to inform medical decision making because of their simplicity in representing complex real-life phenomena (1–4). Examples of applications of STMs include cost-effectiveness analyses of new interventions, clinical decision making to maximize benefits or minimize harm, and optimal screening intervals for disease diagnoses (5).

STMs typically simulate occurrence of events (e.g. disease stage, death) that evolve over time. Though time is continuous, STMs often discretize time in fixed steps known as cycles (e.g. monthly or yearly). A critical step in building STMs is the choice of cycle length. The ISPOR-SMDM Modeling Good Research Practices Task Force report recommends that the cycle length should be short enough to represent the frequency of clinical events and interventions (6). This choice is determined by a number of factors, including availability of data and frequency of clinical follow-up. For example, an annual cycle length may be appropriate for a model evaluating the cost-effectiveness of colorectal cancer screening (7); whereas, a weekly cycle length may be desired when modeling the cost-effectiveness of HIV treatment as disease management and complications develop at a relatively fast time scale (8).

There is a tradeoff when choosing between shorter versus longer cycle lengths. The discretization of time in steps introduces error in the estimates of model outcomes. The error arises mainly because discrete-time STMs assume that state transitions occur only at fixed times, i.e. either at the beginning or end of a cycle; whereas, in most biological and healthcare systems, as time runs continuously, state transitions can occur at any time. Use of half-cycle correction can reduce the error by making appropriate adjustments to outcomes in the first and last cycle (9). This, however, does not completely eliminate the error. The shorter the cycle, the smaller is the error and vice versa (3). Therefore, shorter cycles in STMs can reduce the error by simulating events closer to the continuous time situation, as in real life.

While shorter cycles reduce the error, they increase the computational burden by adding multiple steps to simulate progression of time. This sometimes can impose challenges in conducting model validations, probabilistic sensitivity analysis (PSA), and value of information (VOI) analysis, especially in individual-level STMs. Therefore, increasing the cycle length can improve computational time efficiency by substantially reducing the computer time needed for PSA or VOI analysis.

Cycle length conversion could be required in two scenarios. First, a model exists whose cycle length needs to be increased or decreased. For example, a breast biopsy decision making model by Chhatwal et al. (10) converted an annual cycle length to a six-month cycle length to account for follow-up exams every six-months (11). In another example, an existing hepatitis C virus cost-effectiveness model using annual cycle length (12) was converted to another model that used a weekly cycle length (13). Another scenario where cycle length conversion is frequently required is when a new state-transition model is built using observational data that have a different measurement interval than model’s cycle length. This is almost always the case when developing a de novo STM.

Few publications have discussed issues regarding changing the length of the cycle in STMs. Sonnenberg and Beck (3), and Miller and Homan (14) warned against simply dividing the transition probabilities to shorter cycle when changing the cycle length. For example, when changing the cycle length from annual to monthly, one should not divide the transition probability by 12. Instead they recommended converting an annual probability into a rate and then transforming that rate into a monthly probability. They acknowledged that they considered only the case in which only a single transition within a two-state model is possible. However, the overwhelming majority of STMs have multiple states with multiple transitions, also known as competing risks models. The case of multiple states and competing risks in STMs has received very little attention, and has primarily focused on estimation of transition probabilities using classical or Bayesian statistical techniques given different structures of raw data (15, 16). Despite its relevance to only two-state progressive models, the approach by Sonnenberg and Beck (3) remains ubiquitous in the applied modeling field (17).

The objective of this study is to explore the issues involved when changing the length of the cycle in STMs, and to present an accurate and generalizable approach of converting model inputs (particularly, transition probabilities) to different cycle lengths. We highlight the limitations of commonly used approaches, provide a unified and mathematically correct approach that can lead to more accurate adjustment, explore some mathematical issues with our suggested approach, and offer numerical approximation methods.

We start by assuming that the analyst has all model inputs computed appropriately and expressed in terms of a common cycle length. Thus, the objective is only to convert these inputs into a different cycle length. We later relax this assumption and introduce methods for computing model inputs when the data come from multiple sources, with varying lengths of follow up. We also assume that the cycle length remains fixed throughout the duration of the model. Depending upon the situation, the analyst may need to either increase or decrease the cycle length. We first present the most common case where the desire is to have a shorter cycle length. The case of longer cycle lengths is presented later.

BACKGROUND

Which Model Inputs Change When the Cycle Length Changes?

An STM consists of an initial state distribution, a transition probability matrix, a cycle length, state rewards (costs and utilities), and a termination criterion. Changing the cycle length of a model requires examination of all model inputs that are defined as units per time. These are: costs, discount rates, transition probabilities, and termination conditions if they involve time (e.g., terminate model if current time is greater than a specified time horizon). Because initial state distribution and health state utilities do not have a time dimension, these should not be changed when changing a cycle length.

For simplicity, we assume that the original cycle length is one year, and we divide the year into n periods (cycles) of equal length so that the cycle length is 1/n of a year (e.g., n = 12 indicates that the new model has a monthly cycle).

Costs

STMs involve two types of costs: nonrecurring and recurring (expressed as units per time). Nonrecurring costs (e.g., cost of one-time screening test) are not related to time and are not affected by changing the cycle length. Recurring costs are typically incorporated per state per cycle. For example, many models include a cost of staying in a given health state for a year. The annual cost c of a given state can be converted to a one-nth of a year cycle cost as $\stackrel{\sim }{c}=c/n$. For example, an annual disease recurring cost of $1,200 corresponds to $100 cost per month (i.e., n = 12).

Discount rate

It is very common to have discount rates for future costs and quality-adjusted life years (QALY) be given as rates per year. To convert the annual discount rate r into a one-nth of a year cycle discount rate we use compounding techniques. For example, $1 invested today will yield $(1+r) after one year if the rate is r per year. The same $1 should return $\${\left(1+\stackrel{\sim }{r}\right)}^n$ after one year if it is compounded at a rate of $\stackrel{\sim }{r}$ per 1/n of a year. Thus, $(1+r)={\left(1+\stackrel{\sim }{r}\right)}^n$. Solving this equation for $\stackrel{\sim }{r}$ yields, $\stackrel{\sim }{r}={\left(1+r\right)}^{1/n}-1$. For example converting a discount rate of 3% per year into a monthly rate using the above formula yields the discount rate of 0.247% per month.

Transition probabilities

The transition probabilities between states are typically converted to different cycle lengths using the approach defined in previous studies (3, 14, 17). This approach i) uses the relationship between annual probability p and a constant instantaneous rate z per year, i.e., p = 1 − e^−z to convert the annual probability into a constant rate as z = ln(1 − p); ii) adjusts the rate according to the new cycle length 1/n year by dividing by n; and iii) then converts the rate back into adjusted probability, $\stackrel{\sim }{p}$. Thus, $\stackrel{\sim }{p}=1-e^{-z/n}=1-e^{\text{ln}(1-p)/n}=1-{\left(1-p\right)}^{1/n}$.

Next, we review issues with this widely used approach and show that it is applicable to only two-state STMs and can result in significant error when estimating state distribution or outcomes.

Issues with Traditional Approach for Transforming Probabilities

We present an example demonstrating issues with using the traditional approach for converting annual transition probabilities to monthly transition probabilities. We used a simplified three-state Markov competing risk model of end-stage liver disease with the state of decompensated cirrhosis (DeCirr) transitioning to either hepatocellular carcinoma (HCC) or “Death” (Figure 1). We estimated the transition probabilities from two published clinical studies (details provided in Appendix A) (18, 19). The state-transition probabilities matrix of this model can be written as:

$$P=\left[\begin{array}{ccc}1-p_{12}-p_{13}& p_{12}& p_{13}\\ 0& 1-p_{23}& p_{23}\\ 0& 0& 1\end{array}\right]=\left[\begin{array}{ccc}0.7140& 0.0619& 0.2241\\ 0& 0.5728& 0.4272\\ 0& 0& 1\end{array}\right].$$

We converted the annual transition probabilities p_12, p₁₃ and p₂₃ to monthly probabilities, using the traditional formula $\stackrel{\sim }{p}=1-{\left(1-p\right)}^{1/n}$, where n = 12, and found that ${\stackrel{\sim }{p}}_{12}=0.0053$, ${\stackrel{\sim }{p}}_{13}=0.0209$, and ${\stackrel{\sim }{p}}_{23}=0.0454$.

Figure 1.

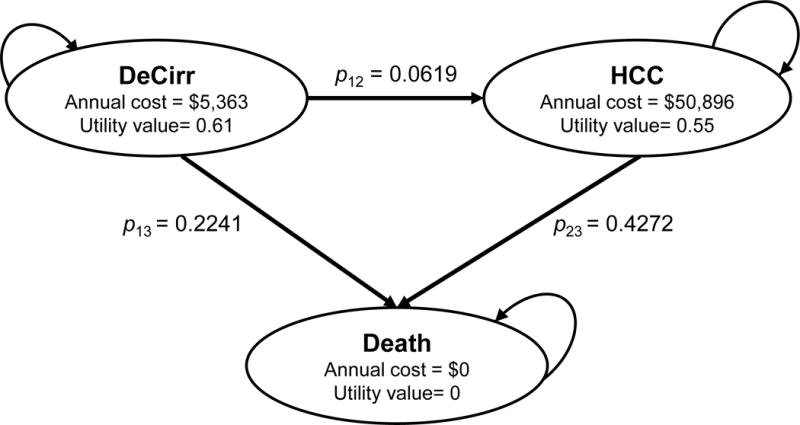
State-transition model showing health states and transitions between states. DeCirr, decompensated cirrhosis; HCC, hepatocellular carcinoma.

Using the above monthly probabilities, we next projected the Markov trace of 10,000 people starting in DeCirr at time 0 to the end of 3 years, i.e. 36 monthly cycles (Table 1). The outcomes at n-th cycle represent the number of patients in HCC and Death after n months. In theory, we expect that the number of patients in each state when observed at the end of 12^th-cycle (i.e. 1 year) should match those observed at the end of 1^st-year using the annual cycle length. We found that at the end of 12^th cycle (i.e. end of 1 year), 427 patients developed HCC and 2,304 patients died. However, using the original probabilities with an annual cycle length, the Markov trace estimated that 619 patients developed HCC and 2241 patients died. Similarly, at the end of 24^th cycle (Year 2) and 36^th-cycle (Year 3), the number of patients in DeCirr, HCC, and Death obtained with the traditional approach did not match those obtained with the original model using the annual cycle. Therefore, the traditional formula to convert transition probabilities to the monthly cycle did not provide identical results. In fact, the use of the traditional formula introduced a different Markov chain. The above discrepancy indicates that the monthly probabilities were not computed correctly.

Table 1.

Markov Trace of 10,000 Patients Starting in Decompensated Cirrhosis State with Traditional and Eigendecomposition Conversion Approach

Month	Original Model (Annual Cycle)			Traditional Approach			Eigendecomposition Approach
	DeCirr	HCC	Death	DeCirr	HCC	Death	DeCirr	HCC	Death
0	10,000	0	0	10,000	0	0	10,000	0	0
1				9,738	53	209	9,723	78	199
2				9,482	102	415	9,454	149	397
3				9,233	148	618	9,192	216	592
4				8,991	190	818	8,938	277	785
5				8,755	230	1,015	8,690	334	975
6				8,526	266	1,209	8,450	386	1,164
7				8,302	299	1,399	8,216	434	1,350
8				8,084	329	1,586	7,989	478	1,533
9				7,872	357	1,770	7,767	519	1,714
10				7,666	383	1,951	7,552	555	1,892
11				7,465	406	2,129	7,343	589	2,068
12 (Year 1)	7,140	619	2,241	7,269	427	2,304	7,140	619	2,241
13				7,078	447	2,475	6,942	646	2,411
14				6,892	464	2,644	6,750	671	2,579
15				6,712	480	2,809	6,563	693	2,744
16				6,536	493	2,971	6,382	712	2,906
17				6,364	506	3,130	6,205	729	3,066
18				6,197	517	3,286	6,033	744	3,222
19				6,035	526	3,439	5,866	757	3,376
20				5,876	534	3,590	5,704	769	3,528
21				5,722	541	3,737	5,546	778	3,676
22				5,572	547	3,881	5,392	786	3,822
23				5,426	552	4,022	5,243	792	3,965
24 (Year 2)	5,098	796	4,106	5,283	556	4,161	5,098	796	4,106
25				5,145	558	4,297	4,957	800	4,243
26				5,010	560	4,430	4,820	802	4,378
27				4,878	562	4,560	4,686	803	4,511
28				4,751	562	4,688	4,556	803	4,641
29				4,626	562	4,812	4,430	802	4,768
30				4,505	561	4,935	4,308	800	4,893
31				4,386	559	5,054	4,188	797	5,015
32				4,271	557	5,172	4,073	793	5,134
33				4,159	555	5,286	3,960	789	5,251
34				4,050	551	5,398	3,850	784	5,366
35				3,944	548	5,508	3,744	778	5,478
36 (Year 3)	3,640	772	5,588	3,840	544	5,616	3,640	772	5,588

Using a monthly cycle length conversion from the traditional approach, the number of people who transitioned to hepatocellular carcinoma (HCC) and Death at the end of 1 year (i.e., cycle 12) were 427 and 2,304, respectively. However, using the eigendecomposition approach, the number of people who transitioned to HCC and Death at the end of 1 year were 619 and 2,241, respectively. Using the original model with annual cycle length, the number of people who transitioned to HCC and Death were same as that obtained with eigendecomposition approach. Similarly, the number of people in DC and HCC at the end of second year and third year were different using the traditional approach when compared with the eigendecomposition approach or original model. DeCirr, decompensated cirrhosis.

EIGENDECOMPOSITION APPROACH

The correct approach to convert transition probabilities requires taking the 12-th root of the annual transition probability matrix, P to find the corresponding monthly transition probabilities. In general, converting an annual cycle length to a shorter, a one-nth of a year cycle, requires finding the n-th root of the annual transition probability matrix (21).

The root of the matrix is found by using eigendecomposition (also known as spectral decomposition) (22). Provided that it is diagonalizable, we can decompose a general k by k matrix P such that P = V ∗ D ∗ V⁻¹, where D is a diagonal matrix consisting of eigenvalues of matrix P, and V is the associated matrix of eigenvectors and V⁻¹ is its inverse. This is called the eigendecomposition of the matrix P (22). Then, P^1/n = V ∗ D^1/n ∗ V⁻¹ which we denote by $\stackrel{\sim }{P}$. The root of the diagonal matrix, D is found by simply taking the root of the diagonal entries.

Using the above approach, we converted the annual transition probability matrix to monthly cycle. Because the matrix P given in the example is upper triangular, its eigenvalues are given by the diagonal elements as 1, 0.7140, and 0.5728. The corresponding eigenvectors can be derived as

$$V=\left[\begin{array}{ccc}0.5774& 1& -0.4016\\ 0.5774& 0& 0.9158\\ 0.5774& 0& 0\end{array}\right]$$

The eigendecomposition yields:

$$\stackrel{\sim }{P}={\left[\begin{array}{ccc}0.7140& 0.0619& 0.2241\\ 0& 0.5728& 0.4272\\ 0& 0& 1\end{array}\right]}^{1/12}=\left[\begin{array}{ccc}0.9723& 0.0078& 0.0199\\ 0& 0.9546& 0.0454\\ 0& 0& 1\end{array}\right].$$

Using the above method, we found ${\stackrel{\sim }{p}}_{12}=0.0078$, ${\stackrel{\sim }{p}}_{13}=0.0199$, and ${\stackrel{\sim }{p}}_{23}=0.0454$. The values of ${\stackrel{\sim }{p}}_{12}$ and ${\stackrel{\sim }{p}}_{13}$ are different from the values obtained by the traditional approach in the previous section. Performing eigendecomposition or taking the root of a matrix are complex matrix operations, but can be easily achieved using most modern mathematical computing packages such as R, MATLAB^®, Maple (Maplesoft™), and Mathematica^® (23–25).

With the above monthly transition probabilities, we again projected the Markov trace of 10,000 people starting in DeCirr at time 0 until the end of 36^th-cycle (Table 1). At the end of year 1, 2 and 3, we found that the number of patients who transitioned to HCC or Death were identical to that obtained using an annual-cycle Markov trace. Unlike the traditional approach, the eigendecomposition method did not alter the underlying Markov chain while changing the cycle length.

ANALYTICAL APPROACH

In some instances, it is feasible to obtain an analytical solution that can accurately convert transition probabilities to different cycle lengths. Below, we derived analytical formulas for our 3-state progressive model to convert annual transition probabilities to a one-nth of a year cycle using the eigendecomposition method. The annual transition probability matrix of this model is given by

$$P=\left[\begin{array}{ccc}1-p_{12}-p_{13}& p_{12}& p_{13}\\ 0& 1-p_{23}& p_{23}\\ 0& 0& 1\end{array}\right],$$

We first make the assumption that p₁₂ + p₁₃ ≠ p₂₃, so that the eigenvalues are distinct and diagonal matrix of the eigenvalues {1,1 − p₁₂ − p₁₃, 1 − p₂₃} is:

$$A=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1-p_{12}-p_{13}& 0\\ 0& 0& 1-p_{23}\end{array}\right].$$

The matrix of eigenvectors V and its inverse are given by:

$$V=\left[\begin{array}{ccc}1& 1& \frac{p_{12}}{p_{12}+p_{13}-p_{23}}\\ 1& 0& 1\\ 1& 0& 0\end{array}\right],$$

$$V^{-1}=\left[\begin{array}{ccc}0& 0& 1\\ 1& -\frac{p_{12}}{p_{12}+p_{13}-p_{23}}& \frac{p_{23}-p_{13}}{p_{12}+p_{13}-p_{23}}\\ 0& 1& -1\end{array}\right].$$

Thus,

$${\mathrm{A}}^{\frac{1}{n}}=\left[\begin{array}{ccc}1& 0& 0\\ 0& {\left(1-p_{12}-p_{13}\right)}^{\frac{1}{n}}& 0\\ 0& 0& {\left(1-p_{23}\right)}^{\frac{1}{n}}\end{array}\right].$$

Performing matrix multiplication we obtain

$$P^{\frac{1}{n}}=V{\mathrm{A}}^{\frac{1}{n}}{V}^{-1}=\left[\begin{array}{ccc}1-{\stackrel{\sim }{p}}_{13}-{\stackrel{\sim }{p}}_{13}& {\stackrel{\sim }{p}}_{12}& {\widehat{p}}_{13}\\ 0& 1-{\stackrel{\sim }{p}}_{23}& {\stackrel{\sim }{p}}_{23}\\ 0& 0& 1\end{array}\right],$$

where

$$\begin{array}{c}{\stackrel{\sim }{p}}_{12}=\frac{p_{12}\left[{\left(1-p_{23}\right)}^{\frac{1}{n}}-{\left(1-p_{12}-p_{13}\right)}^{\frac{1}{n}}\right]}{p_{12}+p_{13}-p_{23}},\\ {\stackrel{\sim }{p}}_{13}=\frac{p_{12}\left[1-{\left(1-p_{23}\right)}^{\frac{1}{n}}\right]+(p_{13}-p_{23})\left[1-{\left(1-p_{12}-p_{13}\right)}^{\frac{1}{n}}\right]}{p_{12}+p_{13}-p_{23}},\\ {\stackrel{\sim }{p}}_{23}=1-{\left(1-p_{23}\right)}^{\frac{1}{n}}.\end{array}$$

Using n = 12, the above formulae will provide monthly transition probabilities, which are identical to the values obtained by the eigendecomposition approach in the numerical example above, $\stackrel{\sim }{P}$. Note that the formulae for ${\stackrel{\sim }{p}}_{12}$ and ${\stackrel{\sim }{p}}_{13}$ are substantially different from the formulae obtained by the traditional approach.

We now consider the case when p₁₂ + p₁₃ = p₂₃ or p₁₂ = p₂₃ − p₁₃ > 0. In this case the transition probability matrix becomes

$$P=\left[\begin{array}{ccc}1-p_{23}& p_{23}-p_{13}& p_{13}\\ 0& 1-p_{23}& p_{23}\\ 0& 0& 1\end{array}\right],$$

with eigenvalues 1, 1 − p₂₃, 1 − p₂₃. Note that one eigenvalue has multiplicity 2. It turns out that matrix P does not have 3 linearly independent eigenvectors. Hence, P is not diagonalizable.

Instead the matrix power can be achieved by diagonalizing P using Jordan decomposition and expressing it as

$$P^{\frac{1}{n}}=S{J}^{\frac{1}{n}}{S}^{-1},$$

where S is a similarity matrix and J is Jordan canonical form:

$$J=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1-p_{23}& 1\\ 0& 0& 1-p_{23}\end{array}\right].$$

Since J is block-diagonal we get the 1/nth power of J as

$$J^{\frac{1}{n}}=\left[\begin{array}{ccc}1& 0& 0\\ 0& {\left(1-p_{23}\right)}^{\frac{1}{n}}& \frac{{\left(1-p_{23}\right)}^{\frac{1}{n}}}{n(1-p_{23})}\\ 0& 0& {\left(1-p_{23}\right)}^{\frac{1}{n}}\end{array}\right]$$

The similarity matrix S and its inverse are given by:

$$\begin{array}{c}S=\left[\begin{array}{ccc}1& 1& 0\\ 1& 0& \frac{1}{p_{23}-p_{13}}\\ 1& 0& 0\end{array}\right],\\ S^{-1}=\left[\begin{array}{ccc}0& 0& 1\\ 1& 0& -1\\ 0& p_{23}-p_{13}& p_{13}-p_{23}\end{array}\right].\end{array}$$

Performing matrix multiplication we obtain

$$P^{\frac{1}{n}}=\left[\begin{array}{ccc}{\left(1-p_{23}\right)}^{\frac{1}{n}}& \frac{{\left(1-p_{23}\right)}^{\frac{1}{n}-1}(p_{23}-p_{13})}{n}& 1-{\left(1-p_{23}\right)}^{\frac{1}{n}}-\frac{{\left(1-p_{23}\right)}^{\frac{1}{n}-1}(p_{23}-p_{13})}{n}\\ 0& {\left(1-p_{23}\right)}^{\frac{1}{n}}& 1-{\left(1-p_{23}\right)}^{\frac{1}{n}}\\ 0& 0& 1\end{array}\right].$$

It is interesting to note that the exact formulas can be obtained by evaluating the limit of the matrix obtained using the eigendecomposition method as p₁₂ → p₂₃ − p₁₃. We used I’Hospital’s rule to evaluate the limit.

Even for a simple three-state STM, the new formulae can be analytically complex. These formulae take into account the competing risks between HCC and Death from the current DeCirr state as well as transitions from the future HCC state. For example, with a cycle length shorter than a year patients can now progress to HCC and die from HCC before the end of the year. Hence, the probability of death from HCC (p₂₃) is included in the formula for the transition probabilities p₁₂ and p₁₃ to account for this. Because there is no competing risk for individuals in HCC and the only future death state is absorbing, the new formula for transition from HCC to Death is identical to the traditional formula. Note that it may not always be possible to obtain a closed-form analytical solution that converts a transition probability from one cycle to another for any STM using eigendecomposition or Jordan decomposition.

ERROR WITH THE TRADITIONAL APPROACH

By altering the Markov chain, the traditional approach introduces error (“conversion error”) in the model’s distribution of health states and outcomes. To estimate the conversion error, we ran the model using a monthly-cycle length with both the traditional and eigendecomposition approach and predicted the number of deaths, cumulative incidence of HCC, total cost, and quality-adjusted life years (QALYs). We defined error as the difference in the outcomes obtained using the traditional versus eigendecomposition approach.

The traditional approach overestimated (i.e. positive error) the number of deaths until year 4 and underestimated (i.e. negative error) the number of deaths afterwards using the monthly cycle length (Figure 2A). Second, the traditional approach underestimated the cumulative incidence of HCC, and the error monotonically increased with time (Figure 2B). These results seem intuitive because the probability of death from DeCirr was overestimated and the probability of progressing to HCC was underestimated by the traditional approach.

Figure 2.

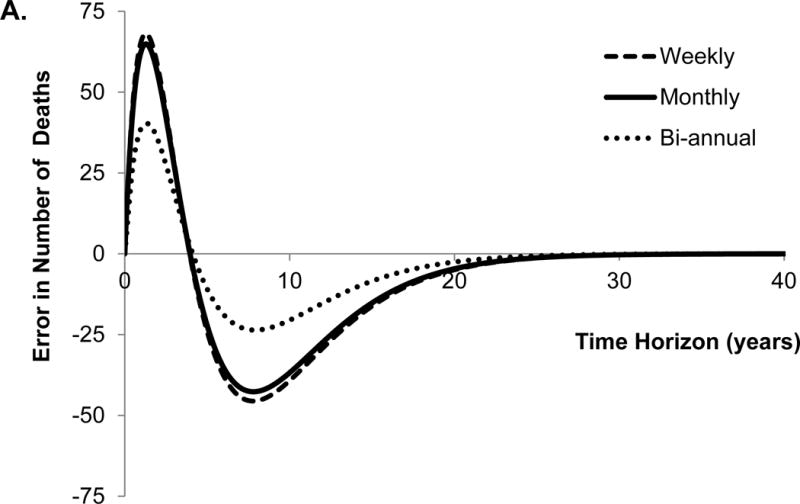
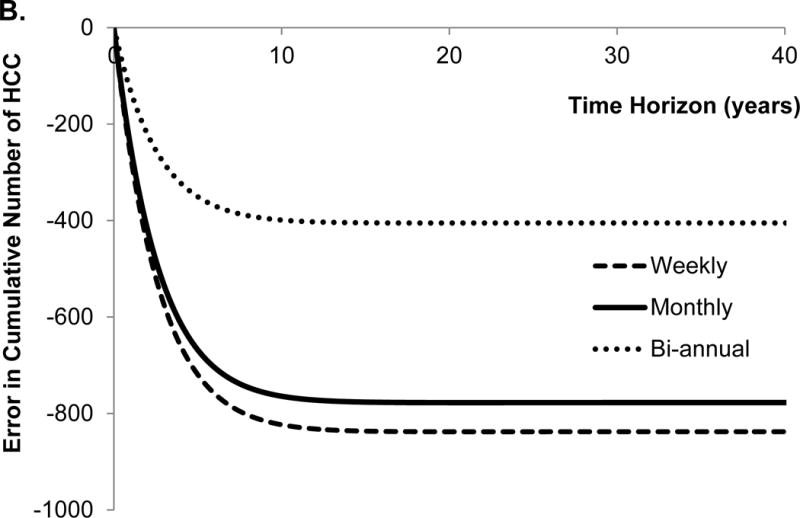
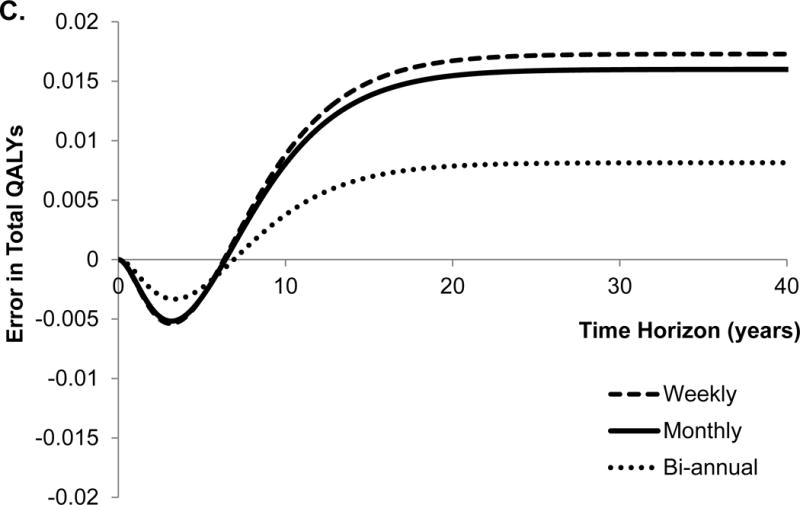
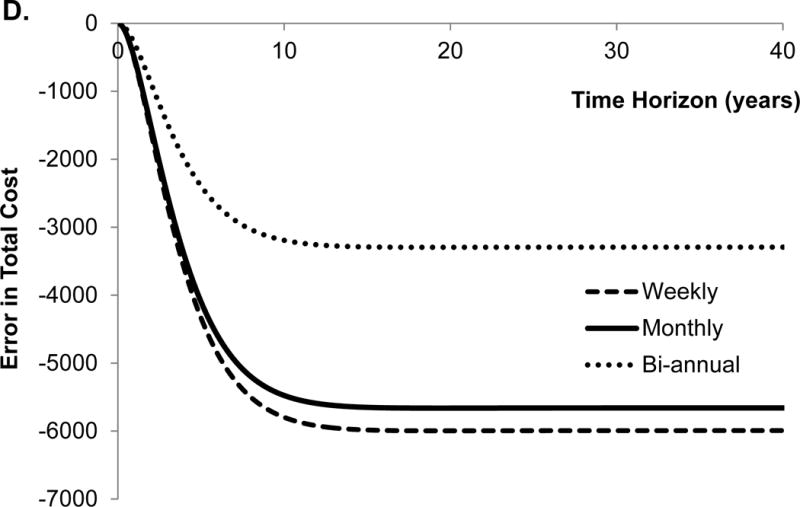
Error in model outcomes using shorter cycle length from traditional approach in comparison to that obtained with eigendecomposition approach. We applied 3% discount rate and within-cycle correction to estimate total costs and quality-adjusted life years (QALYs). HCC, hepatocellular carcinoma.

The traditional approach underestimated the total QALYs until the time horizon of 6 years, and overestimated QALYs afterwards (Figure 2C). Not surprisingly, the conversion error in QALYs is very similar to the error in the number of deaths because QALYs are greatly influenced by death. Finally, the traditional approach underestimated total costs, and the error monotonically increased with the time horizon of the model (Figure 2D). With the lifetime horizon, the total error in the cumulative incidence of HCC, costs and QALYs were −42%, −19% and 0.9%, respectively. The directions of these conversion errors are dependent on the model structure and parameter values, therefore, use of an incorrect approach can under- or over-estimate model outcomes.

We further evaluated the effect of different cycle lengths on the conversion error in model outcomes. For that purpose, we estimated the error in model outcomes obtained with bi-annual and weekly cycle length models (Figure 2A–D). Interestingly, the error in all model outcomes increased as the cycle length decreased from bi-annual to weekly. The reason for such a trend is that by using incorrect conversion of transition probabilities, the error in the model increases, as the cycle lengths decreases even though fine discretization (because of shorter cycle length) in the STMs approach the underlying continuous-time process.

THEORETICAL ISSUES AND PRACTICAL SOLUTIONS

Limitations of the Eigendecomposition Approach

We caution that not all matrices are diagonalizable. A k × k matrix P is diagonalizable if and only if P has k linearly independent eigenvectors. In addition, even if the eigendecomposition approach successfully finds the n-th root of a matrix, it does not guarantee that the resulting matrix root is real (i.e., may include complex entries) or is always stochastic (21, 26). A stochastic matrix must satisfy the following conditions: each element of matrix must be non-negative (because probabilities cannot be negative); and the elements of each row should sum up to one (because the sum of probabilities of staying or leaving any one state should equal to one)(20).

To illustrate limitations of the eigendecomposition approach, we used a previously published Markov model for antiretroviral therapy for human immunodeficiency virus (HIV), first presented by Chancellor et al. (27). This is a well-known example that has been used extensively as a pedagogical tool to illustrate some of the concepts of economic evaluation (28, 29). The following state-transition probability matrix defines annual probabilities with monotherapy for HIV treatment:

$$P=\left[\begin{array}{cccc}0.7215& 0.2018& 0.0669& 0.0098\\ 0& 0.5811& 0.4070& 0.0119\\ 0& 0& 0.7501& 0.2499\\ 0& 0& 0& 1\end{array}\right]$$

We converted the annual transition probabilities to monthly probabilities using the traditional approach (shown by ${\stackrel{\sim }{P}}_T$) and eigendecomposition approach (shown by ${\stackrel{\sim }{P}}_D$).

$$\begin{array}{c}{\stackrel{\sim }{P}}_T=\left[\begin{array}{cccc}0.9748& 0.0186& 0.0058& 0.0008\\ 0& 0.9564& 0.0426& 0.001\\ 0& 0& 0.9763& 0.0237\\ 0& 0& 0& 1\end{array}\right],\\ {\stackrel{\sim }{P}}_D=\left[\begin{array}{cccc}0.9731& 0.0250& 0.0008& 0.001\\ 0& 0.9558& 0.0495& -0.0053\\ 0& 0& 0.9763& 0.0237\\ 0& 0& 0& 1\end{array}\right]\end{array}$$

The 12-step transition matrix using monthly probabilities should yield the distribution of states at the end of 12-th cycle. Alternatively, computing the 12-th power of matrices ${\stackrel{\sim }{P}}_T$ and ${\stackrel{\sim }{P}}_D$ should yield the distribution of states at the end of 12-month (i.e. end of 1 year). We note ${\stackrel{\sim }{P}}_T^{12}\ne P$, which implies that the traditional formulae do not yield the original annual transition probability matrix, P. On the other hand, ${\stackrel{\sim }{P}}_D^{12}=P$. Despite the fact that the eigendecomposition approach yields the original matrix, P at the end of 1 year, ${\stackrel{\sim }{P}}_D$ has a negative probability for the transition from state 2 to 4 given by p₂₄ = −0.0053, which is not a valid probability.

For this specific model structure, we found that the eigendecomposition approach provides a stochastic 12-th root for a different set of transition probabilities, i.e. for p₁₂ = 0.3, p₁₃ = 0.09, p₁₄ = 0.08; p₂₃ = 0.06; p₂₄ = 0.21; p₃₄ = 0.13, where p_ij represents a transition probability from state i to state j. Therefore, the success of eigendecomposition approach is dependent not only on the structure of a model but also on the actual transition probability values.

Later we present a numerical approach that yields a stochastic monthly transition matrix for the above HIV model and compare it with ${\stackrel{\sim }{P}}_T$. We first consider theoretical issues underlying the problem so that we can identify classes of models that do not suffer from these problems.

Conditions for the Existence of Stochastic Roots of a Matrix

Analogous to the traditional conversion of transition probabilities from one time unit to another as done through rates, it is logical to attempt a similar approach for converting transition probability matrices from one cycle length to another. This approach consists of converting the annual probability matrix P into an instantaneous intensity rate matrix by taking the matrix (not element-wise) logarithm of P, adjusting the rate matrix according to a new cycle length 1/n year by dividing by n, and then converting the rate back into adjusted probability by taking the exponential of the intensity rate matrix. In the Mathematics literature, the problem of finding a stochastic root of a transition probability matrix of a discrete-time model is connected to the embeddability problem of continuous-time Markov chains, namely the existence of a unique intensity matrix Q such that P(t) = e^t·Q (21, 26). Some useful necessary conditions have been established for a matrix to be embeddable, which may also be necessary conditions for the eigendecomposition approach to work (26). For a stochastic matrix P, the following conditions are necessary for its embeddability (i.e. existence of the matrix logarithm):

1. determinant (P) > 0,

2. determinant (P) ≤ ∏_i p_ii (i.e, product of diagonal elements),

3. there are no states i and j such that j is accessible from i, but p_ij = 0. We define a state j is accessible from i if there exists a finite sequence of states k₀, k₁, …, k_m such that $p_{k_l}{p}_{k_l+1}>0$ for l = 0, …, m − 1.

In general, if one of the above conditions is not satisfied in the model’s state-transition matrix, then there does not exist a corresponding continuous-time Markov chain. However, note that meeting the conditions above is only necessary for existence of the matrix logarithm but may not be necessary or sufficient to guarantee the existence of a stochastic root. This is clearly illustrated by the HIV example where both the determinant and product of the diagonal elements are given by 0.3142 so condition (i) and (ii) are met. It is also obvious that condition (iii) is satisfied. Yet, the eigendecomposition approach yielded a non-stochastic probability matrix.

Approach for Non-Stochastic Matrix Roots

Several methods exist that can convert a non-stochastic matrix to stochastic matrix. However, we particularly use an algorithm that either finds the stochastic n-th root given by eigendecomposition or approximates the principal n-th root with the closest stochastic matrix if eigendecomposition does not produce a stochastic root (30). The algorithm is based on the distance minimization and aims at choosing elements of a stochastic matrix such that the norm of the difference between its power and the original transition probability matrix is minimum (Appendix B1). We also provide the corresponding MATLAB^® (MathWorks, Natick, MA, USA) code in Appendix B2, and implement the code in MATHEMATICA^® (Wolfram Research, Inc., Champaign, IL, USA) toolbox (Appendix B3). Applying the above approach to our HIV example, we obtained the following monthly transition probability matrix, ${\stackrel{\sim }{P}}_A$:

$${\stackrel{\sim }{P}}_A=\left[\begin{array}{cccc}0.9732& 0.0253& 0.0012& 0.0003\\ 0.0000& 0.9534& 0.0466& 0.0000\\ 0.0000& 0.0000& 0.9772& 0.0228\\ 0.0000& 0.0000& 0.0000& 1.0000\end{array}\right]$$

We compared the error introduced in the HIV model using the approximate n-th root matrix ${\stackrel{\sim }{P}}_A$ generated from our algorithm and the traditional ${\stackrel{\sim }{P}}_T$ matrix formed with the traditionally used formula $\stackrel{\sim }{p}=1-{\left(1-p\right)}^{1/n}$. For that purpose, we compared the original transition probability matrix, P with the 12-th power of ${\stackrel{\sim }{P}}_T$ and ${\stackrel{\sim }{P}}_A$ (which define the state of the system at the end of 1 year). We defined the error between matrices as below:

• Percentage error between the original matrix and traditional approach $=\frac{\Vert {\stackrel{\sim }{P}}_T^{12}-P{\Vert }_F}{\Vert P{\Vert }_F}$,

• Percentage error between the original matrix and our approach $=\frac{\Vert {\stackrel{\sim }{P}}_A^{12}-P{\Vert }_F}{\Vert P{\Vert }_F}$.

Where ‖ . ‖_F represents the Frobenius norm given by $\Vert P{\Vert }_F=\sqrt{{\sum }_i{\sum }_j|p_{ij}{|}^2}$. We found that the error using the traditional and our approach were 5.80% and 3.37%, respectively. Our algorithm introduced less error than the traditional formulas in the HIV model. Though we only compared the numerical error in matrices using the Frobenius norm, the error in long-term outcomes such as QALYs and costs could be even wider.

In Appendix C4, we evaluated six models of varying degrees of complexity. We found that in all models, the traditional approach was incorrect. Note that even for a simple three-state Markov chain, the traditional approach did not work. We used our toolbox to find a stochastic 12-root of each model’s annual transition probability matrix. We compared the error obtained using traditional and numerical approximation approaches. We found that the error using our approach was always less than that obtained with the traditional approach. Further, the range of examples considered suggests that the error disparity does not arise from the size of the matrix, but correlates with the number of transitions in a matrix. Therefore, our approach of numerical approximation provides especially more accurate results than the traditional approach when dealing with models that have a large number of transitions.

The Issue of Identifiability

The second issue concerning finding the root of a stochastic matrix using eigendecomposition approach is that more than one matrix may exist. This is known as the issue of identifiability. The eigendecomposition approach produces the principal n-th root of the original transition matrix, but there are other n-th roots of the matrix that may be stochastic. An example of such roots is provided elsewhere (8). The issue of identifiability could in some cases become important because two different matrices originating from one transition matrix can lead to two different outcomes and potentially different conclusions about the cost-effectiveness of an intervention. However, identifiability issue is not as common as stochasticity issue, therefore, is not considered here.

Converting Inputs to a Longer Cycle Length

Here we investigate the less common case where the analyst wishes to increase the length of the cycle. This could arise because of the need to improve computational efficiency. Adjusting costs and discount rates can be performed in a manner similar to the case where the task is to shorten the cycle length.

The traditional approach to changing cycle lengths may also fail when there is a need to increase a cycle length. In addition, the diagonal elements of the transition probability matrix may become negative when using the tradition approach. Converting an annual cycle length to a longer, m-th cycle (e.g. 5-year cycle) would require taking the m-th power of the annual transition probability matrix. Stochastic matrices have the property that raising a stochastic matrix to any integer power still yields a stochastic matrix. Therefore, the issues of stochasticity, embeddability, and identifiability do not arise when increasing the cycle length of STMs to the multiple of the original cycle length. However, when the cycle length is converted to a non-multiple (i.e. non-integer) value, the resulting matrix is not guaranteed to be stochastic when using the eigendecomposition approach. This is because we will need to find a root of a form “m/n” which is similar to finding the root of a form “1/n.” When the eigendecomposition is not possible or the resulting matrix using the eigendecomposition approach is non-stochastic or complex, we would need to use an approximation algorithm to convert the resulting matrix to a stochastic matrix, similar to the case of finding the root of a matrix.

Converting Probabilities from Different Data Sources

So far we have assumed that the transition probabilities in our examples came from a single source. However, it is typical that transition probabilities are estimated from multiple sources, with varying lengths of follow up. For a specific example, we provide an approach for computing transition probabilities to a common cycle length when these estimates come from multiple sources. We consider a 3-state example whose transition probability matrix takes the following form:

$$\stackrel{\sim }{P}=\left[\begin{array}{ccc}1-{\stackrel{\sim }{p}}_{12}-{\stackrel{\sim }{p}}_{13}& {\stackrel{\sim }{p}}_{12}& {\stackrel{\sim }{p}}_{13}\\ 0& 1-{\stackrel{\sim }{p}}_{23}& {\stackrel{\sim }{p}}_{23}\\ 0& 0& 1\end{array}\right]$$

Each element of the transition probability matrix can come from different sources. The first study may include the probability of transitioning from State 2 to death as p₂₃ over n₁ years. The last two studies provide estimate of p₁₂ and p₁₃ over n₂ and n₃ years, respectively. Because there is only one transition from State 2, and State 3 is an absorbing state, ${\stackrel{\sim }{p}}_{23}$ can be estimated using the traditional formula as

$${\stackrel{\sim }{p}}_{23}=1-{\left(1-p_{23}\right)}^{\frac{1}{n_1}}.$$

By raising the matrix $\stackrel{\sim }{P}$ to the powers n₂ and n₃ we can define p₁₂ and p₁₃ as

$$\begin{array}{c}{p}_{12}=\frac{{\stackrel{\sim }{p}}_{12}\left[{\left(1-{\stackrel{\sim }{p}}_{23}\right)}^{n_2}-{\left(1-{\stackrel{\sim }{p}}_{12}-{\stackrel{\sim }{p}}_{13}\right)}^{n_2}\right]}{{\stackrel{\sim }{p}}_{12}+{\stackrel{\sim }{p}}_{13}-{\stackrel{\sim }{p}}_{23}},\\ p_{13}=\frac{{\stackrel{\sim }{p}}_{12}\left[1-{\left(1-{\stackrel{\sim }{p}}_{23}\right)}^{n_3}\right]+({\stackrel{\sim }{p}}_{13}-{\stackrel{\sim }{p}}_{23})\left[1-{\left(1-{\stackrel{\sim }{p}}_{12}-{\stackrel{\sim }{p}}_{13}\right)}^{n_3}\right]}{{\stackrel{\sim }{p}}_{12}+{\stackrel{\sim }{p}}_{13}-{\stackrel{\sim }{p}}_{23}}.\end{array}$$

With ${\stackrel{\sim }{p}}_{23}$ known, these two equations can be solved for ${\stackrel{\sim }{p}}_{12}$ and ${\stackrel{\sim }{p}}_{13}$ in terms of the known values of p₁₂ and p₁₃ and the follow up periods n₂ and n₃. Unfortunately, these nonlinear equations cannot be solved analytically, so we compute numerical solutions.

To illustrate this point, consider the following values: n₁ = 10, n₂ = 5, n₃ = 3, p₁₂ = 0.10, p₁₃ = 0.05, p₂₃ = 0.20. There are two numerical solutions with real positive roots: $({\stackrel{\sim }{p}}_{12}=0.005,{\stackrel{\sim }{p}}_{13}=0.017,{\stackrel{\sim }{p}}_{23}=0.022)$ and $({\stackrel{\sim }{p}}_{12}=0.023,{\stackrel{\sim }{p}}_{13}=0.017,{\stackrel{\sim }{p}}_{23}=0.022)$. The first solution can be ruled out because it does not yield p₁₂ = 0.10 and p₁₃ = 0.05 when matrix $\stackrel{\sim }{P}$ is raised to the power 5 or 3, respectively.

To avoid obtaining negative or multiple solutions, we suggest following a distance minimization approach similar to the one used to deal with nonstochastic matrices. The algorithm requires defining sum of squared residuals (SSRD) between matrix $\stackrel{\sim }{P}$ and matrix P. In the above example, SSRD is given by

$$\begin{array}{l}\mathit{\text{SSRD}}={\left(p_{12}-\frac{{\stackrel{\sim }{p}}_{12}\left[{\left(1-{\stackrel{\sim }{p}}_{23}\right)}^{n_2}-{\left(1-{\stackrel{\sim }{p}}_{12}-{\stackrel{\sim }{p}}_{13}\right)}^{n_2}\right]}{{\stackrel{\sim }{p}}_{12}+{\stackrel{\sim }{p}}_{13}-{\stackrel{\sim }{p}}_{23}}\right)}^2\\ +{\left(p_{13}-\frac{{\stackrel{\sim }{p}}_{12}\left[1-{\left(1-{\stackrel{\sim }{p}}_{23}\right)}^{n_3}\right]+({\stackrel{\sim }{p}}_{13}-{\stackrel{\sim }{p}}_{23})\left[1-{\left(1-{\stackrel{\sim }{p}}_{12}-{\stackrel{\sim }{p}}_{13}\right)}^{n_3}\right]}{{\stackrel{\sim }{p}}_{12}+{\stackrel{\sim }{p}}_{13}-{\stackrel{\sim }{p}}_{23}}\right)}^2.\end{array}$$

This minimization problem can be solved with many general-purpose optimization routines such as those in R, Mathematica, or Excel. With the values given above, the minimum is achieved by setting ${\stackrel{\sim }{p}}_{12}=0.023$ and ${\stackrel{\sim }{p}}_{13}=0.017$ For complex models, the analytical approach may not be feasible. In that case, a numerical approximation approach would be needed to minimize SSRD, similar to calibration techniques (34).

As observed, changing cycle lengths when transition probabilities are estimated from multiple sources, with varying lengths of follow-up is more complex than when all transition probabilities are expressed in a common cycle length. In this section, we provided an approach to deal with such situations for a specific 3-state STM. However, a general approach to change cycle length for any structure of a STM is needed and is beyond the scope of this study.

DISCUSSION

In this study, we reviewed approaches to changing cycle lengths in STMs, which are commonly used for medical decision making. In particular, we showed anomalies with the commonly used approach of adjusting cycle lengths in STMs. We showed that the traditional approach is not guaranteed to work for any STM with more than two states. Furthermore, we presented an approach based on eigendecomposition to correctly change transition probabilities to different cycle lengths. We also discussed theoretical challenges, and provided a general approach that provides numerical solutions that are more accurate than the traditional approach. We provided MATLAB codes and a user-friendly toolkit to convert transition probabilities to different cycle lengths.

The issue of transforming transition probabilities has been discussed in other fields of social sciences and credit ratings (21, 26). Earlier studies in the medical field have primarily focused on estimation of transition probabilities for Markov chains from partially and fully observed data (15–17). These studies did not discuss the issues that could arise when converting transition probabilities to different cycle lengths. In contrast, we highlighted the problems with the most common approach for conversion of transition matrices. We provided analytic results using eigendecomposition for the three-state progressive model, discussed issues with the eigendecomposition approach, and provided complimentary approaches when those issues are present. We provided several mathematical conditions to evaluate the existence of feasible solutions, and steps to find approximate solutions if they do not exist.

We differentiate between eigendecomposition and the distance minimization algorithms. When it works, the eigendecomposition is exact (no approximation is needed). In this case there is no issue with accuracy. If the eignedecomposition method fails (i.e., the matrix is not diagonalizable or the resulting power of the matrix includes negative or complex entries), the second approach of finding an approximation to the power of the matrix using distance minimization can be used. Our approach always finds a better solution than the traditional approach but its implementation in currently available algorithms cannot always guarantee finding a global minimum. However, we think that our approach is a step in the right direction and further research is warranted to explore this issue further.

Our study also highlights an interesting relationship between the cycle length and accuracy of model outcomes. While discretization of a continuous time function introduces error (discretization error) in model outcomes because of the time spent in each health state, the error decreases as the cycle length gets shorter. On the other hand, incorrect conversion of cycle length adds error (conversion error) to model outcomes because state membership is incorrectly computed. In this case, the error increases as the cycle length get shorter. Therefore, contrary to the common notion that shorter cycle lengths always yield more accurate results, the overall error in model outcomes can in some instances increase as the cycle length becomes shorter. This observation underscores the importance of using the correct approach to adjust probabilities to different cycle lengths. Therefore, only a shorter cycle length obtained using the correct conversion approach would remove the conversion error and reduce the discretization error.

Our study also draws attention to the inherent difficulties in adjusting cycle lengths in STMs. We highlight two potential issues—embeddability and identifiability of a Markov chain. Essentially, the limitation arises from trying to identify which Markov processes arise from shorter time-cycle processes. We note that even the theoretical literature on finding stochastic n-th roots and identifiability is relatively scarce. Therefore, more theoretical advancements are needed before such problems can be addressed in a systematic way.

Our study made some limiting assumptions that provide directions for future research. For simplicity, we only focused on constant (i.e., do not change from cycle to cycle) transition probabilities. However, in practice, almost all state-transition models include some probabilities that change with time. Note that our approach is applicable to time-varying probabilities, however this would require applying the eigendecomposition method to transition probabilities at each cycle. Further research is needed to find a generalizable approach that can be practically implemented without substantial effort. Second, we assumed that all transition probabilities were available for a given cycle length (e.g. monthly, annual, etc.); however, in practice, state-transition probabilities are estimated from different studies reporting values in different time scales. In that case, each parameter cannot be individually converted to a fixed cycle length from each study. Using a simple example, we provided an approach for computing model inputs when the data come from multiple sources, with varying lengths of follow up. To our knowledge, no earlier study has addressed this issue in a systematic way, which warrants further research on finding a generalizable approach. Our study is only the first step to acknowledge the limitations of the commonly used approach of changing cycle lengths in STMs. Finally, we did not evaluate any error in comparative cost-effectiveness results using the traditional approach, which is left for future work. It is possible that in some problems the error in two arms of a cost-effectiveness model cancels each other out when incremental outcomes are computed. However, this does not obviate the need to use our proposed method because there may still be a need to compute accurately total intermediate or final outcomes (e.g., cumulative outcomes, total costs).

In conclusion, we showed that the commonly used approach of converting transition probabilities to different cycle lengths can result in incorrect transformations, thereby leading to incorrect model outcomes. The correct approach based on the eigendecomposition method and distance minimization provides more accurate outcomes; however, further research is needed to easily implement our approach in decision-analytic models.

Appendix A. Estimation of Transition Probabilities of the End-Stage Liver Disease Model

We estimated the transition probabilities of our three-state Markov model of end-stage liver disease using two published clinical studies. Particularly, we estimated progression from decompensated cirrhosis (DC) from Planas et al. (19), which presented data on 187 DC patients with complete follow up over a mean period of 34 months as follows: 72 were still in DC, 33 developed HCC, 75 died from DC, and 7 died from unrelated cause. Note that we cannot calculate probabilities directly for most health states (except remaining in DC state) because of competing risks and progression from future HCC state. Therefore, we use the following approach.

The DC patients evolve in continuous-time as follows:

$$\begin{array}{c}DC\prime (t)=-(\alpha +\mu )DC(t),\\ DC(0)=187.\end{array}$$

We used the following definitions for hazard rates:

• α = progression rate to HCC,

• μ = death from DC,

• δ = death from HCC.

This model can be solved as

$$DC(t)=DC(0)e^{-t(\alpha +\mu )}.$$

We calculated the number of DC patients who developed HCC or remained in the DC state over the follow up period T as

$$\begin{array}{c}\mathit{\text{HCCT}}={\displaystyle \underset{0}{\overset{T}{\int }}\alpha DC(t)}=\frac{DC(0)[1-e^{-T(\alpha +\mu )}]\alpha }{\alpha +\mu },\\ DC(T)=DC(0)e^{-T(\alpha +\mu )}.\end{array}$$

These 2 equations can be solved for α, and μ as

$$\begin{array}{c}\alpha =-\frac{\text{HCCT ln}\frac{DC(T)}{DC(0)}}{T[DC(0)-DC(T)]},\\ \mu =\frac{[\text{HCCT}+DC(T)-DC(0)]\text{ln}\frac{DC(T)}{DC(0)}}{T[DC(0)-DC(T)]}\end{array}$$

Using the values $T=\frac{34}{12}$, DC(0) = 187, DC(T) = 72, HCCT = 33, we find α = 0.0967, μ = 0.2402.

Fattovich et al. (18) report that 17 of the 29 patients with HCC died in the first 19 months, which translates into annual mortality rate of HCC equal to δ = −(12⁄19) ln(1 − 17⁄29) = 0.5573. Writing the intensity matrix Q as

$$Q=\left[\begin{array}{ccc}-0.3369& 0.0967& 0.2402\\ 0& -0.5573& 0.5573\\ 0& 0& 0\end{array}\right].$$

Taking the matrix exponential of Q gives the annual probability matrix as

$$P=\left[\begin{array}{ccc}0.7140& 0.0619& 0.2241\\ 0& 0.5728& 0.4272\\ 0& 0& 1\end{array}\right].$$

The monthly probability matrix is

$$\stackrel{\sim }{P}=\left[\begin{array}{ccc}0.9723& 0.0078& 0.0199\\ 0& 0.9546& 0.0454\\ 0& 0& 1\end{array}\right].$$

Raising this to 34 months, ${\stackrel{\sim }{P}}^{34}$ and multiplying by the vector of initial patients in the original study (187,0,0) we obtain

$$[187,0,0]{\left[\begin{array}{ccc}0.9723& 0.0078& 0.0199\\ 0& 0.9546& 0.0454\\ 0& 0& 1\end{array}\right]}^{34}=\left[\begin{array}{c}72\\ 15\\ 100\end{array}\right],$$

confirming that 72 patients were still in DC state after 34 months, as in the original study by Planas et al. Note that the total number of deaths 100 was more than the number of 82 in Planas et al. because the 100 deaths include additional deaths from patients who also developed HCC. In general, the number of patients in DC state t months from now is 187. (0.9723)^t. The number of people in HCC state at time t is given by

$$\text{HCC}t=(0.0967/12)\ast 187\ast {0.9723}^t.$$

Note that we used the actual monthly hazard rate (0.008055 = 0.0967/12) rather than the monthly probability of HCC (0.00776) as the risk of HCC is continuous over time. Applying the trapezoidal rule for within-cycle correction and summing over 34 months we obtain:

$${\displaystyle \sum _{t=1}^{34}\frac{\text{HCC}(t-1)+\text{HCC(}t)}{2}}=33.$$

Similarly, deaths from DC state can be defined as:

$$\text{Death}t=0.240212\ast 187\ast {\mathrm{0\; .9723}}^t.$$

Similar calculations confirmed that total death from DC after 34 months is

$${\displaystyle \sum _{t=1}^{34}\frac{\text{Death}(t-1)+\text{Death}(t)}{2}}=82.$$

Appendix B: Non-stochastic Matrix Issue and Solution

B1. Distance minimization algorithm

Given where a ∈ Rⁿ where a is the row of the principal n-th root matrix, this computes a row vector xRⁿ, x_i ≥ 0, Σ_ix_i = 1 that minimizes ‖x − a‖:

1)	If Σiai =1 and ai ≥ 0, x = a, quit, end
2)	while true
3)	λ = (Σiai − 1)/n, x =a − λ
4)	if x ≥ 0, quit, end
5)	for i = 1: n
6)	xi = max 0, xi
7)	end
8)	a = x
9)	end

B2. MATLAB code for distance minimization algorithm

Algorithm. % stochroot.m
% This script executes the distance minimization algorithm for a transition
% matrix A with desired pth root. The function nrootmat is the function
% used earlier to calculate the pth root of the matrix.
function b = stochroot(A,p)
Ap = mpower(A,p);
n=length(A);
b = zeros(n,n);
for j=1:n
a = real(Ap(j,:));
while true
 if sum(a)==1 && min(a)>=0
   b(j,:) = a;
   break;
 end
lambda = (sum(a)−1)/n;
x = a − lambda*ones(1,n);
 if min(x)>=0
   b(j,:)=x; break;
 end
  for k=1:n
   x(k) = max(0,x(k));
  end
  a = x;
end
end

B3.Matrix conversion toolbox

We developed a toolbox in MATHEMATICA to convert a transition probability matrix to a different cycle length. The toolbox converts a non-stochastic matrix to stochastic matrix using distance minimization algorithm. Figure B1 below provides the snapshot of the toolbox.

Figure B1.

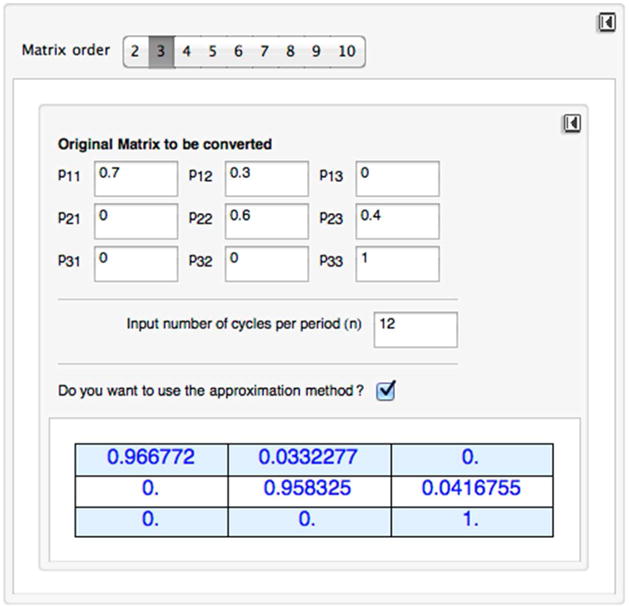
Snapshot of the toolbox for cycle length conversion

To compute a root of a matrix:

1. Select the order of the matrix (i.e., number of heath states). The default is a 3×3 matrix. The current tool can allow up to a 10×10 matrix.

2. Fill in the cell of the matrix. Make sure that the matrix is stochastic by checking that each cell is nonnegative and all rows add up to 1.

3. Select the cycle length by choosing the number of cycles per period (n). For example, if the original matrix has an annual cycle and you want to change it to a monthly cycle, input 12. The default input is 1, which returns the original matrix.

4. If the resulting new matrix is non-stochastic, choose to approximate it by checking the box “Do you want to use the approximation method?”

5. To start over again, use the reset button in the upper right corner. Note that there are two reset buttons, one for resetting the order of the matrix to the default value of 3 and the other for resetting the matrix cells to 0.

B4. Numerical results on non-stochasticity

We present below six Markov chains of increasing complexity. For each model, the original transition probability matrix represents annual probabilities. We converted annual transition probabilities to monthly using both the traditional formula, $\stackrel{\sim }{p}=1-{\left(1-p\right)}^{1/n}$. We also converted the annual transition probabilities to monthly using our toolbox described in Appendix B3, which numerically finds a stochastic 12-th root of the annual transition probability matrix. We compared the two approaches by estimating percentage error in the Frobenius norm. We compared the original transition probability matrix, P with the 12-th power of ${\stackrel{\sim }{P}}_1$ and ${\stackrel{\sim }{P}}_3$ (which defines the state of the system at the end of 1 year). We defined the error between matrices as below:

• Percentage error between the original matrix and traditional approach = $\frac{\Vert {\stackrel{\sim }{P}}_1^{12}-P{\Vert }_F}{\Vert P{\Vert }_F}$,

• Percentage error between the original matrix and our approach = $\frac{\Vert {\stackrel{\sim }{P}}_2^{12}-P{\Vert }_F}{\Vert P{\Vert }_F}$,

where ‖ . ‖_F represents the Frobenius norm given by $\Vert P{\Vert }_F=\sqrt{{\sum }_i{\sum }_j|p_{ij}{|}^2}$.

Example 1. Three-state chain model

Figure B2.

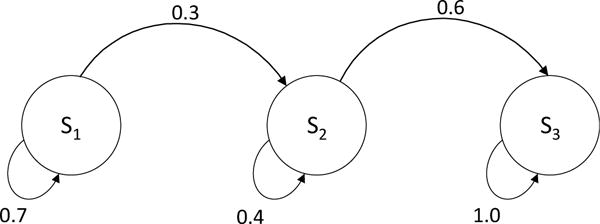
Three-state Markov chain

$$P=\left(\begin{array}{ccc}0.7& 0.3& 0\\ 0& 0.6& 0.4\\ 0& 0& 1\end{array}\right)$$

Figure B2 present a three-state model does not include any competing risks states. Even for this simple structure, the traditional approach did not work. The eigendecomposition approach also failed to provide a stochastic 12-th root; therefore, we applied the numerical approximation. We found that the error using the traditional and distance-minimization approach were 6.21% and 6.03%, respectively. Errors were very similar with both approaches.

Example 2. Five-state chain model

Figure B3.

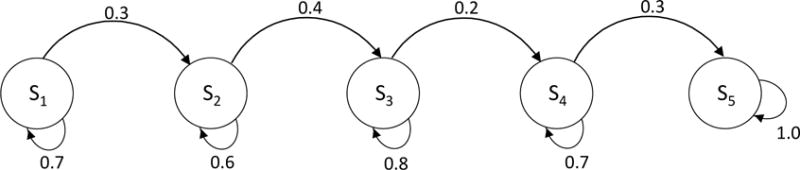
Five-state Markov model

$$P=\left(\begin{array}{ccccc}0.7& 0.3& 0& 0& 0\\ 0& 0.6& 0.4& 0& 0\\ 0& 0& 0.8& 0.2& 0\\ 0& 0& 0& 0.7& 0.3\\ 0& 0& 0& 0& 1\end{array}\right)$$

We next consider a five-state example (Figure B3). In this model structure, the traditional as well eigendecomposition methods did not work. We applied the numerical approximation and compared the error. We found that the error using the traditional and distance-minimization approach were 6.13% and 6.06%, respectively. As in the previous example, errors were very similar with both approaches.

Example 3. Four-state competing risks model A

Figure B4.

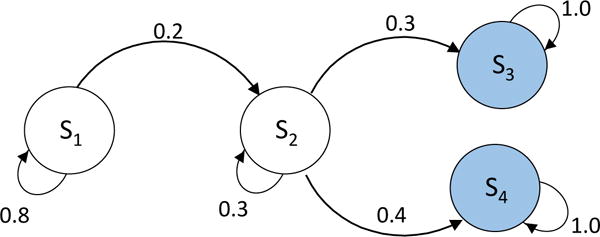
Four-state Markov model with two competing-risks states

$$P=\left(\begin{array}{cccc}0.8& 0.2& 0& 0\\ 0& 0.3& 0.3& 0.4\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)$$

We consider a four-state model with two competing risks states (shaded in Figure B4). We found that the error using the traditional and distance-minimization approach were 9.21% and 6.10%, respectively. In this example, the error was considerably lower with our approach.

Example 4. Four-state competing risks model B

Figure B5.

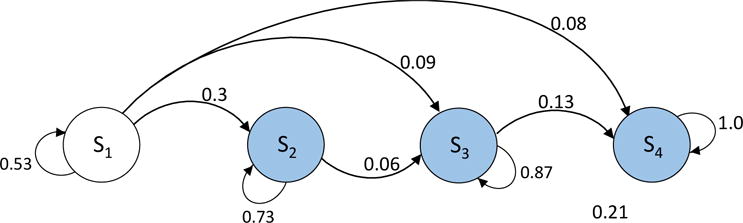
Four-state Markov model with three competing-risks states

$$P=\left(\begin{array}{cccc}0.53& 0.3& 0.09& 0.08\\ 0& 0.73& 0.06& 0.21\\ 0& 0& 0.87& 0.13\\ 0& 0& 0& 1\end{array}\right)$$

We next considered a different four-state model structure that has three competing-risks states (shaded in Figure B5). In this example, the eigendecomposition method provided a stochastic root, and there was no need for any numerical approximation. The error using our approach was 0%, whereas the error using the traditional approach was 5.13%.

Example 5. Four-state competing risks model C

$$P=\left(\begin{array}{cccc}0.57& 0.3& 0.09& 0.04\\ 0& 0.73& 0.06& 0.21\\ 0& 0& 0.87& 0.13\\ 0& 0& 0& 1\end{array}\right)$$

Here we considered the same model structure as in the in the previous example, but used a different set of transition probabilities. In this example, the eigendecomposition methods failed to provide a stochastic root, therefore, we applied numerical approximation to convert the 12-th root matrix to a stochastic matrix. We found that the error using the traditional and distance-minimization approach were 11.66% and 4.83%, respectively. As noted, the error was considerably lower using in our approach than that with the traditional approach.

Example 6. Five-state competing risks model

Figure B6.

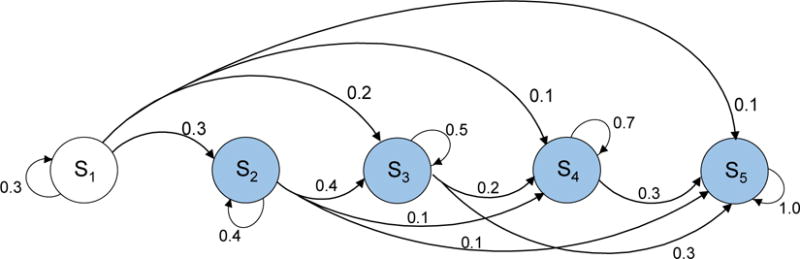
Five-state Markov model with four competing-risks states

$$P=\left(\begin{array}{ccccc}0.3& 0.3& 0.2& 0.1& 0.1\\ 0& 0.4& 0.4& 0.1& 0.1\\ 0& 0& 0.5& 0.2& 0.3\\ 0& 0& 0& 0.7& 0.3\\ 0& 0& 0& 0& 1\end{array}\right)$$

We next provide a five-state model that has four competing-risks states (Figure B6). We found that the error using the traditional and distance-minimization approach were 76.84% and 0.11%, respectively. In this complex model structure, the error was substantially lower when our approach was used. We observed that as the model complexity increased (from example 1 to example 6), the error with traditional approach became increasingly larger than that with our approach.