Quantitative Framework for Retrospective Assessment of Interim Decisions in Clinical Trials

Abstract

This article presents a quantitative way of modeling the interim decisions of clinical trials. While statistical approaches tend to focus on the epistemic aspects of statistical monitoring rules, often overlooking ethical considerations, ethical approaches tend to neglect the key epistemic dimension. The proposal is a second-order decision-analytic framework. The framework provides means for retrospective assessment of interim decisions based on a clear and consistent set of criteria that combines both ethical and epistemic considerations. The framework is broadly Bayesian and addresses a fundamental question behind many concerns about clinical trials: What does it take for an interim decision (e.g., whether to stop the trial or continue) to be a good decision? Simulations illustrating the modeling of interim decisions counterfactually are provided.

What does it take for an interim decision (e.g., whether to stop the trial or continue) to be a good decision? This question is important not only to data and safety monitoring board (DSMB) members and ethicists but also to anyone who wants to be in a position to better understand interim decisions in clinical trials. Most approaches to monitoring and interim analyses do not discriminate effectively between good and bad decisions. While statistical approaches tend to focus on epistemic aspects of monitoring rules (cf. Goldman and Hannan,¹ Proschan and others,² and Gillen and Emerson³),^* often overlooking ethical considerations, ethical approaches to randomized controlled trials (RCTs) tend to overlook key epistemic dimension (cf. Freedman⁵—the principle of clinical equipoise; Buchanan and Miller⁶—the principle of nonexploitation).^† The proposal is a quantitative framework—a second-order decision-analytic framework—that incorporates both ethical and necessary epistemic considerations for the modeling and retrospective assessment of interim decisions.

The 2 most basic tasks of the framework are to deliver the following:

1. A reconstructed justification for a given interim decision

2. A verdict as to whether the decision is ethically permissible

The article proceeds as follows. The first section sets out basic requirements and indicates some important restrictions on the framework. The second section gives an overview of the framework. The third section presents the formal elements constituting the framework and a simulation illustrating the modeling of interim decisions. The article concludes raising further questions of epistemological interest regarding the modeling and evaluation of interim decisions and the public accountability of such decisions.

Basic Requirements and Restrictions

Based on past DSMB experiences from the Women’s Health Initiatives trials,^7–9 as well as human immunodeficiency virus (HIV)/AIDS and oncology trials,^10,11 the proposed framework should meet certain requirements. The most basic requirement (which underlies all others below) is the idea that every DSMB decision should articulate a clear general principle (i.e., a ratio decidendi) that gives reason for the interim decision, and all such decisions should be made public. This section sets out the basic requirements and indicates important restrictions.

Clarity

The framework must provide clear standards of representation (modeling) and clear criteria of evaluation. We need to be clear both about how an interim decision is represented (modeled) and about the principles used for its evaluation.

Scope

The guidelines for representation must be flexible enough to accommodate the wide variety of interim decisions in clinical trials. That is because different types of decisions reflect different types of dilemma, which consequently appeal to contextual factors differently. The framework must be broad enough to accommodate 1) the different types of early stopping decisions typically found in RCTs, 2) common disagreements about decisions based on them, and 3) common types of statistical monitoring procedures—whether based on frequentist or Bayesian philosophies.

Flexibility

The framework should yield answers that vary with changes in problem representation. The framework assists with the identification of a set of relevant decision criteria and with representation of the monitoring rules that govern stopping decisions. Having identified these criteria, the framework tries to represent decisions as optimal, in the following weak sense of optimality: no alternative representation does better on every criterion.

Explanatory Power

The framework should provide public criteria amenable to justification. An adequate framework should show how good interim decisions actually contribute to the permissibility of these decisions. Because a proper evaluation of a DSMB decision requires a reason for its decision, a good decision requires a fully structured justification capable of being communicated to others (i.e., a public rationale or ratio decidendi).^‡ The conception of a good decision proposed by the framework does not judge an interim decision as right or wrong based on whether the DSMB got the outcome (e.g., superior therapy) correctly or incorrectly. The criteria for a good decision focus instead on whether there is a principled reason for the interim decision and then whether the rational decision is ethical, under some ethical principle or maxim (e.g., minimax, since it safeguarded trial participants by minimizing maximal losses).^§

Balancing Epistemic and Ethical Factors

Frameworks currently available tend to focus on the epistemic performance of monitoring rules—such as those in statistical literature—or on meeting the demands of medical ethics applied to clinical research, such as those proposed by the notion of “equipoise disturbed” (cf. Freedman⁵), “therapeutic obligation” (cf. Marquis¹²), “nonexploitation” (cf. Buchanan and Miller⁶), or “risk-benefit relationship as a moral compass” (cf. Iltis).¹³ Yet such approaches lead to the view that interim decisions should be assessed on the basis of either “scientific” or “medical” objectives. The proposed framework, by contrast, represents decisions by combining objectives on the basis of factors contextualized in a particular decision situation.

To meet these requirements, the first step is to appeal to a basic classification of interim monitoring decisions. These are whether or not to stop due to efficacy, futility, or harm.¹¹ This classification permits the identification of relevant criteria that might influence the decision. The next step, given the identification of a set of criteria for representation, is to develop a specialized decision-analytic model, given the existence of a philosophical theory of rational decision making. This means defining the components of the decision-analytic model:

1. A set of available actions (at any interim point in the trial, e.g., stop or continue)

2. Foreseeable consequences of each action

3. Set of possible states of the world (i.e., a set of hypotheses about the effect of interest, e.g., null, alternative)

4. Set of alternative statistical monitoring rules

5. Decision criteria

We call this a complete DSMB decision specification.

A fundamental constraint on the decision specification is the weak optimality requirement: having identified a set of relevant decision criteria, concentrate on representations under which actual DSMB decisions are weakly optimal, in the sense that no alternative under consideration fares better on every criterion. Conflicts of expert opinion can then be analyzed by exploring the distinct ranges of assumptions (scenarios) under which conflicting stopping strategies emerge as optimal choices.

This broadly comparative Bayesian approach offers the hope of meeting all 5 requirements listed above.^** Because we have the components of decision theory within the model, the framework allows us to explicitly account for the epistemic and ethical components that should influence the interim monitoring decision of clinical trials. By being able to represent interim decision options as decisions under risk, each interim decision will, in turn, depend on epistemic elements (e.g., estimated effect size, population frequencies or patient horizon, predictive probability of the test statistic given the stopping rule to reach certain stopping boundaries) and ethical elements (e.g., minimization of maximal losses, expected costs and benefits of possible treatment outcomes). In this light, the decision model can meet the balancing requirement of epistemic and ethical factors.

To conclude this preliminary section, we note 2 important restrictions to the decision-analytic model. The first is that the decision-analytic model is capable of representing only some of the criteria that might, in real life, influence data monitoring decisions. The second is that the framework does not aim to provide an algorithm for making early stopping decisions. It does not propose a theory that takes a description of an RCT decision as input and delivers a sharp verdict about whether or not the trial should be stopped. Instead, it offers a broad general framework that allows modelers to explore and analyze the justification for stopping decisions.

Moreover, the decision framework is not intended as a strict reconstruction of what DSMBs actually have done, or often do, when faced with the complexity of interim decisions. Deliberations from DSMBs are publicly unavailable. When the deliberations do exist, they are often relegated to “Appendix 16.1.9” of reports submitted to regulatory authorities such as the US Food and Drug Administration (FDA).^†† In rare circumstances, there is an actual case study identifying and discussing “lessons learned” specific to the clinical trial (cf. DeMets and others¹⁰), and even then, relevant factors of interim decisions are often missing, making the public transcript an unreliable basis for anyone trying to appraise the DSMB’s deliberations.

Given that the DSMB has an information monopoly during all interim analysis, also having sweeping discretion over the course of the trial precludes most meaningful oversight of its decision making.¹⁵ Decision-making discretion by the DSMB becomes particularly challenging given the added fact that most of its deliberations happen behind closed doors, routinely not reporting publicly its interim decision reasons and recommendations.¹⁶

Although there are practical reasons for DSMBs to keep interim data analysis private under the premise of confidentiality, secret DSMB decision making has at least one important shortcoming: the lack of publicity in decision making prevents the public from getting a proper understanding of the reasons for the DSMB findings and final recommendation. Without a public rationale for its decisions (e.g., early stop, continue, changes to the trial), DSMB decision making prevents others from reaching their own conclusions about the trial’s ethical and scientific appropriateness. And this is an important distinction from the way decision making by court of law happens, for instance, particularly in higher judicial decisions (e.g., setting a precedent) when a judgment is made explicitly and publicly with the inclusion of the judge’s reasoning over the appropriate resolution of the legal issue.

Stanev¹⁷ argues that decision making in legal systems such as judge-made law strikes an optimal balance between the competing demands of conservatism (with stare decisis, the rule that like cases should be decided alike) and innovation (the continuous development of the legal system). Based on similar relationships in the ways DSMBs rely on rules to make decisions in clinical trials, my argument by analogy had focused on conveying plausibility upon the need for publicity and explicitness in DSMB decision making—contrary to current, secretive DSMB practice. If the analogy succeeds, it shows that a similar explanatory hypothesis in clinical trials would explain a similar consequence: DSMB decision making striving for a balance between conservatism and innovation—avoiding dangerous medical treatments and bringing new and effective treatments into use as rapidly as possible—should promote the publicity and explicitness of decisions, the sort of public justification that the framework here proposes for decision making.

The framework begins with an interim decision stripped of some of its complex features. The simplification allows the decision analyst (i.e., modeler) to focus on a limited set of questions about the DSMB interim decision at stake. The particular factors and details that are not stripped vary with the specific type of decision (e.g., early stop due to efficacy, harm, futility). An alternative way of putting this point is that different factors are held fixed depending on the interim decision. This means that the first step of the framework is to provide a simplified description of an interim decision.

Overview of The Framework

The reconstruction of interim decisions requires certain elements. The reconstruction may include the actual stopping rule—if publicly available—or some reasonable reconstruction of the actual prespecified protocol stopping rule. The model is also meant to capture the reasoning that led to the selection of that (actual or reconstructed) stopping rule. This requires the representation of a set of alternative decisions (e.g., continuing with the trial at first interim or stopping), a set of expected losses, and one or more alternative statistical monitoring plans. The statistical monitoring plan includes the trial stopping rule, the number of interim analyses, and the efficacy on primary outcome in which the study was based, as reported in the study’s original publication (or as specified in its protocol).

The representation is considered incomplete until the interim decision (e.g., early stopping) is justified as permissible. The standard for permissibility is the existence of at least one decision criterion on which the interim decision is “optimal” (i.e., it maximizes expected utility). We hinted at the meaning of optimality earlier; a little more about this idea is in order.

According to the framework, a decision criterion prescribes a way in which, for a given representation of an early stopping decision, the criterion picks an “optimal stopping decision.” Because criteria are given by the type of decision (or dilemma) and salient factors of the case, the decision criteria are relative to a set of predefined criteria. We say that a decision is permissible if it is “optimal” according to at least one decision criterion. If we succeed in giving the RCT case a representation and show that the stopping decision is “optimal” on at least one decision criterion, we then say that the decision is permissible, or in principle justifiable.

The last step of the framework is evaluation. Evaluation is composed of 2 stages: a policy stage and a running stage. The first stage reflects a policy decision that is logically prior to the running stage (any data collection or conduct) of the RCT. The first stage is concerned with the choice of the monitoring rule per se (i.e., with the justification of a choice of monitoring rule). The second stage is concerned with the justification of a particular action (i.e., decision) falling under its stopping rule. This second stage may include the “optimal” decision criterion if one is identified during the reconstruction of the early stopping decision.

The need for a 2-stage evaluation is supported by appeal to an intuitive understanding of what ethics (i.e., a just or fair assessment of decisions) requires. An example serves to illustrate the intuition. We seem to give more weight to harm when it is engendered by a rule that is officially adopted by a DSMB than when the harm is due to insufficiently enforced rules or insufficiently protective DSMBs. For instance, burdens on trial participants due to an authorized restriction (e.g., a highly stringent and unrealistic stopping condition) seem morally more serious than burdens engendered by poorly monitored RCTs (e.g., ignoring unforeseen effects) or by DSMB skeptics (e.g., skepticisms about the clinical importance of certain interim results), even if the harms on trial participants are exactly the same—or if the probability of harm faced by trial participants is the same. Unless our criteria of judging the permissibility of a case save this intuitive distinction, an ethical evaluation of interim decisions is incomplete. Thus, we need to make a distinction between the choice of monitoring rule and the decision about whether to stop or continue given a particular stopping rule.

To accommodate this distinction between the choice of a monitoring rule and the choice of a particular action falling under it, our evaluations of monitoring decisions must not simply compute or “tally up” in some way the foreseeable effects each available action would have on trial participants. When judging permissibility, a more complete evaluation of an early stopping decision must weigh these effects differently for distinct types of a causal link connecting the candidate decision to benefits and harms for trial participants. And this can be accomplished with the 2-stage process outlined above.

Consider the following claim: “The DSMB stopped its trial early due to efficacy.” Until the reader knows the type of trial concerned and its governing rules—rules that defined the acts and conditions of early stopping—she or he does not fully understand what the DSMB did. The 2-stage evaluation is necessary not only to account for the fact that exceptions to stopping rules are not uncommon in practice but also because a breach of the stopping rule by the DSMB, which may appear to maximize expected utility according to some representation, may not in fact have an adequate justification. The fact that a decision to continue a trial—increasing the chances of harm to trial participants—appears to be justified as maximizing expected utility given the choice of stopping rule should not be considered an adequate justification—unless the rule under which the action falls is also appropriate to the given RCT context.^‡‡

Another point about the need for a 2-stage evaluation is in order. Even though there is a commitment always to represent the DSMB decision as “optimal” (permissible), the reconstruction of an early stopping decision, by itself, does not imply having a complete evaluation of the early stopping decision. The reason is this: in cases where there are rival opinions about the appropriate stopping rule, it may be demonstrated by comparison that a rival stopping rule is better suited or more appropriate given the RCT context.

By using the framework, decision analysts are able to compare alternative DSMB decisions. Why did the DSMB choose to continue rather than to stop the trial? Given the adoption of a particular statistical monitoring rule, had the foreseeable consequences of its actions been different, would the DSMB have taken a different course of action? Under what realization of expected losses would the DSMB have chosen a different course of action? These counterfactual “what-if” questions reveal a conscious attempt on the part of the reader to provide reasons for the DSMB decision. This point about counterfactual questions indicates a counterfactual-style intuition about explanations—namely, that we have explanations if we can answer counterfactual questions.^§§ The suggestion is that what-if-things-had-been-different information is intimately connected to our judgments of explanatory relevance.

A distinguishing feature of this counterfactual style of explanations is that they are explanations that furnish information that is potentially relevant to control and manipulation. These counterfactual explanations inform us, decision analysts, when we are able to change the value of one or more variables (e.g., monitoring rule R1 to R2, ethical loss function to scientific loss function, or changes in utility values), we could change the value of other variables (e.g., continue the trial v. stop the trial). This conception of explanation has the advantage of fitting a wide range of medical science contexts, particularly clinical trial monitoring and behavioral sciences, where investigators think of themselves as revealing patterns of regularities and constructing explanations.

A key virtue of such explanations is that they show how what is explained depends on other, distinct factors, where the dependence in question has to do with some relationships that hold as a matter of manipulability via a model, which is very useful for decision analysts and those modeling reasoning. This way, decision analysts, by manipulating their model, can see if the model can account for potential, yet plausible, differences of opinions among DSMB members. If it can, we have provided a plausible explanation for reasonable disagreements among expert opinions. If it cannot, then we still have a problem, which is to account for expert opinions that can (might) differ for good reasons.

The idea worth pointing out here is that the decision analyst gains understanding of the DSMB’s interim decision in the ability to grasp a pattern of counterfactual dependence associated with relationships that are potentially exploitable for purposes of manipulation via a model. For instance, we might come to understand how changes in patient health status will change the conservatism of early stopping rules: as health increases, greater efficacy is needed to outweigh possible long-term side effects. Grasping such relationships is the essence of what is required for the analyst to be able to explain the DSMB’s decision to continue the trial despite early evidence for efficacy.^***

Formal Elements and Simulation

According to the framework, the representation of a statistical monitoring plan begins as a decision under uncertainty, represented as a 4-tuple (θ, A, Y, L). θ is the parameter space (the set of possible true states of nature, A is the set of possible actions, Y is the observation (data) model, and L is a specific loss function. Therefore, δ(y): Y→A is a statistical monitoring rule.

To illustrate the framework for modeling decisions, the example is kept as simple as possible. Approximate analysis that considers relevant features shall suffice for the purposes of this article. We treat the progression to AIDS as a binary event. The example involves dichotomous observations, single pair of treatments, 2 hypotheses, 1 loss function, 2 statistical monitoring rules, 1 “overarching” maxim, 3 types of actions, and easy to compute numbers.

Suppose N individuals have HIV. There are 2 treatments: standard T₁ and experimental T₂. To find out which of the 2 treatments is more effective, an RCT is conducted on 2n of the total N patients, with n patients assigned to each treatment. If the trial ends, the remaining N– 2n patients receive the treatment selected as the more effective, unless no treatment is declared superior, in which case the remaining patients are treated with standard treatment T₁.

We restrict to statistical monitoring rules that permit termination after n/2 (half the number of participants assigned to each treatment group) have been treated. That is, the RCT has a single interim analysis halfway through the trial. Keeping calculations relatively simple, N = 100, and of these, we assume the monitoring of 10 + 10 patients (n = 10) so that 5 patients assigned to each treatment are treated by the interim analysis, and 10 patients assigned to each treatment are treated by final analysis.

Observation Model

For each treatment, a single outcome is observed: whether or not the patient recovers. The probability of recovery with T_i is θ_i (i = 1, 2) (assumed constant from patient to patient). y₁ and y₂ denote the number of recoveries among the n patients using T₁ and T₂, respectively. The observations are modeled as to follow a binomial distribution:

$$f(y_i|{\text{θ}}_i)=\left(\begin{array}{c}\hfill n\hfill \\ \multicolumn{1}{c}{y_i}\end{array}\right){\theta }_i^{y_i}{(1-{\theta }_i)}^{n-y_i}(i=1,2).$$

Since the difference between T₁ and T₂ is of interest, let θ stand for the difference in response rates between T₁ and T₂ so that θ = θ₂–θ₁. Thus, the joint distribution of y₁ and y₂ given θ₁ and θ₂ is

$$f(y|\text{θ})=\underset{i=1}{\overset{2}{\Pi }}\left(\begin{array}{c}\hfill n\hfill \\ \multicolumn{1}{c}{y_i}\end{array}\right){\theta }_i^{y_i}{(1-{\theta }_i)}^{n-y_i}(i=1,2),$$

where y and θ denote (y₁, y₂) and (θ₁, θ₂), respectively; yϵY and θϵθ.

Parameter Space θ

The model assumes that the recovery rate of T₁ (θ₁) is 0.5 and that of T₂ (θ₂) is unknown. It assumes that θ takes 1 of 2 possible values:

• H₀: θ = 0 (T₂ is equal to T₁, i.e., θ₂ = θ₁ = 0.5), or

• H₁: θ = 0.2 (T₂ is more effective than T₁, i.e., θ₂ = 0.7).

Set A of Allowable Actions

At the interim analysis, the DSMB can act in 1 of 3 ways:

• a₁: Stop and declare that “T₂ is more effective than T₁,”

• a₂: Stop and declare that “T₂ is equal to T₁,” or

• “recommend a continuation of the trial.”

If DSMB continues the trial at interim, then at the end of the trial, it can act in 1 of 2 ways:

• a_1.f: Stop and declare that “T₂ is more effective than T₁,”

• a_2.f: Stop and declare that “T₂ is equal to T₁.”

At either the interim or the end of the trial, the choice of action among the alternatives is made on the basis of sample data y₁ and y₂. Specific sample data expressed by the pair (y₁, y₂) lead to the choice of action to be taken—a choice that depends ultimately on the decision monitoring rule. A decision monitoring rule is a function of sample data y leading into the set A of allowed actions {a₁, a₂, a_1.f, a_2.f}. It specifies how actions are chosen, given observation(s) y.

Decision Stopping Rule δ(y): Y→A

We first consider decision monitoring rule R₁. This rule is based on frequentist properties (Neyman-Pearson inference), where the focus is on controlling error probabilities. We use an instance of group sequential monitoring procedure, much like an O’Brien-Fleming stopping rule.²³ In this stopping rule, R₁ aims at controlling the overall type I error by having it be no more than 0.05 (approximately). For this, the DSMB considers rejecting H₀ (if H₀ is true) for values (y₂–y₁) ≥ 4^†††; otherwise, the DSMB does not reject H₀.

At interim (when n = 5):

• a₁: Reject H₀ (assume H₀ is false) for values (y₂–y₁) ≥ 4, i.e., for (y₂–y₁) = {4, 5}; stop and declare “T₂ is more effective than T₁”;

• a₂: Accept H₀ (assume H₀ is true) for values (y₂–y₁) ≤–4, i.e., for (y₂–y₁) = {–4, –5}; stop and declare “T₂ is equal to T₁.”

This means that for (y₂–y₁) = {–3, –2, –1, 0, 1, 2, 3}, the DSMB continues with the trial.

At the end of the trial (when n = 10):

• a_1.f: Reject H₀ (assume H₀ is true) for values (y₂–y₁) ≥ 4, i.e., for (y₂–y₁) = {4, 5, 6, 7, 8}; stop and declare “T₂ is more effective than T₁”; otherwise,

• a_2.f: Do not reject H₀ for (y₂–y₁) = {–8, –7, –6, –5, –4, –3, –2, –1, 0, 1, 2, 3}; declare “T₂ is equal to T₁.”

Figure 1 shows how R₁ works as a function of possible values (y₂–y₁), both at interim and at the end of the trial. Specifically, the figure plots the range of (y₂–y₁) values at the end of the trial—indicated by the x-axis, that is, final (treatment − control)—conditional on values (y₂–y₁) at interim—indicated by the y-axis, that is, interim (treatment − control). a₁ is represented by the set of black circles, a₂ is represented by the set of red squares, a₁._f is represented by the set of purple triangles, and a₂._f is represented by the set of white squares. Gray circles represent impossible values for (y₂–y₁). For example, coordinate (X = 6, Y = 0) is not an option, given that (y₂–y₁) = 0 at interim eliminates the possibility of (y₂–y₁) = 6 at the end of the trial.

Figure 1.

Decision rule R₁ as a function of possible values of (y₂–y₁), with (y₂–y₁) at the end of the trial plotted as a function of (y₂–y₁) at interim. Actions: a₁ (black circles), a₂ (red squares), a₁._f (purple triangles), and a₂._f (white squares).

For the alternative monitoring rule (i.e., R₂), we assume a simple Bayesian monitoring rule for comparison. R₂ requires the specification of prior information about θ expressed in terms of a prior probability mass function p(θ). For simplicity, we consider neither an optimistic nor a pessimistic set of priors but “flat”: p(θ = 0) = p(θ = 0.2) = 0.5. When using a Bayesian monitoring rule, the evidence provided by data y is contained in the likelihood ratio, which is multiplied by a factor (the ratio of prior probabilities) to produce the ratio of posterior probabilities. Therefore, when discriminating between H₀ and H₁ on the basis of y, R₂ chooses the hypothesis with the larger posterior probability. For instance, putting it in terms of rejecting H₀, R₂ can reject H₀ when the likelihood ratio is less than 1. If so, with flat priors, R₂ rejects H₀ as long as y₂≥ 6; otherwise, it does not reject H₀.

However, to make the 2 decision rules comparable despite their different statistical philosophies, we chose a cutoff point during the interim analysis—which is my point of contention—so that R₂ would be as close as possible to R₁ on this epistemic factor, while keeping with our choice of easy to compute numbers. Therefore, the sum of the probabilities, whose outcome’s likelihood ratio is more extreme than the 3:1 or 1:3 cutoff, brings us to 0.04, which is the closest the rule gets to the type I error (0.05) used by the DSMB with R₁, given our choice of n = 5 at interim. Figure 2 shows how Bayesian monitoring rule R₂ works as a function of possible values (y₂–y₁), both at interim and at the end of the trial. One relevant difference between Figure 1 and Figure 2 is that, because the evidence provided by data y is contained in the likelihood ratio—given that R₂ is a Bayesian monitoring rule—the probability values of the control group are irrelevant. They cancel out in the ratio because θ₁ = 0.5, regardless of whether H₀ is true or H₁ is true. Only θ₂ varies—namely, the treatment’s effect.

Figure 2.

Decision rule R₂ as a function of possible values of y₂, with y₂ at the end of the trial plotted as a function of y₂ at interim. Actions: a₁ (black circles), a₂ (red squares), a₁._f (purple triangles), and a₂._f (white squares).

$$\frac{p(H_0|y)}{p(H_1|y)}=\frac{p\left(H_0\right)p(y|H_0)}{p\left(H_1\right)p(y|H_1)}=\frac{p\left(H_0\right)p(y_1|H_0)p(y_2|H_0)}{p\left(H_1\right)p(y_1|H_1)p(y_2|H_1)}=\frac{p(y_2|H_0)}{p(y_2|H_1)}$$

when priors $p\left(H_0\right)=p\left(H_1\right)$.

Loss Function

This function is meant to capture ethical and epistemic values associated to possible outcomes of the trial. Following Heitjan and others²⁴ on loss functions, we start with the “ethical” loss function L_E(θ, a). L_E(θ, a) can be used to compare the 2 treatments by paying a penalty for each patient assigned the inferior treatment. One penalty point is assessed for each patient assigned the inferior treatment. One way to think of L_E(θ, a) is to approach it with respect to a particular patient. If H₀ is true, and if the patient is given T₁, the loss incurred with such treatment is 0 (since T₁ and T₂ are considered equivalent), but if the patient is given T₂ in this situation, then there is a cost, which we refer to as cc.^‡‡‡ The other possibility is that H₁ is true. In this case, if the patient is given the inferior treatment T₁, the loss is d (which we assume for now is 1 unit); if given T₂ (superior treatment), the loss is 0.^§§§Table 1 summarizes this situation.

Table 1.

Ethical Loss

	H0	H1
T1	0	d
T2	cc	0

Now we make L_E(θ, a) sensitive to the “effect size” |θ₂–θ₁|. By “effect size,” we mean the percentage difference of no progressions between treatments. Thus, assuming H₁ is true (θ = 0.2), for every n = 5 patients (every segment of interim analysis), the single loss unit is the loss expected (by association) from 1 fewer patient having a positive no progression. That is 0.2 of 5 patients, which equals 1; it is the result that DSMB members should have obtained (or could have expected) had they continued with the trial. Table 2 presents sample losses according to this version of L_E(θ, a), accounting for effect size, n, and N, for values of d = 1 and cc = 0.01.

Table 2.

Ethical Loss w/ Effect Size

Action	True State of Nature
	θ2–θ1 = 0	θ2–θ1 = 0.2
At interim (n = 5)
a1: choose T2	(N – n)cc = 0.95	(θ2–θ1)(nd+ (N– 2n)0) = 1
a2: choose T1	0	(θ2–θ1)(nd+ (N– 2n)d) = 19
At final (n = 10)
a1.f: choose T2	(N – n)cc = 0.9	(θ2–θ1)(nd+ (N– 2n)0) = 2
a2.f: choose T1	0	(θ2–θ1)(nd+ (N– 2n)d) = 18

“Overarching” Maxim

Average loss is obtained by averaging the loss function over all possible observations:

$$E_y[L(\theta ,\delta \left(y\right))|\theta ]=\sum _{y_iϵY}L(\theta ,\delta \left(y\right))f_y(y_i|\theta ).$$

If we have prior information about θ, which can be expressed in terms of a prior probability mass function p(θ), then the Bayes risk of decision rule δ(y) is the expectation of the average loss over possible values of θ:

$$r\left(\delta \left(y\right)\right)=\sum _{\theta ϵ\Theta }\sum _{yϵY}L(\theta ,\delta \left(y\right))f_y(y|\theta )p\left(\theta \right).$$

Simulation

Figure 3 plots, while varying effect sizes, the weighted losses^**** for stopping and continuing, according to R₁ and R₂ decision procedures, when H₁ is true. If one assumes that the DSMB principle for stopping its trial is based on whether stopping it had a lower expected loss than continuing it (where the expectation is with respect to the weighted losses of continuing in light of the fixed set of future actions—a_1.f or a_2.f), then, by averaging the weighted losses of a_1.f and a_2.f, one can compare the weighted losses of stopping v. continuing for a whole range of effect sizes. Notice that for every effect size in the range, the DSMB decision to stop at interim, according to R₁, has a lower expected loss than continuing. The decision to stop is therefore consistent under R₁ given the range of effect size under consideration. This, however, is not the case with alternative decision rule R₂. Given the choice of ethical loss function and assuming that the principle to stop the trial following R₂ is also based on whether stopping the trial had a lower expected loss than continuing it, the only effect size that can warrant a decision to continue is a high expected treatment size (i.e., θ₂ = 0.9). Otherwise, the trial should stop if following R₂ since stopping at interim had a lower expected loss than continuing.

Figure 3.

Weighed losses of stopping (action a₁) and continuing (averaging actions a_1.f and a_2.f) for stopping rules R₁ and R₂, when H₁ is true.

If we focus our attention on the decision to continue the trial (R₁ continuing v. R₂ continuing), for the range of effect sizes, assuming an equal set of priors for every pair of hypotheses (i.e., each pair, H₀ v. H₁, having a different effect size for each H₁), R₁ is outperformed by R₂ with respect to the weighted losses except when the effect size is small, θ₂ = 0.6. This is shown in the upper part of Figure 3. With respect to the weighted losses, R₁ is therefore “less” ethical (has greater weighted losses) than R₂ when the effect sizes are not small, that is, for values θ₂ = {0.7, 0.8, 0.9}. This difference, however, may be of no surprise given the fact that R₂ is a Bayesian monitoring rule. A different set of priors would produce different weighted losses. This result is corroborated by a subsequent Bayes risk comparison.

Comparing R₁ against R₂ with respect to the Bayes risk, we see that the R₁ rule is “less” ethical (has a greater Bayes risk) than R₂’s when the effect sizes are not small, that is, for values θ₂ = {0.7, 0.8, 0.9}. That is, for all effect sizes, except when θ₂ = 0.6, the Bayes risk for R₂’s rule is smaller than the R₁ rule.

Table 3.

Scientific Loss

	H0	H1
T1	0	10
T2	10	0

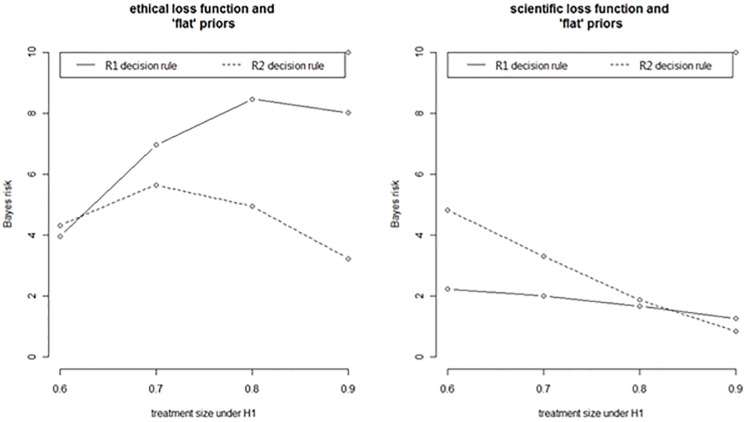
If, however, holding everything else fixed, we vary instead the loss function, we notice how the situation can be reversed. That is, if we shift from the “ethical” to a “scientific” loss function,^†††† the results are reversed. The comparison between the R₁ and R₂ rules is illustrated by the graphs in Figure 4. In the graph on the right, the R₁ monitoring rule outperforms the R₂’s rule with respect to the Bayes risk in all effect sizes, except when effect is large, θ₂ = 0.9. With respect to this function and using Bayes risk as a comparative rationale for adopting a monitoring policy, the R₁ rule is therefore overall “more” ethical then R₂’s except when the effect is large (i.e., θ₂ = 0.9).

Figure 4.

Stopping rule R₁ v. stopping rule R₂ compared with respect to Bayes risk and different loss functions (ethical loss v. scientific loss).

Conclusion

The proposed framework for reconstructing interim decisions, although limited, systematizes reconstructions (in a plausible fashion), making implicit assumptions for interim decision explicit. The fact that the results of RCTs are often provided without public justifications for their interim decision is an important indictment of DSMBs’ early stopping decisions.^23,25,26 If the proposed framework succeeds in providing the means to plausible reconstructions, then justifications for competing decisions exist. Without justifications, the generalizability of DSMBs’ decisions and the subsequent analysis of their decisions are problematic. By providing a common framework that structures justifications in individual cases, one does indeed have the beginnings of a general model for interim decision making.

In pressing a systematic form of justification to which trialists either explicitly or implicitly subscribe, we, decision analysts, may have the means to regard whether a particular interim decision is either permissible or not, according to a given representation of the decision. Because it is not surprising that people often disagree on what is of greatest value or harm for them and for others, it is reasonable to seek an account of interim decisions that saves disagreements, without having to necessarily solve them once and for all. Moreover, when specifying a rationale for an early stopping decision, in a particular context, although different contexts may allow for comparisons between different interim decisions, judgments of superiority cannot be justified as always universally optimal—thus the need for a notion of weak optimality, as we have provided here, where one decision looks optimal in one representation—one set of dimensions—but not necessarily so on another.

Once the point about the balancing of epistemic and ethical factors has been appreciated, the following step is to consider what an early stopping principle of an RCT might look like. If principles of early stopping are to help guide DSMBs’ behavior, these principles must be represented, and they must be capable of being communicated and taught so that they can serve as a public rationale for evaluating early stopping decisions. Any scientific (or ethical) approach whose principles of inference imply that it is not permissible to teach permissible interim decisions, or early stopping principles, violates this publicity standard—that is, it does not meet the public rationale for the early stopping of RCTs. In this fashion, it seems reasonable to say that in contrast to the 2 standard approaches to interim decision (either solely statistical or ethical), the proposed framework seems capable of meeting this publicity standard.