A competitive trade-off limits the selective advantage of increased antibiotic production

Abstract

In structured environments, antibiotic producing microorganisms can gain a selective advantage by inhibiting nearby competing species¹. However, despite their genetic potential^2,3, natural isolates often make only small amounts of antibiotics, and laboratory evolution can lead to loss rather than enhancement of antibiotic production⁴. Here we show that, due to competition with antibiotic resistant cheater cells, increased levels of antibiotic production can actually decrease the selective advantage to producers. Competing fluorescently-labeled Escherichia coli colicin producers with non-producing resistant and sensitive strains on solid media, we found that while producer colonies can greatly benefit from the inhibition of nearby sensitive colonies, this benefit is shared with resistant colonies growing in their vicinity. A simple model, which accounts for such local competitive and inhibitory interactions, suggests that the advantage of producers varies non-monotonically with the amount of production. Indeed, experimentally varying the amount of production shows a peak in selection for producers, reflecting a trade-off between benefit gained by inhibiting sensitive competitors and loss due to an increased contribution to resistant cheater colonies. These results help explain the low level of antibiotic production observed for natural species, and can help direct laboratory evolution experiments selecting for increased or novel production of antibiotics.

Natural microbial isolates, in particular those from soil environments, are known for their potential ability to synthesize a range of antibiotics^5,6. In these dense ecosystems, where antibiotic producers, resistant and sensitive species coexist^7,8,9,10, the ability to inhibit nearby species can give a producer a competitive advantage. Often, however, natural producers are not maximizing their production potential: metabolic engineering of natural species can increase production of antibiotics several-fold without significant reduction in growth^11,12. It is possible that high production levels are still costly in nature, or that antibiotics are produced at small amounts not for inhibition of competitors but because they instead function as signaling molecules at subinhibitory concentrations^{13,14,15,16,17}. Alternatively, it is possible that the low production level of antibiotics does stem directly from their inhibitory role: in complex ecosystems high toxicity against competitors, even at no cost, may not be the most advantageous strategy. It remains unclear whether there are indeed inherent limits on the optimal level of antibiotic production when focusing only on their toxic activity against competing species.

The inhibitory effect of antibiotic production can only be selected for in spatially structured environments. Well-mixed environments present two obstacles to the evolution of antibiotic producers. First, microbially-produced antibiotics can be too dilute to inhibit competitor species and thus producers can only gain when they are already above a critical abundance, leading to density-dependent selection^{18,19,20,21,22}. Second, regardless of their abundance, when producers simultaneously compete not only with antibiotic-sensitive but also with resistant strains, the resistant strain can out-compete the producers²³. These resistant non-producers receive the same benefit of decreased competition without incurring any costs of antibiotic production and can thus be thought of as ‘cheaters’^20,24 (similar to cheaters in other public good systems^19,25). Spatially structured environments, in contrast, circumvent the problem of dilution by concentrating antibiotics around producer colonies, allowing producers even at low abundance to kill sensitive competitors in their immediate vicinity¹. Spatial structure can also limit the success of resistant cheaters by restricting the selective advantage of inhibiting competitors to the locality of producers^23,26. However, even in spatial environments, evolution does not consistently lead to enhancement of antibiotic production^4,27. Here, combining experiments and modeling of competition in spatial environments, we mapped the conditions allowing selection for antibiotic production and asked how the amount of antibiotic produced affects the selective advantage it confers.

To measure selection for antibiotic production, we used a colicin-based three-strain system in which producer and cheater strains compete in the presence of a sensitive strain^1,23,26. Colicins are plasmid-encoded, toxic proteins produced by E. coli that specifically target other E. coli²⁸. The three strains we used share the same genetic background and consist of colicin producers, colicin-resistant “cheaters”, and colicin-sensitive competitors²³. Producers carry the ColE2 plasmid, which encodes a gene for the colicin E2 toxin, a DNA endonuclease that is co-transcribed with immunity and lysis factors²⁹. The colicin operon is repressed by LexA³⁰, allowing its expression to be tuned by inducing DNA damage (Figure 1a; we use mitomycin C). When released, colicin can enter and kill the sensitive strain, but not the resistant strain (Fig. 1b). We differentially labeled each of these three strains with plasmid-encoded fluorescent proteins – CFP, YFP, or mCherry. Plating the strains on agar and imaging in the three fluorescence channels allowed the abundance of each strain to be quantified (total fluorescence of colonies in the appropriate channel, see Supplementary Fig. S1). We defined selection for antibiotic production η as the final ratio of producers to cheaters normalized by their seeding ratio (set to 1).

Figure 1. Colicin producers inhibit sensitive competitors in their vicinity, promoting their own growth as well as that of nearby resistant, non-producing cheaters.

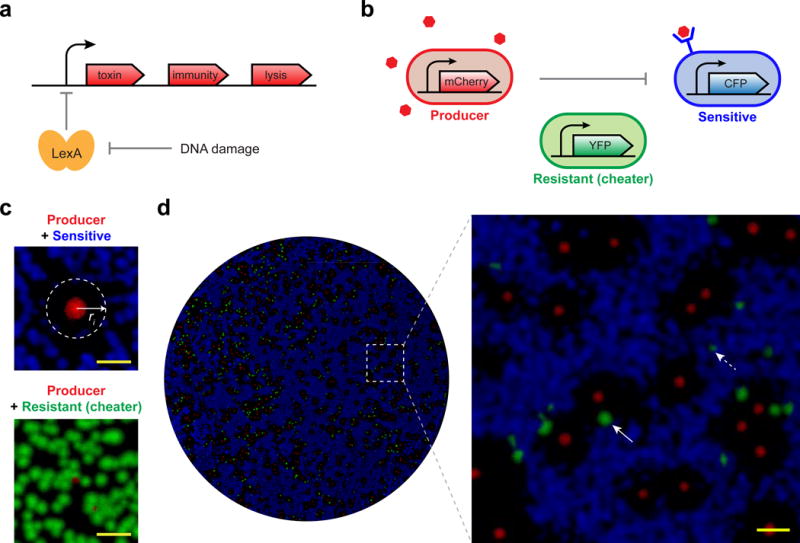
a, The colicin E2 operon contains toxin, immunity, and lysis genes under an SOS promoter induced by DNA damage. b, Producer strain releases colicin (red hexagons) which kills a sensitive strain, but is ineffective against a resistant strain. Strains are differentially labeled with fluoresceist reporters. c, Two-strain co-culture on solid media (containing 16 ng/mL mitomycin C) shows representative producer colonies (red) inhibiting growth of nearby sensitive (blue), but not resistant (green), colonies (scale bars = 1 mm). Sensitive colonies do not grow within the inhibition radius r_i. d, Co-culture of all three strains together, showing the resistant strain can act as a production cheater. Left, growth across entire surface of representative plate; right, zoomed image of 1 cm² box region (scale bar = 1 mm). Resistant colonies are small when competing with the sensitive strain (dash arrow) but they gain in size when growing in the vicinity of producer colonies (solid arrow).

Competing the three strains on solid media showed that producers benefit from the inhibition of nearby sensitive colonies while also allowing cheater colonies in the vicinity to gain from this inhibition. Starting with pair-wise competition, we found that producer colonies make zones of inhibition and grow larger when competing against sensitive versus resistant competitors (Fig. 1c)^1,4. When all three strains were grown together, we observed cheater colonies growing both outside and inside these inhibition zones with the colonies inside growing larger than the colonies outside (Fig. 1d). Proximity to a producer colony thus conferred a gain to these cheater colonies. We therefore asked how the densities of the competing strains affect the outcome of the competition between producers and cheaters.

Varying the seeding densities of the producers and sensitive strains we found that selection for production requires both high density of sensitive competitors and low density of producers (η, Fig. 2a). Selection for production increased with increasing sensitive competitor density (p=2.5×10⁻²¹ and t(61)=15, linear regression), consistent with the benefit of production stemming from the inhibition of sensitive species. Indeed, in separate two-strain competition experiments, we found that the difference in growth of producers when competing against sensitive versus resistant strains appears only above a critical density of these competitors (Fig. 2b, p <.01 at densities above 100 CFU/cm², two-sample t-test), where there is a significant chance of competitors falling within an inhibition zone (critical density ~ 1/πr_i², where r_i = 0.86 mm, Fig. 1c). This difference widens at high competitor density: the growth of producers declined inversely with the density of resistant competitors (indicating a purely competitive interaction between these strains), but plateaued at high sensitive competitor density. The zone of inhibition therefore insures that a fixed amount of resources is available to producer colonies despite increased sensitive competitor density.

Figure 2. Producers have an advantage over resistant cheaters only at high densities of sensitive competitors and low densities of producers.

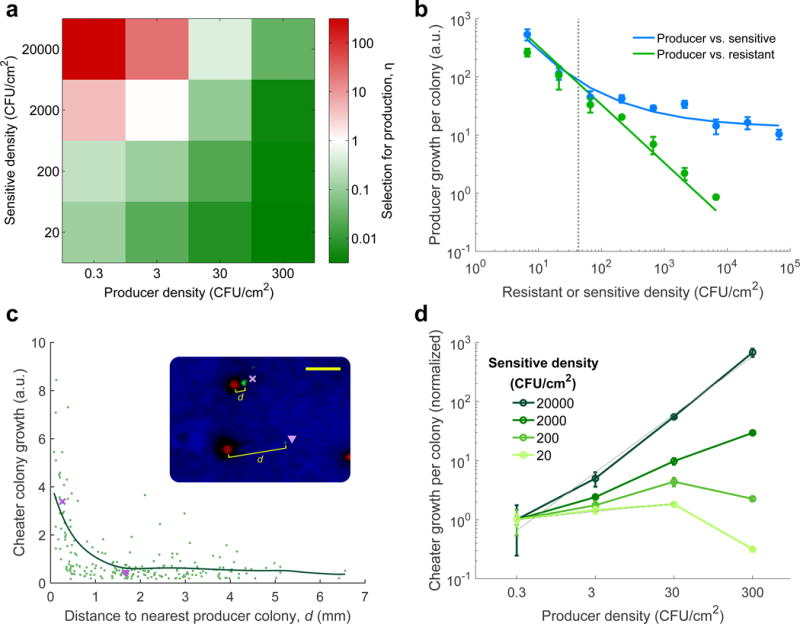
a, Selection for production relative to the non-producing resistant cheater in three-way competitions on agar for varying seeding densities of sensitive and producer cells (producer density [P] = cheater density [C], mean of 4 replicates). b, Mean growth of producer colonies (arbitrary units) in pairwise co-culture with sensitive competitors (blue) versus resistant (green, line showing reciprocal fit, slope=−1). Gain from killing, measured as the difference between the two lines (arrows), appears and further increases as the seeding density of competitors increases beyond a critical density equal to 1/πr_i² (dotted line). Error bars show s.d. of 3 replicate plates, [P]=0.7 CFU/cm². c, The growth of individual cheater colonies (arbitrary units, green dots) decreases with their distance to producer colonies (d is distance to the nearest producer colony; sensitive density [S]=20,000 CFU/cm², [P]=[C]=3 CFU/cm²; pooled data from 4 replicates; line shows smoothened average by local linear regression. Inset: example of two representative cheater colonies indicated by × and ▽ (scale bar = 1 mm). d, Mean cheater growth increases linearly with producers at high sensitive density (solid gray line shows fit, slope = 0.98 ± 0.09 at 95% c.i.), but is not helped by producers at low sensitive density (dashed gray line, slope = 0.13 ± 0.05 at 95% c.i.). Each series is normalized to the mean growth at the lowest producer density (n=4, error bars show s.d.).

While selection for production increased with the density of sensitive colonies, it decreased with the density of producers due to elevated cheating. The relative growth of producers over resistant non-producers (cheaters) in the three-way competition declined with increasing producer density (Fig. 2a, p=3.6×10⁻²⁴ and t(61)= −17, linear regression). At a high density of sensitive competitors, cheater colonies grow much better when they are near a producer (Fig. 2c). As the chance of a cheater to be seeded close to a producer increases linearly with the producer density, the average growth across all cheater colonies is proportional to the producer density (Fig. 2d, darkest line). This relationship stems from the producer inhibiting sensitive cells; when the density of sensitive competitors is low, cheater colony growth is not helped by producer density (Fig. 2d, lightest line). In sum, in a three-way competition, increasing producer density reduces selection for producers by increasing the chance that cheater colonies benefit from inhibition of sensitive competitors by nearby producers.

We developed a simple model to quantitatively understand how selection for producers varies with seeding density and the amount of antibiotic produced. Our model calculates the growth of producer, cheater, and sensitive colonies randomly seeded on a continuous two-dimensional space, interacting through inhibition and competition (Fig. 3a). Each producer colony is surrounded by a circular inhibition zone of radius r_i where sensitive colonies are killed^24,31. The remaining colonies compete for a single limiting resource evenly distributed across space: each colony can access this resource only within a given “grazing zone” of radius r_g around itself and the amount of resource that lies inside overlapping grazing zones is evenly shared. Each colony’s growth is proportional to its total captured resources. As in our experiments, we define selection for antibiotic production η as the ratio between the total growth of all producer colonies relative to that of cheater colonies, normalized by their initial ratio (set to 1).

Figure 3. A simple model of competition and inhibition predicts that selection for antibiotic production is maximized at intermediate production levels.

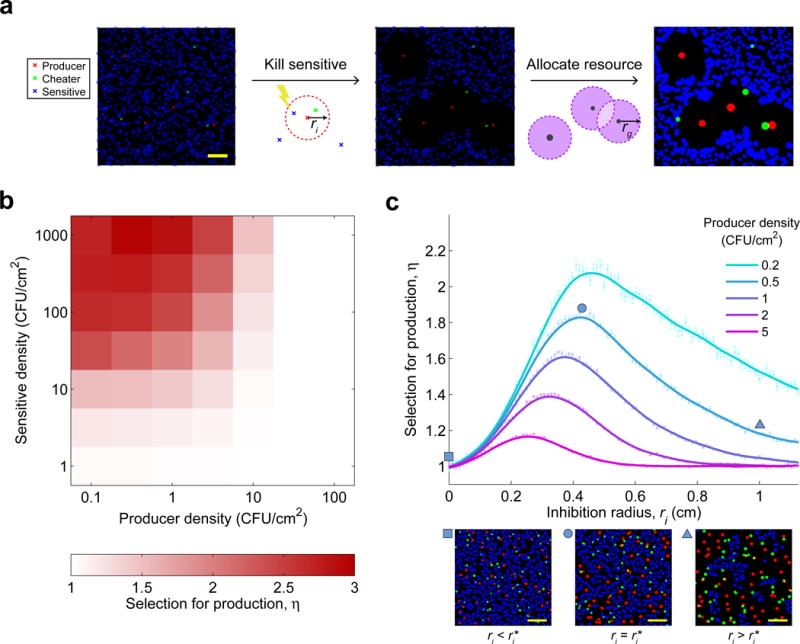
a, Steps in simulating model: (1) Random seeding of producers (red), sensitive (blue) and cheater (green) colonies at given densities (scale bar = 2 mm); (2) killing sensitive colonies inside inhibition zones of radius r_i around producer colonies; (3) final growth of each colony is determined by the amount of resource available to it in a grazing zone of radius r_g around it. Resources in overlapping grazing zones of two or more colonies are equally shared among them. b, Selection for production increases monotonically with the density of sensitive species and decreases with the density of producers (mean of 20 simulations per parameter set). c, Selection for production η is maximized at an intermediate level of production r_i^* (n=50 simulations per parameter set, error bars show s.e.m.). Panels show sample simulations at indicated points (scale bars = 2 cm). Parameter values are given in Supplementary Table 1; see Supplementary Fig. S9 for effects of adding cost to the model and Supplementary Fig. S10 for the effect of varying r_g.

The model predicted that an intermediate level of antibiotic production best optimizes its benefit. We ran simulations of the model, testing how the selective advantage of production depends on the seeded densities of sensitive and producer colonies, as well as on the level of production. In accordance with our experimental data (Fig. 2a), the model showed a monotonic increase in selection for production with the density of the competing sensitive strain and a monotonic decrease with producer density (Fig. 3b). However, when varying the radius of inhibition r_i, we observed a non-monotonic dependence: selection for producers peaked at an intermediate level of production (Figure 3c). A more realistic model accounting for the diffusion of antibiotics from each producer colony yielded similar selection peaks (Supplementary Fig. S2). Interestingly, the reduction in the selective advantage of increased production following the peak arose solely from the competitive interactions accounted for by the model without assuming any direct costs of production. Because selection for production in this model is driven by competitive interactions, the peak selection decreased in magnitude and shifted to lower production levels with increased producer density (Fig. 3c).

To test for the presence of optimal production level as predicted by the model, we performed competition experiments at varying levels of colicin expression. We tuned colicin expression by varying the concentration of mitomycin C (MMC) in the growth media at sub-inhibitory levels (Supplementary Fig. S3), thereby controlling the size of inhibition zones (Supplementary Fig. S4). We measured the relative growth of producers to cheaters in the presence of sensitive competitors under a range of colicin induction levels. Selection for production peaked at intermediate levels of colicin induction (Figure 4a, p=2.8×10⁻⁵ and t(13)= −6.3 at low producer density, see Methods; see Supplementary Fig. S5 for dye swap control). As in the model simulations, higher producer density (which benefits cheaters, Fig. 2c,d) led to a lower selection peak (p<.01 at MMC>0, two-sample t-test) and smaller optimal level of colicin induction.

Figure 4. The advantage of producers over cheaters is maximized at an intermediate level of antibiotic production.

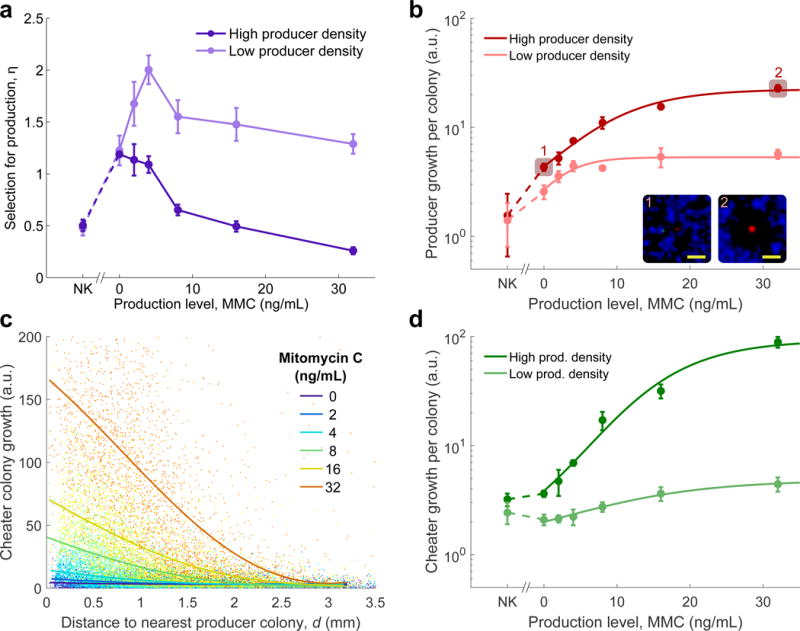
a, Selection for production in three-way competitions as a function of varying levels of colicin induction via mitomycin C ([S]=2,000 CFU/cm²; high density: [P]=[C]=20 CFU/cm², low density: [P]=[C]=2 CFU/cm²; mean of 4 replicate plates for each point, error bars show s.d.). Left-most points represent no-killing (NK) controls, where the sensitive competitor was replaced with resistant. Differences between these experiments and the simulation results (Fig. 3c) may be attributable to model parameters such as production cost (Supplementary Fig. S9), grazing zone radius (Supplementary Fig. S10), cooperative toxicity (Supplementary Fig. S2), or antibiotic diffusivity (Supplementary Fig. S11). b, Mean growth (arbitrary units) of producer colonies increases monotonically with production level (n=4, error bars show s.d.). Insets: representative colonies from highlighted data points. c, Growth (arbitrary units) of individual cheater colonies close to producer colonies increased with colicin induction (each series is pooled data from all replicates in the high [P] condition; solid lines are smoothened averages calculated by local linear regression). See Supplementary Fig. S12 for low [P] data. d, Mean growth (arbitrary units) of resistant colonies at low and high producer density for varying production levels (n=4, error bars show s.d.).

The decline in producer fitness at high colicin induction is not due to the cost of production, but rather the increased benefit gained by cheaters. Because inducing the colicin operon causes cell lysis, production can incur a fitness cost (Supplementary Fig. S3). However, the growth per producer colony increases monotonically over the range of mitomycin C concentration where the peak is observed (Fig. 4b, p<10⁻⁴ and t(18)>5.8, linear regressions), demonstrating that the benefit of production was always higher than its direct cost, both in the presence and absence of cheaters (Supplementary Fig. S6). On the other hand, increasing colicin production also increased the growth of cheater colonies taking advantage of nearby producers (Figure 4c), consistent with larger inhibition zones both increasing the probability of a resistant colony landing inside a zone, and freeing up more nutrients to these cheater colonies. This benefit gained by individual cheater colonies thereby increased the overall cheater growth as a function of colicin induction (Fig. 4d, p<10⁻⁷ and t(18)>9.0, linear regressions). Thus, increased toxin production simultaneously decreases competition from sensitive cells and increases competition from resistant cheaters, leading to a competitive trade-off that sets the optimal level of toxin production.

The selective advantage of antibiotic production depends on the ability of producers to out-compete resistant cheaters. We have found that selection for antibiotic production requires restricted conditions consisting of a high density of competitors but a low density of producers to limit cheating. At any given density, there is an intermediate level of antibiotic production that maximizes producer selection, balancing a trade-off between inhibiting sensitive competitors while limiting the advantage of inevitably appearing cheaters. Considering this trade-off helps to understand the limited quantities of antibiotics produced in nature³², and may explain the prevalence of high molecular weight natural antibiotics (such as colicin) and contact-dependent killing mechanisms³³, which act in shorter ranges and are thus less vulnerable to cheaters. Beyond the ecological implications, this study also provides a framework for designing improved selection schemes for antibiotic drug discovery.

Methods

Strains and media

The original producer, resistant, and sensitive strains derived from BZB1011 are from a previously published study²⁶. Plasmids expressing CFP, YFP, or mCherry under the P_R promoter³⁴ were constructed from the pZ vector system³⁵ and transformed into the base strains.

Cells were cultured on M9 minimal media supplemented with 0.4% glucose and 50 mg/mL kanamycin. Agar plates (1.3% Difco agar) were made in the same media supplemented with mitomycin C (5 ng/mL, unless otherwise indicated). Mitomycin C (VWR) stock solution (1 mg/mL DMSO) was stored at −20°C in 100 μL aliquots for no more than one month; fresh aliquots were thawed for each experiment. Plates were stored in the dark overnight and dried in a sterile hood for 10 minutes before adding cells.

Competition experiments on agar plates

Overnight cultures of individual strains were diluted 1:100 and grown to OD₆₀₀=0.1–0.7. Cultures were mixed at specified ratios, immediately added to plates (100 μL/plate) and spread using glass beads. For experiments measuring selection for antibiotic production, the initial producer to cheater ratio was set to 1. Plates were incubated for 7 days at 37°C (varying density experiments) or at 27°C (varying mitomycin C experiments) in order to limit colicin expression at low mitomycin C induction (Supplementary Fig. S7).

Image processing

1. Image acquisition

Images in bright-field and fluorescence channels were acquired in raw format (CR2) using a Canon EOS T3i digital SLR mounted on a custom scaffold³⁶. Each plate was imaged twice, with the plate rotated approximately 180 degrees between imaging. Consistent exposures were used for each experiment. Dark (no illumination) and bright (uniform fluorescent bacterial lawns) images were acquired for background correction.

2. Basic processing

DCRAW³⁷ was used to convert images from CR2 format to 16-bit TIFFs. We developed a semi-automated MATLAB processing pipeline to extract colony information from the TIFF images. Hot pixels were removed by averaging nearest neighbor pixel values. MATLAB’s built-in demosaic function (gradient-corrected linear interpolation) was used to convert the Bayer pattern encoded images to RGB format. Values below dark and above saturation for each channel were trimmed to enable visualization.

3. Normalization

Background values were subtracted from each image channel based on the dark image controls for each exposure. Flat-field frames for each fluorescence channel were obtained by averaging and smoothing the corresponding bright images (8 images per channel, 2D Wiener filter with 144 pixel window). Illumination correction was performed by dividing each image channel by the flat-field frame. This flat-field correction also served to normalize the intensities of each channel with respect to one another.

4. Segmentation

Global thresholds for each channel were manually selected to segment images into bright (colonies) and dark (no colonies) regions. Areas within 0.5 cm of plate edges were masked. Contiguous bright regions with area greater than 2 pixels were identified as putative colonies. We tabulated the centroid, area, and total intensity of each such object.

5. Colony recognition

Segmented objects consisted of real colonies as well as artifacts caused by light reflections. To remove these artifacts, we aligned the two rotated images of each plate and discarded segmented objects only present in one of the two images and with area less than 65 pixels (0.05 mm²). Alignment in each channel was first performed automatically, by minimizing nearest-neighbor distances between centroids of objects in the two images across three rigid transformation parameters (translation in two dimensions and angle of rotation). Manual setting of alignment parameters was used only when automated alignment failed in all channels.

6. Calculating selection for production

Growth of each colony was calculated as the total intensity minus the mean intensity of the segmented background multiplied by the colony area. Selection for production η was defined as the relative growth of producers to cheaters, normalized to the initial ratio. For the variable-density experiments, we calculated growth of each strain as the summed growth of identified colonies divided by the mean seeding density, since colonies were impossible to separate at high seeding densities. For the colicin induction experiments, we calculated growth of each strain as the mean growth per colony, which yields a more precise value when the number of plated colonies is variable due to low-number fluctuations. Applying the summed-growth analysis to the Fig. 4 data yielded similar, but noisier, results (Supplementary Fig. S8).

Comparison of colony growth measurements

Each strain was individually spread at ~10 CFU/plate on media without MMC and grown for 2–6 days at 37°C. On each day, plates were imaged and 2 colonies of each strain were removed using a 5 mm biopsy punch. The colony-bearing agar cores were each vortexed in 1 mL PBS to suspend cells. Cell suspension was serially diluted to ~100 CFU/mL, then 1 mL of diluted suspension was added to the surface of an agar plate and allowed to dry without spreading. CFU were counted after overnight incubation at 37°C and used to back-calculate total growth of the original colony. Colony growth based on fluorescence intensity was measured using the image processing pipeline described above.

Liquid-culture growth measurements

Overnight cultures were diluted 1:2×10⁴ and grown in 200 μL cultures in a 96-well plate (Corning 3370) for 42 hours at 27°C with shaking. Growth yield was measured using a VICTOR3 plate reader (Perkin Elmer).

Solid-media growth curves

Each strain was individually spread at ~10 CFU/plate on media containing 0–32 ng/mL MMC (4 plates per condition) and incubated at 27°C. Plates were imaged every day; colonies appeared on day 2. Colony growth was measured using the image processing pipeline described above.

Measurement of inhibition zones

Producer colonies were identified as described above. For each plate image, mean fluorescence intensity in the sensitive (CFP) channel (after illumination correction and normalization) was measured for locations r pixels from producer colony centers, varying r from 1–40 pixels. Inhibition zone size was defined as the distance at which sensitive intensity reached half-maximum value (0.14), using linear interpolation between bracketing measurements and setting intensity at r=0 to the minimum value (0.065).

No-cheater competition

Because illumination artifacts in the red channel are difficult to correct without confirming image alignments in the green channel, we used YFP-marked producers in experiments without cheaters. Control experiments with the addition of mCherry-marked cheaters were run in parallel with the no-cheater competitions; experiments were performed as described above.

Simulations

Simulations of the model were implemented in MATLAB. Colonies were seeded in a square environment of area A by sampling location coordinates from a uniform random distribution. Sensitive colonies within r_i of any producer colony were removed. Resource allocation was determined by partitioning the environment into square grid-cells with side length dx. For each grid-cell, resources equal to the area of the grid-cell were partitioned equally among all colonies within r_g of the grid-cell. For visualization of colony growth, colony areas were set to the total resources obtained by each colony, scaled by a constant k. The full parameter set and values for the simulations in Fig. 3 are shown in Supplementary Table S1.

Statistical analysis

Linear regressions were fit to the data in Figures 2a, 2d, 4b, and 4d, testing against a null hypothesis of slope = 0 (t-statistics). In Figures 4b and 4d, we took the log of the x-axis and only used data for MMC>0. A quadratic model was fit to the low producer density data in Figure 4a for MMC = 0–8 ng/mL, testing significance of the squared term coefficient (t-statistic). Two-sample t-tests were performed on the data in Figures 2b and 4a to compare the effects of competitor resistance or producer density, respectively.

Cooperative inhibition simulations

Producer colonies were treated as equivalent instantaneous point sources of antibiotics. Solving the two-dimensional diffusion equation at a time t results in a sum of Gaussian distributions of antibiotic concentration centered on each producer colony:

$$a(x,y)={\displaystyle \sum _{k=1}^P\frac{c}{2\pi {\sigma }^2}\exp (\frac{-{r_k}^2}{2{\sigma }^2})}$$

where r_k is the distance to the k^th producer colony (r_k² = (x−x_k)² + (y−y_k)²), c is the amount of antibiotic production, and σ²=2Dt (where D is the diffusion constant). Sensitive strain colonies were removed where the antibiotic concentration exceeded a threshold concentration MIC.

Code availability

Code for running the image processing pipeline and the model simulations are available upon request.