Critical review on the mechanisms of maturation stress generation in trees

Abstract

Trees control their posture by generating asymmetric mechanical stress around the periphery of the trunk or branches. This stress is produced in wood during the maturation of the cell wall. When the need for reaction is high, it is accompanied by strong changes in cell organization and composition called reaction wood, namely compression wood in gymnosperms and tension wood in angiosperms. The process by which stress is generated in the cell wall during its formation is not yet known, and various hypothetical mechanisms have been proposed in the literature. Here we aim at discriminating between these models. First, we summarize current knowledge about reaction wood structure, state and behaviour relevant to the understanding of maturation stress generation. Then, the mechanisms proposed in the literature are listed and discussed in order to identify which can be rejected based on their inconsistency with current knowledge at the frontier between plant science and mechanical engineering.

1. Introduction

1.1. Wood: the tree muscles

1.1.1. Wood is a multifunctional tissue

Wood takes on several functions in the living tree, including hydraulic, mechanical and other physiological functions such as storage, repair and defence. However, most of investment in biomass is allocated to fibres, the function of which is mechanical. The most studied mechanical functions are support of self-weight and resistance to wind, studied using classical engineering concepts such as beam theory, elastic stability and wood rupture. These ‘skeletal’ functions [1] are well known and documented.

1.1.2. A motor function is necessary for trees to grow in height

Trees are growing organisms, so classical mechanical theories are not sufficient to explain their biomechanical behaviour. A ‘motor’ system, similar to muscles for animals, is also necessary for trees. The most striking functions of this motor system are the ability to recover from mechanical disturbance, e.g. gravitropic uprighting [2,3], or achieve adaptive reorientations, e.g. phototropic movement [4]. Just like in humans, an active motor system is necessary not only to achieve movements but also to control posture and preserve shape in a standing position [1]. For trees, this means the motor system is necessary for stems and branches to grow vertically or at a constant angle [5]. Because the vertical position is challenging gravity, increase in tree weight during growth disturbs the mechanical equilibrium of the tree, bending stems and branches downwards. These downward movements accumulate over time and cannot be corrected by increasing the stiffness or diameter of branches, or by a change in direction of apical extension. An active process is, therefore, needed to control the orientation of tree stems and branches.

1.1.3. Wood maturation provides the motor power

The motor system, necessary to correct tree posture, is provided by wood during its formation. During the development of a wood fibre, its mechanical function switches from a motor function (during the maturation of the cell wall) to a skeletal function (when the cell is dead and has reached its final stiffness). Wood maturation, occurring with the thickening of the cell wall, generates mechanical stresses at the tree periphery, mostly oriented along the stem axis, and thus called longitudinal maturation stress (the term ‘maturation stress’, when the direction is not specified, will hereafter implicitly refer to the longitudinal component of maturation stress). Pre-tension in the stem periphery is beneficial for its strength, since wood is weaker in compression than in tension [6]. The asymmetric distribution of this stress around the stem circumference [7], with higher magnitude on one side of the stem, generates a bending moment, which enables reorientations or compensates for increasing self-weight [5]. Other features, such as eccentric growth and stiffness heterogeneity, only contribute to optimize this process [3].

Mechanisms underlying maturation stress generation are not yet known, while their equivalents are well described for animals (actin–myosin system) and herbaceous plants (changes in turgor pressure). Different hypothetical mechanisms have been proposed in the literature based on observations of wood structure and chemistry, together with mechanical considerations. Recently, this question has been studied through more and more interdisciplinary approaches, using tools of molecular biology [8–10], physics [11,12], physico-chemistry [13,14], biochemistry and immunocytochemistry [15,16], leading to a considerable number of studies and proposed mechanisms. Recent reviews on this issue have gathered knowledge about chemistry [17,18] and the macroscopic action of maturation stress [19] while proposing some hypothetical mechanisms. For an in-depth historical view of the issue of maturation stress, the reader may refer to Kubler [20].

This paper aims at reviewing experimental facts and mechanical consideration relevant to the mechanism underlying maturation stress generation, describe all mechanisms proposed in the literature and try to discriminate between these models, to finally propose candidate mechanisms that appear compatible with all current knowledge.

1.2. Maturation stress is measured through released strains

1.2.1. Evidencing and measuring wood maturation stress

Wood maturation stress can easily be evidenced and measured experimentally. The usual method is stress release: when a stressed piece of material is isolated from the surrounding tissues, it deforms, and this deformation can be measured for example using strain gauges [21–25], linear variable differential transducers [26,27] or other methods [3,28–31]. The result of releasing the stress at the tree periphery is a contraction if the stress is tensile, and an extension if the stress is compressive. The occurrence of such a stress at the periphery of a growing tree is an evidence that it originates in wood maturation, rather than in a passive response to bending loads. For a beam-like object such as a pole, increase in bending load generates maximal stress at the periphery of the pole with tensile stress on the upper side and compressive stress on the lower side. Contrary to a passive pole, in the case of a growing stem the deposition of new wood layers, in the absence of actively generated stresses, would result in an unstressed state at the tree periphery.

1.2.2. Definitions and terminology

There is some confusion in the literature regarding the terminology of maturation stress. The following terms are often used synonymously: maturation stress, maturation strains, released strains, growth stresses and growth strains. ‘Maturation strains’ is a confusing term because wood strains are mostly impeded by the surrounding tissues during the maturation of a wood layer, so that only a little part of maturation stress is released in the tree as strains. This term actually implicitly refers to strains released during evaluation of maturation stress. Growth stress has a distinct meaning: strictly speaking, it refers to all stresses accumulated during growth and their distribution inside the trunk, including support stress and redistribution of maturation stress [20,32]. Growth strains refer to the consequences of growth stresses when the trunk is cut (cracks in log, twist of planks, etc.). Therefore, we advocate using ‘maturation stress’ and ‘released strains’ to describe, respectively, the state of wood inside the tree and its experimental measure.

1.3. Different forms of mechanically active woods

All kinds of wood generate longitudinal maturation stresses (hereafter abbreviated as LMS) although the sign and magnitude of the stress are variable. Reaction woods have the largest magnitude of LMS. Two general categories of reaction woods are distinguished: compression wood (CW) and tension wood (TW). These terms are related to the sign of LMS, compressive for CW, and tensile for TW. ‘Normal’ wood (NW), found in upright stems and on the lateral sides of tilted stem, has a slight tensile stress. ‘Opposite wood’ found on the opposite side of TW has very low tensile stress values, and sometimes slight compressive stress [22]. Opposite wood of CW has tensile stress values similar or slightly larger than NW.

The CW is typically found in gymnosperm species, although it has been also observed in angiosperms such as Buxus [33–35] and some primitive angiosperm species [36,37]. Within species, there is a gradient in CW severity, from light CW generating weak compression to severe CW with larger compression. TW is typically found in angiosperm species, although it has also been found in Gnetales [38], a taxon more related to gymnosperms than angiosperms. Different forms of TW exist. Typical TW has a special cell wall layer, called ‘gelatinous layer’ (G-layer) [39]. Fibres containing this layer are called G-fibres. Other types of TW have been identified, the most frequent of which was previously called ‘tension wood without G-layer’ [26,39,40], which is actually formed of a G-layer which was later lignified [41]. Multi-layered TW, formed of alternating G-layers and S3-layer, has been observed in some botanical families [26,29,42]. In some angiosperm species, no G-layer (whether or not lignified) has yet been identified [43], but it is reasonable to speculate that tissues able to generate stresses amounting to several MPa exist in these species, to ensure their motor function. G-fibres also occur in other mechanically active organs, e.g. roots [44,45], aerial roots [46], tendrils [47,48] and in other plants than trees. In particular, they occur in the phloem of some trees [49] and some herbaceous plants. A lot of studies on G-layers have been performed on flax [17,18,50].

This paper will often focus on mechanisms of stress generation in G-fibres, irrespective of the occurrence of late lignification. G-fibres are taken as model for several reasons: (i) there is currently a consensus on the mechanism generating compression stress in CW, based on the action of matrix swelling and microfibril orientation, (ii) G-fibre is the most abundant among TW types, (iii) this form is the TW type of poplar, which has become a model plant in tree studies, and (iv) when unlignified, G-layers are very easy to identify and can be isolated from the surrounding wall layers [10,51–53].

2. Structure and mechanical properties of reaction woods

2.1. Anatomy and ultrastructure of reaction woods

Reaction woods were considered by wood anatomists long before their mechanical role was elucidated, because of their particular structure. Severe CW typically has rounded cells with intercellular spaces, sometimes helical cavities in the lumen, a thick S2-layer with a large microfibril angle [54]. TW has microfibrils almost parallel to the cell axis [55–58]. Cell walls with a G-layer appear generally thicker than normal wood cell walls when observed in microscopy. It was shown to partially originate in an artefact related to the lateral swelling of the G-layer near its cut surface [59], but remains true even when the border artefact is avoided [23,60]. TW usually lacks an S3 layer [61].

TW cellulose has long been reported to be more crystalline than normal wood [51], meaning that the ratio of amorphous cellulose to crystalline cellulose is lower than in normal wood. The width of cellulose crystallites was reported up to two times larger than that of normal wood cellulose [56,62,63].

Cellulose in wood occurs in the form of aggregates (sometimes termed ‘bundles’ or ‘macrofibrils’). The size of these aggregates varies between NW and TW, although conflicting results have been obtained on this issue: TW aggregates have been reported larger [64] or smaller [65] than NW aggregates. Recent views of cellulose organization in the cell wall involve local aggregation of microfibrils [66], so that cellulose forms a trellis structure, as was long observed using electron microscopy [67–69].

The matrix of the G-layer has a mesoporous structure, similar to hydrogels [14,70,71]. It has long been shown that wood can be treated as a gel [72]. The amount and size of pores are considerably larger in the G-layer than in other wood cell wall layers. Moreover, it was shown that these pores increase in size during the maturation of the cell wall [13].

2.2. Chemical composition of reaction woods

We just mention here that CW has larger lignin content, a different composition in lignin monomers (H/G ratio), more condensed lignin, and a comparatively low cellulose content. TW G-layers have high cellulose content and no lignin or are later lignified during the maturation process in some species but the level of lignification has been shown to be qualitatively lower in lignified G-layers [41]. Regarding CW, complete reviews are already available [54].

The G-layer is made of cellulose microfibrils, representing approximately 75% of the dry mass, in a polysaccharide matrix representing 25% of the dry mass [17]. Recent advances in biochemistry immunocytochemistry and molecular biology have evidenced a complex chemical composition of the matrix, specific to the G-layer as opposed to other secondary layers [50]. Although xyloglucans and xyloglucan endotransglucosylase (XET) activity have been repeatedly reported in the G-layer [10,17,73] other works convincingly argue that they are located at the interface between S2- and G-layers rather than inside the G-layer and that the main constitutive polysaccharide of the G-layer matrix is rhamnogalacturonan I (RG1) pectins, a smaller fraction of the matrix being made of arabino-galactan proteins (AGP) [15,16,18].

2.3. Mechanical state and behaviour of reaction woods

We provide here some knowledge upon the mechanical state and behaviour of reaction woods that are relevant to the purpose of this paper. Other references exist that gather information about other properties of reaction woods [74].

2.3.1. Magnitude of maturation stress and released strains

Maturation stress cannot be measured directly. It is usually estimated using the value of released strain and elastic properties of wood. The magnitude of released strain typically ranges between −0.3% for strong TW and +0.2% for severe CW [7,21,75,76]. These released strains correspond to a magnitude of stress (far higher than for example turgor pressure, which typically amounts some fractions of MPa) typically ranging between +50 MPa and −20 MPa, respectively, for TW and CW. Although the value of released strain is variable, no clear difference in its magnitude has ever been evidenced between species.

Maturation stress also occurs in the tangential direction, and tangential maturation stress is generally compressive. Although this tangential stress does not directly contribute to the motor function of wood, it is noteworthy that its magnitude is correlated to longitudinally released strains [21]: a larger tangential compression is found in TW than in NW and the higher the longitudinal tensile stress, the larger the tangential compressive stress.

2.3.2. The role of microfibril angle

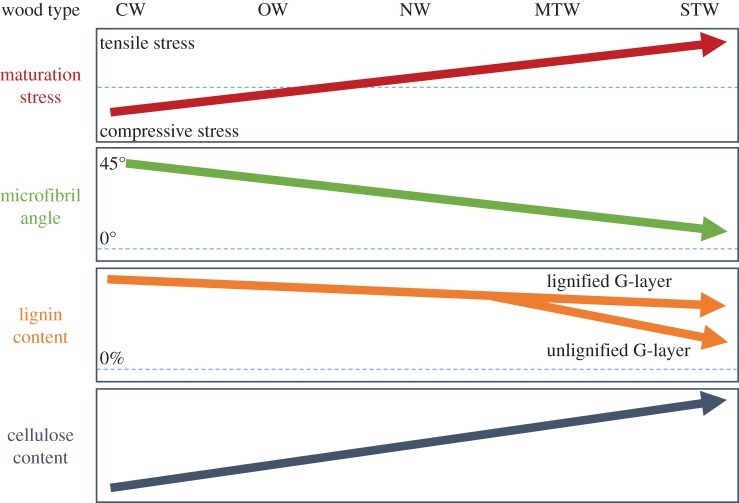
The helical angle of cellulose microfibrils (microfibril angle or MFA) has a key role in wood mechanics. It is correlated to many mechanical properties of wood, such as its stiffness [77–79] and drying shrinkage [80–83]. CW has a large MFA (typically 30°–40°), while normal wood has moderate values (typically 10° to 20°), and TW very low values (probably less than 5°). It should be mentioned that MFA measurements provide an average value, dominated by the main wood layer, namely S2 for CW and NW, and G for TW. When compression and normal woods are considered, a clear correlation can be detected between MFA and maturation stress [79,84]. Together with the changes in chemical composition, these variations suggest that there may be a continuum in structure and function between severe CW, light CW, opposite wood, normal wood and TW, where more tensile stress is associated with higher cellulose content, lower lignin content, and lower MFA. Exceptions to this pattern are species where the TW is lignified at the end of its development (figure 1).

Figure 1.

Schematics of the expected trend in composition and structure of the secondary wall and associated maturation stress from compression wood to tension wood. CW, compression wood; OW, opposite wood; NW, normal wood; MTW, mild tension wood; STW, severe tension wood. For lignin content, branching arrows illustrate the difference between lignified G-layer in the continuation of the slope and unlignified G-layer where lignin content of wood decreases steeply when the G-layers become thicker and S layers thinner. (Online version in colour.)

2.3.3. In situ mechanical state of the gelatinous layer

In TW, the magnitude of tension is directly correlated to the proportion of G-fibres [30,85–87], suggesting that tension originates in the G-fibres. When measuring the G-layer area avoiding the swelling artefact of the G-layer [59], its amount typically ranges between 10 and 30% [88] of the section area. In severe TW induced in artificially bent poplar trees, G-layer represents 65–75% of the G-fibre area (B. Clair 2016, unpublished analysis based on [60]). This indicates that tension in the G-layer itself is larger than that of TW, probably amounting up to 100 MPa.

Tension in the G-layer has also been evidenced directly by different means. First, observation of freshly cut TW sections with atomic force microscopy in topographic mode showed that, once the surface released and before any drying shrinkage, the G-layer appears shrunk when compared to other layers [89]. The same observation can be obtained in light microscopy on longitudinal sections on embedded samples [59]. Another indication of the G-layer tension was provided by an experiment using selective enzymes that hydrolyse the G-layer [90]: once the G-layers are removed from a piece of TW, wood tends to extend longitudinally, consistent with the fact that it was previously shrunk because of the longitudinal tension in the G-layer.

2.3.4. State of crystalline cellulose inside the gelatinous layer

Experimental works using X-ray diffraction provide information about the state of stress at a sub-nanometric scale, namely, inside cellulose crystallites [91–93]. The principle of this method is based on the measurement of lattice spacing, i.e. the distance between monomers along the cellulose chains. Indeed, a change in lattice spacing indicates a deformation of cellulose, accompanied with mechanical stress. A first study of the deformation of cellulose during strain release in wood [12] shows that the cellulose lattice spacing is reduced when LMS is released, and that cellulose strain is close to wood released strain. This provided a first indication that cellulose is in tension in TW, although it was not conclusive on this issue (the same results would be obtained if cellulose was in resting state in TW, and put in compression when releasing the stress). A second set of experiments consisted of measuring the change in lattice spacing along a maturation sequence [11]. It showed that the lattice spacing increases from the cambium to mature wood, clearly demonstrating that cellulose is put in tension during maturation.

2.3.5. Drying shrinkage

Wood shrinks during drying. For normal wood, this shrinkage is very low in the longitudinal direction (few fractions of per cent). However, for reaction woods, both CW and TW, drying shrinkage has much higher values, often larger than 1% (numerous references in [74]). The reason for this has long been identified for CW: shrinkage occurs in the matrix, and, due to the large microfibril angle, is substantially redirected into the longitudinal direction [81,94]. For TW, this high shrinkage appears paradoxical, because cellulose microfibrils, in view of their abundance, stiffness and axial orientation, should prevent longitudinal shrinkage. Only recently was the cause of this behaviour identified as a combination of a small effect of the release of residual auto-stresses [95] and a major effect of the collapse of the porous matrix, leading to a buckling of cellulose microfibrils [14]. Interestingly, using X-ray diffraction, it has been shown that, contrary to the release of LMS, the drying shrinkage generates only a negligible contraction of cellulose [12].

3. Hypothetical mechanisms of maturation stress generation

In this section, we review models which have been proposed to explain the origin of maturation stress. We will first examine models developed for NW and CW, and then concentrate on more recent models developed for TW.

3.1. Lignin swelling, cellulose shrinkage and the ‘unified hypothesis’

The state of stress observed at a macroscopic scale (fibre or tissue level) originates in the mechanical state of the matter at lower levels. Wood cell walls are composite materials with an oriented fibre phase (cellulose microfibrils) and a matrix phase (made of polysaccharide and, when present, lignin). Therefore, the apparition of stress in reaction wood is related to the stress induced in its constituents during maturation, due to physical or chemical transformation of, or interaction between, one or more of them.

3.1.1. The ‘lignin swelling’ hypothesis

When considering the case of CW a necessary condition for a model to be valid is its consistency with the strong relation between maturation stress and MFA. Boyd [84] used an analogy between maturation stress generation and wood drying. The magnitude of wood drying shrinkage in the longitudinal direction depends on the MFA, in a similar way to change in LMS during the progressive change in MFA observed along the continuum from NW to CW. By analogy with this mechanism, Boyd [96] assumed that variations in LMS with MFA were due to the swelling of the matrix. Since lignification is larger for CW than for NW, it was natural to consider that the swelling constituent of the matrix is lignin.

3.1.2. The ‘cell torsion’ hypothesis

There has been a controversy about the boundary condition of the fibre used in mechanical models, namely whether shear strains can happen between adjacent cell walls. Because a cell wall is strongly glued to the neighbouring wall, they form an antisymmetric structure and it has been most of the time concluded that it cannot substantially shear in response to dimensional variations of its constituents [97]. More recently, it was suggested that this condition does not apply to CW, namely that its wall could shear and induce a torsion of the cell [98]. This was supported by a mechanical model, showing that if cellulose is considered inextensible, the swelling of the matrix cannot induce longitudinal deformation without considering that the cell can undergo significant torsion [98].

3.1.3. The ‘cellulose shrinkage’ hypothesis

An alternative to the lignin swelling hypothesis was suggested by Bamber [99,100]. By assuming that cellulose shrinks during maturation, the induction of tensile stress becomes possible. Moreover, because the tensile stress is induced in the direction of microfibrils, its longitudinal component depends on microfibril orientation, so this hypothesis consistently explains the structure–function relationship between TW and NW. Boyd and Bamber strongly argued on this issue, based on microscopic observations and mechanical considerations [99–102]. Note that, in any case, although Bamber tried to find an explanation to both the cases of CW and TW, none of ‘lignin swelling’ and ‘cellulose shrinkage’ hypotheses would explain both cases since cellulose shrinkage by itself does not generate compressive stress.

3.1.4. The ‘unified hypothesis’

This question was studied later using new measurements of maturation stress and a mechanical model [103]. More sophisticated models were developed taking into account different cell wall layers, the kinetics of cell wall deposition during maturation, and explicit modelling at the constituent scale [76]. A ‘unified hypothesis’ was used for the behaviour of constituents, namely the assumption that the ‘lignin swelling’ and ‘cellulose tension’ hypotheses were both valid [86]. With this set of hypotheses, the slight tension of NW and the compression in CW could be simulated at the same time as a consequence of microfibril orientation [76].

3.2. Hypothetical mechanism for tension wood involving factors other than the gelatinous layer

Because of the paradox between TW structure and function, some authors assumed that the cause of TW shrinkage was not directly a tension induced in the cell wall layer constituents, but originated in external actions on the cell wall layers.

3.2.1. The ‘diurnal strain’ hypothesis

By seeking for the cause of the strains induced in constituents of the cell wall, authors of the ‘unified hypothesis’ made the assumption that the origin of this strain was not a modification of the constituents, but a cause external to the cell wall itself, related to the occurrence of diurnal strains, i.e. periodic deformations occurring in wood between day and night as a consequence of the tree transpiration flow [104–106]. There were also indications that the deposition of cell wall material was periodic, deposition of cellulose occurring during the day and deposition of matrix during the night [107,108]. Taken together, these facts could explain both cellulose tension and matrix compression [104,109]: cellulose is deposited when the cell is shrunk, and is, therefore, put into tension during the night when the cell recovers and extends. Conversely, the matrix, deposited during the night, would be put in compression during the day when the wood shrinks. This mechanism would elegantly explain maturation stress in wood without the need of metabolic energy.

3.2.2. Münch's hypothesis revisited

Long ago, Münch [110] proposed a mechanism by which the TW tensile stress does not directly result from the longitudinal shrinkage of the G-layer, but from the interaction between layers. This mechanism was recently revisited [90] and described as follows. The G-layer would swell because of the hydrophilic nature of its polysaccharide matrix. This swelling would occur only laterally because of its low MFA. This would force outer S1 and S2 layers to extend laterally. Because of their large MFA, these layers should have a large Poisson's ratio (i.e. a strain in one direction induces strain of opposite sign in perpendicular directions). This implies that, as a consequence of lateral swelling, the external layers tend to shrink longitudinally, and this would be the source of tensile LMS in TW.

3.3. Hypothetical mechanisms based on a modification of gelatinous layer cellulose

During their synthesis, cellulose microfibrils have one end located at the level of protein complexes inserted into the plasma membrane [111]. In view of the low stiffness of this membrane compared to that of cellulose, this condition is almost equivalent to having a free end. Therefore, if shrinkage is induced in cellulose during this phase, the consequence would just be a displacement of this free end, rather than the accumulation of stress in the cell wall. Induction of tensile stress in microfibrils likely happens after incorporation to the cell wall. As cellulose is mainly crystalline, especially in TW [51], it is difficult to imagine how this material could tend to shrink after its incorporation to the wall. Hereafter, we describe some models that aim at explaining how tension is induced in cellulose.

3.3.1. Lateral crystal growth

Using X-ray measurement and different sources of cellulose, it has been suggested that the lattice spacing of crystalline cellulose depends on the lateral size of the crystal [112]. This is explained by the difference in lattice spacing between cellulose chains located inside the crystal and those located at its surface. Thus, the equilibrium lattice spacing of the microfibril depends on the amount of surface and inner cellulose chains. This implies a size effect on the crystal lattice spacing: the ratio of surface/inner chains decreases when the crystal size increases, so that the lattice spacing changes [112].

The assumption that cellulose crystals may grow laterally would be consistent with the larger crystal size reported for TW than for NW. Lateral growth would provide a mechanism for generating a change in equilibrium lattice spacing of the crystal, and therefore the generation of mechanical stress.

3.3.2. Amorphous cellulose in series with crystallites inside the microfibrils

Cellulose microfibrils are not completely crystalline. Amorphous cellulose regions occur along the microfibrils between crystalline regions [102,113]. This non-crystalline material is sensitive to water and chemically reactive so that it could shrink in response to physico-chemical changes in the environment, and transmit this stress to crystalline material. This assumption was proposed to explain the cellulose shrinkage mechanism in a previously mentioned model [79].

3.3.3. Amorphous cellulose at the surface of microfibrils

The surface of microfibrils is described as para-crystalline [114], an intermediate state between crystalline and amorphous. Therefore, it could potentially be influenced by its physico-chemical environment and tend to shrink, inducing tension. In this case, the tension is induced in amorphous cellulose parallel to crystalline cellulose and transmitted to the TW tissue.

3.3.4. Active binding of microfibrils

Cellulose microfibrils are not exactly parallel to each other, but form a kind of trellis with local lateral connections between them [67–69]. This structure is formed during the aggregation of cellulose. Assuming that some amorphous material helps binding adjacent microfibrils together, a mechanism based on lateral interaction between microfibrils has been proposed (fig. 5.4 in [19]). If active binding occurs, it may generate lateral forces that locally pull the microfibrils towards each other. If this active binding occurs at multiple places along microfibrils, then a global movement of microfibril is prevented (it is pulled on both sides), but local deformations are possible. The pulling force will, therefore, locally bend the microfibrils, and transmit mechanical stress in the longitudinal direction.

3.4. Hypothetical mechanisms based on interaction between cellulose and matrix in the gelatinous layer

Another family of models based on an interaction between microfibrils and the matrix were suggested in the literature, and are presented in this section.

3.4.1. Drying of the gelatinous layer during maturation

The most obvious way to generate longitudinal tension in the G-layer is to dry it, i.e. remove water from the matrix. This mechanism is based on a simple physical action, and is naturally suggested by the large longitudinal drying shrinkage observed in TW [30,115]. This hypothesis was proposed by Bowling & Vaughn [15] based on the hydrophilic nature of TW matrix constituents.

3.4.2. Entrapment of matrix material during cellulose aggregation

Recent advances in biochemistry have led to new models proposed in the literature. These models are designed to explain the molecular function of the chemical constituents found. A first version of this model [73] assumed that xyloglucans, previously considered as the main constituent of the G-layer matrix [10,17], could be entrapped between microfibrils during their aggregation. If the microfibril is initially straight, then the presence of material entrapped during aggregation tends to locally bend the microfibril, and therefore put it in longitudinal tension.

More recently, an alternative to this model was proposed [16–18]. This model is based on the same mechanism of entrapment as mentioned above, but involves a different chemical constituent. Here, the material that locally prevents aggregation is supposed to be an interaction between RG1 backbones and galactans, resulting from the action of β-galactosidase.

3.4.3. A model unifying Münch's hypothesis and the entrapment mechanism

A model has been proposed unifying Münch's hypothesis and the entrapment model [17]. This model assumes that the deformation of the G-layer originates in the entrapment mechanism. This would cause a gradient in longitudinal strain across the wall, inducing a compressive stress towards outer secondary layers. This compressive stress would be the source of additional tensile stress through the coupling with outer layers.

3.4.4. Matrix swelling in a connected cellulose network

Based on the gel-like porous nature of the G-layer matrix and its changes during cell wall development [13], it was proposed that the matrix could swell during maturation [13,19]. This swelling could be the consequence of a change in water potential inside pores, due for example to cell death or changes in osmotic pressure. If it occurs after cellulose aggregation and the formation of a trellis structure, this swelling of the matrix interacts with microfibril aggregates and tends to bend them, inducing tension along the cellulose.

4. Combining models and observations in an integrated approach

4.1. Requirements for a mechanism to be admissible

Here we aim at examining all models reported in §3, and try and discriminate whether they can be rejected or not, by confronting them with mechanical considerations and observations reported in §2.

We will consider three kinds of items in order to examine the models. First, a basic prerequisite for a model to be admissible is its consistency with TW structure at all levels of organization (tissue, cell, cell wall, polymers). Second, the proposed model should be consistent from a mechanical viewpoint. Third, the model should result in a state of stress that is compatible with current knowledge about the in situ mechanical conditions of TW, at all levels of organization. The sign and magnitude of stress at the tissue level must be consistent with observations. The relevant data are the LMS of TW (tensile), and tangential maturation stress (compressive). At the cell wall level, it is known that the G-layer is in a state of longitudinal tensile stress [59]. At the level of microfibrils, crystalline cellulose is also in a state of longitudinal tension [11].

4.2. Models for compression and normal wood

4.2.1. The ‘cell torsion’ hypothesis

It has been suggested that in the case of CW, the cell wall can shear so that the cell may undergo a torsion. This seems consistent with the particular morphology of CW, where rounded cells, intercellular spaces and helical cavities would make this torsion possible.

However, there are at least two weaknesses in this model. First, the hypothesis of cell torsion would imply that shear strain between adjacent cell walls is non-negligible, and, because it is integrated along the cell, this strain would be large at the level of fibre tips. This would imply that the fibre is not correctly glued to the adjacent cell wall, so it cannot efficiently transfer stress to the surrounding tissue, whereas maturation stress is observed at the tissue level. Second, the hypothesis of cellulose inextensibility is a strong mechanical assumption: when finite (although small) extensibility is considered, the results change, and it appears that longitudinal stress can be induced whatever the boundary condition of the fibre.

4.2.2. The ‘lignin swelling’, cellulose tension and unified hypotheses

The lignin swelling hypothesis was formulated to describe the variation in LMS between NW and CW. Assuming the condition of shear restraint, simulations using a mechanical model [76,116] showed that no significant tension can be induced by the mechanism of matrix swelling alone in composite media made of parallel fibres. Although it consistently explains the trend observed along a gradient of CW severity, this model is not valid for NW. Note that, in this model, the origin of matrix swelling was not clear, it was assumed to be the polymerization of lignin, but there is no reference supporting that this polymerization would create a swelling of the matrix.

Adding the cellulose tension hypothesis, the model is able to reproduce the gradient in LMS between NW and CW [76]. These variations result only from the change in MFA, the values of maturation stress induced in the matrix and cellulose being assumed independent of the type of wood. Note that the hypothesis of cellulose shrinkage was not always supported by an underlying microscopic mechanism, but some hypothetical mechanisms presented in this paper provide possible mechanisms by which tensile stress can be achieved in cellulose.

One weakness of the model based on the ‘unified hypothesis’ was that it could not explain at the same time the longitudinal and the tangential maturation stress [79], tangential maturation stress being overestimated. Further modelling effort enabled accounting for the specific boundary conditions of the fibre in the transverse direction, which is completely restrained in the tangential direction, but partly free in the radial direction [116]. This model was able to reproduce at the same time longitudinal and tangential released strains of maturation stress, along a gradient from NW to CW.

4.2.3. The ‘unified hypothesis’ and tension wood

Even when considering both mechanisms of matrix swelling and cellulose shrinkage, the above-mentioned models could not explain the comparatively large longitudinal tensile stress of TW at the same time as NW and CW maturation stress. The effect of MFA alone was not sufficient to predict the LMS in TW. The only way to reproduce at the same time all kinds of wood was assuming that the shrinkage of cellulose is specifically large in TW.

It would be possible to induce large LMS with a model analogous to that of CW, if the MFA is large and shrinkage occurs in the matrix instead of swelling. This mechanism would be similar to other motor systems found in nature, such as in pine cones [117]. This model would be consistent with the case of NW, but is obviously incompatible with the low angle found in TW.

The low MFA of TW appears paradoxical for the same reason as already mentioned for drying shrinkage. Cellulose in wood is mostly in a crystalline state, so it is not easy to imagine a mechanism by which tension should be induced by physico-chemical changes in microfibrils. If cellulose does not create tension, the abundant stiff microfibrils oriented in the longitudinal direction of the cell should prevent movement in the longitudinal direction, whereas its function requires a shortening in that direction. Mechanisms providing an explanation of the origin of cellulose tension are discussed below.

4.3. Examination of mechanisms for tension wood involving factors other than the gelatinous layer

4.3.1. The ‘diurnal strain’ hypothesis

The ‘diurnal strain’ model [109] was designed to explain both matrix compression and cellulose tension on the basis of a purely physical process, requiring no metabolic energy. This model has been proved false by two means.

The first proof was based on an experimental approach, where young trees of both a conifer and an angiosperm species were tilted and submitted to two light conditions: first sample with continuous lighting and control sample with alternating periods of day and night [118]. The uprighting of stems was at least as much for the continuously lighted trees as for the control trees, showing that, when circadian rhythm is suppressed, TW function is maintained, so diurnal strains do not explain maturation stress generation. This experimental evidence was supported by a mechanical simulation of what occurs in a maturing cell if it is submitted to periodic fluctuation of stress at the cell wall boundary on the lumen side (as due to circadian changes in water tension), and periodic deposition of cell wall material (cellulose during the day and matrix during the night). The model was built based on previously developed models to check the ‘unified hypothesis’ in the case of NW and CW [116]. Results (T. Alméras 2006, unpublished) showed that, although the sign of the stress resulting from this interaction was correct in both cellulose and matrix, its order of magnitude was far lower than that required to induce realistic stress in TW.

4.3.2. Münch's hypothesis

Münch's hypothesis assumes that maturation stress results from the lateral swelling of the G-layer and its interaction with external layers [90,110]. The underlying idea is mainly based on the consistency with MFA of each layer and its consequences on their mechanical behaviour in terms of swelling and Poisson's ratio. This mechanism would produce longitudinal tension and lateral compression, consistent with the observed in situ state of stress of TW.

Additional support was provided by experiments [90] measuring the strains of TW resulting from enzyme treatment that supress the G-layer. The results show that when the G-layer is suppressed wood tends to extend longitudinally and shrink tangentially, which seems consistent with the G-layer swelling tangentially, pushing outer layers making the wood shrink. Note, however, that this observation is hardly discriminant, as it is also compatible with the opposite situation where the G-layer would be in longitudinal tension, so that during its release there would be a longitudinal extension accompanied by a lateral shrinkage because of Poisson's effect (as opposed to this model which assumes the G-layer is not pulling directly, but through a coupling effect with outer layers).

The confrontation with other observations and mechanical considerations shows that there are several arguments to reject this model. The main experimental evidence is the assumption that tension is not supported by the G-layer is not compatible with microscopic observations showing that this layer retracts near the cut surface [59,89], neither is it compatible with observations that the cellulose of the G-layer is put in tension during maturation [11]. Also, this model does not consider the fact that pressure inside the G-layer would also act on the lumen side, so that part of the pressure would ‘escape’ inside. It is also noteworthy that this mechanism would be more efficient if a S3-layer prevented deformations on the lumen side, whereas TW specifically lacks a S3-layer [61]. It would also be more efficient if the S2 is thick, whereas it was noted that the thickness of the S2-layer is reduced when more and more severe TW is considered [23]. Theoretical considerations also reveal some inconsistencies. The maturation stress is here supposed to be supported only by the S2 layer. Calculations show that, to achieve longitudinal stresses of the correct order of magnitude, the stress on the S2 layer would be unrealistically large, namely around 1 GPa. It is unlikely that cell wall material can undergo such a stress without being damaged. Finally, the assumption of a purely lateral pressure in the G-layer is strong: pressure may generate mainly lateral strains, but in terms of stress, it can be expected to be isotropic and, therefore, generate longitudinal compressive stress in the G-layer, so that the resulting state of stress of the tissue would be compression rather than tension.

4.4. Micro-mechanical representation of a maturing wood tissue

As the models based on factors other than the G-layer have both been rejected, we will next consider models based on a modification of constituents of the G-layer. All these models are based on a dimensional variation of a constituent (cellulose or matrix) and/or on interactions between cellulose microfibrils.

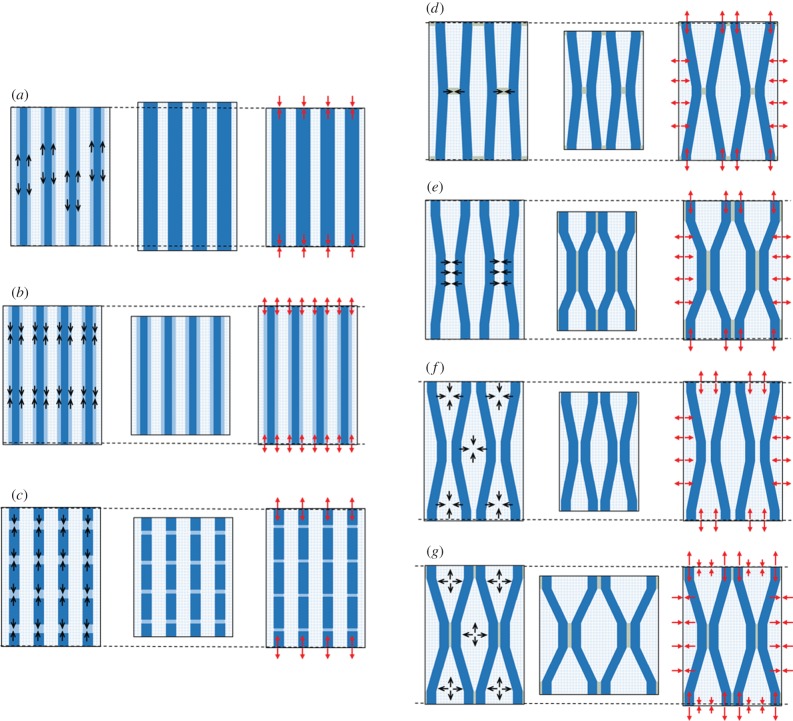
Figures 2 and 3 show a common abstraction of the G-layer material summarizing how the different models work from a mechanical perspective, at least qualitatively. The model concentrates on an elementary volume and the material is supposed made of periodic repetitions of this motif (figure 2). Different compartments are considered: crystalline microfibrils either straight or wavy, amorphous cellulose either located in series or in parallel with crystalline cellulose, a matrix (of unspecified chemical constitution) and an additional compartment standing for connections between microfibrils. Each of these constituents is characterized by geometric parameters. The different values of these parameters enable representing different simplified views of the wall (figure 3): if the angle of microfibril waviness is zero, then straight microfibrils can be considered; if the extension of amorphous cellulose compartments or connecting material is set to zero, then models neglecting them are obtained. The cause of maturation stress is represented by stress induced in one of the compartments, either tensile or compressive.

Figure 2.

Unified representation of the cell wall material. Left: representation of the cell wall material, made of matrix and microfibril trellis. Right: elementary volume of the material. The matrix is represented in textured white, crystalline cellulose in deep blue, amorphous cellulose in light blue, and an additional material in hatched grey.

Figure 3.

Abstract representation of each model: (a) lateral crystal growth, (b) amorphous cellulose at the surface of microfibrils, (c) amorphous cellulose in series with the microfibrils, (d) active binding of microfibrils, (e) entrapment of matrix material during cellulose aggregation, (f) drying of the G-layer during maturation, (g) matrix swelling in a connected cellulose network. For each model, cell wall material is represented in three states: (left) state before maturation, (middle) virtual state of deformation if the volume was free to strain, (right) in situ state of stress. Black arrows inside constituents represent their initial tendency to shrink or swell (convergent arrows indicate shrinkage and divergent arrows indicate swelling). Red arrows represent the final state of stress at the border of the elementary volume (convergent arrows indicate compression and divergent arrows indicate tension). For a complete description of the mechanisms, see text.

Note that for these models to be rigorous, an upscaling to the cell and tissue level is necessary, to take into account the interaction between G-layer and surrounding material. Longitudinal stress is transmitted to surrounding material through shear stress. This requires that the layers are well glued to each other. The G-layer is chemically and structurally very different from the surrounding secondary layer [50]. This difference may cause loose adhesion between layers, as for example suggested by the detachment of the G-layer during sectioning [119], but this detachment has been shown to be due to a cutting artefact and does not occur in the living tree [119]. Specific chemical compounds (xyloglucans and XET) have been located at the interface between layers, and it has been suggested that their function was adhesion between adjacent layers [16].

Also, a rigorous model should take into account the mechanical consequences of the simultaneous occurrence of induced stress and thickening of the wall [76,116]. Nevertheless, we will here neglect this step for clarity. We will assume that the state of stress at the boundary of the elementary volume is the same as that at a boundary of a piece of TW in situ. The boundary conditions considered are completely restrained in both directions, consistent with the fact that longitudinal contraction of maturing TW is impeded because it is glued to the older stiff wood of the stem. The tangential strains are impeded because the circumference of the stem is constant. Figure 3 shows the state of a virtual elementary volume that would be free at its boundaries, before illustrating the in situ state of stress.

4.5. Examination of mechanisms based on a transformation of the gelatinous layer

4.5.1. Lateral crystal growth

The model of lateral crystal growth (figure 3a) is consistent with observation that cellulose lattice spacing is related to crystal size [112], that TW has larger crystal size [62] and with the statement that tension results from cellulose crystallization [101]. However, there is no evidence that lateral crystal growth occurs within the cell wall. Current representations of cellulose synthesis describe cellulose microfibrils synthesized by protein complexes located within the plasma membrane, and aggregation rather than crystallization occurs within the wall [111]. Second, because lattice spacing is increasing with crystal size, it happens that this mechanism would generate compression rather than tension.

4.5.2. Amorphous cellulose at the surface of microfibrils

The model of amorphous cellulose that tends to shrink at the surface of microfibrils (figure 3b) is consistent with the fact that the G-layer is in tension. Note that this model requires the cellulose microfibrils to be straight rather than wavy, otherwise the tension in the microfibril would be partially released by a straightening movement of the microfibrils inside the wall. This is not consistent with current representation of the cell wall [66]. Finally, this model can be rejected because of its inconsistency with the state of cellulose during maturation. If amorphous cellulose is parallel to crystalline cellulose, tension in amorphous cellulose would create tension at the cell boundary, but not inside the core of crystalline cellulose, as opposed to the observation that crystalline cellulose is put in tension during maturation [11].

4.5.3. Amorphous cellulose in series with crystallites inside the microfibrils

If amorphous cellulose is located in series in the microfibril separating crystalline domains (figure 3c) [102,113], then its shrinkage should induce tension in crystalline cellulose, so the resulting state of stress of the G-layer should be tensile. These facts are consistent with the observed state of stress of microfibrils [11] and G-layer [59,89], and the model cannot be rejected on these bases. Note that, just like the model of amorphous cellulose in parallel, this model requires the microfibrils to be straight in order to correctly transmit the stress so current representations of the cellulose network [66] would make this mechanism less efficient. The model also presents two limitations. First the origin of the stress induced in amorphous cellulose is still not specified, but one can assume that the action of a hypothetical enzyme or a change in matrix composition could have this effect. Second, this model does not by itself explain the origin of lateral compression. It is, however, possible that this lateral stress is the consequence of another mechanism, not necessarily related to the generation of LMS.

4.5.4. Active binding of microfibrils

The model assuming active binding between microfibrils (figure 3d) should generate tensile LMS in both crystalline cellulose and at the level of the G-layer, consistent with observations [11,59,89]. This model would also be consistent with the wavy appearance of microfibrils, since it implies bending them. Here, the material laterally binding microfibrils is not specified. It could be for example matrix structural material, such as specific matrix polysaccharides. Xyloglucans (XG) and the action of XET [10] could have been a good candidate since one function of XG in the primary walls is to act as a tether between microfibrils. However, recent analyses showed that XG in the G-fibre are not actually located inside the G-layer, but rather at the interface between G-layer and surrounding lignified layers. Finally, this model, as it pulls microfibrils against each other, should result in lateral tensile maturation stress, which is not consistent with observations that tangential maturation stress is compressive and correlated to the magnitude of longitudinal tension [21].

4.5.5. Drying of the gelatinous layer during maturation

A mechanism based on the drying of the G-layer (figure 3f), i.e. a shrinkage of its matrix due to a loss of water, seems consistent with the large drying shrinkage of this layer [23,89]. This shrinkage would occur when the moisture content of the cell wall decreases, and would be ascribed to hydrophilic polymers such as RG1, AG and AGP [15]. Two arguments, however, tend to reject this model. First, it should be noted that the large shrinkage of TW does not necessarily indicate such a large drying stress, because TW drying shrinkage is a nonlinear inelastic process, involving the collapse of the gel and the buckling of microfibrils [14]. X-ray measurements showed that cellulose lattice distance does not change during drying [12], whereas it becomes larger during maturation, corresponding to tension inside them. Second, this model again would generate lateral tension, which is not consistent with observations.

4.5.6. Entrapment of matrix material during cellulose aggregation

The most recently published models are based on the mechanism of entrapment of material during aggregation (figure 3e) [16,17,73]. These models, by forcing the microfibrils to bend, would generate longitudinal tension inside the G-layer, together with tension in microfibrils, consistent with observations. One strength of these models is that the mechanism is specified at the molecular level. The nature of the entrapped material is specified based on observations from biochemistry and immunocytochemistry. The first version of the model [73] can be rejected since it assumes that the entrapped material is xyloglucans although it has become clear that they are not located inside the G-layer. The newest version [16] of the model is more consistent with current knowledge about the composition of the G-layer, as RG1 is supposed to be the entrapped material. It is also consistent with current representations of microfibril networks and aggregation processes. However, this model should generate lateral tension, which is not consistent with observations.

4.5.7. Model unifying Münch's hypothesis and the entrapment mechanism

This model was an attempt to unify two recent models which have been published, by considering that the entrapment mechanism was the source of lateral swelling of the G-layer, which in turn would cause tensile stress in outer layers. However, the proposed mechanism presents weaknesses from a mechanical viewpoint. The assumption that there is a gradient in strain across the G-layer is based on the gradient of strain that can be observed on a cut section [89] (note that related reference is related to drying shrinkage, not maturation shrinkage). This hypothesis is not consistent with the kinematic conditions of the G-layer in situ, where longitudinal strain gradients are prevented. Additionally, the mechanism by which this gradient could generate lateral compression is unclear. Moreover, the mechanism of aggregation should generate tensile rather than compressive stress in lateral directions, and therefore cannot be the motor of Münch's mechanism.

4.5.8. Matrix swelling in a connected cellulose network

The model assuming the swelling of the matrix inside a connected network (figure 3g) [13,19] is able to generate tension both at the G-layer level and at the microfibril level, consistent with observations. Also, because the cause is a compressive stress inside the matrix, the lateral stress of TW induced by this mechanism should be compressive; moreover, this compression should be correlated to the magnitude of tensile stress. This result is consistent with observations [21]. At a microscopic level, it is consistent with both the observed trellis structure of microfibrils in the wall and the porous nature of the matrix. The matrix presents characteristics of a hydrogel, and a specificity of hydrogels is their ability to swell. Moreover, the increase in pore size during maturation [13] is consistent with the assumed matrix swelling. Use of a mechanical model (T. Alméras 2009, unpublished) showed that the magnitude of the tension generated this way is larger if the microfibrils are tightly bound and if the ratio of matrix to microfibril stiffness is low, both conditions seeming compatible with known structure of the G-layer. A limitation of this model is that the motor of this swelling at a molecular level is unspecified.

4.6. More than one mechanism may be involved

Based on current knowledge, it appears that the cases of TW and CW cannot be modelled by the same mechanism. The model based on the ‘unified hypothesis’ correctly describes the relation between MFA and LMS for NW and CW. This model currently considers that cellulose tension originates in the shrinkage of amorphous cellulose regions inside microfibrils. Alternative hypotheses presented for TW could also be at the origin of this stress.

Regarding TW, four models were found admissible with few limitations: (i) amorphous cellulose along microfibrils, (ii) active binding of microfibrils, (iii) entrapment of material during aggregation, and (iv) swelling of the matrix in a cellulose network. Limitations of models (i), (ii) and (iv) include the fact that the mechanism is not yet identified at the molecular level. Note that models (ii) and (iii) are equivalent from a mechanical perspective. Active binding in (ii) is equivalent to cellulose aggregation in (iii) as both generate forces that pull the microfibrils together. The role of entrapped material in model (iii) is equivalent to the role of the matrix in model (ii): in both cases, this material locally prevents movement of the microfibrils, forcing them to bend and, therefore, generate tension.

Models (i), (ii) and (iii) are not able to reproduce lateral compression, and only model (iv) is consistent with related observations. For this reason, we select model (iv) as our best candidate to date. Note, however, that here each mechanism was considered independently. It is also possible that nature combines different mechanisms to achieve longitudinal tension and lateral compression. For example, if we add a matrix swelling hypothesis to models (i), (ii) or (iii), they become compatible with the state of lateral stress. Moreover, in the case of models (ii) and (iii), this would make the mechanism even more efficient for longitudinal stress, because both the swelling of the matrix and the lateral pulling on microfibrils tend to bend them and, therefore, transmit tension.

5. Conclusion

We examined several models of maturation stress generation in reaction woods, and could reject some of them based on their inconsistency with known cell wall structure, composition, state of stress and mechanical considerations. Information about the in situ state of stress was particularly relevant to discriminate between models. Progress in biochemistry enables the description of hypothetical mechanisms at the molecular level. To further check the models, a quantitative approach based on computational mechanics would make it possible to link the magnitude of maturation stress at the macroscopic level to the magnitude of forces involved in the phenomenon at the microscopic level. Such an approach is currently limited by the lack of quantitative information about some aspects of the microstructure (e.g. characteristic dimensions and three-dimensional structure of the trellis) and behaviour of constituents (e.g. elastic properties and anisotropy of the matrix and the G-layer). Also, information about the timing of events (changes in chemical composition or mechanical behaviour during the maturation process) is essential to achieve a consistent description of the phenomenon. The issue of maturation stress generation is an exemplary case where an interdisciplinary approach, integrating knowledge from many disciplines, should enable rapid progress in the near future.

Authors' contributions

T.A. and B.C. designed the plan and structure of the paper. The manuscript was written by T.A., discussed and modified with B.C. Both authors gave final approval for publication.

Competing interests

We declare we have no competing interests.

Funding

This work was performed in the framework of the project ‘StressInTrees' funded by the French National Research Agency (ANR-12-BS09-0004). EcoFoG benefits from an ‘Investissements d'Avenir’ grant managed by the French National Research Agency (CEBA, ref. ANR-10-LABX-25-01).