The interface of SrTiO₃ and H₂O from density functional theory molecular dynamics

Abstract

We use dispersion-corrected density functional theory molecular dynamics simulations to predict the ionic, electronic and vibrational properties of the SrTiO₃/H₂O solid–liquid interface. Approximately 50% of surface oxygens on the planar SrO termination are hydroxylated at all studied levels of water coverage, the corresponding number being 15% for the planar TiO₂ termination and 5% on the stepped TiO₂-terminated surface. The lateral ordering of the hydration structure is largely controlled by covalent-like surface cation to H₂O bonding and surface corrugation. We find a featureless electronic density of states in and around the band gap energy region at the solid–liquid interface. The vibrational spectrum indicates redshifting of the O–H stretching band due to surface-to-liquid hydrogen bonding and blueshifting due to high-frequency stretching vibrations of OH fragments within the liquid, as well as strong suppression of the OH stretching band on the stepped surface. We find highly varying rates of proton transfer above different SrTiO₃ surfaces, owing to differences in hydrogen bond strength and the degree of dissociation of incident water. Trends in proton dynamics and the mode of H₂O adsorption among studied surfaces can be explained by the differential ionicity of the Ti–O and Sr–O bonds in the SrTiO₃ crystal.

1. Introduction

Understanding the interaction of metal-oxide surfaces and water is a topic of broad interest. Research of these systems is inspired by applications in such fields as geochemistry, catalysis and chemical sensing [1,2]. A particular focus of interest in recent decades has been water-splitting using a metal-oxide anode such as SrTiO₃ or TiO₂ in an electrochemical cell as a photocatalyst, enabling the conversion of solar radiation into chemical potential energy in the form of H₂ [3]. Making this environmentally appealing process efficient and economically viable requires a thorough understanding of the relevant oxide–water interface.

While the photocatalytic capability of SrTiO₃ was demonstrated experimentally over 40 years ago [4], a good understanding of the SrTiO₃/H₂O solid–liquid interface has remained elusive. The general view emerging from temperature-programmed desorption spectroscopy (TPD) [5–7], friction-force microscopy [8], X-ray photoemission spectroscopy [9] and surface X-ray diffraction [10] is that H₂O tends to adsorb strongly and through dissociation on step edges, vacancy sites and onto the SrO-terminated (001) surface, but molecularly and weakly onto the stoichiometric TiO₂-terminated surface. This view is broadly corroborated by static DFT [7,11,12] and hybrid functional [13] calculations as well as molecular dynamics based on empirical interaction potentials [14], all up to one monolayer of H₂O coverage on the planar SrO- and TiO₂-terminated surfaces. In spite of this large body of work, a detailed understanding of the hydration structure of SrTiO₃, the electronic structure of the SrTiO₃/H₂O interface, as well as the vibrational properties at the interface, in particular at high levels of H₂O coverage and non-planar surfaces, is missing.

In this work, we use dispersion-corrected density functional theory molecular dynamics (DFT MD) to attack this problem. We compute the hydration structure of SrTiO₃ at varying levels of H₂O coverage for both planar and non-planar SrTiO₃ surfaces. A strongly mixed mode of molecular and dissociative adsorption is found for planar (001) surfaces, with a crossover to more molecular adsorption on a TiO₂-terminated stepped surface and the ($\sqrt{13}\times \sqrt{13})\mathrm{R}{33.7}^{\circ }$ or ‘RT13’ surface reconstruction [15]. Bonding of covalent character plays an important role alongside surface corrugation, hydrogen bonding and the dispersion interaction in the ordering of the hydration structure. While the electronic structure around the band gap region of the solid–liquid interface displays no features of interest, the vibrational spectrum of adsorbed H₂O is significantly altered at the O–H stretching band frequencies. Proton transfer rates and the degree of surface hydroxylation are highest on the SrO-terminated surface, an effect we trace to the high ionicity of the Sr–O bond with respect to the Ti–O bond in the crystal.

2. Methodology

To gain a thorough understanding of the solid–liquid interface of SrTiO₃ and H₂O, we studied four different surfaces for the oxide: bulk-like SrO-terminated (001), bulk-like TiO₂-terminated (001), the TiO₂-dominated and strongly corrugated RT13 surface reconstruction [15] and a stepped TiO₂-terminated (001) surface. The first two of these are commonly observed in experiment [16], whereas the RT13 surface is believed to be among the most stable SrTiO₃ surfaces near ambient conditions and particularly suitable for homoepitaxial growth of SrTiO₃ and heteroepitaxial growth of other perovskite oxides [17]. We chose the TiO₂ termination for our stepped (001) surface, as experiments suggest that this termination dominates over the SrO termination in step-and-terrace systems [18,19].

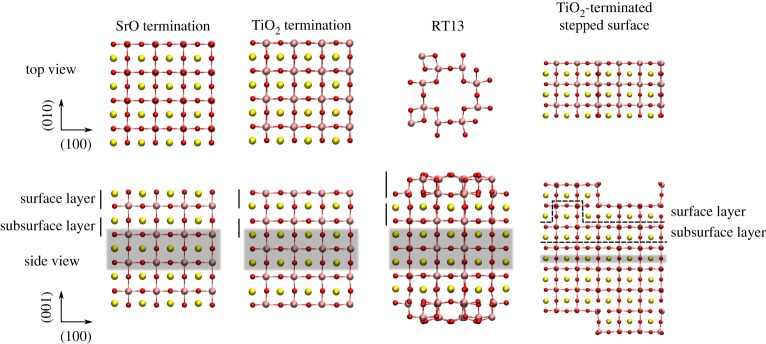
The four different SrTiO₃ surfaces were each modelled with a slab geometry (figure 1). The supercell was periodic in all three dimensions, and a vacuum gap of approximately 20 Å was created in the [001] direction between periodic slab images. In order to achieve a vanishing surface dipole for the overall neutral slabs, all slabs were made mirror-symmetric with respect to the central plane. The SrO and TiO₂-terminated slabs were four and a half unit cells in thickness and 4×4 unit cells in the lateral dimension, whereas the RT13 slab consisted of four unit cells of bulk SrTiO₃ beneath the surface reconstruction and one single surface unit cell in the lateral plane. The size of the stepped surface was 6×3 unit cells in the lateral dimension and six unit cells in the vertical dimension. One to three central atomic planes of each slab were fixed, depending on thickness of the slab (figure 1), with the lattice constant for fixed layers set to its equilibrium bulk value for the exchange-correlation functional in question.

Figure 1.

Visualizations [20] of the relaxed SrO-, TiO₂- and RT13-terminated slabs and the TiO₂-terminated stepped surface in vacuum. Definitions for the surface and subsurfacelayer used in this work are indicated by solid and dashed lines, and the shaded areas indicate fixed atomic layers. O ions are red, Sr is yellow and Ti is pink. Only the top Ti–O layer is shown in the top view of the RT13 surface. (Online version in colour.)

For all static structure optimizations and molecular dynamics runs, we used the CP2K code [21], which hosts a hybrid LCAO and planewave basis set. This set-up is efficient for computations involving surfaces and large vacuum regions, as is the case in this work. We sample the Brillouin zone at the Γ-point, which is justified by the large size of the supercell. Goedecker-Teter-Hutter pseudopotentials [22–24] are used to avoid explicit calculation of the core electrons. We use the DZVP localized basis set [25] as a good compromise between precision and speed.

The standard semi-local formulations of the exchange–correlation functional in DFT exclude, by definition, the long-range dispersion interaction between atoms and molecules [26]. As this electron correlation effect can be important for surface stability, surface–molecule interaction and molecule–molecule interaction [27], dispersion effects should be considered when modelling the present systems of interest. To enable us to include dispersion effects in our model and to still perform large-scale DFT MD simulations, we use the Grimme D3 dispersion correction [28]. To guide us in the choice of exchange–correlation functional, we initially employed a range of functionals (LDA [29], PBE [30], PBEsol [31], PBE-D3, BLYP [32,33], BLYP-D3) to compute the lattice constant, bulk modulus and band gap of SrTiO₃ in the bulk cubic perovskite phase (4×4×4 unit cells), and the ionic displacements upon relaxation of the (001) SrO- and TiO₂-terminated surfaces as well as the surface energy of the bulk-like (001)-terminated crystal. Additionally, using the subset of functionals PBE, PBE-D3 and PBEsol, we performed a set of static structural optimizations of single-molecule adsorption of H₂O onto the SrO- and TiO₂-terminated planar slabs, where the H₂O was initially placed over the most important high-symmetry points on each surface termination. As shown in §3a, this set of static calculations ultimately showed PBE-D3 to offer the overall best results. Therefore, all subsequent MD calculations were done using PBE-D3.

We performed all MD runs at 300 K in the NV T ensemble, employing a time-step of 0.5 fs and the Nosé–Hoover chain thermostat (to all except the fixed atoms in the system) with three links and a time constant of 20 fs, i.e. a frequency of 5×10¹³ Hz, which is in the range of the dominant vibrational frequencies expected in the system (10¹³ Hz for SrTiO₃ and 2–10×10¹³ Hz for H₂O [34]). The total duration of the MD was 10 ps for the SrO-, TiO₂- and RT13-terminated surfaces (448-734 atoms, 3072-3944 electrons per system, 60–150 s ionic⁻¹ step on a Cray XC40 over 384 cores), and 5 ps for the stepped surface (1332 atoms, 6816 electrons, 170 s ionic⁻¹ step over 864 cores) due to the very large size of this system. A drift of no more than −1 meV atom⁻¹ ps⁻¹ was observed in any of the MD runs after an initial equilibration period of 5 and 3 ps, respectively, which indicates that the systems were reasonably close to dynamic equilibrium. We considered three levels of H₂O coverage: 0.5 monolayers (ML, defined here as one H₂O per surface unit cell or cation), 1.0 ML, and bulk H₂O. For the 0.5 ML and 1.0 ML coverages, the H₂O molecules were initially positioned in the middle of the vacuum layer in two or four sheets of 4×4 molecules each, respectively, the molecules being spaced laterally in units of the crystal lattice constant and each molecule being uniformly randomly rotated about the O ion. For bulk water coverage, the gap between two periodic slab surfaces and the number of water molecules were adjusted to give the experimental density of 1 g cm⁻³ for the total density of H₂O between the surfaces. To gain an understanding of how the level of water coverage affects the hydration structure of SrTiO₃, all three levels of coverage were simulated for the SrO- and TiO₂-terminated planar surfaces. On the RT13 and the stepped surface, we considered only bulk water coverage, as this is most relevant for real-world applications in photocatalysis using SrTiO₃.

After an equilibration period of 5 ps (3 ps for the stepped surface), all MD runs were analysed for the vertical density profile of H₂O and the histogram of lateral positioning of H₂O in each hydration layer for the remaining duration of each simulation trajectory (over all time steps). These quantities yield a detailed description of the hydration structure of the SrTiO₃ surface. In addition, to analyse the vibrational properties of H₂O on the photocatalyst surface, we computed the vibrational density of states (VDOS) of H₂O by performing a Fourier transform of the velocity auto-correlation function [35]. The fraction of surface hydroxylation, the fraction of dissociated H₂O in the liquid, and rates of proton transfer within the system were assessed by studying the O–H coordination statistics of O in the slab surface and in the liquid region. By computing the O–H radial distribution function, we found a radial cutoff of 1.25 Å to define the first O–H coordination shell for oxygens in both the liquid and in the slab surface.

Finally, to compute the electronic density of states (EDOS) more precisely than allowed for by the Γ-point sampling of CP2K, we employed the VASP [36–39] code to compute the mean EDOS over five uncorrelated snapshots off each MD trajectory. For the planar surfaces and RT13, a 2×2×1 Γ-centred Monkhorst-Pack [40] grid was used to sample the Brillouin zone, and the energy cutoff for the planewave basis was set to 750 eV. For the stepped surface, a 1×3×1 grid was used, and the planewave cutoff energy was set to 500 eV to fulfil memory constraints on the computation. Only a single representative density of states (DOS) computation is presented for this system, due to computational constraints. The projector-augmented wave method was used in all VASP calculations to avoid explicit treatment of the core electrons.

3. Results

In this section, we first present results from our static calculations, including single-molecule adsorption of H₂O onto SrTiO₃. Then, we present results from our MD simulations at finite temperature and higher levels of water coverage.

(a). Static calculations

(i). Bulk SrTiO₃

Results for bulk SrTiO₃ are presented in table 1. For each functional, we find the equilibrium lattice constant (λ) and bulk modulus at zero pressure (B₀) by fitting a third-order Birch–Murnaghan equation of state [44] to a set of (V,E) data points from a set of static NV T calculations on the crystal. Whereas of the GGA-type functionals PBE and BLYP slightly overestimate λ with respect to experiment, PBEsol gives excellent results. LDA in turn slightly underestimates λ. Correspondingly, the GGA functionals give a softer crystal than LDA does, the former being closer to experiment. Overall, these results on the mechanical properties of SrTiO₃ reflect the usual underbinding exhibited by GGA and overbinding given by LDA. For all functionals, the band gap is about 1.5 eV lower than in experiment. Our findings are in agreement with earlier DFT results on SrTiO₃ [45].

Table 1.

Computed equilibrium lattice constant (λ), bulk modulus at zero pressure (B₀) and minimum band gap (E_g) for cubic SrTiO₃ perovskite at static conditions, along with experimental results at 300 K.

functional	λ (Å)	B0 (GPa)	Eg (eV)
LDA	3.86	204	1.75
PBE	3.94	172	1.74
PBE-D3	3.92	176	1.76
PBEsol	3.90	186	1.75
BLYP	3.98	164	1.70
BLYP-D3	3.94	170	1.75
experiment	3.90 [41]	172 [42]	3.25 [43]

(ii). Clean surface in vacuum

As cleaving the SrTiO₃ crystal reveals both the SrO and TiO₂ terminations, we define the surface energy of the bulk-like (001) termination to be [46]

$$\gamma =\frac{1}{2}({\gamma }_{\mathrm{surf}}^{\mathrm{SrO}}+{\gamma }_{\mathrm{surf}}^{{\mathrm{TiO}}_2}),$$ 3.1

where

$${\gamma }_{\mathrm{surf}}^{\mathrm{SrO}}=\frac{E^{\mathrm{SrO}}-N_{{\mathrm{SrTiO}}_3}^{\mathrm{SrO}}{E}_{\mathrm{bulk}}^{{\mathrm{SrTiO}}_3}}{2A},$$ 3.2

here E^SrO being the total energy of the SrO-terminated slab, N_SrTiO3 being the number of bulk unit cells of SrTiO₃ in the slab ($4\frac{1}{2}\times 4\times 4$), $E_{\mathrm{bulk}}^{{\mathrm{SrTiO}}_3}$ being the total energy per unit cell of bulk SrTiO₃, A being the area of each exposed surface of the slab and correspondingly for ${\gamma }_{\mathrm{surf}}^{{\mathrm{TiO}}_2}$. Before relaxing the structure, the symmetry of the surface was broken by introducing small random displacements for the outermost layer of ions on each side of the slab. Then, to find E^SrO and E^TiO₂, we ran conjugate-gradient relaxation on the ionic structure until the total force acting on any ion was below 0.05 eV Å ⁻¹.

The results for the surface energy are given in table 2. Except for BLYP, our results agree broadly with previous DFT calculations on the quantity [13,46,47]. A slight exception is our result for γ obtained using PBE, which is somewhat lower than previously published values. It is possible that by breaking the symmetry of the surface prior to relaxation and allowing displacements of the ions in all spatial dimensions, we have found a slightly more favourable arrangement for the ionic structure.

Table 2.

Computed surface energy of SrTiO₃ in units of eV/surface (1×1) unit cell and J m⁻² (see text) and the minimum band gap of the slab system with either the SrO or TiO₂ termination at static conditions.

functional	γ (eV/1×1)	γ (J m−2)	ESrOg (eV)	ETiO2g (eV)
LDA	1.28	1.33	1.69	0.87
PBE	0.99	1.03	1.68	0.99
PBE-D3	1.23	1.28	1.72	0.94
PBEsol	1.13	1.18	1.64	0.95
BLYP	2.11	2.20	1.81	0.99
BLYP-D3	2.53	2.64	1.82	0.91

We report the mean atomic displacements in the [001] direction (perpendicular to the slab surface) upon relaxation from the bulk-like structure in table 3. Our results are again in good qualitative agreement with previous DFT calculations [13,46–48]. Experimental results are available for the surface rumpling (S), i.e. the relative displacement of O with respect to the metal cation in the outermost plane of the slab (table 4), and the change in the cation–cation distance between neighbouring planes i and j upon relaxation (D_ij, table 5). While for S our results agree with results from low-energy electron diffraction (LEED) [49] and reflection high-energy electron diffraction (RHEED) [50] experiments, overall our calculated values for the quantity D_ij cannot be reconciled with these measurements. We note, however, that the experimental results on D_ij for the first two planes on the SrO termination and the second and third planes on the TiO₂ termination conflict each other on the sign of the displacement D_ij, a discrepancy which has been noted before and the reason for which is not clear [46]. Our values for these structural parameters are again in good agreement with previous calculations [13,46–48].

Table 3.

Mean displacements of ions (in Å) in the [001] direction upon relaxation of the slab from the bulk-like structure.

layer	ion type	LDA	PBE	PBE-D3	PBEsol
SrO termination
1	Sr	−0.19	−0.17	−0.17	−0.22
	O	0.016	0.048	0.052	0.0059
2	Ti	0.059	0.093	0.091	0.047
	O	0.016	0.045	0.044	−0.0048
3	Sr	−0.048	−0.036	−0.039	−0.062
	O	−0.0026	0.017	0.016	−0.014
TiO2 termination
1	Ti	−0.092	−0.096	−0.092	−0.11
	O	−0.016	0.0083	0.0082	−0.029
2	Sr	0.12	0.13	0.12	0.11
	O	0.012	0.0054	0.0028	−0.0064
3	Ti	−0.015	−0.030	−0.030	−0.030
	O	−0.0033	−0.027	−0.028	−0.026

Table 4.

Surface rumpling (S), i.e. the relative displacement of O in the [001] direction with respect to the metal cation in the topmost plane of the slab (in Å).

	this study				experiment
	LDA	PBE	PBE-D3	PBEsol	LEED [49]	RHEED [50]
SrO termination	0.21	0.22	0.22	0.22	0.16±0.08	0.16
TiO2 termination	0.076	0.10	0.10	0.084	0.08±0.08	0.10

Table 5.

Change in cation–cation distance (in Å) between neighbouring planes i and j (D_ij) in the [001] direction upon relaxing the slab.

	this study				experiment
	LDA	PBE	PBE-D3	PBEsol	LEED [49]	RHEED [50]
SrO termination
D12	−0.25	−0.27	−0.26	−0.26	−0.20±0.04	0.10
D23	0.11	0.13	0.13	0.11	0.08±0.04	0.05
TiO2 termination
D12	−0.21	−0.23	−0.21	−0.22	0.04±0.04	0.07
D23	0.14	0.16	0.15	0.14	−0.04±0.04	0.05

(iii). Single-molecule adsorption of H₂O onto SrTiO₃

We present the energy of adsorption of a single molecule of H₂O onto SrTiO₃ from our static conjugate-gradient relaxations (equivalent to a 1/32 ML water coverage of the surface) along with the adsorption energy from previous computational studies (with varying levels of water coverage) in table 6. For each exchange–correlation functional and surface termination, we report the highest, i.e. most favourable adsorption energy in both the molecular and dissociated configurations of the molecule. In the former, water adsorbs as an intact molecule onto the surface, whereas in the latter, the molecule breaks up into an OH fragment and H, and a covalent bond is formed between the H and a surface O ion. We have applied the counterpoise correction to the basis set superposition error in our results for the adsorption energy, the correction being within the range of −0.001 to −0.065 eV molecule⁻¹ throughout all configurations.

Table 6.

The most favourable adsorption energy of H₂O in the molecular (E^mol_ads) and dissociated (E^diss_ads) mode for each bulk-like surface termination of (001) SrTiO₃. Results from previous studies are presented for comparison. The numbers in parentheses for PBE-D3 signify the contribution of dispersion energy in the total adsorption energy given.

	Emolads (eV)	Edissads (eV)	coverage (ML)
SrO termination
PBE	0.64	1.0	1/32
PBE-D3	0.82 (0.46)	1.1 (0.43)	1/32
PBEsol	1.0	1.3	1/32
PBE [11]	—	1.4	1/18
PBE [12]	0.90	1.3	1/8
B3LYP [13]	0.91	0.92	1/2
TiO2 termination
PBE	0.65	0.52	1/32
PBE-D3	0.86 (0.21)	0.94 (0.20)	1/32
PBEsol	0.94	0.99	1/32
PBE [11]	0.72	0.99	1/18
PBE [12]	0.89	1.1	1/8
PBEsol [12]	2.67	2.83	1/8
B3LYP [13]	0.84	0.74	1/2

Our values for these adsorption energies are slightly lower than the previous literature DFT values, a finding we attribute to the much lower effective H₂O coverage in our calculations. Overall the agreement is reasonable and largely within the spread of previous DFT results. A striking difference can be seen, however, between our PBEsol results and those of Hinojosa et al. [12]. The extremely high adsorption energy of 2.67 eV in the latter work is clearly at odds with the present results as well as those of previous studies. The value of 0.92 eV for molecular adsorption onto the TiO₂-termination as deduced [12] from TPD experiments [6] compares well with our corresponding PBE-D3 value of 0.91 eV. In terms of thermodynamics, these static results imply that the SrO termination clearly favours dissociation, while the difference in preference between the molecular and dissociative modes of adsorption is smaller on the TiO₂ termination. We find the dispersion interaction to make up a significant fraction of the total adsorption energy, contributing approximately 0.4 eV molecule⁻¹ on the SrO termination and 0.1–0.2 eV molecule⁻¹ on the TiO₂ termination, thus making up some 20–50% of the total adsorption energy.

The most favourable adsorption geometries for H₂O on each of the two planar surface terminations as given by PBE-D3 are presented in figure 2, along with the electronic charge density in a two-dimensional plane through the molecule. In the molecular adsorption configuration on the SrO termination, we find the O ion of the H₂O molecule to form an ionic bond with an underlying surface cation, with additional attraction to the surface provided by hydrogen bonds donated from the molecule to the surface. In the dissociated configuration, the OH fragment above the surface is bonded to the surface H through a bond of strong covalent character. In the molecular adsorption configuration on the TiO₂ termination, a bond of covalent character is formed between the O in H₂O and a surface Ti cation, in addition to a hydrogen bond between the molecule and the surface. In the dissociated configuration, the O in the OH fragment above the surface is bonded covalently to the surface cation, similar to the molecular case, with the surface proton additionally donating a hydrogen bond to the OH fragment.

Figure 2.

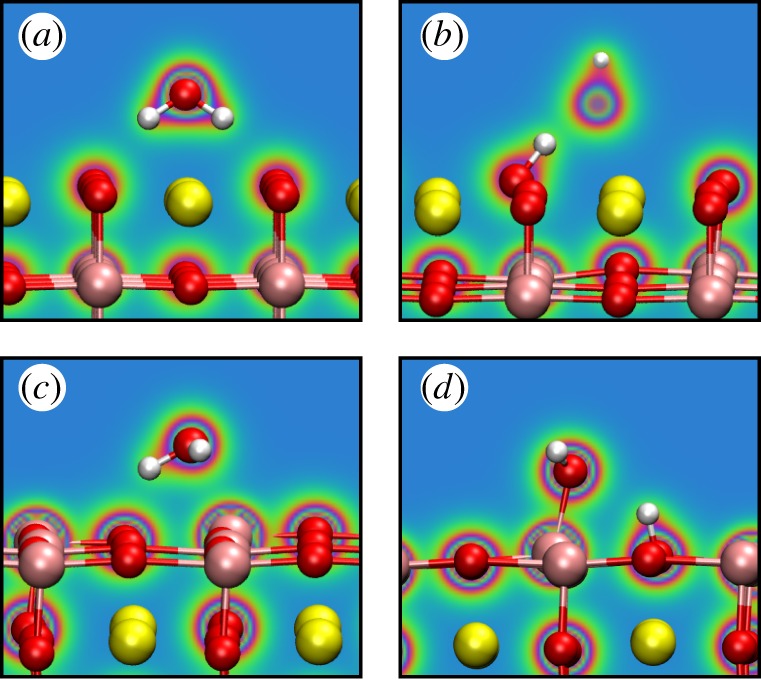
The most favourable adsorption geometries of H₂O onto SrTiO₃, as calculated using PBE-D3, corresponding to the energies in table 6. Colours in the plane indicate electronic charge density, with red being high and blue low. (a) Molecular adsorption onto SrOtermination, (b) dissociative adsorption onto the same, (c) molecular adsorption onto the TiO₂ termination, (d) dissociative adsorption onto the same. The upper oxygen ion in (b) is behind the plane in which the electronic density is plotted. (Online version in colour.)

Based on the presented static results on the SrTiO₃ bulk crystal, the surface in vacuum and H₂O adsorption onto SrTiO₃, we deemed PBE-D3 the overall best functional to use for modelling the SrTiO₃/H₂O solid–liquid interface. Therefore, all simulations to follow were performed using PBE-D3.

(b). Molecular dynamics

(i). Hydration structure

We present the ionic structure of the SrTiO₃/H₂O interface at 0.5 ML, 1.0 ML and bulk H₂O coverage in figures 3, 4 and 5, respectively. Regardless of the level of water coverage and surface termination, the vertical density profiles show that water is strongly structured on the oxide surface, up to at least 7 Å at bulk water coverage. Clear lateral patterns are also evident in the ordering of the water on the surface, as revealed by the histograms of lateral positions. An analysis of the hydration structure of the two surfaces of each slab revealed qualitatively very similar results for the ordering of water and practically identical results for the degree of surface hydroxylation. Therefore, for simplicity, the results presented below are for one surface of each crystal slab. The similarity of results on the two faces of each slab implies that our results for the hydration structure are repeatable and robust.

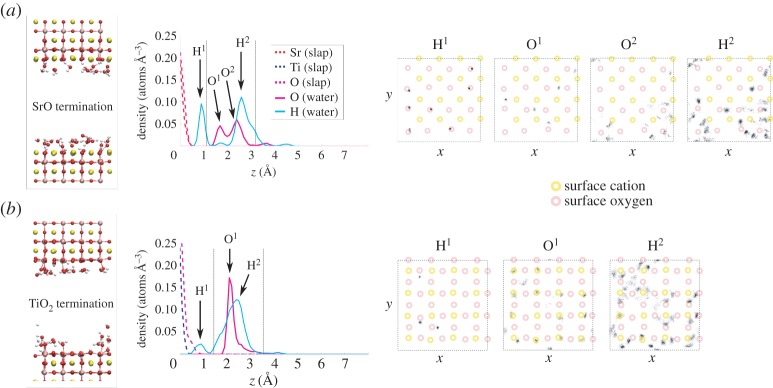
Figure 3.

Results from MD simulations with 0.5 ML of H₂O coverage on the planar SrO termination (a) and TiO₂ termination (b). For each surface, we present a snapshot of the equilibrated structure, the vertical density profile, and the histogram of lateral positions for selected peaks in the hydration structure. In the vertical density profiles, the dashed verticallines denote the first hydration layer. In the lateral position histograms, the surface cation positions are schematically marked by yellow circles and the surface anion positions by red ones. The dashed squares denote simulation cell boundaries. (Online version in colour.)

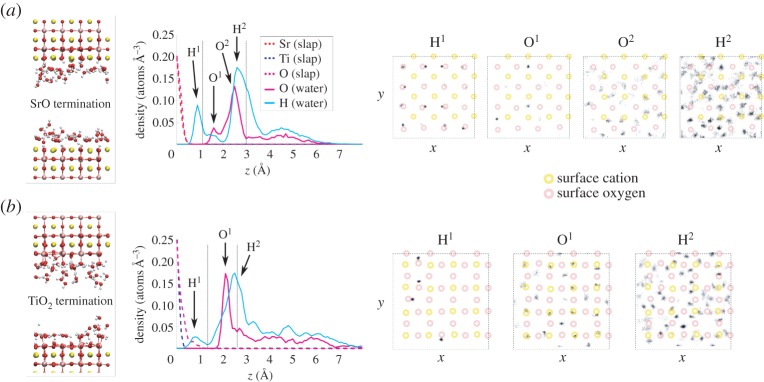
Figure 4.

Results from MD simulations with 1.0 ML of H₂O coverage on the planar SrO termination (a) and TiO₂ termination (b). For each surface, we present a snapshot of the equilibrated structure, the vertical density profile and the histogram of lateral positions for selected peaks in the hydration structure. In the vertical density profiles, the dashed verticallines denote the first hydration layer. In the lateral position histograms, the surface cation positions are schematically marked by yellow circles and the surface anion positions by red ones. The dashed squares denote simulation cell boundaries. (Online version in colour.)

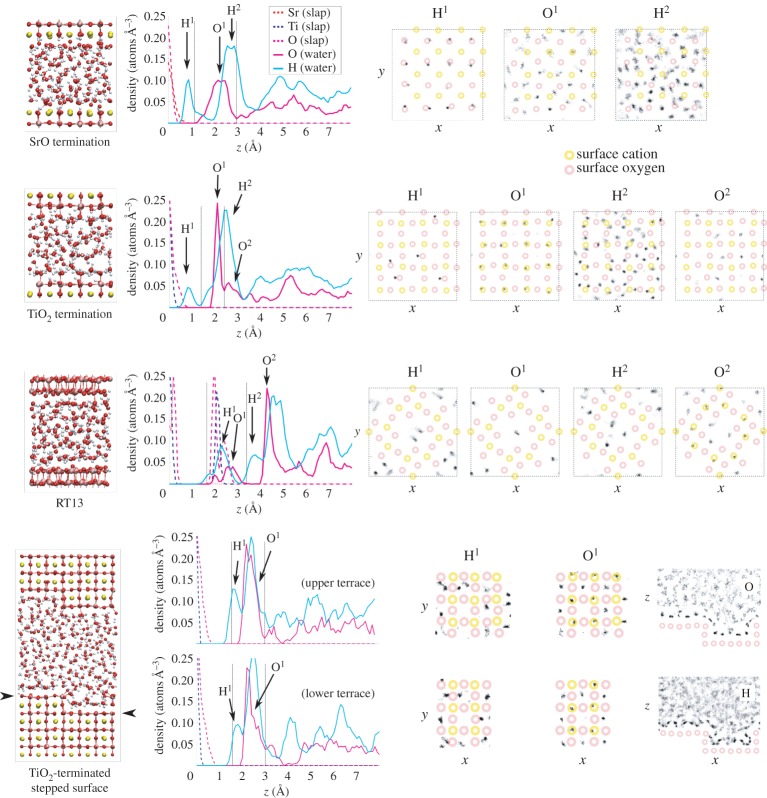
Figure 5.

Results from MD simulations of bulk H₂O coverage on the four studied SrTiO₃ terminations (from top down): planar SrO termination, planar TiO₂ termination, RT13 and stepped TiO₂-terminated (001) surface. For each surface, we present a snapshot of the equilibrated structure, the vertical density profile and the histogram of lateral positions for selected peaks in the hydration structure. In the vertical density profiles, the dashed vertical lines denote the first hydration layer. In the lateral position histograms, the surface cation positions areschematically marked by yellow circles and the surface anion positions by red ones. For the stepped surface, we also show position histograms in the xz-plane. The dashed squares denote simulation cell boundaries. (Online version in colour.)

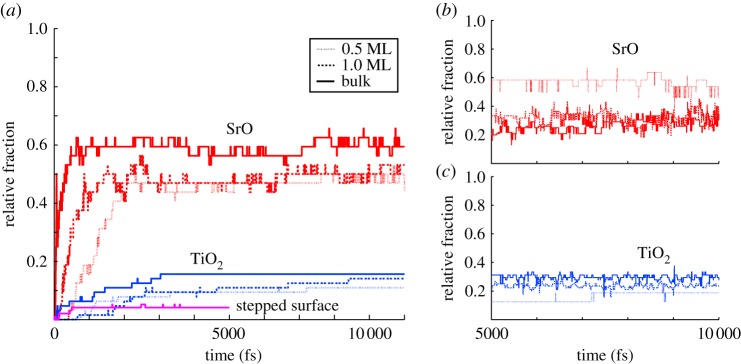
Adsorption of H₂O onto the SrO-terminated surface (figures 3–5) is characterized by a strong tendency for the water to dissociate. Some 50–60% of surface O ions are hydroxylated into OH groups at all water coverages on this termination (figure 6a), the observed large degree of hydroxylation being in qualitative agreement with experiment [8,10]. Also, our static DFT results above as well as previous DFT [11,12] and hybrid functional calculations [13] imply a tendency for water to dissociate, and a slightly lower affinity for molecular adsorption, overall in agreement with the observed strongly mixed mode of adsorption on the SrO termination. The double peak structure of O density seen at low coverages in the first hydration layer (figures 3 and 4) is due to the OH fragments generally assuming a smaller distance from the surface than molecular H₂O. The first hydration layer consists of OH fragments alongside molecular H₂O, the OH dominating this region at 0.5 ML but with a crossover to the molecular component dominating at higher coverages (figures 5 and 6b). The majority of the formed OH fragments are localized in the first hydration layer, the fraction of all OH fragments found in this region of the liquid being 100, 85 and 70% for coverages of 0.5 ML, 1.0 ML and bulk H₂O, respectively. At the lowest coverage of 0.5 ML, we witness some hopping of the OH fragments within the first hydration layer between neighbouring Sr–Sr bridge sites, as observed recently experimentally for dissociated water on the SrO-terminated surface of the perovskite Sr₃Ru₂O₇ [51].

Figure 6.

(a) The fraction of surface O ions which are hydroxylated into OH groups as a function of simulation time for the planar SrO and TiO₂ terminations and the stepped surface (red, blue and magenta, respectively) at all studied water coverages. (b) The fraction of O ions in the first hydration layer of the planar SrO termination which are part of OH fragments as a function of simulation time (after the 5 psequilibration period), the remaining O being part of molecular H₂O. (c) The same for the planar TiO₂ termination. (Online version in colour.)

We find a much lower degree of hydroxylation on the TiO₂-termination (figures 3–5) than on the SrO-termination, with only 10–15% of surface O hydroxylated at all coverages (figure 6a), again in qualitative agreement with experiment [6,8,10]. Our static DFT results, previous DFT [11,12] and hybrid functional [13] calculations indicate an increased tendency for molecular adsorption on the TiO₂ termination with respect to the SrO termination, consistent with the observed shift in the degree of hydroxylation in our MD results. For this surface termination, the first hydration layer is represented at all coverages by a sharp peak in the O density profile (figures 3–5), the peak consisting of both dissociated and molecular H₂O (figure 6c) bound to underlying Ti cations via Ti–O bonds of significant covalent character. The 2 Å distance of this peak from the surface is consistent with results from surface X-ray diffraction experiments of the TiO₂-terminated (001) surface in air, which indicate an overlayer of O (most likely OH) on top of the TiO₂ termination due to adsorbed water vapour [52]. This overlayer was proposed to completely cover the lateral fractional sites (0,0), (0,1/2), (1/2,0) and (1/2, 1/2) of the surface unit cell. At 1.0 ML of water coverage, we find the OH and H₂O to be positioned on most of the cation and some of the bridging O sites (figure 4), and at bulk coverage, O ions of the first hydration layer are on top of the cations (figure 5). Our result for the hydration structure of the TiO₂-terminated surface therefore resembles the surface X-ray diffraction result, but differs crucially in that the overlayer we find does not uniformly cover all surface sites.

Interestingly, although the degree of surface hydroxylation is much lower for the TiO₂-terminated surface than for the SrO termination, the composition of the first hydration layer at bulk water coverage is very similar for the two terminations (some 30% of oxygens belonging to OH fragments, 70% to molecular H₂O, figure 6b,c). This seemingly contradictory result is possible because on the TiO₂ termination, 100% of the OH fragments remain in the first hydration layer, with the total O density of the hydration layer simultaneously being lower than on the SrO termination. All in all, the mode of adsorption is a mixed case of molecular and dissociated H₂O for both terminations at all coverages.

On the RT13 surface (figure 5), water adsorbs almost entirely in the molecular mode, in the first hydration layer filling the cavities between the crests formed by TiO₅ polyhedra on the surface reconstruction (figure 1). This layer of H₂O binds to the surface structure mainly through hydrogen bonding. In the second hydration layer, the adsorbed H₂O forms O–Ti bonds of partly covalent character with the topmost surface cations and also occupies volume above the central cavity of the surface unit cell, the cavity already being occupied by a single water molecule in the first hydration layer. In this system, at the central cavity of the surface reconstruction, we observe a single dissociation event of the form ${\mathrm{H}}_2\mathrm{O}+{\mathrm{H}}_2\mathrm{O}+{\mathrm{H}}_2\mathrm{O}\to {\mathrm{H}}_3\mathrm{O}+{\mathrm{H}}_2\mathrm{O}+\mathrm{OH}$, where no stable surface OH group is formed. We discuss the mechanism behind this event in §4.

The stepped TiO₂-terminated surface (figure 5) also induces a low degree of dissociation of the incident H₂O, again in agreement with experiment [10]. Some 5% of all surface O ions are hydroxylated (figure 6a), these being observed at both terrace and edge sites in the system. Dissociation at step sites has been suggested from experiment decades ago [9], and indeed step edge anion sites are more likely than terrace sites to be hydroxylated in our simulations (1/6 of all step sites being hydroxylated versus 1/30 of terrace sites). The vertical density profiles at the terraces reveal a broader first hydration layer than on the planar TiO₂ termination, with H₂O positioned both on top of the Ti sites through partly covalent bonds and on top of the underlying Sr sites, bonded by hydrogen bonding and dispersion to the crystal surface. This configuration is closer to the hydration structure of TiO₂-terminated SrTiO₃ suggested by Vonk et al. [52] than what we find for the planar TiO₂ surface. We observe strong covalent Ti–H₂O bonding at the step edges alongside the hydroxylated edge anions. Finally, H₂O molecules are strongly hydrogen-bonded to the crystal at the lower corner where the upper and lower terraces meet.

(ii). Electronic structure

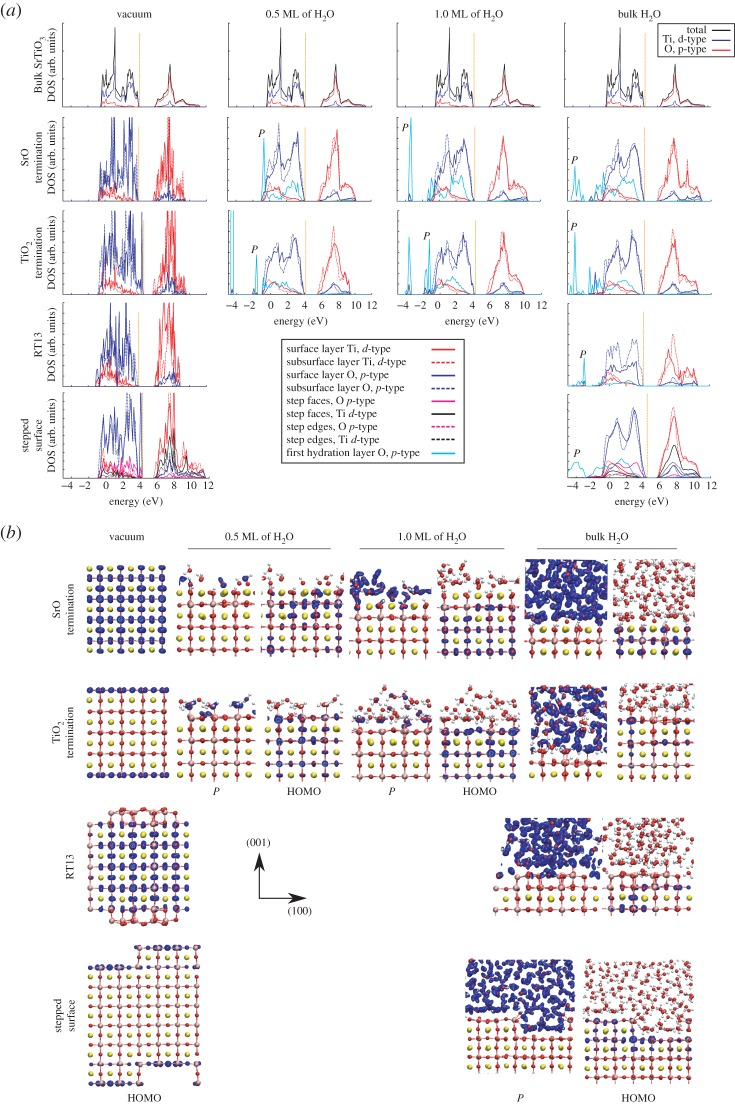
In figure 7a, we present the EDOS for bulk SrTiO₃, the SrTiO₃ surface in vacuum and the surface under H₂O coverage. In all simulated systems, the valence band is dominated by O 2p orbitals and the conduction band by Ti 3d states. The EDOS projected onto either the planar SrO-terminated or RT13 surface is very similar to that of bulk SrTiO₃, including the magnitude of the band gap. The planar and stepped TiO₂-terminated surfaces, however, reveal strongly localized sets of shallow O gap states of p_x and p_y character at the bottom of the band gap. We attribute this difference between the SrO and TiO₂ terminations to the fact that on the SrO termination, all Ti–O₆ octahedra remain intact, while on the TiO₂ termination, the undercoordinated Ti–O₅ polyhedra exposed on the planar surface lead to the formation of the observed ‘dangling bonds’. While such dangling states have been predicted also in earlier DFT studies [48,53–55], they have not been observed in experiment to date. We note that this feature in the EDOS is completely removed already at 0.5 ML of H₂O coverage, and we find even a 1/32 coverage at static conditions to substantially subdue the peak at the bottom of the band gap. Furthermore, these shallow gap states are fully due to the outermost SrTiO₃ layer of the slab, with no contribution from lower lying atomic planes. For these reasons, the present feature may have escaped experimental observation. Interestingly, on the RT13 surface, we see no such dangling states, despite an excess of Ti–O₅ polyhedra on the surface. Instead, the EDOS on the RT13 surface hints that the surface layer is actually more stable than the subsurface layer. It is clearly the particular geometry of the reconstruction which allows for the stability of the surface states and the low surface energy we find for RT13 (0.815 J m⁻²) with respect to the SrO and TiO₂ terminations (1.28 J m⁻², table 2).

Figure 7.

(a) The electronic density of states (EDOS) of the SrTiO₃ surface in vacuum and the surface at different levels of H₂O coverage. The EDOS of bulk SrTiO₃ and the surface in vacuum are from static geometric relaxations, results for the systems with H₂O are from MD. All EDOS involving the surface arealigned to the valence and conduction bands of bulk SrTiO₃ (also shown). The Fermi level is indicated by the dashed orange line. (b) Visualization of the charge density for the surface systems in (a) within an energy window down to 0.5 eV below the Fermi level (HOMO) and for the indicated set of states due to the first hydration layer (denoted by P in (a)). We plot the isosurface of the charge density (in blue) at 10% of the maximum density. For definitions of the surface and subsurface layers, see figure 1. (Online version in colour.)

The electronic states due to the first hydration layer overlap significantly in energy with the valence band energy range for all surfaces and coverages. In addition to these broad bands of Op character, states due to the first hydration layer appear at the bottom of the valence band and also below the valence band minimum upon adsorption of H₂O (denoted by P in figure 7a). On all surfaces, these sharp features in the EDOS are due to O–H bonds in surface OH groups, in OH fragments within the liquid, in H₂O within the liquid, as well as the lone pair charge density in both OH fragments and molecular H₂O (figure 7b).

The band gap of the surface-projected EDOS generally changes by some 0.1 to 0.2 eV upon introduction of the water, decreasing for the stepped TiO₂-surface but increasing for the SrO-terminated and RT13 surfaces. An exception to this is the planar TiO₂-terminated surface, where the band gap increases by approximately 0.5 eV upon saturation of the dangling bond states. These results are, with the exception of the TiO₂-terminated crystal, similar to previous results on rutile TiO₂ (110) [56]. For rutile TiO₂ (110), it was found that the conduction band edge shifts upwards in energy by 1.6 eV upon the adsorption of a monolayer of water [56]. Similarly, we find an upward shift of 0.7 eV for the conduction band minimum of our TiO₂-terminated crystal upon introduction of a monolayer of water, assessed by aligning the computed Kohn–Sham states to the vacuum level between periodic slab surfaces. For the SrO-terminated crystal, in contrast, we find the conduction band minimum to shift downwards by 1.3 eV when a monolayer of water is adsorbed onto the surface. It is clearly the different character of Ti–O and Sr–O bonding which is responsible for the observed difference.

The orbital structure of the top of the valence band (highest occupied molecular orbitals, HOMO) remains fairly intact on the SrO termination upon adding H₂O. By contrast, the dangling surface HOMO states of the TiO₂-terminated slab are stabilized upon introducing the H₂O, as the surface Ti–O₅ polyhedra are effectively made into coordination-saturated Ti–O₆ octahedra. The HOMO then resembles that of the SrO-termination, as can be expected. On the RT13 surface, the interaction between the H₂O and the surface stabilizes the highest energy orbitals of the very top layer of the reconstruction to energies below those of the subsurface layer, leaving the latter to form the HOMO. The H₂O molecules sitting in the cavities of the surface evidently induce a very favourable crystal-to-liquid interaction, which is thus seen in the EDOS.

(iii). Vibrational properties

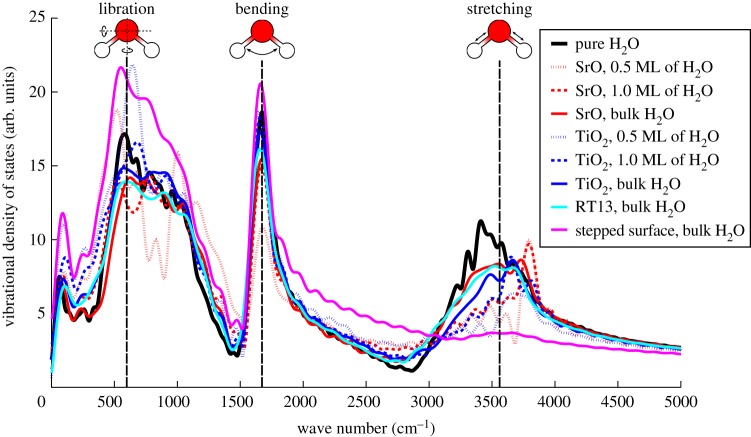
We present the VDOS of H₂O on each of the four surfaces at all considered water coverages in figure 8. In addition, for reference, we plot the computed VDOS of pure H₂O and the frequencies of the vibrational modes of liquid H₂O as found in experiment [34]. Focusing first on the planar and RT13 surfaces, it is immediately apparent that introducing the SrTiO₃ crystal and forming the solid–liquid interface induces significant changes into the vibrational mode as well as the O–H stretching mode of H₂O with respect to pure bulk H₂O. These changes in the VDOS are the largest at the lowest levels of H₂O coverage, which is to be expected, as the strength of the surface-to-molecule interaction per molecule is highest then.

Figure 8.

The vibrational density of states (VDOS) of H₂O on SrTiO₃ for all studied surfaces and all levels of water coverage, along with the VDOS for a pure, periodic supercell of liquid H₂O. The dashed vertical lines are results for the vibrational modes of liquid H₂O from experiment [34]. (Online version in colour.)

Redshifting, i.e. broadening of the low-frequency shoulder of the O–H stretching band is observed for the SrO, TiO₂ and RT13 surfaces at all levels of water coverage. The fundamental reason behind this effect is the weakening of O–H bonds in H₂O due to the molecules donating hydrogen bonds to surface O ions [57–59]. As is well known from previous work on, e.g. TiO₂ [57,58], the stronger the water-to-water or water-to-surface hydrogen bonding, the weaker the covalent O–H bonding within H₂O, and hence the lower the O–H vibrational frequencies. Therefore, as expected, the redshifting effect is strongest for monolayer and sub-monolayer H₂O coverages, where more acceptors of hydrogen bonds are available on the surface per molecule of H₂O than in the case of bulk water coverage. High-resolution electron energy loss spectroscopy experiments find the O–H stretching peak at 3662 cm⁻¹ to become broader and move towards lower energies as water coverage is increased [59]. These observations, reported with respect to the sharp stretching peak of an isolated molecule of H₂O, are consistent with our VDOS results.

Interestingly, we also find a slight blueshifting of the high-frequency shoulder of the O–H stretching band beyond approximately 3700 cm⁻¹ for the case of the SrO-terminated surface. An analysis of the individual velocity autocorrelation functions of H ions reveals that this feature in the VDOS is due to the strong covalent O–H bond of the OH fragments within the liquid. As shown in figure 6, a larger fraction of H₂O dissociates on the SrO than on the TiO₂ termination, which then leads to the blueshifting effect being seen more prominently on the former surface termination.

A conspicuous effect is seen for the vibrational spectrum of H₂O on the stepped TiO₂-terminated surface. The VDOS is altered so that the O–H stretching band is strongly subdued, with the libration band instead being strengthened significantly. While exceptionally strong hydrogen bonding between the H₂O and the surface and ensuing weakening of the O–H bonds within the liquid might explain such a curious effect, we explore other options in §4.

(iv). Proton dynamics

We find various different kinds of proton transfer events taking place in our dynamical simulations. The first type of event is observed in the initial phase of the simulation, at the onset of the dissociation process, when a fraction of the water molecules incident on the slab surface each donate a proton to a surface oxygen. Concurrent to this process, we see resulting OH fragments and neighbouring H₂O molecules exchanging protons in the liquid region of the system. After reaching equilibrium, this latter process continues. Furthermore, in equilibrium, we observe a process where a surface proton is captured back up into the liquid by a nearby OH fragment and then donated back down to the surface again.

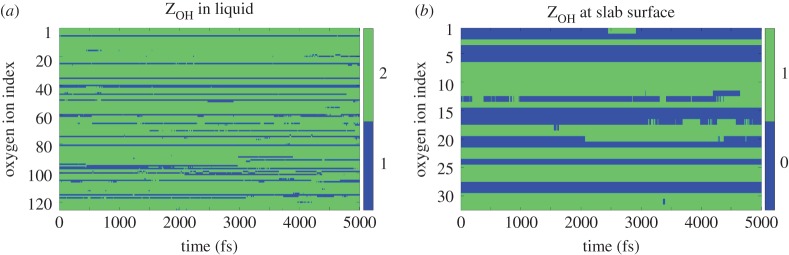
To quantify the rate of these proton transfer events in our simulations, we track the O–H coordination in each system as a function of time. For a given oxygen ion i in the liquid, a change from 2 to 1 in the O–H coordination number Zⁱ_OH is considered a proton donation event, a change from 1 to 2 conversely being considered a proton acceptance event. Correspondingly, for surface oxygens, a change of Zⁱ_OH from 1 to 0 implies a proton donation event and 0 to 1 means acceptance. We find all other changes of Z_OH to have a negligible presence in our simulations.

As an example, in figure 9a,b we plot Zⁱ_OH for all oxygen ions in the liquid and in the slab surface, respectively, for the SrO-terminated SrTiO₃ surface at bulk H₂O coverage. From these data, we compute the mean rate of proton transfer events (treating all donation and acceptance events as separate transfer events), the results being presented for all the relevant simulations in table 7. To enable additional insight, the results are separated into the rate of proton jump events involving oxygens in the liquid region and those involving oxygens in the slab surface, along with the total rate which is the sum of these two. Also, the rates are presented in units scaled by the number of dissociated H₂O molecules in each simulation as well as in units scaled by surface area. Two inferences are immediately apparent. First, in equilibrium, proton transfer takes place mainly among oxygens within the liquid region, the transfer of protons between surface and liquid oxygens being much less efficient for water on all considered surfaces. Second, proton transfer is much more efficient on the SrO termination than either on the planar or stepped TiO₂ termination. We also note that no proton transfer is observed to take place directly between hydroxylated surface oxygens.

Figure 9.

The O–H coordination of oxygen ions as a function of time (after the 5 ps equilibration period) for the SrO-terminated SrTiO₃ slab with bulk H₂O coverage. Results are shown for O ions (a) between the two periodic slab surfaces, i.e. in the liquid region and (b) in the outermost surface layer of the slab. (Online version in colour.)

Table 7.

Mean rate of proton transfer events in all simulated systems, in units of ‘jumps per ps per OH fragment’ and ‘jumps per ps per (1×1) surface unit cell’. Proton transfer events involving changes in O–H coordination for O in the liquid and within the surface are separated.

	jumps/ps/OH			jumps/ps/(1×1)
	0.5 ML	1.0 ML	Bulk	0.5 ML	1.0 ML	Bulk
oxygen in liquid
SrO termination	5.1	13	7.4	2.4	6.3	4.3
TiO2 termination	0.82	1.3	2.2	0.17	0.33	0.69
stepped surface	—	—	2.2	—	—	0.25
RT13	—	—	24	—	—	0.91
oxygen at slab surface
SrO termination	0.58	1.4	0.96	0.28	0.65	0.56
TiO2 termination	0.092	0.050	0.00	0.019	0.013	0.00
stepped surface	—	—	0.75	—	—	0.083
RT13	—	—	2.8	—	—	0.11
total
SrO termination	5.7	14	8.3	2.7	6.9	4.8
TiO2 termination	0.91	1.4	2.2	0.19	0.34	0.69
stepped surface	—	—	3.0	—	—	0.33
RT13	—	—	26	—	—	1.0

4. Discussion

Our DFT MD results show that although the degrees of surface hydroxylation on the planar SrO- and TiO₂-terminated (001) surfaces of SrTiO₃ are very different, the hydration layer in closest proximity to the surface has a similar composition in terms of H₂O and OH in the two cases. However, while the lateral ordering of the liquid on the SrO termination appears close to amorphous, the TiO₂ termination leads to a lattice-like configuration of OH and H₂O covalently bonded to underlying surface cations. These two archetypal surfaces of SrTiO₃ therefore present both striking similarities and differences in hydration structure. Introducing a stepped geometry to the surface leads to covalent bonding between the step edge and incident H₂O and a large density of hydrogen-bond acceptors at the bottom of the step. A qualitatively different situation is found on the RT13 surface, where the lowest lying hydration structure appears completely dominated by the surface corrugation due to the ordering of Ti–O₅ octahedra on the surface, and H₂O remains molecular. The second hydration layer of RT13 already appears dictated by Ti–O bonding, as in the case of the planar TiO₂ termination.

The degree of surface hydroxylation varies in descending order from the planar SrO termination to the TiO₂ termination and finally to the stepped TiO₂-terminated surface. We explain this trend in the basicity of the three surfaces by differences in the ionicities of the bonds between surface cations and anions among the surfaces. In bulk SrTiO₃, the Sr–O bond is known to be much more ionic in character than the Ti–O bond [41,45], a finding we confirm in our own calculations of the bulk crystal. On the surface in vacuum, our computed Bader charges show that this inherent difference in the character of Sr–O and Ti–O bonding leads to the O ion of the planar SrO termination assuming a higher mean accumulation of charge (−1.28 e) than O on either the planar (−1.15 e) or stepped TiO₂ termination (−1.13 e). The more negative the O charge, the stronger the hydrogen-bonding between the average surface anion and the liquid, and therefore the higher the degree of dissociation of H₂O and the basicity of the surface. In table 8, we tabulate the degree of dissociation in units of dissociated molecules per surface anion (as above) alongside the number of dissociated molecules per surface bulk-like (1×1) unit cell.

Table 8.

The equilibrium number of dissociated H₂O molecules per (1×1) surface unit cell and per surface anion in each simulation.

	molecules/(1×1)			molecules/surface O
	0.5 ML	1.0 ML	bulk	0.5 ML	1.0 ML	bulk
SrO termination	0.47	0.48	0.58	0.47	0.48	0.58
TiO2 termination	0.21	0.25	0.31	0.11	0.13	0.16
stepped surface	—	—	0.11	—	—	0.042
RT13	—	—	0.002	—	—	0.0005

Sprik and co-workers have analysed the degree of dissociation of water at solid–liquid interfaces according to the acidity of available hydroxide groups on the crystal surface [56,60]. Specifically, they have shown [56] that the free energy of water dissociation on rutile TiO₂ (110) can be expressed as

$$\mathrm{\Delta }A=2.30k_{\mathrm{B}}T(p{K}_{a1}-p{K}_{a2}),$$ 4.1

where pK_a1 and pK_a2 are the acidities of the two types of sites capable of binding protons under normal pH conditions, these sites being the hydroxylated fivefold coordinated Ti site (Ti–OH⁻) and the bridging oxygen sites. Considering the planar SrO- and TiO₂-terminated surfaces of SrTiO₃, our simulations clearly indicate a favourable (i.e. negative) free energy of water dissociation on both surfaces. If we identify two active sites for each surface, a surface-bound OH fragment (bound to the Ti cation on the TiO₂-terminated surface and more loosely bound at bridging Sr–Sr sites on the SrO-terminated surface) and the oxygen anion of the crystal surface, the favourable free energy of dissociation implies that on both surfaces, it is the surface anion which is more basic of the two active sites. Correspondingly, molecularly bound H₂O can be considered more acidic than a surface-anion-to-H group on both terminations of SrTiO₃.

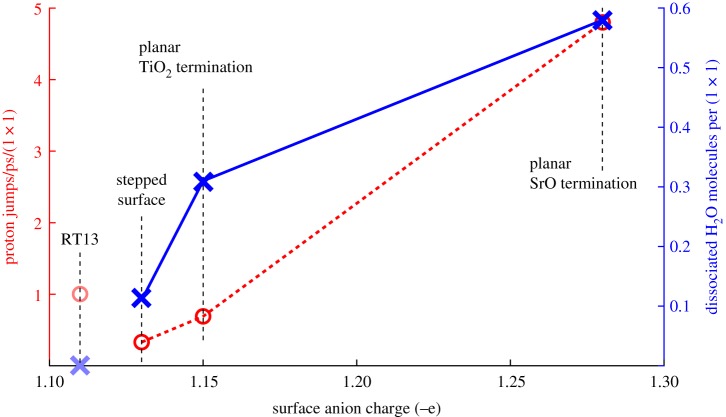
Proton transfer rates were found to be much higher on the SrO-terminated surface than on the TiO₂-terminated planar and stepped surfaces, both between the surface and liquid and within the liquid region. We identify two effects to this end. First, a larger fraction of incident H₂O dissociates on the SrO termination, which simply implies more available hopping sites for protons jumping from H₂O to OH or from surface OH to liquid OH to form molecular H₂O. The second effect is more subtle. It is known that oxygen ions which donate hydrogen bonds accumulate electronic charge at the site of the oxygen ion [61], making strong hydrogen bond donors also strong hydrogen bond acceptors. As noted above, the SrO-terminated surface is the strongest acceptor of hydrogen bonds from the liquid among these three surfaces, which implies that this charge accumulation on the liquid O ions will be strongest on the SrO surface. This strengthens hydrogen-bonding within the liquid region [61], which we see as a smaller mean hydrogen bond length on the planar SrO termination than on the TiO₂ one (1.60 Åversus 1.65 Åat 0.5 ML of water coverage, with the same trend visible for higher coverages and the stepped surface displaying the weakest hydrogen bonds). The decreased hydrogen-to-hydrogen-bond-acceptor distance implies a lower barrier for proton transfer and hence an increased rate. We note that both of the effects contributing to the high proton transfer rate on the planar SrO-terminated surface (higher fraction of dissociation, decreased hydrogen bond length) are thus ultimately attributable to the higher ionicity of the Sr–O bond as compared with the Ti–O bond in the surface of the crystal. In figure 10, we illustrate the clear trend in proton transfer rate and the affinity for water dissociation with respect to the surface anion charge.

Figure 10.

The number of dissociated H₂O molecules per surface (1×1) unit cell and the mean proton transfer rate at bulk H₂O coverage as a function of surface anion charge for the surface in vacuum. The RT13 surface does not follow the same trends in degree of dissociation and proton transfer rate with anion charge as the other surfaces do (see text). (Online version in colour.)

The RT13 surface fails to obey this simple analysis, displaying the lowest surface anion charge (−1.11 e) and correspondingly the lowest degree of dissociation (0.002 molecules/(1×1)), yet having the smallest hydrogen-bond length in the liquid, and correspondingly higher proton transfer rates (1.0 jumps/ps/(1×1)) than the TiO₂-terminated surfaces, despite only a single dissociation event occurring in the system during the simulation. This discrepancy with respect to the other surfaces is likely due to the unusual corrugation of RT13 and the qualitatively different process of dissociation (${\mathrm{H}}_2\mathrm{O}+{\mathrm{H}}_2\mathrm{O}+{\mathrm{H}}_2\mathrm{O}\to {\mathrm{H}}_3\mathrm{O}+{\mathrm{H}}_2\mathrm{O}+\mathrm{OH}$ instead of ${\mathrm{H}}_2\mathrm{O}+\mathrm{O}\to \mathrm{OH}+\mathrm{OH}$) observed on this surface. We suggest that the dissociation process we witness on the RT13 surface, whereby a chain of three H₂O molecules, the first one of which sits inside the central cavity of the surface (figures 1 and 5), breaks up into H₃O in the cavity and H₂O and OH above the cavity, can be explained from the above mechanism of strong hydrogen bond donors becoming strong acceptors. In this view, the H₂O initially inside the cavity is ideally positioned to form strong hydrogen bonds to the O ions at the edge of the central cavity. The strength of these hydrogen bonds then propagates through the chain of three molecules, the last one which ends up donating a proton down the chain to the H₂O in the cavity.

As shown in figure 9a,b, the analysis method for proton transfer rates in our simulations, based on a hard cutoff for O–H coordination, produces some noise into Zⁱ_OH, presumably when a proton is in transition between two O ions. Therefore, the absolute rates of proton jump events presented here are probably overestimates of the actual rates implied by our simulations. In addition, our DFT MD method is by definition a framework of classical nuclear dynamics, whereas taking into account the quantum nature of the proton may be important for the kinds of transfer processes described here [62]. Regardless of these shortcomings, we expect trends in the presented rates between the different regions in the systems (water, surface) and between different surface terminations to be robust. Proton transfer rates of 1.6 jumps/ps/(1×1) or 2.7 jumps/ps/OH found for the rutile TiO₂ (110) surface from DFT MD [61] are within the range of rates that we find here on SrTiO₃.

The drastic effect seen in the VDOS of H₂O on the stepped TiO₂-terminated surface (figure 8) does not seem explainable by the mean strength of surface-to-water hydrogen bonding, because as noted above, hydrogen bonding within this system is weaker than on the planar surfaces, where changes in the VDOS of H₂O upon forming the solid–liquid interface are much smaller. Clearly, the stepped geometry of the surface is an important factor in the observed difference between the two TiO₂-terminated systems. The hydration structure on both surfaces shows a grid-like ordering of O ions on top of the Ti sites (figure 5), but on the stepped surface, this lattice-like Ti-O ordering is complemented by O sitting on the bridging O sites within the same layer, whereas on the planar surface these two components to the vertical density profile are clearly separated. While such an adsorbed grid-like arrangement of O and OH on the stepped surface might lead to the observed anomalous vibrational properties of H₂O in the system, the actual mechanism for this is unclear. We have recently observed a similar effect for H₂O adsorbed onto the (210) surface of brookite TiO₂, and further work is needed to fully understand this feature in the vibrational spectrum of the adsorbed H₂O.

Finally, we examine the significance of our results for the efficiency of photocatalytic water-splitting using SrTiO₃. While electron/hole transfer is generally considered the rate-limiting step for water-splitting using metal-oxide photocatalysts [63], it is interesting to analyse the reaction in terms of proton transfer. We focus on the reduction of H⁺ into H via the electron of the electron-hole pair photogenerated in the SrTiO₃ anode [3]. To the extent that rate of this reaction, $2{\mathrm{H}}^{+}+2e^{-}\rightleftharpoons {\mathrm{H}}_2$, depends on diffusivity of the protons within the solid–liquid interface, higher rates of proton hopping imply higher rates of 2H⁺ reduction. Comparing the proton hopping rates among the different surfaces at bulk water coverage (in units of jumps/ps/(1×1), table 7), it would seem that the SrO-terminated crystal should provide highest efficiency for the reduction process. However, the high reactivity of the surface to H₂O seen as the high degree of surface hydroxylation (table 8) implies that the SrO-terminated surface is not stable with respect to water exposure. RT13, on the other hand, provides a higher rate of proton transfer than the TiO₂-terminated surfaces do, as well as an extremely stable surface, which makes it the most promising candidate for efficient photocatalysis of the surfaces considered here.

5. Conclusion

We used dispersion-corrected DFT MD to predict the structural, electronic and vibrational properties of the SrTiO₃/H₂O solid–liquid interface. A strongly mixed mode of molecular and dissociative adsorption is found on the planar SrO- and TiO₂-terminated (001) surfaces, with a low and negligible degree of dissociation on the stepped TiO₂-terminated and RT13 surfaces, respectively. The ordering of adsorbed water appears dictated by covalent-like surface-cation-to-H₂O bonding and surface corrugation on the various studied SrTiO₃ surfaces. The electronic structure of the solid–liquid interface is featureless in the band gap region, and the vibrational spectrum exhibits features traced back to liquid-to-surface hydrogen bonding and the vibrational frequency of OH fragments in the liquid. We find the inherent difference in the ionicity of the Ti–O and Sr–O bonds of the SrTiO₃ crystal to qualitatively explain observed trends in proton transfer rates and degrees of dissociation of water among the studied surfaces. Based on surface reactivity and proton mobility at the solid–liquid interface, RT13 is suggested to be more suitable than the TiO₂- or SrO-terminated SrTiO₃ surfaces for photocatalytic water-splitting.

Data accessibility

All relevant information and data for reproducing and verifying the results of this work are contained in the manuscript.

Authors' contributions

E.H. designed and performed the simulations and analysis. P.S. and A.S.F. supported the simulations and analysis. A.S.F. conceived the study. All authors contributed to writing the article and gave final approval for publication.

Competing interests

We have no competing interests.

Funding

We were funded through the Academy of Finland through the Centres of Excellence Program (Project No. 251748).