Inevitability and containment of replication errors for eukaryotic genome lengths spanning megabase to gigabase

Significance

Errors in DNA replication can never be completely avoided. By combining a minimal model that takes into account the positions of replication origins (the regions on the DNA where replication initiates) with experimental evidence, we show that genome size strongly influences the frequency of replicative errors. Our work reveals that (i) simple eukaryotes are able to achieve a very low probability of replicative errors by having a moderate number of origins placed at regular intervals; (ii) this strategy is ineffective in eukaryotes with larger genomes, such as human, for which replicative errors are inevitable; and (iii) in these organisms, even moderate numbers of origins can provide containment of replication errors to very low levels, which can be repaired subsequently.

Abstract

The replication of DNA is initiated at particular sites on the genome called replication origins (ROs). Understanding the constraints that regulate the distribution of ROs across different organisms is fundamental for quantifying the degree of replication errors and their downstream consequences. Using a simple probabilistic model, we generate a set of predictions on the extreme sensitivity of error rates to the distribution of ROs, and how this distribution must therefore be tuned for genomes of vastly different sizes. As genome size changes from megabases to gigabases, we predict that regularity of RO spacing is lost, that large gaps between ROs dominate error rates but are heavily constrained by the mean stalling distance of replication forks, and that, for genomes spanning ∼100 megabases to ∼10 gigabases, errors become increasingly inevitable but their number remains very small (three or less). Our theory predicts that the number of errors becomes significantly higher for genome sizes greater than ∼10 gigabases. We test these predictions against datasets in yeast, Arabidopsis, Drosophila, and human, and also through direct experimentation on two different human cell lines. Agreement of theoretical predictions with experiment and datasets is found in all cases, resulting in a picture of great simplicity, whereby the density and positioning of ROs explain the replication error rates for the entire range of eukaryotes for which data are available. The theory highlights three domains of error rates: negligible (yeast), tolerable (metazoan), and high (some plants), with the human genome at the extreme end of the middle domain.

The proper maintenance of genetic information is of fundamental importance to the survival of all organisms, and many molecular mechanisms exist to ensure that the genetic sequence encoded by DNA is maintained unaltered generation after generation (1–3). To preserve the integrity of genetic information and to avoid aberrant ploidy, it is crucial that the entire DNA is copied exactly once; replicating only part of the DNA results in potential corruption of genes, and replicating certain parts of the DNA more than once would perturb chromosome structure and strongly affect gene dosage (4–6). Not surprisingly, regions of underreplicated and overreplicated DNA are common in cancer (7, 8).

DNA replication is a particularly complex process in eukaryotic organisms with large genomes distributed across multiple chromosomes. Multiple checkpoints exist to ensure that, once replication starts, the whole DNA is faithfully replicated before the chromosomes are segregated. Underreplication and overreplication of DNA are prevented by using predefined points of replication initiation called replication origins (ROs) (3, 9).

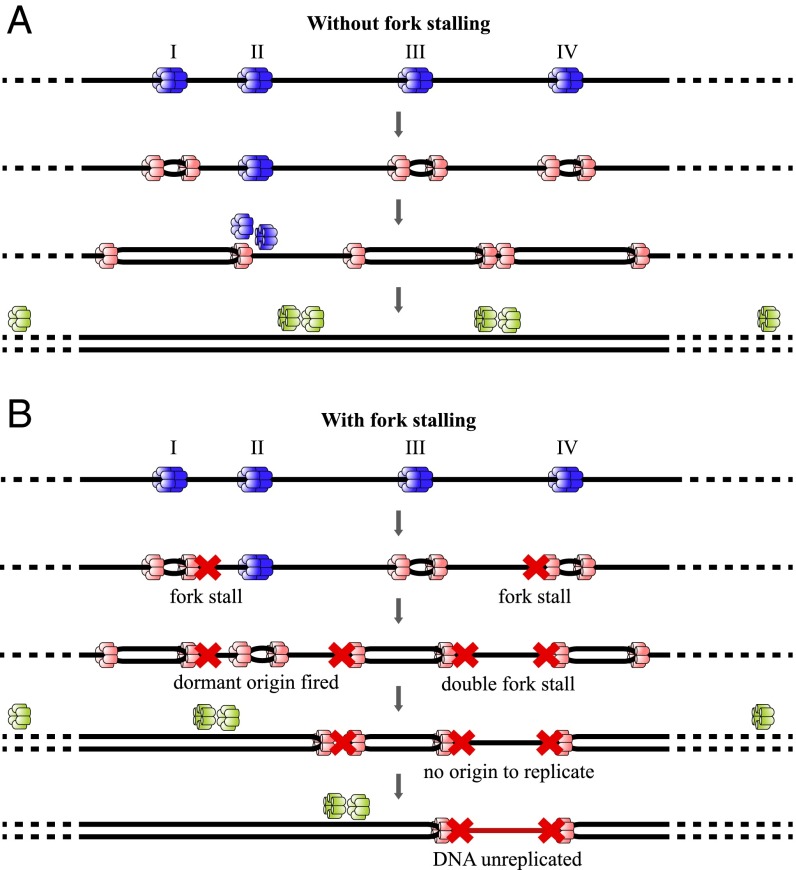
During late mitosis and the G1 phase of the cell division cycle, each potential RO is “licensed” for a single initiation event by being loaded with minichromosome maintenance proteins 2–7 (MCM2-7) double hexamers. To prevent rereplication of DNA segments, the ability to license new origins ceases before cells enter S phase. During this phase, hundreds to thousands of licensed ROs are activated throughout the genome (10). Bidirectional replication forks (RFs) are established at active ROs, each driven by a single MCM2-7 hexamer, allowing DNA polymerases to copy the DNA (Fig. 1A). Despite being highly reliable molecular machines, RFs can, on rare occasions, irreversibly stall (11). The activation of additional ROs can overcome the problem of irreversibly stalled RFs, as a new fork will eventually meet the stalled one, hence replicating all of the intervening DNA. However, if adjacent right-moving and left-moving forks stall and no additional ROs are available between them, the DNA in between the two forks will remain unreplicated (Fig. 1B). This phenomenon constitutes a major replication error for the cell, which is commonly called a double-fork stall (DFS) (Fig. 1). The occurrence of DFSs is therefore a key obstacle for cells to either avoid or overcome to maintain replication fidelity. The molecular processes underlying the management of DFSs are an active field of study, and insults to these processes have been associated with different pathologies (11–13).

Fig. 1.

Potential outcomes arising from ROs licensed on a DNA segment. DNA is denoted as a single black line. Before S-phase entry, four origins (denoted by I, II, III, and IV) are licensed by binding a double hexamer of MCM2-7 proteins (blue). As an origin fires, both MCM2-7 single hexamers are converted into an active Cdc45, Mcm2-7, and GINS complex helicase (pink). (A) RO II is dormant and passively replicated by the fork coming from RO I; replication is complete. (B) Red crosses depict the fork-stalling. Previously dormant RO II is fired to complete the replication of DNA between stalled forks. However, as there is no RO licensed between RO III and IV, the DNA between two stalled forks in this part remains unreplicated, and complete replication is compromised. Adapted from ref. 14.

In our previous work, we introduced a simple probabilistic theory to determine the probability of replication failure arising from DFSs for a given set of ROs in a genome (14). The theory depends on two key assumptions, i.e., that the cell has no time constraint in completing the process (i.e., that all licensed ROs are allowed to be activated as necessary) and that there is a constant small probability per nucleotide for each individual replication fork to irreversibly stall. Mathematical analysis of the theory showed that, in organisms with a genome length comparable to yeasts ($\sim$ 10 Mbp), evenly distributing the ROs throughout the genome optimally reduces the replication errors due to irreversible fork-stalling to levels observed in experiments. In accordance with the theoretical prediction, a strong bias toward evenly distributed ROs was observed in biological data derived from different yeast species (14). The theory relies on a single unknown parameter, the median stall distance (denoted by $N_s$), which describes the typical stalling distance of RFs in eukaryotes (14). Our theory was used to obtain an estimate $N_s$ from the probability of DFS and the RO distribution. The value obtained (12 Mbp) is remarkably close to direct experimental measurements.

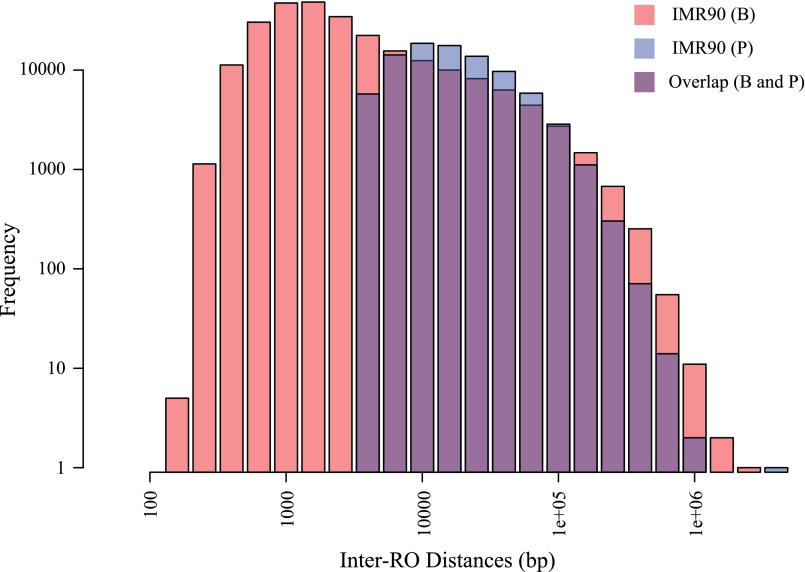
In this article, we extend our theory to study much larger genomes (100 Mbp to 10 Gbp), which are typically found in metazoa and plants. Our theory requires as input the positions of ROs along the genome and yields a number of clear predictions concerning the rates of DFSs, using both mathematical and computational approaches. These predictions were tested on available datasets describing RO distribution in one plant (Arabidopsis) (15), one invertebrate (Drosophila) (16), and two independent human datasets (reporting different human cell lines) (17, 18) (Table S1). Note that the two human datasets have been derived using different approaches to RO detection, and hence the number and positions of ROs vary between them. The two datasets are largely compatible with reported 70% overlap in genomic sites containing ROs in both datasets (18) (see also Fig. S1), and therefore can be used to test the robustness of our theory to experimental and biological variation.

Table S1.

General information from the various datasets for the distribution of ROs

Data	Yeasts		A. thaliana	D. melanogaster	Human cell lines*
	S. cerevisiae	S. pombe			IMR90 (B)	HeLa (B)	hESC (B)	iPSC (B)	IMR90 (P)	HeLa (P)	K562 (P)
No. ROs	1,626	1,476	3,076	12,356	513,934	467,044	416,994	493,686	179,676	180,054	118,346
${\mathit{N}}_{\mathit{g}}$, Mbp	22.45	24.62	229.94	234.18	5,665.42	5,670.47	5,664.43	5,661.91	5,640.31	5,645.12	5,618.98
${\mathit{N}}_{\mathit{l}}$ ± SD, Kbp	14 ± 10	17 ± 13	75 ± 73	19 ± 16	11 ± 36	12 ± 43	14 ± 43	11 ± 41	31 ± 44	31 ± 47	47 ± 72
LR, Kbp	60.70	60.96	773.20	151.39	3,599.33	4,292.70	3,707.84	3,707.94	5,655.11	5,733.72	5,940.84
P(DFS)	0.0011	0.0016	0.077	0.018	0.813	0.884	0.860	0.875	0.702	0.741	0.873
R	0.72	0.77	0.98	0.82	3.23	3.52	3.15	3.57	1.39	1.51	1.53

LR, largest replicon.

^*Besnard et al. data (B) and Picard et al. data (P) were derived using different resolutions in detecting ROs; hence the numbers of total ROs are different, but both datasets are strongly compatible with each other in regards to the genomic locations of ROs (Fig. S1).

Fig. S1.

Inter-RO distances from Besnard et al. (B) and Picard et al. (P) datasets are plotted. Due to the difference in resolution of detection, the minimum inter-RO distance in Picard et al. data is 4001 bp, and, in Besnard et al. data, it is 240 bp. The overlapping bar charts show that the two datasets are compatible. More detail of the compatibility of the two datasets is discussed in ref. 18.

Our theoretical and computational analysis leads to a series of direct predictions, which are all found to be consistent with all datasets analyzed, revealing a picture of great simplicity. The robustness of DNA replication in eukaryotes can be maintained so long as the largest replicon (inter-RO distance) is well below the median stall distance $N_s$. For organisms with larger genomes, such as typical vertebrates and plants, DFSs are highly likely, even if the mean replicon length is small. These organisms therefore require mechanisms to deal with DFSs, and, in related experimental work, we provide experimental evidence for one such postreplicative mechanism (19). For cells with such repair mechanisms, the burden of equally spacing ROs is lifted; far more important is the distribution of larger replicons (relative to $N_s$) from which DFS events are most likely to arise. Our theory also indicates that the number of DFSs becomes unwieldy for genomes significantly greater than 10 Gb, and this additional challenge may play a central role in limiting the genome size of higher eukaryotes.

Results

The “Central Equation” for Determining Replication Errors.

In our previous work (14), we derived a mathematical equation for the genome-wide probability of DFSs, based on the distribution of ROs and $N_s$. The published equations depend on the largest replicon being significantly smaller than $N_s$. Although this limitation holds true for yeast genomes, it does not apply to ROs that have been mapped in mammalian cells. As described in Materials and Methods, we use the same theoretical framework to derive more general equations that are applicable to genomes containing arbitrarily large replicons. To use our theoretical results, we require detailed information on the location of ROs. A number of datasets have been published that provide the locations of ROs in eukaryotes, along with the total genome length (denoted by $N_g$ in the following). In this work, we have used origin-mapping data from Saccharomyces cerevisiae (20), Schizosaccharomyces pombe (21), Arabidopsis thaliana (15), Drosophila melanogaster (16), and five human tissue culture cell lines (IMR-90, HeLa, hESC, iPSC, and K562) from Besnard et al. (17) (denoted by “B” in the following) and Picard et al. (18) (denoted by “P”). Because the work of Picard et al. used more modern techniques (particularly in peak identification), it might be considered a more reliable dataset; comparison with the Besnard et al. dataset is useful in assessing the experimental uncertainties in some of the data.

Because of the very low probability of a DFS in any given replicon, we can show that the statistics of DFSs are Poisson to a very high level of accuracy (SI Text), and that the probability of no DFSs genome-wide has the form $\text{exp}(-\lambda )$. Thus, a great deal of information concerning the probabilities of DFSs for a given genome can be obtained from the single parameter λ. We remind the reader that, for a Poisson distribution, λ also describes both the mean and the variance of the distribution. For a given genome with K ROs, we denote the replicons by the K − 1 values $N_i$ (with i = 1, …, K − 1). These data can then be used in the “central equation” arising from our theory (Eq. 1),

$$\lambda \hspace{0.17em}=\hspace{0.17em}\log \left(2\right)\frac{N_g}{N_s}\hspace{0.17em}-\hspace{0.17em}{\displaystyle \sum }_{i=1}^K\log \left[1\hspace{0.17em}+\hspace{0.17em}\log \left(2\right)\frac{N_i}{N_s}\right].$$ [1]

This expression for λ contains a single unknown parameter $N_s$—i.e., the number of replicated bases along the DNA beyond which 50% of RFs irreversibly stall. The median stalling distance N_s is inversely proportional to the very small probability of stalling per nucleotide (14).

On the right-hand side of Eq. 1, we can identify the two distinct contributions of the genome length (first term) and of the RO distribution (second term). Genome length determines a baseline probability of DFSs that can be lowered by increasing the number of ROs and/or changing their distribution along the genome; indeed, as we have shown previously (14), for a given number of ROs, equally distributing them across the genome is the optimal arrangement to minimize the probability of DFSs. Therefore, the different terms on the right-hand side of Eq. 1 establish a hierarchy of contributions to the probability of DFSs, with genome length being the most important factor, followed by RO number and then RO distribution (Fig. 2).

Fig. 2.

Schematic of the central equation. The genome length is the dominant contributor to the overall replication error due to fork-stalling, followed by the number of licensed ROs and, lastly, by their distribution.

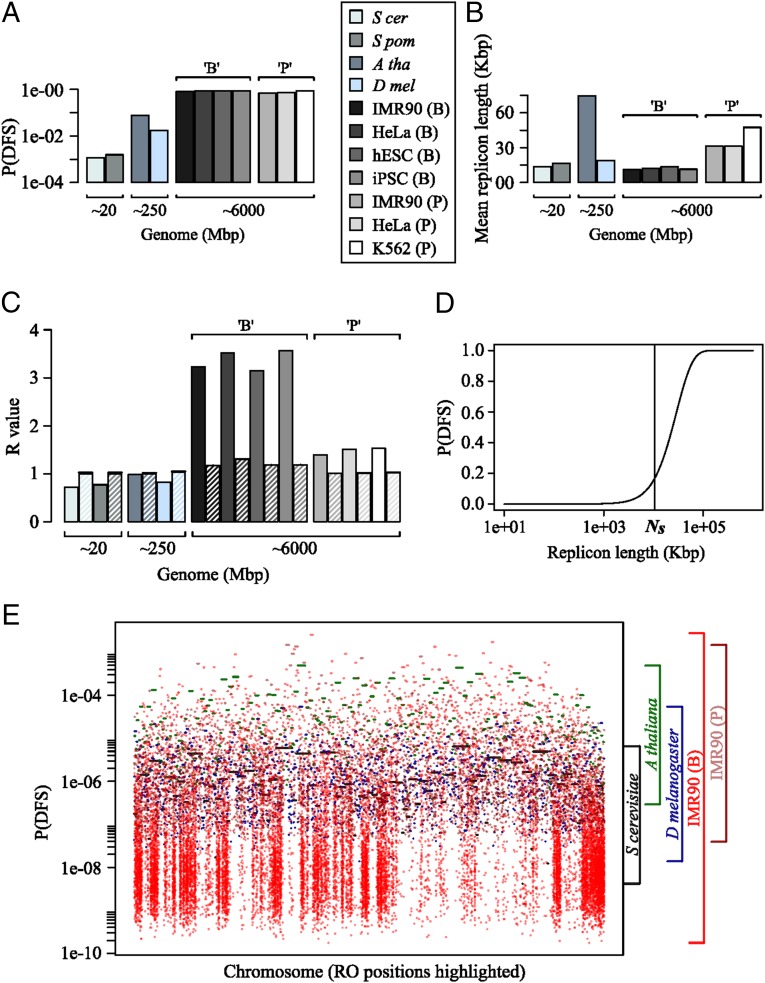
In organisms with relatively small genomes, such as yeasts (∼10 Mbp), an average density of 1 RO per ∼20 Kbp allows the maintenance of very small probabilities of genome-wide DFSs. Application of Eq. 12 to the yeast datasets gives values around 10⁻³ for the probability of one or more DFSs, consistent with our previous analysis. With the increase in genome size from around 10 Mbp (in yeasts) to around 10 Gbp (in human), Eq. 12 shows that the probability of DFSs increases by approximately two orders of magnitude, to more than 0.5 for human genomes (Fig. 3A). This huge increase in error rate occurs despite essentially no shift in the mean replicon size (Fig. 3B). Therefore, it is absolutely necessary for these organisms to have molecular machinery able to repair DFSs.

Fig. 3.

(A) Predicted probability of one or more DFSs for various eukaryotic genomes using the central equation from the model. (B) Measured mean replicon length across the same genomes from the corresponding experimental datasets. (C) Computed R values from the same eukaryotic datasets; note that the dashed bars represent simulated R values for virtual genomes of the same length and RO density but assuming ROs to be randomly distributed. (D) The probability of a DFS, denoted P(DFS), is plotted as a function of increasing replicon length. The estimated median fork-stalling distance, $N_s$ (10 Mbp), is highlighted on the x axis. P(DFS) starts to increase sharply as soon as the replicon size reaches approximately half the value of $N_s$; note that the x axis has a log scale. (E) The calculated probability of a DFS inside replicons plotted against normalized chromosomal lengths for the largest chromosomes in budding yeast, Drosophila, Arabidopsis, and the IMR90 cell line from two human datasets (B and P).

The Bias Toward Uniformly Spaced Replication Origins Is Progressively Lost in Larger Genomes.

The regularity of the RO distribution can be assessed by computing the coefficient of variation of the replicon lengths, denoted by R, defined as the ratio of their SD to their mean. For a perfectly uniform distribution of equally spaced ROs, R is equal to 0. On the other hand, computational analysis indicates that, when ROs are randomly distributed on the genome, the value of R is very close to 1 (14).

In the yeast genomes (diploid genome sizes ∼20 Mbp), we previously showed that their RO distributions were strongly biased toward uniform spacing with values of R ranging from 0.72 to 0.77 (Fig. 3C). The probability of DFSs is very small in yeasts due to the small genome size, and optimization of the RO positions by lowering R reduces this even further. However, as discussed above, organisms with larger genomes have a significantly higher probability of DFS events, which results in the need for additional molecular mechanisms to cope with the consequences (19), and the presence of such mechanisms means there is little to be gained in uniformly ordering ROs on the genomes. Thus, our expectation is that R should be significantly larger in organisms with larger genomes compared with the values found in yeast. Statistical analysis of the available data confirms this expectation (Fig. 3C). Arabidopsis and Drosophila (diploid genome sizes ∼250 Mbp) have values of R around unity (i.e., approximating a random distribution). Particularly striking is the fact that, in human genomes (∼6,000 Mbp), the values of R are significantly larger than unity, indicating that ROs are not spaced purely randomly and that both the number and size of large replicons are significantly greater than expected by chance. This unexpected distribution has important consequences that will be discussed in Large Replicons in Human Genomes.

The probability of a DFS in a given replicon increases with the replicon length according to Eq. 6 (Materials and Methods) and is plotted in Fig. 3D. The probability has a strongly nonlinear form: increasing as the square of the replicon length for lengths much less than the stalling distance, and saturating to unity for lengths significantly greater than the stalling distance. Fig. 3E provides a graphical representation that highlights the dramatic shift in variation of replicon lengths, or, equivalently, the per replicon rate of DFS, by plotting the predicted probability of DFSs across the largest chromosome of different organisms. It is apparent that the variation in probability of error increases by approximately one order of magnitude from yeast to Drosophila, and then again by approximately one order of magnitude from Drosophila to human.

Large Replicons in Human Genomes Cause the Most Errors but Are Bounded by the Stalling Distance.

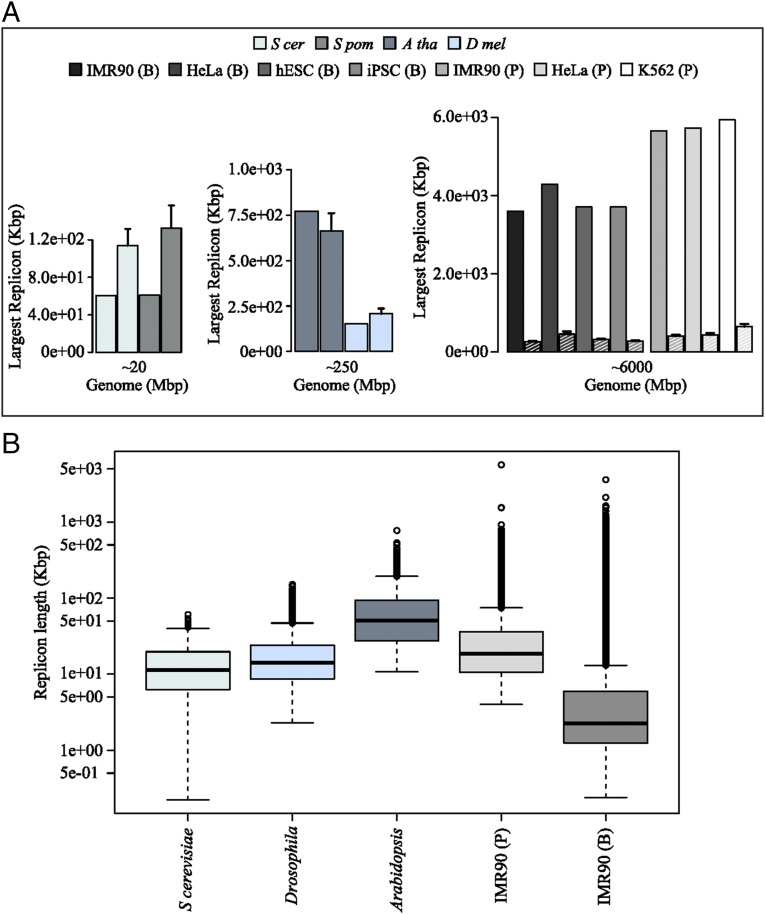
Consistent with our analysis of the values of R, we would expect the largest replicons in the genome to be very significantly different in diploid genomes of size ∼20 Mbp, ∼250 Mbp, and ∼6 Gbp (represented by yeasts, Drosophila/Arabidopsis, and human, respectively), with significantly larger replicons appearing in those genomes with R larger than unity. As seen in Fig. 4A, this is exactly what is observed, with the largest replicons being ∼60 Kbp in yeasts (∼120 Kbp expected for a random distribution), 151 Kbp in Drosophila (207 Kbp expected if random), 773 Kbp in Arabidopsis (663 Kbp expected if random), and ∼5 Mbp in human (∼300 Kbp expected if random). The tendency for larger and larger replicons can also be seen by the significant increase in outliers in the box plots of replicon lengths for the different organisms considered (Fig. 4B). As is clear from Fig. 3D, the probability of a DFS in a given replicon increases dramatically as the length of the replicon approaches $N_s$. To avoid almost inevitable errors arising from a single replicon, we would expect the length of the largest replicon in the entire genome to be bounded by $N_s$, and this is, indeed, what is observed in the data. In the B dataset, we find that the largest replicons in each human cell line are 3.59 Mbp (IMR90), 3.71 Mbp (hESC), 3.71 Mbp (iPSC), and 4.29 Mbp (HeLa), whereas, in P, we find 5.65 Mbp (IMR90), 5.73 Mbp (HeLa), and 5.94 Mbp (K562). Interestingly, the largest replicons appear to be bounded by approximately one half of the stalling distance, which means that the largest replicon in each human cell line contributes a predicted error rate of ∼5%. We note that all of the datasets used for our analysis rely on genomic sequencing data. As such, large regions of repetitive DNA will not be sequenced accurately and yet are likely to contain ROs. These false negatives imply that the largest replicons measured provide an upper bound rather than a definite value, although we do not expect large numbers of missed ROs (19). The future use of more advanced techniques, for example, single-cell sequencing, will shed more light on this aspect.

Fig. 4.

(A) Measured lengths of the largest replicons are shown in each dataset alongside the dashed bars showing the value obtained for virtual genomes of the same length and RO density but assuming ROs to be randomly distributed. (B) The distribution of genome-wide replicon lengths plotted in boxplot format for budding yeast, Drosophila, Arabidopsis, and the IMR90 cell line from two human datasets (B and P).

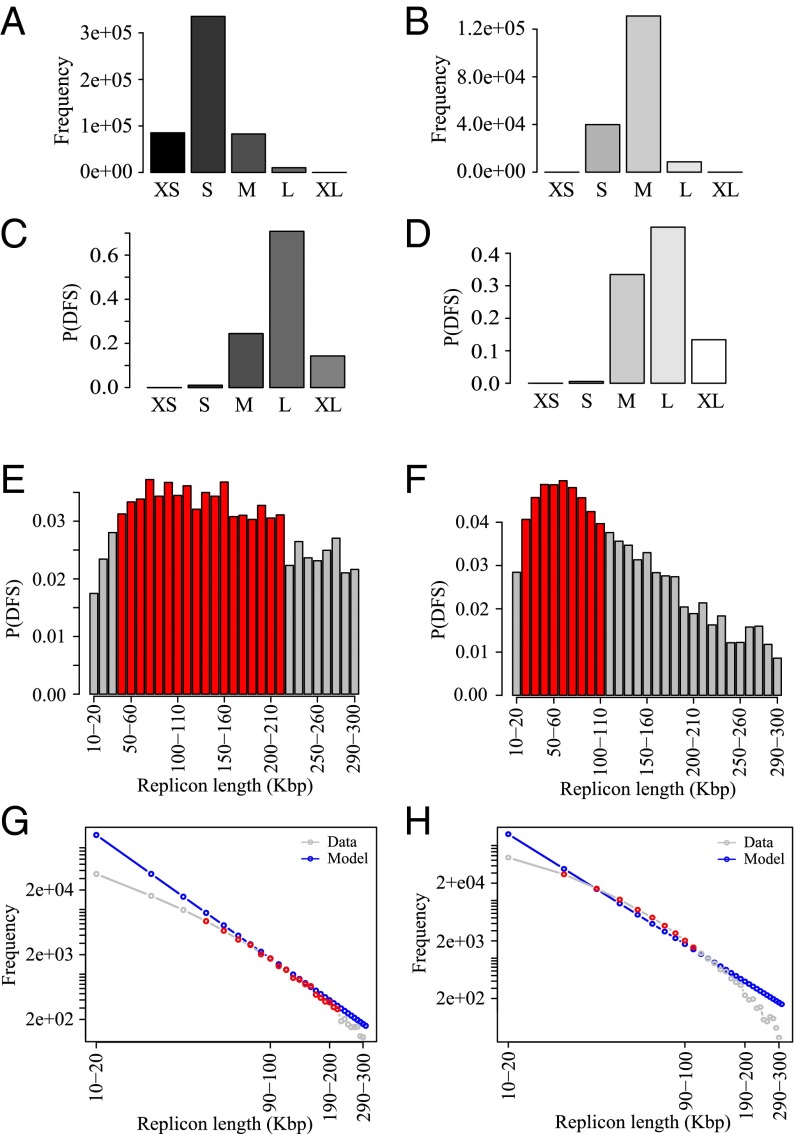
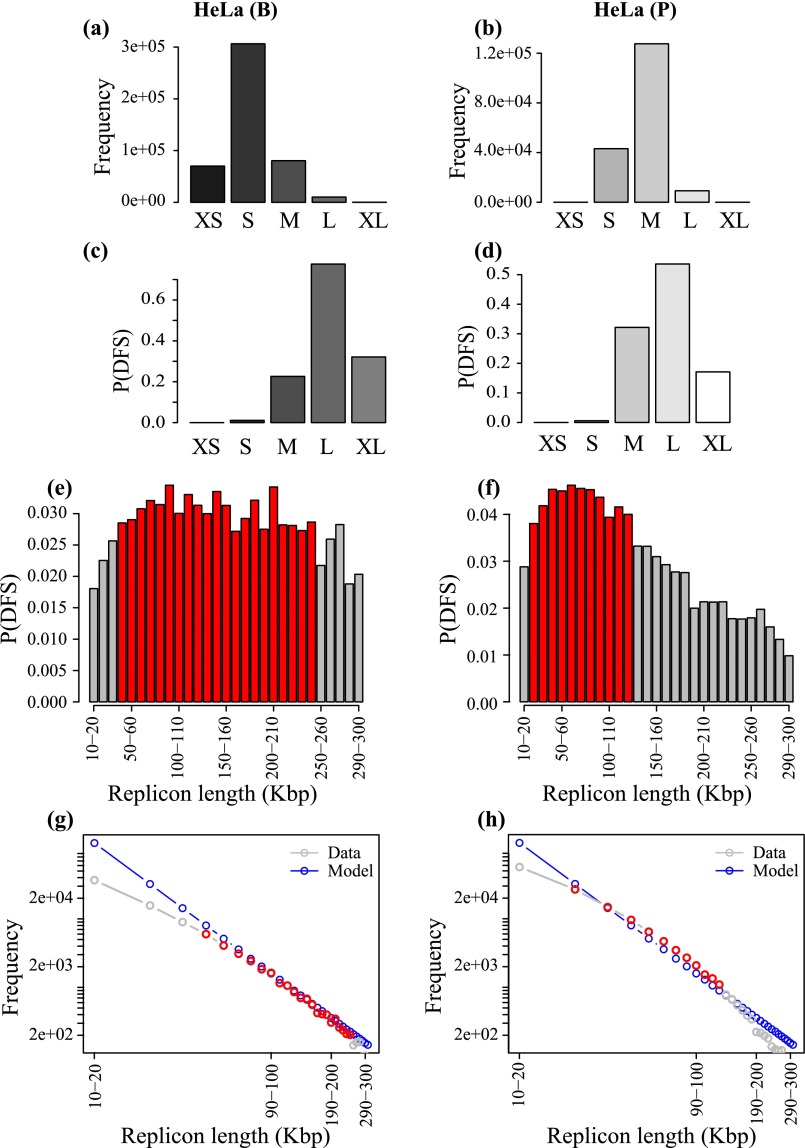
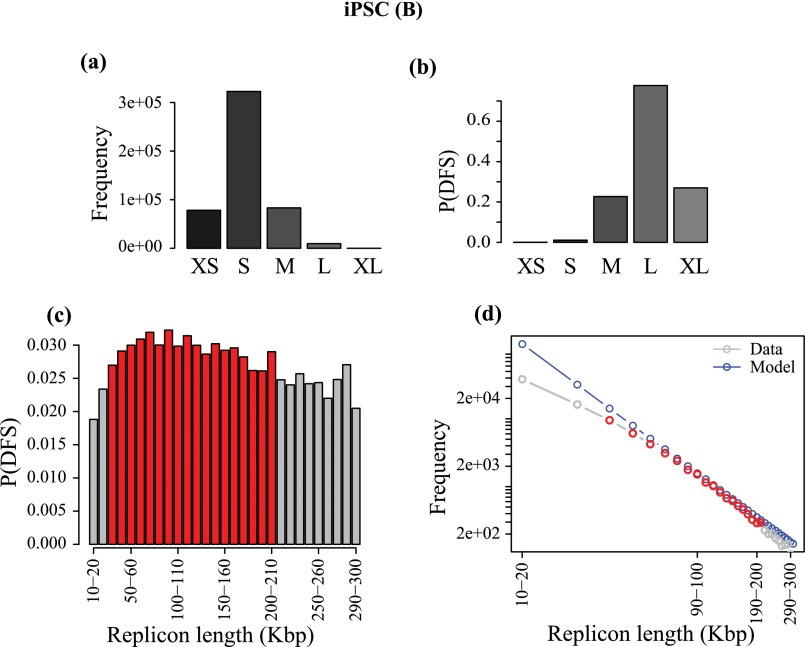
In the human genome, given that errors are very likely, we can determine the range of replicon lengths that are the main contributors to the DFS. We grouped the replicons into five cohorts: very small (XS; <1 Kbp), small (S; 1 to 10 Kbp), medium (M; 10 to 100 Kbp), large (L; 100 Kbp to 1 Mbp), and very large (XL; >1 Mbp). The frequency of replicons in these five cohorts is shown in Fig. 5 A and B for IMR90 from the B and P studies. The most common range of replicons is S, followed by M, the shift from S to M being due to the coalescence of small replicons in the Picard et al. study. L and XL replicons appear only at low frequency. Despite this, Fig. 5 C and D shows that the cohort of L replicons dominates as the source of error, which is due to the fact that the DFS probability increases nonlinearly with the replicon length (Fig. 3D). The error rate due to the small number of XL replicons is significantly smaller compared with the L replicons. An important consequence of this finding is that there will be a very limited impact on genome-wide error rates from false negatives, which primarily affect the distribution of XL replicons.

Fig. 5.

Data are from the IMR90 human datasets (A, C, E, and G) B and (B, D, F, and H) P. (A and B) Frequency of replicons in each cohort, defined according to the following size ranges: <10³ bp, XS; 10³ to 10⁴ bp, S; 10⁴ to 10⁵ bp, M; 10⁵ to 10⁶ bp, L; and >10⁶ bp, XL. (C and D) Probability of DFS in each cohort of the replicons. (E and F) Higher-resolution plot of probability of DFS at the transition from M to L gap cohorts contributing most toward the P(DFS); red bars show the bins with maximum P(DFS) in respective datasets. (G and H) Theoretical frequency distribution of replicons inferred from E and F are presented in blue; gray shows the actual frequency distribution in those bins in the data, and red highlights the red bins in E and F.

Interestingly, in both datasets, for all cell lines, a closer examination of the error rates in the vicinity of the L cohort shows a surprisingly statistically uniform distribution of error rate, which is suggestive of ROs being placed so as to “spread the risk” of error across size scales. In Fig. 5 E and F, the probability of DFS in each 10-kbp interval in the range 10 to 300 kbp is shown for the Besnard et al. (Fig. 5E) and Picard et al. (Fig. 5F) datasets for primary IMR90 cells. These replicons are the ones that contribute the most to the DFS probability. The maxima are relatively broad, particularly for the B dataset, for which the probability of DFS in each 10 kbp is approximately constant at 0.030 to 0.035 across replicons spanning from 40 kbp to 200 kbp. For replicons significantly smaller than the stalling distance, one can infer, from the theory, that ROs are placed in such a way to give a power law, with a frequency of DFSs that decreases as the inverse square of the replicon length thereby spreading the probability of a DFS equally among all size classes (described by Eq. S6). Fig. 5 G and H shows that there is a remarkable concordance between the theoretical frequency distribution (in blue) and the frequency distribution in the data for IMR90 cell line in both datasets (in red). There is also excellent agreement with the theoretical distribution in all of the other cell lines in both datasets (Figs. S2−S4). These results can be interpreted in terms of “spreading the damage” as widely as possible in the replicon size region of maximal DFS errors, as a power law is the most effective way to delocalize errors from any single cohort of replicon lengths.

Fig. S2.

Data are from HeLa human datasets (A, C, E, and G) B and (B, D, F, and H) P. (A and B) Frequency of replicons in each cohort, defined according to the following size ranges: <10³ bp, XS; 10³ to 10⁴ bp, S; 10⁴ to 10⁵ bp, M; 10⁵ to 10⁶ bp, L; and >10⁶ bp, XL. (C and D) Probability of DFS in each cohort of the replicons. (E and F) Higher-resolution plot of probability of DFS at the transition from M to L gap cohorts contributing most toward the P(DFS); red bars show the bins with maximum P(DFS) in respective datasets. (G and H) Theoretical frequency distribution of replicons inferred from E and F are presented in blue; gray shows the actual frequency distribution in those bins in the data, and red highlights the red bins in E and F.

Fig. S4.

Data are from iPSC human dataset in B. (A) Frequency of replicons in each cohort, defined according to the following size ranges: <10³ bp, XS; 10³ to 10⁴ bp, S; 10⁴ to 10⁵ bp, M; 10⁵ to 10⁶ bp, L; and >10⁶ bp, XL. (B) Probability of DFS in each cohort of the replicons. (C) Higher-resolution plot of probability of DFS at the transition from M to L gap cohorts contributing most toward the P(DFS); red bars show the bins with maximum P(DFS) in respective datasets. (D) Theoretical frequency distribution of replicons inferred from C are presented in blue; gray shows the actual frequency distribution in those bins in the data, and red highlights the red bins in C.

Fig. S3.

Data are from hESC and K562 in human datasets (A, C, E, and G) B and (B, D, F, and H) P. (A and B) Frequency of replicons in each cohort, defined according to the following size ranges: <10³ bp, XS; 10³ to 10⁴ bp, S; 10⁴ to 10⁵ bp, M; 10⁵ to 10⁶ bp, L; and >10⁶ bp, XL. (C and D) Probability of DFS in each cohort of the replicons. (E and F) Higher-resolution plot of probability of DFS at the transition from M to L gap cohorts contributing most toward the P(DFS); red bars show the bins with maximum P(DFS) in respective datasets. (G and H) Theoretical frequency distribution of replicons inferred from E and F are presented in blue; gray shows the actual frequency distribution in those bins in the data, and red highlights the red bins in E and F.

Replication Errors Are Common but Low in Number for Higher Eukaryotes.

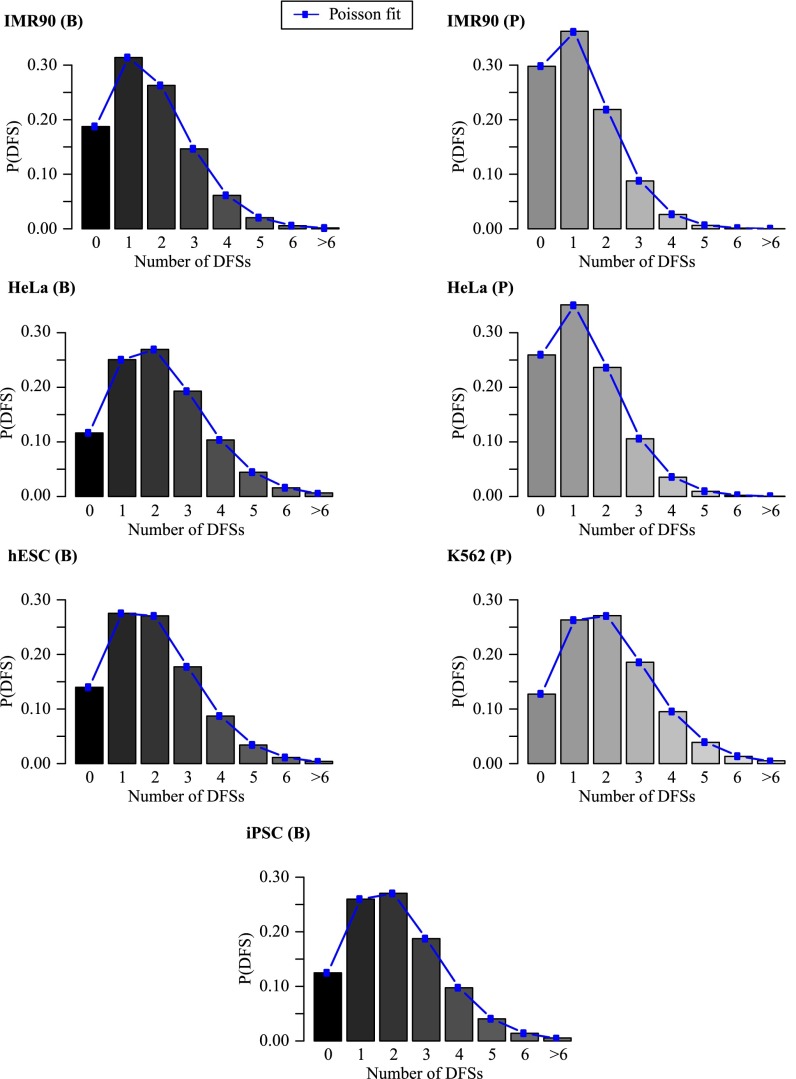
As discussed in The “Central Equation,” our theory predicts that the distribution of the number of DFSs in a given genome is Poisson-distributed to a very high degree of accuracy. We have applied our theory to the human cell lines datasets to test this prediction. As shown in Fig. 6, for all cell lines, from both laboratories, the distribution of DFSs is indeed Poisson-distributed, regardless of being primary or tumoral cell lines. Statistical analysis confirms that the computationally derived probability distribution of DFSs is statistically indistinguishable from the fitted Poisson distribution. Interestingly, we find a very low probability (<10%) of encountering more than three DFSs in the replication of the entire diploid human DNA per cell cycle. Therefore, despite the high probability of the presence of DFSs (∼80%), in ∼90% of cells undergoing DNA replication, the expected number of DFSs is predicted to be three or less, with one or two errors being the most likely occurrences. Indeed, we find that the parameter $\lambda$ (i.e., the mean number of errors) that characterizes the distribution of DFSs ranges from 1.67 to 2.15 in Besnard et al. (17) and from 1.21 to 2.05 in Picard et al. (18).

Fig. 6.

Theoretical prediction for the distribution of the number of DFSs based on the RO positions in each human cell-line dataset (using data from both B and P); also shown, as lines and dots, are best fits to a Poisson distribution.

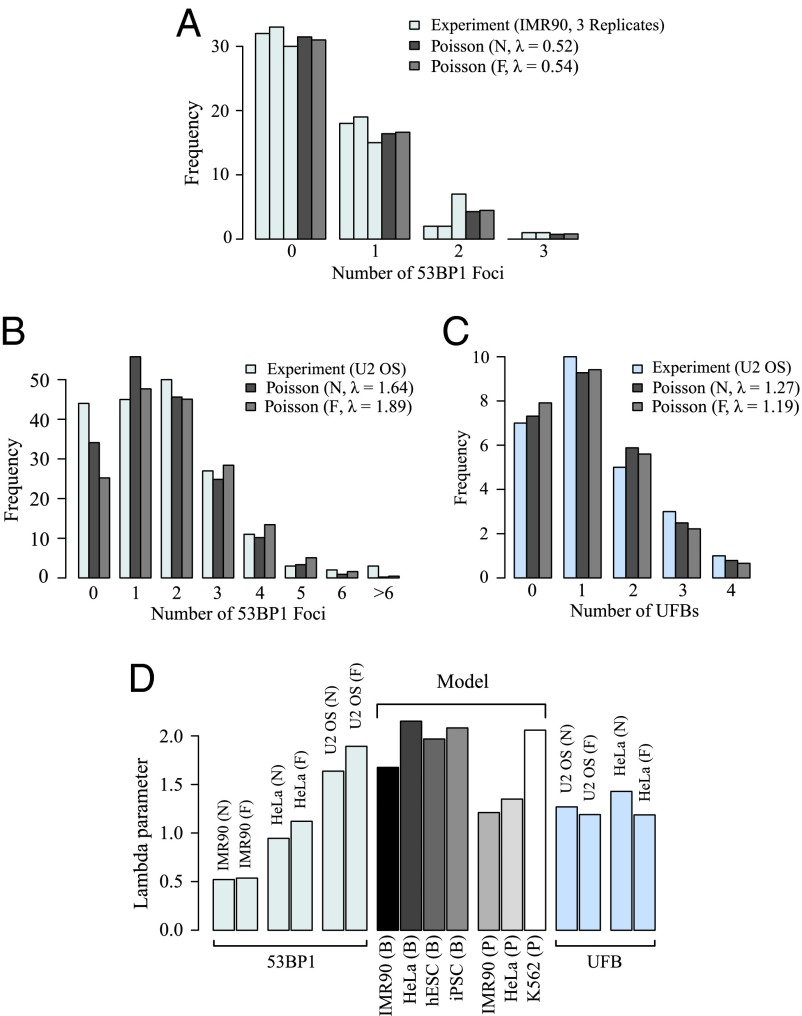
Given that DFSs in human cell lines are almost inevitable, it is somewhat surprising to find that their number is quite sharply constrained to be essentially one, two, or three. This might indicate that the mechanism that deals with such errors has a very low capacity. If, as suggested in Moreno et al. (19), the defects induced by DFSs can be resolved in the following cell cycle by segregating unreplicated DNA to daughter cells, DNA strand breaks could be generated at each DFS. Because the number of illegitimate ways that double-strand breaks could be correctly rejoined increases as the factorial of the number of breaks, this might constrain the number of tolerated DFSs to about three or less. We provide a rationale for putative biological mechanisms in Discussion, and our arguments lead us to consider two different biomarkers for double-strand breaks that would arise from DFS errors; these are the presence of 53BP1 nuclear bodies in the G1 phase of the subsequent cell cycle and the presence of ultrafine anaphase bridges (UFBs) during mitosis. Our theory suggests that the number of both 53BP1 nuclear bodies and UFBs are distributed as a Poisson with a value of $\lambda$ between 1 and 2.

We performed an experimental analysis of 53BP1 in IMR90 cells and both 53BP1 and UFBs in U2-OS cells, and we measured the frequency of their occurrence during the cell cycle at a single-cell level (19). In agreement with our predictions, the experimental distributions of both 53BP1 nuclear bodies and UFBs fit to a Poisson distribution (Fig. 7 A−C). Statistical analyses indicate that both a naïve fitting using the mean of the data and a more advanced approach that accounts for potential errors introduced by the experimental procedure of the immunofluorescence experiments (Fig. 7 A−C) produce distributions that are not statistically different from Poisson distributions for both 53BP1 nuclear bodies (P values between 0.61 and 1 for both IMR90 and U2-OS cells) and UFBs (P values between 0.53 and 1 for U2-OS cells). Additionally, the fitted $\lambda$ values, 0.52 (naïve) and 0.54 (filtered) in IMR90 and 1.64 (naïve) and 1.89 (filtered) in U2-OS cells for 53BP1 nuclear bodies, and 1.27 (naïve) and 1.19 (filtered) for UFBs, are in line with the expectation of a limited number of DFSs. Moreno et al. (19) show that the number of 53BP1 nuclear bodies and UFBs follows a Poisson distribution in the HeLa cell line with $\lambda$ values of 0.94 (naïve) and 1.12 (filtered) for 53BP1 and 1.43 (naïve) and 1.19 (filtered) for UFBs (19). Taken together, these results provide good agreement of our theory with the available data and reinforce the connection between 53BP1 nuclear bodies and UFBs to DFSs. The analysis of UFBs in unperturbed IMR90 cells was not possible due to experimental difficulties related to the fact that this cell line is not immortalized.

Fig. 7.

(A) Experimental distribution of three different replicates of 53BP1 nuclear bodies in the IMR90 cell line fitted with a naïve Poisson (i.e., taking the mean of the data as λ) (gray) and a filtered Poisson (i.e., ignoring the frequencies of zero counts to account for potential error from immunofluorescence staining) (light gray). The single fitting with the average of the three replicates (not statistically different) is shown. (B) Experimental distribution of 53BP1 nuclear bodies in the U2-OS cell line fitted with a naïve Poisson (i.e., taking the mean of the data as λ) (gray) and a filtered Poisson (i.e., ignoring the frequencies of zero counts to account for potential error from immunofluorescence staining) (light gray). (C) Experimental distribution of UFBs in the U2-OS cell line fitted with a naïve Poisson (gray) and a filtered Poisson (light gray). (D) Values of the Possion parameter λ obtained from experimental fits of 53BP1 nuclear bodies in IMR90, U2-OS, and HeLa, and UFBs in U2-OS and HeLa, are compared with theoretical values obtained from different cell lines in Fig. 6.

As a more quantitative analysis, we compared the $\lambda$ values obtained by direct calculation from the RO distribution of different human cell lines and the experimental $\lambda$ values estimated from the distribution of 53BP1 and UFBs. Note that comprehensive RO distribution data are not available for the cell line used for the UFB experiments (U2-OS), and diversity has been observed in RO distribution across different cell lines (17). Moreover, both 53BP1 and UFBs are likely to provide only an approximation of the number of DFSs, as they appear also in the presence of non-DFS-associated double-strand breaks. Despite these limitations, a comparison of the $\lambda$ values indicates that experimental measures are in excellent agreement with theoretical prediction (Fig. 7D). Additional comparisons with the $\lambda$ values obtained from HeLa reinforce our conclusions (Fig. 7D). Interestingly, the range of variation observed in the experimental value of $\lambda$ is matched by the range of variation of our model predictions, suggesting that our methodology is correctly capturing experimental variations.

In both IMR90 and HeLa cells, the experimentally derived $\lambda$ obtained from 53BP1 nuclear bodies data are approximately half of the theoretical estimate obtained from the RO mapping data. This is also true for UFBs in HeLa cells. So long as the density of ROs is small, it is straightforward to show that doubling the density of ROs halves the value of $\lambda .$ Hence the factor of 2 difference in the experimental and theoretical values of $\lambda$ could indicate that around half of the genomic ROs are missing in the current datasets (e.g., due to difficulties in detecting ROs that fire very rarely or ROs positioned in repetitive regions of the DNA). This line of reasoning is also consistent with a potential issue with the largest measured replicon being ∼4 Mbp, the issue being that the replication time for such a gap would be significantly longer than typical S phase (ca. 8 h) (22). If the true RO density is twice that measured, one can show that the largest gap would be halved, giving a value of 2 Mbp, which is in line with the estimate of 2 Mbp for the longest stretch of DNA that could be replicated in the duration of S phase (assuming a fork speed of ∼2 Kbp per minute (23), and remembering that a large replicon will be replicated almost symmetrically by forks traveling from either end).

Effect of Variation of the Stalling Distance.

In applying our theory to the RO position data for various human cell lines, we can vary the numerical value of $N_s$ and measure the effect on the expected number of DFSs. This allows us to gauge the extent to which our conclusions are robust to the variation of the only parameter in our analysis for which we do not have strong experimental data. Both theoretical and biological estimates indicate that $N_s$ is ∼10 Mbp (14, 24). However, a precise estimate of this value is difficult to determine in vivo. The stalling distance is inversely proportional to the very small probability of an irreversible stalling event per nucleotide replicated, which, because of the conservation of the basic replication machinery, is likely to be relatively well conserved across eukaryotes.

First, we analyzed the overall probability of DFSs occurring as $N_s$ is varied. In all of the human cell lines considered, we observe a characteristic transition around 5 Mbp: Below this value, the probability of observing DFSs saturates at 1 (Fig. 8A). Therefore, DFSs are inevitable for smaller values of $N_s$, as one might expect. Importantly, our analysis indicates diminishing returns when $N_s$ is increased to much larger values: Even for $N_s$ around 30 Mbp, error rates are sufficiently high (one in five cells would experience a DFS during S phase) that additional DFS repair mechanisms are still required. Therefore, in higher eukaryotes with large genomes, the pressure to maintain genome stability is most easily resolved by additional safeguard mechanisms to deal with consequences of DFSs, rather than by stabilizing the replication machinery to give such a large $N_s$ that DFSs can be avoided with the regular RO distribution found in eukaryotes with smaller genomes.

Fig. 8.

(A) Based on the RO distributions in the various human datasets, theoretical predictions of the percentage of cells with DFSs are plotted as a function of the parameter $N_s$; the percentage is essentially 100% when $N_s$ < 5 Mbp, and this percentage is still nontrivially high even when $N_s$ > 20 Mbp. (B and C) Theoretical predictions of the probability of one, two, and three DFSs are shown as a function of $N_s$ for the Besnard et al. (B) and Picard et al. (C) data. (D and E) Theoretical predictions of the probability of one, two, or three DFSs are shown as a function of $N_s$ for the Besnard et al. (D) and Picard et al. (E) data. (F and G) Expected numbers of DFSs in different cell lines are plotted against $N_s$ for the Besnard et al. (F) and Picard et al. (G) data; in black, blue, and red are the experimentally obtained expected number of 53BP1 nuclear bodies in IMR90, U2-OS, and HeLa, and UFBs in U2-OS and HeLa cell lines, respectively. Crossing points of the black, blue, and red lines over the curves provide an independent estimate for the plausible range of $N_s$ (vertical lines) by directly comparing experimental data with theoretical predictions.

Our analysis stresses the inevitability of DFS errors during replication of the human genome and calls for a shift in our approach with respect to how the problem has been viewed in the past. On varying the median stalling distance in human cells, the probability of exactly one DFS genome-wide reaches a maximum between 10 and 15 Mbp, depending on the particular cell line and dataset used (Fig. 8 B and C). Furthermore, on varying the stalling distance, we find that the probabilities of exactly two or exactly three DFSs occurring also have peaks in the range 6 to 10 Mbp, again depending on the cell line and the dataset used (Fig. 8 B and C). To probe the likelihood of a small number of errors occurring, we plotted the probability of observing one, two, or three DFSs as stalling distance was varied (Fig. 8 D and E). These results show a very pronounced maximum for $N_s$ around 10 Mbp in the B dataset, and around 8 Mbp in the P dataset. In summary, our analysis of the available RO distribution in a variety of human cell lines and in different datasets indicates that the number of DFSs is constrained between zero and three only for $N_s$ in the vicinity of 10 Mbp.

Finally, we can measure the average number of DFSs when $N_s$ is varied. This number is equal to the $\lambda$ parameter of a Poisson distribution and therefore allows a direct comparison with our experimental measures. As expected, the average number of DFSs decreases from a large value as $N_s$ is increased (Fig. 8 F and G). As explained in Replication Errors Are Common, fitting the Poisson distribution to 53BP1 and UFB experimental data gives values of $\lambda$ between 0.54 and 1.89 (the values are shown in Fig. 8 F and G as black, blue, and red lines). The intersection of the decaying curve with these two lines provides another independent estimate of the stalling distance, which we find to be between 8 and 16 Mbp, depending on the cell line and dataset used. Our analysis of the statistics of DFSs in human cell data on varying the stalling distance therefore provides very strong evidence for the robustness of this parameter, with a value in the range 8 to 15 Mbp, consistent with previous estimates from our analysis of yeast RO distributions, and with direct experimental estimates (14, 24).

Effect of Varying the Number of Licensed ROs.

Interestingly, among the cell types we analyzed, there was no major difference in the mean replicon length (Fig. 3B). Fig. 9 shows how decreasing mean replicon length would reduce the probability of DFSs in a generic organism. The black, light blue, and blue lines illustrate the mean replicon length to achieve a fixed probability of DFSs under the optimal situation of equally spaced ROs. All of the datasets analyzed in the article have a mean replicon length ranging between 10 and 100 Kbp (shaded pink in Fig. 9). Because of the relatively small genome sizes of yeasts, so long as ROs are evenly spaced, this mean replicon length can achieve a tolerable DFS probability of ∼0.1%, similar to the chromosome missegregation rate (14). To maintain a low probability of DFSs as in yeasts, longer genomes would require a much lower mean replicon length or, in other words, much higher density of ROs on the genome. Because the MCM2-7 double hexamer that licenses an RO has a footprint of ∼60 bp (25, 26), this provides an absolute limit to the possible replicon length (dashed line in Fig. 9). It is just about possible for organisms with ∼6,000-Mbp genomes to achieve yeast-like DFS probabilities, but the genome would have to be almost completely packed with MCM2-7, which might leave the genome unable to perform its major function of providing the template for transcription. Because this saturation is implausible for normal cells, additional postreplicative mechanisms must be in place to deal with the inevitable DFSs. For this reason, regularity in RO distribution is not an effective safeguard against DFSs in organisms with larger genomes.

Fig. 9.

Highlighting the issues faced to maintain small DFS error rates for genomes of increasing length: theoretical prediction of the average replicon length as a function of increasing genome length, to maintain a fixed probability of DFS, for three different values of this probability. Diamonds show the positions of yeast, Arabidopsis, Drosophila, and human, obtained from the datasets of RO positions. The pink shadow highlights the biologically relevant range for mean replicon lengths as per all eukaryotic datasets available. The dashed red line marks the footprint for the MCM2-7 double hexamer, below which any replicon length is biologically unrealistic.

Discussion

Faithful DNA replication is fundamental to preserve the genetic content of cells and to avoid the severe pathologies that arise when DNA is improperly replicated. The appropriate location and activation of ROs is fundamental to ensuring that replicative errors are minimized. Here we show that understanding the principles that govern distribution of ROs provides quantitative insights into the way that different organisms maintain genetic integrity. By using a probability theory approach, based on a one-parameter model with simple yet plausible assumptions, we have developed a set of measures and predictions that further this understanding. The excellent agreement of our theoretical predictions with experimental data strongly supports the validity of our model assumptions. Moreover, it allows us to explore the rich system-level diversity of features and constraints associated with DNA replication.

Replicative Errors Are Inevitable in Larger Genomes.

Increased phenotypic complexity of organisms is generally associated with larger genome length, and metazoans have much larger genomes compared with yeast: The diploid human genome is ∼600 times larger than the haploid yeast genome. Despite this large difference in genome size, the replication machinery is essentially conserved (4). Over the past few decades, much effort has been devoted to understanding the molecular mechanisms involved in eukaryotic DNA replication and the associated damage-repair mechanisms. However, less is known about the system-level structures and processes that allow replication fidelity across the different scales of eukaryotic complexity, mirrored by genome lengths spanning over three orders of magnitude across yeast to human. We have used a theoretical approach, previously validated in yeasts (14), to predict the probability of DFSs for different organisms with widely different genome lengths, and for which detailed RO distribution data are available.

Our central equation shows that there is a hierarchy of contributions to the probability of DFS, with genome length being the most important factor, followed by RO number and then RO distribution. This effectively creates different classes of probabilities of DFS errors (∼10⁻³, ∼10⁻², and ∼1) for the respective classes of organisms according to their genome lengths (∼20 Mbp, ∼250 Mbp, and ∼6 Gbp). Interestingly, among the cell types we analyzed, there was no major difference in the density of ROs, i.e., mean replicon length. One possible explanation for this is that to make a significant effect on reducing DFSs, the RO density in organisms with genomes of 250 Mbp or more would lead to excessive clashes with the transcriptional machinery. The third component of our equation—the uniformity of replicon length, i.e., R—also reflects these classes (with values of <1, ∼1, and >1, respectively), indicating that, as the probability of DFSs approaches 1 in larger genomes, the pressure toward a regular RO distribution is lifted.

Inevitability Is Mitigated by Containment in Longer Genomes and Beyond.

DFSs are the primary cause of DNA double-strand breaks during replication (27–29), and are likely to be major contributors to the development of cancer and other pathologies, such as ones associated with aging (30, 31). The inevitability of DFSs in longer genomes requires the presence of cellular mechanisms, which are able to deal with such errors in an efficient manner. In related experimental work, we provide experimental evidence for one such postreplicative mechanism, involving the segregation of unreplicated DNA via UFBs and its protection by 53BP1 before being resolved in the next S phase (19). We have demonstrated very good agreement in the numbers and statistical distribution of experimental measurements of both 53BP1 and UFBs with the predictions of Poisson statistics from our theory, supporting the validity of our conclusions, and indicating that DFSs in the experimental systems are well approximated as independent events.

Analysis of the data available for human cell lines within our theoretical framework shows that RO density and distribution constrain the number of DFSs per cell cycle to three or less for nearly all cells. This limit on the number of DFSs may partially be explained by the difficulty in properly recombining two strands of DNA when end-joining is used. For example, if four DFSs occur and need to be fixed, eight strands will be generated, and only one of the 24 theoretically possible combinations is correct. From our experimental observations, cells with large numbers of 53BP1 nuclear bodies and UFBs showed increased blebbing and apoptosis. This suggests that large numbers of DFSs could compromise the working of the cell and the efficiency of the repair mechanism. Thus, our theory, in light of the experimental data, shows a contingent trade-off between the inevitability of DFS occurrence and the difficulty of its resolution (i.e., apparently requiring sophisticated molecular machinery for detection and repair). It is worth stressing that our central equation for $\lambda$, the mean number of DFSs, contains very large numerical values, i.e., $N_g$ and $N_s$, as well as thousands of replicon lengths. Therefore, in principle, the formula could have produced values for $\lambda$ of almost arbitrary magnitude, either much less than or much greater than unity. It is striking that our theoretical predictions from the central equation yield values for $\lambda$ close to unity and in such strong agreement with experimental data.

Another important requirement for the containment of replicative errors in larger genomes is an upper limit in the length of large replicons. Longer replicons correspond to a higher probability of DFSs (Fig. 3D). Our theory indicates that the largest tolerable replicons in human cell lines are bounded by ∼0.5 $N_s$, and, interestingly, the largest replicons found in experimental datasets are around 0.3 $N_s$. In addition, we have analyzed human cell line data within our theoretical framework, and, by varying $N_s$, we are able to clearly show that the probability of observing a number of DFSs equal to one, two, or three is maximized for $N_s$ in the region of 10 Mbp. This value for $N_s$ is in excellent agreement with previous experimental and theoretical estimates in human cell lines and yeasts (14, 24). Due to the universality of replication machinery across the eukaryotes and the necessity of error containment in larger genomes, we propose this $N_s$ value to be robust and universal in eukaryotes. A further signature of the containment mechanisms associated with the inevitable errors in human genomes can be found in the distribution of the risk among replicons of different sizes: A relatively narrow range of replicons (of size ∼40 to ∼200 kbp) contributes the most to DFSs, with the different replicon sizes in this range contributing approximately equally to the risk.

As a final note, it is worth stressing that some organisms, particularly plants, have very large genomes, with $N_g$ as large as ∼100 Gbp (32). Our theory would predict, in such cases, that the number of DFSs becomes much larger than 3, and in the region of 10 or more. Interestingly, it has been observed that the cell cycle length in plants undergoes a dramatic lengthening as genome size exceeds about 25 Gb (32), potentially reflecting the significantly greater burden of DFS detection and correction in these organisms. We would predict similar effects for ploidy variants within the same species. We currently do not have genome-wide RO distribution data for these organisms to test this idea, but this would provide further opportunities for gaining new understanding of the system-level strategies that eukaryotes use to minimize replication errors.

Materials and Methods

Experimental Setup.

For the 53BP1 and UFBs experiments, U2OS and IMR-90 cell lines from the American Type Culture Collection were maintained in Dulbeccos’s Modified Eagle’s medium (Invitrogen), supplemented with 10% (vol/vol) FBS (Invitrogen) and penicillin and streptomycin at 37 °C in 5% CO₂. Standard immunofluorescence protocols were used for the 53BP1 and UFBs staining. Briefly, cells were fixed with 4% formaldehyde, permeabilized with 0.1% Triton in PBS, and blocked in 0.5% fish gelatin (G-7765; Sigma). Samples were incubated overnight with primary antibodies. To specify G1-phase cells, they were incubated with 40 µM EdU (Invitrogen) for 30 min before fixation, and then incubated with Cyclin A (1:300, ab16726; Abcam). For the detection of 53BP1, cells were also stained with GFP (1:2,000, ab13970; Abcam). To stain incorporated nucleotides, the Click-iT-EdU kit was used as instructed by the manufacturers (C10337; Invitrogen). For staining UFBs, cells were incubated with BLM (1:200, sc-7790; Santa Cruz). Alexa secondary antibodies (Invitrogen) were used for 1 h. Microscopy images were acquired using an Olympus IX70 deltavision deconvolution microscope and a CCD camera. Data from microscopy experiment were analyzed using Volocity 3D analysis software (Perkin-Elmer).

Datasets Used and Statistical Analysis.

Limited direct experimental evidence exists on ROs in plants and metazoan, and most data focus on the genomic density, rather than localization, of ROs (33, 34). Therefore, the main results of our article are framed in the context of available datasets describing genome-wide RO positions. Less high-quality datasets have been considered, where appropriate, to provide additional challenge to the theoretical predictions and their interpretation. Saccharomyces cerevisiae ROs were obtained from the highly curated DNA Replication Origin Database (20) with selection criteria discussed in ref. 14. To provide additional validation, we considered another yeast species in this article: Schizosaccharomyces pombe (21). RO distribution data were also obtained for the following multicellular organisms: Arabidopsis thaliana (15), Drosophila melanogaster (16), and human. Human data for the four cell lines IMR90, HeLa, hESC, and iPSC were derived as discussed in ref. 17, and different datasets for IMR90, HeLa, and K562 cell lines were obtained from ref. 18. The summary of the datasets is presented in Table S1.

When RO positions were defined by genomic ranges, the middle point of the range was used as the genomic location of the RO. Moreover, to limit the problems associated with technological limitations in sequencing the centromeric regions of chromosomes, the largest replicon of each chromosome (corresponding to the centromeric region) was excluded from the analysis in all of the organisms considered.

Probabilities of DFSs were obtained from RO position data using the formulas detailed in the following mathematical derivations. To allow standardized comparisons in computing the probability of DFS, all of the organisms were considered as diploid. Poisson fits of the computationally derived distribution of DFSs were computed using the probability of no DFSs. Poisson fits of the experimental data were computed using the mean (naïve) or by minimizing the difference from the frequencies of DFS strictly larger than zero (filtered). Differences between distributions were computed using Chi-Squared tests.

Model Derivation and Mathematical Details.

The baseline assumptions that have been used to construct the mathematical model have been described elsewhere (14) and will not be discussed here. In yeast, the size of the largest replicon, i.e., inter-RO distance, is significantly smaller than $N_s$. This size difference allowed the introduction of approximations, which could be used to obtain simpler formulas in our previous work (14). This is not valid in human genomes, and therefore we could not rely on the approximations previously used. Hence, various quantities had to be rederived to avoid previously introduced approximations, and we provide the more general derivations below.

Let D be the distance between two adjacent ROs located respectively at n = 0 and n = N, where N − 1 is the number of nucleotides within D. As shown in ref. 14, the probability of a double stall in D (DSD) is given by the following expression:

$$\text{Prob}\left(\text{DSD}\right)={\displaystyle \sum }_{n=0}^{N-1}{(1-q)}^{n}q[1-{(1-q)}^{N-n}].$$ [2]

Therefore,

$$\text{Prob}\left(\text{DSD}\right)\hspace{0.17em}=\hspace{0.17em}q\hspace{0.17em}{\displaystyle \sum }_{n=0}^{N-1}{\left(1-q\right)}^n-q\hspace{0.17em}{\displaystyle \sum }_{n=0}^{N-1}{\left(1-q\right)}^n{\left(1-q\right)}^{N-n}$$

$$=\hspace{0.17em}q\hspace{0.17em}{\displaystyle \sum }_{n=0}^{N-1}{(1-q)}^n-q\hspace{0.17em}{\displaystyle \sum }_{n=0}^{N-1}{\left(1-q\right)}^N.$$

Evaluating the sums using the formula for a geometric series, we have

$$\text{Prob}\left(\text{DSD}\right)\hspace{0.17em}=\hspace{0.17em}\hspace{0.17em}q\left[\frac{1-{(1-q)}^N}{1-(1-q)}\right]-\hspace{0.17em}Nq{(1-q)}^N$$

$$=\hspace{0.17em}1-{(1-q)}^N-Nq\hspace{0.17em}{(1-q)}^N.$$

Thus,

$$\text{Prob}\left(\text{DSD}\right)\hspace{0.17em}=\hspace{0.17em}1-\left(1+Nq\right){\left(1-q\right)}^N.$$ [3]

Expressing the product as the exponential of the sum of the logarithms gives

$${\left(1-q\right)}^N=\exp \left[N\log (1-q)\right].$$ [4]

Because q is an extremely small number, $\log \left(1-q\right)\approx -q$, and hence

$${\left(1-q\right)}^N=\exp (-Nq).$$ [5]

Combining Eq. 3 with Eq. 5, we obtain

$$\text{Prob}\left(\text{DSD}\right)=1-\left(1+Nq\right)\cdot \exp \left(-Nq\right).$$ [6]

Let us define the distance between the adjacent (k + 1)th and kth ROs as N_k. The probability of double stall between this pair of ROs will be denoted as P_k. Thus,

$$P_k=1-\left(1+N_{k}q\right)\exp \left(-N_{k}q\right).$$ [7]

The genome-wide probability of no double stall, which will be denoted as Prob(NDS), is given by the product of probability of no double stalls in each replicon, i.e.,

$$\text{Prob}\left(\text{NDS}\right)={\displaystyle \prod }_k(1\hspace{0.17em}-\hspace{0.17em}{P}_k).$$ [8]

Combining Eq. 7 and Eq. 8, we have

$$\text{Prob}\left(\text{NDS}\right)=\left[{\displaystyle \prod }_k\left(1+N_{k}q\right)\right]\cdot \left\{{\displaystyle \prod }_k\left[\exp \left(-N_{k}q\right)\right]\right\}.$$ [9]

Let N_g be the genome length; then

$${\displaystyle \sum }_k{N}_k=N_g.$$

Thus,

$${\displaystyle \prod }_k\left[\exp \left(-N_{k}q\right)\right]=\text{exp}\left(-q{\displaystyle \sum }_k{N}_k\right)=\text{exp}\left(-q{N}_g\right).$$ [10]

Similarly,

$${\displaystyle \prod }_k\left(1+N_{k}q\right)={\displaystyle \prod }_k\exp \left[\log \left(1+N_k\hspace{0.17em}q\right)\right]\hspace{0.17em}=\exp \left[{\displaystyle \sum }_k\log \left(1+N_k\hspace{0.17em}q\right)\right].$$ [11]

Therefore, combining Eqs. 9, 10, and 11, we have

$$\text{Prob}\left(\text{NDS}\right)=\exp \left(-q\hspace{0.17em}{N}_g\right)\cdot \text{exp}\left[{\displaystyle \sum }_k\text{log}(1+N_k\hspace{0.17em}q)\right]$$

or

$$\text{Prob}\left(\text{NDS}\right)=\text{exp}\left[-q\hspace{0.17em}{N}_g+{\displaystyle \sum }_k\text{log}(1+N_k\hspace{0.17em}q)\right].$$

We have shown before (14) that $q=\log \left(2\right)/N_s$. Hence,

$$\text{Prob}\left(\text{NDS}\right)=\text{exp}\left\{-\frac{\log \left(2\right)N_g}{N_s}\hspace{0.17em}+{\displaystyle \sum }_k\text{log}\left[1+\frac{\log \left(2\right)N_k}{N_s}\right]\right\}.$$ [12]

As given by Eq. 1, where the negative of the quantity in parentheses is denoted by λ. Further derivations and mathematical details are provided in SI Text and Table S2.

Table S2.

Direct calculations on IMR90 cell line suggest that only the leading term is playing a significant role for the value of R_i in Probability of a specific number of DFSs

Probability under consideration	Terms	Numerical value for the term
Terms used to calculate Prob(1DS) (terms in R1)	S1	1.68
Terms used to calculate Prob(2DS) (terms in R2)	S12	2.81
	S2/S12	8.84 × 10−4
Terms used to calculate Prob(3DS) (terms in R3)	S13	4.71
	(S1 × S2)/S13	8.84 × 10−4
	S3/S13	9.25 × 10−6
Terms used to calculate Prob(4DS) (terms in R4)	S14	7.89
	(S12 × S2)/S14	8.84 × 10−4
	(S1 × S3)/S14	9.25 × 10−6
	S22/S14	7.81 × 10−7
	S4/S14	1.40 × 10−7

DS, double stall.

Software Used.

Data analysis was performed using R version 2.15 and RStudio version 0.98.978 (https://www.rstudio.com).

SI Text

Mathematical Derivations.

Probability of a specific number of DFSs.

The previous approach can be extended to calculate the probability of an arbitrary number of double stalls. The probability of exactly one DFS, which will be called Prob(1DS), can be calculated directly as

$$\text{Prob}\left(1\text{DS}\right)={\displaystyle \sum }_k{P}_k.{\displaystyle \prod }_{k_1\ne \hspace{0.17em}k}(1-P_{k_1}).$$ [S1]

Combining Eq. 13 with Eq. 8, we obtain

$$\text{Prob}\left(1\text{DS}\right)\hspace{0.17em}=\hspace{0.17em}\text{Prob}\left(\text{NDS}\right)\cdot {\displaystyle \sum }_k\frac{P_k}{(1-\hspace{0.17em}{P}_k)}.$$

Therefore,

$$\frac{\text{Prob}\left(1\text{DS}\right)\hspace{0.17em}}{\text{Prob}\left(\text{NDS}\right)}={\displaystyle \sum }_k\frac{P_k}{(1-\hspace{0.17em}{P}_k)}.$$

To simplify the next steps, we introduce the following definitions:

$${\text{S}}_1={\displaystyle \sum }_k\frac{P_k}{1-P_k}$$

$${\text{S}}_2={\displaystyle \sum }_k{\left(\frac{P_k}{1-P_k}\right)}^2$$

$$\hspace{0.17em}⋮$$

$${\text{S}}_m={\displaystyle \sum }_k{\left(\frac{P_k}{1-\hspace{0.17em}{P}_k}\right)}^m.$$

Additionally, let Prob(mDS) be the probability of m DFSs; the following conventions will be used:

$$R_1=\frac{\text{Prob}\left(1\text{DS}\right)\hspace{0.17em}}{\text{Prob}\left(\text{NDS}\right)}$$

$$R_2=\frac{\text{Prob}\left(2\text{DS}\right)\hspace{0.17em}}{\text{Prob}\left(\text{NDS}\right)}$$

$$⋮$$

$$\hspace{0.17em}{R}_m=\frac{\text{Prob}\left(m\text{DS}\right)\hspace{0.17em}}{\text{Prob}\left(\text{NDS}\right)}.$$ [S2]

Hence,

$$R_1={\displaystyle \sum }_k\frac{P_k}{(1-P_k)}=S_1$$ [S3]

and

$$R_2=\frac{1}{2!}{\displaystyle \sum }_{k_1}{\displaystyle \sum }_{k_2\ne k_1}\frac{P_{k_1}}{(1-\hspace{0.17em}{P}_{k_1})}\frac{P_{k_2}}{(1-\hspace{0.17em}{P}_{k_2})},$$

which can be rewritten as

$$R_2=\frac{1}{2!}\hspace{0.17em}\left[{\left({\displaystyle \sum }_k\frac{P_k}{1-\hspace{0.17em}{P}_k}\right)}^2-\hspace{0.17em}{\displaystyle \sum }_k{\left(\frac{P_k}{1-\hspace{0.17em}{P}_k}\right)}^2\right]=\frac{1}{2!}\hspace{0.17em}\left(S_1^2-\hspace{0.17em}{S}_2\right).$$

Similarly,

$$R_3=\frac{1}{3!}{\displaystyle \sum }_{k_1}{\displaystyle \sum }_{k_2\ne k_1}{\displaystyle \sum }_{k_3\ne k_1,k_2}\frac{P_{k_1}}{\left(1-P_{k_1}\right)}\frac{P_{k_2}}{\left(1-P_{k_2}\right)}\frac{P_{k_3}}{\left(1-P_{k_3}\right)}$$

$$=\frac{1}{3!}\hspace{0.17em}\left(S_1^3-3\hspace{0.17em}{S}_1\hspace{0.17em}{S}_2+2\hspace{0.17em}{S}_3\right).$$

Iterating the same approach, it is possible to show that

$$R_4=\frac{1}{4!}\hspace{0.17em}\left(S_1^4-\hspace{0.17em}6\hspace{0.17em}{S}_1^2\hspace{0.17em}{S}_2+8\hspace{0.17em}{S}_1\hspace{0.17em}{S}_3+3\hspace{0.17em}{S}_2^2-6\hspace{0.17em}{S}_4\right)$$

$$R_5=\frac{1}{5!}\hspace{0.17em}(S_1^5-\hspace{0.17em}10\hspace{0.17em}{S}_1^3\hspace{0.17em}{S}_2+15\hspace{0.17em}{S}_1\hspace{0.17em}{S}_2^2+20\hspace{0.17em}{S}_1^2\hspace{0.17em}{S}_3-20\hspace{0.17em}{S}_2\hspace{0.17em}{S}_3-30\hspace{0.17em}{S}_1\hspace{0.17em}{S}_4+24\hspace{0.17em}{S}_5)$$

$$R_6=\frac{1}{6!}\hspace{0.17em}(S_1^6-15\hspace{0.17em}{S}_1^4{S}_2+45\hspace{0.17em}{S}_1^2{S}_2^2-15\hspace{0.17em}{S}_2^3+40\hspace{0.17em}{S}_1^3{S}_3-120\hspace{0.17em}{S}_1{S}_2{S}_3+40\hspace{0.17em}{S}_3^2-90\hspace{0.17em}{S}_1^2{S}_4+90\hspace{0.17em}{S}_2{S}_4+144\hspace{0.17em}{S}_1{S}_5-120\hspace{0.17em}{S}_6).$$

Finally, combining R₁, R₂, R₃, R₄, R₅, and R₆ with Eq. S2, we can obtain the probability of one to six DFSs as follows:

$$\text{Prob}\left(1\text{DS}\right)=\text{Prob}\left(\text{NDS}\right)\cdot R_1$$

$$\text{Prob}\left(2\text{DS}\right)=\text{Prob}\left(\text{NDS}\right)\cdot R_2$$

$$\text{Prob}\left(3\text{DS}\right)=\text{Prob}\left(\text{NDS}\right)\cdot R_3$$

$$\text{Prob}\left(4\text{DS}\right)=\text{Prob}\left(\text{NDS}\right)\cdot R_4$$

$$\text{Prob}\left(5\text{DS}\right)=\text{Prob}\left(\text{NDS}\right)\cdot R_5$$

$$\text{Prob}\left(6\text{DS}\right)=\text{Prob}\left(\text{NDS}\right)\cdot R_6.$$

As shown in Table S2, direct calculations on the IMR90 cell line suggest that only the leading power is playing a significant role for the R_i. Therefore, we write

$$R_2\approx \frac{1}{2!}\hspace{0.17em}\left(S_1^2\right)$$

$$⋮$$

$$R_k\approx \frac{1}{k!}\hspace{0.17em}\left(S_1^k\right)$$

and hence

$$\text{Prob}\left(k\text{DS}\right)=\text{Prob}\left(\text{NDS}\right)\cdot R_k\approx \text{Prob}\left(\text{NDS}\right)\frac{1}{k!}\left(S_1^k\right).$$

The probability density function of a Poisson distribution is

$$\text{Prob}\left(\text{n}\right)=\exp \left(-\lambda \right)\frac{{\lambda }^n}{n!}.$$

Therefore, for our distribution to follow a Poisson, we have to show that

$$\text{Prob}\left(\text{NDS}\right)=\exp \left(-\lambda \right).$$ [S4]

This formula implies S₁ = λ.

Now, from Eq. 8 and Eq. S4, we have

$$\lambda =-\log \left[{\displaystyle \prod }_k\left(1-P_k\right)\right]=-{\displaystyle \sum }_k\log \left(1-P_k\right)={\displaystyle \sum }_k\log \left(\frac{1}{1-P_k}\right)={\displaystyle \sum }_k\log \left(1+\frac{P_k}{1-P_k}\right).$$

The value $P_k/(1-P_k)$ is very small, and we can use a Taylor expansion to obtain

$$\lambda ={\displaystyle \sum }_k\left[\frac{P_k}{1-P_k}+O\left(P_k^2\right)\right]\approx {\displaystyle \sum }_k\left(\frac{P_k}{1-P_k}\right)=S_1.$$

Because the $P_k$ are very small, this approximation is generally very good.

Frequency of replicons of particular size.

We have shown in Eq. 3 that the probability of a DFS in the region of DNA between a pair of adjacent ROs separated by N nucleotides is

$$\text{Prob}\left(\text{N}\right)\hspace{0.17em}=\hspace{0.17em}1-\left(1+Nq\right){\left(1-q\right)}^N.$$ [S5]

Now, we calculate the probability of DFS in a cohort of M replicons whose size is in the vicinity of N. The probability of no error occurring from this cohort would be the following product: ${\displaystyle \prod }_k\left[1\hspace{0.17em}-\hspace{0.17em}P\left(N_k\right)\right],$ where the product is restricted to those replicons within the cohort. This probability will be very close to 1, and we denote it by θ. Substituing Eq. S5 into this expression, and recognizing that all of the N_k are close to N, enables us to rewrite the probability of no error from the cohort as

$${\left(1+Nq\right)}^M\cdot {\left(1-q\right)}^{MN}=\theta .$$

Now, taking the natural logarithm,

$$M\cdot \text{log}\left(1+Nq\right)+MN\cdot \text{log}\left(1-q\right)=\text{log}\left(\theta \right).$$ [S6]

Because q << 1, $\log \left(1-q\right)\approx -q$, and thus we write

$$M\cdot \text{log}\left(1+Nq\right)-\hspace{0.17em}MNq=\text{log}\left(\theta \right).$$

Hence,

$$M=\frac{\text{log}\left(\theta \right)}{\left[\text{log}\left(1+Nq\right)-\hspace{0.17em}Nq\right]}.$$ [S7]

For Nq << 1, it is straightforward to show, from expanding the denominator, that M ≈ 1/N².