Significance
Lithium metal is an ideal anode material for rechargeable Li-ion batteries, but its use is prevented by the growth of lithium deposits, or “dendrites,” during charging that can cause performance loss and serious safety concerns. Understanding the growth of dendrites in situ is crucial for the progress of this technology. MRI has been limited to directly studying the lithium signal until now, resulting in low sensitivity, limited resolution, and long experiment times. We present here an approach that detects the “shadows” of dendrites growing through the electrolyte, allowing the dendrites’ growth to be imaged very quickly in 3D with high resolution. This technique can also be applied to other electrodes, such as those based on sodium, zinc, and magnesium.
Keywords: Li-ion batteries, in situ MRI, dendrite growth
Abstract
Lithium metal is a promising anode material for Li-ion batteries due to its high theoretical specific capacity and low potential. The growth of dendrites is a major barrier to the development of high capacity, rechargeable Li batteries with lithium metal anodes, and hence, significant efforts have been undertaken to develop new electrolytes and separator materials that can prevent this process or promote smooth deposits at the anode. Central to these goals, and to the task of understanding the conditions that initiate and propagate dendrite growth, is the development of analytical and nondestructive techniques that can be applied in situ to functioning batteries. MRI has recently been demonstrated to provide noninvasive imaging methodology that can detect and localize microstructure buildup. However, until now, monitoring dendrite growth by MRI has been limited to observing the relatively insensitive metal nucleus directly, thus restricting the temporal and spatial resolution and requiring special hardware and acquisition modes. Here, we present an alternative approach to detect a broad class of metallic dendrite growth via the dendrites’ indirect effects on the surrounding electrolyte, allowing for the application of fast 3D 1H MRI experiments with high resolution. We use these experiments to reconstruct 3D images of growing Li dendrites from MRI, revealing details about the growth rate and fractal behavior. Radiofrequency and static magnetic field calculations are used alongside the images to quantify the amount of the growing structures.
Lithium metal is a promising anode material for secondary lithium batteries because it has the highest theoretical specific capacity of possible anode materials (3,860 mAh/g), and the most negative voltage. The metal’s use is currently limited due to irregular microstructure buildup on the electrode during charging (1). These mossy, needle-like, or dendritic structures severely compromise battery performance and can eventually penetrate the separator and cause overheating and short circuiting, thus presenting serious safety concerns. Preventing dendrite growth has proven to be extremely challenging, due in part to the current poor understanding of the conditions under which the dendrites’ growth is initiated and the factors that contribute to their continued growth (2, 3). The development of new analytical techniques that are sensitive to dendrite growth and amenable to studying electrochemical cells in situ is crucial to future efforts of improving battery designs and performance (4, 5).
In situ NMR spectroscopy and MRI are powerful noninvasive methods that can provide time-resolved and quantitative information about the changes within the electrolyte and the electrodes. NMR measurements are sensitive to dendrite growth and are also able to resolve different lithium microstructure morphologies through chemical shift measurements (6–9). MRI approaches provide additional spatial information, allowing specific structural changes to be localized, thereby enhancing the utility of the methods and simplifying interpretation (7, 10, 11). Previous work relied on the measurement of 7Li and 6Li signals, where the identification of dendrites could be achieved via changes in the intensities and frequencies of the Li-metal signals due to skin-depth effects and susceptibility shifts, respectively (6–10, 12). The main limitations of resolution and imaging time arise from the inherent insensitivity of the lithium isotopes and relaxation phenomena.
Here, we demonstrate a previously unidentified approach; rather than imaging dendrites directly, their interactions with the electrolyte can be used to measure their growth indirectly. Three effects are considered: (i) the displaced volume in the electrolyte, (ii) the magnetic-susceptibility effects on the electrolyte, and (iii) the radiofrequency (rf) field effects on the electrolyte signal. The electrolyte is typically composed of proton-rich material [e.g., the electrolyte with the brand-name LP30 is composed of 1 M LiPF6 in 1:1 ethylene carbonate (EC):dimethyl carbonate (DMC)], thereby providing excellent sensitivity for measurements of 1H spins. As a result, full 3D measurements become possible that track dendrite growth as a function of time.
Results and Discussion
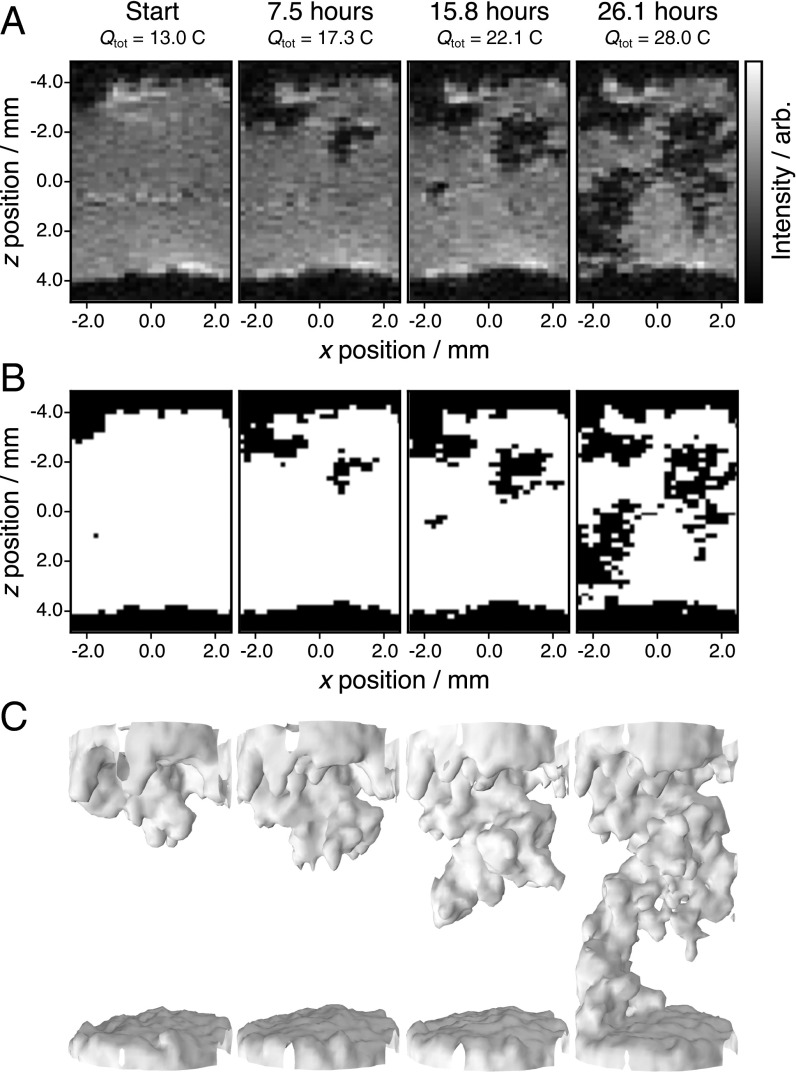
Fig. 1 shows a time series of 3D images of dendrite growth in a symmetrical Li-metal electrode cell geometry. The images, acquired using 1H FLASH (fast low angle shot) imaging performed in situ on the electrochemical cell (Fig. 1A), show there to be a relatively uniform intensity in the electrolyte region initially, with dark regions extending from z = 4 and −4 mm corresponding to the two Li electrodes. Fig. 1A (Left) shows the starting configuration of the cell after dendrite growth had been initiated by charging at 50 μA (0.16 mA cm−2) for 72 h (total charge applied, C) (7). As further current is passed (referred to here as “charging” because this is the direction of current flow in a full cell when Li plating occurs) (Fig. 1A, Left to Right), a feature grows out from the left side of the top electrode into the middle of the electrolyte region and spans the full electrolyte cavity to reach the bottom electrode by t = 26.1 h ( C). The morphology and progressive “growth” of this feature between the electrodes is indicative of a dendritic microstructure.
Fig. 1.
In situ 1H 3D FLASH imaging results from the electrochemical cell, with each 3D image acquired in 16 min 40 s. The cell was charged at 50 μA (0.16 mA cm−2) for 72 h before these measurements and then charged at 160 μA (0.51 mA cm−2) for the times specified, with the total charge applied also given in coulombs. (A) Two-dimensional slices from four time points. (B) Segmented images of the results from A, where . (C) Three-dimensional segmented images of the same time points with an additional Gaussian filter applied to smoothen the visualization.
Segmenting the images into regions above and below a threshold intensity, (Fig. 1B), emphasizes the position and growth of the microstructure. was chosen to provide good image contrast while maintaining the 3D structure of the reconstructed dendrite. Factors affecting the choice of are discussed in more detail below. Movie S1 shows the full time series of images collected every 17 min during a 26.1-h charge, and Movie S2 illustrates the reconstructed dendrite geometry from the final MRI image (same data as Fig. 1C, Right).
This methodology offers considerable advantages over 3D imaging techniques observing 7Li metal, which require longer scan times (13). Our current approach offers 180-μm isotropic resolution within 16 min 40 s scans, with potential for further optimization due to the increased signal-to-noise ratio and favorable MR properties of the 1H nucleus, and the contrast enhancement afforded by the long-range susceptibility effects. The ability to observe microstructural lithium growth in situ and in 3D provides a unique opportunity to study the mechanisms underlying these processes. For example, the image series in Fig. 1C shows that the dendrite growth is not unidirectional, even on macroscopic length scales, but instead twists before growing to short circuit the cell in the final image frame. There have been reports that microstructure growth could occur at the base of existing dendrites (14). This process can clearly be ruled out for the applied currents and cell geometry used here because once the growth zones move past a given region, the observed microstructure does not change for the remainder of the experiment. This effect is observed when comparing, for example, the third to fourth images in Fig. 1C (and the associated time steps in Movie S1), where new growth is observed on both the left- and right-hand sides of the cell during the same time period.
Understanding the source of the observed image contrast around the dendrites is important if the methodology is to be fully exploited. The microstructures are expected to be very small, of the order of 1–3 μm in diameter (5, 14, 15), making it unlikely that the 80% drop in signal intensity of the 180 × 180 × 180 μm image voxels can be due solely to the local displacement of the electrolyte by the dendrites. Furthermore, local displacement effects would not result in any attenuation of the total image intensity, and yet the intensity decreases approximately linearly during charging (Fig. 2) and by a total of ca. 18% by the end of charging. Assuming that the concentration of the protonated species in the electrolyte is uniform, the signal changes can be correlated to a change in the observed electrolyte volume (right-hand axis in Fig. 2). This conversion allows for a direct comparison with the volume of Li microstructure that grows if all of the deposited lithium grows as microstructure (dashed line in Fig. 2). Under these assumptions, the microstructure occupies 2.03 mm3 by the end of charging, whereas the signal lost in the images corresponds to a lost volume of over 40 mm3. This 20-fold difference between the expected microstructure volume and the affected region of the proton signal can be explained on the basis of susceptibility effects and rf inhomogeneities close to the conducting microstructure.
Fig. 2.
Trends in the total MRI image intensity correlated with microstructure volume. The image intensity is converted to volume by assuming volume signal intensity (i.e., concentration is uniform) and then normalizing by the starting volume of the electrolyte as estimated from the image at (236 mm3). The dendrite volume is estimated by converting the total charge transferred, (current times time) to the number of moles of lithium, , where is the Faraday constant, and then to a volume, , using the density of lithium metal, . Numerical errors associated with the experimental image intensity are within the marker size. arb., arbitrary units.
These mechanisms can be quantified through and field calculations. A section of the reconstructed dendrite from the MRI results is chosen as a model system on which to perform these calculations, as described in Materials and Methods. Dendrites can be thought of as fractal (16), and hence this macroscopic shape is expected to be representative of the dendrite shape on the microscopic scale. The chosen structure resembles sections of lithium microstructures seen in SEM (15) and X-ray phase-contrast imaging (17).
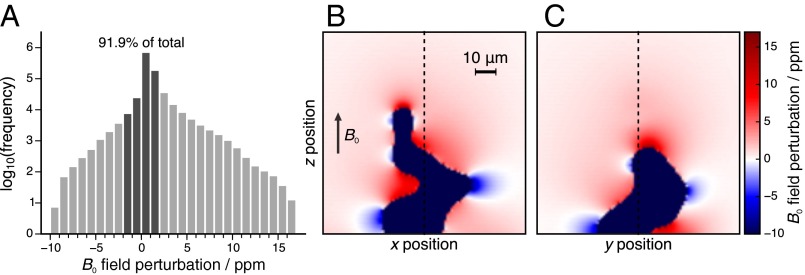
Lithium metal is strongly paramagnetic (volume susceptibility, ) (18); thus a strong local field is induced in the direction of an applied B0 field, leading to changes in the observed frequencies of the nuclear species in the electrolyte around the object. The modification to B0 is calculated using a fast Fourier transform (FFT) method (12, 19, 20) that operates on a Cartesian grid of susceptibility values representing the Li dendrite used for the field calculations. Fig. 3 displays orthogonal cross-sections of the B0 field map obtained from the susceptibility calculations and a histogram showing the variation in the B0 field across the full voxel. A significant perturbation of 10–15 ppm is observed in the field close to the dendrite, matching well with 7Li MRI (7, 10) and NMR (6, 8, 21) results, where the signals from the dendrites are observed to shift by up to 15 ppm relative to the bulk metal resonance. The effects are long-ranged, impacting the local field for all of the positions inside the voxel, albeit by small amounts. For example, the field around a spherical object falls off with and around a cylindrical object with . The histogram combining all of the positions inside the voxel (Fig. 3A), plotted on a logarithmic scale, shows that 91.9% of the locations experience a field perturbed by less than 2 ppm. We note that these effects can result in minor misregistration of some of the detected signals in the frequency-encoded dimension (96 points were acquired in the read or directly observed dimension with a spectral width of 80 kHz, so a frequency shift of ca. 2 ppm will result in signal misregistration by 1 voxel). This effect results in minor additional image contrast and could be reduced using an increased spectral width for the acquisition.
Fig. 3.
Results from the susceptibility calculations. (A) Histogram of the B0 field perturbations at every position in the 3D voxel. (B and C) B0 field maps at orthogonal slices through the simulation voxel. B0 is aligned along z as indicated in B; dotted lines on B and C show the slice positions.
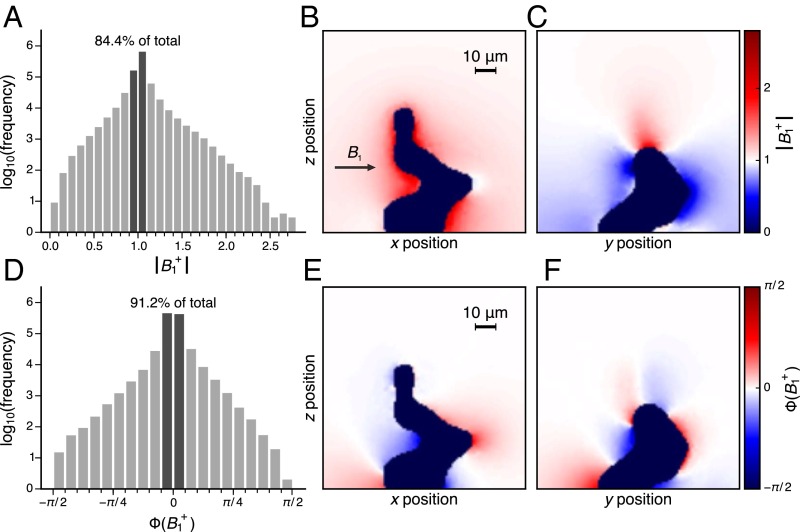
The calculated field distribution is shown for two orthogonal planes in Fig. 4, including the absolute magnitude of the field (Fig. 4 B and C) and its phase (Fig. 4 E and F), as well as histograms showing the distribution of each quantity over all of the electrolyte sites in the voxel (Fig. 4 A and D). The lithium dendrite is modeled as a perfect conductor. The rf field, expected to be homogenous in the absence of the dendrite, has changed to a highly anisotropic distribution, For the most part, the magnitude of the field is increased in the x-z plane and reduced in the y-z plane. According to the boundary conditions, the field perpendicular to a metal surface is significantly attenuated, as also demonstrated in previous calculations and MRI experiments (12). The maximum deviations from the unperturbed magnetic field occur close to the surface of the metal, in electrolyte regions that are less than 5 μm away from the metal surface. There are also strong changes in the phase of the field close to the dendrite structure (Fig. 4 E and F). However, the analysis of the rf field distribution over the whole voxel (Fig. 4 A and C) shows that the rf field is not significantly perturbed for the majority of the electrolyte locations in the voxel (93.9% are within 20% of the unperturbed field amplitude, and 91.2% are within radians of its phase). The histograms also show there to be an approximately equal distribution of sites in the voxel where an increase in the field intensity/phase is observed versus a decrease. Both the amplitude and the phase change in impact the excited and detected signal for this voxel in the MRI experiment.
Fig. 4.
Results from the rf field intensity and phase calculations. (A and D) Log-scale histograms for the amplitude and phase of across the whole voxel. (B, C, E, and F) Maps of the amplitude (B and C) and phase (E and F) of in two orthogonal slices through the voxel. propagates in the direction as indicated in B.
The B0 and field maps in Figs. 3 and 4 are used to calculate the detected signal intensity of the dendrite-occupied voxel in a gradient-echo (T2*-weighted) MRI experiment. Spin echo MRI experiments could also be used, but the inhomogeneities in the rf field would compromise the use of fast/turbo spin echo sequences, wherein the acquisition of consecutive lines of k-space with (imperfect) refocusing π-pulses under a single excitation would lead to image distortions. Slower experiments would therefore be required and would not be amenable to in situ studies.
In the vector model used to describe the dynamics of the bulk MR magnetization vector, the spatial variation of impacts the NMR signal excited by an rf pulse according to
| [1] |
where is the equilibrium magnetization at the jth position in the voxel and is the flip angle defined as with the gyromagnetic ratio of the nucleus and the pulse duration. From Eq. 1, it is clear that changes in the phase of are manifested in the phase of .
In steady-state imaging experiments such as FLASH, low flip angles and repetition times (TR) are used to reduce experiment times, partially saturating the equilibrium magnetization until an equilibrium value is reached. The spatial variation in leads to a spatial variation in the equilibrium magnetization that must also be accounted for, and is given by
| [2] |
where is the length of the fully relaxed magnetization vector, TR is the repetition time used in the experiment, and is the spin-lattice relaxation of the nuclear spin, which is assumed to be constant () within the voxel.
According to the principle of reciprocity (22), the local variation in the phase and amplitude of the field also impacts the detected signal,
| [3] |
where is complex and represents the signal amplitude and phase, and is the Larmor frequency. All of the signals from each position inside the voxel, , are summed to give the overall intensity, , that is predicted for the single voxel in the image. Depending on the type of imaging experiment used, further weighting of the signal intensity is expected (i.e., by , , or ). Gradient echo (GE) sequences such as FLASH are -weighted and are sensitive to these types of inhomogeneities within the voxel. The detected signal intensity is consequently modified to
| [4] |
where is the angular frequency offset in the rotating frame for the jth location in the voxel (obtained from the susceptibility calculations) and , the echo time (TE) used in the experiment. The signals are normalized by , the expected signal intensity for the voxel when no dendrite is present (i.e., no scattered rf field, , and , , and ). All experimental parameters used in the calculation correspond to the values from the FLASH experiments used to acquire the images from Fig. 1.
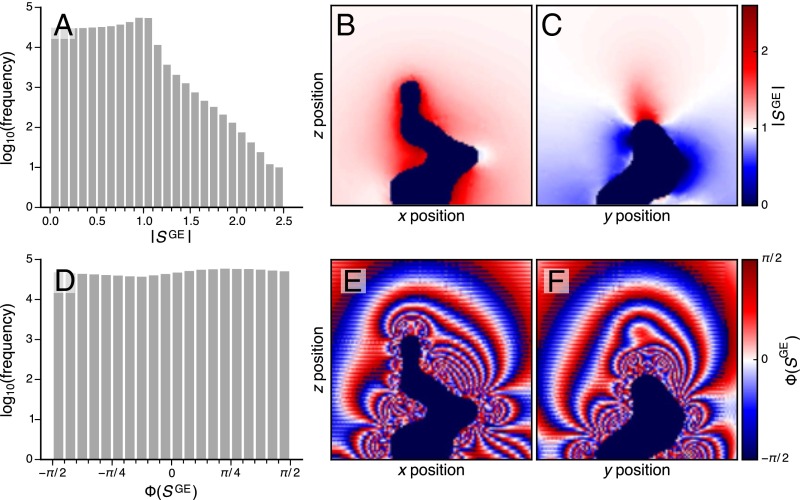
Maps of the signal intensity, (Fig. 5 B and C), follow the trends shown in the field maps (Fig. 4 B and C). This similarity is seen because the FLASH experiment uses a low flip-angle pulse and in the regime where TR is sufficient to avoid saturation of then is proportional to the amplitude of . Maps of the signal phase, (Fig. 5 E and F), show there to be significant changes over relatively short distances in the voxel, with particularly strong fluctuations close to the dendrite. These effects are predominantly due to the changing B0 field throughout the volume and the resulting differences in the relative phase that is accumulated during the TE in the experiment, although the changing phase will also play a role. The changes in the signal phase have a profound effect on the total signal intensity of the voxel because of partial signal cancellations, resulting in significant attenuation of the detected signal.
Fig. 5.
Results from the signal intensity and phase calculations. (A and D) Log-scale histograms for the amplitude and phase of the detected signal across the whole voxel. (B, C, E, and F) Maps of the amplitude (B and C) and phase (E and F) of the detected signal in two orthogonal slices through the voxel.
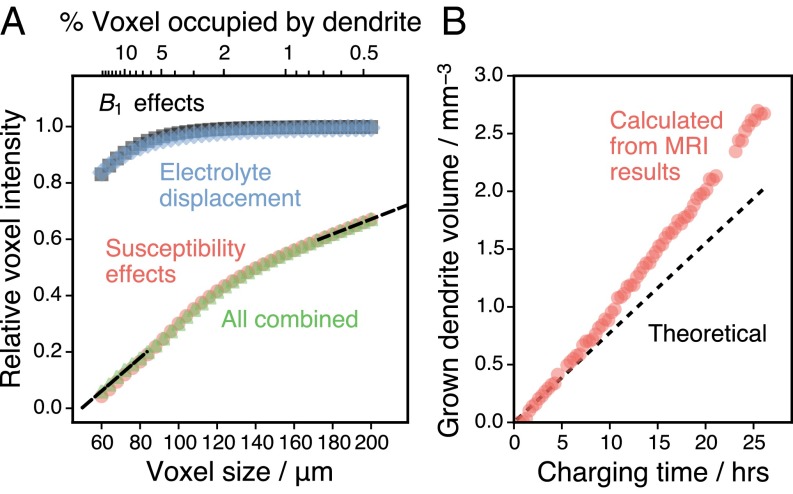
The voxel considered in Figs. 3–5 has a volume of 1003 μm3 with ∼3.5% of the total volume occupied by dendritic lithium metal. To understand the dominant effects that contribute to the signal intensity under different growth conditions, voxels of different sizes were also considered, containing the same dendrite structure but enlarging the surrounding region. The sum of the signal intensities is shown in Fig. 6A, where the individual contributions from the susceptibility and field effects are also considered. It is seen that the inhomogeneities lead to almost no change in the detected signal. This effect can be attributed to the fact that increases in some regions around the voxel while it decreases in others. Meanwhile, the susceptibility effects can explain almost all of the complete signal attenuation when only a modest fraction of the cell is occupied by dendrites (603-μm3 voxel; 15% occupied by dendrite). In the MRI experiment results, a threshold of 20% of the maximum signal amplitude of a given voxel () is used to designate locations where dendrites are growing. In Fig. 6A, this condition is satisfied for the 803-μm3 voxel with 7% of its volume occupied by the dendrite. This observation confirms that high levels of contrast are possible without individual voxels containing a significant volume of metal displacing the electrolyte.
Fig. 6.
Analysis of calculated voxel size effects. (A) Calculated signal attenuations for differently sized voxels, given relative to the maximum signal for each cell size. Contributions of different sources of signal attenuation are calculated separately (for alone and for susceptibility alone for all , with both conditions used to isolate displacement effects). Black dashed lines illustrate the linear extrapolation of the combined results. (B) Comparison between the calculated and theoretical dendrite volume in the battery throughout the experimental time series. Numerical errors associated with the calculated dendrite volume are within the marker size.
The results in Fig. 6A relate the dendrite volume in a single voxel to the MRI signal intensity of that voxel and can be extrapolated to cover the full signal range (dashed black lines in Fig. 6A). This relationship can then be used to convert the experimental MRI signal intensities of each voxel, , into estimates of the local dendrite volume and therefore the overall volume of dendrites that have grown inside the battery (Fig. 6B, methodology described in more detail in SI Text). The results are close to the calculated theoretical volume (dashed line in Fig. 6B, calculation described in the caption of Fig. 2). The total dendrite volume is predicted to be 2.7 mm3, whereas 2.0 mm3 is expected if all of the deposited lithium forms dendrites with the same density as bulk lithium metal. Additional calculations performed on highly symmetric (spherical and cylindrical) and random lithium geometries (detailed in SI Text and Fig. S1) produce lower estimates of the total grown dendrite volume (1.6 mm3 for the sphere and random morphologies and 2.2 mm3 for a rotationally averaged cylinder). The model dendrite geometry does, therefore, help in examining the influence of morphology on the quantification. On the other hand, the relatively small range of the estimates, which fall within ∼80–135% of the theoretical dendrite volume, suggest that the role of morphology is minor, and although there is some uncertainty in the quantification of the dendrite volume, there is currently no alternative methodology that would allow one to perform such an assessment in situ. Indeed, the agreement between the current experiment and theory is quite surprising, considering that a naïve analysis simply based on signal intensities would overestimate the dendrite volume by a factor of 20 (Fig. 2). Therefore, this analysis shows that and especially effects allow a nearly accurate explanation of the experimentally observed signal attenuation.
Fig. S1.
Comparison of signal decay due to susceptibility differences for objects of different shapes. (A) Relationship between voxel signal intensity and occupation of the voxel for a cylinder oriented at different angles, θ, with respect to the to B0 field. arb., arbitrary units. (B) The average of the cylinder orientations compared with spherical and random lithium geometries and the model dendrite geometry presented in the main text. (C) Calculation of the dendrite volume based on the experimental signal intensities using the results from B for the different shapes (legend from B applies). The theoretical dendrite volume is based on the electrochemistry and assumes that all plated lithium forms dendrites, as described in the legend of Fig. 2.
In summary, we present here a methodology for the noninvasive assessment of Li-ion battery cells, where the growth of microstructure and dendrites is monitored indirectly via 1H MRI in 3D at different charging states. One of the main advantages of the method is a dramatic increase in sensitivity, because direct observation of low-sensitivity nuclei such as 7Li is not required, thus enabling wide-ranging applications to different battery chemistries (e.g., sodium), including the use of electrodes with insensitive or inactive NMR nuclei such as zinc. Furthermore, the speed afforded by this 1H method offers a significant advantage over current approaches, which will be an important factor for the study of different cycling behaviors. The approach provides a “one nucleus fits all” solution for studying a broad range of different battery models (for example, Li, Na, Zn, and Mg cells) under the same conditions, with no special hardware demands. Significant image contrast amplification (up to a factor 20) is demonstrated to arise from the local inhomogeneities originating from the susceptibility differences. These techniques could be used for testing dendrite growth models and the effectiveness of dendrite-suppressing approaches such as pulsed charging (23, 24) or the use of advanced electrode, electrolyte, or separator materials.
SI Text
Susceptibility calculations were performed on model lithium geometries to explore the dependence of the quantification of the lithium dendrite volume on morphology. The following geometries were constructed on a 2563 Cartesian grid (nominally representing a 2563-μm voxel):
-
i)
An infinite cylinder (radius, 11 μm) with the direction of the B0 field varied from to , where is the angle between the field direction and the long axis of the cylinder. The susceptibility-induced distortions around the cylinder are zero for the orientation (i.e., B0 field aligned with long axis of cylinder); hence this orientation was not included.
-
ii)
A random distribution of lithium within the central 303-μm region of the cell, with 75% of the volume of this region assigned to lithium.
-
iii)
A sphere (radius, 20 μm).
Sites inside the structure were assigned a susceptibility (where ), with elsewhere, roughly approximating the electrolyte susceptibility. The sizes of the shapes were chosen to obtain cells containing similar amounts of Li (and to maintain this similarity as the box size is reduced during the processing steps, as described in step 3 below).
The calculations were performed using the same FFT method referenced in the main text, resulting in 3D B0 field maps over a region that is used to represent a single voxel in the FLASH MRI image. The results were processed in the following way to produce estimates of the total dendrite volume from the MRI image intensities. For step 1, Eqs. 1–4 are used to calculate the expected signal intensity of the voxel for the experimentally used FLASH sequence. Inhomogeneities in the rf field are ignored because these are shown to be insignificant in comparison with the impact of B0 inhomogeneities for the gradient echo experiment ( is used in the equations). In step 2, the number of lithium positions in the 2563-μm susceptibility cell are used to calculate the percentage of the voxel occupied by lithium. Thus, with the result from step 1, a single data point relating %Li with MRI signal intensity is obtained. In step 3, the B0 field map is cropped to reduce the effective voxel size (i.e., reduce the cell size from 2563 μm to something smaller such as 2403 μm) surrounding the same lithium geometry. Steps 1 and 2 are then repeated to calculate the MRI signal intensity for the cell with the new %Li (the lithium structures are centered in the cell so reducing the cell size increases the %Li). This procedure results in a series of data points relating the signal intensity and the %Li in the voxel for the calculated lithium geometry (shown in Figs. S1 A and B for the different geometries/relative B0 orientations). In step 4, the relationships from step 3 are linearly extrapolated to cover the full signal range (between 0 and 1) so that the relationships can be used to provide a lookup table to convert the measured voxel intensities in the MRI experiments [scaled according to for the jth voxel at time ] into estimates of the %Li contained within each voxel. The %Li is then converted into a volume using the MRI voxel size (1803 μm) and summed over all of the voxels in each image to give the total grown dendrite volume at each time, as plotted in Fig. S1C.
The calibration curves for the different lithium geometries are shown in Fig. S1 A and B. Orienting the cylindrical lithium geometry at different angles with respect to B0 (Fig. S1A) results in a large range in the predicted voxel signal intensity, which is expected because susceptibility effects are highly anisotropic, with different impacts on the local field in directions parallel and perpendicular to the B0 direction. The lithium dendrite structures that grow in the experiment are expected to be directionally disordered (5, 8, 14–17) and therefore should be better represented by a linear combination of the different cylinder orientations. The predicted signal attenuation due to this linear combination is shown in Fig. S1B and compares favorably with the result from the model dendrite geometry, as well as the spherical and random lithium geometries. The agreement between the calibration curves leads to similar predictions for the grown dendrite volume in the experiments (Fig. S1C), with the spherical and random morphologies giving an estimate of ca. 1.6 mm3, the cylinder 2.2 mm3, and the model dendrite 2.7 mm3, whereas the theoretical maximum volume based on the duration of the applied current is 2.0 mm3. The calibration curves and volume estimates from the spherical and random lithium geometries are almost identical, strongly indicating that the quantification results are largely insensitive to the lithium morphology. On the other hand, it is unlikely that both morphology and Li quantification can be determined from the MRI image alone. Based on the lithium geometries explored here, the quantification is accurate to within a factor of about two, and accuracy could be improved by including further prior knowledge about morphology.
Materials and Methods
Sample Preparation.
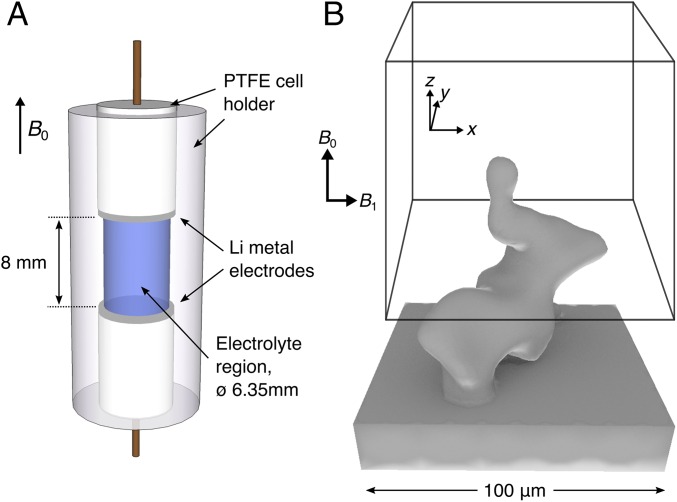
A schematic of the electrochemical cell used is shown in Fig. 7A. The cell consists of two 6.35-mm-diameter, circular lithium metal (Sigma-Aldrich) electrodes, separated by an 8-mm electrolyte region filled with 1 M LiPF6 in 1:1 by volume EC:DMC electrolyte (LP30, Novolyte) mixed with 5% (wt/wt) poly(methyl methacrylate). Copper mesh current collectors were pressed into the lithium metal electrodes and attached to stranded copper wire that connected them to the external circuit. The cell was prepared in an argon glove box (O2 and H2O, <0.2 ppm). Electrochemical cycling was performed using a Biologic VSP potentiostat, with the current applied in the direction from the bottom electrode (positive electrode) to the top electrode (negative electrode). Dendrite growth was initiated before the collection of the in situ 1H images by charging the cell at 50 μA (0.16 mA cm−2) for 72 h. During the MRI experiments, the cell was charged at 160 μA (0.51 mA cm−2) for a total of 26.1 h.
Fig. 7.
Schematics of the electrochemical cell (A) and the model dendrite used for the calculations (B), with the box drawn to illustrate a given MRI voxel position around the dendrite.
Magnetic Resonance Imaging.
The MRI experiments were performed on a Bruker Ultrashield 9.4 T Avance I spectrometer containing a Bruker Micro2.5 gradient assembly and operating at 400.1 MHz for 1H. A Bruker Micro2.5 imaging probe was used to collect all of the data, with a Bruker WB40 coil insert (internal diameter, 25 mm) for 1H experiments. The cell was aligned in the magnet such that B0 (and the z axis of the gradients) was aligned perpendicular to the face of the electrodes (as illustrated in Fig. 7A). The cells were centered in the coil, the excitation profile of which was found to be ∼15 mm, thus ensuring uniform excitation over all the components in the cell. Three-dimensional 1H MRI experiments were performed using the 3D FLASH sequence implemented in Paravision 5.1, using a TE of 2 ms, TR of 100 ms, nominal flip angle (α) of 10°, and four scans for signal averaging. The field of view was 11.52 × 11.52 × 17.28 mm in the x, y, and z direction, respectively, with a k-space consisting of 64 phase-encoded points in the x and y directions and 96 points in the readout direction along z. Only the central 50 k-space points in the phase directions were acquired to accelerate the acquisition. The application of the FLASH sequence resulted in a 3D image covering both electrodes and the electrolyte region in the cell with an isotropic resolution of 180 μm, with a total experiment time of 16 min 40 s.
rf Field Calculations.
The interaction between a microscopic conducting object and an applied rf field was simulated using finite element calculations to solve Maxwell’s equations in 3D. The calculation was performed within the COMSOL simulation suite (COMSOL Multiphysics; https://www.comsol.com; COMSOL AB). A 3D geometry representing a lithium dendrite structure was constructed from a section of the FLASH MRI data. The raw voxel data were first converted to an STL format using the vtk Python module (25). The STL mesh was then imported into Blender, where a cuboid base representing the electrode surface was added and the surface closed. Minor meshing errors in the resulting structure were fixed using Gmsh (26) before the object, displayed in Fig. 7B, was imported into COMSOL. The dendrite was placed at the center of a 280-μm-radius sphere, filled with electrolyte surrounding the dendrite. Compared with the dendrite electrical conductivity of 3.774 × 107 , the conductivity of the electrolyte region was approximated as zero, The finite element mesh consisted of 67,400 tetrahedral and 5,942 triangular elements, covering the surface of the dendrite and spherical boundary, and volume between the two. Dirichlet boundary conditions were used on the surface of the sphere to specify the incoming field, , whereas perfect conductor boundary conditions were used on the surface of the dendrite. When using calculations with finite conductivity, the magnitude of an object’s conductivity has a negligible effect on distortions (12, 27). The computations were performed in the rotating frame at a frequency of 400 MHz (the Larmor frequency of 1H in the MRI experiments) using the BiCGStab solver. The calculation took ∼1 h running on a desktop computer with 32 gigabytes of random access memory and an Intel i7 processor with 6 cores. Only the and components of the calculated field are included in the MR signal calculations as the components perpendicular to the direction of the external magnetic field, , where are the and components of the scattered field and the values are normalized according to the incoming field. These quantities were extrapolated onto a 200 × 200 × 200 grid covering a 200-μm3 region centered on the dendrite and exported to Python for further analysis. The exported fields are used to calculate the rf fields in the positively and negatively rotating frames (22, 28),
| [5] |
| [6] |
because these are the fields that interact with the nuclear spin magnetization in the rotating frame, where the and are complex quantities.
Susceptibility Calculations.
The susceptibility-induced modification to B0 caused by the paramagnetic lithium metal structure inside the voxel was calculated using a FFT method that has been described elsewhere (19, 20). A regular 3D grid of volume-susceptibility values is taken as the calculation input, which was constructed directly from the gridded COMSOL output, with (where ) (18) for grid points inside the dendrite and elsewhere, roughly approximating the electrolyte susceptibility. This 2503 cell was padded with zeros to make a 5123 cell on which the calculations were performed. The output from the calculations is the susceptibility-induced offset to the field at each of the points in the grid, , in units of parts per million.
Supplementary Material
Acknowledgments
The NMR/MRI methodology, as well as rf and static field calculations were supported by US National Science Foundation Grant CHE 1412064. The electrochemistry and battery components of the work were supported as part of the NorthEast Center for Chemical Energy Storage (NECCES), an Energy Frontier Research Center funded by the US Department of Energy (DOE), Office of Science, Basic Energy Sciences, under Awards DE-SC0001294 and DE-SC0012583 (in situ methodology), including NECCES matching funds from the New York State Energy Research Development Authority (to H.J.C.), by the Assistant Secretary for Energy Efficiency and Renewable Energy, Office of FreedomCAR and Vehicle Technologies of the US DOE under Contract DE-AC02-05CH11231, under the Batteries for Advanced Transportation Technologies (BATT) Program Subcontract 7057154.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1607903113/-/DCSupplemental.
References
- 1.Tarascon J-M, Armand M. Issues and challenges facing rechargeable lithium batteries. Nature. 2001;414(6861):359–367. doi: 10.1038/35104644. [DOI] [PubMed] [Google Scholar]
- 2.Sannier L, et al. Room temperature lithium metal batteries based on a new gel polymer electrolyte membrane. J Power Sources. 2005;144(1):231–237. [Google Scholar]
- 3.Crowther O, West AC. Effect of electrolyte composition on lithium dendrite growth. J Electrochem Soc. 2008;155(11):A806–A811. [Google Scholar]
- 4.Brissot C, Rosso M, Chazalviel J-N, Baudry P, Lascaud S. In situ study of dendritic growth in lithium/PEO-salt/lithium cells. Electrochim Acta. 1998;43(10–11):1569–1574. [Google Scholar]
- 5.Orsini F, et al. In situ scanning electron microscopy (SEM) observation of interfaces within plastic lithium batteries. J Power Sources. 1998;76(1):19–29. [Google Scholar]
- 6.Bhattacharyya R, et al. In situ NMR observation of the formation of metallic lithium microstructures in lithium batteries. Nat Mater. 2010;9(6):504–510. doi: 10.1038/nmat2764. [DOI] [PubMed] [Google Scholar]
- 7.Chang HJ, et al. Correlating microstructural lithium metal growth with electrolyte salt depletion in lithium batteries using ⁷Li MRI. J Am Chem Soc. 2015;137(48):15209–15216. doi: 10.1021/jacs.5b09385. [DOI] [PubMed] [Google Scholar]
- 8.Chang HJ, et al. Investigating Li microstructure formation on Li anodes for lithium batteries by in situ 6Li/7Li NMR and SEM. J Phys Chem C. 2015;119(29):16443–16451. [Google Scholar]
- 9.Hu JZ, et al. In situ 7Li and 133Cs nuclear magnetic resonance investigations on the role of Cs+ additive in lithium-metal deposition process. J Power Sources. 2016;304:51–59. [Google Scholar]
- 10.Chandrashekar S, et al. 7Li MRI of Li batteries reveals location of microstructural lithium. Nat Mater. 2012;11(4):311–315. doi: 10.1038/nmat3246. [DOI] [PubMed] [Google Scholar]
- 11.Salager E, et al. Solid-state NMR on the family of positive electrode materials Li2Ru1-ySnyO3 for Li-ion batteries. Chem Mater. 2014;26(24):7009–7019. [Google Scholar]
- 12.Ilott AJ, et al. Visualizing skin effects in conductors with MRI: (7)Li MRI experiments and calculations. J Magn Reson. 2014;245:143–149. doi: 10.1016/j.jmr.2014.06.013. [DOI] [PubMed] [Google Scholar]
- 13.Romanenko K, Forsyth M, O’Dell LA. New opportunities for quantitative and time efficient 3D MRI of liquid and solid electrochemical cell components: Sectoral Fast Spin Echo and SPRITE. J Magn Reson. 2014;248:96–104. doi: 10.1016/j.jmr.2014.09.017. [DOI] [PubMed] [Google Scholar]
- 14.Yamaki J, et al. A consideration of the morphology of electrochemically deposited lithium in an organic electrolyte. J Power Sources. 1998;74(2):219–227. [Google Scholar]
- 15.López CM, Vaughey JT, Dees DW. Morphological transitions on lithium metal anodes. J Electrochem Soc. 2009;156(9):A726–A729. [Google Scholar]
- 16.Fleury V. Branched fractal patterns in non-equilibrium electrochemical deposition from oscillatory nucleation and growth. Nature. 1997;390(6656):145–148. [Google Scholar]
- 17.Eastwood DS, et al. Three-dimensional characterization of electrodeposited lithium microstructures using synchrotron X-ray phase contrast imaging. Chem Commun (Camb) 2015;51(2):266–268. doi: 10.1039/c4cc03187c. [DOI] [PubMed] [Google Scholar]
- 18.Gugan D. Martensitic transformation of lithium: Magnetic susceptibility measurements. Phys Rev B. 1997;56(13):7759–7762. [Google Scholar]
- 19.Salomir R, de Senneville BD, Moonen CT. A fast calculation method for magnetic field inhomogeneity due to an arbitrary distribution of bulk susceptibility. Concepts Magn Reson. 2003;19B(1):26–34. [Google Scholar]
- 20.Marques JP, Bowtell R. Application of a Fourier-based method for rapid calculation of field inhomogeneity due to spatial variation of magnetic susceptibility. Concepts Magn Reson Part B Magn Reson Eng. 2005;25B(1):65–78. [Google Scholar]
- 21.Trease NM, Zhou L, Chang HJ, Zhu BY, Grey CP. In situ NMR of lithium ion batteries: Bulk susceptibility effects and practical considerations. Solid State Nucl Magn Reson. 2012;42:62–70. doi: 10.1016/j.ssnmr.2012.01.004. [DOI] [PubMed] [Google Scholar]
- 22.Hoult DI. The principle of reciprocity in signal strength calculations—A mathematical guide. Concepts Magn Reson. 2000;12(4):173–187. [Google Scholar]
- 23.Mayers MZ, Kaminski JW, Miller TF. Suppression of dendrite formation via pulse charging in rechargeable lithium metal batteries. J Phys Chem C. 2012;116(50):26214–26221. [Google Scholar]
- 24.Aryanfar A, et al. Dynamics of lithium dendrite growth and inhibition: Pulse charging experiments and Monte Carlo calculations. J Phys Chem Lett. 2014;5(10):1721–1726. doi: 10.1021/jz500207a. [DOI] [PubMed] [Google Scholar]
- 25.Schroeder W, Martin K, Lorensen B. The Visualization Toolkit. 4th Ed Kitware; New York: 2006. [Google Scholar]
- 26.Geuzaine C, Remacle J-F. Gmsh: A 3-D finite element mesh generator with built-in pre- and post-processing facilities. Int J Numer Methods Eng. 2009;79(11):1309–1331. [Google Scholar]
- 27.Vashaee S, Goora F, Britton MM, Newling B, Balcom BJ. Mapping B(1)-induced eddy current effects near metallic structures in MR images: A comparison of simulation and experiment. J Magn Reson. 2015;250:17–24. doi: 10.1016/j.jmr.2014.10.016. [DOI] [PubMed] [Google Scholar]
- 28.Collins CM, Smith MB. Calculations of B(1) distribution, SNR, and SAR for a surface coil adjacent to an anatomically-accurate human body model. Magn Reson Med. 2001;45(4):692–699. doi: 10.1002/mrm.1092. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.