Illusory Late Heavy Bombardments

Significance

The vast majority of evidence marshaled for the Late Heavy Bombardment comes from ⁴⁰Ar/³⁹Ar age spectra of Apollo samples, interpreted through “plateau” ages, which show an apparent cluster at ∼3.9 Ga. Whether such data can be uniquely inverted to constrain impact histories in the Earth−Moon system has never been tested. We show that diffusive loss of ⁴⁰Ar from a monotonically declining impactor flux coupled with the early and episodic nature of lunar crust formation tends to create clustered distributions of apparent ⁴⁰Ar/³⁹Ar ages at ca. 3.9 Ga. Instead, these ⁴⁰Ar/³⁹Ar data can be reconciled with a continuously decreasing bollide flux. Thus, impacts may have played a minimal role in terrestrial habitability, early Earth dynamics, and the formation of Hadean zircons.

Abstract

The Late Heavy Bombardment (LHB), a hypothesized impact spike at ∼3.9 Ga, is one of the major scientific concepts to emerge from Apollo-era lunar exploration. A significant portion of the evidence for the existence of the LHB comes from histograms of ⁴⁰Ar/³⁹Ar “plateau” ages (i.e., regions selected on the basis of apparent isochroneity). However, due to lunar magmatism and overprinting from subsequent impact events, virtually all Apollo-era samples show evidence for ⁴⁰Ar/³⁹Ar age spectrum disturbances, leaving open the possibility that partial ⁴⁰Ar* resetting could bias interpretation of bombardment histories due to plateaus yielding misleadingly young ages. We examine this possibility through a physical model of ⁴⁰Ar* diffusion in Apollo samples and test the uniqueness of the impact histories obtained by inverting plateau age histograms. Our results show that plateau histograms tend to yield age peaks, even in those cases where the input impact curve did not contain such a spike, in part due to the episodic nature of lunar crust or parent body formation. Restated, monotonically declining impact histories yield apparent age peaks that could be misinterpreted as LHB-type events. We further conclude that the assignment of apparent ⁴⁰Ar/³⁹Ar plateau ages bears an undesirably high degree of subjectivity. When compounded by inappropriate interpretations of histograms constructed from plateau ages, interpretation of apparent, but illusory, impact spikes is likely.

Earth contributes relatively little to our knowledge of the early impactor flux to the inner solar system, due to its constant resurfacing by the combined effects of erosion and cratonic growth. Although the Moon’s longstanding stability and relatively short duration of crustal growth in principle transcends these terrestrial limitations, after nearly 50 y of lunar sample analysis, our understanding of the Earth−Moon impact history remains limited (1–3); reasons for this include the relatively small area of the lunar surface from which we have documented sample locations and the potentially cryptic nature of impact thermal signatures (4). Despite these limitations, there is broad consensus that impact rates were higher during and immediately after accretion of the terrestrial planets (5) and possibly during a spike in impact rates (i.e., the Late Heavy Bombardment; LHB) at either ∼3.9 (1, 6, 7) or ∼4.1 Ga (8, 9). The existence of an LHB (we use this term to describe any postulated spike in impact rate; e.g., 3.9 or 4.1 Ga), however, is not universally accepted. The apparent spike could instead reflect impact saturation of the surface, termed the “stonewall” effect (2).

The shape of impact curves and the existence of an LHB has profound implications for the geological and biological development of our planet. The geologic effects implied by these impact histories range from planetary sterilization (10), to a Hadean (>4 Ga) Earth covered by ca. 20 km of flood basalts (11), to generation of hydrothermal systems providing enhanced environments for extremophiles (12). Whether or not impact rates during the Hadean could have sterilized Earth is of particular relevance, as no microfossils older than ∼3.5 Ga (13) have been identified. However, a record of isotopically light carbon consistent with biologic activity extends back to 4.1 Ga (14–16), leaving open the possibility that life may have existed during the hypothesized bombardment episodes. The existence of an LHB-type event has broader implications to other planets, and its origin has been linked to dramatic changes in giant planet orbital dynamics (17) and ejected debris from a large Mars impact (18).

The ⁴⁰Ar/³⁹Ar data are not the only source of evidence that has been used to support the LHB hypothesis. Indeed, the original proposal of a “terminal lunar cataclysm” (6) was based on the observation of widespread U−Pb fractionation at ca. 3.9 Ga together with nine Rb−Sr internal isochrons ranging from 3.85 to 4.0 Ga. In some ways, it is surprising that global inferences were drawn from such a small sample population, more than half of which were derived from Apollo 14 collections; this further underscores the earlier noted issue that all Apollo-era samples are restricted to only ∼4% of the lunar surface (19). Thus, these data are equally consistent with a single, local event rather than a planetary-wide bombardment episode.

The bulk of the evidence now marshaled in support of the LHB comes from ⁴⁰Ar/³⁹Ar step-heating analyses (1, 7, 8). Specifically, compilations of ⁴⁰Ar/³⁹Ar “plateau” ages are constructed under the assumption that a compilation of these ages can be related to impact intensity. However, ⁴⁰Ar* is not retentive in rocks at moderately elevated temperatures, resulting in partial resetting of the isotopic system (20–22). The pioneering studies that established ⁴⁰Ar/³⁹Ar as a viable dating method explicitly addressed the importance of diffusive ⁴⁰Ar* loss in extraterrestrial materials (23) and devised corrections for partial resetting effects (24, 25). Over the intervening five decades, this approach was generally abandoned in favor of assigning age significance to seemingly flat portions of the age spectra, termed “plateau ages.” In contrast with the flat release patterns from which this concept was first introduced (26, 27), lunar and meteorite samples are rarely observed to have undisturbed age spectra. Because the vast majority of analyzed meteorite and lunar samples have been assigned plateau ages despite evidence of significant disturbance to the ⁴⁰Ar/³⁹Ar system, a potentially significant bias can be introduced by the assignment of plateau ages.

An additional problem is that lunar crustal growth and meteorite parent body petrogenesis were episodic and limited to a relatively short duration (<500 Ma). As the majority (∼85%) of the exposed surface of the Moon is thought to be a floatation crust formed during crystallization of a magma ocean (28), it must have formed relatively quickly after lunar accretion. The observed age spread for lunar samples (with the exclusion of Mare basalts and other impact derived samples) is ∼300 Ma for the ferroan anorthosites, lunar zircons, and the Mg gabbroic suite (29, 30). Additionally, essentially all known meteorite parent bodies formed and differentiated between 4.57 and 4.52 Ga (31, 32). The episodic nature of petrogenesis on these bodies suggests the possibility that apparent spikes in the compilation of ⁴⁰Ar/³⁹Ar ages could reflect crust formation shifted toward younger ages due to partial ⁴⁰Ar* resetting with a monotonic impact flux.

To examine how well histograms of plateau ages represent the actual impact record and its support of an LHB-type event, we have reevaluated the interpretation of ⁴⁰Ar/³⁹Ar data for extraterrestrial samples using a physical model describing ⁴⁰Ar* diffusive loss during postformation heating events. This model, which accounts for partial resetting, permits us to assess whether or not ⁴⁰Ar/³⁹Ar data can even, in principle, act as evidence for an impact spike or if the apparent spikes are simply artifacts due to episodic crust formation.

Method

Our model simulates ⁴⁰Ar* distributions in synthetic samples produced in response to a random impact history. This simulation is then compared with a compilation of ⁴⁰Ar/³⁹Ar data from Apollo samples (Model Constraints). In all interpretations, even those involving an episodic flare-up, the background impact intensity is assumed to follow an exponential decline following accretion (33, 34). Thus, we use an exponential decay with an added a linear component to allow a greater parameter range to be evaluated. The impact history is constrained to monotonically increase back in time from the present and is given by

$$IC\left(t\right)=A+B\times t+C\times e^{Dt},$$ [1]

where A, B, C, and D are free parameters. In each time step (100 Ma), the sampled locations that experienced impact-related ⁴⁰Ar* degassing are randomly chosen without replacement from a set of 1,000 targets with equal probability of selection. When a randomly chosen sample is “impacted” during a time step, we assign a fractional loss of ⁴⁰Ar* representing the thermal effect of that collision. Because we have no prior information regarding fractional loss of ⁴⁰Ar* in impact events, we use two models with differing assumptions. The first model assumes a uniform probability distribution between 0 and 1 for fractional loss of ⁴⁰Ar* resulting from each impact (see Supporting Information for justification).

To specifically test the assumptions inherent in model 1, model 2 assumes no a priori knowledge of the specific shape of the fractional ⁴⁰Ar* loss probability distribution. We assume, instead, that fractional loss follows a beta distribution (35) and constrain the two shape parameters to produce normally distributed plateau ages at either 3.9 or 4.1 Ga (±0.2 Ga; 1σ). We characterize each target using a spherical diffusion geometry for ⁴⁰Ar* and invert the fractional loss to the dimensionless parameter Dt/r² (where D is diffusion coefficient, t is duration, and r is the characteristic diffusion length scale), which, in turn, is used to calculate the age spectrum of the target from which a plateau age, that is, the asymptotic portion of the late gas release (at 90% ³⁹Ar release; Supporting Information), is assigned. Lastly, to compare the fractional loss seen in lunar samples to the synthetic targets, in model 2, we define the width of the plateau to be the fractional ³⁹Ar released from the age reaching 90% of the maximum age to complete degassing (Supporting Information). Although using only a single diffusion domain is an oversimplification—real samples are composed of multiple phases and a distribution of domain sizes (4)—this assumption is unlikely to significantly influence our results. Indeed, more sophisticated modeling of existing Apollo ⁴⁰Ar/³⁹Ar data are currently not possible given the lack of accurate temperature control during the step-heating analyses and problematic heating schedules (4).

Model Constraints

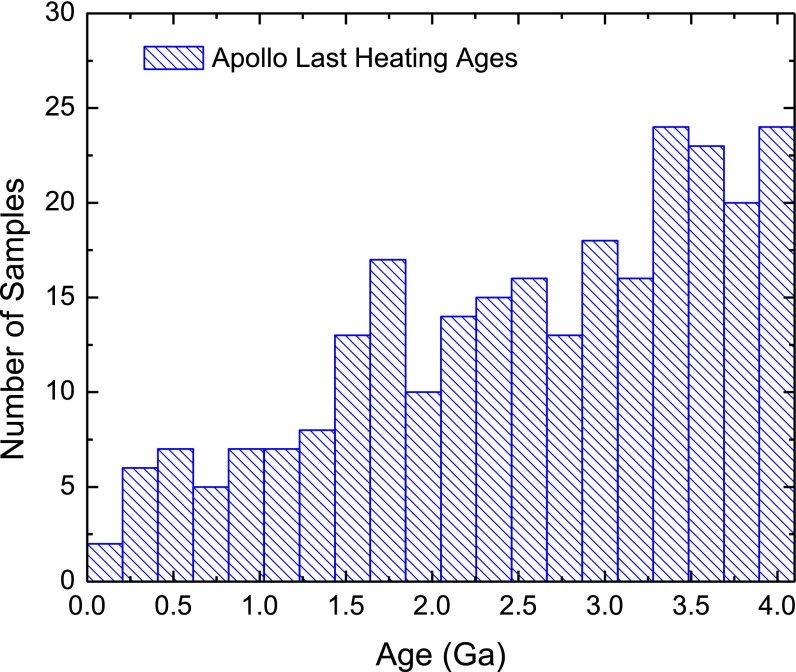
In samples that were partially reset during postformational heating, the apparent age obtained during initial laboratory degassing is the best estimate for the timing of that loss (20, 24). This is because early heating steps (typically ∼400 °C for <30 min) liberates ⁴⁰Ar* held near grain/subgrain boundaries. We thus tabulated “Last Heating Ages” (LHAs; i.e., the age of the initial gas released) for 267 Apollo ⁴⁰Ar/³⁹Ar analyses (see Supporting Information and Dataset S1 for data and references). This age distribution is the primary constraint for all models and is similar, albeit more comprehensive, to the compilation of “initial” ages in ref. 36. Our compilation (Fig. 1) shows an approximately linear increase in LHAs going back to 4 Ga followed by a sharp drop-off at ∼4 Ga. This drop-off is consistent with the loss of ⁴⁰Ar* generated before that time by subsequent thermal activity, akin to a stonewall effect (2). Before we discuss model results, we note that interpretation of these data in terms of >3-Ga impacts is problematic due to intense endogenous magmatism (37). Furthermore, rock comminution, mixing, and recoil effects can further obscure interpretation of ⁴⁰Ar/³⁹Ar data. Despite these effects, our LHA compilation would appear to suggest a monotonic decrease in impacts over at least the past ∼3 Ga.

Fig. 1.

Compilation of 267 LHAs, which is the age of the gas released during the early heating steps.

Both models require knowledge of the basement crystallization age distribution and we assume that lunar zircon ²⁰⁷Pb/²⁰⁶Pb ages (38–41) approximates this function (see Dataset S1 for compilation). Although this could skew results to those compositions more likely to saturate zircon, compiled lunar Sm−Nd whole rock ages (29) lead to a similar age distribution.

Results

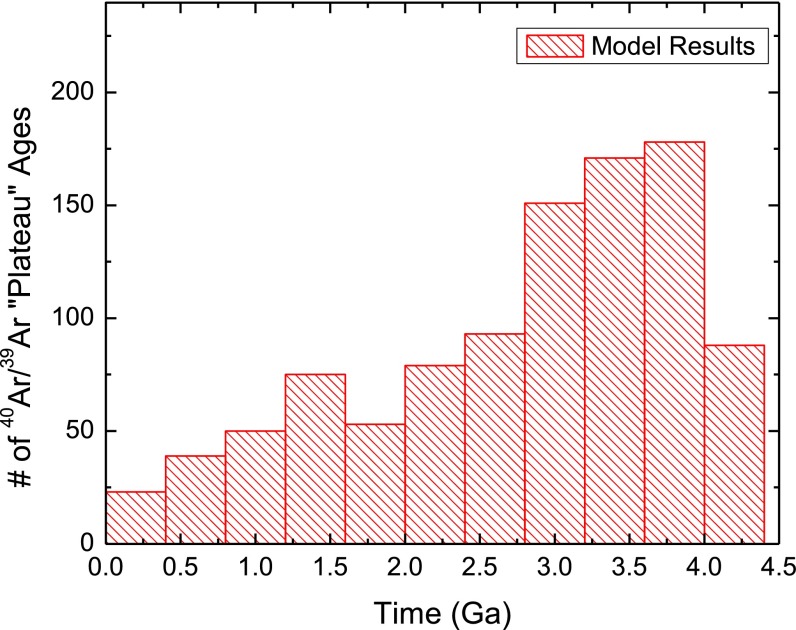
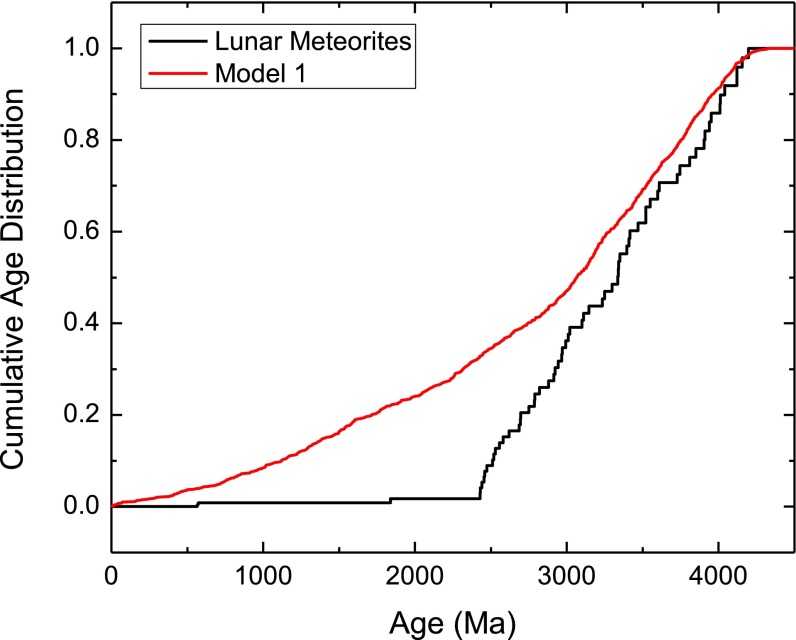
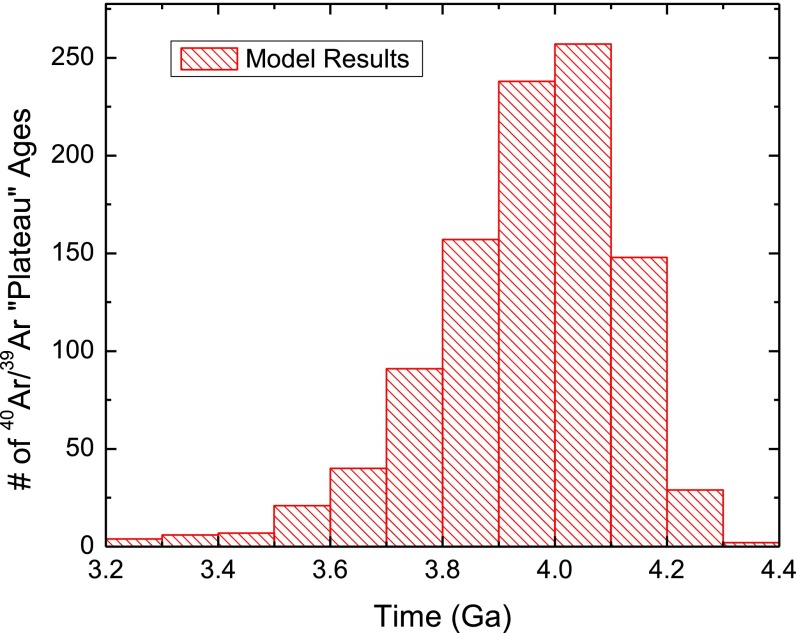
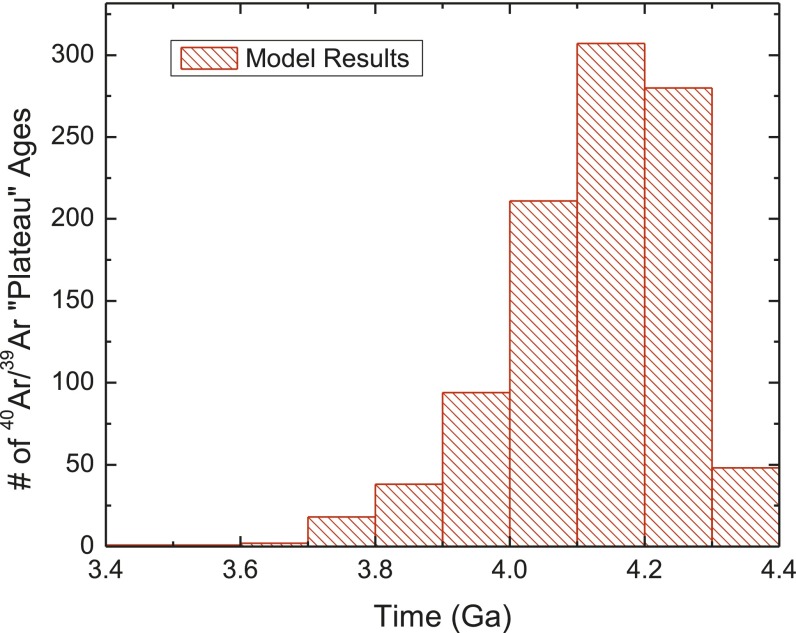
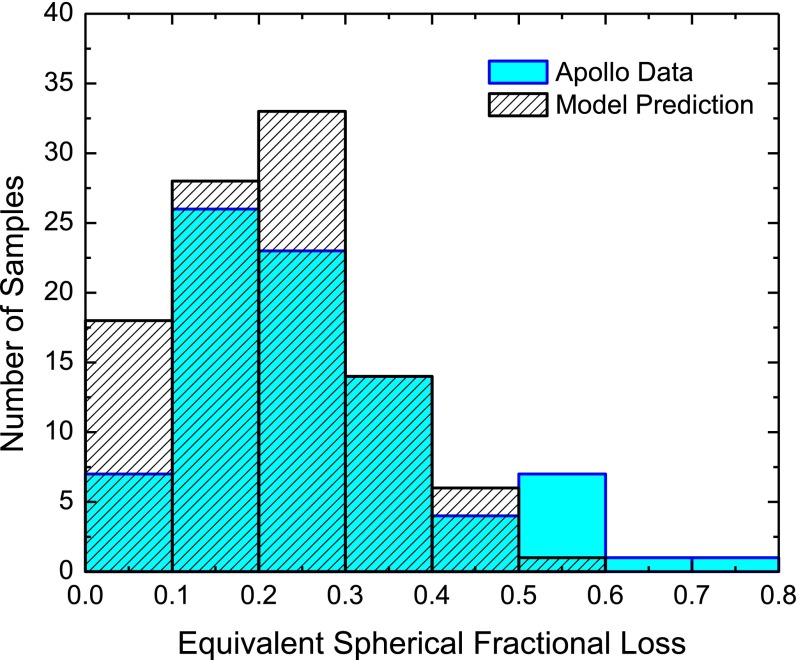
Apparent plateau ages returned by model 1 (Fig. 2) reveal an age distribution characterized by an illusory bombardment spike between 3.5 and 4.0 Ga. This result shows that episodic, pre-4-Ga crust formation coupled with partial ⁴⁰Ar* loss due to the monotonically decreasing impact flux can bias age compilations toward the appearance of an impact spike. The model 1 results agree well for >3 Ga compared with the distribution of lunar meteorite ⁴⁰Ar/³⁹Ar plateau ages, but our model overpredicts young plateau ages (Fig. S1). Results of model 2 (Figs. S2 and S3) can reproduce both a canonical spike at 3.9 Ga and one at 4.1 Ga. We note that we do not specifically compare the shape of our spike to that of the literature data, as, to our knowledge, the specific shape of the plateau age distributions has never been used to constrain impact histories. That is to say, the literature interpretation is that a spike in plateau ages at 3.9 Ga is evidence for the LHB, but the specific distribution has not been cited in support. Because model 2 is fixed to require an impact spike, we instead assess the plausibility of the underlying assumptions by examining the probability distribution of impact-induced fractional ⁴⁰Ar* loss that is required to match the desired impact spike age. To compare the resulting distribution to that for Apollo samples, we need to calculate the fractional loss for each sample. Because there are virtually no published Apollo ⁴⁰Ar/³⁹Ar data that have been fit by a diffusion model (cf. ref. 36), we compiled the fraction of gas included in the plateau for ∼100 Apollo samples (42–45). Model 2 output agrees well with this compilation (Fig. 3), suggesting that the assumptions embodied in the model are reasonable despite the considerable complications in Apollo ⁴⁰Ar/³⁹Ar data.

Fig. 2.

Distribution of plateau ages resulting from model 1. Although there are more broad features than observed in the Apollo data, there is a peak between 3.5 and 4 Ga showing that apparent bombardment spikes are common in plateau age histograms.

Fig. S1.

Model 1 results compared with the distribution of ⁴⁰Ar/³⁹Ar plateau ages from lunar meteorites. The meteorite data are our compilation of the references listed in ref. 8.

Fig. S2.

Model 2 results for a 3.9-Ga impact spike.

Fig. S3.

Model 2 results for a 4.1-Ga impact spike.

Fig. 3.

Actual spherical loss estimated to result in an impact event from the Apollo data compared with the distribution resulting from running model 2 with an LHB at 3.9 Ga. The agreement between the two distributions shows that even selecting samples with little fractional loss (i.e., “good” plateaux) still introduces a significant bias to the inferred bombardment history.

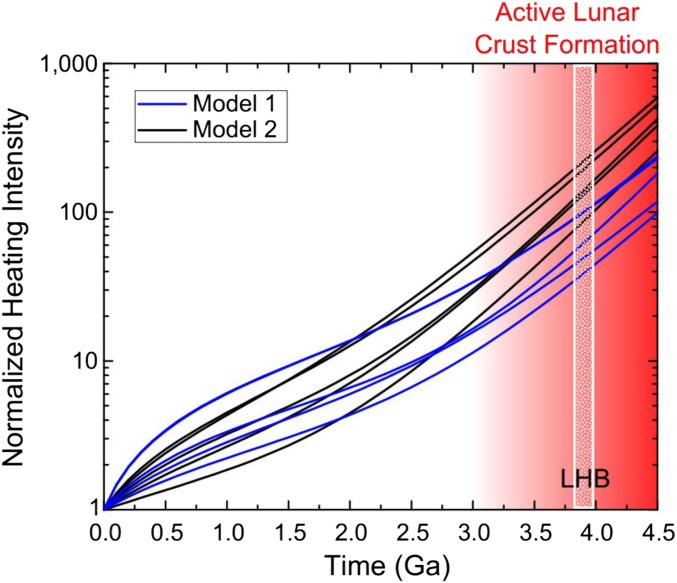
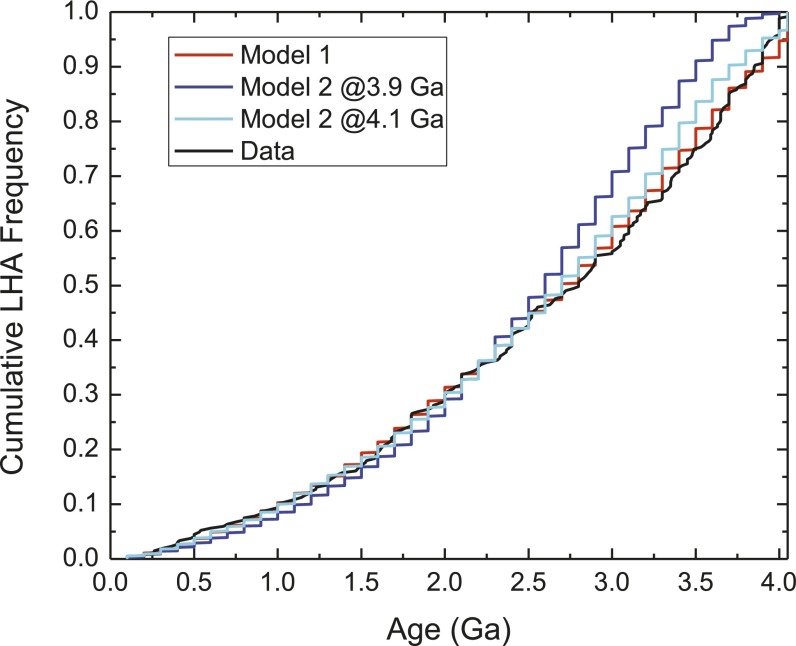
For both models, the simulated impact rates both exponentially and monotonically decrease with time (Fig. 4). Comparison of model 1 with the cumulative frequency distribution for LHAs matches well. For model 2, the fit to a 4.1-Ga impact spike is better than one at 3.9 Ga, although both are visually adequate solutions (Fig. S5 and Supporting Information).

Fig. 4.

Selected model runs for both model 1 and model 2 normalized to the present-day impact rate. Both models suggest a drop in impacts of 2× to 5× over the last 2 Ga, and neither has a spike at the timing of the LHB at ∼3.9 Ga. Also shown is the timing of active crust formation and volcanism on the Moon in red and the LHB in white. During the interval shaded in red, we do not believe ⁴⁰Ar/³⁹Ar to be uniquely interpretable in terms of impacts due to the generally high thermal activity on the Moon.

Discussion

Implications for Other Extraterrestrial Bodies.

Our modeling shows that, due to the nature of declining impact rates and the early but episodic nature of crust formation on extraterrestrial bodies, apparent bombardment episodes can be a common artifact in ⁴⁰Ar/³⁹Ar plateau age histograms. Indeed, age compilations of samples from H chondrites and howardite–eucrite–diogenite (HED) meteorites also show apparent spikes in impact activity between 3.5 and 4 Ga (8, 46, 47). Model 1, in general, produced curves that imply increased activity around 3 to 4 Ga and feature a paucity of >4 Ga ages. Although our model is based on a lunar crustal age distribution that is too young to characterize meteorite parent bodies, the qualitative agreement between our results and meteorite data suggests that episodic petrogenesis coupled with a monotonically decreasing impact flux can explain meteorite ⁴⁰Ar/³⁹Ar histograms.

A distinctive characteristic of meteorite ⁴⁰Ar/³⁹Ar ages is the lack of plateaux between 4.1 and 4.4 Ga. This can be understood if those samples with bulk cooling ages of ≥4.5 Ga were shielded from impact thermal effects by their location away from the parent body surface, only becoming thermally affected during their last (typically <1 Ga) breakup event. Meteorite samples with ⁴⁰Ar/³⁹Ar ages between 3.5 and 4 Ga are those that lay closer to parent body surfaces and thus experienced a protracted impact history. Thus, the view that the lack of intermediate plateau ages in meteorites reflects an impact hiatus (8) is nonunique and at least as well explained by relative position in parent bodies.

Mass Constraints.

Based on estimates of highly siderophile elements’ concentrations in Earth’s mantle (48–50) and mantle noble gas systematics (51), it has been suggested that 0.5 to 1.5% of an Earth mass was accreted following core formation (the “Late Veneer”). Although this estimate is not universally accepted (52, 53), it is widely used to constraint impact models (11) and mantle dynamic models (54). As we have shown, the act of inverting a distribution of ⁴⁰Ar/³⁹Ar plateau ages into an impact curve, even to relatively late stages of planetary evolution (i.e., 3.9 to 4.1 Ga), is nonunique. Thus, proposed bombardment histories for the period >4.1 to 4.5 Ga (9, 11) are speculative. Indeed, these histories (9, 11) result in geochemical consequences that are incompatible with the terrestrial record. For example, virtually all workers agree that the Hadean (>4 Ga) zircon record requires a terrestrial hydrosphere (55–59); this is fundamentally incompatible with the models for the Hadean derived from impact histories (9, 11). Other geochemical inferences include the existence of an evolved, likely granitic continental crust (60, 61), possibly formed by a subduction-like process (59, 62). Furthermore, the hypothesis that Hadean zircons formed in impact melts was explicitly tested and rejected (63). Instead, models from the impact history of the Earth−Moon system (11), based on extrapolated impact curves based on ⁴⁰Ar/³⁹Ar plateau age histograms, propose that impacts delivering the Late Veneer caused Hadean Earth to be covered with ∼20-km-thick flood basalts. To reconcile the Late Veneer with constraints inferred from Hadean zircons, we propose that the majority of all impacts happened at >4.4 Ga and that more recent cratering contributed only negligible mass and energy to the Earth−Moon system. Indeed, a recent reevaluation of lunar basin-forming impactors (64) similarly agrees that estimates of delivered mass to the Moon based on observed crater sizes are substantially overestimated due to misestimated target properties. Our modeling is insensitive to the magnitude of >4.4-Ga impacts and thus consistent with a higher, early impactor flux being responsible for the Late Veneer. Further evidence for a significant drop-off in impact flux is that there are no lunar or terrestrial zircons (or samples of any kind) significantly older than 4.4 Ga (29, 65), and the Hf isotopes in those zircons point to a differentiation event at ≥4.5 Ga (38, 59). Although it may seem paradoxical that Late Veneer impacts, which would likely melt the crust and mantles of both Earth and the Moon, did not reset their Hf isotope systems, the large disparity in Lu and Hf concentrations between both the terrestrial crust/mantle (66, 67) and ferroan anorthosite/KREEP (68, 69) works against leaving a record of such an event. That is, although impact mixing of crust and mantle is unlikely to significantly affect crustal Hf isotope evolution, it destroys or resets the chronology of rocks older than 4.4 Ga. A scenario consistent with our reanalysis of the meaning of lunar ⁴⁰Ar/³⁹Ar data, environmental constraints inferred from Hadean zircons (59), the reevaluation of lunar basin-forming impactor size (64), and the >4.5-Ga age of core formation of ref. 31 is that a Late Veneer was delivered to Earth between 4.5 and 4.4 Ga, followed by relatively low impact rates.

Summary

To examine the possibility of monotonically decreasing impact curves combined with episodic crust formation yielding the observed distribution of ⁴⁰Ar/³⁹Ar plateau ages, we constructed three simulations. They are constrained to fit a compilation of LHAs of Apollo samples, which represent an estimate of the last time each sample experienced heating sufficient to cause measurable ⁴⁰Ar loss. Model 2 is further constrained to create a spike in impacts at 3.9 or 4.1 Ga. We show that ⁴⁰Ar/³⁹Ar plateau age histograms can show apparent (but illusory) bombardment episodes under monotonically decreasing impact rates for bodies with early and episodic crust formation when coupled with the effects of partial resetting of the ⁴⁰Ar/³⁹Ar system. Finally we note that, while the most widely used evidence to support the LHB hypothesis yields unreliable impact histories, it does not preclude the existence of such events.

Future work using improved chronological methods, such as in situ ⁴⁰Ar/³⁹Ar dating (70) as well as quantitative thermochronologic modeling (36), can aid in establishing evidence for or against an LHB-type event. Until such evidence is gathered, we conclude that a monotonic decrease in impactor flux explains all existing ⁴⁰Ar/³⁹Ar data from both lunar and meteoritic samples.

Detailed Model Description

We chose to generate trial solutions using a Markov chain Monte Carlo approach, as it is more efficient than the standard Monte Carlo method, although similar outcomes would result from both. For each iteration of the simulation, we performed the following steps: (i) choose values for the constants A, B, C, and D (and, in model 2, the shape parameters for the beta distribution); (ii) generate a distribution of target ages using the lunar zircon ²⁰⁷Pb-²⁰⁶Pb age distribution; (iii) for each time step, randomly select impact targets and assign a fractional loss, either from a uniform distribution (model 1) or from the specified beta distribution (model 2); based on the fractional loss in each impact, calculate the plateau age for each target based on its ⁴⁰Ar/³⁹Ar spectrum at 90% ³⁹Ar loss (i.e., a laboratory heating was simulated and the age selected at which the spectrum asymptotically approaches uniform values—the plateau); and (v) evaluate the goodness of fit for each simulated solution relative to the distribution of LHAs (models 1 and 2) and the distribution of plateau ages (model 2).

Normalized example age spectra are shown in Fig. S4. Once each simulation was run, we had thousands of potential parameters with fits of varying quality to the data; we selected the best set of parameters (A, B, C, and D as well as beta distribution shape parameters; model 2 only) for this work. That is to say, out of all of the potential solutions, we selected the one that best fit the available constraints. We made this choice because we are only interested in whether or not our model can reproduce the observed data, rather than what the uncertainties on each parameter are. To visually assess whether or not the best model parameters reproduce the LHA distribution, we have plotted the cumulative frequency distribution for our models and the data (Fig. S5). Note that each model run fits well visually with a 4.1-Ga LHB and provides a better fit than a 3.9-Ga LHB in model 2.

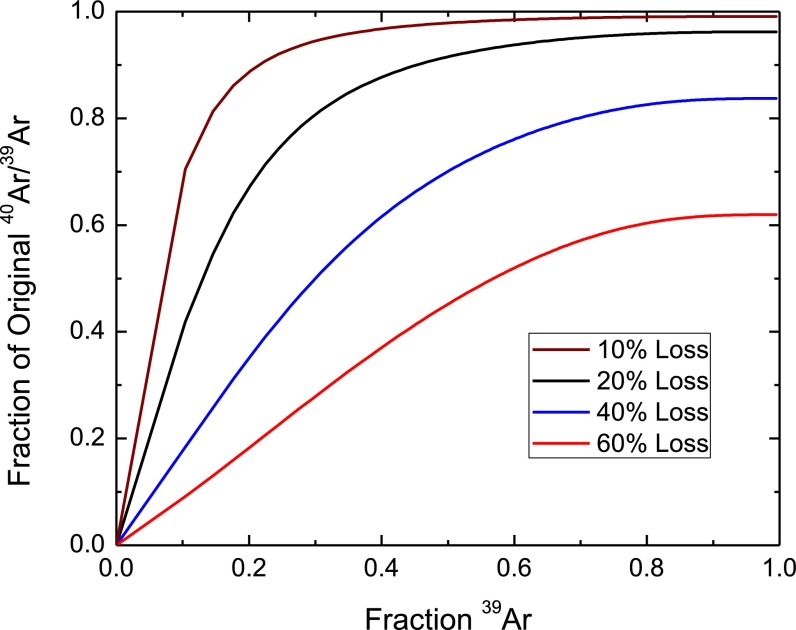
Fig. S4.

Age spectra showing the effects of diffusive loss at ⁴⁰Ar/³⁹Ar = 0 of a sample that originally formed at ⁴⁰Ar/³⁹Ar = 1. We show here examples with 10, 20, 40, and 60% loss to show how the age spectra changes. The specific form of the age spectra is dependent on the geometry chosen, but the general behavior is the same (that is, diffusive loss in all geometries leads to plateau ages that are too young). Additionally, the shape does not change considerably from one event to multiple events, and, therefore, this is a general example of one or multiple loss events.

Fig. S5.

A comparison of the cumulative LHA distribution between the models and data. Note the good visual agreement between the data and model 1. Formodel 2, although both model runs fit the data well, the simulation constrained to a bombardment at 4.1 Ga provides a better fit than the one at 3.9 Ga.

Age at 90% ³⁹Ar Release

We chose to use the age at 90% of the ³⁹Ar release for two reasons: (i) It is usually on the flat part of the age spectrum, and (ii) it is computationally required to define a cutoff value. In model 1, changing the value to, say, 95 or 85% provides no change to the result. In model 2, where a beta distribution is fit to the fractional ⁴⁰Ar loss, changing the ³⁹Ar value to another one would simply shift the distribution of fractional ⁴⁰Ar loss. That is, choosing a higher value of ³⁹Ar loss would shift the distribution to higher fractional ⁴⁰Ar loss and vice versa. Therefore, the specific choice in value does not strongly influence our results.

Model 2 “Gas in Plateau”

To assess the fractional loss, we assume that each sample can be described by a spherical diffusion geometry. To convert from fraction of gas in the plateau in the literature data to fractional loss, we calculate the loss required to match the modeled plateau width to that of each sample. Because Apollo samples have complex age spectra due to numerous potential causes, including diffusive loss, rock comminution, and recoil effects, our analysis is necessarily imprecise. Therefore, the agreement between our model 2 results and the information gleamed from analyses of Apollo samples suggests, but does not prove, that our model is reasonable. We note that our model presents a best-case scenario, as these other factors further obscure the true impact chronology.

Justifying a Uniform Distribution for Fractional Loss

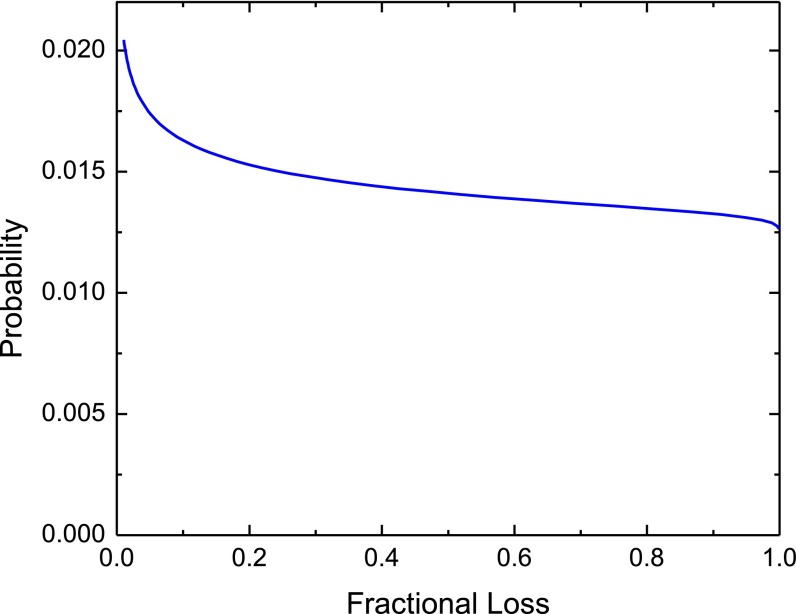
Model 1 assumes a uniform distribution for fractional loss within a volume heated by an impact (e.g., the same proportion experience 10% as 80% loss). Although the primary justification is that a uniform distribution in 1D represents maximum entropy when a parameter can vary continuously in a certain range (71), it closely resembles a diffusive approximation. We simulated the distribution of fractional loss occurring from a hemispherical melt. Using a hemispherical melt (radius = 100 m) and the standard analytical solution (72), we calculated the temperature−time history along a trajectory away from the hemisphere. Our choice of radius is purely illustrative, and our calculation is independent of impactor size. Once the thermal structure was calculated, we used typical diffusion parameters for Apollo samples (36) to calculate the probability distribution of each fractional loss. That is to say, we find the fraction of material that experienced 1% loss, 2% loss, etc., up to 99% (Fig. S6). The distribution we find is well described by a uniform probability distribution of fractional loss outside of the melt region. Although our model does not account for impact ejecta, the thermal effects of the shockwave, or the fact that real impact melt sheets are not truly hemispherical, it represents a reasonable first approximation. Indeed, accounting for these factors is likely a minor effect relative to the degree of our understanding the retentiveness of ⁴⁰Ar in the average lunar sample.

Fig. S6.

The probability distribution for fractional ⁴⁰Ar loss as calculated for a hemispherical impact. We approximate this as a uniform distribution for model 1.

LHA Data Compilation

Each LHA represents one Apollo sample; for samples with multiple analyses, we chose the most recent. Papers that did not include sufficient information to determine an LHA were not used in our analysis. Specifically, we used data found in ref. 44 and refs. 73–95. We followed a similar methodology as ref. 36 in compiling our LHAs, and our compilation is similar to theirs (see figure 4 in ref. 36).