A MODEL TO STUDY ARTICULAR CARTILAGE MECHANICAL AND BIOLOGICAL RESPONSES TO SLIDING LOADS

Abstract

In physiological conditions, joint function involves continuously moving contact areas over the tissue surface. Such moving contacts play an important role for the durability of the tissue. It is known that in pathological joints these motion paths and contact mechanics change. Nevertheless, limited information exists on the impact of such physiological and pathophysiological dynamic loads on cartilage mechanics and its subsequent biological response. We designed and validated a mechanical device capable of applying simultaneous compression and sliding forces onto cartilage explants to simulate moving joint contact. Tests with varying axial loads (1 – 4 kg) and sliding speeds (1 – 20 mm/s) were performed on mature viable bovine femoral condyles to investigate cartilage mechanobiological responses. High loads and slow sliding speeds resulted in highest cartilage deformations. Contact stress and effective cartilage moduli increased with increasing load and increasing speed. In a pilot study, changes in gene expression of extracellular matrix proteins were correlated with strain, contact stress and dynamic effective modulus. This study describes a mechanical test system to study the cartilage response to reciprocating sliding motion and will be helpful in identifying mechanical and biological mechanisms leading to the initiation and development of cartilage degeneration.

1. Introduction

The integrity of the extracellular matrix (ECM) of articular cartilage is controlled by a balance of anabolism and catabolism. Normal physiological forces lead to adaptation and physiological remodeling of the matrix so that it can distribute compressive loads and enable a low-friction motion. On the contrary, abnormal or non-physiological forces can result in over-expression of matrix enzymes such as matrix metalloproteinases (MMPs) and disintegrin and metalloproteinase with thrombospondin motifs (ADAMTS’) that lead to tissue destruction as observed in joint diseases and osteoarthritis (OA).¹⁷ In OA, the equilibrium between anabolism and catabolism is shifted towards catabolic processes which impairs ECM integrity.¹⁶ A persistent predominance of catabolic stimuli results in tissue deterioration, compromises its ability to cope with mechanical stresses and ultimately results in inferior mechanical properties what expedites further degeneration and tissue breakdown.^2,9 The balance between mechanics and biology led researchers to investigate the gene expression response of ECM genes and degradative enzymes to mechanical forces. Applied loads in the physiological range generally stimulated chondrocytes to up-regulate genes for matrix proteins such as collagen type II and aggrecan.^29,31 On the other hand, supra-physiological loads resulted in overexpression of catabolic enzymes and inflammatory cytokines.²³ While these studies offer important insight into mechanobiological processes, the mechanical loading was applied to isolated explants over a stationary contact area. It is known however, that joint surfaces move relative to each other and the area of contact stress is in continuous motion.^15,21 From a tribological standpoint, these moving contacts/stress-fields are an important component of joint kinematics to produce high fluid pressurization and a sustainably low coefficient of friction.^3,24,28

Pathological changes in joints can alter these stress-field kinematics and result in changes in loading paths and patterns.^14,21 Such altered kinematics can have negative consequences for articular cartilage biomechanics. They potentially expose previously unloaded or less conditioned cartilage areas to mechanical forces.² In the knee joint, anterio-posterior (AP) translation can be as high as 6 mm in healthy joints but almost double that after anterior cruciate ligament (ACL) injury.²¹ In addition, the relative sliding velocity between the femur and tibia has been shown to significantly increase after ACL section in a dog model.¹ This in turn changes loading frequencies and evokes an altered deformational response due to the tissue’s poroelasticity. Some of these changes have already been proposed as possible inducers for OA.^1,5 For this reason, parameters such as sliding speed, loading time, path length and contact area have already been investigated from a mechanical perspective.^5,6,8 However, the use of this fundamental knowledge of joint kinematics in a mechanobiological model is missing. Questions still remain on how variations in sliding speed, loading paths and contact geometries influence cartilage mechanics and biology. This paper describes a test system for examination of such moving stress-fields on cartilage. Our goal was to investigate articular cartilage mechanical and biological responses to contact forces applied over a relatively large area, such as a bovine knee condyle. For that reason, a new mechanical test system was developed and preliminary mechanical and biological results on cartilage explants are presented.

We hypothesized that (1) high axial forces in combination with low speeds would result in increased cartilage strain, contact stress and dynamic effective modulus, and (2) that these increases would be positively correlated with the gene expression of catabolic enzymes.

To test hypothesis (1) we applied 1, 2, 3 and 4 kg axial loads in combination with 1, 2, 5, 10 and 20 mm/s sliding speeds and measured the resulting cartilage strains, contact stresses and dynamic effective moduli during dynamic loading. For hypothesis (2), we applied the different axial loads to bovine femoral condyles at a sliding speed of 10 mm/s and measured the gene expression of anabolic (collagen type II, aggrecan, sox 9, fibronectin) and catabolic (MMP-3, MMP-13, ADAMTS-4 and ADAMTS-5) proteins. We found that high loads and slow sliding speeds resulted in the highest cartilage deformations, while the contact stress and effective cartilage moduli increased with increasing load and speed. In addition, changes in gene expression of extracellular matrix proteins correlated with increases in strain, contact stress and dynamic effective moduli. However, the gene expression for degradative enzymes was not correlated with the changes in dynamic loading.

2. Materials and Methods

2.1 Device and Components

A mechanical test apparatus for mechanobiological studies of articular cartilage was designed and constructed. The device, called “Dynamic Articular Cartilage Test System” (DACTS) was designed to apply dynamic sliding or rolling and axial force onto the articular surface of a cartilage explants. The DACTS mimicked the migrating contact area during articular joint motion where two opposing cartilage surfaces slide or roll against each other under the compressive force of muscles, ligaments and other soft tissues, and body weight. The goal of using this type of test apparatus was to investigate the mechanical and biological response of articular cartilage to such sliding and rolling forces. Even though the DACTS was designed to apply sliding and rolling, this study only focused on the application of sliding loads onto articular cartilage explants.

To load the cartilage, we used a spherical Delrin ball (diameter = 2.54 cm) to apply a constant normal (perpendicular) force onto the surface of the articular cartilage layer of a femoral condyle. In brief, the DACTS is composed of a dead-weight load-frame attached by movable linear bearings to two parallel, vertically aligned rods. To control the applied dead–weight force, the frame is suspended by a 111.2 N load cell (MLP-25, sensitivity 2 mV/V, Transducer Techniques, Temecula, CA) and a frictionless air cylinder (E16DU, Airpot, Norwalk, CT) (Figure 1). The Delrin sphere is attached to a horizontal rod, which was fixed to prevent it from rolling in order to have pure sliding contact with the cartilage. The test specimen (condyle) is held using a vise clamp mounted in a tank attached to a linear stage (Design Components Inc., Palatine, IL) driven by a stepper motor (LE57-51, Parker Compumotor, Rohnert Park, CA). The stepper motor displacement (X-direction, 1 μm resolution), velocity and acceleration are controlled via a computer-interface (Laboratory Technologies Corporation, Wilmington, MA). The X-displacement was monitored using a ± 50.8 mm linear variable differential transformer (LVDT) (Sensotec, Columbus, OH; model VL7A, 10 μm/mV resolution) and the vertical Y-displacement using two ± 5.08 mm LVDTs (model DS400A, 1 μm/mV resolution).

Figure 1.

Image of the Dynamic Articular Cartilage Test System (DACTS). Inset on the right shows a close-up view of the Delrin ball on the osteochondral explant.

2.2 DACTS Validation

To validate the system’s performance (accuracy and precision), tests were run with different loads (1, 2, 3 and 4 kg) and speeds (1, 10 and 40 mm/s). The different test cases were applied to a metal femoral condyle, with the x-displacement = ± 12 mm. Twenty cycles were run for each load/speed-combination to determine accuracy and precision of the system. The applied velocity profile was trapezoidal with equal times for acceleration and deceleration. Acceleration/deceleration for all test cases was chosen to be 400 mm/s².

2.3 Stiffness/Compliance of the System

In order to correct for the system’s stiffness, the compliance was measured and subtracted from the raw data before analysis. The indenter sphere was lowered onto a rigid metal plate with increasing load and the load and Y-displacement continuously recorded. The Y-displacement was plotted against the load and a polynomial compliance curve fitted to the resulting load-displacement response.

2.4 Corrections for the Curvature of the Condyle

To obtain the curvature of the specimen, the indenter was repeatedly lowered onto the surface, yielding force-deformation responses, which were used to determine the surface geometry (at contact) and initial effective modulus (E₀), calculated from Hertzian theory (see Equation 4). First, the compliance of the system was subtracted from the raw data and the values from both Y-LVDTs averaged. The data obtained from the LVDTs represent the location of the center of the indenter as it moves along the surface. All coordinates of the ball center at surface contact were then fitted using a 3^rd order polynomial. Displacements and contact forces were then corrected according to the slope of the condyle (Figure 2). The slope of the curvature at each point along the X-axis was derived from the polynomial and the corrected X- and Y-displacement – the real contact point of indenter and cartilage – calculated via the sine of the angle at any given location. A second polynomial was then fitted to the corrected X- and Y-coordinates representing the true cartilage surface. After completion of the loading experiments, the cartilage was removed from the bone with a surgical blade and the bone surface was identically mapped in order to obtain the spatial variation of the cartilage thickness.

Figure 2.

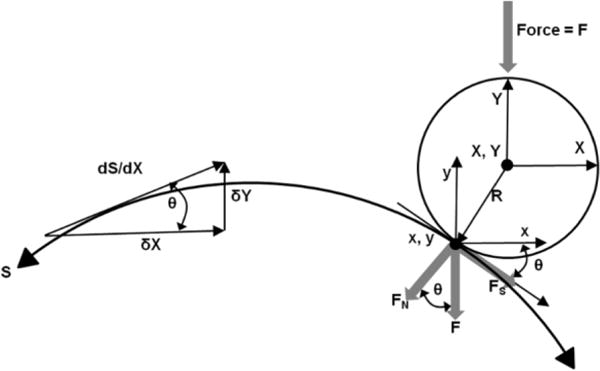
Schematic drawing to illustrate the correction of the Y-LVDT’s to calculate the actual surface contact point (x, y) from (X, Y) as well as the true (normal) force (F_N) from the applied force F. Shear forces were not measured.

To calculate contact stresses and elastic moduli, Hertzian theory of elastic deformation was used to calculate a single reduced radius (R’) for the curved surfaces of the indenter and the condyle. The reduced radius was calculated with 1/R’ = 1/R_a + 1/R_b where a (body a) represents the Delrin indenter and b (body b) the condyle. Since the Delrin indenter is a sphere, R_a = 1.27 cm. For the condyle, the R_b was calculated from the polynomial fit to the cartilage surface given by

$$R_b=\frac{{\left[1+{\left(\frac{dy}{dx}\right)}^2\right]}^{\frac{3}{2}}}{\left|\frac{d^{2}y}{d{x}^2}\right|}$$ (1)

To obtain the initial cartilage thickness, the shortest distance between the cartilage surface and bone was calculated with a Matlab (MathWorks, Natick, MA) routine.

For each cycle during the loading process, a 3^rd order polynomial was obtained according to the procedure described above. These polynomials represented the cartilage contact surface at any given time under the applied loading conditions. With this information, cartilage deformation (δ), total strain (ε), maximum dynamic contact stress (σ_max) and dynamic effective modulus (E*) could be calculated at each location along the condyle for each individual cycle using Hertzian theory. The bone was considered incompressible.

2.5 Calculations of Mechanical Parameters

Total strain (ε) was calculated by a change in thickness (deformation, δ) as measured by the LVDTs, divided by the initial thickness (l₀) of the cartilage specimen

$$(\epsilon =\frac{\delta }{l_0}).$$ (2)

By using Hertzian theory of elastic deformation²⁰ the contact radius (a) between the indenter and the cartilage was calculated with

$$a=\sqrt{\delta \cdot R^{\prime }}$$ (3)

and the effective modulus (E*) by using

$$E=\frac{3\cdot F\cdot {R\prime }^{-0.5}\cdot {\delta }^{-1.5}}{4}$$ (4)

The axial force (F) was measured by the load cell and R’ and δ calculated as described in paragraph 2.4. Note that E* is not a true material property. Amongst others, it depends on material properties (elastic modulus, permeability) of the cartilage explant and Delrin sphere, the sliding speed (deformation rate), and the reduced radius. However it does provide a valid tool to measure relative changes between the different loading conditions used in this study.

We modeled the cartilage layer as a thin elastic compressible layer bonded to a rigid substrate (bone). Using the formulas from Jaffar¹⁹, the maximum contact stress (σ_max) was calculated with

$$p_{\mathit{max}}=\frac{2\cdot F}{\pi \cdot a^2}$$ (5)

2.6 Loading of Cartilage Explants

Unless otherwise indicated, all chemicals were purchased from Life Technologies, Grand Island, NY.

Mature bovine knees were obtained from a local abattoir within 24 hours of death. Viable femoral condyles were removed, rinsed with sterile PBS to remove blood and bone marrow, and either incubated overnight in culture medium (Dulbecco’s modified eagle’s medium (DMEM) supplemented with 1% antibiotic-antimycotic and 10 mM Hepes buffer) for live studies or wrapped in PBS (phosphate buffered saline)-soaked gaze and frozen at −80° C for mechanical tests. All tests were performed at room temperature.

2.6.1 Mechanical Response to Sliding Loads

Frozen bovine condyles were thawed overnight at 4°C and mounted into the DACTS, the cartilage kept wet by a continuous flow of PBS for the duration of the experiment. The indenter was fixed to prevent it from rotating, therefore only allowing a sliding motion. The cartilage surface was mapped as described above using 12 N load, yielding force-deformation curves which were converted to stress-strain using Hertzian theory. Following a 20-minute recovery period, the sphere was lowered onto the apex of the condyle and cyclically slid over the cartilage (x = ± 15 mm amplitude in X-direction), at speeds of 1, 2, 5, 10 or 20 mm/s with applied loads of 1, 2, 3 or 4 kg for 25 cycles. After each test the cartilage surface was checked for visual cartilage damage with India ink (Speedball Art, Statesville, NC), rinsed and left unloaded to recover for 20 minutes before the next test was started. Prior the start of each test the indenter was lowered to touch the cartilage surface (x=0) in order to guarantee full recovery of the tissue to its initial height. After the cartilage was loaded with all speed and load combinations, the cartilage layer was removed and the bone surface mapped.

2.6.2 Mechanobiological Response to Sliding Load

For the mechanobiological study, explants were removed from the culture medium immediately before the mechanical loading was applied and kept wet by a continuous flow of culture medium. The indenter was prevented from rotating and the cartilage surface was mapped as previously described. Following the 20-minute recovery period, the indenter was cyclically slid on the cartilage (x = ± 18 mm) at 10 mm/s and 1.2, 2.4, 3.6 or 4.8 kg for 400 cycles (48 minutes loading time) at room temperature. After each test, 6 mm diameter full-depth cartilage samples (N_total = 15) were harvested along the loading path (± 18 mm), incubated for 72 minutes (loading + incubation = 2 hours) and processed for mRNA analysis. The entire cartilage layer was then removed to map the bone surface, as described above. At each biological sampling location (Figure 3), the following mechanical parameters were calculated: initial cartilage thickness, initial effective cartilage modulus, applied normal force, deformation, strain, stress and dynamic effective modulus. For each mRNA sample, the gene response was analyzed by real-time quantitative polymerase chain reaction (RT-qPCR). A linear regression model was used to correlate the mechanical parameters with mRNA. Adjacent unloaded cartilage specimens were used as controls. Input values for the mechanical parameters were the final values after 400 cycles.

Figure 3.

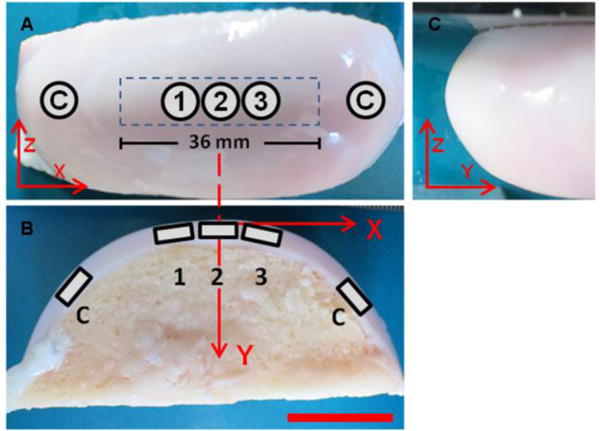
Proximal-distal (A), medio-lateral (B) and anterior-posterior (C) view of the explanted condyle. Five samples were immediately removed at the end of each loading. Loaded samples (1, 2, 3) were removed along the 36 mm loading path (locations X = −5 mm, 0 mm, 5 mm). Two unloaded control samples (labeled “C”) were also removed. Scale bar = 2 cm.

2.7 Gene Expression

Genes, commonly associated with degenerative states of cartilage, were analyzed and divided in two groups: anabolic genes for the ECM constituents (collagen type II, aggrecan, fibronectin, sox 9) and catabolic genes for degrading ECM constituents (MMP-3, MMP-13, ADAMTS-4, ADAMTS-5). Glyceraldehyde-3-phospahte dehydrogenase (GAPDH) and ribosomal protein L13a (RPL13a) were used as housekeeping genes. Forward and reverse primers for each gene can be found in Table 1. Delta-delta Ct (ΔΔCt) values were calculated for each gene followed by the fold change in expression with the formula 2^−ΔΔCt.

Table 1.

Forward and reverse primers

Gene	Forward Primer	Reverse Primer
MMP-3	GCAAGCCATTAAGACCACATCA	TTCTAGATATTGCTGAACAAGCTCC
MMP-13	TCCAGTTTGCAGAGAGCTACC	CTGCCAGTCACCTCTAAGCC
ADAMTS-4	CATCCTACGCCGGAAGAGTC	CATGGAATGCCGCCATCTTG
ADAMTS-5	TGGAAAGGGACGATTCGGTG	AGAGGTCAAAGACTGCCAGC
Collagen 2	GCTTCCACTTCAGCTATGGA	CAGGTAGGCAATGCTGTTCT
Aggrecan	GGGAGGAGACGACTGCAATC	CCCATTCCGTCTTGTTTTCTG
Fibronectin	CTACCCTCACGTTGTGGGAC	TTCCAGGAACTCGGAACTGT
Sox 9	ACGCCGAGCTCAGCAAGA	CACGAACGGCCGCTTCT
RPL13a	GCCTACTCGCAAGTTTGCCT	GCCGTTACTGCCTGGTACTT
GAPDH	GGGTCATCATCTCTGCACCT	GGTCATAAGTCCCTCCACGA

2.8 Statistics

The relationship between the mechanical parameters and the biological response was assessed with univariate and multiple linear regressions using the r-squared (r²) value to determine the best fit model. For each regression coefficient an α-level = 0.05 was considered statistically significant.

3. Results

3.1 System Validation

System compliance was determined by fitting a 2^nd order polynomial to the load vs. Y-deformation using the full weight of the load frame (4828 ± 43.2 g). The X-displacement vs. time profile used was a triangle waveform with constant acceleration of 400 mm/s², the speeds of 1, 10 and 40 mm/s reached their maximum value in 0.1 sec., 0.025 sec., and 0.0025 sec, respectively. Calculations of the actual speed from 20 cycles at 1, 10 and 40 mm/s input (at full load, 4.8 kg normal load) was 1.012 mm/s ± 0.004 mm/s, 10.08 mm/s ± 0.09 mm/s and 39.45 mm/s ± 1.25 mm/s, respectively. The air cylinder was able to control the dead-weight loads for all speeds with an accuracy >93% and the coefficient of variation < 7% (Table 2).

Table 2.

Load accuracy during dynamic loading; Mean ± SD

	1 mm/s	10 mm/s	40 mm/s
1000 g	929.92 ± 21.37	1031.59 ± 71.03	973.37 ± 37.4
2000 g	1950.04 ± 10.75	1914.87 ± 94.58	2039.31 ± 31.99
3000 g	2991.52 ± 14.96	3016.35 ± 66.79	2994.33 ± 38.02
4000 g	3989.47 ± 11.00	4026.40 ± 36.03	3992.54 ± 16.44

3.2 Mechanical Response to Sliding Loads

One condyle was used to measure cartilage deformation for each load and speed combination. Results are presented only for the X-position = 0 (X=0). However the same responses were found for any given location along the condylar surface. All condyles underwent creep deformation (Figure 4) that was more evident at higher loads. The application of different axial forces led to a variety of strains, contact stresses and dynamic effective moduli (Figure 5 and 6, respectively). The initial cartilage thickness at x=0 was 1.48 mm while the mean thickness at the start of all tests was 1.43 mm ± 0.0856 mm. No visual cracks were observed with Indian ink after the tests were performed. An increase in axial load led to increased deformation of the tissue and higher strains (Figure 4). Total strain increased from the first loading cycle, reaching a plateau after 5–10 cycles, independent of the load and sliding speed applied. An increase in sliding speed resulted in decreased deformational response of the tissue and lower strains. Additionally, an increase in axial load as well as sliding speed resulted in higher contact stresses and an increased dynamic effective modulus (Figure 5 and 6).

Figure 4.

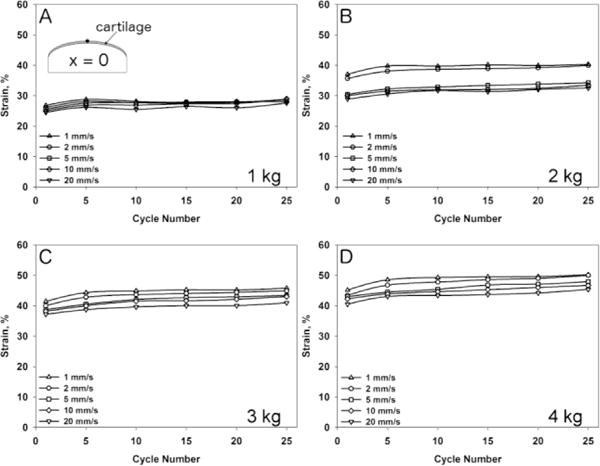
Strain at X-location = 0 mm during 25 cycles of loading for axial loads of 1 kg (A), 2 kg (B), 3 kg (C) and 4 kg (D) at 1 mm/s, 2 mm/s, 5 mm/s, 10 mm/s and 20 mm/s sliding speed.

Figure 5.

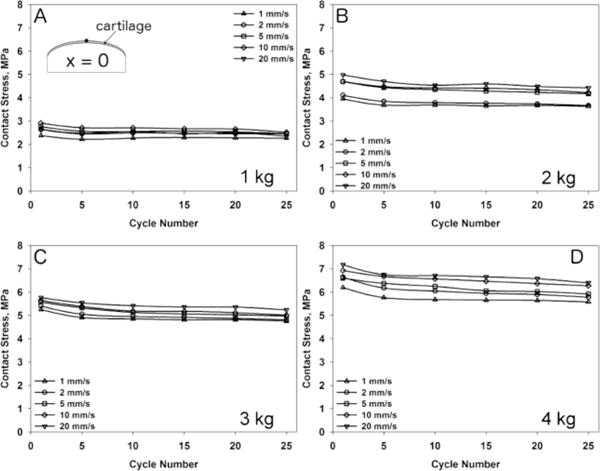
Calculated contact stress at X-location = 0 mm during 25 cycles of loading for axial loads of 1 kg (A), 2 kg (B), 3 kg (C) and 4 kg (D) at 1 mm/s, 2 mm/s, 5 mm/s, 10 mm/s and 20 mm/s sliding speed.

Figure 6.

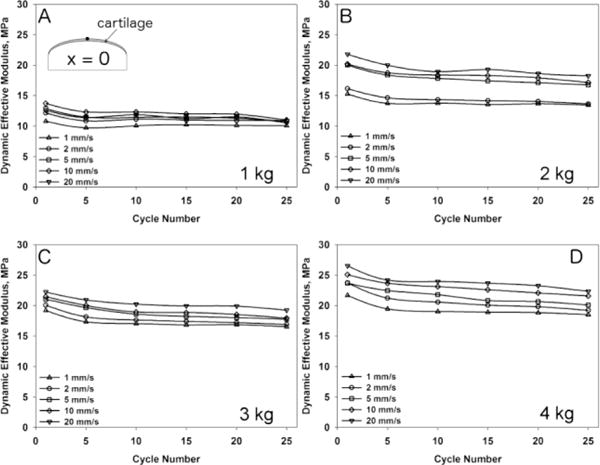
Change in the cartilage dynamic effective modulus at X-location = 0 mm during 25 cycles of loading for axial loads of 1 kg (A), 2 kg (B), 3 kg (C) and 4 kg (D) at 1 mm/s, 2 mm/s, 5 mm/s, 10 mm/s and 20 mm/s sliding speed.

3.3 Mechanobiological Response to Sliding Loads

Regression analysis between mechanical parameters and gene expression (N = 15) found several significant correlations. Contact stress, strain and dynamic effective modulus had the largest effect on gene expression of ECM molecules. Results are presented for univariate linear regression in Figure 7. The multiple regression analysis showed that only fibronectin gene expression was significantly influenced by more than one mechanical parameter. Sixty-six percent of the increase in fibronectin gene expression was due to the increase in strain (ε) and initial effective modulus (E₀) where fibronectin gene expression = 1.303 – 0.0569 ε [%] + 0.1120 E₀ [MPa].

Figure 7.

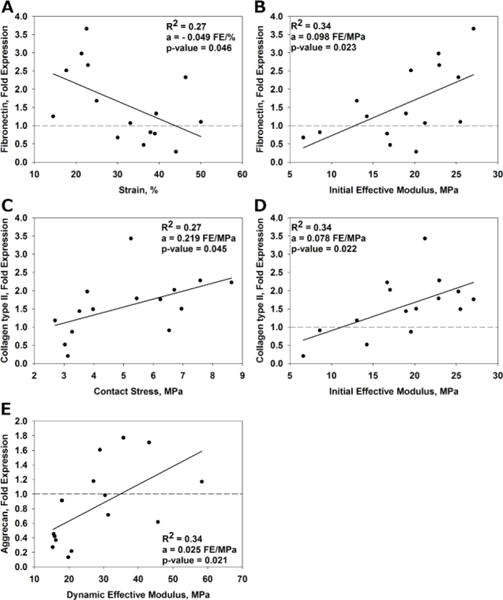
Scatterplots showing gene expression vs. individual mechanical parameters. The gene expression was normalized (fold change) to the unloaded control (dashed lines). Significant correlations (p < 0.05) are shown for fibronectin vs. strain (A) and initial effective modulus (B), collagen type II vs. contact stress (C), and initial effective modulus (D) and aggrecan vs. dynamic effective modulus (E). The fit of the linear model is denoted R² and the slope of the line is equal to a. The units of the slope are fold expression (FE) per unit of the mechanical parameter.

4. Discussion

In this paper we present the design and validation of a new cartilage testing system (DACTS) capable of applying a constant sliding load to the surface of articular cartilage of osteochondral explants of different geometric shape. This system is an approach to more realistically mimic the in vivo joint kinematics where relative sliding and rolling between articulating surfaces induces moving contact points. The capability of loading curved surfaces⁸ is an advantage over other devices which load flat tissue sections.^11,27,30 Velocity profiles had good accuracy between input and output speeds with the largest difference at 40 mm/s speed with 3.2 %. The use of an air cylinder allowed consistent application of constant loads with variations of less than 7 %.

The mechanical analysis of bovine condyles subjected to different sliding loads has found a load- and speed-dependent deformational response of the articular cartilage (Figure 4). Beside an expected increase in deformation (strain) with increasing axial load, we also found decreased deformation (strain) with increasing speed. A four-fold increase in load (from 1 kg to 4 kg) had a larger effect on deformation than a twenty-fold increase in speed (1 mm/s to 20 mm/s).

The speed-dependency of the deformation can be explained by the poroelastic nature of articular cartilage. According to the biphasic theory, the compressive behavior of articular cartilage depends on the resistance or permeability of fluid flow through the solid matrix.²⁶ Increased cyclic contact speeds result in higher loading frequencies and loading rates where the fluid component has less time to escape the solid matrix. This results in higher tissue stiffness (dynamic effective modulus) (Figure 6) and consequently less strain. This nonlinear behavior has already been described in compression experiments²² and microtribology studies⁶ over a wide range of loading frequencies and speeds. Since contact speed has a direct influence on loading rate and instantaneous compressive modulus, it will also affect other mechanical parameters such as contact area and contact stress. Contact stress depends on the contact area, therefore it is imperative to understand the deformational properties of the tissue under the indenter in order to make accurate assumptions on the area in contact. According to Ateshian and Wang⁴ the symmetry of the contact depends on the Peclet number (Pe) and is defined as Pe = (V A)/(H_a κ) where V is the sliding velocity, A the cartilage thickness, H_a the aggregate modulus and κ the permeability of the cartilage. The contact becomes perfectly symmetrical at Pe > 100. In our case, Pe increased from ~1,500 (1 mm/s) up to ~30,000 (20 mm/s) based on an aggregate modulus of 1 MPa and a permeability of 0.001 mm⁴/Ns,²⁶ leading to symmetric contact areas. Since higher speeds produced less deformation, the contact stress increases due to a smaller contact area. In fact, by increasing the sliding speed we found decreased contact radii (data not shown) and increasing contact stresses for all loads applied (Figure 5).

In order to investigate the mechanobiological response of the tissue, we quantified and correlated the mechanical response with the biological response. As can be seen in Figure 8, a short-term application of cyclic compressive sliding applied to the articular surface resulted in substantial location- and time-dependent changes in strain, contact stress and dynamic effective modulus. Amongst other factors, both location- and time dependence is due to varying intrinsic, geometric material and mechanical properties of the cartilage ECM along the load path (surface), which also caused different magnitudes of the applied force due to changing sphere-surface contact angles. The fact that different locations within a joint can have different reactions to mechanical loads has already been demonstrated by other researchers.²⁵ Another factor that needs to be taken into consideration is that due to the cyclic, reciprocating motion, different locations will have different loading/unloading patterns. Whereas the apex of the condyle (x = 0) has a symmetric loading/unloading pattern, locations further away from the apex, towards the end of the loading path (x = −18/+18 in our case), generally have shorter times between two loadings or “hits” in the same cycle and longer recovery times in between (minimum and maximum at the ends, respectively). These are factors, which influence the mechanical response over time and might ultimately determine the biological outcome. Therefore, it is safe to assume that chondrocytes in the ECM were subjected to different strains and stresses depending on their location and the morphological, material and mechanical properties of their surrounding ECM.

Figure 8.

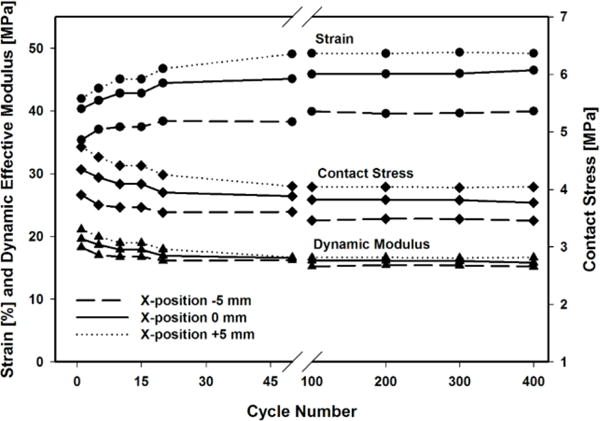
Typical strain, contact stress and dynamic effective modulus during 400 cycles of dynamic sliding with a 3.6 kg axial load at 10 mm/s sliding speed. X-position represents the location along the femoral condyle with respect to the apex (X-position = 0).

Mechanical parameters such as strain and contact stress are known to influence chondrocyte gene expression.^23,31 We performed a multiple regression analysis in order to determine what mechanical parameters influenced the gene expression. As found in previous studies, we found an increase in collagen type II and aggrecan expression with dynamic loading,^12,29 suggesting an attempt by the chondrocytes to adapt the ECM in response to the dynamic loading conditions. Fibronectin was the only gene that showed a significant correlation with multiple parameters; 66% of the fibronectin regulation in our model was correlated with strain (extrinsic) and the initial effective modulus (intrinsic). A higher initial effective modulus (stiffer material) resulted in lower fibronectin gene expression, whereas an increase is generally considered an indicator for cartilage degeneration.⁷ No genes for matrix degradation had a significant correlation with the dynamic mechanical loading in this study. This is consistent with a study reporting no change in MMP gene expression with compressive dynamic loading up to 12 MPa.¹³ It may be that the contact stresses and strains were not high enough to reach a threshold to influence the gene expression. Even the highest measured contact stress in this study (~ 8 MPa) is still considered physiological, and might not induce catabolism. It may also be that the genes studied are not influenced by the mechanical parameters we investigated. In this study, only one speed was used. Different speeds would provide us with different stress rates and loading frequencies, two factors known to be major regulators for the biological response of cartilage.¹⁰

In our study we loaded the articular surface of bovine articular cartilage using a Delrin sphere. While this does not represent in vivo human joint conditions, it is an easy-to-quantify mechanical environment. One major limitation of the study was that the cartilage loading was performed at room temperature. It has been shown that temperature can influence gene expression in isolated chondrocytes.¹⁸ Thus it is possible that at physiological temperature the gene expression response to the mechanical loading will be different then found here, both in absolute magnitude and relative expression of the ECM proteins studied. For future studies it will be important to address this limitation by controlling the temperature, such as placing the entire test system in an incubator or using a small enclosure around the specimen.

Another limitation of our test system was the inability to measure the cartilage rebound or recovery after each loading cycle. The cartilage deformations (strains) reported are relative to the initial (unloaded) cartilage surface (thickness) and not the actual real-time cyclic strains per cycle (to the previous loading cycle). As such, the stress and dynamic effective modulus, calculated via deformation (strain), do not necessarily represent the true stresses and moduli. In addition, the mechanobiological study used one sliding speed (10 mm/s) to eliminate confounding variables. Future studies will need to address such issues, and experiments with different speeds must be performed. Also, the difference between sliding (no rotation) and rolling (free rotation) is of interest and will be studied in future experiments.

To summarize, modeling dynamic contact parameters to mimic gait is complex, and DACTS is a simplified model to investigate cyclic sliding and rolling contact mechanics applied to articular cartilage. DACTS is a versatile loading apparatus, which in addition to mechanobiological studies, could also be used to test implants and their behavior in the host tissue. By introducing migrating contacts into mechanical and biological studies, the analysis becomes more physiological but also more complex. Not only does the application of moving contacts in a mechanobiological study need a relatively large tissue surface (availability of tissue for sampling) but also these larger tissue areas are likely to have dissimilar tissue properties at different spatial locations along the path of motion. Thus, a profound analysis of spatial and temporal changes in articular cartilage mechanics and biology are imperative to fully characterize and understand the mechanobiology of chondrocytes during physiological joint motion. This study describes a new approach to investigate the effect of sliding joint contact on cartilage mechanics and biology. It provides valuable insight into how cartilage responds to reciprocating motion, as occurs during gait. This information will be helpful in identifying mechanical and biological mechanisms that lead to the initiation and development of cartilage degeneration and ultimately OA, as after traumatic events such as ACL tears.