Estimating and testing high-dimensional mediation effects in epigenetic studies

Abstract

Motivation: High-dimensional DNA methylation markers may mediate pathways linking environmental exposures with health outcomes. However, there is a lack of analytical methods to identify significant mediators for high-dimensional mediation analysis.

Results: Based on sure independent screening and minimax concave penalty techniques, we use a joint significance test for mediation effect. We demonstrate its practical performance using Monte Carlo simulation studies and apply this method to investigate the extent to which DNA methylation markers mediate the causal pathway from smoking to reduced lung function in the Normative Aging Study. We identify 2 CpGs with significant mediation effects.

Availability and implementation: R package, source code, and simulation study are available at https://github.com/YinanZheng/HIMA.

Contact: lei.liu@northwestern.edu

1 Introduction

Mediation analysis plays an important role in biomedical, behavioral, and psychosocial research studies, typically to understand the mechanism whereby change in one variable causes change in another (MacKinnon, 2008). Analytical methods for mediation analysis have been published extensively in the literature. For example, MacKinnon et al. (2002) compared several methods to test the statistical significance of the mediation effect via a Monte Carlo study; Wang and Zhang (2011) considered estimating and testing mediation effects in censored data; Taylor and MacKinnon (2012) investigated four applications of permutation tests to the single-mediator model; Pearl (2012) presented the causal mediation formula based on the counterfactual approach; Zhang and Wang (2013) introduced and compared four approaches to dealing with missing data in mediation analysis; Boca et al. (2014) developed a permutation approach for testing multiple mediators. For more details about mediation analysis, we refer to the review papers by Ten Have and Joffe (2010) and Preacher (2015). A comprehensive list of literature on mediation analysis is given in a webpage maintained by David Kenny (http://davidakenny.net/cm/mediate.htm).

Most of the above results are concerned with a single or multiple but low-dimensional mediators. To the best of our knowledge, there is very limited research on the high-dimensional mediation effects. However, with the development of advanced data collection techniques, high-dimensional data become increasingly common in many areas of scientific research. Our motivating example is an epigenome-wide DNA methylation study. In the methylation process, methyl groups are added to DNA at binding sites typically referred to as cytosine-phosphate-guanine (CpG) islands, which results in changes (typically down-regulation) to the expression of that DNA. Illumina Infinium HumanMethylation450 BeadChip array is a widely used platform that allows to measure DNA methylation levels of roughly 480K probes, resulting in high-dimensional data.

Specifically, our clinical interest lies in the effect of smoking (measured in pack-years) on lung function, and the extent to which this effect may be mediated by methylation changes. Prior studies have identified CpG sites associated with cigarette smoking in both epigenome-wide or gene-specific analyses, e.g. Gao et al. (2015), Harlid et al. (2014), Zeilinger et al. (2013). Identifying which markers mediate the effect of smoking on lung function is highly desirable from a public health perspective as it can lead to improved techniques for disease early detection and prevention. However, currently there are no appropriate statistical methods developed for use in the high-dimensional mediation analysis.

In this article, we will adopt the multiple mediator model’s framework (Preacher and Hayes, 2008) and extend it to the high-dimensional setting. Then, we propose a method to estimate and test mediation effects in high-dimensional epigenetic studies. Our key ideas are: first, reduce the pool of potential mediators from a very large to a moderate number (i.e. less than the sample size); next, conduct the variable selection with the minimax concave penalty (MCP, Zhang 2010); third, carry out joint significance testing for mediation effects.

The structure of the article is given as follows. In Section 2, we introduce the high-dimensional mediation regression model and propose the estimation and inference procedures. In Section 3, we illustrate the performance of our proposed procedure via extensive simulation studies. In Section 4, we apply our method to study the mediating effect of high-dimensional DNA methylation markers on the causal effect of smoking on lung function in the Normative Aging Study. Section 5 presents some concluding remarks and discusses further research topics.

2 Model and methodology

Mediation models are used to evaluate mechanism by which an exposure has an effect on an outcome. The simplest case of mediation analysis with one mediator is shown in Figure 1 with three variables: exposure X, mediator M, and outcome Y. The variable M mediates the effect of X on Y; that is: X causes M and then M causes Y. In the case of high-dimensional mediators (Fig. 2), we consider the following regression equations to assess the mediation effects:

$$\begin{array}{l}Y=c^{\ast }+{\gamma }^{\ast }X+{\mathrm{ϵ}}_1,\\ M_k=c_k+{\alpha }_{k}X+e_k, k=1,\cdots ,p,\\ Y=c+\gamma X+{\beta }_1{M}_1+\cdots +{\beta }_p{M}_p+{\mathrm{ϵ}}_2,\end{array}$$ (1)

where M_k, $k=1,\cdots ,p$ are the mediating variables (potential mediators); ${\gamma }^{\ast }$ represents the “total effect” of the independent variable X on the dependent variable Y; γ is the parameter relating X and Y via the direct effect, after adjusting for all mediators of interest. Moreover, $\alpha ={({\alpha }_1,\cdots ,{\alpha }_p)}^{\text{T}}$ is the parameter vector relating the independent variable to the mediating variables, and $\beta ={({\beta }_1,\cdots ,{\beta }_p)}^{\text{T}}$ is the parameter vector relating the mediators to the dependent variable adjusting for the effect of the independent variable. The “indirect effect” is denoted by the path $X\to M\to Y$ in Figure 1, and in the high-dimensional case is denoted by ${({\alpha }_1{\beta }_1,\cdots ,{\alpha }_p{\beta }_p)}^{\text{T}}$. Furthermore, $c^{\ast }$, c and c_k, $k=1,\cdots ,p$ are the intercept terms; ϵ₁, ϵ₂ and $e_k,k=1,\cdots ,p$ are residuals. Note there are p functions in the second equation of (1), one for each mediator.

Fig. 1.

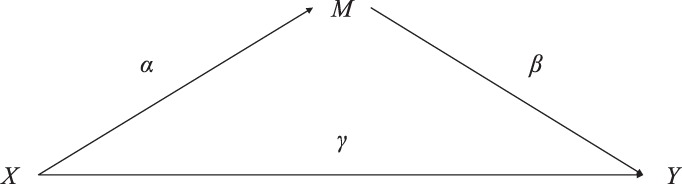
A scenario with a single mediator between exposure and outcome (plotted similarly to Boca et al., 2014)

Fig. 2.

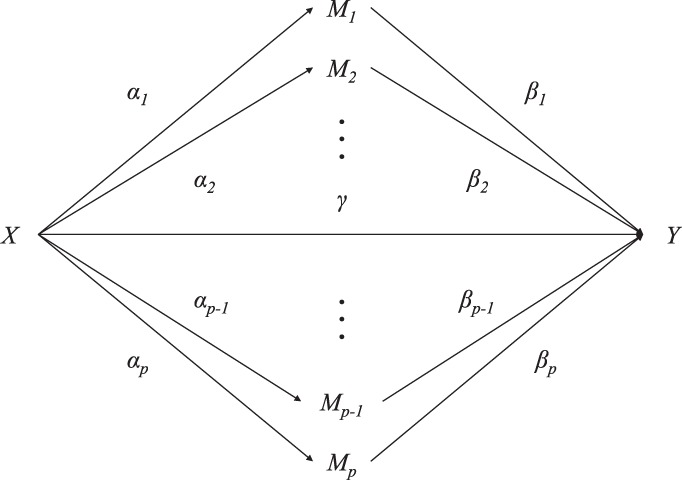
A scenario with high-dimensional mediators between exposure and outcome (plotted similarly to Boca et al., 2014)

Since the number of mediators p is much larger than the sample size n, traditional regression analysis fails to work in the third equation of (1). To tackle this problem we will first employ the sure independence screening (SIS, Fan and Lv, 2008) to identify those M_k’s with large absolute effect $\left|{\beta }_k\right|$, which form an index set denoted by $\mathcal{I}\subset \{1,\cdots ,p\}$. We will then perform variable selection using MCP. Details of the proposed procedure are as follows:

Step 1. (Screening). Use the SIS (Fan and Lv, 2008) to identify a subset $\mathcal{I}=\{1\le k\le p:$ M_k is among the top $d=[2n/\log (n)]$ largest effects for the response Y}. Of note, the methylation markers are standardized to ensure that the coefficients are in the same scale.

Step 2. (MCP-penalized estimate). Compute {${\widehat{\beta }}_k,\hspace{0.17em}k\in \mathcal{I}$} by minimizing the MCP penalized criterion,

$$Q^{\text{ols}}={\displaystyle {\sum }_{i=1}^n{\left(Y_i-c-\gamma X_i-{\displaystyle {\sum }_{k\in \mathcal{I}}{\beta }_k}{M}_{ik}\right)}^2}+{\displaystyle {\sum }_{k\in \mathcal{I}}{p}_{\lambda ,\delta }}({\beta }_k),$$ (2)

where $p_{\lambda ,\delta }(·)$ is the MCP:

$$\begin{array}{l}{p}_{\lambda ,\delta }({\beta }_k)=\lambda \left[\left|{\beta }_k\right|-\frac{|{\beta }_k{|}^2}{2\delta \lambda }\right]I\{0\le |{\beta }_k|<\delta \lambda \}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\frac{{\lambda }^2\delta }{2}I\left\{\right|{\beta }_k|\ge \delta \lambda \}.\end{array}$$

Here $\lambda >0$ is the regularization parameter, and $\delta >0$ determines the concavity of MCP. The MCP procedure has been implemented in R package ncvreg (Breheny and Huang, 2011). We prefer MCP over other penalty functions, e.g. elastic net (Zou and Hastie, 2005) since MCP can select the correct model with probability tending to 1 (Zhang, 2010). Further, we set $d=[2n/\log (n)]$ in Step 1 instead of $d=[n/\log (n)]$ in Fan and Lv (2008) to increase the chance to identify important mediators, since we need to consider both $X\to M$ and $M\to Y$ simultaneously.

Step 3. (Joint significance test). Let $\mathcal{S}=\{k:{\widehat{\beta }}_k\ne 0\}$, which is based on the MCP-penalized estimate in Step 2. The raw P-value for testing $H_0:{\beta }_k=0$ is given as

$$P_{\text{raw},1k}=2\left\{1-\Phi \left(\frac{\left|\widehat{{\beta }_k}\right|}{{\widehat{\sigma }}_{1k}}\right)\right\},$$

where $k\in \mathcal{S},\hspace{0.17em}\Phi (·)$ is the cumulative distribution function of N(0, 1), and ${\widehat{\sigma }}_{1k}$ is the estimate of standard error for ${\widehat{\beta }}_k$ that can be obtained from the oracle property of MCP (Fan and Li, 2001; Zhang, 2010). To control the family wise error rate (FWER), it is necessary to adjust for multiple comparisons by Bonferroni's method. Thus, we propose to use the following corrected P-value

$$P_{\text{corr},1k}=\min (P_{\text{raw},1k}·|\mathcal{S}|,1),$$ (3)

where $k\in \mathcal{S},$ and $\left|\mathcal{S}\right|$ is the cardinality, i.e. the number of elements in set $\mathcal{S}$. Notice that the MCP has the model selection consistency (Zhang, 2010), which ensures the validity of the joint significance test procedure.

Similarly, the raw P-value for testing $H_0:{\alpha }_k=0$ is

$$P_{\text{raw},2k}=2\left\{1-\Phi \left(\frac{\left|\widehat{{\alpha }_k}\right|}{{\widehat{\sigma }}_{2k}}\right)\right\},$$

where $k\in \mathcal{S},\hspace{0.17em}\widehat{{\alpha }_k}$ is the ordinary least squares estimator for α_k and ${\widehat{\sigma }}_{2k}$ is the corresponding estimated standard error. Similar to (3), the Bonferroni corrected P-value is

$$P_{\text{corr},2k}=\min (P_{\text{raw},2k}·|\mathcal{S}|,1).$$ (4)

We will reject the null hypothesis of no mediation effect with M_k only if both α_k and β_k are significant. The Bonferroni corrected P-value for the joint significance test is defined as

$$P_{\text{corr},k}=\max (P_{\text{corr},1k},P_{\text{corr},2k}),$$ (5)

where the corrected P-values $P_{\text{corr},1k}$ and $P_{\text{corr},2k}$ are defined in (3) and (4) respectively. If $P_{\text{corr},k}<0.05$, we can conclude that there exists significant mediation effect for M_k on Y, $k\in \mathcal{S}$.

Remarks 1: Another approach (Liu et al., 2013) is to test the mediation effect by the following model:

$$\begin{array}{l}Y=c^{\ast }+{\gamma }^{\ast }X+{\mathrm{ϵ}}_1,\\ M_k=c_k+{\alpha }_{k}X+e_k, k=1,\cdots ,p,\\ Y=c+\gamma X+{\beta }_k{M}_k+{\epsilon }_k, k=1,\cdots ,p.\end{array}$$ (6)

In the last equation of Model (6), Y depends on only one mediator M_k. However, as shown in Figure 2, multiple mediators contribute to the outcome Y. Preacher and Hayes (2008) described several advantages of the single multiple mediation Model (1) over the separate simple mediation Model (6). First, failure to adjust for other P – 1 mediators could lead to either inefficiency (if mediators are independent of each other) or even bias (if mediators are correlated with each other). The latter issue may be more troublesome as the correlation among probes close to one another can be as high as 0.6 (Moen et al., 2013) in cell lines or even stronger in our Normative Aging Study (NAS) data collected directly by blood sample. Furthermore, including multiple mediators in one model allows us to determine to what extent the specific indirect effects are associated with mediators, as shown in our Application. Finally, it is not feasible to predict Y using only one mediator.

3 Simulation studies

In this section, we will conduct some simulation studies to assess our proposed procedure. We generate data from model (1), where X is generated from $N(0,1.5)$, the first 8 elements of β $({\beta }_k,k=1,\cdots ,8)$ are ${(0.20,0.25,0.35,0.40,0.50,0.50,0,0)}^{\text{T}}$, and the first 8 elements of α $({\alpha }_k,k=1,\cdots ,8)$ are ${(0.25,0.15,0.25,0.55,0,0,0.55,0.55)}^{\text{T}}$. The rest of β and α are all 0. Let c = 1, $\gamma =0.5$. c_k is chosen as a random number from U(0, 2). e_k and ϵ₂ are generated from $N(0,1.2)$ and N(0, 1), respectively. The direct effect $\gamma =0.5$ and the total effect ${\gamma }^{*}=\gamma +{\sum }_{i=1}^P{\alpha }_k{\beta }_k=0.895$, so the percentage of total effect mediated by methylation markers is 0.395/0.895 = 44%.

We fit the model by the proposed method and use the joint significance test procedure to derive the P-values. We also compare our procedure with the naive joint significance test based on model (6), where we use Bonferroni's adjustment by the total number of methylation markers p. In the above setting, let ${\mathcal{S}}_0=\{1,2,3,4\}$ denotes the index set of significant mediators. Following Dezeure et al. (2015), we define FWER=P$(\exists k\in {\mathcal{S}}_0^c:P_{\text{corr},k}<0.05$), where $P_{\text{corr},k}$ is given in (5). Similarly, $\text{Power}=\sum _{k\in {\mathcal{S}}_0}\text{P}(P_{corr,k}<0.05)/\left|{\mathcal{S}}_0\right|$. Table 1 presents the estimator and mean square error (MSE) for the indirect effect ${\alpha }_k{\beta }_k,\hspace{0.17em}k=1,\cdots ,9$. The FWER and power are reported in Tables 2 and 3, respectively. All simulations are based on 500 replications, with sample size n = 100, 200 and 300, respectively.

Table 1.

Estimator and MSE (in parenthesis) for the indirect mediation effect ${\alpha }_k{\beta }_k$

	p = 1000			p = 10 000
(${\alpha }_k,{\beta }_k)$	n = 100	n = 200	n = 300	n = 100	n = 200	n = 300
(0.25,0.20)	0.0256	0.0415	0.0475	0.0154	0.0222	0.0298
	(0.0226)	(0.0206)	(0.0159)	(0.0160)	(0.0146)	(0.0156)
(0.15,0.25)	0.0191	0.0313	0.0365	0.0135	0.0187	0.0249
	(0.0174)	(0.0177)	(0.0139)	(0.0136)	(0.0126)	(0.0121)
(0.25,0.35)	0.0511	0.0764	0.0866	0.0311	0.0454	0.0577
	(0.0331)	(0.0253)	(0.0217)	(0.0247)	(0.0197)	(0.0229)
(0.55,0.40)	0.1376	0.1876	0.2138	0.0844	0.1187	0.1461
	(0.0622)	(0.0492)	(0.0351)	(0.0552)	(0.0390)	(0.0448)
(0,0.50)	−0.0010	0.0008	−0.0026	0.0010	−0.0009	0.0004
	(0.0282)	(0.0270)	(0.0224)	(0.0196)	(0.0163)	(0.0156)
(0,0.50)	0.0005	−0.0006	0.0005	−0.0003	−0.0009	−0.0010
	(0.0269)	(0.0248)	(0.0231)	(0.0173)	(0.0167)	(0.0153)
(0.55,0)	−0.0005	−0.0001	0.0001	−0.0002	0.0000	0.0000
	(0.0077)	(0.0094)	(0.0034)	(0.0054)	(0.0000)	(0.0000)
(0.55,0)	−0.0001	0.0008	0.0000	−0.0001	0.0000	0.0001
	(0.0109)	(0.0081)	(0.0000)	(0.0061)	(0.0034)	(0.0035)
(0,0)	−0.0001	−0.0000	0.0000	0.0000	0.0000	−0.0000
	(0.0021)	(0.0004)	(0.0002)	(0.0015)	(0.0004)	(0.0002)

Table 2.

FWER at significance level 0.05

	p = 1000			p = 10 000
Method	n = 100	n = 200	n = 300	n = 100	n = 200	n = 300
Proposed	0.0380	0.0360	0.0240	0.0240	0.0140	0.0200
Naive	0	0	0	0	0	0

Table 3.

Power at significance level 0.05

	p = 1000			p = 10 000
Method	n = 100	n = 200	n = 300	n = 100	n = 200	n = 300
Proposed	0.2635	0.6735	0.8845	0.1325	0.4445	0.6990
Naive	0.0595	0.2770	0.4630	0.0325	0.1770	0.3770

From the results in Table 1, we can see that the estimators are close to the true values of indirect effect and the MSE decreases as the sample size n increases. Table 2 indicates that the proposed joint significance test procedure has reasonably well controlled type I error, while a little conservative. In contrast, the naive procedure has poor type I error control. In Table 3, our method has better power than the naive method. Therefore, our method is preferred in practice.

4 An application

Methylation markers are often considered potential mediators between exposures and health outcomes. For example, Bind et al. (2014) found that the effect of air pollution on coagulation and inflammation was significantly mediated by several methylation markers in the Normative Aging Study. However, they only considered 5 specific methylation markers. An epigenome-wide mediation analysis will allow for more thorough and systematic identification of all the possible mediation effects due to DNA methylation.

Our data come from the US Department of Veterans Affairs Normative Aging Study, an ongoing longitudinal cohort of elderly, predominantly white American veterans. In 1963, 2280 men aged 21–80 years and free of hypertension or other chronic conditions were enrolled. Between January 1, 1999 and December 31, 2013, 686 were randomly selected and had blood samples profiled using the Illumina Infinium 450K BeadChip DNA methylation array. A total of 500ng of DNA was used to perform bisulfite conversion. The DNA methylation level was calculated as M values (logit of methylated probe intensity) which approximate a normal distribution (Du et al., 2010). Batch effect and potential confounding effects of blood cell subtype were estimated by Housemandn method (Houseman et al., 2012) and corrected for using ComBat (Johnson et al., 2007). We include 484 548 probes in the analysis.

We are interested in how these methylation markers mediate the relationship between smoking and lung function. Lung function is measured by four outcomes: FEV1 (forced expiratory volume in 1 second), FVC (forced expiratory vital capacity), FEV1/FVC, and MMEF (maximum mid expiratory flow). We conduct separate mediation analysis for each measure. We exclude subjects with lung-related diseases, e.g. asthma, emphysema and COPD, resulting in a sample size of 290. Smoking status and frequency were assessed via questionnaire between 1999 and 2006, defined as ‘baseline’ for our analyses. Methylation was measured at baseline, and outcomes were measured between 2001 and 2006 (e.g. 2+ years post-baseline for each subject), allowing us to ensure the proper temporal relationship (exposure → methylation → lung function). Our analysis also adjusts for age, height, and weight in each equation of model (1).

Of note, in the Normative Aging Study, there are much stronger correlations between M’s and Y than those between X and M’s. Therefore, in Step 1 we also add the top $d=[2n/\log (n)]$ CpGs in the path from $X\to M$ to increase the possibility to identify significant mediators. In the second step we run a variable selection on the screened CpGs. In Step 3 we use the joint significance test to derive the P-values. Since smoking reduces lung function, we filter out mediators with indirect effect ${\alpha }_k{\beta }_k>0$.

In Table 4 we list the summary results for each of the four outcomes. We identify 2 CpGs as mediators, which are associated with at least one lung function outcome. Specifically, cg05575921 (in the gene region of AHRR) is associated with three measures of lung function, methylation of which has been shown to be a sensitive marker of smoking history (Gao et al., 2015; Harlid et al., 2014). Another CpG, cg24859433 in the intergenic region 6p21.33 is associated with MMEF of the lung function (Ambatipudi et al., 2016; Zeilinger et al., 2013). Therefore, our Epigenome-Wide Association Study (EWAS) results are supported by the current literature for their potential roles in smoking and lung function, demonstrating the validity of our approach.

Table 4.

Estimators and corrected P-values for significant mediation effects

	CpG	CHR	Gene Name	$\widehat{\alpha }$	$\widehat{\beta }$	P-value	% TE
FEV1	cg05575921	5	AHRR	−0.0231	0.1141	0.0003	50.5
FVC	cg05575921	5	AHRR	−0.0231	0.1327	0.0017	57.5
FEV1/FVC	cg05575921	5	AHRR	−0.0231	0.6065	0.0453	38.9
MMEF	cg24859433	6	*	−0.0117	13.366	0.0324	15.9

‘*’denotes CpGs in the intergenic region; ‘%TE’ denotes the percentage of total effect: ${\alpha }_k{\beta }_k/{\gamma }^{*}$.

We are also interested in the relative magnitudes of the total effect mediated through methylation markers, defined as ${\alpha }_k{\beta }_k/{\gamma }^{*}$ for each methylation marker. The results are listed in the last column of Table 4. About 50% of total effect between smoking and FEV1 (or FVC), and 40% between smoking and FEV1/FVC is mediated through cg05575921, and 16% between smoking and MMEF through cg24859433. We note that the percentage of total effect mediated by methylation markers for FEV1 is close to the Simulation Setting (44%), demonstrating the applicability of our method to real scenarios. Intervention could be explored on these CpGs to modify the lung function among smokers. Finally, we use the naive joint significance test for the NAS data. However, it fails to identify any significant mediators.

5 Conclusion and remarks

We developed a new method to estimate mediation effects with high-dimensional mediators. We used the sure independent screening and the MCP methods, and the joint significance test for mediation effects. We illustrated the proposed method via simulation studies and a real data example. We identified 2 CpGs which could mediate the effects of smoking and lung function. Our method can be widely used in high-dimensional DNA methylation analysis from population studies.

Several other issues may complicate the testing of high-dimensional mediation effects, which will be studied in the future research. e.g. confounders (Li et al., 2007), non-linearity (Albert, 2012) and measurement error (Valeri et al., 2014; Zhao and Prentice, 2014). Particularly, for measurement error, two classical correction approaches including the method of moments and regression calibration (Valeri et al., 2014) may be employed in the high-dimensional mediators case.

In reality, many exposures or risk factors may work simultaneously on DNA methylation. For example smoking and physical activity can both affect lung function through DNA methylation. If these exposures are independent of each other, we can simply add the other risk factor in Model (1). For example, in the second equation of Model (1), we have a total of 2p parameters (${\alpha }_{1k},{\alpha }_{2k},k=1,\dots ,p$). The estimation and inference can be carried out similarly. However, complications arise when there factors are correlated or have interaction effects. It is of further interest to incorporate multiple exposures into the mediation analysis of high-dimensional methylation markers.

Funding

This work was supported by AHA 14SFRN20480260, 12GRNT12070254 and National Institute of Environmental Health Sciences (R01ES021357, R01ES021733 and R01ES015172), National Natural Science Foundation of China (11301212, 11401146), and China Postdoctoral Science Foundation (2014M550861). The VA Normative Aging Study is supported by the Cooperative Studies Program/Epidemiology Research and Information Center of the US Department of Veterans Affairs.

Conflict of Interest: none declared.