Skip to main content
PMC home page
NeuroImage : Clinical logoLink to NeuroImage : Clinical
. 2016 Sep 14;12:615–623. doi: 10.1016/j.nicl.2016.09.010

Statistical estimation of white matter microstructure from conventional MRI

Leah H Suttner a,⁎, Amanda Mejia b, Blake Dewey c, Pascal Sati c, Daniel S Reich b,c, Russell T Shinohara a
PMCID: PMC5048084  PMID: 27722085

Abstract

Diffusion tensor imaging (DTI) has become the predominant modality for studying white matter integrity in multiple sclerosis (MS) and other neurological disorders. Unfortunately, the use of DTI-based biomarkers in large multi-center studies is hindered by systematic biases that confound the study of disease-related changes. Furthermore, the site-to-site variability in multi-center studies is significantly higher for DTI than that for conventional MRI-based markers. In our study, we apply the Quantitative MR Estimation Employing Normalization (QuEEN) model to estimate the four DTI measures: MD, FA, RD, and AD. QuEEN uses a voxel-wise generalized additive regression model to relate the normalized intensities of one or more conventional MRI modalities to a quantitative modality, such as DTI. We assess the accuracy of the models by comparing the prediction error of estimated DTI images to the scan-rescan error in subjects with two sets of scans. Across the four DTI measures, the performance of the models is not consistent: Both MD and RD estimations appear to be quite accurate, while AD estimation is less accurate than MD and RD; the accuracy of FA estimation is poor. Thus, in some cases when assessing white matter integrity, it may be sufficient to acquire conventional MRI sequences alone.

Keywords: Image synthesis

Highlights

  • •

    Conventional MR images are used to estimate four DTI measures.

  • •

    Mean diffusivity and radial diffusivity are estimated well.

  • •

    MRI may be used to study certain microstructural changes in white matter.

1. Introduction

Diffusion tensor imaging (DTI) has become the predominant modality for studying white matter integrity in multiple sclerosis (MS) and other brain disorders, including Alzheimer's disease, traumatic brain injury, epilepsy, depression, and stroke. In MS, DTI is generally understood to provide information about diffuse changes in the microstructure and integrity in the white matter of patients. Numerous studies have shown that certain DTI measures differ between MS subjects and controls. In particular, researchers have found that patients with MS have increased mean diffusivity (MD) and decreased fractional anisotropy (FA) in normal appearing white matter (NAWM) compared to healthy controls (Vrenken et al., 2006, Ciccarelli et al., 2003, Senda et al., 2012, Werring et al., 1999). As traditional MRI based measures of white matter changes in MS show only limited associations with disability, these DTI findings have been noted for their promise of clinical utility (Barkhof, 2002); (Zivadinov, 2016). Moreover, many studies promote the use of DTI by suggesting that DTI can measure microstructural changes, whereas conventional magnetic resonance imaging (MRI) is only able to identify changes at the macrostructural level (Senda et al., 2012, Rocca et al., 2006, Wilson et al., 2003).

Unfortunately, the use of DTI-based biomarkers in large multi-center studies is hindered by systematic biases (Pfefferbaum et al., 2003, Vollmar et al., 2010), which confound the study of disease-related changes. Furthermore, the site-to-site variability in multi-center studies is significantly higher for DTI (Zhu et al., 2011, Teipel et al., 2012) than that for conventional MRI-based markers (Teipel et al., 2010, Ewers et al., 2006). These issues necessitate larger sample size in multi-center studies using DTI and highlight the potential for less generalizable findings from single-scanner studies. Additionally, DTI sequences require additional scanning time, which increases the cost of MRI in both clinical and research settings. In this paper, we investigate whether conventional MRI can be used to detect microstructural changes and estimate DTI measures.

Synthesizing or estimating a specific imaging modality or sequence from other imaging sequences can be advantageous for several reasons. Doing so allows for larger multicenter imaging studies in which patients, or even entire centers, are missing particular types of images. It also allows researchers to capitalize on imaging datasets that have already been acquired. For example, the Alzheimer's Disease Neuroimaging Initiative (ADNI) database (Mueller et al., 2005) contains thousands of conventional MRIs, and the Comprehensive Longitudinal Investigation of Multiple sclerosis at the Brigham and Women's Hospital (CLIMB) contains conventional MRI from thousands of MS patients (Gauthier et al., 2006); there are also numerous well controlled phase 3 studies that have acquired conventional MRI data. Using image estimation, these and other databases could be used to conduct large-scale studies with quantitative imaging not acquired at every study site. Image synthesis also has significant applications in multi-modal image registration (Michel and Paragios, 2010, Jog et al., 2013a, Ye et al., 2013) and normalization (Jog et al., 2013a). Thus, there has been a growing interest in this field in recent years. A recent study on image synthesis showed that it is possible to synthesize T2-weighted contrasts from T1-weighted images and to synthesize 3-tesla T1-weighted magnetization prepared rapid gradient echo (MPRAGE) images from 1.5-tesla MPRAGEs using an atlas image-based nonlinear regression (Jog et al., 2013b, Ye et al., 2013) uses a generalized patch-based label propagation method to synthesis arbitrary target image modalities. Specifically, they use T1-weighted MRI to synthesize T2 MRI and, with much less accuracy, DTI-fractional anisotropy.

In our study, we adopt the methods introduced by Mejia et al. (2016), in which quantitative T1 maps (qT1) are estimated from the conventional MRI sequences: T1-weighted (T1w), T2-weighted (T2w), proton density-weighted (PDw), and T2-weighted fluid attenuated inversion recovery (FLAIR) images. We apply their Quantitative MR Estimation Employing Normalization (QuEEN) model to estimate the four DTI measures: MD, FA, radial diffusivity (RD) and axial diffusivity (AD).

2. Methods

2.1. Study sample

The dataset we use in this study includes 73 subjects with clinically diagnosed MS and at least one set of MRI and DTI scans. After performing quality control to exclude images that exhibit subject movement, major segmentation errors, and registration problems, we have 50 subjects, including 14 with relapsing-remitting MS (RRMS), 12 with secondary-progressive MS (SPMS), and 24 with primary-progressive MS (PPMS). The resulting study sample is 64% female with a mean age of 53 (S.D. 11). Additionally, a second set of MRI and DTI scans was acquired for 19 subjects, which we use to evaluate the predictive accuracy of the model. The median time between scans is 181 days (range 147–301). Additional summary statistics are provided in Table 1. The distributions of these summary statistics are similar in males and female, though the males have slightly higher EDSS scores (Appendix Table A.1, Table A.2).

Table 1.

Study sample summary statistics.

All MS PPMS RRMS SPMS
n 50 24 14 12
% Female 64.0 50.0 85.7 66.7
Mean age (SD) 52.9 (11.4) 56.6 (7.4) 44.4 (15.0) 55.4 (8.3)
Disease duration (SD) 14.9 (10.8) 13.5(9.5) 15.0 (7.9) 25.7 (9.2)
Median EDSS score (range) 3.5 (1.0–7.5) 5.5 (1.5–7.5) 1.5 (1.0–6.0) 6.25 (1.5–7.0)
Open in a new tab

2.2. Imaging protocol

Each MRI study includes the following volumes, all collected on a Siemens Skyra 3 T scanner equipped with a 32-channel receive coil: T1-MPRAGE (Magnetization-Prepared RApid Gradient Echo) [TR = 3000 ms, TE = 3.03 ms, TI = 900 ms, FA = 9]; PDw and T2w images from a dual-echo turbo-spin-echo (TSE) sequence [TR = 3000 ms, TE = 11 ms/101 ms, FA = 150, ETL = 14]; and a 3D T2-weighted FLAIR image acquired using a T2-selective inversion pulse optimized for T2 of 120 ms [TR = 4800 ms, TE = 354 ms, TI = 1800 ms, variable FA]. All scans are acquired at 1.0 mm isotropic resolution except the PDw/T2w TSE sequence, which is acquired at 0.93 × 0.93 × 3.0 mm resolution.

Each DTI study was obtained using a two-acquisition method with opposite phase encode directions to minimize influence of B0-related image distortions. Each acquisition acquired 1 reference image without diffusion weighting and 30 images with radially spaced diffusion directions and a diffusion weighting of b = 1000 s/mm2. Diffusion weighted images were acquired at 2 × 2 × 2 mm isotropic resolution.

2.3. Image processing

We perform image preprocessing as described in Mejia et al. (2016). Briefly, we rigidly align all images to the MNI152 1.0 mm nonlinear template. To remove extracerebral voxels, we use the SPECTRE skull-stripping algorithm (Carass et al., 2011). To segment tissue classes, we use Lesion Topology Preserving Anatomy Driven Segmentation (Lesion-TOADS) (Shiee et al., 2010). We visually inspect the segmentations and exclude subjects with major errors, but we do not manually tune the segmentation method. We correct for ventricular segmentation errors using non-topologically constrained maximum membership classes. We generate brain masks by excluding cerebrospinal fluid (CSF), hypointense voxels in FLAIR, and any voxels outside the field of view on any image. To create conservative tissue class masks, we use a 3 × 3 × 3 diamond-shaped kernel for erosion of the Lesion-TOADS segmentation. We use the conservative masks for training and validation, but we use the full masks for whole-image predictions. Overall, the image processing takes approximately one to two hours per subject on a single computer core.

2.4. Image normalization

As conventional structural MRI is acquired in arbitrary units, intensity normalization is required to compare values across images acquired at different sites; using different hardware, software or protocols; or even on different dates using the same scanner and protocol. Historically, image normalization has been performed with respect to NAWM (Shinohara et al., 2014) or CSF Pujol et al., 1992, van Waesberghe et al., 1998, Bakshi et al., 2002, Tjoa et al., 2005, Brass et al., 2006, Neema et al., 2009) as a reference region. However, both of these tissue classes are less than optimal for this study. CSF is highly variable in intensity, which can lead to inconsistent normalization. Changes in NAWM are of primary interest, and thus normalizing with respect to NAWM could obscure disease-related changes.

Instead, we utilize the adaptation of the z-score normalization method (Shinohara et al., 2014, Shinohara et al., 2011) proposed by Mejia et al. (2016). The z-score method subtracts a measure of location and divides by a measure of scale; we refer to these two steps as scaling and shifting, respectively. The adapted method proposed by Teipel et al. (2010) utilizes a combination of NAWM and cerebellar gray matter (CBGM). Although using NAWM alone as a reference can confound the normalization, the standard deviation of NAWM is well estimated and can be used for scaling. Abnormalities of CBGM in MS are poorly detected by conventional MRI methods, and thus CBGM signal intensity should be similar between subjects and disease groups. Thus, CBGM can be used for shifting. Previously, CBGM has been used for normalization in positron emission tomography (PET) in MS (Ratchford et al., 2012) and Alzheimer's disease (Kropholler et al., 2007).

The normalized units are given by

MiNv=Miv−μi,mCBGMσi,mNAWM

Mi(v) denotes the intensity of voxel v for subject i in modality M ∈ {FLAIR, PDw, T1w, T2w}. For subject i in modality M, μi,MCBGM is the mean intensity in CBGM, and σi,MNAWM is the standard deviation of intensities within NAWM.

2.5. Statistical prediction model

To model each DTI modality, we apply the QuEEN statistical model to generate “statistical DTI” measures of MD, FA, RD and AD. QuEEN uses a voxel-wise generalized additive regression model to relate the normalized intensities of one or more conventional MRI modalities to a quantitative modality, such as qT1 or DTI. We specify a set of models to use the standard MRI modalities, T1w, T2w, PDw, and FLAIR, to predict the DTI measures MD, FA, RD, and AD. As in the QuEEN T1 model, we fit a separate model for each tissue class, c. Here we use the nine tissue classes identified as lesion, CBGM, GM, caudate, thalamus, putamen, brainstem, CBWM, and NAWM. Thus, for each DTI measure, we relate the value at each voxel v in class c of subject i to the corresponding predictor modalities by:

DTIjiv∼fj1cT1wiNv+fj2cT2wiNv+fj1cPDwiNv+fj1cFLAIRiNv+ϵ1v

where j = 1 , 2 , 3 , 4 indexes the four DTI measures we wish to predict. The smooth functions fjkc(·), k = 1 , 2 , 3 , 4, relate predictor modality k to DTI measure i within tissue class c. We implement the models in R using the gam function from the mgcv package (version 1.7-28, (Wood, 2006, Wood, 2011) as described in Mejia et al. (2016). The gam function represents the smooth curves as penalized regression splines. The degree of smoothness is estimated using generalized cross-validation, and the smoothing parameter estimation criterion is optimized using the Newton method (Chong and Wahba, 1991). The statistical DTI measures (stat-MD, stat-FA, stat-RD, and stat-AD) are estimated by applying the estimated regression curves to the respective predictor modalities.

2.6. Model validation

To evaluate each model, we assess the accuracy and utility of the statistical DTI measures. First, we assess the accuracy of the models by comparing the scan-rescan mean square error (MSE) to the statistical prediction MSE in subjects with two sets of scans. We define the scan-rescan MSE as the voxel-wise squared difference in intensity between the original acquired images and the second set of images (the rescan images) averaged across voxels. In contrast, we define the statistical prediction MSE as the voxel-wise squared difference in intensity between the statistical DTI measure and the rescan image, averaged across voxels. We summarize both measures by tissue class. These two MSEs describe how accurately the statistical and acquired DTI measures predict a second acquired DTI measure obtained within one year. Assuming that the best available prediction of the acquired rescan DTI measure is the acquired DTI measure from the first visit, we use these MSEs as benchmarks for predictive performance.

Second, we assess the utility of the model. Liu et al. (2012) found evidence that RRMS patients had decreased FA and increased MD, RD, and AD in white matter regions compared to healthy controls, so we compare the mean DTI values in NAWM across MS subtypes for the statistical and acquired images. For each DTI measure, we conduct two-sided Wilcoxon rank sum tests between each subtype.

2.7. Associations with clinical measures

To investigate the use of these images as potential biomarkers we conduct a preliminary assessment of the association of the observed and predicted DTI measures and two commonly used scores for disability and cognition. First, we test the correlations between mean MD and mean RD in NAWM and the Expanded Disability Status Scale (EDSS) score (Kurtzke, 1983), a common measure designed to assess neurological impairment in MS. We also test the correlation of mean MD and mean RD in NAWM with the Symbol Digit Modality Test (SDMT) (Smith, 1982) score, a tool for measuring cognitive function. We use the nonparametric Kendall's Tau coefficient for assessing correlations.

3. Results

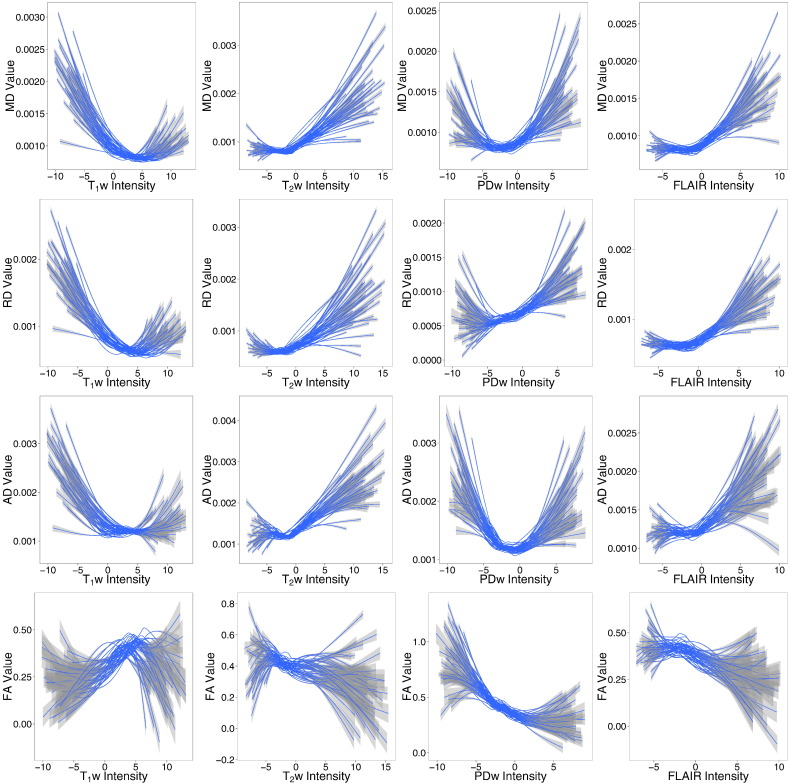
The normalization method relies on the assumption that the distribution of intensities in CBGM is similar across the MS subtype groups. We check this assumption using Kruskal–Wallis tests of association between each acquired DTI measure and MS subtype. Indeed, there are no significant associations (Table 2). Fig. 1 shows the relationships between the normalized predictor images and each acquired DTI measure within NAWM. The relationships between the normalized predictor images and MD (top row) and RD (second row) appear to be similar across subjects, while the relationships between the normalized images and AD (third row) appear less similar. In FA (bottom row), there appears to be a large amount of heterogeneity across subjects in the relationships with the normalized predictor images.

Table 2.

Kruskal-Wallis tests of association between the acquired DTI measure in CBGM and MS subtype.

Acquired DTI p-Value
MD 0.86
RD 0.83
AD 0.78
FA 0.51
Open in a new tab

Fig. 1.

Fig. 1

Open in a new tab

Acquired DTI versus normalized predictor images within NAWM. Each line is a smoothed curve from a single subject, and confidence bands for each curve are shown in gray. The relationships between MD and RD and the normalized predic-tor images appear much more similar across subjects, whereas the relationships between AD and FA and the normalized predictor images varies greatly across subjects.

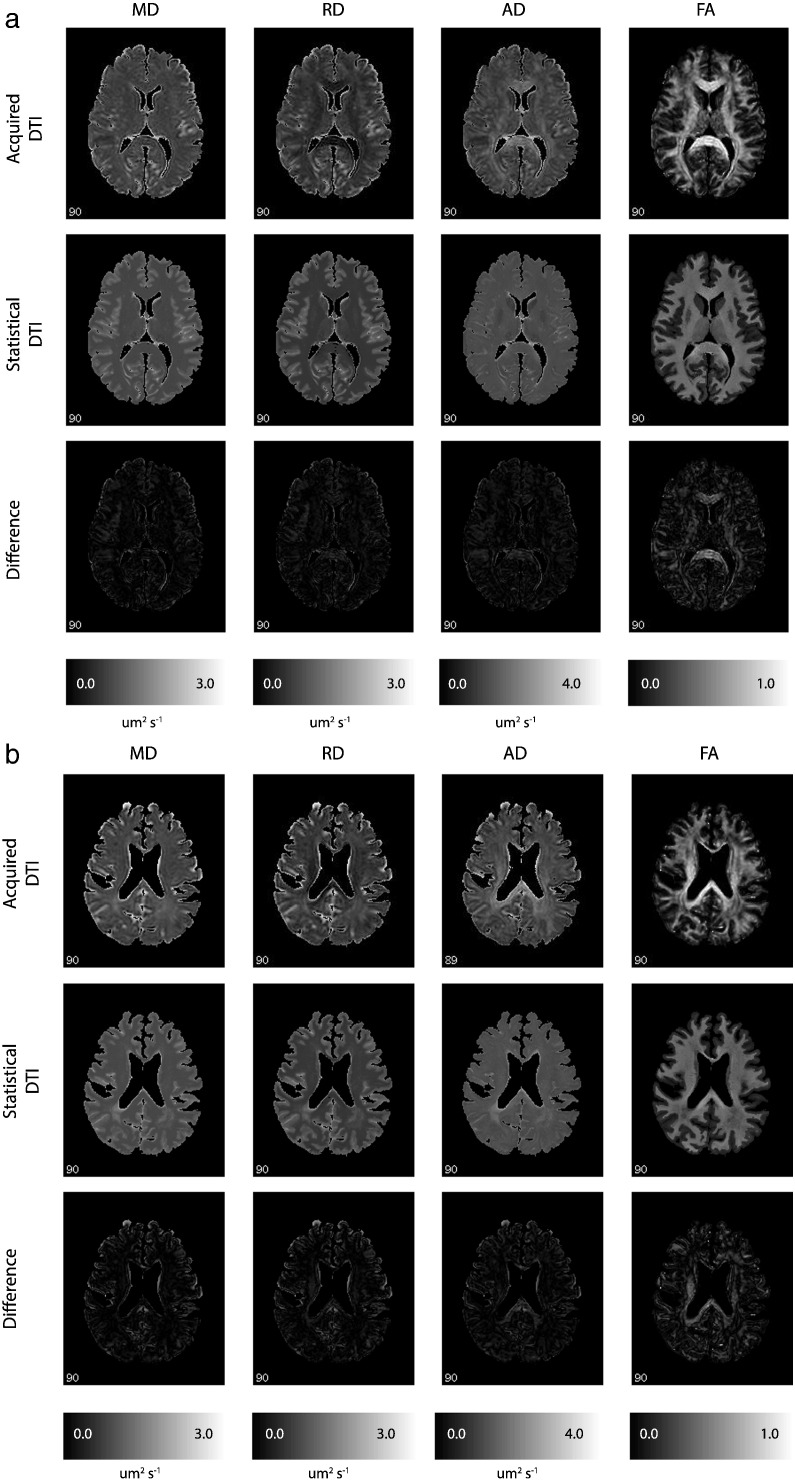
Sample images from two randomly selected subjects are shown in Fig. 2. The subject in Fig. 2a has PPMS and the subject in Fig. 2b has SPMS. The top rows in Fig. 2a/b show the acquired DTI images, the middle rows show the statistical DTI images estimated using the leave-one-subject-out cross-validation (LOOCV), and the bottom rows show the absolute value of the difference between the acquired and statistical DTI images. Both stat-MD and stat-RD appear to be quite accurate estimates of MD and RD, respectively, while stat-AD is less accurate than stat-MD and stat-RD, and the accuracy of stat-FA is poor (although stat-FA still captures the strong gray/white differentiation typical of FA maps).

Fig. 2.

Fig. 2

Open in a new tab

a DTI images from a PPMS subject. The four DTI measures are shown for a PPMS subject. The top row shows the acquired DTI, the middle row shows the statistical DTI, and the bottom row shows the abso-lute value of the difference between the acquired and statistical DTI. The models for MD and RD perform relatively well, while the models for AD and FA appear to fail. 2b DTI images from a SPMS subject. The four DTI measures are shown for a SPMS subject. The top row shows the acquired DTI, the middle row shows the statistical DTI, and the bottom row shows the absolute value of the difference between the acquired and statistical DTI. The models for MD and RD perform relatively well, while the models for AD and FA appear to fail.

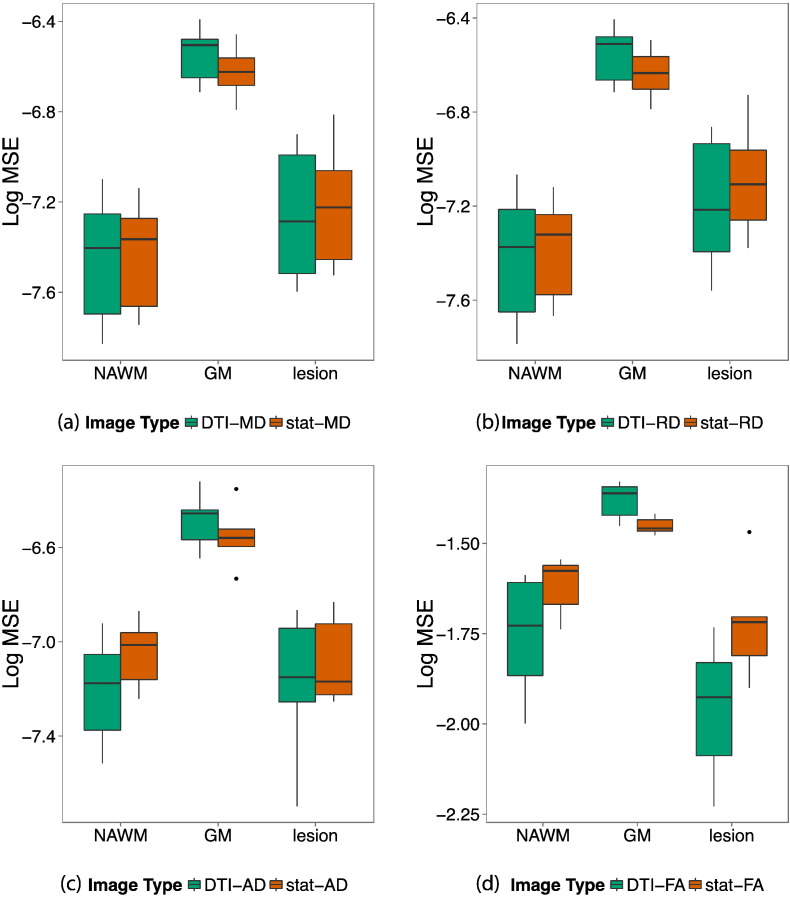
To assess the accuracy of our statistical DTI models, we compare the prediction MSE of the statistical DTI images to the scan-rescan MSE of the acquired images. Fig. 3 shows boxplots of the scan-rescan log-MSE for the acquired DTI images (shown in green) and the prediction log-MSE for the statistical estimate of each DTI image (shown in orange) for three tissue classes of interest: NAWM, GM, and lesions. Each boxplot was constructed based on the MSE from 19 subjects with two sets of DTI scans. In MD and RD, the MSEs are comparable in NAWM and lesions. In MD, the prediction log-MSE in the statistical images and the scan-rescan log-MSE in the acquired images have means in NAWM of − 7.4 mm2 s− 1 (25th percentile = − 7.5, 75th percentile = − 7.3) and − 7.4 mm2 s− 1 (− 7.5, − 7.3), respectively, and means in lesions of − 7.4 mm2 s− 1 (− 7.5, − 7.1) and − 7.5 mm2 s− 1 (− 7.6, − 7.3), respectively. In RD, the prediction log-MSE and the scan-rescan log-MSE have means in NAWM of − 7.3 mm2 s− 1 (− 7.5, − 7.3) and − 7.3 mm2 s− 1 (− 7.5, − 7.2), respectively, and means in lesions of − 7.2 mm2 s− 1 (− 7.3, − 7.1) and − 7.4 mm2 s− 1 (− 7.6, − 7.1), respectively. Across all four DTI measures, the statistical prediction log-MSE of the estimated images is smaller in GM compared to the scan-rescan log-MSE of the acquired images, indicating that our models can accurately estimate GM. However, in FA and AD, the prediction log-MSE is much larger in NAWM and lesions compared to the scan-rescan log-MSE of the acquired images, suggesting that the FA and AD models may be incorrect.

Fig. 3.

Fig. 3

Open in a new tab

Scan-rescan and statistical prediction MSEs. For each DTI measure, acquired scan-rescan MSE (green) and statistical prediction MSE (orange) are shown in lesion, GM, and NAWM. In NAWM the prediction MSEs in MD (a) and RD (b) are similar to scan-rescan MSEs, but these are slightly larger in AD (c) and FA (d). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

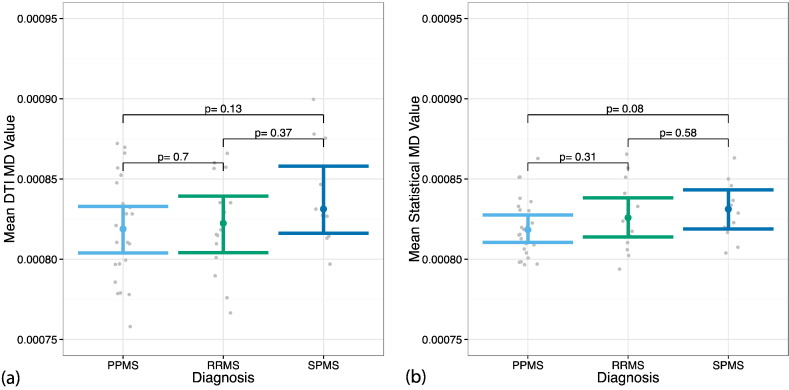
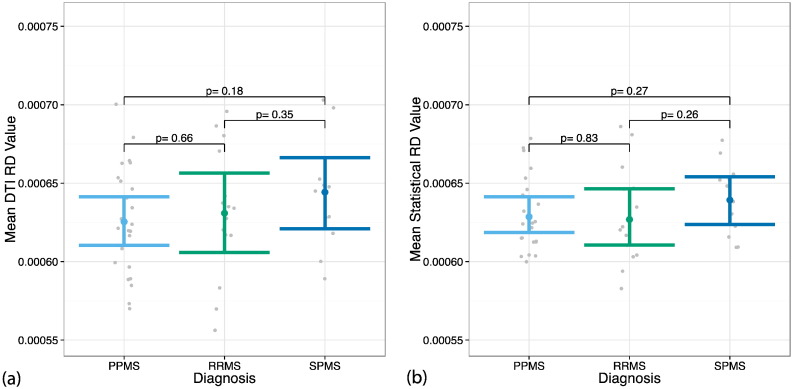
Fig. 4, Fig. 5 show the MS subtype group differences for mean MD and mean RD, respectively, in NAWM. In all comparisons, the differences between subgroups were not significant. However, the spread of the data is tighter in the statistical images compared to the acquired images. As shown in Fig. 5, the level of significance between groups was similar for the statistical and acquired RD images. Fig. 4 shows more pronounced differences in statistical MD between PPMS and each of the other subtypes compared to the acquired images as well as a smaller spread.

Fig. 4.

Fig. 4

Open in a new tab

Distribution of MD in NAWM between MS subtypes. Differences in MD in NAWM between MS subtypes were tested using (a) the acquired DTI images and (b) the statistical MD images. The plots show the mean MD in NAWM for each subject (gray) and the Wilcoxon 95% confidence intervals for each subtype. The p-values are reported for the two-sided Wilcoxon tests. There are no significant differences between the subgroups in either DTI MD or statistical MD. However, the variance of the data is smaller in the statistical MD images compared to the acquired MD images.

Fig. 5.

Fig. 5

Open in a new tab

Distribution of RD in NAWM between MS subtypes. Differences in RD in NAWM between MS subtypes were tested using (a) the acquired DTI images and (b) the statistical RD images. The plots show the mean RD in NAWM for each subject (gray) and the Wilcoxon 95% confidence intervals for each subtype. The p-values are reported for the two-sided Wilcoxon tests. There are no significant differences between the subgroups in either DTI RD or statistical RD.

Table 3a provides the results of the exploratory analyses of the correlations between mean MD in NAWM and EDSS and SDMT scores, respectively. Table 3b provides the correlations between mean RD in NAWM and the EDSS and SDMT scores. None of the results withstand the multiple comparisons correction, however these results suggest that higher RD values may be associated with lower SDMT scores, and this association is stronger using the statistical RD measure.

Table 3a.

Correlations between mean MD and clinical scores.

MD Score Correlation p-Value
Acquired EDSS 0.133 0.20
Statistical EDSS 0.0378 0.72
Acquired SDMT − 0.19 0.07
Statistical SDMT − 0.141 0.17
Open in a new tab

Table 3b.

Correlations between mean RD and clinical scores.

RD Score Correlation p-Value
Acquired EDSS 0.133 0.20
Statistical EDSS 0.171 0.10
Acquired SDMT − 0.184 0.07
Statistical SDMT − 0.248 0.02
Open in a new tab

4. Discussion

Here, we have used conventional MRI to estimate several common DTI measures, namely MD, RD, AD, and FA. Across the four DTI measures, the performance of the models is not consistent: while MD and RD are accurately estimated within NAWM using statistical methods, AD and FA are less so. It is currently unclear whether the inaccuracies in the AD and FA predictions are due to failures of the model or due to missing information. It may be that the differences in the performance of the models are explained by what each DTI measure describes. MD is a global measure sensitive to tissue microstructure, and in practice it is highly correlated to RD, which, in NAWM, represents diffusivity perpendicular to white matter bundles. On the other hand, AD quantifies diffusivity along the major orientation of the axon bundles and is substantially less sensitive to pathology, such as diffuse inflammation, demyelination, and edema – all of which are detectable by the conventional MRI approaches. Finally, FA represents tissue anisotropy as a measure of contrast between AD and RD; thus, any prediction errors for either AD or RD are likely to be magnified in the FA prediction (Song et al., 2002, Alexander et al., 2007). Furthermore, the four MRI contrasts that we use in the estimation are not sensitive to fiber orientation, but another contrast, T2*, can be quite sensitive to fiber orientation. Thus, if the failure of the model to predict AD and FA is due to inadequacies of the standard MRI modalities, then including T2* in our statistical model may improve the accuracy of our AD and FA estimations.

As described above, we fit a separate model within each tissue class for each DTI prediction model. Model performance differs by tissue class both within and across DTI measures, as seen by the prediction MSE plots. Across all DTI measures, we predict GM well with respect to the acquired DTI scans. This is likely due to the lack of variation in structured diffusion across the brain in GM. In NAWM, we can accurately predict MD and RD but not AD and FA, again indicating that the model is insufficient for the latter DTI measures or that additional information exists in the AD and FA maps. In lesions, the statistical DTI predictions are generally worse than the acquired DTI predictions for each measure, which may be due to the greater amount of variability in DTI measures within lesions.

In addition, although none of the MS subtype group differences in NAWM are significant, we show that there are more pronounced differences in the statistical MD images than in the acquired MD images. This finding needs further examination in a larger sample which would provide more power to detect true group differences in MD, which has been shown to be sensitive to diffuse and focal white matter pathology as well as changes in the gray matter in MS (Senda et al., 2012, Ontaneda et al., 2014, Harrison et al., 2013).

Implementation of these models as a tool for studying and monitoring MS requires that the images produced are accurate and reproducible. We have shown that the proposed models perform well for the specific imaging protocols used in this study. The fj(v) elements of the model are functions estimated from a large number of voxels whose intensities are known to be highly reproducible (Teipel et al., 2010, Ewers et al., 2006). However, it remains to be shown how the models perform across different DTI protocols and platforms. Such validation studies will be crucial before this methodology can be adopted in the clinic.

5. Conclusions

We have discussed the differences in the performance of our statistical estimation across the four DTI measures and various tissue classes. Although we do not present accurate estimation models for AD or FA maps, we can accurately estimate MD and RD. Thus, we have shown that the information in the latter image types is not unique, and that the information may be captured using statistical methods on conventional imaging. Therefore, in studies that are not interested in anisotropy, or only interested in MD, it may be sufficient to acquire only conventional MRI sequences.

Acknowledgments

We thank Dr. Govind Nair for his insightful comments and discussions about this work. We acknowledge the contribution of the NINDS Neuroimmunology Clinic, which recruited the patients and performed clinical evaluations, and the NIH Functional MRI Facility, where scanning took place. Suttner, Mejia, and Shinohara are partially funded by the NIH grant RO1 NS085211 from the National Institute of Neurological Disorders and Stroke (NINDS) (Z01-NS003119). Shinohara was also partially funded by R21 NS093349. The study was supported in part by the Intramural Research Program of NINDS. This work represents the opinions of the researchers and not necessarily that of the granting organizations.

Appendix A.

Table A.1.

Study sample summary statistics in females.

All MS PPMS RRMS SPMS
n 32 12 12 8
Mean age (SD) 51.5 (12.5) 56.6 (6.8) 44.2 (16.2) 55.0 (7.2)
Disease duration (SD) 15.2 (11.9) 15.2 (11.1) 8.0 (7.3) 26.1 (11.5)
Median EDSS score (range) 2.5 (1.0–6.5) 3.25 (1.5–6.5) 1.5 (1.0–3.5) 6.0 (1.5–6.5)
Open in a new tab

Table A.2.

Study sample summary statistics in males.

All MS PPMS RRMS SPMS
n 18 12 2 4
Mean age (SD) 55.3 (8.9) 56.6 (8.1) 45.8 (7.1) 56.2 (11.0)
Disease duration (SD) 14.2 (8.9) 11.9 (7.7) 7.0 (5.8) 25.0 (2.2)
Median EDSS score (range) 6.0 (1.5–7.5) 6.0 (2.5–7.5) 3.75 (1.5–6.0) 6.5 (2.5–7.0)
Open in a new tab

References

  1. Alexander A.L., Lee J.E., Lazar M., Field A.S. Diffusion tensor imaging of the brain. Neurotherapeutics. Jul. 2007;4(3):316–329. doi: 10.1016/j.nurt.2007.05.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Bakshi R., Benedict R.H.B., Bermel R.A., Caruthers S.D., Puli S.R., Tjoa C.W., Fabiano A.J., Jacobs L. T2 hypointensity in the deep gray matter of patients with multiple sclerosis: a quantitative magnetic resonance imaging study. Arch. Neurol. Jan. 2002;59(1):62–68. doi: 10.1001/archneur.59.1.62. [DOI] [PubMed] [Google Scholar]
  3. Barkhof F. The clinico-radiological paradox in multiple sclerosis revisited. Curr. Opin. Neurol. Jun. 2002;15(3):239–245. doi: 10.1097/00019052-200206000-00003. [DOI] [PubMed] [Google Scholar]
  4. Brass S.D., Benedict R.H.B., Weinstock-Guttman B., Munschauer F., Bakshi R. Cognitive impairment is associated with subcortical magnetic resonance imaging grey matter T2 hypointensity in multiple sclerosis. Mult. Scler. Houndmills Basingstoke Engl. Aug. 2006;12(4):437–444. doi: 10.1191/135248506ms1301oa. [DOI] [PubMed] [Google Scholar]
  5. Carass A., Cuzzocreo J., Wheeler M.B., Bazin P.-L., Resnick S.M., Prince J.L. Simple paradigm for extra-cerebral tissue removal: algorithm and analysis. NeuroImage. Jun. 2011;56(4):1982–1992. doi: 10.1016/j.neuroimage.2011.03.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Chong G., Wahba G. Minimizing gcv/gml scores with multiple smoothing parameters via the Newton method. SIAM J. Sci. Stat. Comput. 1991;12(2):383–398. [Google Scholar]
  7. Ciccarelli O., Werring D.J., Barker G.J., Griffin C.M., Wheeler-Kingshott C.A.M., Miller D.H., Thompson A.J. A study of the mechanisms of normal-appearing white matter damage in multiple sclerosis using diffusion tensor imaging--evidence of Wallerian degeneration. J. Neurol. Mar. 2003;250(3):287–292. doi: 10.1007/s00415-003-0992-5. [DOI] [PubMed] [Google Scholar]
  8. Ewers M., Teipel S.J., Dietrich O., Schönberg S.O., Jessen F., Heun R., Scheltens P., van de Pol L., Freymann N.R., Moeller H.-J., Hampel H. Multicenter assessment of reliability of cranial MRI. Neurobiol. Aging. Aug. 2006;27(8):1051–1059. doi: 10.1016/j.neurobiolaging.2005.05.032. [DOI] [PubMed] [Google Scholar]
  9. Gauthier S.A., Glanz B.I., Mandel M., Weiner H.L. A model for the comprehensive investigation of a chronic autoimmune disease: the multiple sclerosis CLIMB study. Autoimmun. Rev. Oct. 2006;5(8):532–536. doi: 10.1016/j.autrev.2006.02.012. [DOI] [PubMed] [Google Scholar]
  10. Harrison D.M., Shiee N., Bazin P.-L., Newsome S.D., Ratchford J.N., Pham D., Calabresi P.A., Reich D.S. Tract-specific quantitative MRI better correlates with disability than conventional MRI in multiple sclerosis. J. Neurol. Feb. 2013;260(2):397–406. doi: 10.1007/s00415-012-6638-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Jog A., Roy S., Carass A., Prince J.L. Pulse sequence based multi-acquisition MR intensity normalization. Proc. SPIE Int. Soc. Opt. Eng. 2013;8669 doi: 10.1117/12.2007062. (Mar.) [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Jog A., Roy S., Carass A., Prince J.L. Magnetic resonance image synthesis through patch regression. Proc. IEEE Int. Symp. Biomed. Imaging Nano Macro IEEE Int. Symp. Biomed. Imaging. 2013;2013:350–353. doi: 10.1109/ISBI.2013.6556484. (Dec.) [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Kropholler M.A., Boellaard R., van Berckel B.N.M., Schuitemaker A., Kloet R.W., Lubberink M.J., Jonker C., Scheltens P., Lammertsma A.A. Evaluation of reference regions for (R)-[(11)C]PK11195 studies in Alzheimer's disease and mild cognitive impairment. J. Cereb. Blood Flow Metab. Off. J. Int. Soc. Cereb. Blood Flow Metab. Dec. 2007;27(12):1965–1974. doi: 10.1038/sj.jcbfm.9600488. [DOI] [PubMed] [Google Scholar]
  14. Kurtzke J.F. Rating neurologic impairment in multiple sclerosis: an expanded disability status scale (EDSS) Neurology. Nov. 1983;33(11):1444–1452. doi: 10.1212/wnl.33.11.1444. [DOI] [PubMed] [Google Scholar]
  15. Liu Y., Duan Y., He Y., Yu C., Wang J., Huang J., Ye J., Parizel P.M., Li K., Shu N. Whole brain white matter changes revealed by multiple diffusion metrics in multiple sclerosis: a TBSS study. Eur. J. Radiol. Oct. 2012;81(10):2826–2832. doi: 10.1016/j.ejrad.2011.11.022. [DOI] [PubMed] [Google Scholar]
  16. Mejia A., Sweeney E., Dewey B., Nair G., Sati P., Shea C., Reich D.S., Shinohara R.T. Statistical estimation of T1 relaxation time using conventional magnetic resonance imaging. NeuroImage. 2016 doi: 10.1016/j.neuroimage.2015.12.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Michel F., Paragios N. 2010. Image Transport Regression Using Mixture of Experts and Discrete Markov Random Fields; pp. 1229–1232. [Google Scholar]
  18. Mueller S.G., Weiner M.W., Thal L.J., Petersen R.C., Jack C., Jagust W., Trojanowski J.Q., Toga A.W., Beckett L. The Alzheimer's disease neuroimaging initiative. Neuroimaging Clin. N. Am. Nov. 2005;15(4):869–877. doi: 10.1016/j.nic.2005.09.008. (xi–xii) [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Neema M., Arora A., Healy B.C., Guss Z.D., Brass S.D., Duan Y., Buckle G.J., Glanz B.I., Stazzone L., Khoury S.J., Weiner H.L., Guttmann C.R.G., Bakshi R. Deep gray matter involvement on brain MRI scans is associated with clinical progression in multiple sclerosis. J. Neuroimaging Off. J. Am. Soc. Neuroimaging. Jan. 2009;19(1):3–8. doi: 10.1111/j.1552-6569.2008.00296.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Ontaneda D., Sakaie K., Lin J., Wang X., Lowe M.J., Phillips M.D., Fox R.J. Identifying the start of multiple sclerosis injury: a serial DTI study: Prelesion DTI. J. Neuroimaging. Nov. 2014;24(6):569–576. doi: 10.1111/jon.12082. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Pfefferbaum A., Adalsteinsson E., Sullivan E.V. Replicability of diffusion tensor imaging measurements of fractional anisotropy and trace in brain. J. Magn. Reson. Imaging. Oct. 2003;18(4):427–433. doi: 10.1002/jmri.10377. [DOI] [PubMed] [Google Scholar]
  22. Pujol J., Junqué C., Vendrell P., Grau J.M., Martí-Vilalta J.L., Olivé C., Gili J. Biological significance of iron-related magnetic resonance imaging changes in the brain. Arch. Neurol. Jul. 1992;49(7):711–717. doi: 10.1001/archneur.1992.00530310053012. [DOI] [PubMed] [Google Scholar]
  23. Ratchford J.N., Endres C.J., Hammoud D.A., Pomper M.G., Shiee N., McGready J., Pham D.L., Calabresi P.A. Decreased microglial activation in MS patients treated with glatiramer acetate. J. Neurol. Jun. 2012;259(6):1199–1205. doi: 10.1007/s00415-011-6337-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Rocca M.A., Ceccarelli A., Falini A., Tortorella P., Colombo B., Pagani E., Comi G., Scotti G., Filippi M. Diffusion tensor magnetic resonance imaging at 3.0 tesla shows subtle cerebral grey matter abnormalities in patients with migraine. J. Neurol. Neurosurg. Psychiatry. May 2006;77(5):686–689. doi: 10.1136/jnnp.2005.080002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Senda J., Watanabe H., Tsuboi T., Hara K., Watanabe H., Nakamura R., Ito M., Atsuta N., Tanaka F., Naganawa S., Sobue G. MRI mean diffusivity detects widespread brain degeneration in multiple sclerosis. J. Neurol. Sci. Aug. 2012;319(1–2):105–110. doi: 10.1016/j.jns.2012.04.019. [DOI] [PubMed] [Google Scholar]
  26. Shiee N., Bazin P.-L., Ozturk A., Reich D.S., Calabresi P.A., Pham D.L. A topology-preserving approach to the segmentation of brain images with multiple sclerosis lesions. NeuroImage. Jan. 2010;49(2):1524–1535. doi: 10.1016/j.neuroimage.2009.09.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Shinohara R.T., Crainiceanu C.M., Caffo B.S., Gaitán M.I., Reich D.S. Population-wide principal component-based quantification of blood-brain-barrier dynamics in multiple sclerosis. NeuroImage. Aug. 2011;57(4):1430–1446. doi: 10.1016/j.neuroimage.2011.05.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Shinohara R.T., Sweeney E.M., Goldsmith J., Shiee N., Mateen F.J., Calabresi P.A., Jarso S., Pham D.L., Reich D.S., Crainiceanu C.M. Australian imaging biomarkers lifestyle flagship study of ageing, and Alzheimer's disease neuroimaging initiative, “statistical normalization techniques for magnetic resonance imaging. NeuroImage Clin. 2014;6:9–19. doi: 10.1016/j.nicl.2014.08.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Smith A. Western Psychological Services; Los Angeles: 1982. Symbol Digit Modalities Test: Manual. [Google Scholar]
  30. Song S.-K., Sun S.-W., Ramsbottom M.J., Chang C., Russell J., Cross A.H. Dysmyelination revealed through MRI as increased radial (but unchanged axial) diffusion of water. NeuroImage. Nov. 2002;17(3):1429–1436. doi: 10.1006/nimg.2002.1267. [DOI] [PubMed] [Google Scholar]
  31. Teipel S.J., Ewers M., Wolf S., Jessen F., Kölsch H., Arlt S., Luckhaus C., Schönknecht P., Schmidtke K., Heuser I., Frölich L., Ende G., Pantel J., Wiltfang J., Rakebrandt F., Peters O., Born C., Kornhuber J., Hampel H. Multicentre variability of MRI-based medial temporal lobe volumetry in Alzheimer's disease. Psychiatry Res. Jun. 2010;182(3):244–250. doi: 10.1016/j.pscychresns.2010.03.003. [DOI] [PubMed] [Google Scholar]
  32. Teipel S.J., Wegrzyn M., Meindl T., Frisoni G., Bokde A.L.W., Fellgiebel A., Filippi M., Hampel H., Klöppel S., Hauenstein K., Ewers M., EDSD study group Anatomical MRI and DTI in the diagnosis of Alzheimer's disease: a European multicenter study. J. Alzheimers Dis. 2012;31(Suppl. 3):S33–S47. doi: 10.3233/JAD-2012-112118. [DOI] [PubMed] [Google Scholar]
  33. Tjoa C.W., Benedict R.H.B., Weinstock-Guttman B., Fabiano A.J., Bakshi R. MRI T2 hypointensity of the dentate nucleus is related to ambulatory impairment in multiple sclerosis. J. Neurol. Sci. Jul. 2005;234(1–2):17–24. doi: 10.1016/j.jns.2005.02.009. [DOI] [PubMed] [Google Scholar]
  34. van Waesberghe J.H., van Walderveen M.A., Castelijns J.A., Scheltens P., Lycklama G.J., Nijeholt à., Polman C.H., Barkhof F. Patterns of lesion development in multiple sclerosis: longitudinal observations with T1-weighted spin-echo and magnetization transfer MR. AJNR Am. J. Neuroradiol. Apr. 1998;19(4):675–683. [PMC free article] [PubMed] [Google Scholar]
  35. Vollmar C., O'Muircheartaigh J., Barker G.J., Symms M.R., Thompson P., Kumari V., Duncan J.S., Richardson M.P., Koepp M.J. Identical, but not the same: intra-site and inter-site reproducibility of fractional anisotropy measures on two 3.0 T scanners. NeuroImage. Jul. 2010;51(4):1384–1394. doi: 10.1016/j.neuroimage.2010.03.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Vrenken H., Pouwels P.J.W., Geurts J.J.G., Knol D.L., Polman C.H., Barkhof F., Castelijns J.A. Altered diffusion tensor in multiple sclerosis normal-appearing brain tissue: cortical diffusion changes seem related to clinical deterioration. J. Magn. Reson. Imaging. May 2006;23(5):628–636. doi: 10.1002/jmri.20564. [DOI] [PubMed] [Google Scholar]
  37. Werring D.J., Clark C.A., Barker G.J., Thompson A.J., Miller D.H. Diffusion tensor imaging of lesions and normal-appearing white matter in multiple sclerosis. Neurology. May 1999;52(8):1626–1632. doi: 10.1212/wnl.52.8.1626. [DOI] [PubMed] [Google Scholar]
  38. Wilson M., Tench C.R., Morgan P.S., Blumhardt L.D. Pyramidal tract mapping by diffusion tensor magnetic resonance imaging in multiple sclerosis: improving correlations with disability. J. Neurol. Neurosurg. Psychiatry. Feb. 2003;74(2):203–207. doi: 10.1136/jnnp.74.2.203. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Wood S.N. Chapman & Hall/CRC; Boca Raton, FL: 2006. Generalized Additive Models: An Introduction with R. [Google Scholar]
  40. Wood S.N. Fast stable restricted maximum likelihood and marginal likelihood estimation of semiparametric generalized linear models: estimation of semiparametric generalized linear models. J. R. Stat. Soc. Ser. B Stat Methodol. Jan. 2011;73(1):3–36. [Google Scholar]
  41. Ye D.H., Zikic D., Glocker B., Criminisi A., Konukoglu E. Modality propagation: coherent synthesis of subject-specific scans with data-driven regularization. Med. Image Comput. Comput. Assist. Interv. MICCAI Int. Conf. Med. Image Comput. Comput. Assist. Interv. 2013;16(Pt 1):606–613. doi: 10.1007/978-3-642-40811-3_76. [DOI] [PubMed] [Google Scholar]
  42. Zhu T., Hu R., Qiu X., Taylor M., Tso Y., Yiannoutsos C., Navia B., Mori S., Ekholm S., Schifitto G., Zhong J. Quantification of accuracy and precision of multi-center DTI measurements: a diffusion phantom and human brain study. NeuroImage. Jun. 2011;56(3):1398–1411. doi: 10.1016/j.neuroimage.2011.02.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Zivadinov R. Multiple Sclerosis: A Mechanic View. 2016. Role of neuroimaging in multiple sclerosis. [Google Scholar]

Articles from NeuroImage : Clinical are provided here courtesy of Elsevier

RESOURCES