Abstract
In biomedical, data security is the most expensive resource for wireless body area network applications. Cryptographic algorithms are used in order to protect the information against unauthorised access. Advanced encryption standard (AES) cryptographic algorithm plays a vital role in telemedicine applications. The authors propose a novel approach for design of substitution bytes (S-Box) using second-order reversible one-dimensional cellular automata (RCA2) as a replacement to the classical look-up-table (LUT) based S-Box used in AES algorithm. The performance of proposed RCA2 based S-Box and conventional LUT based S-Box is evaluated in terms of security using the cryptographic properties such as the nonlinearity, correlation immunity bias, strict avalanche criteria and entropy. Moreover, it is also shown that RCA2 based S-Boxes are dynamic in nature, invertible and provide high level of security. Further, it is also found that the RCA2 based S-Box have comparatively better performance than that of conventional LUT based S-Box.
Keywords: cellular automata, body area networks, telemedicine, cryptography, security of data, table lookup
Keywords: substitution bytes, S-box, second-order reversible cellular automata, wireless body area network applications, data security, advanced encryption standard, AES cryptographic algorithm, telemedicine applications, second-order reversible one-dimensional cellular automata, RCA2, look-up-table, LUT, cryptographic properties, nonlinearity correlation immunity bias, avalanche criteria
1. Introduction
Cryptography plays a vital role in secure data transmission for wireless body area network (WBAN) applications [1–3]. The cryptographic algorithms are generally based on secret key and public key systems [4]. However at present, a lot of emphasises was made on the secret key system which uses a symmetric key on both encryption as well as decryption. The data encryption standard (DES) algorithm was first published by Federal Information Processing Standards (FIPS) in 1999 [5]. However, it has been vulnerable to many attacks which results in less data security [6]. Moreover in 2001, FIPS selected Rijndael algorithm for advanced encryption standard (AES) as a replacement to DES [7]. The main criteria for choosing Rijndael was its symmetric key length, confusion and diffusion [8]. The AES algorithm has been standardised and adopted in latest IEEE Standard 802.15.6 for WBAN application due to its best performance and security [9].
The substitution bytes (S-Box) in AES algorithm plays an important role as it provides confusion in the cipher text [10, 11]. The basic function of S-Box is to transforms the 8 bits input data into 8 bits secret data using a precomputed look-up-table (LUT). Traditionally, the conventional S-Box architectures used in AES algorithm are based on LUT's which demands large number of memory cells. Moreover, the conventional LUT based S-Boxes are also not secure enough against differential cryptographic attacks due to rigid architecture [12]. The works so far reported in the literature above mainly emphasised only on cryptanalysis of S-Box. On the other hand, there is a need to develop alternative architecture of S-Box, which is sufficiently secure against cryptanalysis, dynamic in nature with low hardware complexity which results in less power dissipation. The WBAN applications demand a ultra-low energy architecture for AES to increase the life time of battery.
In this Letter, we proposed a flexible and dynamic S-Box architecture using RCA2 in order to overcome the limitations of the classical S-Box. We also analysed the level of security provided by classical LUT based S-Box and proposed RCA2 based S-Box of AES algorithm using cryptographic properties such as strict avalanche criterion, input/output entropy, nonlinearity, correlation immunity bias (CIB).
This Letter is organised as follows. In Section 2 the concept of AES algorithm is revisited. The basic of cellular automata (CA) is discussed in Section 3. Formulation of RCA2 based S-Box is discussed in Section 4. Furthermore, the performance of LUT based S-Box and RCA2 based S-Box is evaluated using cryptographic properties in terms of security in Section 5. Section 6 concludes the Letter.
2. Method
The AES is a symmetric block cipher algorithm with secret key. The length of the secret key recommended by the latest IEEE Standard 802.15.6 for WBAN application is 128 bits [9]. The AES algorithm consists of four transformations, namely, the S-Box, ShiftRows (SR), MixColumns (MC) and AddRoundKey (ARK) by which it generates cipher text over data in order to provide enough security [13]. The AES algorithm encryption and decryption process is shown in Fig. 1, the number of rounds of transformations is given by
| (1) |
Using (1), the AES with 128 bits secret key algorithm results a total of ten rounds, out of which from 1 to Nr − 1 rounds have four transformations S-Boxes, SR, MC and ARK except the last Nr round have only three transformations S-Box, SR and ARK. The input bits are arranged in 4 × 4 matrix of bytes known as state array and each column as well as row are known as a word.
Fig. 1.
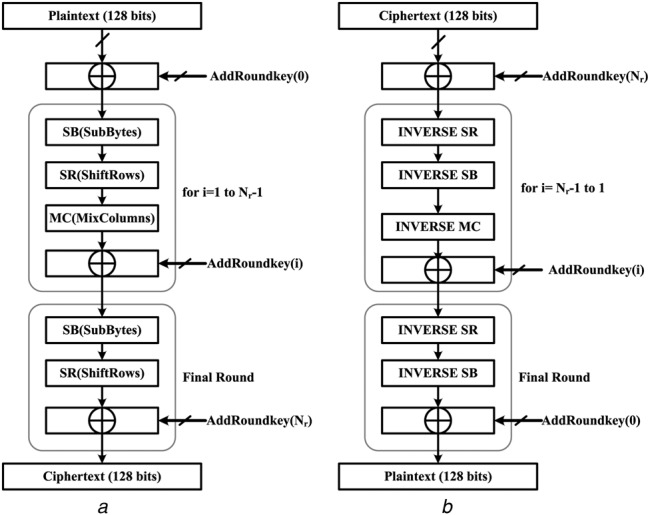
Sequential flow of AES encryption
a Encryption
b Decryption
2.1. SubBytes
In S-Box transformation, each element (byte) of input data is substituted with another data (byte) using precomputed LUTs as shown in Table 1. These S-Boxes are computed by the multiplicative inverse of each element in the state using GF(28) with an irreducible polynomial and followed by an affine transformation. In order to transform 128-bit input data, a total of 16 ROM structures of S-Box are utilised which enormously increase the hardware complexity in the AES algorithm. The new developing cryptanalysis makes the ROM structure more prone to attacks [12]. However, in order to overcome the limitation, we proposed a RCA2 based S-Box which is cryptographically secure against cryptanalysis and also it is dynamic in nature. The LUT based S-Box in hexadecimal form is represented in Table 1. For example, if the input data is c6, then the substituted value of S-Box is determined from Table 1 by the intersection of c row and 6 column which results in b4.
Table 1.
LUT based S-Box
| y | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | a | b | c | d | e | f | |
| 0 | 63 | 7c | 77 | 7b | f2 | 6b | 6f | c5 | 30 | 01 | 67 | 2b | fe | d7 | ab | 76 | |
| 1 | ca | 82 | c9 | 7d | fa | 59 | 47 | f0 | ad | d4 | a2 | af | 9c | a4 | 72 | c0 | |
| 2 | b7 | fd | 93 | 26 | 36 | 3f | f7 | cc | 34 | a5 | e5 | f1 | 71 | d8 | 31 | 15 | |
| 3 | 04 | c7 | 23 | c3 | 18 | 96 | 05 | 9a | 07 | 12 | 80 | e2 | eb | 27 | b2 | 75 | |
| 4 | 09 | 83 | 2c | 1a | 1b | 6e | 5a | a0 | 52 | 3b | d6 | b3 | 29 | e3 | 2f | 84 | |
| 5 | 53 | d1 | 00 | ed | 20 | fc | b1 | 5b | 6a | cb | be | 39 | 4a | 4c | 58 | cf | |
| 6 | d0 | ef | aa | fd | 43 | 4d | 33 | 85 | 45 | f9 | 02 | 7f | 50 | 3c | 9f | a8 | |
| 7 | 51 | a3 | 40 | 8f | 92 | 9d | 38 | f5 | bc | b6 | da | 21 | 10 | ff | f3 | d2 | |
| 8 | cd | 0c | 13 | ec | 5f | 97 | 44 | 17 | c4 | a7 | 7e | 3d | 64 | 5d | 19 | 73 | |
| 9 | 60 | 81 | 4f | dc | 22 | 2a | 90 | 88 | 46 | ee | b8 | 14 | de | 5e | 0b | db | |
| a | e0 | 32 | 3a | 0a | 49 | 06 | 24 | 5c | c2 | d3 | ac | 62 | 91 | 95 | e4 | 79 | |
| b | e7 | c8 | 37 | 6d | 8d | d5 | 4e | a9 | 6c | 56 | f4 | ea | 65 | 7a | ae | 08 | |
| c | ba | 78 | 25 | 2e | 1c | a6 | b4 | c6 | e8 | dd | 74 | 1f | 4b | bd | 8b | 8a | |
| d | 70 | 3e | b5 | 66 | 48 | 03 | f6 | 0e | 61 | 35 | 57 | b9 | 86 | c1 | 1d | 9e | |
| e | e1 | f8 | 98 | 11 | 69 | d9 | 8e | 94 | 9b | 1e | 87 | e9 | ce | 55 | 28 | df | |
| f | 8c | a1 | 89 | 0d | bf | e6 | 42 | 68 | 41 | 99 | 2d | 0f | b0 | 54 | bb | 16 | |
2.2. ShiftRows
The transformation is used to create diffusion in cipher text by shifting of elements by one byte. The bytes in the first row remain unchanged whereas the second, third and fourth rows are shifted to the left by 1, 2, 3 bytes, respectively.
2.3. MixColumns
This transformation is used for attaining diffusion in the block cipher and a column operation where each column is expressed as a four term polynomial over GF(28) field and multiplied by fixed polynomial with Modulo x4 + 1. Mathematically, these operations are written in matrix form as follows, where 0 ≤ C < 4
| (2) |
| (3) |
2.4. AddRoundKey
In ARK transformation, the round cipher keys are generated in the key expansion by bitwise XOR operation. After key schedule in key expansion, the key can be divided into 11 groups of 4 byte words. The first 4 byte word is the initial 128-bit secret key and subsequent keys are generated in the key expansion using SubWord, Rotation Word (RotWord) and Rcon. Each ARK is four words output from the key expansion block denoted by ARK , where i = 0 to Nr. SubWord means nonlinear transformation of each byte of key using S-Box. The RotWord is a cyclic left shift of each byte in a word by one byte. Rcon is an array of constant words and the left most byte in a word is non-zero involved in direct XOR operation with the plain text and rest of the ten rounds use subsequent four words for the generation of ARKs.
3. Basics of CA
The basic CA structure is shown in Fig. 2, which consists of a groups of cells with a finite size of length from S0 to S7 which evolve using deterministic rule with each cell can store one of the two states 0 and 1. If the right most and left most (extreme) cells of this CA structure are considered to be adjacent to each other, then the CA is called as circular boundary CA. The one-dimensional (1D) circular boundary CA evolves with different neighbourhood configurations of elementary CA [14]. Each elementary CA consists of central cell i which is surrounded by neighbourhood cells of a defined radius r, therefore the total number of cells in elementary CA is given as ni = 2r + 1, including the central cell i. We considered r = 1, which results in the total number of possible different neighbourhood configurations of elementary CA L = 2ni with , , cells. The next state of the cell i at time (t + 1) depends on the current state of central cell i and also neighbourhood i + 1, i − 1 cells, respectively, at time t with a deterministic rule of function fp. Mathematically, can be expressed as
| (4) |
Fig. 2.
Lattice structure of CA
The function fp is referred as deterministic rule which is represented by decimal form in Table 2. The total number of deterministic rules considered are given by 2L = 256 where L = 2ni. The next state of central cell at a time step t + 1 depends on the central cell and neighbouring cells with a defined rule fp.
Table 2.
Truth table for rules 90 and 75
| 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 | ||
|---|---|---|---|---|---|---|---|---|---|
| 111 | 110 | 101 | 100 | 011 | 010 | 001 | 000 | ||
| rule 90 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | decimal 90 |
| rule 75 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | decimal 75 |
If the rule in CA are derived using EXOR logic and/or EXNOR logic, then it is called as additive CA. The additive CA is used in bit-error correcting code, very large scale integration (VLSI) testing and data encryption. If all the cells in CA evolve using the same deterministic rule, then the CA is said to be uniform CA. The dynamic nature of 1D periodic uniform CA depends on deterministic rule fp and the number of iterations.
4. Formulation of S-Box using second-order reversible 1D CA
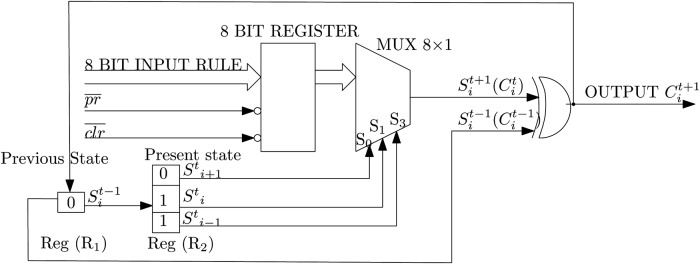
The basic function of S-Box is transforming one byte of input data to another one byte secret data using predefined LUT. The truth table of S-Box is basically a function f: Bn → Bm. The LUT based S-Box architecture requires more memory cells and these S-Boxes are more prone to differential cryptanalysis due to absence of dynamic in nature [12]. In order to meet the requirements of WBAN, in this Letter, we proposed a reversible CA based S-Box realisation which is dynamic in nature and cryptographically secure compared with that of classical S-Box. A CA is said to be first-order 1D CA, if the next configuration is the function of defined rule and present neighbourhood configuration , , cells. The reversibility of 1D CA system of a given length in each output state is based on rules and the output can be realised using Boolean function [15]. If the function is invertible then the rule is reversible which is a desired property in cryptography. If the Boolean function is not one on one, then a value in the range set can map to many values in domain set, which in the process of decryption the plain text is not retrieved from the cipher text. We observed that in the first-order 1D CA only six rules are reversible. Moreover to overcome the limitations, we proposed RCA2 in which there are 64 reversible rules and the mapping of Boolean function is one on one. The basic function of RCA2 based S-Box is to transform 8 bits input data to another secret data using a combinational logic. The block diagram of proposed RCA2 based S-Box shown in Fig. 3 indicates vectors composed of length of the secret key, deterministic rule for encryption or decryption, number of time steps and size of the lattice. The 8 bits input data for RCA2 based S-Box is iteratively computed from 1 to 50 time steps using a defined deterministic rule and 8 bits input secret key. The structure of RCA2 is slightly different as that of first-order 1D CA, the results obtained with first-order 1D CA are XORed with the previous value of the central cell i at time step t − 1 in order to achieve the new configuration of RCA2 at a time step t + 1. The next configuration of central for RCA2 at t + 1 depends not only on present cell but also on the previous cell , as shown in Fig. 4. Mathematically, the RCA2 is represented by
| (5) |
where , respectively, at discrete time step t + 1 and t–1. The switches of multiplexer are activated and deactivated according to the control signals (input secret key) and the output of multiplexer is mapped according to the stored 8 bits rule in the register with the control signals as shown in Fig. 4. Initially, the 8 bits register is loaded with a deterministic rule, the register R1, R2 are used to store the secret key and the secret key of register R2 used as control signal to the multiplexer. The output of the multiplexer is XORed with the previous value stored in the register R1 iteratively. The RCA2 structure is based on combinational logic and control signals as shown in Fig. 4. The output of the combinational logic depends on the control signals. The control signal used in RCA2 can dynamically implement various functions according to the different rules. This makes the RCA2 dynamic in nature as the rule can be changed at any instant of time subsequently the output of multiplexer also changes accordingly (Fig. 5).
Fig. 3.
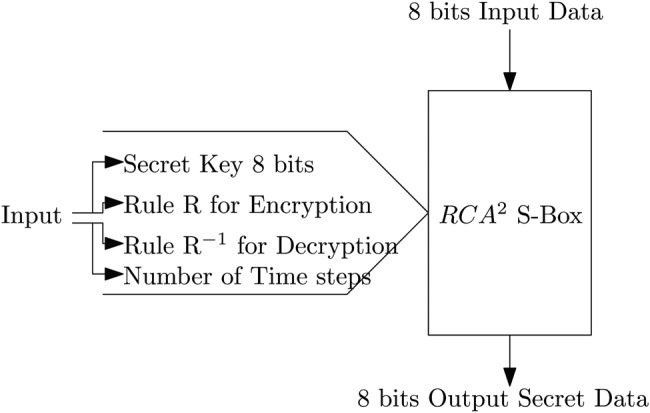
Block diagram of RCA2 based S-Box
Fig. 4.
Structure of RCA2 using a rule
Fig. 5.

RCA2 with 256 rules
In RCA2 algorithm, D is the initial data loaded on the array of registers, fp is the input rule vector ranging from [1:256] and NOI means the number of iterations [1:50] and S0–S7 is defined as size of the lattice. Hence, in RCA2 algorithm there exists 28 possible random initial states which are taken into consideration. However, the 8-bit random initial states of RCA2 evolve using different 256 deterministic rules and number of iterations which are considered from time step 1 to 50. There exist a relationship between time step t and group of CA cells S0–S7 in a lattice as the variation of output is high if the time step t ≥ size of the lattice.
5. Results and discussions
The functioning of S-Box is to map 8 input bits to 8 output bits using predefined table known as LUT μ : GF(Bn) GF(Bm) [16]. Mathematically, the LUT based S-Box and RCA2 based S-Box are derived using Boolean function in order to study the level of security using cryptographic properties. In cryptography, the Boolean function used to encrypt the plain data must be diverse and mapping from input to output should be one on one, so as to provide enough security and proper decryption. Finally, the 28 output bits are transformed into a single output bit using Boolean function fi: Bn → B. In a S-Box, if μ: Bn → Bm and hence there exists m number of function μ = {f1, f2, …, fm}, where i ∈ [1, m]. The truth table in polarity form is written as follows:
| (6) |
fβ is a Boolean function of the linear combination of m functions , i ≤ m, where αi ∈ Bm are coefficient of the linear function.
The RCA2 based S-Boxes are flexible, dynamic in nature and more resistant to differential cryptanalysis as these provide enough level of security compared with that of LUT based S-Box. We considered size of the RCA2 lattice to be 8 bits, the secret key of 8 bits and examined with different 256 number of rules for 28 different combinations of 8 bit lattice iteratively from 1 to 50 time steps. The level of security of S-Box is observed using the cryptographic properties, namely, the CIB, strict avalanche criteria (SAC), nonlinearity and entropy. If an S-Box satisfies these cryptographic properties then the S-Box is cryptographically secure against cryptanalysis. The observed boundary values of nonlinearity, CIB, strict avalanche criterion and entropy for a standard LUT based S-Box of AES algorithm are presented in Table 3. It is clear from Table 3 that the proposed RCA2 based S-Box attained 10% better nonlinearity compared with that of Clark et al. [18], Millan [19] and Nedjah and Mourelle [20]. The value of CIB is 15% better than that of Clark et al. [18]. The attained value of nonlinearity and SAC for proposed RCA2 based S-Box are comparatively better than Hussain et al. [17].
Table 3.
Cryptographic property values for RCA2 based S-Box and LUT based S-Box
| RCA2 rule no. | Time step | Nonlinearity | Entropy | CIB | SAC |
|---|---|---|---|---|---|
| RCA2 rule 30 | 13 | 100 | 0.9872 | 17 | 16 |
| RCA2 rule 57 | 9 | 106 | 0.9914 | 14 | 16 |
| RCA2 rule 86 | 24 | 101 | 0.9857 | 18 | 16 |
| RCA2 rule 99 | 9 | 106 | 0.9914 | 14 | 16 |
| RCA2 rule 135 | 13 | 100 | 0.9857 | 18 | 16 |
| RCA2 rule 149 | 16 | 104 | 0.9823 | 20 | 16 |
| RCA2 rule 169 | 12 | 104 | 0.9857 | 18 | 16 |
| RCA2 rule 225 | 12 | 101 | 0.9840 | 19 | 16 |
| Hussain et al. [17] | NA | 105 | NP | NP | 16 |
| 96 | NP | NP | 10 | ||
| Clark et al. [18] | NA | 90 | NP | 19 | 44 |
| 100 | NP | 24 | 48 | ||
| Millan [19] | NA | 80 | NP | NP | 16 |
| NP | NP | 18 | |||
| Nedjah and Mourelle [20] | NA | 70 | NP | NP | NP |
| 102 | NP | NP | NP | ||
| standard AES S-Box | NA | 112 | 0.9887 | 16 | 14 |
NA, not applicable; NP, not provided.
5.1. Strict avalanche criteria
If one input bit is changed in a Boolean function, then half of the output bits should be changed [21]. For a Boolean function, if f is to satisfy SAC the following condition, should be balanced, where the Hamming weight of α is 1 and SAC is represented by
| (7) |
Bn consists of all the possible inputs in the n variable function which is basically 2n different inputs consisting of all the elements in Bn whose Hamming weight is 1
| (8) |
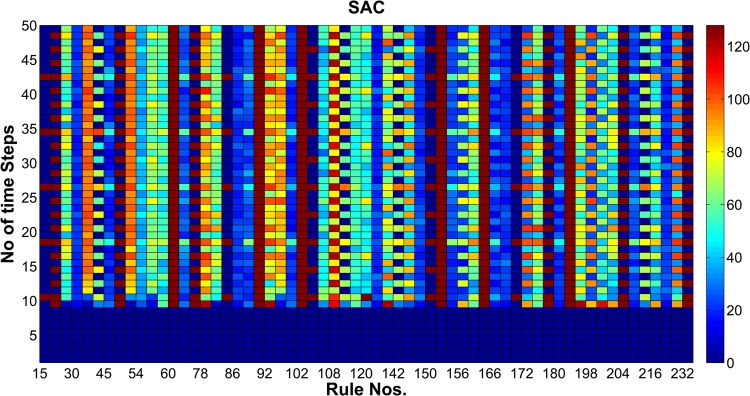
If the value of SAC is less, then the observed cipher is secure enough against cryptographic attacks. We infer that the achieved value of SAC is best for rule numbers 30, 45, 89, 90, 141 as shown in Fig. 6. Moreover, we found that 31.0323% RCA2 rules out of 256 had better SAC value than that of LUT based S-Box as shown in Table 3.
Fig. 6.
Value of SAC for RCA2 based AES S-Box
5.2. Entropy
This property provides us the amount of information in the input bits, when output bit are already known [22]. There exists 2n possible inputs and 2m outputs for a Boolean function of n input and m output. The input/output bit to bit entropy of S-Box is computed with and represented by HS
| (9) |
where Pi is the fraction of ones in the output side
| (10) |
| (11) |
where is the entropy corresponding to the probability .
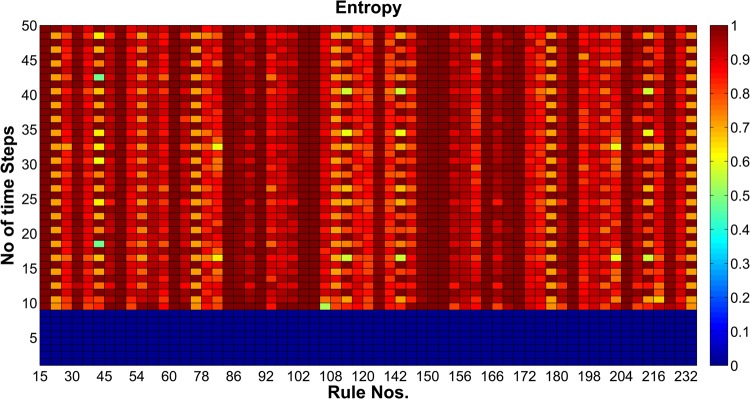
For an observed cipher, if the entropy value is high then the data is highly secure. The best value observed for entropy is 0.9972 as shown in Fig. 7 and also best values of entropy are achieved at rule numbers 30, 57, 86, 99, 135, 149 which are presented in Table 3. We also found that for RCA2 based S-Box 26.0323% out of 256 RCA2 rules have better entropy value than that of standard LUT based S-Box.
Fig. 7.
Values of entropy for RCA2 based AES S-Box
5.3. Nonlinearity
The nonlinearity of a Boolean function is the minimum distance from the function to the set of affine functions and nonlinearity is represented by
| (12) |
where An is the set of all the affine function
| (13) |
where η, β represent the binary sequence of f, g, respectively, and 〈η, β〉 define the scalar product of sequence. Hence, for a function f: Bn → B
| (14) |
where βj belongs to sequence of all linear functions
| (15) |
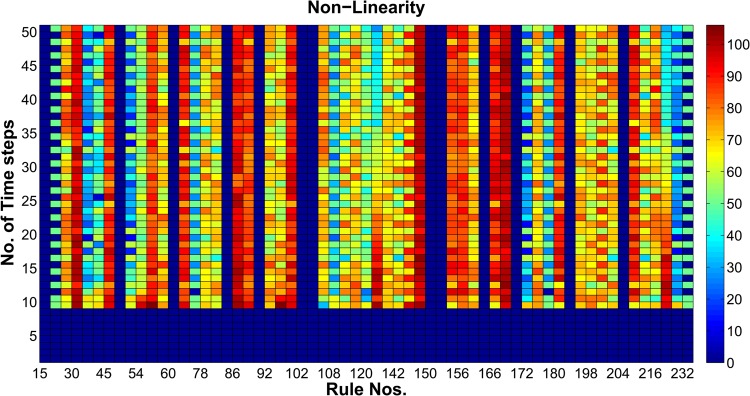
The cipher is highly secure if the nonlinearity value is high. We observed that the value of nonlinearity is high for rules 30, 85, 147, 166 and also found that 6.098% out of 256 RCA2 rules have higher values of nonlinearity. The maximum value of nonlinearity attained was 106 in case of RCA2 based S-Box as presented in Table 3.
5.4. Correlation immunity bias
A Boolean function is said to satisfy CIB of order l, if it is statistically independent of combination of any l input bits. Mathematically, if l input bits are fixed then we can get n Cl2l g functions. So for f: Bn → B, the CIB is represented as
| (16) |
where belongs to the Hamming weight of all the possible functions keeping m bits in the function f fixed. W(f) corresponds to the Hamming weight of function f
| (17) |
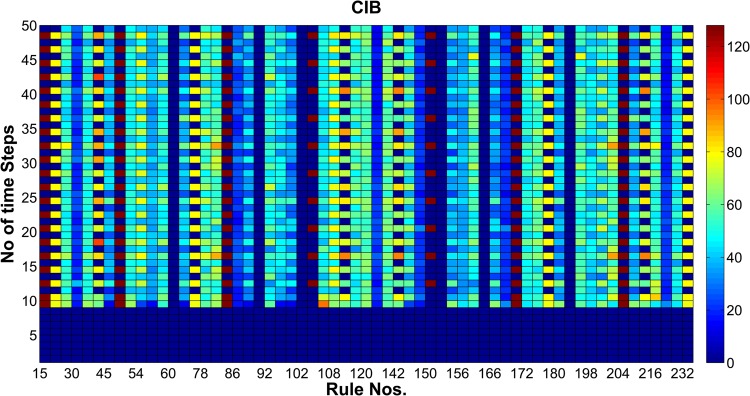
If the achieved CIB value is low then the cipher is cryptographically secure. The values of CIB are found to be better at rule numbers 30, 178, 195, 216 and also found that 36.3548% out of 256 RCA2 rules had better value of CIB, as indicated in Fig. 9. Moreover, we observed that the results of nonlinearity, CIB, entropy and SAC for RCA2 based S-Box are comparatively better than that of classical LUT based S-Box. The value of SAC, CIB, nonlinearity and entropy of RCA2 based S-Box is presented along with few reversible rules in Table 3. The process overhead to compute (number of time steps) proposed RCA2 based S-Box depends on the specified number of iterations. As WBAN applications deal with low-frequency biomedical signals, the process overhead incurred will not affect the overall performance of the system [9].
Fig. 8.
Value of nonlinearity for RCA2 based AES S-Box
Fig. 9.
Value of CIB for RCA2 based AES S-Box
6. Conclusion
We proposed a RCA2 based S-Box for AES algorithm to overcome the limitations of standard classical LUT based S-Box. In future, proposed RCA2 based S-Box can be implemented using complementary metal–oxide–semiconductor technology library cells in order to evaluate low power dissipation and less energy consumption for WBAN application. The classical S-Box has been designed using predefined LUTs which are more prone to cryptographic attacks. Moreover, the proposed RCA2 based S-Box eliminates inefficient memory tables and possibility to create an S-Box, which are dynamic in nature and also cryptographically secure than the conventional S-Box used in AES. The comparative analysis with respect to level of security for LUT based conventional S-Box and RCA2 based S-Box was evaluated using cryptographic properties. Therefore, it has been observed that the values corresponding to RCA2 based S-Box outperform that of LUT based S-Box realisations.
7. Funding and Declaration of Interests
Conflict of interest: None declared.
8 References
- 1.Kamal A., Islam M.M.: ‘Facilitating and securing offline e-medicine service through image steganography’, Healthc. Technol. Lett., 2014, 1, (2), pp. 74–79 (doi: ) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lewy H.: ‘Wearable technologies – future challenges for implementation in healthcare services’, Healthc. Technol. Lett., 2015, 2, (1), pp. 2–5 (doi: ) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Kumar M.: ‘Security issues and privacy concerns in the implementation of wireless body area network’. 2014 Int. Conf. on Information Technology (ICIT), December 2014, pp. 58–62 [Google Scholar]
- 4.Alam M., Ghosh S., Mohan M., et al. : ‘Effect of glitches against masked AES S-box implementation and countermeasure’, IET Inf. Secur., 2009, 3, (1), pp. 34–44 (doi: ) [Google Scholar]
- 5.National Institute of Standards and Technology: ‘FIPS PUB 46-3: data encryption standard (DES)’, October 1999, supersedes FIPS 46-2
- 6.Zodpe H., Wani P., Mehta R.: ‘Design and implementation of algorithm for des cryptanalysis’. 2012 12th Int. Conf. on Hybrid Intelligent Systems (HIS), December 2011, pp. 278–282 [Google Scholar]
- 7.Advanced Encryption Standard (AES): ‘Federal information processing standards publication 197 Std., 2011’, 26 November 2001
- 8.Al-Haj A., Abandah G., Hussein N.: ‘Crypto-based algorithms for secured medical image transmission’, IET Inf. Secur., 2015, 9, (6), pp. 365–373 (doi: ) [Google Scholar]
- 9.IEEE Standard for local and metropolitan area networks – part 15.6: wireless body area networks, Std., February 2012
- 10.Kuo H., Verbauwhede I.: ‘Architectural optimization for a 1.82 Gbits/sec VLSI implementation of the AES Rijndael algorithm’. Cryptographic Hardware and Embedded Systems CHES 2001, 2001 (LNCS, 2162), pp. 51–64 [Google Scholar]
- 11.Li H.: ‘Efficient and flexible architecture for AES’, IEE Proc., Circuits Devices Syst., 2006, 153, (6), pp. 533–538 (doi: ) [Google Scholar]
- 12.Bechtsoudis A., Sklavos N.: ‘Side channel attacks cryptanalysis against block ciphers based on FPGA devices’. 2010 IEEE Computer Society Annual Symp. on VLSI (ISVLSI), July 2010, pp. 460–461 [Google Scholar]
- 13.Bahrak B., Aref M.-R.: ‘Impossible differential attack on seven-round AES-128’, IET Inf. Secur., 2008, 2, (2), pp. 28–32 (doi: ) [Google Scholar]
- 14.Gangadari B.R., Ahamed S.R., Mahapatra R., et al. : ‘Design of cryptographically secure AES S-Box using cellular automata’. 2015 Int. Conf. on Electrical, Electronics, Signals, Communication and Optimization (EESCO), January 2015, pp. 1–6 [Google Scholar]
- 15.A New Kind of Science. Champaign, Ilinois, US, United States: Wolfram Media Inc., 2002
- 16.Rothaus O.: ‘On bent functions’, J. Comb. Theory A, 1976, 20, (3), pp. 300–305 (doi: ) [Google Scholar]
- 17.Hussain I., Shah T., Gondal M.A., et al. : ‘Construction of cryptographically strong 8 × 8 S-Boxes’, World Appl. Sci. J., 2011, 13, (11), pp. 2389–2395 [Google Scholar]
- 18.Clark J.A., Jacob J.L., Stepney S.: ‘The design of sboxes by simulated annealing’, New Gener. Comput., 2005, 23, (3), pp. 219–231 (doi: ) [Google Scholar]
- 19.Millan W.: ‘How to improve the nonlinearity of Bijective S-Boxes’. Proc. Third Australasian Conf. on Information Security and Privacy, ser. ACISP ’98, London, UK, 1998, pp. 181–192 [Google Scholar]
- 20.Nedjah N., Mourelle L.D.M.: ‘Designing substitution boxes for secure ciphers’, Int. J. Innov. Comput. Appl., 2007, 1, (1), pp. 86–91 (doi: ) [Google Scholar]
- 21.Webster A., Tavares S.: ‘On the design of S-Boxes’. Advances in Cryptology CRYPTO 85 Proc., 1986 (LNCS, 218), pp. 523–534 [Google Scholar]
- 22.Adams C., Tavares S.: ‘Good S-Boxes are easy to find’. Advances in Cryptology ‘CRYPTO’ Proc., 1990 (LNCS, 435), pp. 612–615 [Google Scholar]