Effects of Stone Size on the Comminution Process and Efficiency in Shock Wave Lithotripsy

Abstract

The effects of stone size on the process and comminution efficiency in shock wave lithotripsy (SWL) are investigated by experiments, numerical simulations, and scale analysis. Cylindrical BegoStone phantoms with approximately equal height and diameter of either 4-, or 7- or 10-mm, in a total aggregated mass of about 1.5 g, were treated in an electromagnetic shock wave lithotripter field. The resultant stone comminution (SC) was found to correlate closely with the average peak pressure, P_+(avg), incident on the stones. The P_+(avg) threshold to initiate stone fragmentation in water increased from 7.9 to 8.8 to 12.7 MPa, respectively, when the stone size decreased from 10 to 7 to 4 mm. Similar changes in the P_+(avg) threshold were observed for the 7- and 10-mm stones treated in 1,3-butanediol where cavitation is suppressed, suggesting that the observed size dependency is due to changes in stress distribution within different size stones. Moreover, the slope of the correlation curve between SC and $\ln \left({\stackrel{‒}{P}}_{+\left(avg\right)}\right)$ in water increased with decreasing stone size, while the opposite trend was observed in 1,3-butanediol. The progression of stone comminution in SWL showed a size-dependency with the 7- and 10-mm stones fragmented into progressively smaller pieces while a significant portion (> 30%) of the 4-mm stones were stalemated within the size range of 2.8 ~ 4 mm even after 1,000 shocks. Analytical scaling considerations suggest size-dependent fragmentation behaviour, a hypothesis further supported by numerical model calculations that exhibit changing patterns of constructive and destructive wave interference, and thus variations in the maximum tensile stress or stress integral produced in cylindrical and spherical stone of different sizes.

INTRODUCTION

Following the original Dornier HM3, contemporary shock wave lithotripters have evolved progressively in the technologies for shock wave generation, focusing, patient coupling, imaging, and overall functionality of the system (Rassweiler et al. 1992; Lingeman 1997). Despite this, the efficiency of shock wave lithotripsy (SWL) has not improved appreciably in the past two decades (Graber et al. 2003; Gerber et al. 2005; Lingeman et al. 2009). This lack of progression in SWL efficacy has been attributed, in part, to an incomplete understanding of the fundamental mechanisms and associated dynamic processes responsible for stone comminution (SC), as well as identification of key lithotripter field parameters (Lingeman et al. 2003; Zhong 2013) and other factors such as coupling interface quality (Lingeman et al. 2003; Pishchalnikov et al. 2006; Leighton and Cleveland 2010) that may influence the treatment outcome.

Multiple mechanisms of stone fragmentation have been proposed, including spalling (Chaussy et al. 1980; Whelan and Finlayson 1988; Lubock 1989), cavitation (Coleman et al. 1987; Crum 1988; Holmer et al. 1991), compression-induced tensile failure (Chaussy et al. 1980; Chaussy 1982; Lokhandwalla and Sturtevant 2000), quasi-static squeezing (Eisenmenger 2001) and dynamic squeezing with emphasis on shear wave generation (Sapozhnikov et al. 2007). Among them, spalling (Xi and Zhong 2001; Mihradi et al. 2004), cavitation (Zohdi and Szeri 2005) and shear wave stress (Cleveland and Sapozhnikov 2005) have been shown to depend critically on the size or geometry of the stone. Furthermore, acoustic pulse energy E_eff (Koch and Grunewald 1989; Granz and Köhler 1992; Delius et al. 1994; Eisenmenger 2001) and peak average pressure (P_+(avg)) incident on the stone (Smith and Zhong 2012) are two of the lithotripter field parameters that have been correlated with SC. However, the size dependency in the thresholds of P_+(avg) and E_eff required to initiate stone fragmentation has not been investigated.

This study is motivated by the general observation that the rate of stone comminution during SWL is not uniform (Smith and Zhong 2013), but rather characterized by a rapid initial increase to a maximum within a few hundred shocks, followed by a slow progressive decay within a few thousand shocks towards the end of treatment (Zhong 2013). When a stone is disintegrated, the refraction of the incident lithotripter shock wave (LSW) into the resulting fragments and the interaction of different stress waves inside the stone material will change (Xi and Zhong 2001), leading to varied stone comminution rates (Xi and Zhong 2001; Zhong 2013). Similarly, reflection of the LSW from the fragments and its impact on cavitation produced in the surrounding fluid may also change as the treatment progresses (Calvisi et al. 2008; Iloreta et al. 2008). These two fundamental and constantly evolving processes in SWL, coupled with the continuing change in the intrinsic (i.e., pre-existing) flaw distribution inside the residual stone and the extrinsic flaw population created by cavitation bubbles on the surface of the fragments (both are being further disintegrated as the treatment progresses) will dictate the overall comminution processes (Zhong 2013). Furthermore, treatment strategy will influence how these two critical processes may eventually contribute to the SWL outcome (Zhou et al. 2004; Maloney et al. 2006; Pishchalnikov et al. 2006). Although stress waves and cavitation can act synergistically in SWL to produce effective SC (Zhu et al. 2002), the influence of continuously evolving fragment size during SWL on treatment progression and outcome is largely unknown.

Insight into the relative importance of various fragmentation mechanisms has been sought by numerical modeling of the propagation of acoustic pulses into kidney stone simulants. Finite difference studies of two-dimensional elasticity models (Dahake and Gracewski 1997a; Dahake and Gracewski 1997b), ray tracing analysis (Xi and Zhong 2001), and numerical studies based on finite element method (Mihradi 2006) highlighted the importance of focusing effects induced by stone geometry. Axisymmetric finite difference models (Cleveland & Sapozhnikov, 2005) refined previous studies by consideration of the realistic strain rates produced by rapid lithotripter pulse rise time. Additional studies with the same numerical model in combination with experiments (Sapozhnikov et al. 2007) assessed the role of various possible stone breakup mechanisms, and showed that tensile stress induced by shear waves emanating from the lateral boundary of cylindrical U30 stones (placed at the lithotripter focus with its flat surfaces aligned parallel to the incident LSW front) dominates over spallation mechanism in the creation of the first fracture in the posterior region of the stone. Furthermore, fracture of individual cylindrical stones in a lithotripter field was analyzed by using a finite element model that incorporates cohesive interface elements, and the results were compared to experimental observations (Mota et al. 2006).

This study combines experiment, scaling analysis, and numerical simulation to investigate the effect of stone size on the comminution process and efficiency in SWL. Comminution experiments were carried out using artificial kidney stones in different size groups either individually, or in groups with approximately matched total mass. Similarity theory considerations are invoked to assess the possibility of self-similar behavior in LSW-stone interaction upon a change of scale. Numerical simulations of the refraction or reflection of an incident pressure pulse by isolated, single stones of different shape and size illustrate the origin of various stress waves, and how their interactions may lead to the maximum tensile stress or stress integral produced inside the stone. The numerical results are discussed in comparison with the experimental observations.

MATERIALS AND METHODS

To assess the effect of stone size on comminution efficiency, artificial kidney stones of cylindrical shape with approximately equal diameter and height (4, 7, 10 mm) were prepared from BegoStone Plus (BEGO USA, Lincoln, RI) with a powder-to-water mixing ratio of 5:1. These artificial stones mimic the acoustic and mechanical properties of calcium oxalate monohydrate and brushite stones, which are known to be difficult to fragment in SWL (Dretler 1988; Zhong et al. 1993; ZHONG and PREMINGER 1994; Liu and Zhong 2002; Esch et al. 2010). To reduce the influence of stone mass on treatment outcome, either one 10-mm^‡ stone (~1.50 g), or three 7-mm stones (~3 × 0.40 = 1.20 g) or fourteen 4-mm stones (~14 × 0.11 = 1.54g) were used in each experiment so that the total mass of the stone materials in each group was approximately matched. In addition, experiments employing single cylindrical stones of different sizes (4 or 7 or 10 mm) were carried out at the lithotripter focus to determine the number of shocks required to produce the first fracture so that the results can be directly compared with numerical model calculations.

Stone fragmentation tests were conducted using an electromagnetic (EM) shock wave generator, similar to those used in Siemens Modularis lithotripters, mounted at the bottom of a Lucite tank (L × W × H = 40 × 40 × 30 cm) filled with 0.2 µm-filtered and degassed water (<3 mg/L O₂ concentration, 23°C) (Smith and Zhong 2012). The shock wave generator was operated at 14 kV with a pulse repetition frequency (PRF) of 1 Hz, corresponding to a peak pressure of 46 MPa and a −6 dB focal width of about 8 mm. As shown in Fig. 1, stones placed in a flat-base tube holder (inner diameter = 14 mm) were aligned to different positions in the lithotripter field using a 3-D positioning system (VXM-2 step motors with BiSlide-M02 lead screws, Velmex, Bloomfield, NY) so that stone comminution produced at different pressure levels could be assessed. The tube holder was filled with either water or 1,3-butanediol to discern the contribution of cavitation to stone comminution (Smith and Zhong 2012). The lithotripter field was characterized by using a fiber optic probe hydrophone (FOPH 500, RP Acoustics, Leutenbach, Germany) at a low PRF of 0.03 Hz to avoid cavitation interference. Based on the hydrophone measurements, the average peak pressure (P_+(avg)) distribution inside the tube (or stone) holder was calculated using the middle Riemann summation of the peak pressure distribution (Smith and Zhong 2012) with a grid size of 0.01 mm in the trinomial fit, normalized by the total surface area of the holder. Although the projected surface area along the LSW propagation direction may differ initially for stones in different size groups, the fragments produced by the shock wave treatment will quickly spread out to cover the entire surface of the sample holder during majority of the treatment. Considering axisymmetry in the shock wave field, a cylindrical coordinate system was set up with its origin coinciding with the lithotripter focus. Table 1 summarizes the values of P_+(avg) and E_eff in the stone holder at different locations of the lithotripter field used for the comminution tests.Following the first series of experiments, additional tests were conducted near the thresholds of P_+(avg) for stones in different size groups (also shown in Table 1) to strength the power of statistical analysis of the results.

Figure 1.

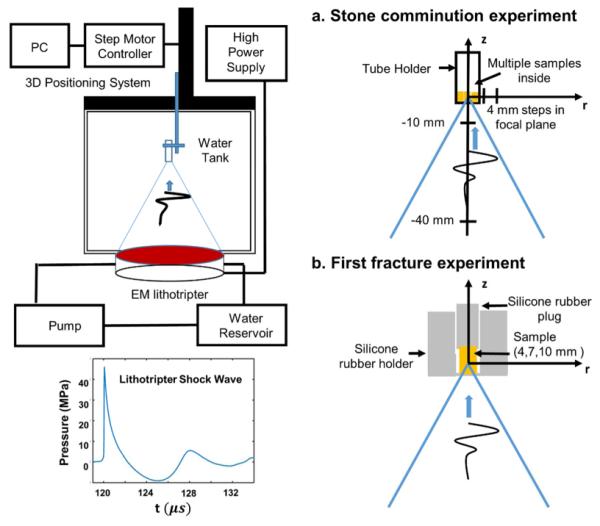
Diagram of the experimental setup: (a) positions of the tube holder during stone comminution experiments using different size groups of approximately matched total mass (b) the stone holder and placement of individual stone of different sizes to determine the number of shocks required to produce the first fracture.

TABLE 1.

Average peak pressure (P_+(avg)) and effective acoustic energy (E_eff) inside the stone holder at different lithotripter field positions

P+(avg) (MPa)	19.6	17.1	15.8	14.2	12.6	11.0	9.6	9.0	8.5	8.1	16.8	13.7
Eeff (mJ)	37.8	31.4	28.0	24.0	19.6	15.1	10.8	8.7	6.6	4.6	35.0	30.6
r (mm)	0	4	5	6	7	8	9	9.5	10	10.5	0	0
z (mm)	0	0	0	0	0	0	0	0	0	0	−10	−40
Stone size (mm)	4,7,10	4,7,10	4	4	4	4,7,10	7,10	7	7,10	10	4,7,10	4,7,10

Relationships between stone size and comminution efficiency were also investigated by numerical simulations using the axisymmetric elasticity solver within the BEARCLAW finite- volume code (Fovargue et al. 2013). This is a high-resolution method that uses second-order Riemann solvers and flux limiters (Langseth 1995) to accurately capture sharp gradients, as produced by LSWs with fast rise time or obtained by sharp changes in material properties.

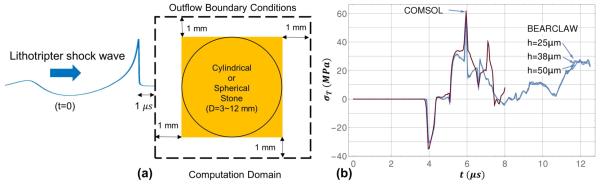
Simulation of the full comminution process is beyond the scope of the present paper. Rather, simulations were constructed to assess effects associated with stone size in the absence of cavitation effects. Cylindrical and spherical stones of density ρ_s = 1995 kg/m³ with a longitudinal (or P) wave speed c_P = 4159 m/s and a transverse (or S) wave speed c_S = 2319 m/s (5:1 Begostone, (Esch et al. 2010)) were placed in water with c₀ = 1500 m/s and density ρ₀ =1000 kg/m³. A plane waveform with a pressure time dependence corresponding to the experimentally measured waveform at the lithotripter focus at 14 kV was input from the left-side computational boundary, situated at 1 mm from the stone edge (Fig. 2a). Simulations were carried out for both radially uniform pressure pulses, and validated radial pressure distributions produced by the Siemens Modularis lithotripter (Fovargue et al. 2013). The radially uniform incident LSW pulses allow us to assess the effect of stone size on resultant stress field without the influence of the lithotripter focal width (Cleveland and Sapozhnikov 2005).

Figure 2.

(a) Diagram of the numerical simulation setup. The incident lithotripter shock wave is 1 μs away from entering the computation domain at the beginning of the simulation. (b) Convergence plot of tensile stress time history at center of D = 4 mm spherical stone obtained by BEARCLAW finite volume code for h = 0.050, 0.033, 0.025 mm grid spacing. In the finite volume model the stone is modeled as a sharp jump in material properties over one cell width. For comparison, a structure-acoustic interaction simulation using the COMSOL finite element package is also presented. The structure-acoustic simulation matches normal displacement and stress between an acoustic domain (water) and an elastic domain (stone). Differences in the shear stress boundary condition between the two models can lead to differing waveform predictions, even though position and amplitude of peak stress is consistent.

To enable comparisons with first stone fracture as observed in cavitation-suppressed experiments with 1,3-butanediol, single cylindrical stones of various sizes were subjected to LSW pulses with realistic radial pressure distribution. Assessment of size-dependent behavior upon further fragmentation in different size stone groups with matched total mass was carried out using spherical stones of equivalent volume, a reasonable approximation to the irregularly shaped fragments that appear in SWL (Eisenmenger 2001; Zhu et al. 2002; Qin et al. 2010). A grid convergence study was performed (Fig. 2b) to determine the mesh cell size required for accurate resolution of the steep pressure pulse. All computations reported here were carried out using grid cells of h = 0.025 mm and explicit time stepping with time step size of ${\delta }_T=5.89ns$ (such that Courant- Friedrichs- Lewy number $CFL=\frac{C_p{\delta }_T}{h}=0.98$). To aid interpretation of the finite volume results, acoustic ray-tracing results are also presented.

Normal theory linear models were used to characterize the associations between SC and the lithotripter field summaries P_+(avg) or E_eff, the former on the log scale, and the dependence of these on stone size and media. The lithotripter field summaries were analyzed separately, applying to each a nested hierarchy of regression models with increasing dependence on stone size and media. These included models (M1) with media-specific slopes and size specific x-intercept terms, (M2) with size- and media-specific slopes and size-specific x-intercepts and (M3) with size- and media-specific slopes and size- and media-specific x-intercepts. We compared pairs of nested models using an F test (Weisberg 2005). All computations were carried out in the R statistical language (Team 2014). The nonlinear least squares routine nls (Bates et al. 1988) was used to fit the models with constrained x-intercept terms. Estimates of the x-intercept values for these models were computed using bootstrap resampling (Efron and Tibshirani 1986).

RESULTS

Experiments

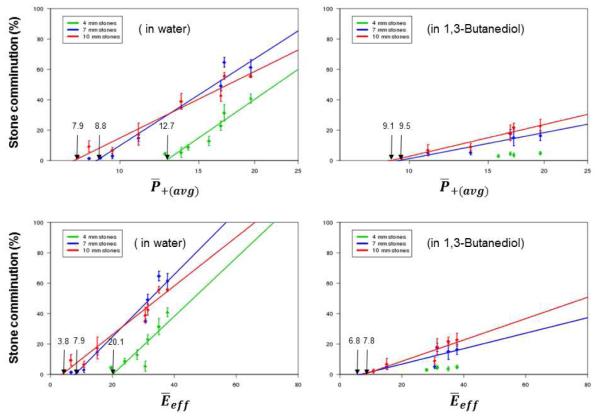
Significant differences were observed in stone comminution after 1,000 shocks from various size groups and in dissimilar fluid media (Fig. 3). Stone comminution (SC) is quantified by the ratio of weight of dried fragments smaller than 2 mm in diameter to the initial weight of the stones. Overall, the results confirm the general correlation between SC and P_+(avg) or E_eff observed previously using 10-mm spherical Begostone samples (Smith and Zhong 2012; Smith and Zhong 2013). The correlation between SC and P_+(avg), expressed in a linear-log relation of $SC=k_1\ln \left({\stackrel{‒}{P}}_{+\left(avg\right)}\right)$ + b₁ where k₁ and b₁ are constants, and ${\stackrel{‒}{P}}_{+\left(avg\right)}=\frac{P_{+\left(avg\right)}}{P_0}$ with P₀ = 1 MPa, was used to determine the P_+(avg) threshold [calculated by using $P_{0}exp(-b_1∕k_1)$ and the slope of the correlation curve (k₁) for different size groups in water and 1,3-butanediol, respectively. Similarly, the correlation between SC and E_eff was expressed in a linear relation $[SC=k_2\ln \left({\stackrel{‒}{E}}_{eff}\right)+b_2]$ where k₂ and b₂ are constants, and ${\stackrel{‒}{E}}_{eff}=\frac{E_{eff}}{E_0}$ with E₀ = 1 from which the E_eff thresholds and the slope of the correlation curve for different size groups were determined. The general fit of the correlation curves are good with the coefficient of determination R² = 0.64 to 0.96, except for the fit between SC and E_eff in 1,3-butanediol, which varies in the range of R² = 0.41 to 0.71. As summarized in Table 2, both parameters were found to vary with stone size and fluid medium.

Figure 3.

Correlation between stone comminution and ${\stackrel{‒}{P}}_{+\left(avg\right)}$ and ${\stackrel{‒}{E}}_{eff}$ in water and 1,3- butanediol after 1000 shocks for three size groups: 4 mm (green), 7 mm (blue) and 10 mm (red). The ${\stackrel{‒}{P}}_{+\left(avg\right)}$ and ${\stackrel{‒}{E}}_{eff}$ thresholds for each size group are indicated by arrows. Note ${\stackrel{‒}{P}}_{+\left(avg\right)}$ and ${\stackrel{‒}{E}}_{eff}$ and normalized P_+(avg) and E_eff, respectively. Four samples were used under each specific test condition and at each location in the lithotripter field.

TABLE 2.

Thresholds of P _+(aVg) and E_eff, and slope of regression curve for SC vs. $\ln \left({\stackrel{‒}{P}}_{+\left(avg\right)}\right)$ or SC vs. E_eff after 1,000 shocks in water and 1,3-Butanediol.

Medium in the holder	Size (mm)	Threshold P+(aVg)(MPa)/Eeff(mJ)	Slope SC vs. $\ln \left({\stackrel{‒}{P}}_{+\left(avg\right)}\right)∕E_{eff}$
Water	4	12.7 (12.3, 13.1)/ 20.1 (18.4, 22.5)	0.88(0.75, 1.02)/ 0.019 (0.015,0.023)
	7	8.8 (8.7,9.1)/ 7.9 (7.2,8.8)	0.82 (0.77,0.88)/ 0.021 (0.019,0.022)
	10	7.9 (7.5,8.3)/ 3.8 (2.1,5.6)	0.63 (0.58,0.68)/ 0.016 (0.015,0.018)
1,3-Butanediol	4	−	−
	7	9.5 (8.3,11.0)/ 6.8 (-0.2,14.9)	0.25(0.14,0.36)/ 0.005 (0.002,0.008)
	10	9.1 (8.4,9.8)/ 7.8 (3.7,11.2)	0.30 (0.22,0.38)/ 0.007 (0.005,0.009)

For both lithotripter field parameters, M2 was strongly preferred to M1 ($\ln \left({\stackrel{‒}{P}}_{+\left(avg\right)}\right)$ p-value = 2.53×10⁻⁶; ${\stackrel{‒}{E}}_{eff}$ p-value = 6.53×10⁻⁴), while M3 was not found to be discernibly better than M2 ($\ln \left({\stackrel{‒}{P}}_{+\left(avg\right)}\right)$ p-value = 0.236; ${\stackrel{‒}{E}}_{eff}$ p-value = 0.640). Hence the data support size- and media-specific slopes and (at minimum) size-specific x-intercepts. While differences in size-specific x-intercepts between the two media were too small to detect with high confidence, we base our summary of these data on the more general model in which the threshold (x-intercept) terms vary by size and media.

In water, P_+(avg) threshold (p-value=9.2 × 10⁻⁸) and slope (p-value=2.8 × 10⁻⁶) were both found to increase with decreased stone size (Fig. 4a). When the stone size decreased from 10 to 7 to 4 mm, the estimate of the P_+(avg) threshold was found to increase from 7.9 (95% confidence interval (CI) from 7.5 to 8.3) to 8.9 (95% CI from 8.7 to 9.1) to 12.7 (95% CI from 12.3 to 13.1) MPa, respectively. In contrast, while a similar increase in P_+(avg) threshold was observed in 1,3-butanediol (9.1 MPa, 95% CI from 8.4 to 9.8 MPa for 10-mm stones; 9.5 MPa, 95% CI from 8.3 to 11.0 MPa for 7-mm stones; p-value=0.55) the slope was estimated to decrease with decreased stone size (p-value=0.43; Fig. 4a). The slope for the 4-mm stones treated in 1,3-butanediol was very shallow and no quantifiable SC was observed at P_+(avg) below 15.8 MPa. Therefore, the threshold for P_+(avg) in 1,3-butanediol for the 4-mm stones could not be determined exactly, but should exist in the range of 14.2 to 15.8 MPa. In comparison, one of the most notable contrasts between the stones treated in water vs. those treated in 1,3-butanediol is the opposite change in the slope of the regression curve when stone size decreases, but additional data will be needed to confirm the reversed trend in 1,3-butanediol. These results may indicate the dissimilar roles that stress waves and cavitation play in stone comminution and their synergistic interaction in a cavitation supportive fluid, such as water or urine (Zhu et al. 2002).

Figure 4.

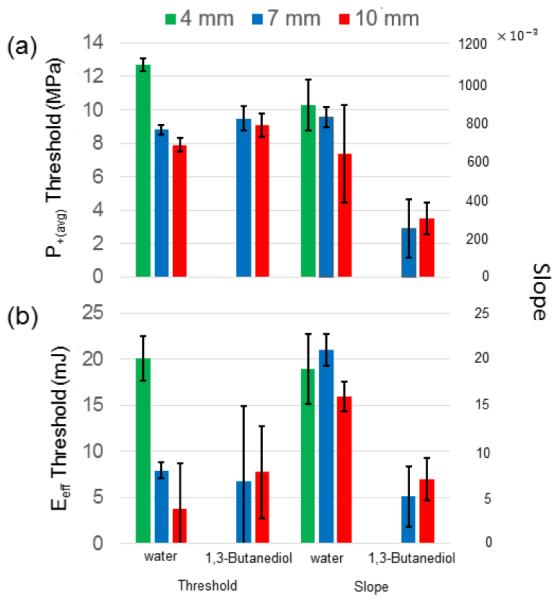
Threshold and slope with associated error bars determined from the regression analysis between stone comminution (SC) and ${\stackrel{‒}{P}}_{+\left(avg\right)}$ and ${\stackrel{‒}{E}}_{eff}$ in water and 1,3-butanediol after 1000 shocks for three size groups : 4 mm (green), 7 mm (blue), and 10 mm (red)

In water, the E_eff threshold was also found to increase (p-value= 2.4 × 10⁻⁷) with decreased stones size from 3.8 (95% CI from 2.1 to 5.6) to 8.0 (95% CI from 7.2 to 8.8) to 20.1 (95% CI from 18.4 to 22.5) mJ for 10-, 7-, and 4-mm stone groups, respectively, while the slope was found to initially increase (from 10-mm to 7-mm) and then decrease slightly (from 7-mm to 4-mm) with reduced stone sizes (0.016, 95% CI from 0.015 to 0.018 for 10-mm stones; 0.021, 95% CI from 0.019 to 0.022 for 7-mm stones; 0.019, 95% CI from 0.015 to 0.023 for 4-mm stones, p-value = 9.8×10⁻⁴). However, in 1,3-butanediol we were unable to discern size dependence in the relationship between SC and E_eff (size specific threshold p-value=0.74; size specific slope p-value=0.34).

Figure 5 shows the comminution dose dependence and rate of SC in three different size groups. A Weibull model (Smith and Zhong 2013) in the form of, $SC=1-\exp [-{\left(\frac{dose-c}{d}\right)}^e]$ where c, d and e represent the dose threshold, a normalization factor and the Weibull modulus, respectively, was used to fit the data (R² = 0.97 to 1.00) from which the rate of SC was calculated for each size group. Although stones disintegrate progressively with increased shock number in all three groups, the efficiency of SC is significantly higher in the 7- and 10-mm groups than the 4-mm group beyond 500 shocks. More importantly, the SC rate curves further confirm that two distinct phases of stone comminution exist during SWL (Zhong 2013). At the beginning, the SC rate increases rapidly, reaching a maximum within a few hundred shocks, and thereafter, decays monotonically within a few thousand shocks towards the end of the treatment. Overall, the general features in the SC rate curves are not sensitive to the threshold value of c (in the range of 20 to 100 shocks) required for initiating fragmentation. Interestingly, the SC rate of 4-mm stone group was found to reach its maximum earlier than those of 10- and 7-mm stone groups. This observation of a progressively reduced SC rate that prevails for the longest treatment duration in the 4-mm stone group is consistent with its lowest SC compared to the other two size groups.

Figure 5.

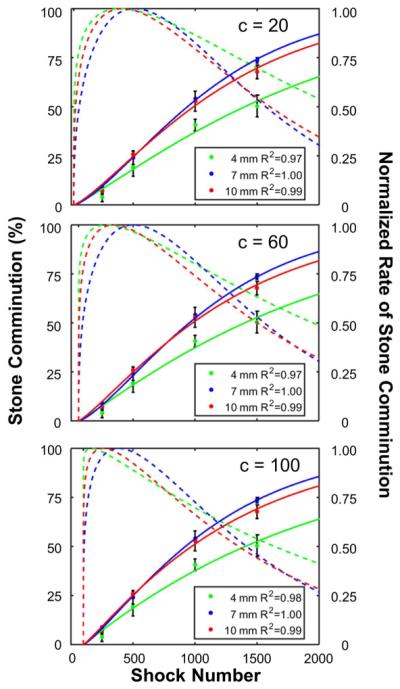
Dose dependence in stone comminution (solid lines) and normalized rate of stone comminution (dashed lines) for three different size groups treated at the lithotripter focus. The experimental results are fitted using the Weibull model for three different values for the shock dose threshold (c = 20, 60 and 100 shocks) to initiate fracture.

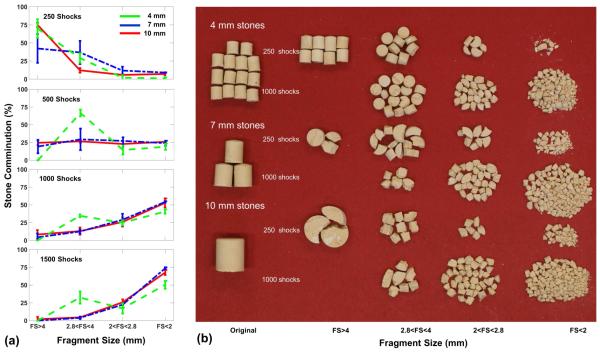
It is worth noting that the fragment size distributions after 250 shocks vary significantly among the three size groups (Fig. 6). In particular, the size distribution curves for the 10- and 7-mm size groups begin to converge after 500 shocks and overlap with each other by 1500 shocks. In these two size groups, as the shock number increases the peak in the fragment size distribution curve shifts gradually from larger than 4 mm to between 2.8 and 4 mm, to less than 2 mm. In contrast, the fragment size distribution of the 4-mm group is noticeably different with a significant portion of the fragments stagnated within the 2.8 ~ 4 mm size range even after 1500 shocks while its counterparts in the 7- and 10-mm size groups were reduced to insignificant levels. This observation exemplifies the influence of stone size on comminution processes and efficiency in SWL.

Figure 6.

(a) Variations of fragment size (FS) distributions in three different stone size groups after treatment in water at the lithotripter focus. (b) Representative photos of original stones of different sizes (left column) and corresponding fragment distribution in different size ranges after 250 shocks and 1000 shocks.

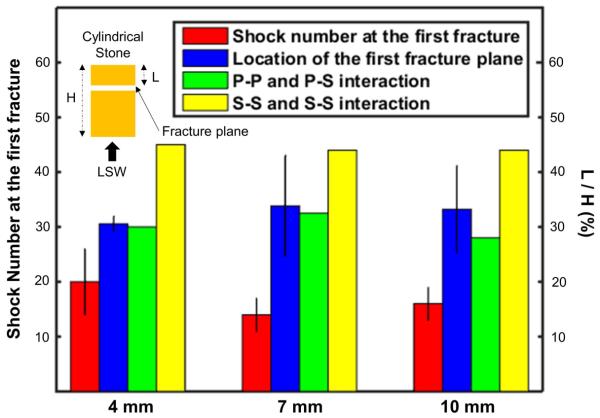
The number of shocks (mean ± s.d.) to initiate the first fracture in single cylindrical stones of 4-, 7-, and 10-mm treated at the lithotripter focus was found to be 20 ± 6, 14 ± 3, and 16± 3 (n = 4), respectively, as shown in Fig. 7, and the results are statistically similar (p = 0.20 based on ANOVA test). In all cases, the fracture plane was formed approximately parallel to the back surface of the stone at a nominal distance about 30% to 34% of the stone height.

Figure 7.

The number of shocks delivered to produce the first fracture in individual 4-, 7-, 10- mm cylindrical stones (red bar), locations of the first fracture plane (blue bar), locations of P-P wave and P-S wave interaction (green bar), and location of S-S and S-S wave interaction (yellow bar). Note, P-S: Shear waves generated by the reflection of incident longitudinal waves; P-P: Longitudinal waves generated by the reflection of incident longitudinal waves; S-S: Shear waves generated by the reflection of shear waves.

Numerical Model Calculations

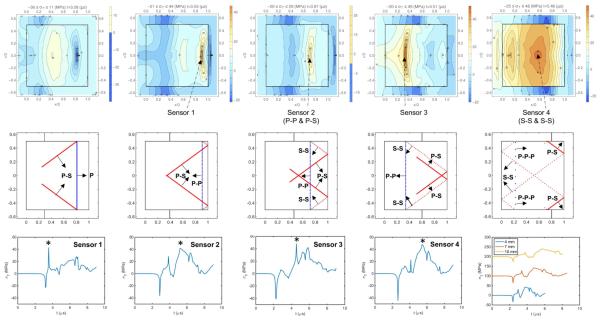
The interaction of a LSW with a 7-mm cylindrical stone at the lithotripter focus and the formation of regions of high tensile stress inside the stone are shown in Fig. 8, together with ray tracing plots created following methods described previously (Ting and Lee 1969) at five time steps to facilitate the interpretation of the various stress wave interactions. When the incident LSW impinges the stone at the left boundary, a P-wave will be generated and propagates at a faster speed in the stone with a wavefront parallel to the left (wave entrance) boundary, which later reflects off the right (wave exit) boundary (denoted by P-P). During this period, the reflection of the advancing P-wave from the lateral cylindrical surface (i.e., upper and lower boundaries) of the stone generates an S-wave (i.e., P-S wave), which converges towards the center axis of the stone. In soft artificial kidney stones such as E-30 where c₀ is approximately equal to c_S, the slower moving pressure wave in water outside the cylindrical surface of the stone will further induce a second and stronger shear wave, also known as head wave (Cleveland and Sapozhnikov 2005). However, in BegoStone phantoms where c_S is much greater than c₀, no strong head wave is produced from the pressure wave in water gliding along the cylindrical surface of the stone.

Figure 8.

Wave propagation and interaction in a 7-mm cylindrical BegoStone phantom. Top row: tensile stress contours at 5 MPa spacing. Second row: ray-tracing plots at corresponding times of the tensile stress contour plots. Third row: tensile stress signal detected by four sensors placed at different locations inside the stone (* is used to mark the peak in each sensor signal) together with the tensile stress signals detected by three sensors placed at the P-P and P-S interaction point in 4-, 7-, and 10-mm cylindrical stones, respectively. The sensor signals are displayed with different baseline shifts for clarity of comparison.

Four regions where local maximum tensile stress is produced during the LSW-stone interaction were identified. Sensors were placed in these regions to extract the tensile stress time history from the numerical results. The first tensile peak was observed shortly after the reflection of the P-wave (i.e., P-P) from the back surface at a location (L) about 10% of the stone height (H). The second tensile peak was produced when the reflected P-wave in tension constructively interferes with the converging P-S wave on the center axis of the stone in the posterior region of the stone with L/H = 0.3. The third tensile peak was noted in the anterior region of the surface aligned with the back propagating P-P wavefront at L/H = 0.7. Finally, a fourth tensile peak was observed when the reflected S-wave from the back surface (denoted by S-S) crosses the central axis of the stone at L/H = 0.44.

It is interesting to note that the location of the first stone fracture observed experimentally (see Fig. 7) is most closely matched with the location of the second tensile stress peak produced by P-P and P-S interaction, and reasonably matched with the location of the fourth tensile stress peak produced by S-S and S-S interaction. Although the peak tensile stresses at the four sensor locations are comparable, the duration of the tensile stress peak in the stone fracture region is significantly broader than the other locations (see last row in Fig. 8). Consequently, the tensile stress integral [i.e., $\int {({\sigma }_T-{\sigma }_0)}^{2}dt$ for σ_T > σ₀ where σ₀ is the quasistatic failure strength of the material ], such as calculated from the Tuler-Butcher criterion for dynamic fracture of a brittle material (Freund 1998; Wijerathne et al. 2010), is significantly higher in the fracture region than in the locations of the other peaks. This general feature is observed in all three-sized stones (Table 3). More importantly, as the stone size decreases, the peak tensile stress calculated inside the stone does not change appreciably. However, the corresponding tensile stress integral values will decrease substantially with stone size.

Table 3.

Sensor locations in cylindrical stones of different sizes and the peak tensile stress and stress integral $[\int {({\sigma }_T-{\sigma }_0)}^{2}dt]$ from each sensor

Stone size (mm)	Sensor	$\frac{L}{H}(\%)$	Max(δT) (MPa)	$\int {({\sigma }_{\mathbf{T}}-{\sigma }_0)}^2\mathbf{dt}(\times {10}^8\mathrm{P}{a}^{2}s)$
4	1	10	44	3.12
	2	33	43	9.05
	3	78	53	4.51
	4	45	49	9.36
7	1	10	44	4.39
	2	30	41	13.81
	3	70	50	11.46
	4	44	48	16.05
10	1	13	35	6.10
	2	28	40	15.70
	3	64	47	16.10
	4	44	46	19.68

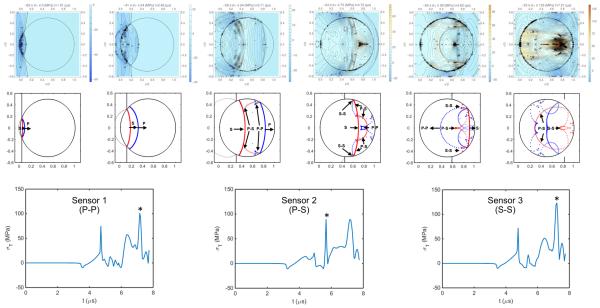
The more complex patterns of the generation and interaction of various stress waves inside spherical stones are shown in Fig. 9. Analysis of the tensile stress distribution in conjunction with ray tracing of different wavefronts revealed three distinct tensile stress peaks generated in the posterior region of the stone. The first peak was observed at P-P focusing with L/H = 0.25 while the second and third peaks were produced by P-S and S-S focusing at L/H =0.37 and 0.28, respectively. The stone geometry induces curvature of the refracted and reflected P- and S-waves. The maximum tensile stress is produced by the interaction of S-waves that are generated by the incident pressure wave (i.e., P_i) refraction at the front surface and subsequent convergence at the distal end of the stone upon reflection (i.e., S-S waves).

Figure 9.

Tensile stress contours (top row) and corresponding ray-tracing plots (second row) at six different times in a 10-mm spherical stone subjected to a weakly focused incident lithotripter pulse: (1) 1.91 µs, wavefronts of P and S waves attached, (2) 2.49 µs, wavefronts of P and S waves detached from each other, (3) 3.71 µs, high tensile stress generation at the boundary, (4) 4.72 µs, during P-P wave interaction, (5) 5.62 µs, during P-S wave interaction, and (6) 7.21 µs, during S-S wave interaction. In the tensile stress contours, 5 MPa spacing is used between contour lines at t = 1.91 and 2.49 µs, while 2 MPa spacing is used elsewhere. Third row: tensile stress signal from three sensors placed at the locations of the maximum P-P wave interaction, P-S wave interaction, and S-S wave interaction, respectively.

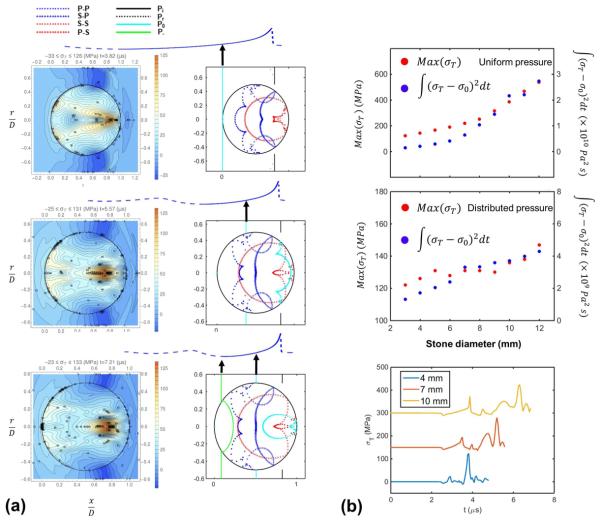
Figure 10 shows a comparison of the stress fields for different stone sizes during the focusing interaction of the S-S waves. The times were chosen for each stone to correspond to approximately equal positions of the S-wave reflected from the distal end of the stone. Even so, there are notable differences in the overall aspect of the stress field due to varying degrees of constructive and destructive interference of the waves. For example, in small stones destructive interference may occur between the S-S wave and a large portion of the leading compressional component of the refracted P wave that is still propagating towards the back surface of the stone. In large stones when the S-S wave focuses, the tensile part of the incident LSW has already transmitted into the stone, which will further increase the tensile stress built up at the S-S wave focus. In contrast, when the S-S wave focuses in small stones, the tensile part of the incident LSW has not yet entered the stone (see ray tracing plots in Fig. 10). Overall, the numerical results clearly show a trend of significantly decreased maximum tensile stress and stress integral with reduced stone size for an incident LSW with either uniform or distributed pressure at the shock front. This result is consistent with the experimental observation of initially increasing stone comminution efficiency followed by decreasing efficacy in stone breakdown.

Figure 10.

(a) Tensile stress contours (left column, 5 MPa spacing) and corresponding ray- tracing plots (right column) in 4-, 7-, and 10-mm spherical stones during the S-S wave interaction. Note, P-P: longitudinal waves in stones generated by reflection of longitudinal waves, S-P: longitudinal waves in stones generated by reflection of transverse waves, S: transverse waves in stone, S-S: transverse waves generated by reflection of transverse waves, P-S: transverse waves generated by reflection of longitudinal waves, P_i: incident pressure wave in water, P_r: reflected pressure wave in water. P_o: the wave front in the incident pressure wave in water with pressure equaling to zero. P_-: the wave front in the incident pressure wave in water with maximum negative (tensile) pressure. (b) Variations of Peak tensile stress Max (σ_T) and tensile stress integral $\int {({\sigma }_T-{\sigma }_0)}^{2}dt$ inside a spherical stone vs. stone diameter. The stones are subjected to an incident lithotripter pulse with either a uniform or a distributed pressure at the leading shock front, and (c) tensile stress signals detected by three sensors placed at the S-S interaction in the 4-, 7-, and 10-mm spherical stones, respectively. The sensor signals are displayed with different baseline shifts for clarity of comparison.

DISCUSSION

Using groups of stones with similar initial shape and approximately equivalent total mass but different individual sizes, we have demonstrated clearly a size-dependency in stone comminution in water during SWL. As stone size changes, there are significant variations in the threshold of P_+(avg) or E_eff (independent of surrounding fluid medium under the test conditions used in this study) to initiate stone fragmentation, the slope of SC vs. $\ln \left({\stackrel{‒}{P}}_{+\left(avg\right)}\right)$, and the rate of SC in relation to the number of shocks delivered. Specifically, the P_+(avg) or E_eff threshold is found to increase as stone size decreases - a feature that is generally observed in different size groups both in water and in 1,3-butanediol (except for the 4-mm stones). This characteristic change in P_+(avg) or E_eff threshold with stone size may reflect the variations either in the flaw population of the stone material or the stress field produced by the LSW-stone interaction or a combination of both factors. To fracture a stone, tensile or shear stresses of sufficient amplitude must be generated in the stone to open up pre-existing flaws through three principal modes of fracture (Lokhandwalla and Sturtevant 2000; Zhong 2013). Although it is conceivable that the flaw population in the stone or residual fragments may change progressively during SWL, a quantitative assessment of this change both experimentally and theoretically is beyond the scope of this work and warrants future investigations.

We thus only assess the changes in the stress field based on numerical simulations of LSW interactions with cylindrical and spherical stones of different sizes. Our results show that the calculated maximum tensile stress inside a spherical stone^§ is produced primarily by the focusing of the S-S wave. The corresponding stress integral also reaches the maximum inside the stone (see Table 4). The maximum tension, and more importantly, the tensile stress integral does decrease appreciably with stone size, presumably due to the increased level of destructive interference of different stress waves in small stones (see Fig. 10). This speculation is supported not only by the reduction in the maximum tensile stress with decreased stone size, but also by the more dramatically squeezed pulse duration of the tensile stress peak. For example, the −6 dB pulse width of the tensile peak produced by the S-S interaction in Fig. 10 decreases from 0.30 μs in the 10-mm stone to 0.15 μs in the 7-mm stone, and further down to 0.11 μs in the 4-mm stone.

Table 4.

Sensor locations in spherical stones of different sizes and the peak tensile stress and stress integral $[\int {({\sigma }_T-{\sigma }_0)}^{2}dt]$ from each sensor

Stone size (mm)	Sensor	$\frac{L}{H}(\%)$	Max(δT) (MPa)	$\int {({\sigma }_{\mathbf{T}}-{\sigma }_0)}^2\mathbf{dt}(\times {10}^9\mathrm{P}{a}^{2}s)$
4	l	28	75	1.19
	2	N/A	N/A	N/A
	3	15	124	1.69
7	1	26	103	2.32
	2	39	93	2.18
	3	29	131	2.94
10	1	25	101	2.67
	2	37	89	2.98
	3	28	136	3.70

The dependence of the P_+(avg) threshold on stone size may also be appreciated using dimensional analysis. Scale independence in stone comminution, i.e., no effect of stone size upon P_+(avg) threshold, would occur only under conditions of geometric, kinematic, and dynamic similarities (Langhaar 1951; Sonin 2001). The interaction of a lithotripter pulse with stones exhibits multiple time scales related to the characteristic length of the pulse and the propagation time of elastic waves in the stone. In our experiments, the independent geometric and kinematic parameters characterizing the LSW-stone interactions are the pulse rise time t_RT, pulse length t_L, wave speeds c_o, c_p, c_s, stone diameter D and lithotripter focal width (FW), which can all be described by two physical units (length and time). Using the Buckingham π theorem (Langhaar 1951), one can easily obtain non-dimensional groups such as $\frac{C_P}{c_0},\frac{C_S}{c_0},\frac{C_{P}t}{D},\frac{C_{S}t}{D}$, and $\frac{FW}{D}$ where t is a characteristic time (e.g., t_RT or t_L). The kinematic and dynamic similarities will exist when these non-dimensional groups are matched among different sized stone groups. Therefore, self- similarity in SWL will only occur under extreme conditions such as t_RT, t_L → 0 , and equivalently, for very large stone sizes where the details of the lithotripter pulse shape are no longer resolved. In other words, for pulses with sharp jumps there is no dependence of maximum stresses formed by constructive interference on the stone size. However, for pulses with changes in amplitude observable on the time scale $\frac{D}{c}$ where c is the wave speed in stone (i.e., c_p, c_s), stone size effects are expected, and indeed observed both numerically and experimentally. Consideration of cavitation would add at least two more independent parameters (cavity average size, cavity breakdown time), which would again indicate dependence of stone breakdown (such as measured by the P_+(avg) threshold) upon stone size with no self-similar regime.

Our results have demonstrated clearly the influence of fluid medium around the stone on comminution efficiency, which is consistent with the observation from previous studies on the role of cavitation in stone fragmentation during SWL (Zhu et al. 2002). In cavitation suppressive medium such as 1,3-butanediol, the slope in the SC vs. $\ln \left({\stackrel{‒}{P}}_{+\left(ave\right)}\right)$ curve decreases with decreasing stone size, indicating again the diminishing possibility of effective constructive wave interference and focusing to build up high tensile or shear stresses inside the stone to initiate fracture from intrinsic flaws. Moreover, as SWL treatment progresses the density of the largest intrinsic flaw population inside fragments will also likely decrease, requiring either a higher stress or larger number of shocks to produce the next fracture (Zhong 2013). In contrast, in cavitation supportive medium such as water or urine, the slope of the SC vs. $\ln \left({\stackrel{‒}{P}}_{+\left(ave\right)}\right)$ curve increases with decreasing stone size despite that a high P_+(avg) threshold is needed to initiate fragmentation. It is plausible that the higher rate of SC increment in relation to increased pressure above the P_+(avg) threshold is facilitated by the augmented cavitation activities in water around small-size stones due to their large surface area and presumably more cavitation nuclei produced during SWL. Under such a scenario, increased cavitation damage could be produced on the surface of the stone and served as extrinsic flaws that may precipitate fracture from the surface into the interior of the stone (Vakil and Everbach 1993; Zhu et al. 2002; Zhong 2013; Neisius et al. 2014).

Furthermore, it is worth noting that stone (or fragment) size also significantly affects the progression and eventual outcome of comminution in SWL. In particular, our results show that large size stones tend to break into multiple fragments of irregular shapes and sizes, consistent with the observations from previous studies (Eisenmenger 2001; Zhu et al. 2002). As shown in Fig. 6, comminution of the 10- and 7-mm size stones leads to progressively smaller and smaller fragments as the treatment progresses. In contrast, comminution of the 4-mm size stones produces unevenly distributed fragments, with a large portion of the fragments stalemated within the size range of 2.8 ~ 4 mm even after 1,000 to 1,500 shocks. The fragments in the 2.8 ~ 4 mm size range are often resulted from initial fracture of the 4-mm stones into two pieces (see Fig. 6). This observation may be caused by the minimal distance (or dimension) of c_p*t⁺/2 (= 4.8 mm for the hard BegoStone samples used in this study) where t⁺ is the compressive pulse duration of the LSW required to avoid destructive interference between the incident compressive wave and the reflected tensile wave from the back (or boundary) surface of the stone. Being small in size, these fragments, spread out in the stone holder, are more difficult to break because of their increased P_+(avg) threshold.