Who Really Gets Strep Sore Throat? Confounding and Effect Modification of a Time-Varying Exposure on Recurrent Events

Abstract

Unmeasured confounding is the fundamental obstacle to drawing causal conclusions about the impact of an intervention from observational data. Typically, covariates are measured to eliminate or ameliorate confounding, but they may be insufficient or unavailable. In the special setting where a transient intervention or exposure varies over time within each individual and confounding is time constant, a different tack is possible. The key idea is to condition on either the overall outcome, or the proportion of time in the intervention. These measures can either eliminate the unmeasured confounding by conditioning or by use of a proxy covariate. We evaluate existing methods and develop new models from which causal conclusions can be drawn from such observational data even if no baseline covariates are measured. Our motivation for this work was to determine the causal effect of Streptococcus bacteria in the throat on pharyngitis (sore throat) in Indian schoolchildren. Using our models, we show that existing methods can be badly biased and that sick children who are rarely colonized have a high probability that the Streptococcus bacteria is causing their disease.

1. Introduction

The potential for unmeasured confounding makes causal conclusions about an exposure from observational data problematic. A common strategy to attack this problem is to measure covariates so that conditional on the covariates, the intervention is effectively assigned at random. In the causal literature there are at least four main methods for controlling confounding in a observational trial to allow for causal inference to be made; confounder adjustment or regression analysis, instrumental variable analysis [1], matching [2], and propensity score adjustment [3]. When potential confounding variables or instrumental variables are available these methods can work well and are straightforward to implement. However, it is not always possible to measure sufficient covariates and so the assumption of no unmeasured confounders is often suspect.

If there is a time-varying intervention, e.g. periodic use of a transiently acting drug, so subjects are observed during both exposed and nonexposed states, a different tack is possible. If intervals of drug exposure are randomly assigned, one can compare outcomes on drug versus off drug within an individual. Conceptually this is no different from a repeated crossover trial. Crossover trials require that the effect of the exposure be achieved by the end of the exposure period and that there is no lingering effect of the exposure beyond the period of exposure. Analysis of intermittently administered interventions for survival type data has been discussed in [4] and [5], while [6] considered the setting of recurrent event data. In observational studies, the time-varying intervention or exposure is not assigned at random and may be related to an individual's underlying risk of an event. Maclure [7] introduced the case-crossover design for such data where the effect of transient exposures on an event are estimated by comparing exposure status just prior to the event to a matched control period in the past; see also [8] and [9]. Navidi [10] extended the case-crossover design approach to recurrent events, while [11] discussed different ways to generalize this method to recurrent events where multiple event periods are matched with multiple control periods. A related approach is the self-controlled case series (SCCS), introduced in [12]. Here each individual follows their own nonhomogeneous Poisson process with some parameters common to all subjects. A parametric multinomial model for the common parameters was derived by conditioning on the number of events for each person. This approach has been used extensively in the study of vaccine safety [13]. Finally, the method of Huang et al. [14] can also be applied to this setting. They specified a semiparametric intensity with a person-specific baseline intensity and some parameters common to all subjects. By applying the pairwise conditional likelihood approach [15] to all pairs of subjects with at least one event, the baseline intensity function is eliminated.

This research was motivated by a study of school children in Vellore, India where throat colonization by Group A Streptococcus (GAS) bacteria was measured over time along with events of pharyngitis (sore throat) [16]. Of major interest was to estimate the probability of causation (PC) or the probability that GAS colonization is responsible for pharyngitis in a child who presents with both. The probability of causation was introduced by Levin [17] and discussed by Greenland [18] who cautions against its uncritical use. Because a child's (unmeasured) immune system impacts both colonization by GAS and clinical disease, it is difficult to pretend that GAS colonization is effectively randomized and methods that address confounding are needed.

The idea of this paper is to use the individual follow-up data on the colonization and pharyngitis event rates to act as proxies for the unmeasured confounding. We review methods that condition on the pharyngitis events and show that the SCCS and pairwise conditioning approach of Huang et al. [14] can be applied to this setting. We introduce a new approach where the colonization rate is used as a proxy for a time-constant unmeasured confounder. The new approach naturally handles effect modification where the probability of causation depends on the unmeasured confounder. The SCCS and Huang et al. methods cannot directly handle such modification. This new approach is similar in spirit to pattern mixture models for missing data where models for the observed (nonmissing) data are created conditional on the patterns of missingness [19]. Simulations show that the SCCS and Huang et al. methods work well if there is no effect modification but can be badly biased otherwise. Using the colonization rate as a covariate proxy for the confounder can provide accurate inference under both settings. For the Vellore schoolchildren study, we show strong effect modification where children who are rarely colonized have a high probability of causation while for frequently colonized children the probability of causation is nearly zero. These results suggest it may be beneficial to tailor antibiotic therapy based on a child's history of colonization.

2. CAUSAL FRAMEWORK

In this section we develop a causal framework that applies to a time-varying binary exposure on a recurrent event under the strong assumption that transient periods of exposure are assigned at random.

To talk of causation, it is natural to think of counterfactual outcomes and so we imagine whether a child would have had the event (pharyngitis) if they were positive for exposure (GAS colonized) and if they were not. For now, we consider the probability of causation for a small interval [t, t + Δ). Let Y (Z) be the event indicator for a child who has exposure state Z = 0, 1 in this interval. Thus of the pair Y (0), Y (1), one is observed, the other is counterfactual, and the observed data is Y = Y (1)Z + Y (0)(1 – Z). There are four possibilities for these pairs of outcomes which are provided in Table 1 along with a meaningful label.

Table 1.

The four kinds of individuals and their proportions in the population during a small interval of time [t, t + Δ). Different outcomes are observed depending on the exposure status, Z.

Label	Proportion	Event if Z = 0 Y (0)	Event if Z = 1 Y (1)
Immune	θ 00	0	0
Exposure caused disease	θ 01	0	1
Exposure prevented disease	θ 10	1	0
Doomed	θ 11	1	1

At a given point in time, some children will have Z = 1 and others will have Z = 0. In this section, we make the strong assumption that the true proportions of Table 1 for the four categories are the same for these two types of children. If the Z values were randomly assigned, this would be automatically satisfied.

Under the assumption that exposure cannot prevent the event or θ₁₀ = 0 we write the probability of causation as

$$\mathrm{PC}=\mathrm{pr}(\text{Z caused the event}\mid \text{have the event and Z}=1)=\frac{{\theta }_{01}}{{\theta }_{01}+{\theta }_{11}}$$ (1)

$$=\frac{\mathrm{pr}(Y=1\mid Z=1)-\mathrm{pr}(Y=1\mid Z=0)}{\mathrm{pr}(Y=1\mid Z=1)}.$$ (2)

The PC measures a causal effect at an individual level and is estimable under the assumption that θ₁₀ = 0 since pr(Y = 1 | Z = z) can be estimated using sample proportions. Note that if, peculiarly, the exposure Z = 1 prevented disease in a proportion θ₁₀, then the PC estimated by the right hand side (2) would estimate (θ₀₁ − θ₁₀)/(θ₀₁ + θ₁₁), an underestimate of the true probability of causation.

For our setting, PC is of interest as it additionally provides the probability that effective antibiotics will cure a child of disease, for a child who presents with disease and GAS colonization of the throat. The probability of causation was introduced by Levin [17] and discussed by Greenland [18] for the setting of a long term exposure on a terminal event.

In principle, we could make many tables like Table 1 for the partition of Δ-sized intervals of the time axis and aggregate the estimated θs and thus PCs. A better way is to postulate a model for the instantaneous risk of the event as a function of current exposure. To proceed, let Z(t) be the indicator of exposure at time t, N(t) the number of events occurring at or before time t. We first assume that, conditioning on Z(t), the recurrent event process N(t) is a nonhomogeneous Poisson process with intensity function

$$\lambda \left(t\right)={\lambda }_0\left(t\right)\exp \left\{Z\left(t\right){\beta }_1\right\}.$$

This specification is known as the proportional intensity model and is the recurrent event analogue to the proportional hazards model for survival data [20, ?]. It follows that in a small interval [t, t + Δ), the probability of having a pharyngitis event is ${\int }_t^{t+\Delta }\lambda \left(u\right)du\approx \lambda \left(t\right)\Delta$. Thus under the proportional intensity model with random exposure, the probability of causation for a small interval is

$$\begin{array}{cc}\hfill \mathrm{PC}=& \frac{\mathrm{pr}\{N(t+\Delta )-N\left(t\right)>0\mid Z\left(t\right)=1\}-\mathrm{pr}\{N(t+\Delta )-N\left(t\right)>0\mid Z\left(t\right)=0\}}{\mathrm{pr}\{N(t+\Delta )-N\left(t\right)>0\mid Z\left(t\right)=1\}}\hfill \\ \hfill \approx & \frac{{\lambda }_0\left(t\right)e^{{\beta }_1}\Delta -{\lambda }_0\left(t\right)\Delta }{{\lambda }_0\left(t\right)e^{{\beta }_1}\Delta }=1-\frac{1}{e^{{\beta }_1}}.\hfill \end{array}$$

Another important metric is the attributable fraction (AF) or fraction of cases that are attributable to the exposure. Arguing as before, we consider a short period of time and consider the expected number of cases in the current environment (i.e. where Z = 1 with probability p over the interval and over the population) compared to an environment where the exposure has been eliminated (e.g., a perfect vaccine which eliminates GAS colonization and therefore disease). We obtain an attributable fraction as

$$AF\left(p\right)=\frac{E_{ZC}\left[\Delta {\lambda }_0\left(t\right)e^{{\beta }_{1}Z\left(t\right)}\right]-\Delta {\lambda }_0\left(t\right)}{E_{ZC}\left[\Delta {\lambda }_0\left(t\right)e^{{\beta }_{1}Z\left(t\right)}\right]}=1-\frac{1}{E_{ZC}\left[e^{{\beta }_{1}Z\left(t\right)}\right]}=1-\frac{1}{e^{{\beta }_1}p+(1-p)}$$

where E_ZC denotes the expectation of Z(t) in the current environment. The attributable fraction measures a causal effect on a population. If θ₀₁ > 0, the estimate of AF(p) can be less than 0 if, for example, GAS prevented more cases of pharyngitis than it caused. The reasoning here is analogous to that of a randomized trial where we can imagine the causal population impact of a harmful intervention would be a net increase in disease.

3. UNMEASURED CONFOUNDING

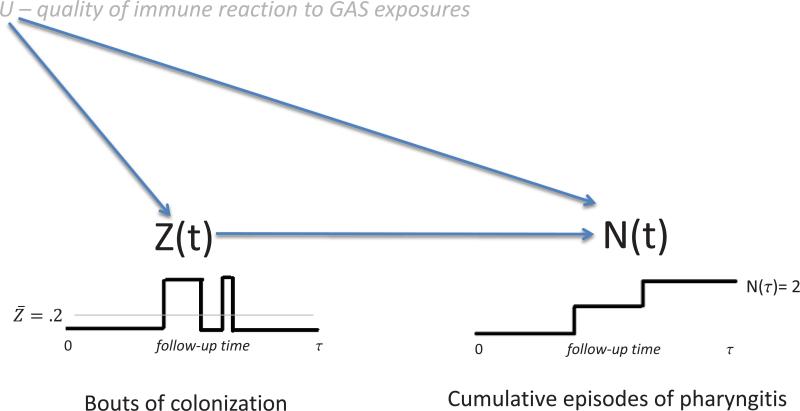
While the methods of the previous section are appropriate when Z(t) is effectively assigned at random, such pseudo-randomization is unlikely to be the case. In our example, children who tend to get colonized may have a different intrinsic risk of pharyngitis than children who tend to be free of colonization. More specifically, the components of the immune system that thwart colonization may be related to the components that fight clinical disease. A simple schematic of how the unmeasured immune system U might impact observable data is given in Figure 1. If the arrow from U to Z(t) were missing, then U can be viewed as a subject specific frailty variable and confounding would not be a concern. If the arrow from U to N(t) were missing, then standard methods that condition on Z(t) could be used to estimate the models. Importantly, this schematic assumes that U is a time-constant quality of a child that impacts both Z(t) and N(t). Relaxation of the assumption of time constancy will be discussed later.

Figure 1.

Schematic of how a time-constant unmeasured confounder U, a measure of the immune system's response to GAS exposure, impacts periods of colonization and episodes of pharyngitis.

A common approach to deal with confounding is to measure baseline covariates X that are related to both the intervention/state Z(t) and the outcome N(t). With perfect covariate selection, X essentially allows identification of U. More specifically we could formalize a model for the intensity function conditional on the history to time t,

$$\lambda \left(t\right)={\lambda }_0\left(t\right)\exp \{Z\left(t\right){\beta }_1+{\mathit{X}}^{\prime }{\beta }_2+\mathit{S}{\left(t\right)}^{\prime }{\beta }_3\},$$ (3)

where X is a vector of baseline covariates that are correlated with U so that U ≈ X′ β₂ and S(t) is a vector of time-varying covariates that can include functions of the recurrent event history of the child prior to t.

In (3) it is assumed that the effect of changes in Z(t) are immediate and complete. More sophisticated models could allow for gradual effects. For example, a ‘carryover’ impact of a change in Z(t) from 1 to 0 at time t_s could be modeled by replacing Z(t)β₁ in (3) by, {1 – t/(ω + t_s)} I {t ∈ (t_s, t_s + ω)}β₁, so that the impact of the switch gradually diminishes post shift for a period of time of length ω. For simplicity, we will focus on the simpler (3) in the sequel.

In the Vellore pharyngitis study no baseline covariates were measured so we need to develop a different way to address unmeasured confounding. For simplicity, our subsequent development ignores X and S(t) though they could be easily added as could gradual effects for switches in Z(t). Our thinking is that with long follow-up we can reliably estimate each child's long term probability of being colonized, $\overline{Z}={\int }_0^{\tau }Z\left(t\right)dt∕\tau$, and also their rate of pharyngitis, Ȳ = N(τ)/τ, where τ is the duration of follow-up. These can essentially act as separate proxies for U so the unmeasured confounder is increasingly revealed with the passage of time. In the next subsections we formalize these ideas.

3.1. Conditioning on outcome

Let N(·) = {N(t); 0 ≤ t ≤ τ} and Z(·) = {Z(t); 0 ≤ t ≤ τ}. For notational simplicity, we assume a common follow-up time τ for all subjects. This can be relaxed so subject i has followup time τ_i. In general a model for our data can be informally represented as f{N(·), Z(·), U} which can be decomposed as

$$f\{N(\cdot ),Z(\cdot ),U\}=f\{N(\cdot )\mid Z(\cdot ),U\}\times f\{Z(\cdot ),U\}.$$ (4)

An exponential model consistent with the strong pseudo-randomization assumption of the previous section can be written in this form by assuming that f{N(·) | Z(·), U} = f{N(·) | Z(·) | Z(·)}, for example by the specification

$$\lambda \left(t\right)=\exp \{{\beta }_0+Z\left(t\right){\beta }_1\}.$$ (5)

Note that f{Z(·), U}, i.e. the way the pseudo-randomization of Z(t) depends on U, is arbitrary, can vary idiosyncratically across individuals, and is ignorable under the pseudo-randomization assumption.

A more realistic model that formalizes confounding is to assume that f{N(·) | Z(·), U} is given by the proportional intensity model

$$\lambda \left(t\right)={\lambda }_0\left(t\right)\exp \{Z\left(t\right){\beta }_1+U{\beta }_2\},$$ (6)

where U follows some distribution. This model basically allows each child their own proportional deviation exp(U β₂) from the overall rate of pharyngitis λ₀(t) exp|Z(t)β₁}, as if each child is conducting their own randomized trial with periods of exposure(Z(t) = 1 or colonization) and control (Z(t) = 0, lack of colonization).

Given U and {Z(t), 0 ≤ t ≤ τ}, the number of pharyngitis events at time τ, i.e. N(τ), is a Poisson random variable with conditional mean

$$E\{N\left(\tau \right)\mid U,Z\left(t\right),0\le t\le \tau \}={\int }_0^{\tau }{\lambda }_0\left(s\right)\exp \{Z\left(s\right){\beta }_1+U{\beta }_2\}ds.$$

Suppose the time interval [0, τ] is partitioned into K subintervals {I₁, . . ., I_k} and assume that the baseline intensity function λ₀(t) is piecewise constant within each interval with values λ₀₁, . . . , λ_0K. We further assume that the covariate process is constant within each subinterval, that is, Z(t) takes values of z₁, . . . , z_K in the K subintervals. Then, given (z₁, . . . , z_K), N(τ) is a Poisson random variable with mean

$$\sum _{k=1}^K{\lambda }_{0k}{L}_k{e}^{z_k{\beta }_1+U{\beta }_2},$$

where L_k is the length of the kth interval. Moreover, the number of pharyngitis events with GAS colonization is a Poisson random variable with mean

$$\sum _{k=1}^K{\lambda }_{0k}{L}_k{e}^{z_k{\beta }_1+U{\beta }_2}I(z_k=1).$$

Let Y_k denote the number of pharyngitis episodes in the kth interval for a single individual. Then the conditional likelihood contribution for that individual's (Y₁, . . . , Y_K) given N(τ) is proportional to

$$\prod _{k=1}^K{\left(\frac{{\lambda }_{0k}{L}_k{e}^{z_k{\beta }_1+U{\beta }_2}}{{\sum }_{j=1}^K{\lambda }_{0j}{L}_j{e}^{z_j{\beta }_1+U{\beta }_2}}\right)}^{Y_k}=\prod _{k=1}^K{\left(\frac{e^{{\beta }_{0k}+z_k{\beta }_1}}{{\sum }_{j=1}^K{e}^{{\beta }_{0j}+z_j{\beta }_1}}\right)}^{Y_k},$$ (7)

where β_0k = log{λ0kL_k}. Equation (7) elegantly eliminates Uβ₂ and is a special case of the SCCS method [12, 13]. Asymptotic normality follows from the theory of a parametric multinomial likelihood and sandwich estimates of standard errors can be used to protect against model mis-specification (White 1982). Subjects with Z̄ = 0 or 1 and subjects who have no events do not provide information to this likelihood.

When λ₀(t) is a constant function, that is, λ₀₁ = · · · = λ_0K, the above model simplifies to a binomial model. The outcome is N₁ the number of events when Z(t) = 1. The binomial parameters are N(τ) the total number of events and the binomial success probability is given by

$$\frac{\stackrel{‒}{Z}∕(1-\stackrel{‒}{Z})e^{{\beta }_1}}{\stackrel{‒}{Z}∕(1-\stackrel{‒}{Z})e^{{\beta }_1}+1},$$ (8)

where $\stackrel{‒}{Z}={\sum }_{k=1}^K{L}_{k}I(z_k=1)∕{\sum }_{j=1}^K{L}_j$ is the proportion of time with Z(t) = 1.

In these conditional approaches, we assumed a piecewise constant baseline intensity λ₀(t). We can completely eliminate an arbitrary nuisance intensity function with a clever kind of conditioning applied to (6). Following [14], we consider a pair of event times from person i and k, say t_ij and t_kℓ. Define a pair of event times as comparable if both persons i and k are under observation at times t_ij and t_kℓ, that is max(t_ij, t_kℓ) ≤ min(τ_i, τ_k), where τ_i, τ_k are the follow-up duration for persons i and k, respectively. Define the indicator of this event as I_ik = max(t_ij, t_kℓ) ≤ min(τ_i, τ_k). By conditioning on the order statistics of comparable event times, the pairwise pseudo-likelihood contribution for that pair reduces to

$$\frac{1}{1+\exp \left([\{Z_i\left(t_k\right)+Z_k\left(t_i\right)\}-\{Z_i\left(t_i\right)+Z_k\left(t_k\right)\}]{\beta }_1\right)}.$$

Note that both λ₀(t) and Uβ₂ are eliminated from (6) by this pairwise conditioning. Estimation of β follows from maximizing the pairwise pseudo-likelihood

$$\prod _{i<k}\prod _{j=1}^{m_i}\prod _{\ell =1}^{m_k}{\left\{\frac{1}{1+\exp \left([\{Z_i\left(t_{k\ell }\right)+Z_k\left(t_{ij}\right)\}-\{Z_i\left(t_{ij}\right)+Z_k\left(t_{k\ell }\right)\}]{\beta }_1\right)}\right\}}^{I_{ik}},$$ (9)

where m_i is the number of events for person i and t_ij is the jth event time for person i. Huang et al. [14] proved asymptotic normality and provided sandwich estimates of variance to protect against model mis-specification [14].

A more general model would allow for effect modification where the impact of Z(t) on the risk of pharyngitis might vary with U. This might make sense for our example if children who tended to be colonized had a different probability of causation from children who tended to not be colonized. A model reflecting this interaction between U and the intervention is

$$\lambda \left(t\right)={\lambda }_0\left(t\right)\exp \{Z\left(t\right){\beta }_1+U{\beta }_2+Z\left(t\right)U{\beta }_3\}.$$ (10)

Unfortunately, neither conditioning on N(τ) nor pairwise conditioning eliminates U from the resultant model. A simple method to address such effect modification will be introduced in the next section.

3.2. Conditioning on Z̄

Another kind of decomposition leads to a different class of models. We can informally write

$$\begin{array}{cc}\hfill f\{N(\cdot ),Z(\cdot ),U\}=& f\{N(\cdot )\mid Z(\cdot ),U\}\times f\{Z(\cdot ),U\}\hfill \\ \hfill =& f\{N(\cdot )\mid Z(\cdot ),\overline{Z},U\}\times f\{Z(\cdot ),\overline{Z},U\}.\hfill \end{array}$$

We postulate that f{N(·) | Z(·), Z̄, U} = f{N(·), Z̄}. This can be justified by either thinking that U is unnecesary once Z̄ is known, or as an approximation if Z̄ is a good proxy for U. Detailed justifcation of the latter is given in the appendix. In this model Z̄ is the confounder while U is an unobserved reflection of it. Of course Z̄ is determined by Z(·) so the last assumption is equivalent to assuming f{N(·) | Z(·), U} = f{N(·) | Z(·)}. An example of this decomposition is to assume that f{N(·) | Z(·) | Z̄} is given by

$$\lambda \left(t\right)={\lambda }_0\left(t\right)\exp \{Z\left(t\right){\beta }_1+h\left(\overline{Z}\right){\beta }_2+Z\left(t\right)h\left(\overline{Z}\right){\beta }_3\}.$$ (11)

where h() is a known function such as the identity or logit. This allows the impact of Z(t) = 1 to be different for children with different Z̄s. With β₃ = 0, (11) is similar to (10) but with Z̄β₂ taking the place of Uβ₂. Note that as in the previous section, this decomposition obviates specification of f{Z(·), Z̄, U}—the method by which U determines Z(·). The model can be estimated as described in Lin et al. (2000). As before, sandwich estimators of the variance can be used to effectively weaken the assumption that conditional on Z(·), event times are independent.

In the proportional intensity model defined by (11) the risk of an event at time t depends on Z̄ which depends on data measured after time t. This seems odd, but this kind of modeling parallels pattern mixture models for missing data [19]. In such models, outcomes are modeled conditional on patterns of missingness (e.g. early dropout versus late dropout), and then an overall model for outcome is obtained by averaging over the patterns of missingness. Similar to our setting, the patterns of missingness are discerned in the future, relative to the outcomes being modeled. Equation (11) can lead to useful inference. First, we can always marginalize over the distribution of Z̄ to obtain unconditional inference. Using this maneuver, the (unconditional) probability of causation is given by

$$\mathrm{PC}=\int 1-\frac{1}{e^{{\beta }_1+h\left(\overline{Z}\right){\beta }_3}}dF\left(\overline{Z}\right),$$

where F (Z̄) can be estimated by the empirical distribution function of Z̄. Second, the dependence of PC on Z̄ may be of scientific interest. For example, with Z̄ the proportion of time colonized with GAS, a β₃ < 0 might suggest a commensal or benign relationship between the pathogen (GAS) and host (child) for larger Z̄ and a parasitic or harmful relationship between pathogn and host for small Z̄. Having the relationship between GAS and host change with Z̄ would refute the idea that GAS is always parasitic. Finally, once the data are collected, the best estimate of the future PC for a child with a historically measured Z̄_i would be the conditional PC

$$\mathrm{PC}\left(\overline{Z}\right)=1-\frac{1}{e^{{\beta }_1+h\left({\overline{Z}}_i\right){\beta }_3}}.$$

In addition to (11) being a model in its own right, it can be viewed as a kind of approximation to (10) for a time-constant confounder U. Under weak conditions, for example as given in the appendix, one can show that as τ → ∞, h(Z̄_i) → h(z_i) = U_i. Thus with a long followup, h(Z̄) becomes a proxy for U.

This approximation is predicated on the idea that τ is ‘large enough’. If τ is not large enough, the approximation may be poor and one can explore different corrections. Under the assumption of a time-constant confounder and weak conditions on the distribution of sojourn times, we have h(Z̄_i) ≈ N{U_i, ω²(U_i)} for large τ (see Appendix). Put another way we have

$$h\left({\overline{Z}}_i\right)\approx U_i+e_i$$ (12)

where e_i has a normal distribution with variance ω²(U_i). Juxtaposing (12) with (11) reveals a classic Gaussian measurement error model where we observe the error-prone h(Z̄_i) instead of the true covariate U_i. Measurement error corrections could be entertained if we could estimate ω²(U_i), but this is not estimable without further assumptions. Another approach would be to use the decomposition (4) with f{Z (·),|Z(·), U} given by (10) and f{Z(·)|U} = f{Z(·)|U}f(U) where f(U) is Gaussian and f{Z(·)|U} follows some parametric process. This development parallels shared parameter model for missing data (see e.g. [21] and [22]). Here the shared parameter is U_i and it governs the observable event times and Z̄_i. In shared parameter models for missing data, the shared parameter governs both the outcomes and the missingness indicators. Formal development of these approaches is beyond the scope of this paper but could be interesting future work.

4. SIMULATIONS

In this section we evaluate 6 different methods of estimation under different scenarios by simulation.

1. Naive: Here we fit the simple proportional intensity model with no confounding,

   $$\lambda \left(t\right)={\lambda }_0\left(t\right)\exp \left\{Z\left(t\right){\beta }_1\right\}.$$
2. Binomial: We assume the proportional intensity model has a constant baseline intensity function modulated by an unmeasured confounder U,

   $$\lambda \left(t\right)=\exp \{{\beta }_0+Z\left(t\right){\beta }_1+U{\beta }_2\},$$

   and condition on the number of events. This leads to a binomial likelihood with parameter β₁ from equation (8) and is a simple SCCS approach.
3. Multinomial: We assume a piecewise constant exponential baseline rate function modulated by an unmeasured confounded U,

   $$\lambda \left(t\right)=\exp \{\sum _{k=1}^5{\beta }_{0k}I(t\in I_k)+Z\left(t\right){\beta }_1+U{\beta }_2\}$$

   where I_k defines the intervals (0, 0.2), (0.2, 0.4), . . . , (0.8, 1). Conditioning on N(τ) leads to a multinomial likelihood with 4 β_0k parameters and β₁. This method is a more sophisticated SCCS approach.
4. Pair: We maximize the pairwise pseudo-likelihood given by (9) to estimate β₁. This eliminates λ₀(t) and U from the proportional intensity model with arbitrary baseline intensity

   $$\lambda \left(t\right)={\lambda }_0\left(t\right)\exp \{Z\left(t\right){\beta }_1+U{\beta }_2\}.$$
5. Z̄ : We fit a proportional intensity model where the intervention interacts with Z̄

   $$\lambda \left(t\right)={\lambda }_0\left(t\right)\exp \{Z\left(t\right){\beta }_1+\overline{Z}{\beta }_2+\overline{Z}Z\left(t\right){\beta }_3\},$$

   This approximates both (6) (with β₃ = 0) and (10).
6. Omni: We fit the correct “omniscient” proportional intensity model that has knowledge of U

   $$\lambda \left(t\right)={\lambda }_0\left(t\right)\exp \{Z\left(t\right){\beta }_1+U{\beta }_2+UZ\left(t\right){\beta }_3\}.$$

   Based on these regression parameter estimates, we evaluate estimates of PC which equals $1-1∕\exp \left({\widehat{\beta }}_1\right)$ for the first four methods of estimation. For Method 5, $\widehat{\mathrm{PC}}$ equals $E_Z\{1-1∕\exp ({\widehat{\beta }}_1+Z{\widehat{\beta }}_3)\}$ where E_Z(·) is over the empirical distribution of the sample ${\overline{Z}}_i\mathrm{s}$. For the omniscient Method 6, $\widehat{\mathrm{PC}}=E_U\{1-1∕\exp ({\widehat{\beta }}_1+U{\widehat{\beta }}_3)\}$ where E_U(·) is over the empirical distribution of the U_is.

To generate data we use the decomposition

$$f\{N(\cdot ),Z(\cdot ),U\}=f\{N(\cdot )\mid Z(\cdot ),\overline{Z},U\}\times f\{Z(\cdot ),\overline{Z}\mid U\}\times f\left(U\right).$$

We specify

• f(U) is given by $U\stackrel{D}{=}N(0,{\sigma }_U^2)$

• f(Z(), Z̄|U) is given b Z(t) = 1 if t ≤ exp (μ + U + ϵ)/{1 + exp(μ + U + ϵ)} and Z(t) = 0 otherwise, where $ϵ\stackrel{D}{=}N(0,{\sigma }_e^2)$, and thus $\overline{Z}={\int }_0^{1}Z\left(s\right)ds$

• f(N(·) | Z(·), U) is determined by the proportional intensity model

  $$\lambda \left(t\right)={\lambda }_0\left(t\right)\exp \{{\beta }_{1}Z\left(t\right)+U{\beta }_2+UZ\left(t\right){\beta }_3\}$$

For our first scenario, we assume λ₀(t) = exp(β₀). We let μ = −2 and μ = 0, the latter induces a symmetry in the distribution of Z̄ around 0.5, while μ = −2 better approximates the Vellore study. We consider three settings for β = (β₀, β₁, β₂, β₃): (0, 1, 0, 0), (0, 1, 1, 0), and (0, 1, 1, −1); these correspond to no confounding, confounding, and confounding with interaction. For each β we vary σ_e, σ_U = (2,1),(2,.5),(1,1), (1,.5), (.5,1), and (.5,.5). Decreasing σ_U tends to reduce the impact of unmeasured confounding while decreasing σ_e tends to make Z̄ a better proxy for U as would happen with a larger study. However, smaller σ_U, σ_e induce less variation in Z̄ which makes it harder to estimate the coefficients associated with Z̄ in (11), namely β₂, β₃.

Table 2 presents selected results for μ = −2. For all simulation results we use robust estimators of the mean and variance (median and scaled median absolute deviation) due to occasional outlier estimates of PC, especially for the simpler methods. The robust estimates more clearly reveal performance of the estimators.

Table 2.

Performance of different estimates of the probability of causation.

Simulation Settings						Probability of Causation
β 2	β 3	σ e	σ U	$\overline{N_{+}}$	P̂ +	Naive	Bin	Mult	Pair	Z̄	Omni
0	0	1.0	1.0	201	0.512	0.633	0.631	0.632	0.633	0.631	0.630
						0.019	0.029	0.030	0.031	0.030	0.021
						0.001	−0.001	0.000	0.001	−0.001	−0.002
						0.019	0.029	0.030	0.031	0.030	0.021
0	0	0.5	0.5	168	0.451	0.634	0.634	0.636	0.635	0.634	0.629
						0.024	0.031	0.032	0.032	0.046	0.025
						0.002	0.002	0.004	0.003	0.002	−0.003
						0.024	0.031	0.032	0.032	0.046	0.025
1	0	1.0	1.0	431	0.499	0.807	0.630	0.630	0.631	0.632	0.635
						0.009	0.014	0.016	0.017	0.026	0.025
						0.175	−0.002	−0.002	−0.001	0.000	0.003
						0.320	0.014	0.016	0.017	0.026	0.025
1	0	0.5	0.5	211	0.449	0.698	0.634	0.635	0.634	0.576	0.628
						0.015	0.024	0.026	0.026	0.067	0.034
						0.066	0.002	0.003	0.002	−0.056	−0.004
						0.059	0.024	0.026	0.026	0.098	0.034
1	−1	1.0	1.0	265	0.521	0.487	0.244	0.249	0.230	0.384	0.381
						0.059	0.200	0.190	0.170	0.100	0.098
						0.093	−0.150	−0.145	−0.164	−0.010	−0.013
						0.145	0.425	0.400	0.439	0.101	0.100
1	−1	0.5	0.5	187	0.456	0.598	0.536	0.539	0.528	0.582	0.580
						0.030	0.059	0.058	0.062	0.049	0.032
						0.015	−0.047	−0.044	−0.055	−0.001	−0.003
						0.032	0.081	0.077	0.092	0.049	0.032

NOTE: The proportional rate function is given by exp(0 + Z(t)1 + Uβ₂ + UZ(t)β₃) with $U\stackrel{D}{=}N(-2,{\sigma }_U^2)$. Each set of four rows provides medians,robust variance (×10), median bias, and robust MSE (×10) for the different estimators over 1000 simulated studies, each with 200 subjects. Columns 5 and 6 report the average number of events and proportion of patients with at least 1 event, averaged over the simulations.

For Setting 1, with no confounding, β = (0, 1, 0, 0), we are simulating a randomized trial and all methods are unbiased for PC. For (σ_e, σ_U) = (1, 1) the naive and omniscient methods have the smallest MSE while for (σ_e, σ_U) = (0.5, 0.5) the Z̄ method has the largest MSE. For Setting 2, β = (0, 1, 1, 0), U has an impact in terms of confounding but no effect modification. Here the naive method is quite biased for all (σ_U, σ_e) = (1, 1). while the other methods are all unbiased. The proportional rate Z̄ method is unbiased but has larger variance than the binomial, multinomial, and pairwise methods. Note that the binomial, multinomial, and pairwise methods are properly specified here while the proportional intensity model with Z̄ is a kind of poor man's approximation for U and is unnecessarily estimating an interaction term. For (σ_U, σ_e) = (.5, .5) the naive and Z̄ methods are mildly biased and the Z̄ method has the largest MSE. For setting 3, β = (0, 1, 1, −1), U is both a confounder and an effect modifier. Here we see that only the Z̄ and omniscient methods are unbiased. Interestingly for (σ_U, σ_e) = (1, 1) the MSE of the Z̄ and omniscient methods are similar.

Over all settings, the pairwise conditional model of Huang et al. looks similar to the SCCS multinomial model in terms of bias and variance. In these simulations with an exponential baseline rate function, methods that allow for nonconstant or arbitrary baseline rate functions are unnecessarily flexible. The simple proportional intensity model with Z̄ is unbiased for nearly all scenarios and the only reliable choice for Scenario 3. In summary, the pairwise conditional approach of Huang et al. is preferred unless scenario 3 holds in which case the Z̄ model is necessary. Simulations with μ = 0 reveal very similar results for the means of the estimates but generally smaller variances as more events result from μ = 0. Simulations where the Z(t) = 1 epochs are randomly assigned over time (instead of always at the start) reveal similar behavior. The behavior for the unreported σ_U, σ_es is similar.

For our next set of simulations we set λ₀(t) to be piecewise constant, −0.45, −0.15, 0.15, 0.45, 0.75, over 5 intervals of equal length. We set Z̄* = [|5Z̄|]/5 + 1 * B, where Z̄ was generated as above, [|·|] is the greatest integer function, and B is Bernoulli(1/2). Thus Z̄* is a kind of discretized version of Z̄ that can equal 0, 0.2, . . . ,1, and Z̄* is a poorer proxy for U than Z̄. Based on Z̄* we either randomly assigned the epochs of 0 and 1 over the 5 intervals, or placed all the 1s over the first intervals. For this latter scenario Z(t) tends to be conflated with the piecewise λ₀(t).

Table 3 reports selected results for μ = −2 and conflation of Z(t) = 1 with followup time. We see again that the proportional intensity model does best for Scenario 3 while the pairwise and multinomial models do best for Scenario 2. The pairwise and multinomial methods fail quite spectacularly if there is differential confounding i.e. β₃ ≠ 0, but are unbiased when β₃ = 0. The behavior for the unreported σ_U, σ_es is similar. When we re-ran the simulation with epochs of Z(t) = 1 randomized, the performance of the methods were similar to Table 2. Simulations with μ = 0 reveal generally very similar results for the means of the estimates but generally smaller variances as more events result when μ = 0;

Table 3.

Performance of different estimates of the probability of causation.

Simulation Settings						Probability of Causation
β 2	β 3	σ e	σ U	$\overline{N_{+}}$	P̂ +	Naive	Bin	Mult	Pair	Z̄	Omni
0	0	1.0	1.0	220	0.533	0.631	0.200	0.635	0.634	0.627	0.629
						0.041	0.160	0.083	0.087	0.120	0.061
						−0.001	−0.432	0.003	0.002	−0.005	−0.003
						0.041	2.000	0.083	0.087	0.120	0.061
0	0	0.5	0.5	184	0.468	0.631	0.183	0.634	0.636	0.636	0.625
						0.087	0.180	0.120	0.110	0.190	0.110
						−0.001	−0.449	0.002	0.004	0.004	−0.007
						0.087	2.200	0.120	0.110	0.190	0.110
1	0	1.0	1.0	467	0.510	0.886	0.201	0.620	0.622	0.644	0.634
						0.008	0.070	0.043	0.041	0.079	0.045
						0.254	−0.431	−0.012	−0.010	0.012	0.002
						0.650	1.900	0.044	0.042	0.080	0.045
1	0	0.5	0.5	232	0.467	0.771	0.187	0.639	0.641	0.578	0.633
						0.033	0.140	0.081	0.083	0.250	0.084
						0.139	−0.445	0.007	0.009	−0.054	0.001
						0.230	2.100	0.081	0.084	0.280	0.084
1	−1	1.0	1.0	322	0.527	0.555	−0.860	−0.016	−0.015	0.377	0.383
						0.066	1.300	0.750	0.720	0.260	0.160
						0.161	−1.254	−0.410	−0.409	−0.017	−0.011
						0.325	17.000	2.430	2.390	0.263	0.161
1	−1	0.5	0.5	213	0.472	0.627	−0.056	0.471	0.477	0.567	0.575
						0.076	0.310	0.210	0.210	0.240	0.110
						0.044	−0.639	−0.112	−0.106	−0.016	−0.008
						0.095	4.390	0.335	0.322	0.243	0.1110

NOTE: The proportional rate function is given by exp(A_k + Z(t)1 + Uβ₂ + UZ(t)β₃) for k = 1,. . ., 5 with $U\stackrel{D}{=}N(-2,{\sigma }_U^2)$. Each set of four rows provides medians,robust variance (×10), median bias, and robust MSE (×10) for the different estimators over 1000 simulated studies, each with 200 subjects. Columns 5 and 6 report the average number of events and proportion of patients with at least 1 event, averaged over the simulations.

In practice one would pick a method that is informed by inspection of the data, thus one might fit a model which allows for interaction with Z̄ or functions of Z̄. If an interaction model is not necessary, then the pairwise conditional model would be appealing as it eliminates arbitrary subject specific baseline intensity functions with little loss of efficiency.

5. ANALYSIS OF THE VELLORE STUDY

A World Health Organization report estimates that there are over 616 million new cases per year of GAS pharyngitis, of which over 550 million occur in less developed countries. Pharyngitis is most frequently due to viruses, but several bacteria, including Group A streptococci (GAS), persist as a common cause of pharyngitis even in the era of antibiotics. For a child who presents with GAS and pharyngitis, it is not at all certain that the GAS is responsible as the GAS may be incidental to a viral cause. Because there can be serious complications following untreated streptococcal pharyngitis such as rheumatic heart disease and toxic shock syndrome, the standard practice is to treat with penicillin or other antibiotics, even though there is recognition that some unknown proportion of these will be treated unnecessarily. Overuse of antibiotics is a serious worldwide public health concern as it can lead to the development of resistant strains of bacteria which are not treatable by current antibiotics [23, 24]. Thus it is of substantial interest to estimate the probability of causation and possibly tailor antibiotic therapy to those with a high probability of a bacterial cause.

To address these issues, a study of 307 school children in a rural area near Vellore, India was conducted between March 2002 and March 2004 [16]. The enrolled children were followed longitudinally in two different ways. Cases of pharyngitis were identified weekly and throat swabs were obtained on those with pharyngitis to identify the presence of GAS. We call this the pharyngitis data. Children with GAS positive pharyngitis were treated with a brief course of penicillin.were obtained on the student volunteers to determine the prevalence of GAS. We call this the carriage data. Statistically, GAS colonization is a time-varying covariate with pharyngitis the recurrent event.

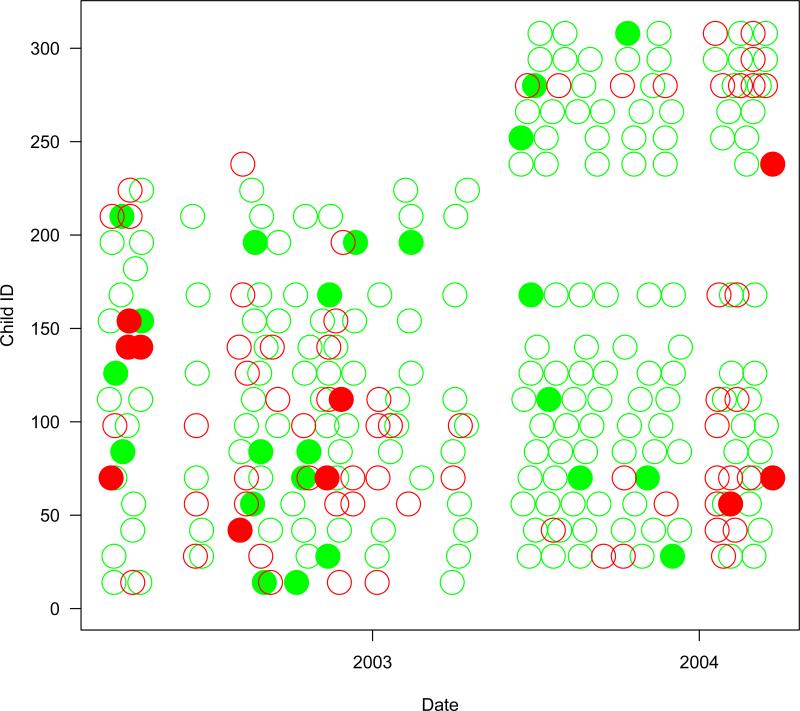
Overall, 218 of the 307 children had at least one episode of pharyngitis. The median number of episodes was 2 with a maximum of 12. The median colonization rate was 0.08 with 25th and 75th percentiles of 0 and 0.17, respectively; 125 children were never colonized while 3 were always colonized. Table 4 provides a tally of the data while Figure 1 provides data trajectories for 22 selected children. Notable are gaps during school holidays and the enrollment of additional children to make up for those who left at the end of a school year.

Table 4.

Episodes of pharyngitis (sore throat) and carriage visits classified by the presence of Group A Streptococcus in the throat.

	Carriage Data Monthly Visit	Event Data # Pharyngitis Events
No Group A Strep	2504	530
Group A Strep	323	110
Total	2827	640

We begin our analysis by fitting the simple proportional intensity model

$$\lambda \left(t\right)={\lambda }_0\left(t\right)\exp \left\{Z\left(t\right){\beta }_1\right\}.$$

The carriage data does not provide continuous measurement of Z(t) so we use the value from each monthly visit to specify Z(t) until the next monthly visit, except at event times when the GAS readout from the pharyngitis visit is used.

Under this naive model we obtain an estimate of the probability of causation as 1 – 1/ exp(0.25) = 0.22 with a 95% bootstrap confidence interval of (0.04, 0.38). This estimand has a casual interpretation if Z(t) is essentially randomly assigned, however this assumption is suspect. We next condition on the total number of events from each child, forming the binomial model with offset of log{Z̄(1 – Z̄)} as given in (8). This requires a constant baseline intensity function and eliminates confounding due to a main effect. Only children with at least 1 event and both positive and negative carriage visits contribute to the likelihood. This filtering results in reducing the 307 children to 136 and the number of events from 640 to 446. The median Z̄ over the 136 selected children is 0.15. The resultant PC is 0.14 with a 95% bootstrap confidence interval of (−0.08, 0.35). We also estimate PC using the pairwise approach which allows for an arbitrary baseline intensity; this gives a PC of 0.12 with a 95% bootstrap confidence interval of (−0.18, 0.32). Of course a probability cannot be less than zero. The negative values here reflect the sampling variability in the estimate of PC. If the estimated PC were reliably negative it would call into question the assumption that GAS colonization cannot prevent disease (i.e. that θ₁₀ = 0 of Table 1).

Our final analysis allows for different effects of Z(t) for children who are either above or below the overall median colonization rate. We fit the proportional intensity model

$$\lambda \left(t\right)={\lambda }_0\left(t\right)\exp [Z\left(t\right){\beta }_1+I\{\overline{Z}>\text{median}\left(\overline{Z}\right)\}{\beta }_2+I\{\overline{Z}>\text{median}\left(\overline{Z}\right)\}Z\left(t\right){\beta }_3],$$ (13)

where median(Z̄) = .08. This model uses all children including those with no events. While it is an easy-to-interpret model in its own right, it can also be viewed as a direct proxy for the model

$$\lambda \left(t\right)={\lambda }_0\left(t\right)\exp [Z\left(t\right){\beta }_1+I\{U>\text{median}\left(U\right)\}{\beta }_2+I\{U>\text{median}\left(U\right)\}Z\left(t\right){\beta }_3],$$ (14)

under the weak assumption that E(Z̄_i) → _g(U_i) for any monotone g(). In other words, the covariate choice of U as above or below the median obviates concern about what function maps U_i to $\overline{z_i}$.

For this model, the three β coefficients are, respectively .98, .33 and −.99 with p < .005 for each based on Wald tests with sandwich-based standard errors. This indicates strong effect modification and casts doubt on the estimates of the previous paragraph. The estimated probabilities of causation are 0.62 with a 95% CI of (0.40, 0.76) and −0.01 with a 95% CI of (−0.34, 0.22), for children who are colonized less than or more than the median, respectively. Thus for children who are colonized rarely, the novel insult of GAS has a high probability of causing the pharyngitis, while for children who have repeated colonizations the familiar GAS colony in the throat is unlikely to cause the pharyngitis. In practice, if one knew a child's history of colonization the PC conditional on Z̄ could be used to guide therapy with antibiotics strongly recommended for children with a rare bout of colonization. These estimates can also be used to provide an overall estimate of the probability of causation for a randomly selected child without knowledge of past colonization status. The marginalized PC is .62 × 0.5 – 0.01 × 0.5 = 0.31 which has 95% bootstrap confidence interval of (0.12, 0.44).

For (13) to be an approximation to (14) requires that τ be large enough. We reasoned that if estimates with τ/2 follow-up were close to those with τ follow, then we would have evidence that τ were large enough. We thus created two datasets, one for each of the two school years, and reran the analysis. This provides us with two estimates, each based on approximately τ/2 follow-up. We obtained marginalized PC estimates of .33 for year 1 and .27 for year 2, both close to the .31 based on the entire dataset. We also fashioned a test to see if either were statisticaly far from the .31 based on the entire dataset. We simulated a null distribution by randomly selecting half the children (and their entire followup) and calculating the marginalized PC. Under the null that $E\left\{\widehat{PC}(\tau ∕2)\right\}=E\left\{\widehat{PC}\left(\tau \right)\right\}$, this simulated distribution should approximate the distribution of an estimate of $\widehat{PC}(\tau ∕2)$, in this dataset as both are based on half the total information. The year 1 and year 2 marginalized PCs fall at the 38th and 67th percentiles of this distribution, corresponding to two-sided p-values of .76 and .66, respectively. We thus have evidence that τ (or even τ/2) is large enough for the approximation of (13) to (14) to be accurate.

Finally, we performed a sensitivity analysis for the assumption of “no carryover” i.e. that the effect of Z(t) switching from 1 to 0 is immediate and complete. We created an additional time-varying covariate which was 1 for a window of length m months following a 1 to 0 switch and 0 otherwise. For m=2 and 4, the effect of this covariate was near zero and there was minimal change in the estimates of the other βs.

Another estimand of interest is the attributable fraction. This estimates the proportion reduction in clinical pharyngitis in a new world where clinical pharyngitis due to GAS is eliminated. In this development we assume that GAS colonization cannot prevent disease. For the proportional intensity model with an interaction term for Z(t) and Z̄ the construction is somewhat tricky. The subtly here is how to calculate the risk of pharyngitis for a child who had Z̄ = p in the Vellore study in this new world. Because Z̄ is essentially a proxy for an unmeasured confounder U, it is an intrinsic quality of the child and from (13) her risk of pharyngitis at time t when she is uncolonized is

$${\lambda }_0\left(t\right)\exp \left[{\beta }_{2}I\{p>\text{median}\left(p\right)\}\right].$$

It follows that the attributable fraction can be expressed as

$$AF=1-\frac{E_{\overline{Z}}\left[\Delta {\lambda }_0\left(t\right)\exp \left\{{\beta }_{2}I(\overline{Z}>\text{median}\left(\overline{Z}\right))\right\}\right]}{E_{ZC}\left[\Delta {\lambda }_0\left(t\right)\exp \{{\beta }_{1}Z\left(t\right)+{\beta }_{2}I(\overline{Z}>\text{median}\left(\overline{Z}\right))+{\beta }_{3}I(\overline{Z}>\text{median}\left(\overline{Z}\right))Z\left(t\right)\}\right]}.$$

Here E_Z̄ is the expectation over the distribution of Z̄, while E_ZC is the expectation of Z(t) in the current environment. We can estimate AF as

$$1-\frac{{\sum }_{i=1}^n\exp \left\{{\widehat{\beta }}_{2}I({\overline{z}}_i>\text{median}\left({\overline{z}}_i\right))\right\}]∕n}{{\sum }_{i=1}^n[{\overline{z}}_i\exp \{{\widehat{\beta }}_1+I({\overline{z}}_i>\text{median}\left({\overline{z}}_i\right))({\widehat{\beta }}_2+{\widehat{\beta }}_3)\}+(1-{\overline{z}}_i)\exp \left\{I({\overline{z}}_i>\text{median}\left({\overline{z}}_i\right)){\widehat{\beta }}_2\right\})]∕n}.$$

An attributable fraction is of policy interest as it can estimate the impact on pharyngitis disease of a perfectly effective vaccine with perfect community uptake. We estimate the AF as −.01 with a 95% bootstrap confidence interval of (−.19,.14). As mentioned earlier, the AF can be truly less than 0 if, on average, GAS prevents more cases of pharyngitis than it causes. An estimated AF can be less than 0 due to sampling variability. In the Vellore study, 530 of 640 cases of pharyngitis had no GAS present. Thus over 80% of pharyngitis cases could not be caused by GAS and the fraction of pharyngitis cases attributable to GAS is near zero with uncertainly about the estimate reflected in the confidence interval. This analysis suggests that a perfect vaccine would have little impact on pharyngitis disease in this population.

6. DISCUSSION

This paper has examined how different methods can be used to draw causal conclusions for a transient exposure on recurrent event data in the presence of a time-constant confounder. We considered methods that conditioned on the total number of events, the timing of pairs of events, and the overall intervention rate for each person. Without effect modification, but allowing for confounding and arbitrary baseline intensity the pairwise conditional approach of [14] is appealing as it eliminates the nuisance confounding and the nuisance baseline intensity function. With effect modification, a simple proportional intensity model that allows for an interaction with Z̄—a proxy for the unmeasured confounder—does best, while other methods can be badly biased. The key trick underling the proportional intensity model with interaction is to use the future Z(t), via Z̄ as a proxy for unmeasured confounding. This trick is similar to pattern mixture models for missing data.

For simplicity (and necessity for the Vellore study) our development avoided the incorporation of other covariates, however, they can be easily incorporated into the methods. These may serve as additional proxies for unmeasured confounding or be of scientific interest by themselves for the proportional intensity model. Methods that condition on outcome (binomial, multinomial, pairwise) eliminate time-constant covariates, however, time-varying covariates are not eliminated and can be used in these conditional methods, or generalizations of them. Our development assumed that the data were conditionally independent, given the conditioning variables (for example, Z(t) and/or N(τ)). In practice there might be auto-correlation in the outcomes even given these conditioning variables. To address this, time-varying functions of the outcome history might be incorporated as additional covariates in our models to weaken the assumption of conditional independence.

We made the strong assumption that the confounder did not vary with time. In practice, this assumption can be weakened by partitioning the data into sets within which the confounder is approximately time-constant, estimating parameters within these sets and then combining the estimates using inverse variance weights. For example, we could break the data in half by calendar time and stratify. Or for each person we could partition their time axis into 4ths, calculate Z̄ for each and then stratify by the 2 high Z̄s versus the 2 low Z̄s This would allow for different probabilities of causation during transient epochs where Z(t) tended to be relatively common for an individual, or relatively rare for an individual. Further development of such approaches is left to future research.

Figure 2.

The presence of Group A Streptococcus in the throat for 22 selected children during the study. Monthly carriage visits are denoted by an open circle. Any weekly positive pharyngitis visit during the month is denoted by a closed circle. Green circles denote GAS negative visits, while red circles denote GAS positive visits.

APPENDIX

In this appendix we sketch out a class of models where h(Z̄) → U τ → ∞. Rather than working directly with the process {Z(s); 0 ≤ s ≤ τ} consider the representation of {Z(s); 0 ≤ s ≤ τ} as the alternating sojourn times in state 0 and 1, say $T_1^0,\dots ,T_{N^0\left(\tau \right)}^0$ and $T_1^1,\dots ,T_{N^1\left(\tau \right)}^1$ respectively, where N^z(τ) is the random number of sojourn times in state z by time τ. We assume that $E\left(T_j^z\right)={\mu }_z\left(U\right)$, $\mathrm{var}\left(T_j^z\right)={\sigma }_z^2\left(U\right)$, that sojourn times are independent conditional on U.

We have N^z(τ) → ∞ as τ → ∞. Consider the random sum

$$\overline{T^z}\left(\tau \right)=\sum _{j=1}^{N^z\left(\tau \right)}\frac{T_j^z}{N^z\left(\tau \right)},$$

which is random because N^z(τ) is random. Now by the law of large numbers as τ → ∞, we have

$$\overline{T^z}\left(\tau \right)\to {\mu }_z\left(U\right),$$

in probability as τ → ∞.

By the central limint theorem for iid random variables we have

$$\sqrt{N^z\left(\tau \right)}\{\overline{T^z}\left(\tau \right)-{\mu }_z\left(U\right)\}\to \mathrm{N}\{0,{\sigma }_z^2\left(U\right)\}.$$

Next, consider the proportion of time that the generic person is in state 1 over the interval (0, τ). This is

$$\overline{Z}\left(\tau \right)=\frac{{\sum }_{j=1}^{N^1\left(\tau \right)}{T}_j^1}{{\sum }_{j=1}^{N^1\left(\tau \right)}{T}_j^1+{\sum }_{j=1}^{N^0\left(\tau \right)}{T}_j^0}=\frac{{\sum }_{j=1}^{N^1\left(\tau \right)}{T}_j^1∕\overline{N}\left(\tau \right)}{{\sum }_{j=1}^{N^1\left(\tau \right)}{T}_j^1∕\overline{N\left(\tau \right)}+{\sum }_{j=1}^{N^0\left(\tau \right)}{T}_j^0∕\overline{N\left(\tau \right)}},$$

in distribution as τ → ∞ where N̄(τ) = {N¹(τ) + N⁰(τ)}/2. Note that |N¹(τ) – N⁰(τ)| is either 0 or 1 for all τ as the sojourn times alternate. We can thus show that the asymptotic results for

$$\overline{T^z}\left(\tau \right)=\sum _{j=1}^{N^z\left(\tau \right)}\frac{T_j^z}{N^z\left(\tau \right)}$$

are the same as the asymptotic results for

$$\sum _{j=1}^{\overline{N\left(\tau \right)}}\frac{T_j^z}{\overline{N\left(\tau \right)}}.$$

Thus as τ → ∞.

$$\overline{Z}\to \frac{{\mu }_1\left(U\right)}{{\mu }_1\left(U\right)+{\mu }_0\left(U\right)}=\overline{z}\left(U\right),$$

in probability.

By the delta method we obtain

$$\sqrt{\overline{N}\left(\tau \right)}\{\overline{Z}-\overline{z}\left(U\right)\}\to \mathrm{N}\left(0,{\tau }^2\left(U\right)=\frac{{\mu }_0{\left(U\right)}^2}{{\{{\mu }_0\left(U\right)+{\mu }_1\left(U\right)\}}^4}{\sigma }_1^2\left(U\right)+\frac{{\mu }_1{\left(U\right)}^2}{{\{{\mu }_0\left(U\right)+{\mu }_1\left(U\right)\}}^4}{\sigma }_0^2\left(U\right)\right),$$

in distribution as τ → ∞.

Define h() as satisfying

$$U=h\left(\frac{{\mu }_1\left(U\right)}{{\mu }_1\left(U\right)+{\mu }_0\left(U\right)}\right).$$

By another application of the delta-method we have

$$\sqrt{\overline{N\left(\tau \right)}}\{h\left(\overline{Z}\right)-U\}\to \mathrm{N}\{0,{\left\{h^{\prime }\left(U\right)\right\}}^2{\tau }^2\left(U\right)\}$$ (15)

in distribution as τ → ∞.

Based on (15) we obtain the classical measurement error model which can be written as

$$h\left(\overline{Z}\right)\approx U+ϵ$$

where ϵ is distributed N[0, ω²(U) = {h′(U)}²τ²(U)].