Prediction of response factors for gas chromatography with flame ionization detection: Algorithm improvement, extension to silylated compounds, and application to the quantification of metabolites

Abstract

We previously showed that the relative response factors of volatile compounds were predictable from either combustion enthalpies or their molecular formulae only 1. We now extend this prediction to silylated derivatives by adding an increment in the ab initio calculation of combustion enthalpies. The accuracy of the experimental relative response factors database was also improved and its population increased to 490 values. In particular, more brominated compounds were measured, and their prediction accuracy was improved by adding a correction factor in the algorithm. The correlation coefficient between predicted and measured values increased from 0.936 to 0.972, leading to a mean prediction accuracy of ± 6%. Thus, 93% of the relative response factors values were predicted with an accuracy of better than ± 10%. The capabilities of the extended algorithm are exemplified by (i) the quick and accurate quantification of hydroxylated metabolites resulting from a biodegradation test after silylation and prediction of their relative response factors, without having the reference substances available; and (ii) the rapid purity determinations of volatile compounds. This study confirms that Gas chromatography with a flame ionization detector and using predicted relative response factors is one of the few techniques that enables quantification of volatile compounds without calibrating the instrument with the pure reference substance.

Abbreviations

BSTFA

N,O‐bis(trimethylsilyl)trifluoroaceta‐mide

DFT

density functional theory

FID

flame ionization detector

ISTD

internal standard

MRF

molar response factor

RRF

relative response factor

TMCS

trimethylchlorosilane

1. Introduction

GC with flame ionization detection (FID) is one of the most popular techniques to quantify volatile compounds. In the scientific literature on flavors, fragrances, and essential oils, the raw percentages of peak areas are often used as such, or in association with that of an internal standard (ISTD) and assuming that all response factors are equal to unity. We have previously reported that such an approach leads to poor accuracy 2. In contrast, quantifying by rigorous methods (internal standardization, internal normalization) is accurate but time‐consuming, because it requires the building of calibration curves, or to experimentally determine the response factors relative to a given ISTD 3. To skip this step, several authors have proposed predicting the response factors by using different theoretical models: quantitative structure–property relationships 4, 5, 6, 7, 8 or empirical models, such as the “effective carbon number” 9. The former are often characterized by their complexity, which discourages analysts from using them. The latter is based on an incremental calculation involving the contribution of the different functional groups of the compound 9, which requires additional experimental work when a new functional group is considered 10.

To avoid the experimental determination of relative response factors (RRFs) for each GC quantification, we have demonstrated that they are reproducible enough over time and from one instrument to another to be compiled in a database and reused afterward 2. Although this considerably shortens the quantification procedure, it does not solve the challenge of compounds that are not available in pure state to be used as standards, or those that are not stable enough to be stored before use for the determination of their RRFs. To overcome these difficulties, we previously developed a new approach to predict the RRFs 1: based on the fact that an FID is a burner, it was hypothesized that the RRFs would be correlated with the combustion enthalpies of compounds. The latter were determined by ab initio calculations and were linearly correlated with RRFs. However, these combustion enthalpies were themselves linearly correlated to the molecular formulae of corresponding compounds (R = 0.999), and so the RRFs were also predicted on the sole basis of molecular formulae with an accuracy of better than ±10% for 81% of the 351 database compounds (the accuracy being expressed here, and in the present work, as the relative difference from the predicted to the measured RRF). The algorithm included most of the atoms found in compounds analyzed by GC (C, H, O, S, N, F, Br, Cl, and I), and was tested on a variety of functional classes (hydrocarbons, alcohols, phenols, aldehydes, ketones, esters, lactones, ethers, sulfur compounds, nitrogen compounds, halogenated compounds, benzene derivatives). Although the real combustion enthalpy of hydrocarbons is supposed to yield HCO⁺ ions in most cases, this did not seem to be valid for benzene derivatives, because a correction term was required for such species. Therefore, we correlated the FID signal with the enthalpy of a full combustion, knowing that this is an indirect correlation.

In another paper, the capabilities of the RRF calculation were tested for the quantification of a complex mixture (essential oil) 10. The workload was shortened from three days with an experimental determination of RRFs to 3 h by using the predictive algorithm, while maintaining good accuracy (mean relative bias between the composition using the predicted RRF compared with that using internal standardization: 0.9%). In the same paper, the approach was also used to quantify unstable or noncommercially available substances. The results were confirmed by using alternative techniques, such as quantitative NMR spectroscopy.

Since the publication of this predictive model, several papers have reported applications not only to the flavor and fragrance domain, but to new areas as well. Delort et al. 11, for example, quantified the aroma compounds of oyster leaf by using compiled and predicted RRFs. Because metabolomic studies require the production of hugely large data sets, a very time‐consuming process, Mehl et al. quantified the constituents of 64 lemon essential oils by GC–FID, also by using compiled and predicted RRFs 12. Similarly, comprehensive 2D GC (GC × GC) generates hundreds of peaks and the individual measurement of corresponding RRFs is not conceivable. Filippi et al., however, used predicted RRFs to quantify, for the first time, 123 constituents of a very complex essential oil, Vetiver, by internal standardization and GC × GC 13. In the context of bio‐oils, Olcese et al. quantified about 160 volatiles generated by the pyrolysis of lignin by multidimensional GC 14, 15. Dalluge et al. 16 quantified volatiles resulting from the pyrolysis of a carbohydrate‐rich biomass by GC–FID, after having determined the molecular formula of the unknowns by TOF‐MS. The kinetics of a chemical reaction was monitored by Neuenschwander et al. 17, and an original study by Young et al. 18 investigated the applicability of calculated RRFs to HPLC with superheated water as a mobile phase and an FID detector hyphenated to the column through a nebulizer and a cyclonic spray chamber: “the LC–FID responses for many of the volatile analytes, such as the alkanols were very similar to the predicted values,” but lower responses were observed for nonvolatile analytes, presumably due to the mechanism of aerosol formation in the spray chamber.

The present work aims to increase the accuracy of the RRF prediction, to improve not only the reliability of quantification, but also the measurement of compound purities. In addition, a new atom (Si) and more brominated compounds were added to extend the model's scope. This also allowed the prediction of combustion enthalpies to be extended to these atoms.

2. Materials and methods

2.1. Materials

All compounds came from the Firmenich collection except the following: N,O‐bis(trimethylsilyl)trifluoroacetamide/1% trimethylchlorosilane (BSTFA/1% TMCS) from Supelco (Bellefonte, USA); vanillic acid (>97%), maleic acid (>99%), and acetylsalicylic acid (99.5%) from Sigma (Steinheim, Germany); pyridine, hydrochloric acid (37%), and dichloromethane from Carlo Erba (Val de Reuil, France); methyl octanotate (99%) from Alfa Aesar (Karlsruhe, Germany); and halogenated compounds from Aldrich, Alfa Aesar, or Carlo‐Erba.

The compounds that were suspected to contain nonvolatile impurities were redistilled by using a short Vigreux column.

2.2. Metabolite extraction from biodegradation tests

Tests were performed according to OECD 301F guideline 19 to evaluate the ready biodegradability of chemicals, with the test duration extending to 60 days 20. Before being submitted to the 301F test, the purity of analytes was assessed by using the predicted RRFs 10. After the test, an ISTD (methyl octanoate, about 20 mg, precisely weighed to the nearest 0.01 mg) was added to the aqueous media (200 mL). The latter was acidified with 1 mL of hydrochloric acid at a concentration of 37%, extracted three times with 50 mL of CH₂Cl₂, and then extracted two times with 20 mL of CH₂Cl₂. The solvent of the combined extracts was removed in a rotatory evaporator and the concentrate was diluted in 3 mL of ethyl acetate.

2.3. Typical derivatization procedure

Two solutions were freshly prepared at 0.5 g/kg in pyridine before derivatization, one with the ISTD (methyl octanoate), the second with the compound to be derivatized. In a vial were mixed 0.6 mL of the latter plus 0.4 mL of pyridine (both precisely weighed to the nearest 0.01 mg), as well as 200 μL of BSTFA/1% TMCS. The vial was then closed, heated to 50°C for 1 h, and cooled to room temperature. Next, 0.6 mL (precisely weighed) of the ISTD solution were added, and 1 μL of the prepared solution was injected in the GC–FID instrument. Measurements of reference RRFs for the database were done in triplicate from three different vials prepared as described above.

2.4. GC–FID analyses

GC analyses were performed by using a GC–FID (Agilent, model 6890; Agilent Wilmington, DE, USA) equipped with a ZB‐1 column from Phenomenex (Torrance, CA, USA) or a DB‐1ms column from J&W Scientific (Folsom, CA, USA), both 30 m × 0.25 mm × 0.25 μm. The injector and FID temperatures were 280 and 250°C, respectively. The carrier gas was helium under a constant flow of 1 mL/min (velocity: 25 cm/s). The sample (1 μL) was injected by using a syringe of 10 μL and an Agilent 7683 autosampler, with a split ratio of 50:1 and a total flow of 52.7 mL/min in the injector. The oven was maintained at 50°C for 5 min; then the temperature was increased by 3°C/min to 120°C and then by 5°C/min to 280°C and maintained for 5 min. The H₂ and the air flows were set at 35 and 400 mL/min, respectively. All RRFs refer to methyl octanoate as the ISTD.

2.5. RRF measurements

The RRF of nonderivatized compounds was determined as previously described 1. All determinations were made relative to the same ISTD: methyl octanoate. Both the ISTD and the compound(s) to be quantified were diluted in the solvent (usually, ethyl acetate) at a concentration of about 1 g/L. The robustness of RRF measurements as a function of experimental conditions has been investigated in a previous study 2.

2.6. GC–MS analyses

The mass spectrometer was an HP 5973 from Agilent. The GC conditions (chromatograph model, column, oven program, gas velocity) were the same as for GC–FID analyses. The GC column outlet was directly coupled to the electron impact ionization source. The transfer line was heated to 250°C and the electron impact ionization source itself operated at 230°C, with collision energy of 70 eV. The data acquisition rate was 20 Hz with a mass range of 40–450 or 45–600 Da, depending on the molecular mass of the analyte.

2.7. Response factor calculation

In this work, the combustion enthalpies were first correlated with the molar response factors (MRFs), defined as follows:

$$\mathit{MRF}=\frac{\left(A_{\mathrm{i}}\right)\left(M_{\mathrm{ISTD}}\right)}{\left(M_{\mathrm{i}}\right)\left(A_{\mathrm{ISTD}}\right)}$$ (1)

With $A_{\mathrm{i}},A_{\mathrm{ISTD}}$: Peak area of the compound i and the ISTD, respectively.

And $M_{\mathrm{i}},M_{\mathrm{ISTD}}$: Molarities of the compound and the standard, respectively.

The RRFs were calculated as follows:

$$\mathrm{RRF}=\frac{\left(m_{\mathrm{i}}\right)\left(A_{\mathrm{ISTD}}\right)}{\left(m_{\mathrm{ISTD}}\right)\left(A_{\mathrm{i}}\right)}$$ (2)

With $m_{\mathrm{i}},m_{\mathrm{ISTD}}$: mass of the compound and the ISTD, respectively.

Therefore, both response coefficients can be converted one into the other by:

$$\mathrm{RRF}=\frac{1}{\mathrm{MRF}}\frac{\mathrm{M}{\mathrm{W}}_{\mathrm{i}}}{\mathrm{M}{\mathrm{W}}_{\mathrm{ISTD}}}$$ (3)

With MW_ISTD and MW_i : the molar weight of the ISTD and the compound, respectively, both expressed to the first decimal place throughout this paper.

2.8. Response factor prediction

In our previous publication 1, we showed that the MRFs can be calculated with good accuracy from the combustion enthalpies by using the following linear equation:

$$MRF=-0.0708+8.57.{10}^{-4}\Delta H_{\mathrm{Comb}}+1.27.{10}^{-1}{n}_{\mathrm{Benz}}$$ (4)

With n _Benz : the number of benzene rings

For the sake of simplification, in Eq. (4) (as well as in the rest of this paper and in previous papers), ΔH _Comb represents the absolute value of the combustion enthalpy (expressed in kcal/mol) because this parameter should have a negative value for all compounds detected in the FID. ΔH _Comb can be obtained from experimental data, density functional theory (DFT) calculations, or atomic composition.

2.8.1. Enthalpy of combustion from experiment

When experimental data exist in the literature 21, the enthalpies can be calculated as the difference of the heat of formation of the molecules from the heat of formation of the combustion products: CO₂, H₂O, N₂, SO₂, HF, HCl, Br₂, Cl₂. In this work, the heat of formation in the gas state was considered for all chemical compounds under standard conditions (1 atm; 298.15 K). Other products such as H₂SO₄ and HBr could be considered as possible combustion products but were not used in this study, as they did not improve our model. These experimentally derived values were used to calibrate the prediction of enthalpies of combustion from both the DFT and the atomic composition (see Sections 2.8.2 and 2.8.3). Reference 21 also contains a method based on group contribution for estimating the heat of formation of chemicals.

2.8.2. Enthalpy of combustion from DFT calculations

In this work, we refer to our previously published calculation of combustion enthalpy from DFT calculations 1. The enthalpy of a molecule was calculated as the difference between DFT (B3LYP/6.31G**) energies of the molecule and the energies of the combustion products. Energies were calculated (after energy minimization) with the computer software Jaguar, version 8.2 22. As DFT methods are known to produce systematic errors, the DFT energies of O₂ and the combustion products (CO₂, H₂O, N₂, SO₂, HF, HCl, Br₂, Cl₂) were replaced by values derived from least square fitting of predicted against experimental enthalpies of combustion. The known prediction bias for acetylenic compounds was significant only for small compounds (fewer than four carbons) and was not corrected (see Supporting Information). Prediction of combustion enthalpies by this model was very accurate and precise (R = 0.999, SD = 1.66 kcal/mol for values ranging from 150 to 1000 kcal/mol, N = 51). For Br‐ and I‐containing compounds, the LACVP** basis set was used instead of 6.31G**. No ZPE energy correction was introduced in our calculations. As the prediction accuracy of the enthalpies was largely superior to the precision of our GC response factors, no other DFT methods were investigated. In this work, we applied the same method to calculate heat of formation of Si‐containing compounds. As no experimental data exist in Ref. 21 for these compounds, the DFT energy of the combustion product SiO₂ was not corrected.

2.8.3. Enthalpy of combustion from atomic composition

The combustion enthalpies from atomic composition, ΔH _Comb, when they referred to the previously published 1 equations, were calculated by using the following formula (in kcal/mol):

$$\begin{array}{ccc}\hfill \Delta H_{\mathrm{Comb}}& =& 11.06+103.57n_{\mathrm{C}}+21.85n_{\mathrm{H}}-48.18n_{\mathrm{O}}\hfill \\ & +& 7.46n_{\mathrm{N}}+74.67n_{\mathrm{S}}-23.57n_{\mathrm{F}}-27.43n_{\mathrm{Cl}}\hfill \\ & -& 11.90n_{\mathrm{Br}}-2.04n_{\mathrm{I}}\hfill \end{array}$$ (5)

with n _C, n _H, n _O, etc. being the number of carbon, hydrogen, oxygen, etc. atoms in the compound.

Coefficients of Eq. (5) were obtained by minimizing the squared differences against experimental combustion enthalpies (see Sec. 2.8.1). This equation still gave very accurate combustion enthalpies (R = 0.999, SD = 6.68 kcal/mol, N = 51), but they were slightly less precise than in the DFT model. Both calculations gave a similar accuracy for the MRF prediction when used in combination with Eq. (4).

To shorten these steps, we directly calculated the predicted RRFs by using the following formula, combining Eqs. (3), (4), and (5) 10:

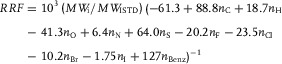(6)

with n _Benz being the number of benzene rings in the compound.

2.9. Purity prediction

2.9.1. Quick procedure

The purity p of a given compound i is estimated as $p_i={\mathit{RRF}}_{\mathit{i}}^{\mathit{Pred}}/{\mathit{RRF}}_{\mathit{i}}^{\mathit{App}}$,with ${\mathrm{RRF}}_{\mathrm{i}}^{\mathrm{Pred}}$ and ${\mathrm{RRF}}_{\mathrm{i}}^{\mathrm{App}}$ the predicted and the apparent RRF of i, respectively. ${\mathrm{RRF}}_{\mathrm{i}}^{\mathrm{App}}$ is experimentally determined by assuming that the substance i is pure 10.

2.9.2. Full procedure

All constituents must be amenable to GC (compounds with a calculated vapor pressure up to 3.62 × 10^–7 Pa at 25°C have been tested 23) and their molecular formulae should be known. The amount m_i of each of them is determined by using Eq. (2), an ISTD, and the predicted RRF_i. The purity of a given constituent i in the mixture is $p_i=m_i/\sum m_i$

3. Results and discussion

With the previously published algorithm, some RRFs were inaccurately predicted, leading to a bias in excess of 10% in about 20% of cases, whereas the distribution of biases was approximately normal. A first explanation could lie in a lack of accuracy in the experimental data, such as the purity of standards used to build the database. Redetermining the experimental RRFs of outliers under stricter conditions, for example, using purer reference substances, would thus improve the correlation. Other causes could be a lack of accuracy of the enthalpies of the combustion model, or some compounds not behaving according to the initial assumption made to develop the algorithm; that is, their combustion enthalpies are not directly correlated to the response factors.

3.1. Database improvement

To improve the reliability of the database, all compounds exhibiting a bias of more than 10% between the predicted and measured RRF were reinvestigated. Most of these outliers consisted of impure substances, highly volatile substances, and compounds not populated enough in the database to be representative (halogenated compounds). The RRFs of impure compounds were redetermined whenever a purer source was identified. Alternatively, they were repurified when rapidly feasible. In both cases, their purity was increased from about 90% to at least 95% or even 98% whenever possible. For instance, some monoterpenes that were suspected to be prone to oxidation or polymerization were flash‐distilled, and their RRFs immediately redetermined. The resulting samples led to RRFs close to the predicted values (e.g. γ‐terpinene: bias of 11.5% and 6% before and after distillation, respectively). Only the compounds exhibiting objective evidence of insufficient purity were disregarded. Similarly, the chemicals that were too volatile to be accurately weighed were also not taken into account in the revised database.

3.1.1. Brominated compounds

Using the former model (Eq. (6)), the experimental RRFs of brominated compounds were well correlated with the predicted values (R = 0.98), but the latter were overestimated with a mean bias of 14.5% relative to experimental values. After the purity of standards was checked and the data set extended, this bias persisted, which suggested that the algorithm had to be improved, rather than the experimental data (see Section 3.2).

3.1.2. Silylated compounds

The database initially used did not contain any silylated compound. However, analyzing products with labile protons in GC often requires their derivatization into a trimethylsilyl compound. Therefore, 25 hydroxylated compounds (alcohols, phenols, carboxylic acids) were derivatized with BSTFA/1% TMCS. In the previously developed algorithm (Eq. (6)) 1, an increment k _Si n _Si (where n _Si is the number of Si atoms in the compound and k _Si a scalar to be determined) was added to the denominator increment in bold in Eq. (7).

The optimization versus experimental values based on a series of five aliphatic alcohol derivatives gave a correlation R = 0.92 for k _Si = 43.9 kcal/mol in equation 6. Therefore, the incremental approach appears suitable for the prediction of silylated compounds, and k _Si was recalculated by ab initio methods from combustion enthalpies (section 3.2.1).

$$\begin{array}{ccc}\hfill \Delta H_{\mathrm{Comb}}& =& 11.06+103.57n_{\mathrm{C}}+21.85n_{\mathrm{H}}-48.18n_{\mathrm{O}}\hfill \\ & & +7.46n_{\mathrm{N}}+74.67n_{\mathrm{S}}-23.57n_{\mathrm{F}}-27.43n_{\mathrm{Cl}}\hfill \\ & & -11.90n_{\mathrm{Br}}-2.04n_{\mathrm{I}}+\mathbf{46}.\mathbf{5}{n}_{\mathrm{Si}}\hfill \end{array}$$ (7)

3.2. Algorithm improvement

3.2.1. Improvement of MRF calculation

In Ref. 1, the prediction of MRF from atomic composition was performed in two steps: First, the combustion enthalpy of compounds was calculated from the molecular formula (Eq. (5)). In a second step, the MRF was calculated by a linear combination based on this calculated enthalpy of combustion and one corrective term to account for the number of benzene rings (Eq. (4)).

To extend our model to Si‐containing compounds, we added a new term to Eq. (5). As no experimental combustion enthalpies were available, we used DFT calculation, as proposed in our previous publication 1 (see Section 2.8.2), to calculate the enthalpy of combustion of three Si‐containing compounds (Me₃SiH, Me₄Si, and Me₃SiOMe). These three values were used to determine the Si contribution ($k_{Si}^{\prime }$ = 46.5 kcal/mol) to ΔH _Comb (Eq. (7)) by minimizing the squared differences between these DFT calculated enthalpies and those calculated from atom count. For simplicity, the equation used for the calculation of ΔH _Comb was based only on atom count.

In our previous model, the parameter for Br resulting from the experimental heats of formation systematically gave underestimated predicted MRF values (Eqs. (4) and (5)). A possible explanation for this difference could be that the combustion would produce HBr instead of Br₂ as used in ref. 1. Because a recalculation based on this hypothesis did not significantly improve the prediction, the Br coefficient, k _Br = –11.90, was left unchanged in the prediction of ΔH _Comb and was assumed to represent the true contribution of Br in the global combustion enthalpy of the compound. The MRF prediction was reoptimized (Eq. (4)) by using the response factors measured above and a corrective term for Br. The differences (sum of squared differences) were minimized between the MRF model (combination of Eqs. (4) and (5)) and experimental values to determine the Br corrective term in Eq. (8) (corrected parameters in bold):

$$\begin{array}{ccc}\hfill \mathit{MRF}& =& -0.0708+8.57.{10}^{-4}\Delta H_{\mathrm{Comb}}+1.27.{10}^{-1}{n}_{\mathrm{Benz}}\hfill \\ & +& \mathbf{6}.\mathbf{18}.\mathbf{1}{\mathbf{0}}^{-\mathbf{2}}{n}_{\mathbf{Br}}\hfill \end{array}$$ (8)

When we compared the MRFs predicted with Eqs. (7) and (8) and the improved experimental data set (R = 0.991; SD = 0.053, N = 490) to those resulting from the previous model (Eq. (4)) and the old data set (R = 0.936, SD = 0.116, N = 381), both the correlation coefficient and the SD were improved (Fig. 1). The statistical results for the Si compounds (R = 0.973, SD = 0.053, N = 26) exhibited an accuracy identical to that of the global set (SD = 0.053). This prediction level is notable for a new chemical family (Si compounds) because it has been obtained only by ab initio calculation without taking into account any experimental measurement.

Figure 1.

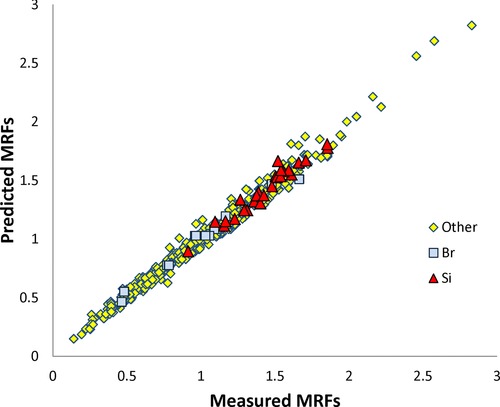
Molar response factors: predicted versus measured values (R = 0.991; SD = 0.053; N = 490).

The fact that the number of compounds was large for each introduced parameter (26 for Si and 15 for Br) favored a robustness of the model. However, we applied a “leave one out” procedure to evaluate the predictive power of the model from the bromo compounds. In this procedure, we successively reoptimized parameters for Br after leaving one compound aside, and then the removed compound was predicted from this model. All Br‐containing compounds predicted by using this procedure gave good statistical results for true prediction: R = 0.987, SD = 0.052, N = 15.

Equations (3), (7), and (8) can be combined into a single equation to facilitate the routine calculation of RRFs:

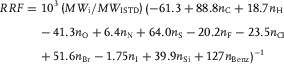(9)

It is notable that the k _Si value resulting from this DFT prediction (39.9, Eq. (9)) is close to the above‐mentioned experimental estimation based on a small series of alcohol derivatives (43.9, Section 3.1.2).

3.2.2. Accuracy of the prediction

Because the objective of the present work was to increase the accuracy of quantifications, the biases of predicted RRFs resulting from the present optimization were compared with those of the previous model (Fig. 2). The distribution was much narrower, with 93% of the 490 values of the new database predicted to be better than ± 10%, versus 81% with the previous algorithm and the old database of 351 values. The relative mean bias, measured by the RSD of predicted versus measured RRFs, decreased from 10.4% with the previous model to 6.0% with the new one. This represents a significant improvement resulting from both the reliability of the experimental data set and the algorithm reoptimization.

Figure 2.

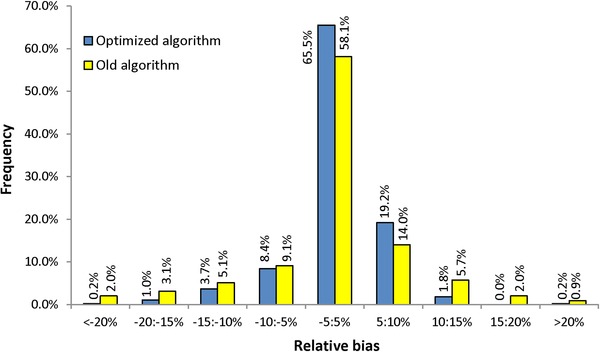
Distribution of RRF biases predicted by using the initial and optimized algorithms.

3.3. Application to the quantification of metabolites

Nowadays, chemical legislation requires that new products be tested for their potential environmental impact before market introduction, such as their ability to biodegrade. When performing a biodegradation assay, small amounts of tested compounds are used, and the resulting metabolites are sometimes unexpected, if not unknown. Isolating them to confirm their structures by NMR spectroscopy is either not feasible, or leads to quantities that are too small to be isolated and used for GC calibration. In the former case, their structures need to be hypothesized from their MS spectra and then they need to be resynthesized. Because many metabolites are carboxylated species, they are first extracted from the acidified reaction medium and then silylated. After addition of an ISTD, the mixture can be analyzed by GC. After the identity of the metabolites, or, at least, their molecular formula, is determined, their RRFs are calculated and the quantification can be completed without having the authentic substance at one's disposal. This is particularly time‐saving when the metabolites are not available (e.g. identified using data from the literature or from their isolation at mg‐scale from the reaction mixture).

Such a procedure is exemplified below with the biodegradation of 1‐(bicyclo[2.2.1]hept‐2‐yl)‐2‐hexanone, using OCDE test 301F at 60 days of incubation (Fig. 3) 19. After the silylation of analytes extracted from the test medium, their quantification, based on a predicted RRF, led to a molar balance of 84%. The missing 16% was assumed to have been incorporated into the biomass. The ester function of ISTD was not hydrolyzed during the acidic extraction, as verified in a separate experiment by using a second, nonhydrolyzable ISTD (see Supporting Information).

Figure 3.

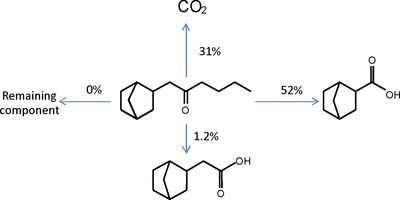
Biodegradation of 1‐(bicyclo[2.2.1]hept‐2‐yl)‐2‐hexanone subjected to OECD 301F test (molar percentages).

The two acids were then synthesized to confirm their identification, and their RRFs were determined in comparison with predicted values (Table 1). The agreement between both values strongly supports the fact that the derivatization reaction was quantitative, which was also confirmed by the same observation for many other silylated metabolites. Had the derivatization ever been incomplete, the “apparent” RRF measured from the derivatization mixture would have been greater than the predicted value. In addition, for those compounds that are GC amenable without derivatization (e.g. short chain alcohols), the unreacted substance would have been detected, which was not the case.

Table 1.

Predicted and measured RRFs of 1‐(bicyclo[2.2.1]hept‐2‐yl)‐2‐hexanone metabolites

Compounds	RRFPred	RRFMeas	Bias
2‐Bicyclo[2.2.1]heptane acetic acid trimethylsilyl ester	1.042	1.040	0.2%
2‐Bicyclo[2.2.1]heptane carboxylic acid trimethylsilyl ester	1.076	1.023	5.2%

This rapid quantification strategy was applied to the biodegradation of a series of cyclohexyl‐ and norbornyl‐derived ketones. These results were used to elucidate the biodegradation pathway of this chemical family, as reported in a separate paper 20.

3.4. Application to the purity measurement of chemicals

3.4.1. Influence of the solvent

To check the possible dependence of RRF on the dilution solvent, we analyzed the purity of a series of 27 fragrance allergens by using the quick procedure (Section 2.9.1) and four different solvents: dichloromethane, ethyl acetate, toluene, and methyl pivalate. The RSD of the resulting purity measurement of allergens gave a median value of 4.2% over the four solvents, but it decreased to 1.9% when CH₂CL₂ was omitted (details are given in Supporting Information Table S1). The latter exhibited the lowest boiling point, systematically giving lower experimental RRF values, and so it predicted purities up to 20% higher than the mean value in the three other solvents. In conclusion, different solvents can be used, except for those that are very volatile.

3.4.2. Purity of a defined mixture

Checking the purity of a chemical by GC is a potential issue because all constituents must be volatile and available to determine their RRFs. As a frequent approximation, all response factors are considered to be equal to unity, whereas 17% of these RRFs deviate from unity by more than 30%, according to our database. To exemplify the usefulness of predicted RRFs to overcome these difficulties, we intentionally made a chemical (4‐bromophenol) impure by mixing it with small amounts of diphenylether, 1,4‐dibromobenzene, and 4‐isopropyl‐3‐methylphenol (Table 2). All constituents had a certified purity higher than 99%. Because of the presence of hydroxyl groups, the mixture was silylated before its analysis.

Table 2.

Predicted purity of a sample after silylation, according to the quick and the full procedures

	phenol‐TMS	Diphenyl‐ether	1,4‐Dibromo‐benzene	4‐Isopropyl‐3‐methylphenol‐TMS
Predicted RRFs (silylated)	1.337	0.766	1.919	0.862
Real amounts	89.4%	5.4%	3.9%	1.4%
Purity (quick procedure)	87.7% (0.3)	5.4% (0.05)	3.7% (0.01)	1.4% (0.01)
Purity (full procedure)	89.3% (0.03)	5.5% (0.03)	3.8% (0.01)	1.4% (0.004)

TMS, trimethylsilyl.

Measurement of three different derivatization reactions.

SDs in parentheses.

The quick procedure previously reported consists of predicting the purity by dividing the predicted RRF by the apparent RRF of the whole mixture (see Section 2.8.1). It gave a satisfactory estimate of the main compound purity (87.7% instead of 89.4%). Using the same approach, the impurities were also well evaluated (Table 2, quick procedure). It is noteworthy that this quick procedure remains applicable when “nonvisible” impurities are present, such as nonvolatiles. If we assume that diphenyl ether had been replaced by a nondetected impurity, the other percentages would have remained unchanged, because their calculation requires only the knowledge of their predicted RRFs, the mass of the ISTD, and the mass of the impure sample analyzed by GC and the resulting peak areas.

The full procedure is applicable only if the main constituents and all impurities are GC amenable and their molecular formulae are known. The amount of each constituent is then determined by using the predicted RRFs, which allows determination of the proportions of all constituents (Table 2, full procedure).

This single case is not representative of all possible situations, because the accuracy of the purity determination directly depends on the accuracy of the RRF prediction. Because the latter was good (RSD = 6.0%), the purity prediction should be satisfactory in most cases. However, the database included only compounds with one or two mono‐ and bisilylated derivatives. To check whether the technique was also applicable to compounds with more silyl groups, we derivatized products with three to six hydroxyl groups. Starting from compounds that were pure at more than 99%, we found their calculated purities after derivatization to be higher than 90% (Supporting Information Table S2).

4. Concluding remarks

The fact that the experimental MRF values were not used to determine the Si coefficient in the new algorithm confirms the validity of the theoretical approach in consisting of a correlation between the FID response factors and the combustion enthalpies. This allows extension of the model to other chemical families either from measurements of heat of combustion enthalpies, or directly from the DFT calculation. However, the case of bromine suggests that this RRF/ΔH _Comb relationship would not exactly match the reaction occurring in the FID, and so a correction factor may sometimes be useful for improving the prediction accuracy. As in the case of benzene rings, the real ionized Br species detected in the FID remain unknown. For Br and benzene rings, this could explain the small shift of predicted RRFs when using true ΔH _Comb values because our prediction hypothesizes full combustion, whereas the detected species might be precursors of these fully oxidized species. Nevertheless, the new algorithm remains extremely simple: it allows very rapid quantification procedures with good accuracy, as illustrated in the case of silylated metabolites and purity determination.

The large data set used in the present work confirms the broad applicability of the proposed model. The use of experimentally determined RRFs clearly remains the most accurate means whenever pure authentic standards are available. However, when this is not the case, or when a complex multicomponent mixture makes the experimental RRF measurement too time‐consuming, the predicted RRFs are a valid alternative, with a mean accuracy of 6.0%. The different atoms included in the algorithm allow prediction of the vast majority of compounds that are amenable to GC. The extension to Si now extends the prediction to the semi‐volatile hydroxylated compounds after their derivatization.

The authors have declared no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supporting Information