Identifying lineage effects when controlling for population structure improves power in bacterial association studies

Abstract

Bacteria pose unique challenges for genome-wide association studies because of strong structuring into distinct strains and substantial linkage disequilibrium across the genome^1,2. Although methods developed for human studies can correct for strain structure^3,4, this risks considerable loss-of-power because genetic differences between strains often contribute substantial phenotypic variability⁵. Here, we propose a new method that captures lineage-level associations even when locus-specific associations cannot be fine-mapped. We demonstrate its ability to detect genes and genetic variants underlying resistance to 17 antimicrobials in 3,144 isolates from four taxonomically diverse clonal and recombining bacteria: Mycobacterium tuberculosis, Staphylococcus aureus, Escherichia coli and Klebsiella pneumoniae. Strong selection, recombination and penetrance confer high power to recover known antimicrobial resistance mechanisms and reveal a candidate association between the outer membrane porin nmpC and cefazolin resistance in E. coli. Hence, our method pinpoints locus-specific effects where possible and boosts power by detecting lineage-level differences when fine-mapping is intractable.

Mapping genetic variants underlying bacterial phenotypic variability is of great interest owing to the fundamental role of bacteria ecologically, industrially and in the global burden of disease^6–8. Hospital-associated infections including Staphylococcus aureus, Escherichia coli and Klebsiella pneumoniae represent a serious threat to the safe provision of healthcare^9,10, while the Mycobacterium tuberculosis pandemic remains a major global health challenge¹¹. Treatment options continue to be eroded by the spread of antimicrobial resistance, with some strains resistant even to antimicrobials of last resort¹².

Genome-wide association studies (GWASs) offer new opportunities to map bacterial phenotypes through inexpensive sequencing of entire genomes, enabling direct analysis of causal loci and functional validation via well-developed molecular approaches^2,13–22. However, bacterial populations typically exhibit genome-wide linkage disequilibrium and strong structuring into geographically widespread genetic lineages or strains that are probably maintained by natural selection^1,5. Approaches to controlling for this population structure have allowed for systematic phenotypic differences based on cluster membership^15,16 or, in clonal species, phylogenetic history^13,19–21. However, these and other approaches common in human GWASs^3,4 risk masking causal variants because differences between strains account for large proportions of both phenotypic and genetic variability.

Here, we describe a new approach for controlling bacterial population structure that boosts power by recovering signals of lineage-level associations when associations cannot be pinpointed to individual loci because of strong population structure, strong linkage disequilibrium and a lack of homoplasy. We base our approach on linear mixed models (LMMs), which can control for close relatedness within samples by capturing the fine structure of populations more faithfully than other approaches²³ and enjoy greater applicability than phylogenetic methods because recombination is evident in most bacteria^24,25. Our approach offers biological insights into strain-level differences and identifies groups of loci that are collectively significant, even when individually insignificant, without sacrificing the power to detect locus-specific associations.

Controlling for population structure aims to avoid spurious associations arising from (1) linkage disequilibrium with genuine causal variants that are population-stratified, (2) uncontrolled environmental variables that are population-stratified and (3) population-stratified differences in sampling³. In the four species we investigated, we observed genome-wide linkage disequilibrium and strong population structure, with the first ten principal components (PCs)²⁶ explaining 70–93% of genetic variation, compared with 27% in human chromosome 1 (Supplementary Fig. 1). Controlling artefacts arising from population structure therefore risks a loss of power to detect genuine associations in this large proportion of population-stratified loci.

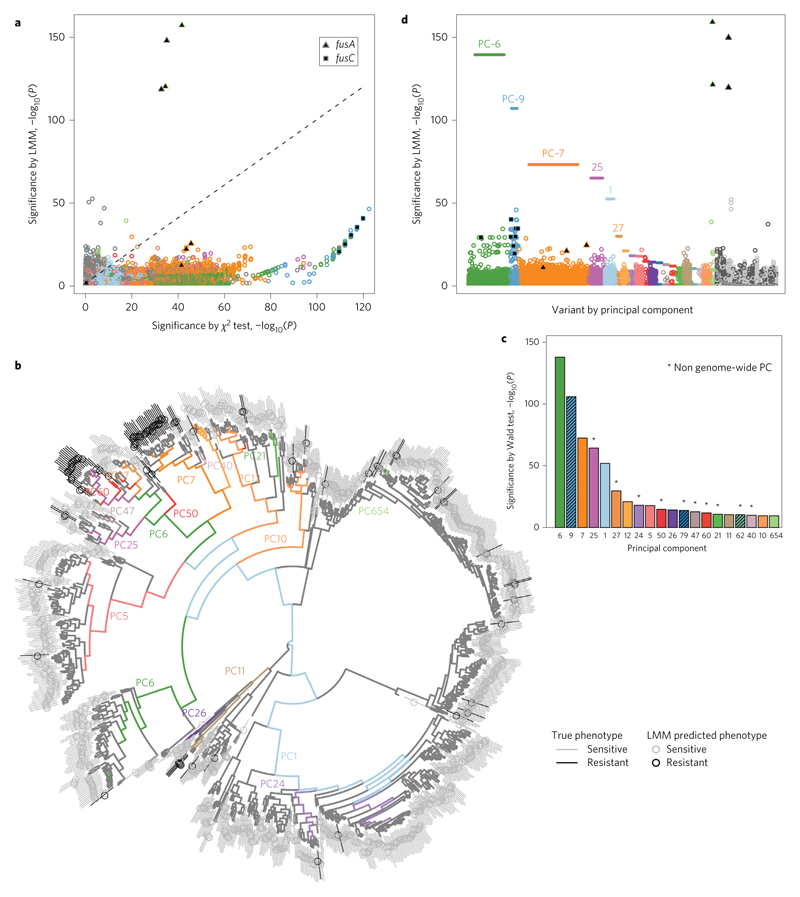
For example, we investigated associations between fusidic acid resistance and the presence or absence of short 31 bp haplotypes or ‘kmers’ in S. aureus (see Methods and Supplementary Fig. 2). The kmer approach aims to capture resistance encoded by substitutions in the core genome, the presence of mobile accessory genes, or both¹³. Kmers linked to the presence of fusC, a mobile element-associated resistance-conferring gene whose product prevents fusidic acid interacting with its target EF-G (ref. 27), showed the strongest genome-wide association by χ² test (P = 10⁻¹²²).

However, fusC-encoded resistance was observed exclusively within strains ST-1 and ST-8. Thus, controlling for population structure using LMM²⁸ reduced the significance to P = 10⁻³⁹, below other loci (Fig. 1a and Supplementary Fig. 3). Kmers capturing resistance-conferring substitutions in fusA, which encodes EF-G, were propelled to greater significance, because these low-frequency variants were unstratified and LMM improves power in the presence of polygenic effects²⁹ (P = 10⁻¹¹ by χ² test, P = 10⁻¹⁵⁷ by LMM). However, fusA variants explain only half as much resistance as fusC overall.

Figure 1. Controlling for population structure in bacterial GWASs for fusidic acid resistance in S. aureus.

a, Effect of controlling for population structure using LMM on the significance of the presence or absence of 31 bp kmers. The 200,000 most-significant kmers prior to control for population structure and a random 200,000 are plotted. Each kmer is colour-coded according to the principal component to which it is most strongly correlated, and grey if it is not most strongly correlated to one of the 20 most significant principal components. b, Principal components correspond to lineages in the clonal genealogy. Branches are colour-coded by one of the 20 most significant principal components to which they are most correlated. Individual genomes are colour-coded with black or grey lines to indicate fusidic acid resistance and susceptibility, respectively. The circle passing through the line is colour-coded to indicate the phenotype predicted by the LMM. c, Wald tests of significance of lineage-specific associations. Some principal components, for example, PC-9, are hashed to indicate that no branch in the clonal genealogy was most strongly correlated with it. Asterisks above the bars, for example PC-25, indicate evidence for lineages associated with particular genomic regions. d, Manhattan plot showing significance of unique variants after controlling for population structure, with variants clustered by principal component. The horizontal ordering is randomized. This allows identification of the variants corresponding to the most significant lineage-specific associations.

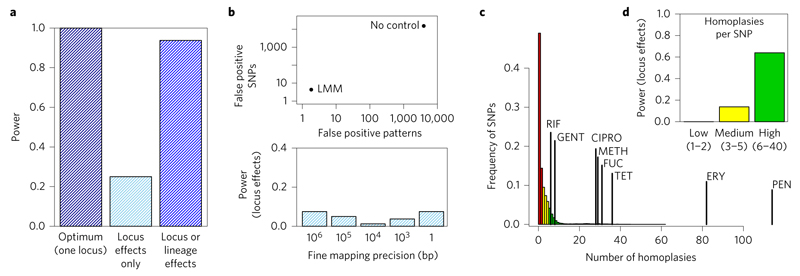
Although kmers linked to fusC did not suffer an outright loss of significance, as penetrance (proportion of fusC carriers expressing resistance) was very high, simulations show that for phenotypes with modest effect sizes (for example, odds ratios of 3), controlling for population structure risks loss of genome-wide significance at 59, 75, 99 and 99% of high-frequency causal variants in M. tuberculosis (n = 1,573), S. aureus (n = 992), E. coli (n = 241) and K. pneumoniae (n = 176) simulations, respectively, with the power loss being greatest when the sample size is low and the number of variants is high (Fig. 2a and Supplementary Fig. 4a).

Figure 2. Power, false positives, fine mapping and homoplasy in S. aureus. Simulation results.

a, Controlling for population structure and multiple testing lead to a drastic reduction in power to detect locus effects, compared with the theoretical optimum power for a single locus. The Wald test improves the power several-fold by detecting lineage-specific effects. b, Top: mean numbers of false-positive SNPs and patterns (that is, unique distributions of SNP alleles among individuals) are drastically reduced by controlling population structure with LMM. Bottom: fine mapping precision is very coarse owing to genome-wide linkage disequilibrium. Interpreting lineage effects is useful when the locus-specific signal cannot be fine-mapped. c, Number of times that common SNPs (minor allele frequency (MAF) > 20%) and antibiotic resistance phenotypes have emerged on the phylogeny. d, When homoplasy is high, the power to detect locus effects is much improved, explaining the good power to map antibiotic resistance phenotypes. In the simulations, causal loci were selected at random from high-frequency SNPs (MAF > 20%) in the n = 992 isolates and phenotypes simulated per genome with case probabilities of 0.25 and 0.5 for the common and rare alleles, respectively (odds ratio of 3). Genome-wide significance (to detect locus effects) was based on a Bonferroni-corrected P value threshold of α, equal to 0.05 divided by the number of SNP patterns.

Methods to limit loss of power such as ‘leave-one-chromosome-out’²⁹ are impractical in bacteria, which typically have one chromosome. Instead, we developed a method to recover information discarded when controlling for population structure. In cases where population stratification reduces the power to detect locus-specific associations, our method infers lineage-specific associations, similar to a phylogenetic regression^30,31, without sacrificing the power to detect locus-specific associations when possible.

We observed that leading principal components tend to correspond to major lineages in bacterial genealogies (or ‘clonal frames’³²) despite substantial differences in recombination rates (Fig. 1b and Supplementary Fig. 5), reflecting an underlying relationship between genealogical history and principal component analysis³³. Principal components are commonly used to control for population structure by including leading principal components as fixed effects in a regression²⁶. The regression coefficients estimated for principal components could therefore be interpreted as capturing lineage-level phenotypic differences, and each principal component tested for an effect on the phenotype. Because principal components are guaranteed to be uncorrelated, defining lineages in terms of principal components, rather than as phylogenetic branches or genetic clusters, minimizes the loss of power to detect lineage-level associations caused by correlations between lineages.

To identify lineage effects we exploited a connection between principal components and LMMs. In an LMM, every locus is included as a random effect in a regression. This is equivalent to including every principal component in the regression as a random effect³⁴. We thus decomposed the random effects estimated by the LMM to obtain coefficients and standard errors for every principal component (see Methods). We then used a Wald test³⁵ to assess the significance of the association between each lineage and the phenotype.

Our method, implemented in the R package bugwas, revealed strong signals of association between fusidic acid resistance and lineages including PC-6 and PC-9 (P = 10⁻⁷⁰), comparable in significance to the low-frequency variants at fusA (Fig. 1c and Supplementary Fig. 6). We next reassessed locus-specific effects by assigning variants to lineages according to the principal component to which they were most correlated, then comparing the significance of variants within lineages. This showed that fusC and variants in linkage disequilibrium with fusC accounted for the strongest signals within PC-6 and PC-9 (P = 10⁻³⁴ and 10⁻⁴⁵ respectively, Fig. 1d), with the strongest locus-specific associations localized to a 20 kb region containing the staphylococcal cassette chromosome (SCC), the most significant hit mapping to the gene adjacent to fusC. Thus, identifying loci contributing to the most significant lineages provides an alternative to prioritizing variants for follow-up based solely on locus-specific significance.

In simulations, our method was able to recover signals of lineage-level associations in cases where significance at individual loci was lost by controlling for population structure, increasing the power 2.5-fold (M. tuberculosis) to 22.0-fold (E. coli) (Fig. 2a and Supplementary Fig. 4a). LMM reduced the number of falsely detected single nucleotide polymorphisms (SNPs) by 30-fold (K. pneumoniae) to 3,600-fold (S. aureus). However, fine-mapping of causal variants to specific chromosomal regions frequently suffered from genome-wide linkage disequilibrium, because linkage disequilibrium is not generally organized into physically linked blocks along the chromosome (Fig. 2b and Supplementary Fig. 4b), underlining the importance of recovering power by interpreting lineage effects.

We noted a trade-off to interpreting lineage effects, because they are susceptible to confounding with population-stratified differences in environment or sampling (Supplementary Fig. 7). Therefore, non-random associations between lineages and uncontrolled variables that influence phenotype risk false detection of lineage-level differences.

Confronted with a strong population structure and genome-wide linkage disequilibrium in bacteria, we wished to test empirically the ability of GWASs to pinpoint genuine causal variants more generally. We therefore conducted 26 GWASs for resistance to 17 antimicrobials in 3,144 isolates across the major pathogens M. tuberculosis³⁶, S. aureus³⁷, E. coli and K. pneumoniae³⁸ (Supplementary Fig. 8).

We supplemented the kmer approach by surveying the variation in SNPs and gene presence or absence. We imputed missing SNP calls by reconstructing the clonal frame followed by ancestral state reconstruction, an approach that generally outperformed imputation using Beagle (Supplementary Table 1, see Methods).

Correlated phenotypes caused by the presence of multi-drug-resistant isolates led to significant results in unexpected loci or regions in some analyses. A combination of first-line drug regimens contributes to multi-drug resistance co-occurrence in M. tuberculosis, which led to spurious associations as the top hit before controlling for population structure between ethambutol and pyrazinamide resistance and SNPs in rifampicin resistance-conferring rpoB. Even after controlling for population structure, these associations remained genome-wide significant at P = 10⁻⁴⁵ and P = 10⁻⁵⁴.

Antimicrobial resistance has arisen over 20 times per drug in the M. tuberculosis tree, through frequent convergent evolution (Supplementary Fig. 4c and Supplementary Fig. 8). Within a single gene, such as rpoB, there are multiple targets for selection. Both SNP and kmer-based approaches correctly identified variants in known resistance-causing codons, but greater significance was attained in the latter because the targets for selection were typically within 31 bp (Supplementary Fig. 9a). In these cases, absence of the wild-type allele was found to confer resistance, with power gained by pooling over the alternative mutant alleles.

For each drug and species, we evaluated whether the most significant hit identified by GWAS matched a known causal variant^36–38 (Supplementary Table 2). By this measure, the performance of GWASs across species was very good, identifying genuine causal loci or regions in physical linkage with those loci for antimicrobial resistance in 25/26 cases for the SNP and gene approach and the kmer approach after controlling for population structure (Table 1 and Supplementary Table 3). For accessory genes such as β-lactamases, in particular, mobile element-associated regions of linkage disequilibrium were often detected together with the causal locus (Supplementary Fig. 9b).

Table 1. Number of resistant and sensitive isolates by species and antibiotics, known mechanisms of resistance and main results.

Antibiotic	R	S	Resistance mechanism	Resistance determined by	SNP/gene rank	SNP/gene LMM rank	Kmer rank	Kmer LMM rank
E. coli
Ampicillin	189	52	β-lactamase genes blaTEM	Gene presence	1	1	6 (tnp)*	6 (tnp)*
Cefazolin	139	102	β-lactamase genes blaCTX-M	Gene presence	2 (nmpC)**	3 (nmpC)**	121,710 (nmpC)**	3,690 (nmpC)**
Cefuroxime	81	160	β-lactamase genes blaCTX-M	Gene presence	1	1	1,598 (162-192 upstream blaCMY-2)*	470 (162-192 upstream blaCMY-2)*
Ceftriaxone	55	186	β-lactamase genes blaCTX-M	Gene presence	1	1	1,403 (tnp)*	470 (tnp)*
Ciprofloxacin	91	150	SNPs in gyrA#, gyrB, parC## or parE or presence of PMQR‡	Gene presence or SNPs, or both	1##	1##	1##	1#
Gentamicin	48	193	aac (aac(3)-II), ant, aph or rRNA methylase	Gene presence	1	1	1	1
Tobramycin	67	174	aac (aac(3)-II), ant or rRNA methylase	Gene presence	1	1	1	1
K. pneumonia
Cefazolin	53	123	β-lactamase genes blaCTX-M	Gene presence	1 + HP + wbuC	1	762 (tnp)*	837 (tnp)*
Cefuroxime	46	130	β-lactamase genes blaCTX-M	Gene presence	1 + HP + wbuC	1+ HP + wbuC	762 (tnp)*	1,480 (tnp)*
Ceftriaxone	35	141	β-lactamase genes blaCTX-M	Gene presence	1 + HP + wbuC	1 + HP + wbuC	771 (tnp)*	812 (tnp)*
Ciprofloxacin	34	142	SNPs in gyrA, gyrB, parC or parE or presence of PMQR (qnr-B1#, qnr-B19##)	Gene presence or SNPs, or both	2# (tnp)*	2# (tnp)*	1,853## (tnp)*	4,427## (tnp)*
Gentamicin	31	145	aac (acc(3)-II), ant, aph or rRNA methylase	Gene presence	1	1	1	79 (tmrB_2)*
Tobramycin	36	140	aac (acc(3)-II), ant or rRNA methylase	Gene presence	1	1	1	1
M. tuberculosis
Ethambutol	41	1,589	embB	SNPs	2 (rpoB)**	1	1	1
Isoniazid	239	1,470	katG, fabG1	SNPs	1	1	1	1
Pyrazinamide	45	1,662	pncA	SNPs	142 (rpoB)**	1	126 (rpoB)**	1
Rifampicin	86	1,487	rpoB	SNPs	1	1	1	1
S. aureus
Ciprofloxacin	242	750	grlA or gyrA	SNPs	1	1	1	1
Erythromycin	216	776	ermA, ermC, ermT or msrA	Gene presence	1	1	1	1
Fusidic acid	84	908	SNPs in fusA# or presence of fusB or fusC##	Gene presence or SNPs, or both	4## (SAS0037)*	1#	75## (SAS0040)*	1#
Gentamicin	11	981	aacA/aphD	Gene presence	1 + GNAT acetyltransferase	1 +GNAT acetyltransferase	1 + 415 bases upstream to 100 bases downstream	1 + 415 bases upstream to 100 bases downstream
Penicillin	824	168	blaZ	Gene presence	1	1	2 (blaI)*	2 (blaI)*
Methicillin	216	776	mecA	Gene presence	1	1 + mecR1	1 + SCCmec genes	1 + SCCmec genes
Tetracycline	46	946	tetK, tetL or tetM	Gene presence	2 (repC)*	2 (repC)*	1 + plasmid genes	1 + plasmid genes
Trimethoprim	15	308	SNPs in dfrB, presence of dfrG or dfrA	Gene presence or SNPs, or both	1	1	1	1
Rifampicin	8	984	rpoB	SNPs	1	1	1	1

For each antibiotic, the most significant variant was the expected mechanism, unless indicated by *(most significant variant was in physical linkage (PL) with the expected mechanism) or **(most significant variant was not the expected mechanism or in PL with the expected mechanism). The rank of the most significant result for an expected causal mechanism for each GWAS is reported, plus, in brackets, the gene that was most significant when it was not causal. Where more than one gene or mechanism causes resistance, the variant we found is underlined, or referred to by ^# and ^##. R, resistant; S, sensitive; HP, hypothetical protein; tnp, transposase; PMQR, plasmid mediated quinoline resistance. See Supplementary Tables 3–6 for more detail.

Genuine resistance-conferring variants were detected in all but one study, demonstrating that the high accuracy attained in predicting antimicrobial resistance phenotypes from genotypes known from the literature^37,39 is mirrored by good power to map the genotypes that confer antimicrobial resistance phenotypes using GWASs. However, these results also reflect the extraordinary selection pressures exerted by antimicrobials. High homoplasy at resistance-conferring loci caused by repeat mutation and recombination breaks down linkage disequilibrium, assisting mapping (Fig. 2c and Supplementary Fig. 4c).

For one drug, cefazolin, in E. coli, we identified a variation in the presence of an unexpected gene as the most strongly associated with resistance, nmpC (P = 10^−12.4). This gene encodes an outer membrane porin over-represented in susceptible individuals. Permeability in the Salmonella typhimurium homologue mediates resistance to other cephalosporin β-lactams⁴⁰, making this a strong candidate for a novel resistance-conferring mechanism discovered in E. coli.

Population structure presents the greatest challenge for GWASs in bacteria, because of the inherent trade-off between the power to detect genuine associations of population-stratified variants and robustness to unmeasured, population-stratified confounders. By introducing a test for lineage-specific associations, we allow these signals to be recovered even in the absence of homoplasy, while acknowledging the increased risk of confounding. Detecting lineage effects is valuable, because characterizing phenotypic variability in terms of strain-level differences is helpful for biological understanding and it permits the prediction of traits, including clinically actionable phenotypes, from strain designation.

Identifying loci that contribute to the most significant lineage-level associations offers flexibility in the interpretation of bacterial GWASs, where it will often be difficult to pinpoint significance to individual locus effects and where linkage disequilibrium can make the fine-mapping of causal loci a genome-wide problem. Loci can be prioritized for follow-up by identifying groups of lineage-associated variants that collectively show a strong signal of phenotypic association, but which cannot be distinguished statistically. This strategy provides an alternative to prioritizing variants based solely on locus-specific significance, but it carries risks, because lineage-associated effects are more susceptible to confounding with population-stratified differences in environment or sampling. This trade-off between power and robustness underlines the importance of functional validation for bacterial GWASs going forward.

Methods

Linear mixed model

In the LMM^41–45, the phenotype is modelled as depending on the fixed effects of covariates including an intercept, the ‘foreground’ fixed effect of the locus whose individual contribution is to be tested, the ‘background’ random effects of all the loci whose cumulative contribution to phenotypic variability we will decompose into lineage-level effects, and the random effect of the environment:

$$\text{phenotype}=\text{covariates}+\text{foreground}\hspace{0.17em}\text{locus}+\text{background}\hspace{0.17em}\text{loci}+\text{environment}$$

Formally,

$$y_i=w_{i1}{\alpha }_1+\dots +w_{ic}{\alpha }_c+X_{il}{\beta }_l+X_{il}{\gamma }_1+\dots +X_{il}{\gamma }_L+{\epsilon }_i$$

where there are n individuals, c covariates, L loci, l is the foreground locus, y_i is the phenotype in individual i, W_ij is covariate j in individual i, α_j is the effect of covariate j, X_ij is the genotype of locus j in individual i, β_l is the foreground effect of locus l, γ_j is the background effect of locus j and ε_i is the effect of the environment (or error) on individual i. Biallelic genotypes are numerically encoded as −f_j (common allele) or 1−f_j (rare allele), where f_j is the frequency of the rare allele at locus j. This convention ensures that the mean value of X_ij over individuals i is zero for any locus j. Because triallelic and tetrallelic loci are rare, we use only biallelic loci to model background effects. When the foreground locus is triallelic (K = 3) or tetrallelic (K = 4), the genotype in individual i is encoded as a vector indicating the presence (1) or absence (0) of the first (K − 1) alleles and β_l becomes a vector of length (K − 1).

Treating the background effects of the loci as random effects means the precise values of coefficients γ_j are averaged. The γ_j are assumed to follow independent normal distributions with common mean 0 and variance λτ⁻¹ to be estimated. As most loci are expected to have little or no effect on a particular phenotype, this tends to constrain the magnitude of the background effect sizes to be small. The environmental effects are also treated as random effects assumed to follow independent normal distributions with mean 0 and variance τ⁻¹. The model can be rewritten in matrix form as

$$\mathbf{\text{y}}=\mathbf{\text{W}}\alpha +\mathbf{\text{X}}{.}_l{\beta }_l+\mathbf{\text{u}}+\mathbf{\epsilon }$$

with

$$\mathbf{\text{u}}=\mathbf{\text{X}}{.}_1{\gamma }_1+\dots +\mathbf{\text{X}}{.}_L{\gamma }_L$$

$$\mathbf{\mu }\sim {\text{MVN}}_n\left(0,\lambda {\tau }^{-1}\mathbf{\text{K}}\right)$$

$$\mathbf{\epsilon }\sim {\text{MVN}}_n\left(0,{\tau }^{-1}{\mathbf{\text{I}}}_n\right)$$

where u represents the cumulative background effects of the loci, MVN denotes the multivariate normal distribution, I_n is an n × n identity matrix, and K is an n × n relatedness matrix defined as K = XX′, which captures the genetic covariance between individuals.

Testing for locus effects

To assess the significance of the effect of an individual locus l on the phenotype, controlling for population structure and background genetic effects, the parameters of the linear mixed model α₁…α_c, β_l, λ and τ were estimated by maximum likelihood, and a likelihood ratio test with (K − 1) degrees of freedom was performed against the null hypothesis that β_l = 0 using the software GEMMA²⁸.

Testing for lineage effects

Because controlling for population structure drastically reduces the power at population-stratified variants, and because a large proportion of variants are typically population-stratified in bacteria, we recovered information from the LMM regarding lineage-level differences in phenotype.

We defined lineages using principal components because we observed that principal components tend to trace paths through the clonal frame genealogy corresponding to recognizable lineages (as seen by the branch colouring in Fig. 1b and Supplementary Fig. 5) and because principal components are mutually uncorrelated, minimizing loss of power to detect differences between lineages due to correlations. Principal components were computed based on biallelic SNPs using the R function prcomp(), producing an L by n loading matrix D and an n by n score matrix T where T = X D. D_ij records the contribution of biallelic SNP i to the definition of principal component j, while T_ij represents the projection of individual i onto principal component j.

Point estimates and standard errors for the background locus effects are usually overlooked because the assumed normal distribution with common mean 0 and variance λτ⁻¹ tends to cause them to be small in magnitude and not significantly different from zero. However, cumulatively, the background locus effects can capture systematic phenotypic differences between lineages. We therefore recovered the post-data distribution (equivalent to an empirical Bayes posterior distribution) of the background locus random effects, γ, from the LMM, and reinterpreted it in terms of lineage-level differences in phenotype.

Empirically, we found that the post-data distribution of the background random effects was generally insensitive to the identity of the foreground locus and comparable under the null hypothesis (β_l = 0). We therefore calculated the mean and variance–covariance matrix of the multivariate normal post-data distribution of γ in the LMM null model. These are equivalent to those of a ridge regression⁴⁶ and were computed as

$$\mu ={({\mathbf{\text{X}}}^{\prime }\mathbf{\text{X}}+1/\lambda {\mathbf{\text{I}}}_L)}^{-1}{\mathbf{\text{X}}}^{\prime }\text{y}\hspace{0.17em}\text{and}\hspace{0.17em}{\displaystyle \sum {(\tau {\mathbf{\text{X}}}^{\prime }\mathbf{\text{X}}+1/\lambda {\mathbf{\text{I}}}_L)}^{-1}}$$

respectively. Both λ and τ were estimated by GEMMA under the LMM null model. Using the inverse transformation of the biallelic variants from PCA, X = TD⁻¹, the background random effects can be rewritten in terms of the contribution of the n principal components:

$$\begin{array}{l}\mathbf{u}=\mathbf{\text{X}}{.}_1{\gamma }_1+\dots +\mathbf{\text{X}}{.}_L{\gamma }_L\\ =\mathbf{\text{X}}\mathbf{\gamma }={\mathbf{\text{TD}}}^{-1}\mathbf{\gamma }=\mathbf{\text{Tg}}\\ =\mathbf{\text{T}}{.}_1{\text{g}}_1+\dots +\mathbf{\text{T}}{.}_n{\text{g}}_n\end{array}$$

where g = D⁻¹γ, and g_j is the background effect of principal component j on the phenotype. We computed the mean and variance of the post-data distribution of g as m = D⁻¹μ and S = D⁻¹ΣD, respectively, using the affine transformation for a multivariate normal distribution. To test the null hypothesis of no background effect of principal component j (that is, g_j = 0), we used a Wald test with test statistic $w_j=m_j^2/S_{jj},$ which we compared against a χ² distribution with one degree of freedom to obtain a P value.

Although we identified and tested for lineage effects in the LMM setting, lineage effects could also be identified and tested for by interpreting the coefficients of leading principal components or genetic cluster membership included as fixed effects in a regression, both of which represent alternative methods for controlling for population structure.

Identifying non genome-wide principal components

Some principal components capture variation localized to particular areas of the genome. We identified non genome-wide principal components by testing for spatial heterogeneity of the loading matrix W for biallelic SNPs across the genome. SNPs were grouped into 20 contiguous bins (indexed by j ) of nearly equal sizes N_j, and the mean O_ij and variance V_ij in the absolute value of the SNP loadings for principal component i in bin j were calculated, as well as the mean absolute value E_i of the SNP loadings for principal component i across all SNPs. The null hypothesis of no heterogeneity was assessed by comparing the test statistic χ_i² = Σ_j (O_ij − E_i)²/(V_ij/N_j) to a χ² distribution with degrees of freedom equal to the number of bins minus one to obtain a P value.

Antimicrobial resistance testing, genome sequencing and SNP calling

We investigated 241 E. coli and 176 K. pneumoniae UK clinical isolates newly reported here, together with 992 S. aureus and 1,735 M. tuberculosis isolates reported previously^36,37. All isolates were tested for resistance to multiple antimicrobials based on routine clinical laboratory protocols, and DNA was extracted and sequenced on Illumina platforms as previously described^36–38. We called SNPs using standard methods^47,48, employing Stampy⁴⁹ to map reads to reference strains CFT073 (genbank accession no. AE014075.1), MGH 78578 (CP000647.1), H37Rv (NC_000962.2) and MRSA252 (BX571856.1) for E. coli, K. pneumoniae, M. tuberculosis and S. aureus, respectively. The distributions of biallelic SNP frequencies are provided in Supplementary Table 4.

Defining the pan-genome

To investigate gene presence or absence we created a pan-genome for each set of isolates. To obtain whole genome assemblies, reads were de novo assembled using Velvet⁵⁰. We annotated open reading frames on the de novo assemblies for each isolate. We then used the Bayesian gene-finding program Prodigal⁵¹ to identify a set of protein sequences for each de novo assembly. These annotated protein sequences were clustered using CD-hit⁵², with a clustering threshold of 70% identity across 70% of the longer sequence. We converted the output of CD-hit into a matrix of binary genotypes denoting the presence or absence of each gene cluster in each genome (Supplementary Fig. 2).

Kmer counting

Some diversity such as indels and repeats is difficult to capture using standard variant calling tools. To capture non-SNP variation, we pursued a kmer or word-based approach¹³ in which all unique 31 base haplotypes were counted from the sequencing reads using dsk⁵³ following adaptor trimming and removal of duplicates and low-quality reads using Trimmomatic⁵⁴. If a kmer was counted five or more times in an isolate, then it was counted as present; if not, it was treated as absent (Supplementary Fig. 2). This produced a deduplicated set of variably present kmers across the data set, with the presence or absence of each determined per isolate. The total number of SNPs, kmers and gene clusters per species can be found in Supplementary Table 5.

Phylogenetic inference

Maximum likelihood phylogenies were estimated for visualization and SNP imputation purposes using RAxML version 7.7.6 (ref. 55), with a general time reversible (GTR) model and no rate heterogeneity, using alignments from the mapped data based on biallelic sites, with non-biallelic sites being set to the reference.

SNP imputation

Because Illumina sequencing is inherently more error-prone than Sanger sequencing, strict filtering is required for reliable mapping-based SNP calling, contributing to a small but appreciable frequency of uncalled bases in the genome due to ambiguity or deletion. Restricting analysis to sites called in all genomes is undesirable, while ignoring uncalled sites by removing individuals with missing data at individual sites generates P values that cannot be validly compared between sites because they are calculated using data from differing sets of isolates.

SNP imputation is therefore generally considered necessary for GWASs⁵⁶. We imputed missing base calls using two approaches, ClonalFrameML⁵⁷ and Beagle⁵⁶. Imputation using ClonalFrameML⁵⁷ involves estimating the clonal frame by maximum likelihood⁵⁸, then jointly reconstructing ancestral states and missing base calls by maximum likelihood utilizing the phylogeny reconstructed earlier⁵⁹. To use Beagle, the mapped data were coded as haploid (one column per individual) and input as phased data^56,60.

Testing imputation accuracy

To simulate data for testing imputation accuracy, 100 sequences were randomly sampled from each GWAS data set across the phylogeny. Maximum likelihood phylogenies were estimated for the 100 sequences of each species using RAxML⁵⁵, as above. Any columns in the alignment corresponding to ambiguous bases in the reference genome were excluded. One round of imputation was performed using ClonalFrameML to produce complete data sets with no ambiguous bases (Ns), which were then treated as the truth for the purpose of testing. The empirical distributions of Ns per site in the data sets of 100 sequences were determined, and these were sampled with replacement to reintroduce Ns to the variable sites in 100 simulated data sets. These sequences were then imputed again using ClonalFrameML and Beagle. Accuracy was summarized per site as a function of the frequency of Ns per site and the minor allele frequency. Overall, ClonalFrameML was more accurate than Beagle, so ClonalFrameML was used for all GWAS analyses (Supplementary Table 1).

Calculating association statistics before controlling population structure

We wished to compare the significance of associations before and after controlling for population structure. For the SNP and gene presence or absence data, an association between each SNP or gene and the phenotype was tested by logistic regression implemented in R. For the kmer analyses, an association between the presence or absence of each kmer was tested using a χ² test implemented in C++. For each variant a P value was computed.

Correction for multiple testing

Multiple testing was accounted for by applying a Bonferroni correction⁶¹; the individual locus effect of a variant (SNP, gene or kmer) was considered significant if its P value was smaller than α/n_p, where we took α = 0.05 to be the genome-wide false-positive rate and n_p to be the number of SNPs and genes, or kmers, with unique phylogenetic patterns, that is, unique partitions of individuals according to allele membership. Because the phenotypic contribution of multiple variants with identical phylogenetic patterns cannot be disentangled statistically, we found that pooling such variants improved the power by demanding a less conservative Bonferroni correction than correcting for the total number of variants (Supplementary Fig. 10).

The genome-wide −log₁₀ P value threshold for SNPs and genes (or kmers) was 6.1 (7.3) for S. aureus ciprofloxacin, erythromycin, fusidic acid, gentamicin, penicillin, methicillin, tetracycline and rifampicin, 5.9 (6.7) for S. aureus trimethoprim, 6.5 (7.3) for all antimicrobials tested for E. coli, 6.6 (7.3) for all antimicrobials tested for K. pneumoniae and 5.0 (7.6) for all antimicrobials tested for M. tuberculosis. We also accounted for multiple testing of lineage effects by applying a Bonferroni correction for the number of principal components, which equals the sample size n.

Running GEMMA

For the analyses of SNPs, genes and kmers, we computed the relatedness matrix K from biallelic SNPs only. We tested for foreground effects at all biallelic, triallelic and tetrallelic SNPs, genes and kmers. GEMMA was run using a minor allele frequency of 0 to include all SNPs. GEMMA was modified to output the ML log-likelihood under the null, and alternative and −log₁₀ P values were calculated using R.

To perform LMM on tri- and tetra-allelic SNPs, each SNP was encoded as K − 1 binary columns corresponding to the first K − 1 alleles. For each column, an individual was encoded 1 if it contained that allele and 0 otherwise. The first column was input as the genotype, and the others as covariates into GEMMA. The log-likelihood of the null from the biallelic SNPs, together with the log-likelihood under the alternative for each of the SNPs, was used to calculate the P value per SNP.

Due to the large number of kmers present within each data set, it was not feasible to run LMM on all kmers. We therefore applied the LMM to the top 200,000 most significant kmers from the logistic regression, plus 200,000 randomly selected kmers of those remaining. The randomly selected kmers were used to indicate whether some were becoming relatively more significant than the top 200,000, providing a warning in the case where large numbers of kmers became significant only after controlling for population structure.

Variant annotation

SNPs were annotated in R using the reference fasta and genbank files to determine SNP type (synonymous, non-synonymous, nonsense, read-through and intergenic), the codon and codon position, reference and non-reference amino acid, gene name and gene product.

Unlike the SNP approach, where we can easily refer to the reference genome to find what gene the SNP is in and the effect that it may have, annotation of the kmers is more difficult. We used BLAST⁶² to identify the kmers in databases of annotated sequences. Each kmer was first annotated against a BLAST database created of all refseq genomes of the relevant genus on NCBI. This enabled automatic annotation of all kmers that gave a sufficiently small e-value against the genus-specific database. All kmers were also searched against the whole nucleotide NCBI database, first to compare and confirm the matches made against the first database and second to annotate the kmers that did not match anything in the within-genus database. Finally, when the resistance-determining mechanism was a SNP, the top 10,000 kmers were mapped to a relevant reference genome using Bowtie2 (ref. 63). This was used to determine whether the most significant kmers covered the position of the resistance-causing SNP or whether they were found elsewhere in the gene.

Genes were annotated for each CD-hit gene cluster by performing BLAST⁶² searches of each cluster sequence against a database of curated protein sequences downloaded from UNIPROT⁶⁴.

Testing power by simulating phenotypes

To assess the performance of the method for controlling population structure, we performed 100 simulations per species. In each simulation, a biallelic SNP was chosen randomly (from those SNPs with minor allele frequency above 20%) to be the causal SNP. Binary phenotypes (case or control) were then simulated for each genome with case probabilities of 0.25 and 0.5, respectively, in individuals with the common and rare allele at the causal SNP (an odds ratio of 3). For each simulated data set, we tested for locus effects at every biallelic SNP, and for lineage effects at every principal component, as described above. The power to detect locus effects was defined as the proportion of simulations in which the causal SNP was found to have a significant locus effect. This was compared to a theoretically optimum power computed as the proportion of simulations in which the causal SNP was found to have a significant locus effect when population structure and multiple testing were not controlled for. The power to detect lineage effects was computed as the proportion of simulations in which the principal component most strongly correlated to the causal SNP was found to have a significant lineage effect. We defined fine mapping precision as the distance spanned by SNPs within two log-likelihoods of the most significant SNP in the test for locus effects, in those simulations in which the causal locus was genome-wide significant. We calculated the number of homoplasies per SNP by counting the number of branches in the phylogeny affected by a substitution based on the ClonalFrameML ancestral state reconstruction, and subtracting the minimum number of substitutions (K − 1).

Code availability

We have created an R package, bugwas, implementing our method for controlling population structure, and an end-to-end GWAS pipeline using R, Python and C++. Both can be downloaded from www.danielwilson.me.uk/virulogenomics.html.

Supplementary Material

Supplementary information is available online. Reprints and permissions information is available online at www.nature.com/reprints.