Influence of tree shape and evolutionary time-scale on phylogenetic diversity metrics

Abstract

During the last decades, describing, analysing and understanding the phylogenetic structure of species assemblages has been a central theme in both community ecology and macro-ecology. Among the wide variety of phylogenetic structure metrics, three have been predominant in the literature: Faith’s phylogenetic diversity (PD_Faith), which represents the sum of the branch lengths of the phylogenetic tree linking all species of a particular assemblage, the mean pairwise distance between all species in an assemblage (MPD) and the pairwise distance between the closest relatives in an assemblage (MNTD). Comparisons between studies using one or several of these metrics are difficult because there has been no comprehensive evaluation of the phylogenetic properties each metric captures. In particular it is unknown how PD_Faith relates to MDP and MNTD. Consequently, it is possible that apparently opposing patterns in different studies might simply reflect differences in metric properties. Here, we aim to fill this gap by comparing these metrics using simulations and empirical data. We first used simulation experiments to test the influence of community structure and size on the mismatch between metrics whilst varying the shape and size of the phylogenetic tree of the species pool. Second we investigated the mismatch between metrics for two empirical datasets (gut microbes and global carnivoran assemblages). We show that MNTD and PD_Faith provide similar information on phylogenetic structure, and respond similarly to variation in species richness and assemblage structure. However, MPD demonstrate a very different behaviour, and is highly sensitive to deep branching structure. We suggest that by combining complementary metrics that are sensitive to processes operating at different phylogenetic depths (i.e. MPD and MNTD or PD_Faith) we can obtain a better understanding of assemblage structure.

Introduction

During the last decades, the phylogenetic structure of species assemblages has received much attention in community ecology and macro-ecology since it holds promise to help unravel the drivers of species coexistence at various spatial scales (Webb et al. 2002, Lozupone and Knight 2005, Mouquet et al. 2012, Warren et al. 2014).

Community ecologists have considered phylogenetic distances between species as a substitute for niche differences and have used phylogenetic structure to disentangle the relative effects of biotic and abiotic environments in shaping present day species distributions (Webb et al. 2002, Mouquet et al. 2012). Coexistence theory predicts that species sharing the same niches compete more strongly than dissimilar species (HilleRisLambers et al. 2012), it is therefore commonly expected that competition-driven coexistence will generate patterns of phylogenetic ‘over-dispersion’ (i.e. distantly related species with less niche overlap co-occur). Conversely, phylogenetic ‘clustering’ is thought to indicate the coexistence of closely related species because of shared environmental niches (Webb et al. 2002, Mouquet et al. 2012, O’Dwyer et al. 2012). Although the link between pattern and process has been a matter of some debate (for example, see Mayfield & Levine 2010), non-random phylogenetic community structure appears common. Recently, macro-ecologists have also used the phylogenetic structure of assemblages to understand the effects of historical processes on large scale biodiversity distribution (Davies et al. 2011, Kissling et al. 2012). For example, explosive radiation of species within a given area may result in the co-occurrence of closely related species resulting in phylogenetic clustering, while multiple allopatric speciation events may lead to phylogenetic over-dispersion (Warren et al. 2014).

Among the plethora of phylogenetic structure metrics that have been developed and used in both fields (Pavoine and Bonsall 2011), the three most commonly used are Faith’s phylogenetic diversity (named PD_Faith hereafter), which represents the sum of the branch lengths of the phylogenetic tree linking all species of a particular assemblage (Faith 1992), the mean pairwise distance between all species in an assemblage (MPD) and the pairwise distance between the closest relatives in an assemblage (MNTD) (Webb et al. 2002). As PD_Faith correlates closely and positively with species richness (SR, e.g. Tucker and Cadotte 2013), the use of a null model that keeps SR constant while randomizing phylogenetic relationships allows comparisons of assemblages with different SR. Using this null model, standard effect size (SES, Eq. 1) and relative position of observed values with respect to the null distribution can be calculated. SES can be defined as:

$$\mathit{\text{ses}}.\mathit{\text{Metric}}=\frac{{\mathit{\text{Metric}}}_{\mathit{\text{obs}}}-\mathit{\text{mean}}({\mathit{\text{Metric}}}_{\mathit{\text{null}}})}{\mathit{\text{sd}}({\mathit{\text{Metric}}}_{\mathit{\text{null}}})}$$ (Eq. 1)

where Metric_obs is the observed metric in a given assemblage, and Metric_null is the same metric but calculated n times with n randomised assemblages. The relative position of the observed value with respect to the null distribution is computed as the proportion of null values that are lower than the observed values. It represents the probability to draw the observed value from the null distribution and thus corresponds to a p-value (H_null being the null model). For normally distributed data, significance at p-value<0.05 is equivalent to a standard effect size > 1.96 (or < -1.96).

The standard effect size (and associated p-value) of MPD (ses.MPD hereafter) and MNTD (ses.MNTD hereafter) are commonly used in the community phylogenetic literature (also referred to as NRI and NTI, respectively, Webb et al. 2002), and can be directly compared to the standard effect size of PD_Faith (ses.PD_Faith hereafter). All three standardized metrics quantify the relative excess (overdispersion) or deficit (clustering) in phylogenetic diversity for a given species set relatively to the species pool (whose phylogenetic relationships between species are depicted by the “regional tree”). As a consequence, a negative standardized metric reflects a relative clustering of species while a positive standardized metric reflects a relative overdispersion of species.

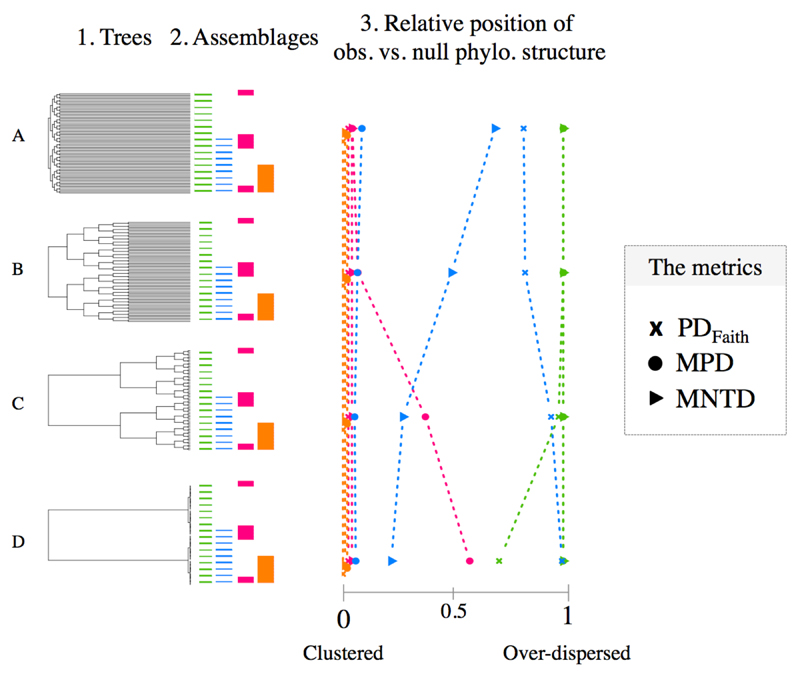
MPD and MNTD highlight phylogenetic structure of assemblages at different evolutionary depths since MPD is more strongly influenced by the ‘basal’ structure of the phylogenetic tree while MNTD describes the more ‘terminal’ structure of the phylogenetic tree (Webb et al. 2002). This is an important aspect since different processes may act at different evolutionary time scales. Some processes may produce basal clustering, while others may create terminal over-dispersion, generating “clusters of overdispersion” (see e.g. blue assemblages in Fig. 1). For example, a cluster of overdispersion could be due to environmental filtering at large evolutionary time scales and competition between close relatives at fine evolutionary time scale (Hardy and Senterre 2007). Conversely, “overdispersion of clusters” would correspond to basal overdispersion and terminal clustering (see e.g. pink assemblages in Fig. 1). Consequently, owing to their property to detect phylogenetic structure on restricted phylogenetic scales, existing metrics may be limited in their ability to capture complex structural patterns and may suffer from decreased power (i.e. inflated false negative) in case clustering and overdispersion occur in concert at different phylogenetic scales. In other words, if clustering and overdispersion occur at different phylogenetic scales, using a metric that averages the information over the entire tree may mask these two opposing patterns.

Figure 1. Sensitivity of PD_Faith, MNTD and MPD to different assemblage structures and tree shapes.

The figure depicts four balanced trees (column ‘Tree’) along with four potential assemblage (column ‘Assemblage’): coloured segments indicate that the corresponding tips on the phylogeny are present in the assemblages (i.e. species presence); from left to right: simple simple overdispersion in green; clustering of overdispersion in blue; overdispersion of clusters in red; and simple clustering in orange. The corresponding diversities are presented in the third column. Values on the X-axis correspond to the relative position of observed value compared to a null distribution (interpreted as a p-value). For example, a value of 0 indicates that the observation is lower than all null expectations (‘clustering’) while a value of 0.5 indicates that the observation equals to the median of the null distribution. The different metrics are represented by different symbols (see legend).

While differences in the performance of ses.MPD and ses.MNTD are widely recognised, ses.PD_Faith has mostly been considered independently or as interchangeable with ses.MPD and ses.MNTD (see Table 1 and Supplementary Material 1 for examples and their detailed justifications, respectively). To our knowledge, this assumed equivalence has never been validated empirically. Comparisons between studies using either jointly MPD and MNTD or PD_Faith (either SES of metrics and/or corresponding p-values) are thus difficult to interpret, and it is possible that apparently opposing patterns of phylogenetic structure simply reflect differences in metric properties. While a number of macro/micro ecological studies have explored patterns of phylogenetic metrics, making unique and important contributions to the literature (e.g. Morlon et al. 2011, Fritz and Rahbek 2012, O’Dwyer et al. 2012, see Table 1), for the most part they have focussed only on PD_Faith, limiting our understanding of the phylogenetic scale at which processes structuring species assemblages operate. In constrast, community phylogeneytic studies frequently measure both MPD and MNTD, but rarely consider PD_Faith. Choice of metric, however, is often poorly justified, and we currently lack a comparative analysis comparing the performance of these three widely used indices.

Table 1. Hypotheses tested, key papers and corresponding metrics used across fields to depict the phylogenetic structure of species assemblages.

The table depicts for each of the two considered field of research (column 1) the hypotheses tested behind classic phylogenetic patterns (column 2) and key papers using either MPD/MNTD or PD_Faith (column 3).

	Hypotheses related to the two patterns:		Metrics used to quantify the pattern; examples of key publications
Fields	Clustering	Over-dispersion	Biotas	MPD/MNTD	PDFaith
Community ecology	Environmental filtering*	Competition	Micro-biotas	Goberna et al. 2014 Bryant et al. 2008	O’Dwyer et al. 2012
			Macro-Biotas	Webb et al. 2002; Graham et al. 2009;	Cadotte et al. 2009; Morlon et al. 2011
Macro-ecology	In-situ speciation	Biogeographic contact zones; Vicariance; Competition at large scale	Cardillo 2011b; Davies & Buckley 2011		Fritz & Rahbek 2012

^*but see Mayfield & Levine 2010

Here, we perform the first comprehensive comparative analysis of MPD, MNTD and PD_Faith using both simulations and emprical data. We first used simulation experiments to understand the relative effect of (1) the size and the shape of the regional tree, and, (2) the richness and structure of the observed community, on the mismatches between the three metrics. Second, we evaluated metric behaviour on real world datasets for gut microbes and terrestrial mammals. Overall, we show that MNTD and PD_Faith, are both ‘terminal’ metrics, and thus could be used interchangeably, while MPD, a ‘basal’ metric sensitive to deeper branching structure, captures a distinct, but complementary dimension of phylogenetic structure. Their combined use allow for a better understanding of assemblage structure, especially when different processes operates at different phylogenetic depths simultaneously, while the use of only one metric could lead to incomplete interpretations and biased conclusions.

Material and Methods

Simulation experiments

In a first set of simulations, we illustrated the sensitivity of PD_Faith, MPD and MNTD to tree shape and phylogenetic structure using a straightforward toy example. We generated four balanced phylogenetic trees with different basal vs. terminal branch lengths (see Fig. 1 column 1). For each tree, we compared the response of the three metrics to four extreme assemblage structures: phylogenetic clustering and overdispersion, clustering of overdispersion and overdispersion of clusters (Fig. 1)

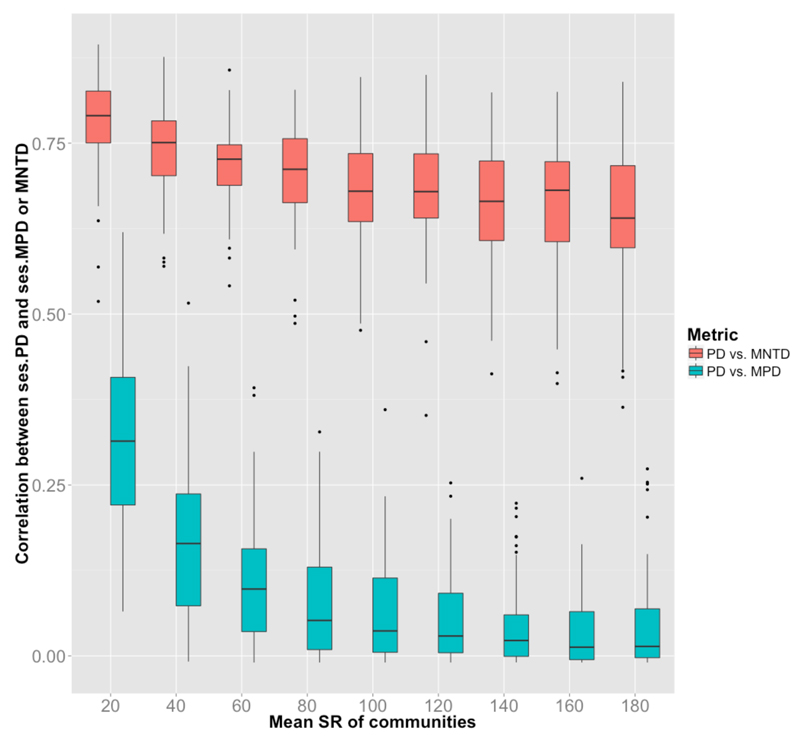
In a second set of simulations, we tested the influence of regional pool sizes, regional tree shapes and species richness of the assemblage on the three metrics. We first created four regional species pools of different sizes (n = 20, 40, 100 and 200 species). For each regional species pool, we simulated 100 regional phylogenetic trees of size n using a pure birth model (function sim.bdtree of the geiger R package; Harmon et al. 2008) for which we reported two tree shape statistics: imbalance (Colless 1982) and Gamma values, quantifying the “tippiness” vs. “stemminess” of the tree, respectively (Pybus and Harvey 2000). For each of these 400 regional pools (100 regional trees * 4 tree sizes), we constructed local species assemblages by randomly drawing without replacement m species from the regional pool (m thus equals the species richness of the corresponding community). We repeated this procedure varying m from 2 to n-1 and randomly drawing five assemblages for a given species richness m. To test the influence of the size of the species assemblage on our three metrics, we then grouped assemblages according to their SR and reported the mismatches between metrics for each group independently. For example, with a regional species pool of 200 species, we created 10 sets of species assemblages with different ranges of SR (from 10 to 30 species for the first set, 30 to 50 for the second, and so on until 170 to 190 species for the last set). For each tree and each set of assemblages we calculated the strength of the relationship between ses.PD_Faith and ses.MPD or ses.MNTD as the R² of the linear regression between them (we also checked for more complex models, see Results).

Real world empirical data

To compare the three metrics in realistic examples, we compiled two empirical datasets that differed in spatial scale and assemblage structure: mammal gut microbial assemblages and global terrestrial carnivore assemblages.

Mammal gut microbial assemblages

Species assemblages were here defined as the set of microbial Operational Taxonomic Units (OTUs, a taxonomic concept based on DNA sequence similarities commonly used for microbes) living in the gut of different mammalian species. We used the 16S rRNA genes dataset from Muegge et al. (2011) to derive occurrences of 2,820 OTUs (defined at 97% of similarity to create species-like entities) in the gut of 33 mammalian species (i.e. 33 bacterial species assemblages from a regional pool of n = 2,820 OTUs) and to reconstruct a regional phylogenetic tree (see Supp. Mat.2. for details).

Global carnivore assemblages

We used the distribution maps provided by the Mammal Red List Assessment (http://www.iucnredlist.org/) to derive the occurrence of 241 terrestrial carnivores (regional species pool). We then defined a species assemblage as all carnivores co-occurring in a given 50x50km grid cell. Analyses were thus carried out over 52,346 assemblages around the world. For phylogenetic relationships, we used the recent update of the carnivoran phylogeny proposed by Nyakatura and Bininda-Emonds (2012) as the regional tree.

Metric calculation

For both simulated and empirical datasets, we computed the observed PD_Faith, MPD and MNTD for each assemblage using the function pd, mpd and mntd in the R package picante (Kembel et al. 2010). We then randomly shuffled the tips of the regional phylogeny and calculated PD_Faith, MPD and MNTD for the random assemblages, and repeated this procedure 100 times to obtain a null distribution of values for each assemblage and for each metric. We calculated standard effect sizes using eq.1, as well as the relative position of the observed index in the null distribution to derive p-values (e.g. Fig 1). All analysis were performed using R (R Development Core Team 2014).

Results & Discussion

In our first set of simulations (see Material & Methods and Figure 1), we used extreme assemblage structures to illustrate the different phylogenetic signal captured by PD_Faith, MPD and MNTD, respectively. All three metrics produce very similar predictions in the case of simple patterns where a single process structures species’ assemblages (Fig. 1, clustered patterns in orange and over-dispersed patterns in green). We also explored more complex phylogenetic structures such as clusters of overdispersion or overdispersion of clusters. These patterns might arise when different processes acting at different depth of the tree jointly influence assemblage phylogenetic structure. In these more complex cases, the different metrics suggested different phylogenetic structures, with these differences being further affected by phylogenetic tree shape (Fig. 1).

In the case of clusters of overdispersion (blue line in Fig. 1) on a very ‘tippy’ tree (i.e. one with relatively short internal to tip branch lengths; tree A in Fig. 1) the relative rank of observed MPD versus null MPD suggests clustering while PD_Faith (and even more MNTD) tends towards over-dispersion (see Fig. 1). This difference can be explained by the sensitivity of MPD to deep branching structure in the tree, which are counted multiple times when computing pairwise distance between all species in the assemblage (Webb et al. 2002). Thus, MPD tends to emphasise the basal clustering rather than the overdispersion within the cluster. In contrast, PD_Faith and MNTD are less influenced by internal branches (they are completely ignored by MNTD and counted only once for PD_Faith), and therefore tend to be more sensitive to patterns occurring at the tips of the tree. When keeping the same community structure (a cluster of overdispersion, blue curve) but switching to a “stemmy” tree (i.e. one with relatively long internal to tip branch lengths; tree D in Fig. 1), MPD still suggests clustering and MNTD over-dispersion but PD_Faith shifts towards clustering. In this case only, PD_Faith is closer to MPD than to MNTD because, even though PD_Faith counts internal branches only once, in our simple simulation they have a profound effect because they are disproportionally (and perhaps unrealistically) long compared to tip lengths. When considering overdispersion of clusters (red curve) on the same stemmy tree, PD_Faith and MNTD were more sensitive to the signal of clustering, whereas MPD was more sensitive to the signal for overdispersion. This simple example illustrates that different metrics can identify apparently contrasting patterns in the same dataset, and that changes in tree structures can alter metric behaviour, and thus the inferences we might draw from them. Overall, PD_Faith and MNTD tend to identify similar structure (although not always), but are decoupled from MPD.

Our second set of simulations aimed at investigating whether the observed mismatch between PD_Faith and MPD was still apparent with a less-extreme range of community structures, but more realistic regional tree shapes and richer species assemblages. We found that ses.PD_Faith and ses.MPD were still largely decoupled while ses.PD_Faith and ses.MNTD showed congruent results (Fig 2 and Supp. Mat. 3-4). While regional phylogenetic tree shape and species pool size did not influence the discrepancies between ses.PD_Faith and ses.MPD (Supp. Mat. 5-6) correlation strength between metrics decreased with increasing species richness (mean SR) of assemblages (Fig 2 and 3-4). The richer the community, the more complex they are, and the more divergent are the metrics. Conversely, species poor communities likely have less complex structures that are easily detected by all three metrics.

Figure 2. Influence of assemblage species richness on diversity metrics.

Boxplots represent R² of the linear regressions between ses. PD_Faith and ses.MPD, and between ses. PD_Faith and ses.MNTD for 10 sets of simulated assemblages that differ in species richness (SR): from 10 to 30 species for the first set, 30 to 50 for the second, and so on, until 170 to 190 species for the last set. For each of these sets, we computed the standard effect size of each metric and the R² of the linear relationship between the metrics. We repeated the whole procedure 100 times to obtain a distribution of R² for each level of SR.

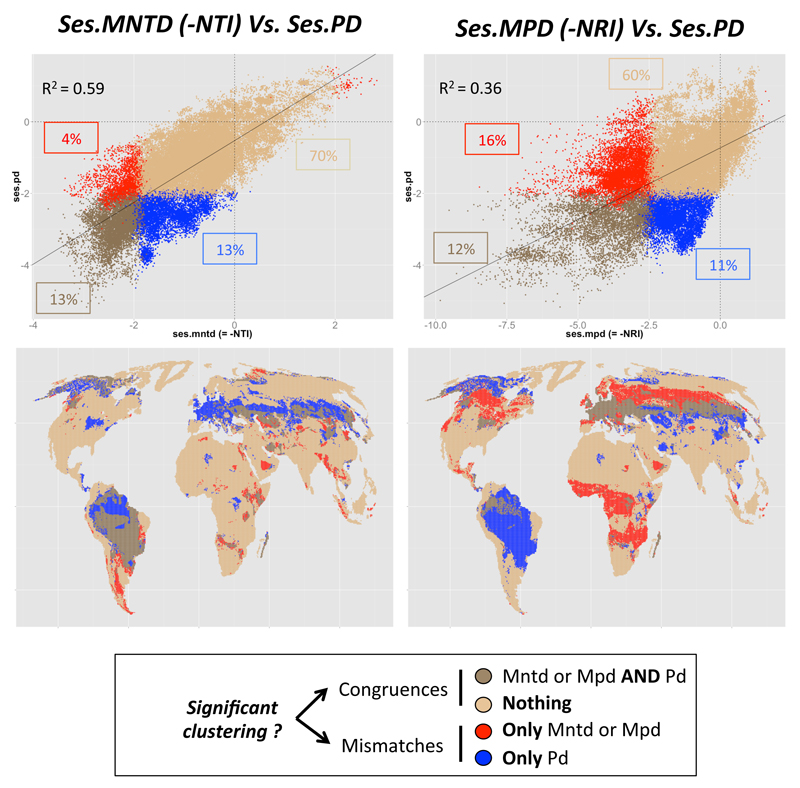
Figure 3. Phylogenetic structure of carnivoran assemblages.

The top graphs represent the relationships between ses.PD_Faith and ses.MPD or ses.MNTD together with the R² of their linear relationship. The proportion of congruence and divergence are also represented in four groups: whether PD_Faith and MPD (or MNTD) show congruent (significant/non-significant clustering: dark and light brown dots, respectively) or diverging results (only significant PD_Faith / only significant MPD (or MNTD); blue and red dots, respectively). Bottom graphs show the spatial structure of these four types of assemblages.

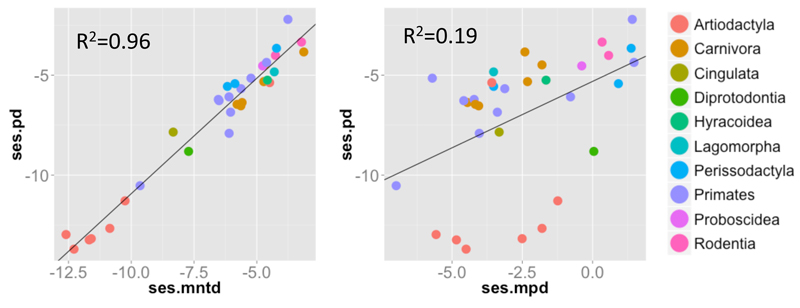
Figure 4. Mammalian guts phylogenetic structure.

Raw relationship between ses.PD_Faith(Y-axis) and ses.MPD/ses.MNTD (X-axis) across 33 mammalian gut assemblages. Host orders are represented by different colours (see legend). The R² of linear models between metrics are reported on each graph.

The analyses of empirical data match to the results from the simulations. Phylogenetic pattern of both carnivore diversity and gut microbiomes revealed a clear mismatch between ses.PD_Faith and ses.MPD (R² = 0.36 and 0.19, for carnivores and microbes respectively, Figs 3-4), and greater congruence between ses.PD and ses.MNTD (R² = 0.59 and 0.96, for carnivores and microbes respectively, Figs 3-4). These results were almost identical when testing for linear or non-linear relationships between the metrics (see Supp. Mat. 7-8). The clear mismatch between indices further reveals complex structures that cannot be summarized by a single number (i.e. a single metric).

Comparing phylogenetic structure using metrics sensitive to process operating at different evolutionary scales sheds new light on the distribution of diversity. Indeed, for carnivores, the differences between metrics were strongly spatially structured (Fig. 4). In some parts of South America, both ses.PD_Faith and ses.MNTD suggested phylogenetic clustering which were not evident from patterns of ses.MPD. Recent radiations of particular clades within the neotropics following the Great American Biotic Interchange (Webb 2006, Woodburne 2010) - for example, the ocelot genus leopardus (Johnson et al. 2006) - likely results in the co-occurrence of closely related species (Pedersen et al. 2014) at the continental scale. Niche partitioning via fine-scale habitat preferences may then have allowed these close relative species to co-occur at the scale of our analysis (Araújo and Rozenfeld 2014), leading to ‘terminal’ phylogenetic clustering (as detected by ses.PD_Faith or ses.MNTD). At the same time, because South American carnivore assemblages also contain species from the two major clades of carnivores (i.e. dog- and cat-like clades: caniformia and feliformia, respectively), which are evolutionarily distinct from each other, but contain approximately equal numbers of species (see Pedersen et al. 2014, and Supp. Mat. 9), regional assemblages tend to show random phylogenetic patterns (as indicated by ses.MPD scores).

In contrast to patterns in South America, the Congo basin and some parts of Eurasia and North America show significant ‘basal’ clustering (as indicated by a significant negative ses.MPD values), but little structure towards the tips (as suggested by non-significant patterns of ses.PD_Faith and ses.MNTD). This pattern may reflect the very unbalanced distribution of caniformia and feliformia in these regions (see Sup. Mat. 9) suggested to be the outcome of the interrelation between large-scale competition and historical biogeography (Pedersen et al. 2014). In Eurasia and North America, caniformia are over-represented, while feliformia dominate in the Congo basin (Pedersen et al. 2014; see also Supp. Mat. 9). Thus, these regions show taxonomic dominance by a single subclade, which is apparent in the “basal” clustering pattern, while there is little regional phylogenetic structure within clades. Taken together these findings demonstrate that one single phylogenetic diversity metric is not able to fully describe the complex structure of assemblage at macro-ecological scales where different processes may operate in different geographical regions and are evident at different phylogenetic depths. It is thus important to use multiple metrics that focus on different evolutionary scales, to be able to draw more precise and robust interpretations of phylogenetic diversity patterns (see e.g. Davies and Buckley 2011). Our results further stress the importance of using multiple metrics in the analysis of large datasets, as complex macro-ecological phylogenetic structures can emerge when studying relatively large groups (see O’Meara 2012, for a macro-evolutionnary perspective on this subject).

Our findings at large spatial scale also extend to micro-biology, as we observe very similar trends for gut microbial assemblages (Fig. 4 and Sup. Mat. 9). For example, rodent microbial gut assemblages appear clustered with ses.PD_Faith or ses.MNTD, but over-dispersed with ses.MPD (Fig. 4). Therefore, when using only metrics of ses.PD_Faith or ses.MNTD, one would have concluded that rodent microbial gut assemblages mainly consist of some closely related lineages. Whereas, when using only the ses.MPD metric, one would have concluded the opposite: microbial guts assemblages consist of distantly related lineages.

Again, these mismatches among metrics seem to be caused by an over-dispersion of clusters (see Supp. Mat. 10); the capybara (Hydrochoerus hydrochaeris) is an interesting example. Because it is a hindgut-fermenter herbivore, plant residuals reaching the fermentative part of the gut are complex to digest (e.g. cellulose and lignin, Ley et al. 2008) and a variety of plant secondary metabolites need to be broken-down (Dearing et al. 2000). Consequently, very different bacterial clades with different enzymatic equipment inhabit the gut of hindgut herbivores, possibly generating observed patterns of ‘basal’ overdispersion, i.e. co-occurrence of distantly related bacterial lineages. However, within these clades, host-specific processes structuring bacterial assemblages, such as mucus barriers, oxygen concentration and the innate and adaptive immune systems, may select for specific bacterial lineages (Salzman et al. 2010, Bevins & Salzman 2011, Hooper et al. 2012) favouring clustering of bacterial lineages. Thus, similarly to the case for global carnivoran communities discussed above, we show that a set of complementary metrics is needed to accurately describe the complex phylogenetic structure of micro-biomes.

We have classified phylogenetic metrics as either ‘terminal’ or ‘basal’, and we show that ses.PD_Faith is a ‘terminal’ metric that reflects the phylogenetic structure that is dominant near the tip of the tree. Recent reviews on metrics of phylogenetic beta diversity (Swenson 2011) and evolutionary isolation (i.e. phylogenetic “structure” at the species level, Redding et al. 2014) have followed a similar classification, placing emphasis on the phylogenetic depth at which patterns emerge. For example, Swenson (2011) classified Unifrac (Lozupone and Knight 2005) and PhyloSor (Bryant et al. 2008), the beta diversity equivalents of PD_Faith, as ‘terminal’ while Dpw (Webb et al. 2008), the beta diversity equivalent of MPD, as ‘basal’. Similarly, Redding et al. (2014) suggested that the fair proportion evolutionary distinctiveness metric (Isaac et al. 2007), the equivalent of PD_Faith at the species level, best captures ‘terminal’ isolation, while the ‘average phylogenetic distance’ (Ricotta 2007), the equivalent of MPD at the species level, is more closely linked to the ‘basal” isolation of species.

Our analysis focused on the three most widely used metrics in (macro) ecology. There are, however, a large number of available metrics in the literature that have been proposed over the last decades (see Pavoine and Bonsall, 2011, for a synthetic review). It is beyond the scope of the paper to review and compare all available metrics, and additional studies are needed to extend our results to other metrics. For example, the Rao Quadratic Entropy (Rao QE, e.g. Pavoine and Bonsall 2011) is also widely used to describe phylogenetic structure (e.g. Devictor et al. 2010). Interestingly, when using presence/absence data, Rao QE has a non-linear relationship with MPD (Rao QE = (m-1)/m * MPD, with m being the species richness of the assemblage) so that the two metrics essentially carry the same information. As a consequence, our results suggest that Rao QE would also represent a ‘basal’ metric of phylogenetic diversity, although this remains to be verified.

To better link macro-ecology, community ecology and microbial ecology, our analysis only focused on presence-absence data since abundance data is often not available at macro- and micro-ecological scales. However, we suggest that issues raised here for presence-absence data are likely to also occur when metrics are computed with abundance data. It is nonetheless not trivial to extend our simulation framework to incorporate abundances because additional assumptions have to be made on the relative abundances of species within the simulations, for which many possible scenarios exist. Additionally, since other metrics and recent developments have been proposed to specifically include abundances (e.g. Chao et al. 2010, Faith 2013), more comprehensive tests need to be conducted to evaluate the influence of species’ abundance on detected patterns.

Conclusion

The use of PD_Faith, MPD and MNTD to characterize the phylogenetic structure of assemblages and regional species assemblages is common in the ecological literature. However, the choice of one metric over another seems more the product of historical contingencies rather than methodological properties. For example, studies linking phylogenetic diversity to area (Morlon et al. 2011), productivity (Cadotte et al. 2008) or functional diversity (Safi et al. 2011) have adopted PD_Faith as the natural extension of species richness (SR). This is an interesting avenue but explores only one single –recent- dimension of the phylogenetic structure of communities. Adding metrics that detect deeper phylogenetic structures (such as MPD or Rao QE) may in fact reveal different processes and thus complete our understanding of diversity distribution.

Here, we have demonstrated that the choice of metric can significantly impact inferences on dominant patterns and thus interpretation with regard to potential underlying processes. We show that MNTD and PD_Faith behave similarly, but that MPD is more sensitive to deeper branching structures. Our results extend the findings of Swenson (2011) for beta diversity metrics to alpha diversity metrics in distinguishing between relatively ‘basal’ or ‘terminal’ metrics. We call for the joint use of complementary metrics (i.e. MPD and PD_Faith or MNTD) to better understand patterns of species assemblage.