Penalized Regression for Genome-Wide Association Screening of Sequence Data

Abstract

Whole exome and whole genome sequencing are likely to be potent tools in the study of common diseases and complex traits. Despite this promise, some very difficult issues in data management and statistical analysis must be squarely faced. The number of rare variants identified by sequencing is apt to be much larger than the number of common variants encountered in current association studies. The low frequencies of rare variants alone will make association testing difficult. This article extends the penalized regression framework for model selection in genome-wide association data to sequencing data with both common and rare variants. Previous research has shown that lasso penalties discourage irrelevant predictors from entering a model. The Euclidean penalties dealt with here group variants by gene or pathway. Pertinent biological information can be incorporated by calibrating penalties by weights. The current paper examines some of the tradeoffs in using pure lasso penalties, pure group penalties, and mixtures of the two types of penalty. All of the computational and statistical advantages of lasso penalized estimation are retained in this richer setting. The overall strategy is implemented in the free statistical genetics analysis software Mendel and illustrated on both simulated and real data.

1. Introduction

Deep resequencing is emerging as a new and potent means for mapping Mendelian disease genes.^1,2 The initial successes raise the question of whether the search for rare variants is apt to be as promising a route to mapping genes for common complex diseases and traits. In our opinion, the answer is likely to be in the affirmative, but too few studies have been completed to form a strong opinion. The recent finding of an association between copy number variation and autism is one argument in favor of the rare variant common disease hypothesis.³ This association is not too surprising given the correlation between autism and paternal age, which is known to increase the risk of deleterious mutations. The paternal age argument applies to other psychiatric traits such as schizophrenia⁴ and bipolar disorder.⁵ The rare variant hypothesis is also more plausible on evolutionary grounds than the common variant hypothesis because genetic variants with a negative impact on fitness should in theory be driven to extinction. The lessons classical population genetics teaches about the balance between selection and mutation are still relevant today. Thus, there is good reason to explore the statistics of rare variation detection in anticipation of sequence based genetic studies.

Resequencing will deliver both rare and common variants. It would be counterproductive to discard the common variants because in reality there is no sharp dividing line between common and rare. Thus, statistical methods that can analyze both rare and common variants simultaneously are preferable. Furthermore, some form of model selection is absolutely necessary because the number of SNP predictors in most studies far exceeds the number of participants. The rare variants uncovered in resequencing will exacerbate the excess of predictors over responses. The recent papers^10–13 have stressed the role of penalized estimation in statistical genetics. Lasso penalties^18–20 have the interesting capacity to force many parameter estimates to zero. Model selection with a predetermined number of predictors can be achieved by tuning the strength of the lasso penalty. If model fitting is carried out by coordinate ascent or descent, then lasso penalized estimation is exceptionally fast.^12,25

A particular rare disease predisposing allele may be present in only a handful of patients. Hence, statistical tests that capture only marginal effects are doomed to low power. This sad fact suggests focusing on disease gene discovery rather than disease variant discovery. One of the most attractive strategies for combining signals is to group variants by gene or pathway. Li and Leal⁷ proposed a group-wise test exploiting both multivariate and collapsing strategies that possesses higher power than a simple multivariate test or simple collapsing. Madsen and Browning⁸ extended the method by incorporating weights (dependent on allele frequency) into the group-wise statistics and approximating p-values by permutations within each group. Both methods consider rare variants with minor allele frequencies falling below a pre-specified threshold and exclude more common variants from analysis. The pooling strategy of Price et al⁹ circumvents the issue of arbitrarily chosen frequency threshold by calculating a group-wise statistic under a variety of thresholds. Higher power is achieved at the cost of an increased computational burden.

These methods have certain drawbacks. Environmental predictors are excluded from analysis even though they may contribute significantly to an association. Multiple testing remains an issue. More importantly, existing methods are sensitive to the classification of variants. If all types of variants (causal, protective, or neutral) coexist, then the various signals can cancel one another and potentially compromise statistical power. Our recent paper¹¹ explores a remedy that groups variants by gene or pathway membership in penalized regression. The encompassing multiple regression framework allows simultaneous consideration of genetic and environmental predictors and overcomes the unfortunate cancelations of causal and protective variants. Here we continue our exploration of group penalties, with emphasis on weighted penalties that keep both common and rare variants in play. In accord with the notion that variants with large deleterious effects should be rarer than variants with small deleterious effects, lower weights should be assigned to variants with lower population frequencies.^8,9

In pursuing group effects, we have attempted to retain the following advantages of lasso penalized estimation: (a) it applies to both ordinary regression (quantitative traits) and logistic regression (case-control studies), (b) it puts genetic and environmental predictors on the same footing, (c) it keeps both rare and common SNP predictors in play, (d) it partially circumvents the vexing issue of multiple comparisons, (e) it is computationally very efficient, (f) it offers a principled approach to model selection when the number of predictors exceeds the number of study participants, (g) it identifies protective variants as well as deleterious variants, and (h) it is amenable to finding interactions among predictors. We have previously demonstrated that Euclidean group penalties preserve these advantages.¹¹ Group penalties make it easier for related predictors to enter a model once one of the predictors does. Lasso penalties are retained to discourage the inclusion of neutral mutations in disease susceptibility genes. When disease genes harbor one or more borderline-rare variants with substantial risk, a mixture of lasso and group penalties performs well.

The major innovation in the current paper is the imposition of weights modulating lasso and group penalties. Ideally the weights should be chosen to reflect prior biological knowledge. In reality, we need better systems for rating the potential severity of point mutations. There is a severity hierarchy extending from non-synonymous mutations to synonymous mutations and ultimately to frameshift and protein truncating mutations. A non-synonymous mutation in a highly conserved codon is more important than the corresponding mutation in a less conserved codon. If both copies of a gene are disabled, this is a clear sign of trouble. If several genes in a common pathway are disabled or disregulated, the pathway as whole may be compromised. Integration of prior knowledge in penalized regression is an obvious priority, but until sequence data becomes more widely available, it is probably premature to pursue such elaborations.

The remainder of the paper is organized as follows. Section 2 describes the penalized regression framework with mixed lasso and group penalties, suggests a few plausible weighting schemes, and explains how both group penalties and weights can be implemented. Fortunately, the coordinate descent algorithms found successful in lasso penalized regression require trivial changes. Coordinate descent is exceptionally quick and permits optimal tuning of the penalty constant by cross-validation. Section 3 applies the mixed penalty method with weights to simulation examples. Section 4 provides a detailed description of the user interface to our implementation of penalized model selection in our statistical genetics program Mendel. We illustrate the mechanics of problem definition using the breast cancer data analyzed in our previous paper.¹¹ Finally, the discussion mentions some strengths and weaknesses of model selection under mixed penalties and suggests potentially helpful extensions.

2. Methods

Genome-wide association testing is one application field challenging current model selection procedures. All generalized linear models involve an n × 1 response vector y and an n × p predictor matrix X. If the number of predictors p far exceeds the number of responses n, then some form of model selection is mandatory. Indeed, the ability to estimate parameters consistently requires the ratio p/n to tend to 0. Traditional model selection techniques include forward and backward stepwise regression and minimization of AIC (Akaike) and BIC (Bayesian) information criteria; the latter two lead to a combinatorial search over a space with 2^p possible submodels. For this reason statisticians have substituted penalized estimation for combinatorial search. Generally the objective function being minimized is a convex combination of a loss function (or negative loglikelihood) and a penalty function. Penalty functions act like priors in Bayesian statistics and must be carefully constructed to steer parameter estimates in productive directions. The following reasons are cause for optimism in applying penalization estimation in statistical genetics:

1. Speed. Standard algorithms often choke when confronted with genomic-scale data. Efficient algorithms such as coordinate descent have been devised for solving convex optimization problems.^10,12,25

2. Flexibility. The modeling of complex biological phenomena is naturally embedded in the design of the loss and penalty functions. In association studies, biological meaningful units such as genes and pathways can be examined by introducing group penalties.¹¹ In copy number variation (CNV) reconstruction, copy number should change infrequently along a chromosome. Such smoothness is enforced by the fused lasso penalty.¹⁵

3. Theoretical Justification. Recent advances in theoretical statistics justify the use of penalized estimation in high dimensional settings. Model selection consistency is especially relevant to association testing. Under certain regularity conditions, the predictors singled out by penalized estimation have a high probability of coinciding with the true predictors.^16,17

4. Empirical Justification. There are many success stories of penalized regression methods in natural language processing, remote sensing, financial engineering, and other application areas outside genetics.

2.1. Penalized Regression with Weights

In lasso penalized linear regression^12,18,19 estimates of the intercept μ and the regression coefficients β_j are derived by minimizing the objective function

$$f(\theta )=\frac{1}{2}{\Vert y-\mu -X\beta \Vert }_2^2+\lambda {\Vert \beta \Vert }_1,$$

where θ = (μ, β), ${\Vert z\Vert }_2={({\sum }_j{z}_j^2)}^{1/2}$ is the Euclidean (ℓ₂) norm, and ‖z‖₁ = Σ_j |z_j| is the taxicab (ℓ₁) norm. The sum of squares ${\Vert y-\mu -X\beta \Vert }_2^2$ represents the loss function minimized in ordinary least squares; the ℓ₁ contribution ‖β‖₁ is the lasso penalty function. Its multiplier λ > 0 is the penalty constant. The order in which predictors enter a model as λ decreases is roughly determined by their impact on the response. Exceptions to this rule occur for correlated predictors. Because the intercept is felt to belong to any reasonable model, the lasso penalty omits it, and the intercept freely moves off zero.

Logistic regression is handled by replacing the sum of squares by the negative loglikelihood. The loglikelihood amounts to

$$L(\theta )=\sum _{i=1}^n[y_{i}log{p}_i+(1-y_i)log(1-p_i)],$$ (1)

where the success probability p_i for response i is defined by

$$p_i=\frac{e^{\mu +x_i^t\beta }}{1+e^{\mu +x_i^t\beta }}.$$ (2)

Here the response y_i is 0 (control) or 1 (case), and $x_i^t$ is the ith row of the predictor matrix X. To put the regression coefficients on an equal penalization footing, all predictors are centered around 0 and scaled to have approximate variance 1. There is a parallel development of lasso penalized regression for generalized linear models.²⁰ In each case the objective function is written as

$$f(\theta )=L(\theta )-\lambda {\Vert \beta \Vert }_1$$

as the difference between the loglikelihood and the lasso penalty. Because we now maximize f(θ), we subtract the penalty.

To construct a weighted lasso penalty, we assign a positive weight s_j to each predictor j and substitute the sum Σ_j s_j|β_j| for ‖β‖₁. A larger weight s_j corresponds to a higher penalty and discourages the j-th predictor from entering the model. Conversely, a smaller weight s_j exerts less penalty and encourages selection of the corresponding predictor. Eliminating a weight (s_j = 0) forces the j-th predictor to be retained in the model. In association testing, there are several sources of prior knowledge pertinent to assigning lasso weights:

1. Genotyping Error. Variants that cannot be typed reliably should be penalized more.

2. Allele Frequencies. In a different context, Madsen and Browning⁸ propose the weight $s=\sqrt{p(1-p)}$ for a variant with population frequency p. This scheme assigns smaller penalties to rarer variants as suggested by classical population genetics theory. The more extreme weights s = p(1 – p) risk giving rare variants too much influence.

3. Properties of Point Mutations. Several programs predict the functional effects of non-synonymous changes. The SIFT software of the Venter Institute,²² PolyPhen-2,²³ and MAPP²⁴ represent a good start in quantifying the risk entailed by coding mutations.

4. Conservation Across Species. Conservation scores are particularly valuable for assigning weights to noncoding mutations not covered by SIFT.

Integrating the weights derived from different types of information is a challenge. For the sake of simplicity, we adopt the allele frequency weights $s=2\sqrt{p(1-p)}$ in our examples. The factor of 2 makes the weights scale between 0 and 1.

Yuan and Lin²¹ have suggested Euclidean penalties as a natural way to group predictors. The lasso penalty ‖β‖₁ and the ridge penalty ${\Vert \beta \Vert }_2^2$ separate parameters. If a parameter enters a model, then it does not strongly encourage or inhibit other associated parameters from entering the model. Euclidean penalties act more subtlely. Let G denote a group label and t_G a corresponding group weight. The objective function

$$f(\theta )=L(\theta )-\lambda \sum _G{t}_G{\Vert {\beta }_G\Vert }_2$$

incorporates a Euclidean penalty on each group. Here β_G is the subvector of the regression coefficients corresponding to group G. For the purposes of this paper, we take all t_G = 1. In studies with good candidate genes or pathways, it makes sense to reduce t_G for a candidate group. Groups with a single predictor are allowed. Singleton groups are advisable for dispersed variants far from any gene.

Euclidean group penalties run the risk of letting in response-neutral predictors. As soon as one predictor from a group enters a model, it opens the door for other predictors from the group to enter the model. For this reason we favor a mixture of group and lasso penalties.¹¹ Lasso penalties maintain the pressure for neutral mutations to be excluded, even if they occur in causal genes or pathways. There is no need to group SNPs that occur outside coding or obvious regulatory regions. Simultaneous imposition of lasso and Euclidean penalties has further advantages. In addition to enforcing model parsimony and selecting relevant parameters, both penalties improve the convergence rate in minimizing the objective function. Because the penalties are convex, they also increase the chances for a unique minimum point when the loss function is non-convex.

2.2. Algorithms

Traditional algorithms such as Newton's method and scoring falter on high-dimensional, non-smooth problems. Cyclic coordinate ascent-descent is a better choice. Block relaxation, a generalization of cyclic coordinate descent, cycles through disjoint blocks of parameters and updates one block rather than one coordinate at a time. Meier et al²⁶ use block relaxation to fit logistic regression with purely group penalties. The extreme efficiency of cyclic coordinate descent-ascent in penalized estimation stems from the low cost of the univariate updates and the fact that most parameters never budge from their initial value of 0. Here we summarize cyclic coordinate ascent-descent for linear and logistic regression with mixed lasso and group penalties. Full algorithmic details appear in our previous papers.^10–12 Adding weights imposes trivial changes to the algorithms.

In coordinate ascent we increase f(θ) by moving one parameter at time. If a slope parameter β_j is parked at 0, when we seek to update it, its potential to move off 0 is determined by the balance between the increase in the loglikelihood and the decrease in the penalty. The directional derivatives of these two functions measure these two opposing forces. The directional derivative of L(θ) is the score $\frac{\partial }{\partial {\beta }_j}L(\theta )$ for movement to the right and the negative score $-\frac{\partial }{\partial {\beta }_j}L(\theta )$ for movement to the left. An easy calculation shows that the directional derivative of λ‖β_G‖₂ is λ in either direction when β_G = 0. In this case note that ‖β_G‖₂ = |β_j|. If β_G ≠ 0, then the partial derivative of λ‖β_G‖₂ with respect to β_j is λβ_j/|β_G‖₂. Hence, the directional derivatives both vanish at β_j = 0. In other words, the local penalty around 0 for each member of a group relaxes as soon as the regression coefficient for one member moves off 0.

2.2.1. Logistic Regression

In logistic regression the penalized loglikelihood with group and lasso penalties is

$$f(\theta )=L(\theta )-{\lambda }_{\mathrm{L}}\sum _j{s}_j|{\beta }_j|-{\lambda }_{\mathrm{E}}\sum _G{t}_G{\Vert {\beta }_G\Vert }_2,$$

where j ranges over all variants and G ranges over all groups. In practice, we fix the ratio of λ_L to λ_E and define λ = λ_L + λ_E. Formulas for the score vector ∇L(θ) and the expected information matrix E[−d²L(θ)] are well known¹¹ and need not be repeated here. The expected and observed information matrices coincide in logistic regression.

In penalized maximum likelihood estimation, coordinate ascent is implemented by replacing the loglikelihood by its local quadratic approximation based on the relevant entries of the score and observed information. The penalty terms are likewise approximated locally by linear or quadratic functions in the parameter being updated. The one-dimensional updates are not exact, but they can be computed easily by Newton's method. To update a slope parameter β_j, one resets β_j = 0 and commences maximization. If the directional derivatives to the right and left of 0 are both negative, then no progress can be made, and β_j remains at 0. Otherwise, maximization is confined to the left or right half-axis, whichever shows promise. Because the objective function is concave, the two directional derivatives at 0 cannot be simultaneously positive. Newton's method almost always converges within five iterations. At each iteration one should check that the objective function is driven uphill. If the ascent property fails, then the simple remedy of step halving is available.

2.2.2. Linear Regression

In ordinary linear regression, the objective function to be minimized is

$$f(\theta )=\frac{1}{2}{\Vert y-\mu -X\beta \Vert }_2^2+{\lambda }_{\mathrm{L}}\sum _j{s}_j|{\beta }_j|+{\lambda }_{\mathrm{E}}\sum _G{t}_G{\Vert {\beta }_G\Vert }_2.$$

Coordinate descent for linear regression also yields to Newton's method. Owing to the discontinuities in the penalties, once again iteration is confined to the left or right half-axis, provided either passes the directional derivative test. In contrast to unpenalized linear regression, minimization takes more than a single iteration. This complication just reflects the fact that the group penalty is neither linear nor quadratic.

2.3. Selection of Tuning Constants

In principle, cross validation can be invoked to determine the optimal values λ_L and λ_E. As we show in our simulation, setting them equal works well. Given a fixed ratio of the two penalties, the total penalty λ = λ_L + λ_E can be adjusted to deliver a predetermined number of genes or SNP variants. Because the number of non-zero predictors entering a model is generally a decreasing function of λ, a bracketing and bisection strategy is effective in finding a relevant λ.¹⁰ Of course, the smaller the number of predictors desired, the faster the overall computation proceeds. If computing time is not a constraint, it is helpful to optimize the objective function over a grid of points and monitor how new predictors enter the model as λ decreases. Another way to choose λ is to minimize either the BIC or AIC criterion as a function of λ. Recall that the purpose of convex relaxation is to avoid the combinatorial search entailed by the traditional application of the AIC and BIC criteria. Guiding the choice of λ by these criteria is a better tactic.

3. Analysis of Simulated Data

Our first simulation example, admittedly a toy example, involves 1000 controls and 1000 cases under different scenarios reflecting heterogeneity in both minor allele frequencies (MAF) and relative risks (RR). We assume 10 participating genes, each with 5 rare variants. Across the variants the MAFs are simulated from the Wright-Fisher distribution under balancing selection

$$f(p)\propto c{p}^{{\alpha }_s-1}{(1-p)}^{{\alpha }_n-1}{e}^{\sigma (1-p)},$$

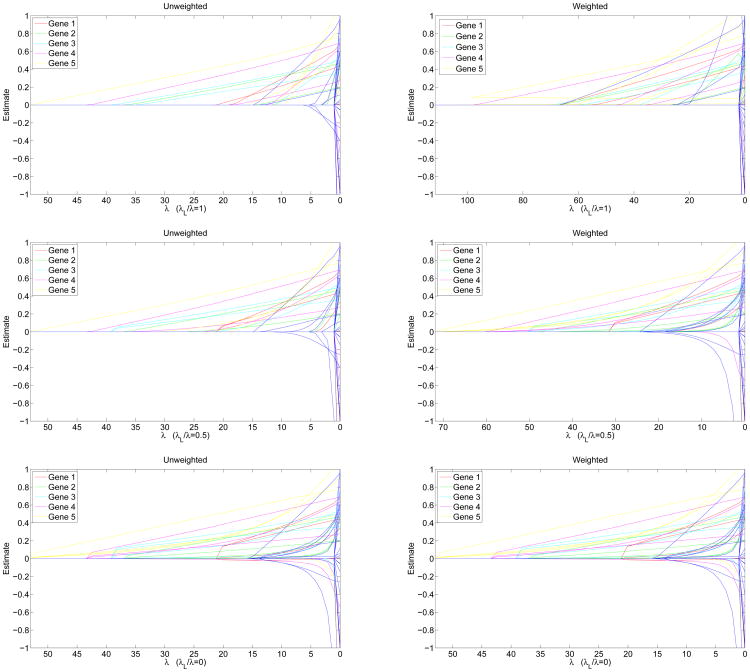
where c is a scaling constant such that ${\int }_0^{1}f(p)dp=1$ and σ is a selection coefficient. We take α_s = 0.2, α_n = 0.002, and σ = 15.²⁷ For i = 1, …, 5, gene i has i causal rare variants. Therefore, the model has 15 causal rare variants dispersed over 5 genes and 35 neutral rare variants dispersed over 10 genes. All neutral variants have relative risk (RR) 1; causal variants' RRs are drawn uniformly from the interval [1.2,5]. The wild-type penetrance f₀ is set at 0.01. For more details on data simulation algorithm, see our previous paper.¹¹ Figure 1 shows the solution paths of lasso, mixed penalty, and group penalty estimates with and without weights $s_j=2\sqrt{p_j(1-p_j)}$, where p_j is the MAF estimated from the controls. All group weights are set to 1. The pure lasso penalty (λ_L/λ = 1) picks up significant variants sequentially. The pure group penalty (λ_L/λ = 0) picks up genes (groups) 1, 2, and 3 sequentially. The mixed group plus lasso penalty (λ_L/λ = 0.50) achieves a good compromise between the two.

Fig. 1.

Solution paths of parameter estimates under lasso penalties (top row), mixed penalties (middle row), and group penalties (bottom row). Left column: s_j ≡ 1 and t_G ≡ 1 (no weighting). Right column: $s_j=2\sqrt{p_j(1-p_j)}$ and t_G ≡ 1.

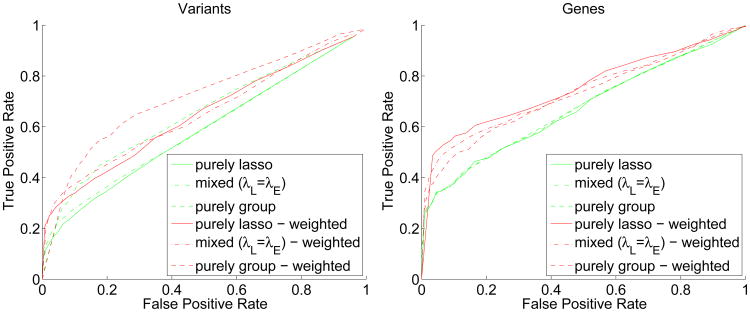
To discern the effects of weighted and unweighted penalized estimation, we repeat the same simulation 100 times and plot ROC curves for selected variants and genes in Figure 2. Each point of the ROC curves records the true and false positive rates of the selected variants (left panel) and genes (right panel) at a specific λ value. A true positive for selection of a gene is defined as choosing any true variant within that gene. In all three situations, adding weights improves the selection of causal variants and genes. Indeed, the ROC curves shift visibly toward the upper left. Also notice that for acceptable false positive rates (less than 0.05) the mixed-weight penalty provides the best true positive rates for selection of both variants and genes.

Fig. 2.

ROC curves based on 100 simulations using the setup of Figure 1.

4. Software Implementation and Illustration of Real Data

The methods we have described are implemented in the statistical genetics software Mendel⁶ and will be freely available in its next public release, version 10.5 or higher. Mendel is available for Linux, MacOS, and Windows at http://www.genetics.ucla.edu/software. Within Mendel the SNP association option handles GWAS (genome-wide association study) data, both simple marginal p-value calculations and the above lasso based analyses.

We previously applied mixed penalized logistic regression to a familial breast cancer dataset¹¹ with SNPs assigned to genes involved in double strand break repair. We now take advantage of these data to illustrate the mechanics of our implementation in Mendel. The data originate from genotype samples of participants enrolled in the UCLA Family Cancer registry. We performed penalized logistic regression in which the response, breast cancer status (affected versus unaffected), is coded as a binary outcome. Our sample contains 399 Caucasian participants, of whom 196 were affected and 203 were unaffected. Covariates include age, Ashkenazi Jewish heritage, and education level. We imputed missing non-genetic predictors using the mean value for a continuous variable and the most frequent category for a categorical variable. Overall 148 SNPs from 17 genes in the DSBR pathway were typed and grouped by gene. Missing SNP data were imputed using the SNP Imputation option of Mendel.⁶ For a complete description of the data, results, and insights gained from mixed penalized analysis, see our companion paper.¹¹ Mendel takes less than five seconds on a standard desktop computer to complete all analyses on this dataset. On a more challenging dataset with 10,000 SNPs and 2,200 individuals, Mendel completes all marginal and lasso analyses in under 30 seconds.

The input files used for the breast cancer and other analyses adhere to the usual Mendel conventions. In particular, the compressed SNP genotype data file conforms to the standard binary format adopted by both Plink and Mendel. SNP group designations and weights are optional. If they are desired, then they should be deposited in the SNP definition input file alongside the name, chromosome, and base pair position of each SNP. If no group is specified for a SNP, it is considered to be a singleton group. If no weight is specified for a SNP, then the SNP is assigned the default weight $2\sqrt{p(1-p)}$, where p is its MAF. The user may specify a value for the ratio λ_L/λ by invoking the keyword lasso_proportion in the Control file. Mendel reads all optional parameter settings from the Control file. To provide flexible modeling, the user can force any predictor or group to be retained in the lasso model by assigning to the keywords retained_predictor or retained_group the corresponding predictor or group name. If a retained group is specified, then all predictors within that group are retained. For example, the Control file snippet

Analysis_option = SNP_Association

Model = 2

Quantitative_trait = BC

Marginal_analysis = True

Lasso_analysis = True

Desired_predictors = 50 ∷ marginal

Desired_predictors = 20 ∷ lasso

Lasso_proportion = 0.5

Predictor = Grand ∷ BC

Predictor = Age ∷ BC

Transform = standardize ∷ Age

Retained_predictor = rs11571476

Retained_predictor = Age

Retained_group = XRCC4

instructs Mendel to perform SNP association analysis using cases and controls. The value 2 for the keyword Model implies logistic regression; the default value 1 implies ordinary linear regression. The third command in the above Control file indicates that affection status pertains to the trait BC. Both a marginal and lasso analysis will be performed, with the top 50 marginal predictors and the top lasso set of 20 predictors reported in a Summary output file. Marginal results on all predictors are always reported in another output file intended for plotting. For this analysis run, the ratio λ_L/λ ratio is set to 0.5. If the keyword lasso_proportion is not specified, the ratio has its default value of 1. All defined SNPs are always included as predictors unless specifically excluded in a SNP exclusion file. In this example two non-SNPs are named as predictors for the trait BC, a mandatory grand mean and an optional variable Age. The Transform keyword specifies that the Age variable will be normalized prior to analysis; we recommend normalization for all quantitative predictors. Finally, the above Control file specifies that the two predictors rs11571476 and Age and all predictors in the group XRCC4 should be retained in the lasso model.

As mentioned, most results are presented in a Summary output file. At the top of this file appear the results for each predictor individually. For example, the first few rows of marginal results might be

PREDICTOR NAME	MARGINAL P-VALUE	REGRESSION ESTIMATE	STANDARD ERROR	HARDY- WEINBERG P-VALUE	MINOR ALLELE FREQUENCY	GENOTYPING SUCCESS RATE	GROUP NAME
Grand Mean	-	-0.03509	-	-	-	-	-
Age	0.2347E-04	0.43700	0.10660	-	-	-	-
rs9634161	0.00760	-	-	0.19917	0.15539	1.00000	RAD52
rs16889040	0.00768	-	-	0.49854	0.25815	1.00000	RAD21
rs4986763	0.01123	-	-	0.20101	0.37469	1.00000	BRIP1
rs16888997	0.01298	-	-	0.67786	0.25815	1.00000	RAD21
rs16888927	0.01932	-	-	0.17591	0.26817	1.00000	RAD21
rs1120476	0.02024	-	-	0.48503	0.43233	1.00000	XRCC4

To decrease computation time, regression estimates are only calculated for predictors with marginal p-values more significant than 0.001. This default threshold can be reset by the user. A table of false discovery rates for the marginal p-values appears after the single predictor summary.

The results of the lasso analysis are listed after the marginal results in the Summary file. For example, the first few rows of lasso results might be

PREDICTOR NAME	MARGINAL P-VALUE	LEAVE-ONE-OUT INDEX	REGRESSION ESTIMATE	HARDY- WEINBERG P-VALUE	MINOR ALLELE FREQUENCY	GENOTYPING SUCCESS RATE	GROUP NAME
Age	0.2347E-04	0.1645E-05	0.50391	-	-	-	-
rs9634161	0.00760	0.00166	-0.42841	0.19917	0.15539	1.00000	RAD52
rs2061783	0.35871	0.01508	1.46004	0.2611E-10	0.03509	1.00000	XRCC4
rs10514249	0.02687	0.02757	-0.80396	0.86985	0.43985	1.00000	XRCC4
rs2075685	0.34106	0.05623	-0.38380	0.05712	0.42105	1.00000	XRCC4
rs2887531	0.50526	0.08627	-0.24576	0.11833	0.23183	1.00000	RAD52
rs11571476	0.05510	0.08633	0.30271	0.68282	0.42481	1.00000	RAD52

Since our example Control file specified that group XRCC4 should be retained, all members of that group will be included in the complete lasso output set. The lasso output is sorted by the leave-one-out index, which is simply the p-value of the likelihood ratio test of the full regression model, using all predictors in the lasso set, versus the model leaving out the specified predictor. Because of the prior selection of predictors, the leave-one-out index is not a legitimate p-value.

5. Discussion

This paper presents penalized estimation as a framework for association testing in the presence of both common and rare variants. Our results partially vindicate the twin strategies of mixed group penalties and penalty weights acting at either the single predictor or the group level. Penalty weights provide a flexible way of incorporate prior biological knowledge and have the potential to increase power in association mapping. Even choosing to weight individual variants by their population frequencies makes a difference in sorting through the confusion of causal genes and neutral variants within them. Although our recommended tactics improve both false positive and false negative rates, they represent an incremental improvement rather than a panacea. In our opinion, there is still room for further improvement. More progress is apt to come through more nuanced weights or propensity scores cumulating risks across the whole spectrum of variants within a gene or pathway. Replacing variant predictors by group-wise propensity scores may serve to reduce the number of predictors and the need for differential penalty weights altogether.