Enhanced DNA imaging using super-resolution microscopy and simultaneous single-molecule orientation measurements

Abstract

Single-molecule orientation measurements provide unparalleled insight into a multitude of biological and polymeric systems. We report a simple, high-throughput technique for measuring the azimuthal orientation and rotational dynamics of single fluorescent molecules, which is compatible with localization microscopy. Our method involves modulating the polarization of an excitation laser, and analyzing the corresponding intensities emitted by single dye molecules and their modulation amplitudes. To demonstrate our approach, we use intercalating and groove-binding dyes to obtain super-resolved images of stretched DNA strands through binding-induced turn-on of fluorescence. By combining our image data with thousands of dye molecule orientation measurements, we develop a means of probing the structure of individual DNA strands, while also characterizing dye-DNA interactions. This approach may hold promise as a method for monitoring DNA conformation changes resulting from DNA-binding proteins.

1. INTRODUCTION

The fluorescence microscope is an effective tool for measuring the orientations of single molecules. By directly measuring the tilt and wobble of individual fluorescent probes, researchers have gained an understanding of the mechanical properties of DNA [1,2], the acrobatics of motor proteins [3-5], as well as measures of molecular order (and disorder) in single cells, biological filaments [6-8], and polymers [9-11]. To derive physical understanding from single-molecule orientation measurements, it is necessary to relate the orientation of the fluorescent probe to the structure to which it is bound—be it other macromolecules or cellular organelles. In this regard, the emergence of widefield localization microscopy techniques beyond the diffraction limit (such as (f)PALM, STORM and PAINT) [12-15] presents an opportunity to combine molecular orientation datasets with super-resolution images.

Localization microscopy utilizes the following principles: First, by optical or chemical means, the concentration of actively fluorescing molecules labeling a structure is diluted to such an extent that fluorescence images of individual molecules are separately discernable on a camera sensor (throughout this article, we will refer to these single-molecule images as point-spread functions or PSFs). By fitting the PSF shapes, the positions of the molecules are estimated, i.e. they are localized separately in time. Finally, by plotting the coordinates of all localized molecules, a ‘pointillist’ reconstruction is generated with resolution typically an order of magnitude finer than the diffraction limit, thus achieving super-resolution [16]. In this article, we demonstrate how, in addition to spatial position, in-plane molecular orientation and rotational immobility may be ascertained over the course of a typical super-resolution imaging experiment.

2. BACKGROUND

The fluorescence emission pattern from a single molecule is closely approximated by an oscillating electric dipole. Dipoles produce distinctive PSFs, which vary with respect to their orientation relative to the microscope objective lens [17]. Orientational effects become especially prominent when the microscope objective is slightly defocused [18]. Accordingly, image-analysis methods have proliferated as a means of estimating orientation [19-26]. However, these approaches require exceptionally bright and photostable fluorophores, and sophisticated computational algorithms that must jointly estimate orientation and ideally the 3D position of molecules [27], while also accounting for any optical aberrations that may be introduced by the sample. Additionally, when a single-molecule’s PSF is altered (using microscope defocus or other means) such that its orientation is easier to estimate, single-molecule emission is spread over a larger region on a camera sensor than would be required using the standard PSF. This implies that the overall density of simultaneously emitting molecules must be further reduced, in order to prevent the PSFs of multiple molecules from overlapping—thus limiting the overall throughput of an imaging experiment. These combined challenges have impeded the rapid application of image-based orientation measurements in super-resolution imaging.

Use of polarization optics considerably simplifies matters. By placing a polarizing beamsplitter in the emission pathway of a microscope, and simultaneously collecting two polarized images, researchers have combined single-molecule polarization measurements with localization microscopy [6-8]. Unfortunately, in high numerical-aperture microscopes, the emission polarization of a molecule is a function of both its azimuthal orientation (ϕ), and its polar tilt (θ) with respect to the (optical) z-axis (inset, Fig. 1(a)). As a consequence, a single emission polarization measurement does not provide enough information to uniquely determine ϕ or θ. In order to measure either of these two parameters without incurring systematic bias, it is essential to measure polarized single-molecule intensity along a minimum of three unique polarization axes. (See e. g. [28-31] for alternative schemes.) Furthermore, dye molecules may rapidly rotate or wobble [32-34], emitting fluorescence at many distinct orientations. Emission polarization measurements will, in turn, be affected by the degree of rotational freedom that a molecule experiences over a single camera frame, leading to further ambiguity when attempting to interpret emission polarization data. A key feature of our method is the capacity to distinguish rotationally mobile molecules from fixed ones, while simultaneously measuring the molecules’ mean azimuthal orientations without bias.

Fig. 1.

Experimental overview. (a) By augmenting a conventional fluorescence microscope with an electro-optic modulator (EOM), the excitation laser is modulated to three distinct nearly linear polarization states (pink arrows). The brightness of single molecules, as measured on an electron-multiplying charge coupled device (EMCCD) camera sensor, will vary in proportion to the degree of alignment between the molecule’s absorption dipole moment and the excitation polarization. In principle, we desire a programmable half-wave plate which is normally achieved by aligning the EOM phase modulation axis to 45° with respect to an input linear polarizer (LP), and placing a quarter-wave plate (QWP) after the EOM with fast axis perpendicular to the linear polarizer. In practice, for different laser lines we used different combinations of dichroics and waveplates to optimize the overall linearity of the rotated polarizations at the sample (see Supplement 1). Inset: The absorption dipole moment is parameterized by an azimuthal angle ϕ and a polar angle θ. Our method permits us to measure the mean azimuthal orientation ϕ of a molecule over the course of a measurement period. In addition, we measure the rotational immobility parameter γ, which quantifies how much a molecule deviates from its mean azimuthal orientation. Using a theoretical model for constrained rotational diffusion, γ is related to an azimuthal arc-angle δ, which specifies the full aperture within which the molecule may ‘wobble’. (b) Fluorescence images of single rhodamine 101 molecules in polymers illustrate our technique. Over a series of camera frames, the excitation polarization (denoted by a pink arrow) is set at three different angles, and the emission intensity from a single-molecule is recorded. ϕ is determined by the relative intensities measured in three consecutive camera frames, while γ is related to the overall modulation amplitude of the signal. Images of two relatively immobile molecules (high γ) embedded in poly(methyl methacrylate) (PMMA) are shown, in addition to a rotationally mobile molecule (low γ) in Mowiol. ϕ values are reported between 0°−180° due to the inherent two-fold degeneracy of the absorption dipole moment.

An additional difficulty of emission polarization-based approaches is the need to simultaneously detect single molecules in multiple (polarized) imaging channels, projected onto separate camera sensors, or separate regions of a single sensor. Accurate localization of single molecules using a multichannel detection scheme requires that positions from one imaging channel be mapped into the other, using a process termed image registration. In order to avoid incurring systematic localization errors, which may lead to degraded resolution and imaging artifacts, accurate image registration requires specialized instrumentation, image-processing software and calibration procedures [35-37]. In contrast, our method conducts orientation measurements using a single imaging channel, sidestepping the need for image registration entirely.

3. METHOD

To address the drawbacks associated with emission polarization schemes, we have devised a simple widefield extension of the first confocal experiment to perform single-molecule orientation measurements at room temperature [1]. By inserting an electro-optic modulator (EOM) into the beam-path of our excitation laser (Fig. 1(a)), we modulate the excitation polarization over successive camera frames, while simultaneously performing epifluorescence localization microscopy. As the excitation polarization is adjusted, the emission intensity (brightness) U of detected molecules will fluctuate (Fig. 1(b)) in proportion to how closely their absorption dipole moments μ align with the polarization vector E of the excitation electric field:

$$U=\frac{A}{T}{\int }_0^T{\mid {\mu }^{†}\left(t\right)\mathit{E}\mid }^{2}dt$$ (1)

In Eq. (1), we assume a partially mobile dipole μ(t) that may rotate over time, with camera exposure time T, and A a proportionality constant. In the classic experiment [1], the excitation polarization was continuously rotated from 0^o to 90^o in the x-y plane. Here, in order to conserve photons over a shorter measurement sequence, we elect to use only three distinct excitation polarizations, each rotated roughly 60^o from the other two. By synchronizing our camera frame to our EOM, we change the excitation polarization for each successive exposure. For the subset of molecules that remain in a fluorescent state for at least three complete camera frames, our data analysis procedure enables us to characterize their (azimuthal) rotational dynamics. Specifically, we measure the following two parameters (see the next section for data analysis procedure): We determine the mean azimuthal orientation ϕ of the absorption dipole moment, in addition to azimuthal rotational immobility—a parameter that we term γ. In the absence of measurement noise, the value of γ varies from 0 to 1. A completely immobilized molecule will have a γ of 1, while a molecule that is freely rotating (visiting each ϕ with equal frequency over a single camera frame) will have a γ of 0. Intermediate γ values characterize how closely a given molecule resembles each of these two extremes (Fig. 1(b)). To further interpret the measured parameters ϕ and γ, we employ a rotational diffusion model similar to that of [2] (Supplement 1) that assumes molecules rotate about the z-axis at a constant polar orientation θ. We derive an expression relating γ to an azimuthal ‘arc-angle’ δ (inset, Fig. 1(a)), describing the range of orientations to which a given molecule is rotationally constrained:

$$\gamma =\frac{sin\left(\delta \right)}{\delta }$$ (2)

Additionally, in Supplement 1, we provide a detailed discussion of our measurements using the more complex rotational diffusion models considered by [32-34]. As a future enhancement to our method, the polar orientation θ and the three-dimensional rotational mobilities of probes may be determined by introducing z-polarized excitation using total internal reflection [5,38-40]. However, this modification requires additional camera frames and thus additional photostability. θ can also be measured by altering a confocal excitation field using annular illumination or a radially polarized beam [41-43].

4. MATHEMATICAL FRAMEWORK

In essence, our method measures a subset of the second moments of a single-molecule’s dipole orientation with respect to time. From the second moments, we estimate the mean azimuthal orientation ϕ and rotational immobility γ. Using the coordinate system diagrammed in Fig. 1(a), the absorption dipole moment μ of a molecule may be expressed interchangeably in terms of azimuthal and polar angles { ϕ , θ } or as a 3-component unit vector:

$$\mu =\left[\begin{array}{c}\hfill cos\left(\varphi \right)sin\left(\theta \right)\hfill \\ \hfill sin\left(\varphi \right)sin\left(\theta \right)\hfill \\ \hfill cos\left(\theta \right)\hfill \end{array}\right]=\left[\begin{array}{c}\hfill {\mu }_x\hfill \\ \hfill {\mu }_y\hfill \\ \hfill {\mu }_z\hfill \end{array}\right]$$ (3)

The integral from Eq. (1) may now be simplified using the following considerations: Since the excitation field E remains constant over a single camera frame, it may be brought outside the integral:

$$\begin{array}{cc}\hfill U& =\frac{A}{T}{\mathit{E}}^{†}\left({\int }_0^T\mu \left(t\right){\mu }^{†}\left(t\right)dt\right)\mathit{E}\hfill \\ \hfill & ={\mathit{AE}}^{†}\left[\begin{array}{ccc}\hfill \langle {\mu }_x^2\rangle \hfill & \hfill \langle {\mu }_x{\mu }_y\rangle \hfill & \hfill \langle {\mu }_x{\mu }_z\rangle \hfill \\ \hfill \langle {\mu }_x{\mu }_y\rangle \hfill & \hfill \langle {\mu }_y^2\rangle \hfill & \hfill \langle {\mu }_y{\mu }_z\rangle \hfill \\ \hfill \langle {\mu }_x{\mu }_z\rangle \hfill & \hfill \langle {\mu }_y{\mu }_z\rangle \hfill & \hfill \langle {\mu }_z^2\rangle \hfill \end{array}\right]\mathit{E}\hfill \end{array}$$ (4)

Where we have used angled brackets < > to denote temporal averaging. By employing an epi-illumination excitation geometry, we ensure that the excitation field has a negligible z-polarization component. Re-writing only the x and y polarization components of E as a 2-dimensional vector ${\mathit{E}}_{xy}=\left[\begin{array}{c}\hfill E_x\hfill \\ \hfill E_y\hfill \end{array}\right]$ permits us to further simplify Eq. (4):

$$U=A{\mathit{E}}_{xy}^{†}\left[\begin{array}{cc}\hfill \langle {\mu }_x^2\rangle \hfill & \hfill \langle {\mu }_x{\mu }_y\rangle \hfill \\ \hfill \langle {\mu }_x{\mu }_y\rangle \hfill & \hfill \langle {\mu }_y^2\rangle \hfill \end{array}\right]{\mathit{E}}_{xy}$$ (5)

Suppose that a single molecule’s emission intensity is measured over three complete camera frames $\{U_1,U_2,U_3\}$, using three distinct excitation polarizations $\{{\mathit{E}}_1,{\mathit{E}}_2,{\mathit{E}}_3\}$, which in general may be complex valued to describe elliptical polarization states. (Each vector E_j has non-zero components only in the x-y plane, $\{E_{x,j},E_{y,j}\}$). For our analysis, we assume that partially mobile molecules rotate on a timescale much faster than the camera integration time T. In addition, we require that the second moments of a given molecule’s orientation do not change over each successive camera exposure. In other words, we assume ergodicity. In this case, the measured intensities U_j are related to the second moments by $\left\{\langle {\mu }_x^2\rangle ,\langle {\mu }_y^2\rangle ,\langle {\mu }_x{\mu }_y\rangle \right\}$ the following system of linear equations:

$$\begin{array}{cc}\hfill \left[\begin{array}{c}\hfill U_1\hfill \\ \hfill U_2\hfill \\ \hfill U_3\hfill \end{array}\right]& =A\left[\begin{array}{ccc}\hfill {\mid E_{x,1}\mid }^2\hfill & \hfill {\mid E_{y,1}\mid }^2\hfill & \hfill 2\mathfrak{R}\left\{E_{x,1}{E}_{y,1}\right\}\hfill \\ \hfill {\mid E_{x,2}\mid }^2\hfill & \hfill {\mid E_{y,2}\mid }^2\hfill & \hfill 2\mathfrak{R}\left\{E_{x,2}{E}_{y,2}\right\}\hfill \\ \hfill {\mid E_{x,3}\mid }^2\hfill & \hfill {\mid E_{y,3}\mid }^2\hfill & \hfill 2\mathfrak{R}\left\{E_{x,3}{E}_{y,3}\right\}\hfill \end{array}\right]\left[\begin{array}{c}\hfill \langle {\mu }_x^2\rangle \hfill \\ \hfill \langle {\mu }_y^2\rangle \hfill \\ \hfill \langle {\mu }_x{\mu }_y\rangle \hfill \end{array}\right]\hfill \\ \hfill & =A\mathit{P}\left[\begin{array}{c}\hfill \langle {\mu }_x^2\rangle \hfill \\ \hfill \langle {\mu }_y^2\rangle \hfill \\ \hfill \langle {\mu }_x{\mu }_y\rangle \hfill \end{array}\right]\hfill \end{array}$$ (6)

In Eq. (6), we denote the matrix containing electric field information as P, as it acts as a ‘probe matrix’ relating molecular orientation to raw intensity measurements. In Supplement 1, we provide a detailed calibration procedure for determining P prior to each imaging experiment. By inverting the probe matrix, it is thus possible to measure $\left\{\langle {\mu }_x^2\rangle ,\langle {\mu }_y^2\rangle ,\langle {\mu }_x{\mu }_y\rangle \right\}$ up to the proportionality constant A:

$$A\left[\begin{array}{c}\hfill \langle {\mu }_x^2\rangle \hfill \\ \hfill \langle {\mu }_y^2\rangle \hfill \\ \hfill \langle {\mu }_x{\mu }_y\rangle \hfill \end{array}\right]={\mathit{P}}^{-1}\left[\begin{array}{c}\hfill U_1\hfill \\ \hfill U_2\hfill \\ \hfill U_3\hfill \end{array}\right]$$ (7)

Once the relative values of the second moments have been measured, we assemble them into a 2-by-2 matrix M_xy and subsequently compute its eigenvalues ${\lambda }_1,{\lambda }_2$ and eigenvectors $v_1,v_2$:

$${\mathit{M}}_{xy}=A\left[\begin{array}{cc}\hfill \langle {\mu }_x^2\rangle \hfill & \hfill \langle {\mu }_x{\mu }_y\rangle \hfill \\ \hfill \langle {\mu }_x{\mu }_y\rangle \hfill & \hfill \langle {\mu }_y^2\rangle \hfill \end{array}\right]=\sum _{j=1}^2{\lambda }_j{v}_j{v_j}^{†}$$ (8)

How do we interpret the measurements contained in the matrix M_xy? We consider two limiting cases: A completely immobilized molecule, and a freely rotating molecule, which visits all azimuthal orientations with uniform frequency over a single camera frame. In the case of an immobile dipole, $\langle {\mu }_x^2\rangle ={\mu }_x^2$, $\langle {\mu }_y^2\rangle ={\mu }_y^2$, and $\langle {\mu }_x{\mu }_y\rangle ={\mu }_x{\mu }_y$. Therefore, M_xy will have a single non-zero eigenvalue λ₁, with corresponding eigenvector: ${v_1}^{†}=\left[{\mu }_x{\mu }_y\right]∕\sqrt{{{\mu }_x}^2+{{\mu }_y}^2}$. In the latter case, we observe that $\langle {\mu }_x^2\rangle =\langle {\mu }_y^2\rangle$ and $\langle {\mu }_x{\mu }_y\rangle =0$, hence M_xy will be a multiple of the identity matrix I.

With these two limiting cases in mind, the matrix M_xy associated with an arbitrary (partially mobile) molecule may be decomposed as follows:

$${\mathit{M}}_{xy}=({\lambda }_1+{\lambda }_2)\left[\gamma \left({\mathit{v}}_1{{\mathit{v}}_1}^{†}\right)+\left(1-\gamma \right)\mathbf{I}\right]$$ (9)

Where the parameter γ is calculated as:

$$\gamma =\frac{{\lambda }_1-{\lambda }_2}{{\lambda }_1+{\lambda }_2}$$ (10)

Furthermore, the mean azimuthal orientation ϕ is calculated using the components $\{{\mu }_x,{\mu }_y\}$ of the eigenvector v₁:

$$\varphi =\text{atan}2({\mu }_y,{\mu }_x)$$ (11)

The function $\text{atan}2\left(\right)$ denotes the two-argument arctangent. Due to the twofold degeneracy of the dipole orientation, values of ϕ between 0° and −180° are rotated 180° such that $\varphi \in [0°,180°)$. The decomposition of M_xy used in Eq. (9) is useful, as it permits us to realize that as far the second moment measurements are concerned, a (partially mobile) molecule can be viewed as a superposition of a completely immobilized dipole with azimuthal orientation pointing in the direction v₁, and a freely rotating dipole. Accordingly, the parameter γ describes how closely the measured signal from a given molecule resembles each of the two limiting cases. To summarize, our orientation measurements are obtained as follows:

1. Single molecules that stay in a fluorescent (bright) state over at least three complete camera frames are identified from the raw data. Their total (background-subtracted) intensity in each frame is computed.

2. The relative sizes of the second moments $\left\{\langle {\mu }_x^2\rangle ,\langle {\mu }_y^2\rangle ,\langle {\mu }_x{\mu }_y\rangle \right\}$ are computed up to the proportionality constant A using Eq. (7).

3. The matrix M_xy is assembled. Its eigenvalues ${\lambda }_1,{\lambda }_2$ and eigenvectors $\{v_1,v_2\}$ are calculated.

4. The parameters γ and ϕ are computed according to Eqs. (10) and (11) respectively.

5. arc-angle δ is estimated using Eq. (2).

In the context of bulk steady-state fluorescence polarization measurements, it has been previously noted [44] that a minimum of three excitation polarization measurements are required to determine the mean azimuthal orientation of absorption dipole moments and the degree of molecular order existing within a sample. However, by applying a similar analysis framework to single-molecule datasets, we differentiate ‘static’ disorder—in which an ensemble of rotationally immobilized molecules have no clear orientation with respect to each other—from ‘dynamic’ disorder, which occurs when the individual molecules in an ensemble are free to rotate. (These two cases cannot be distinguished using bulk steady-state measurements.) While bulk approaches often use more than three excitation polarizations to gain additional measurement precision [45], we must contend with the limited number of photons emitted by single molecules before photobleaching. Hence, we stick to the bare minimum of three unique polarization states.

5. RESULTS

We demonstrate the technique by imaging DNA using intercalating dyes. Dye molecules induce structural changes in DNA [46], which disrupt the functions of DNA-binding proteins and enzymes [47]. A detailed understanding of how fluorescent dyes bind with host DNA may prove essential to drug development efforts [48], or DNA curtains studies [49]. Using single-molecule orientation measurements, we characterized the dye SYTOX Orange—a DNA stain that has recently shown promise for live cell imaging applications [50]. While the chemical structure of SYTOX Orange is proprietary, this dye is reported to be monomeric, and to intercalate when binding to DNA (dye molecules are expected to slot between adjacent base pairs, orienting roughly perpendicular to the DNA axis) [51]. We prepared samples of stretched, linear lambda phage DNA (λ-DNA) strands adhered to silanized glass coverslips, using the ‘dynamic molecular combing’ technique used in Ref. [52]. To perform localization microscopy, we employed a scheme similar to PAINT [15,53] previously described in [54-56], in which dyes in solution continuously bind to the DNA, becoming bright spots which can be localized sequentially (see Supplement 1). Samples were imaged in 15.5 μm × 15.5 μm fields of view for periods of approximately 13.5 minutes (15,000 camera frames), yielding between 100,000-300,000 localizations and 10,000-30,000 single-molecule orientation measurements.

Figs. 2(a) and 2(b) show super-resolved λ-DNA strands. When using SYTOX Orange, we estimate our localization precision to be 27 nm (Supplement 1). We observe overall alignment of molecules perpendicular to DNA strands (Fig. 2(a)), and as the DNA axis bends, the mean dye molecule orientation rotates accordingly (Fig. 2(b)). By fitting a spline (Supplement 1) to localizations from a DNA strand, we histogram the orientations of dye molecules relative to the DNA axis (Fig. 2(c)), in addition to corresponding γ measurements (Fig. 2(d)). Our orientation measurements strongly suggest that the fluorophore of SYTOX Orange inserts between adjacent DNA base-pairs (inset, Fig. 2(a)), enforcing perpendicular alignment of the absorption dipole moments. However, the median absolute deviation of orientation measurements (18°) is substantially greater than the precision of our measurement method (Supplement 1). We estimate a precision of 5.8° based on a median of 1603 photons detected per orientation measurement (fluorescence background was 27 photons per pixel per camera frame). This ‘broadening’ of the orientation distribution may be due to the presence of secondary binding modes, either to the minor/major groove or to the DNA phosphate backbone. Furthermore, there may be curvature in the DNA that is beneath our localization precision to detect. A median γ value of 0.91 indicates that the dyes are predominantly rotationally immobilized (we measure γ with a precision of 0.11). Using Eq. 2, we estimate that dye molecules are restricted to an arc-angle δ of 44°. This result is similar to previous rotational mobility measurements obtained using the bis-intercalating dye YOYO-1 [8,57].

Fig. 2.

Super-resolved images and single-molecule orientation measurements acquired using the intercalating dye SYTOX Orange. (a) Images of λ-DNA strands, color-coded according to mean azimuthal orientation of dye molecules measured within 30 nm voxels. Inset: Due to the intercalative binding mode, absorption dipole moments align perpendicular to DNA axis. (b) As a DNA strand bends, mean molecular orientation rotates to remain perpendicular to the DNA axis. This effect is evidenced by the changing color of the curved DNA strands. Inset: Visualization of all orientation measurements localized along a short strip of DNA (green box). Lines point in the direction of ϕ, and are color coded to denote γ. (c) Histogram of orientation measurements localized along the strip of DNA denoted by the white dotted lines in a. Using spline interpolation, the DNA axis was estimated. Accordingly, ϕ measurements are reported relative to the DNA axis. Median orientation with respect to the DNA axis is measured to be 87°, and median absolute deviation is 18°. (d) Histogram of γ measurements, corresponding to the same molecules used in c. δ is estimated to be 44° from the median γ of 0.91. Photon shot-noise causes a portion of γ measurements to be greater than 1.

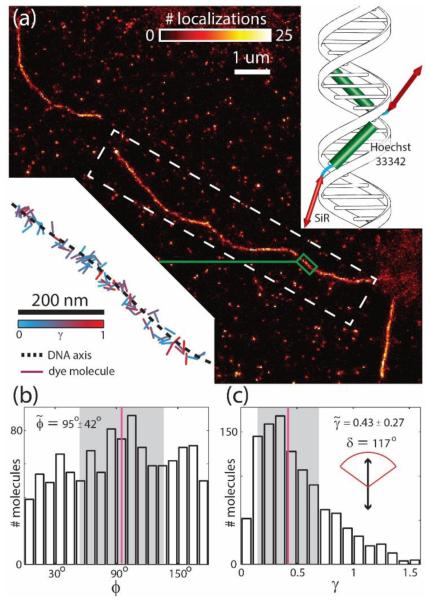
From our experiments involving SYTOX Orange, we believe that intercalation is the primary mechanism that causes dye molecules to be rotationally constricted – since the fluorophores are sandwiched in between adjacent DNA base-pairs, they are unable to freely wobble over the course of an orientation measurement. Will a non-intercalating dye enjoy greater rotational freedom? To test this hypothesis, we repeated our imaging experiments using the recently reported dye SiR-Hoechst [52]. This dye is synthesized by attaching a silicon-rhodamine (SiR) derivative to the minor groove-binding moiety Hoechst 33342, and imaged with 641 nm light to efficiently pump only the SiR. We reason that since the SiR is tethered to Hoechst 33342 via a flexible four-carbon linker, and not directly attached to the DNA strand, we will observe a decline in the rotational immobility parameter γ. In Fig. 3(a), we present a super-resolved image of a DNA strand obtained using the dye SiR-Hoechst, and again measure the orientations of dye molecules along the DNA strand (Fig. 3(b)). In contrast to the results obtained using SYTOX Orange (Fig. 2(c)), we observe no overall molecular order relative to the DNA axis. After determining the respective γ values for molecules detected along the DNA strand, we measure a median γ of 0.43, and estimate an enhanced arc-angle δ of 117°. Based on a median of 8424 total photons detected per orientation measurement (with 158 photons fluorescence background per pixel per frame), we estimate measurement precision to be 2.5° for ϕ, 0.05 for γ, and a localization precision of 22 nm (Supplement 1).

Fig. 3.

Results acquired using the dye SiR-Hoechst. (a) Super-resolved image of a DNA strand. In this case, the absorption dipole moments of silicon-rhodamine are not constrained, because they are not directly bound to DNA strands (right inset). Hence we elect not to color-code our image, as no overall alignment with respect to the DNA axis is expected. This feature is evidenced from a visualization of all orientation measurements localized within a small strip of DNA (green boxed region and lower left inset). (b) Histogram of all orientation measurements localized along the strip of DNA denoted by the white dotted lines in a (ϕ measurements are reported relative to DNA axis). We observe no preferential alignment. (c) Histogram of γ measurements, corresponding to the same molecules used in b. As γ measurements are significantly smaller, the rotational immobility is enhanced, and the arc-angle δ (estimated from the median γ) is found to be significantly larger (117°) than that measured for intercalating dyes.

Due to the fact that intercalating dyes generally orient perpendicular to the DNA axis, single-molecule orientation measurements may be combined with localization data to detect deformations that have been induced within DNA strands. In Fig. 4(a), we show a λ-DNA strand stained with SYTOX Orange that became bent as it was deposited upon a coverslip. By inspecting areas of high curvature along the DNA axis (Fig. 4(b)), we observe patches approximately 100 nm in length that contain markedly fewer detected molecules. We note that at alternate ends of these regions, dye molecules undergo an abrupt change in orientation, indicating an acute bend along the DNA axis. As previously observed by [58], the stretching forces exerted upon the DNA during deposition on a microscope coverslip are great enough to cause individual strands to break. In this case, we believe that as the DNA was bent, a conformation change or a complete DNA breakage was induced, which effectively prevented the intercalation of dye molecules. On some DNA strands (Fig. 4(c)), we have noticed discrete regions in which our spline interpolation procedure does not effectively predict the orientations of dye molecules. In Fig. 4(d), we show a 100 nm patch of DNA where the dye molecule orientation varies wildly, followed by a 300 nm strip along which the density of detected molecules declines. From these measurements, we speculate that upon adhering to the microscope coverslip, a tangle was introduced into the DNA. This DNA-tangle may have also caused a conformation change in the neighboring strip of DNA, leading to a drop in localization density.

Fig. 4.

Visualizing bending and tangling of DNA using the intercalator SYTOX Orange. (a) Super-resolution image of a λ-DNA strand containing multiple ‘bends’. For comparison, a diffraction-limited image was also produced, by summing all frames of data contained in our acquisition sequence. (b) Plots of single-molecule positions and orientations demonstrate that when the DNA axis abruptly bends, labeling density drops (see arrows). (c) Super-resolution image of a λ-DNA strand exhibiting ‘tangles’. (d) By plotting single-molecule positions and orientations, we show an example of a tangle (arrow), in which dye molecules do not align perpendicular to the DNA axis, as estimated using spline interpolation. The tangle is followed by a region in which few molecules are detected, indicating a possible conformation change in the DNA.

6. DISCUSSION

Combining polarization modulation with localization microscopy has permitted us to measure single-molecule rotational dynamics, detect nanoscale deformations in individual DNA strands, and characterize the binding modes of different types of DNA staining dyes. This work suggests that intercalating dyes may serve as an exquisite sensor for studying DNA-binding proteins at the single-molecule level. For example, nucleosome complexes play a vital role in DNA compaction and regulating gene expression by virtue of the manner in which they wrap DNA into ‘loops’. The formation of such loops may be readily monitored in real-time by using single-molecule orientation data to detect bends in the DNA substrate. Our measurement approach is accomplished using a simple modification of the excitation pathway of a standard fluorescence microscope – no changes to the microscope body itself are required. In the future, this feature will permit our technique to be seamlessly integrated with other imaging modalities, such as 3D super-resolution imaging, which relies upon PSF modulating optics placed in the microscope emission pathway. Our use of only three unique excitation polarizations and our data analysis procedure may also prove applicable to related imaging methods that rely upon rotationally fixed fluorophores, and deconvolution algorithms that estimate molecular density and average molecular orientation within an imaging volume in order to achieve super-resolution [59].

Furthermore, our scheme provides a rapid and straightforward means of identifying samples for which molecular-orientation induced localization errors may prove to be significant. When single molecules are rotationally constrained, their PSFs are anisotropic, and appear to ‘shift’ in spatial position as a function of microscope defocus [60-62]. For the samples imaged in this study, we estimate orientation-induced localization errors to be less than 35 nm (see Supplement 1), due to the fact that for in vitro DNA samples, all fluorescent emitters are constrained to a relatively narrow range of depths. However, when imaging biological structures inside cells, emitters inhabit an extended range of z-positions, and orientation-induced localization errors may be 100 nm or more. Using our method, the prevalence and severity of such orientation-induced errors may be ascertained, and appropriate correction schemes may be implemented, when necessary [27,63,64]. A wide range of single-molecule imaging experiments stand to benefit.