Too Many Covariates and Too Few Cases? – A Comparative Study

Abstract

Prior research indicates that 10–15 cases or controls, whichever fewer, are required per parameter to reliably estimate regression coefficients in multivariable logistic regression models. This condition may be difficult to meet even in a well-designed study when the number of potential confounders is large, the outcome is rare, and/or interactions are of interest. Various propensity score approaches have been implemented when the exposure is binary. Recent work on shrinkage approaches like lasso were motivated by the critical need to develop methods for the p >> n situation, where p is the number of parameters and n is the sample size. Those methods, however, have been less frequently used when p ≈ n, and in this situation, there is no guidance on choosing among regular logistic regression models, propensity score methods, and shrinkage approaches. To fill this gap, we conducted extensive simulations mimicking our motivating clinical data, estimating vaccine effectiveness for preventing influenza hospitalizations in the 2011–2012 influenza season. Ridge regression and penalized logistic regression models that penalize all but the coefficient of the exposure may be considered in these types of studies.

1. Introduction

In observational studies, potential confounders must be accounted for due to lack of randomization. A multivariable logistic regression model (LRM) is the most commonly used technique to control the confounders when the outcome of interest is binary. The advantage of multivariable LRM (mLRM) is its capability to simultaneously control for many covariates. This appealing property is jeopardized when the number of parameters is relatively large compared to the number of events (or the number of nonevents if fewer).

For mLRM, prior research indicates that 10–15 cases or controls, whichever fewer [1–4], are required per parameter to reliably estimate regression coefficients. This condition is, however, hard to meet even in a well-designed study when the number of confounders is large, a rare disease is studied, and/or interactions are of interest. In our motivating influenza vaccine study [5, 6], we estimated influenza vaccine effectiveness (VE) against influenza-associated hospitalizations in adults ≥ 50 years of age, using the case positive control negative design (similar to the case control design except that the controls have tested negative for the same disease that the cases are positive for) [5]. We were challenged by the relatively large number of potential confounders including comorbidities in older adults as well as a relatively small number of influenza hospitalizations.

Propensity score (PS) based approaches have also been advocated for controlling for confounding when exposure is binary or categorical. See, among many others, [7–20]. PS is the conditional probability of a subject being exposed given the set of baseline covariates. The seminal paper [7] shows that if exposure status is strongly ignorable given the baseline variables, then it is strongly ignorable given the PS score. In other words, if the observed covariates are sufficient to control the confounding effect of exposure, then adjustment for PS is also sufficient. Rosenbaum and Rubin [7] also demonstrated that conditioning on the PS yields unbiased estimation of the expected outcome difference between the exposure and unexposure groups. There exist many ways to use PS to control imbalance. For example, logit PS can be included as a single covariate (or expanded into multiple variables if nonlinearity exists) in the outcome model in addition to the exposure as if it were a single confounder [9]; if used in stratification, PS can partition the data into at least five strata and the univariable LRM is fitted within each stratum [21, 22]; the PS can be used in matching [23]; or be used as sampling weights in an inverse probability weighting approach [24]. In the medical literature, PS methods are frequently used in the LRM to estimate odds ratios. However, due to non-collapsibility of the odds ratio [25], the PS-based approaches can provide unbiased estimation of the risk difference, but not the adjusted odds ratios [13, 14, 26]. As for our motivating influenza vaccine study, the scientific interest is to estimate the adjusted odds ratio, for which the usage of PS-based approaches without covariate adjustment is criticized [13, 26]. In this paper, we include the PS covariate adjustment approach as one of the comparison approaches as research has advocated its validity in the similar setting [9].

Another approach that has potential to control for covariate imbalance is shrinkage, such as penalized maximum likelihood estimation (PMLE) [27], also called ridge regression (RgR), with quadratic penalty or L2-norm, and least absolute shrinkage and selection operator regression (LASSO) [28] with L1 or absolute value norm. Although both RgR and LASSO are shrinkage approaches, they have different properties. Since RgR was developed to avoid over-parameterization, it shrinks estimates towards zero. On the other hand, The LASSO and LASSO motivated shrinkage methods have been developed recently for the variable selection problem in high-dimensional data analysis when the number of parameters is much bigger than the sample size, usually stated as a p >> n problem. The penalty function of LASSO is chosen so that the model can yield zero estimates when the parameter values are close to zero and hence can perform variable selection. The primary goal of LASSO and others is to lead to models with parsimony when the number of covariates is greater than the sample size. Although intensively used in genetic and imaging research with p >> n, the utility of lasso and other shrinkage approaches has not been evaluated in the more traditional observational studies and are less frequently used as tools to control confounders [29]. Since in typical observational studies, the number of parameters rarely exceeds the sample size, we considered both LASSO and RgR approaches in this paper. (See reference [30] for a detailed description of LASSO, RgR, and mixture of the two, elastic net).

The goal of this study is to conduct Monte Carlo simulations to evaluate and compare the performance of mLRM, PS adjustment, and shrinkage regression methods in studies when the number of confounders is relatively high compared to the number of events when the outcome model is mLRM and the parameter of interest is the adjusted odds ratio of exposure.

2. Methods

We denote Z as the measured confounding covariates, Y as the binary outcome with 1 indicating positive disease status, and X as the exposure variable with 1 indicating exposed. We will consider nine methods in this comparative study.

2.1. Univariable Logistic Regression Model (uLRM)

We defined the uLRM to be

$$\text{logit}\mathrm{P}({\mathrm{Y}}_{\mathrm{i}}=1|{\mathrm{X}}_{\mathrm{i}})={\alpha }_0+{\alpha }_1{\mathrm{X}}_{\mathrm{i}},\mathrm{i}=1,\cdots ,\mathrm{n}$$ (1)

where Y_i and X_i are the outcome and exposure status of the ith subject, respectively. The parameter of primary interest is α₁. The whole set of parameters in this approach is (α₀, α₁) with 2 degrees of freedom. The uLRM tells how large the asymptotic bias is if the analyses were not adjusted by any confounders compared to correct adjustment.

2.2. Multivariable Regular Logistic Regression Model (mLRM)

The mLRM method is defined as

$$\text{logit}\mathrm{P}({\mathrm{Y}}_{\mathrm{i}}=1|{\mathrm{X}}_{\mathrm{i}},{\mathbf{Z}}_{\mathrm{i}})={\alpha }_0+{\alpha }_1{\mathrm{X}}_{\mathrm{i}}+{\mathit{\alpha }}_2^{\prime }{\mathbf{Z}}_{\mathrm{i}},\mathrm{i}=1,\cdots ,\mathrm{n}$$ (2)

where Z_i is the p × 1 vector of confounders from the ith subject with its corresponding p × 1 vector of parameters, α₂. The whole set of parameters in this approach is (α₀, α₁, ${\mathit{\alpha }}_2^{\prime }$) with p + 2 degrees of freedom.

2.3. Propensity Score Adjustment (PSA) and Propensity Score Trimming (PST)

In order to implement the PS method, an mLRM is fitted with the exposure variable X as the dependent variable and the confounding covariates Z as the independent variables. We call this logistic regression model the propensity score model. The individual PS is then defined as the estimated probability of exposure given the confounding covariates, or P̂(X = 1|Z). To estimate the effect of the exposure on the outcome, another logistic regression model with the outcome Y as the dependent variable is considered and denoted as outcome model. The independent variables of the outcome model include at least the exposure variable. The other independent variables included in the outcome model vary for different approaches and will be explained for each method.

To implement PSA, we consider another mLRM model (outcome model):

$$\text{logit}\mathrm{P}({\mathrm{Y}}_{\mathrm{i}}=1|{\mathrm{X}}_{\mathrm{i}},{\mathbf{Z}}_{\mathrm{i}})={\alpha }_0+{\alpha }_1{\mathrm{X}}_{\mathrm{i}}+{\mathit{\alpha }}_2\mathrm{g}({\mathrm{W}}_{\mathrm{i}}),$$ (3)

where W_i is the logit function of PS of the ith subject, g(W_i) is a nonparametric smooth function of W_i, and α₂ is the parameter corresponding to g(W_i). We modeled g(W_i) with a restricted cubic spline function [3] in this paper. In PSA, W enters into the outcome model as it was the only confounder. We adjust for W but not PS itself because we expect the linear predictor to be more linearly related to the log odds of P(Y = 1).

PST approach is similar to PSA except that the non-similar subjects in the exposure and the unexposed groups are excluded (trimmed) from the outcome model. The trimming step is included because the goal of PS is to construct comparable cohorts. As we are interested in rare disease with a limited number of cases, the trimming step in our simulation studies only trimmes the control group and is conducted by excluding the controls with propensity scores outside the range of the propensity score values of the cases.

2.4. Propensity Score with Additional Heterogeneity Adjustment (PSH)

The inclusion of the confounder variables in the outcome model not only makes the comparison between the exposed and unexposed groups meaningful but also accounts for the heterogeneity in the population and hence leads to adjusted odds ratio. The latter capability cannot be done by PSA alone. To see this, let α_1,mLRM be the α₁ defined in (2) and α_1,PSA be the α₁ defined in (3). It is easy to show that

$$\text{exp}({\alpha }_{1,mLRM})=\frac{P(Y=1|X=1,\mathbf{Z})P(Y=0|X=0,\mathbf{Z})}{P(Y=0|X=1,\mathbf{Z})P(Y=1|X=0,\mathbf{Z})},$$

and

$$\text{exp}({\alpha }_{1,PSA})=\frac{P(Y=1|X=1,W)P(Y=0|X=0,W)}{P(Y=0|X=1,W)P(Y=1|X=0,W)},$$

where W is the logit of PS and is a summary scalar of Z. The estimate of α_1,mLRM is the adjusted odds ratio, which is the primary parameter of interest, and is usually different from the estimate of α_1,PSA. This is known as non-collapsibility of the odds ratio [25]. The idea of PSH approach is to include an additional pre-specified subset of confounder variables with relative large effect size to control some level of heterogeneity and hence lessen the problem of non-collapsibility.

2.5. Ridge Logistic Regression With (RgR) or Without Penalizing Exposure Variable (RgRNoExp)

Ridge regression or quadratic PMLE is a shrinkage method allowing the covariates to be included in the model but with shrunken coefficients. To introduce shrinkage approaches, we assume (X, Z) are normalized so that (X, Z)′(X, Z) = I, where I is the identity matrix. The parameter estimates of RgR maximize the likelihood function of model (2) under the constraint of ${\alpha }_1^2+{\sum }_{j=1}^p{\alpha }_{2j}^2\le s$, where s is the constraint, and α₁, α_2j’s, and p are defined in Section 2.1 and 2.2. Note that as suggested by [27], the intercept, α₀, is not included in the constraint, and therefore, not shrunk in all the shrinkage methods considered in this paper. In practice, the constraint s can be determined by minimizing the user defined loss function with a cross-validation procedure [30] or effective Akaike information criterion [3].

RgRNoExp is similar to RgR except the regression coefficient of the exposure variable X is not penalized in the model. In other word, with α₁ being the regression coefficient of the exposure X, the parameter estimates of this approach are to maximize the likelihood function of model (2) under the constraint of ${\sum }_{j=1}^p{\alpha }_{2j}^2\le s$. Comparing to RgR, RgRNoExp doesn’t include α₁ in the constraint and therefore, doesn’t penalize the corresponding exposure of interest.

2.6. Lasso Logistic Regression With (LASSO) or Without Penalizing Exposure Variable (LASSONoExp)

LASSO is a shrinkage method with L1-norm penalty, which means it maximizes the likelihood function of model (2) under the constraint of $|{\alpha }_1|+{\sum }_{j=1}^p|{\alpha }_{2j}|\le s$, where α₁, α_2j’s, p, and s are defined in Section 2.5. The L1-norm penalty in LASSO is referring to the absolute function in the constraint and the L2-norm penalty in Ridge is referring to the quadratic function in its constraint. Because LASSO has L1-norm penalty, it can yield zero estimates when the parameter values are close to zero and hence performs variable selection [28].

LASSONoExp approach is similar to LASSO except the regression coefficient of the exposure variable X is not penalized in the model. In other words, it maximizes the likelihood function of model (2) under the constraint of ${\sum }_{j=1}^p|{\alpha }_{2j}|\le s$. Different from LASSO, LASSONoExp will allow us to obtain a non-zero estimate of the regression coefficient of interest even if its effect is close to null, while at the same time, to shrink the parameter estimates of the confounders to avoid model overfitting. The reasoning behind LASSONoExp and RgRNoExp is that shrinkage intentionally biases parameter estimates to minimize overfitting whereas we do not want to bias the exposure effect estimator.

3. Simulation Studies

In our motivating VE study [6], the outcome was the influenza status and the exposure was the vaccination status. Covariates included age in years, sex, race, home oxygen use, insurance, five individual medical conditions, smoking, immunosuppression, and timing of admission relative to the onset of influenza season. In the study, 135 patients had complete influenza virus testing, information on vaccination status, and complete demographic data. There were 13 patients with detectable influenza virus, of whom 5 were immunized, and 122 participants were negative for influenza, of which 89 were immunized with the influenza vaccine. The choice of simulation design and parameter values in this section was to mimic this motivating influenza vaccine study, in which outcome was rare in the population and case-control sampling design could deal with the extremely low incidence.

For PSH approach, we included the top three predictors with largest effect size in the outcome model in addition to propensity score and the exposure variable.

3.1. Simulation Procedures

Monte Carlo simulations were performed to simulate a case-control study and to mimic the data collection procedures of the VE study. The simulation was composed of the following two steps.

In step 1, we simulated 5 million samples from the following models:

$$\text{logit}\mathrm{P}(\mathrm{X}=1|\mathbf{Z})={\beta }_0+{\mathit{\beta }}_1^{\prime }\mathbf{Z}$$

$$\text{logit}\mathrm{P}(\mathrm{Y}=1|\mathrm{X},\mathbf{Z})={\alpha }_0+{\alpha }_{1}X+{\mathit{\alpha }}_2^{\prime }\mathbf{Z},$$

where X was the exposure of interest, Z was the vector of 13 confounders including two continuous variables and eleven binary variables, and Y was the dependent variable. The population parameters including the parameters in the distribution function of the confounder variables and the regression coefficients in the two logistic regression models took the values of the estimates from the VE study. In particular, the variables (z₁, …, z₁₁) represented the confounders of race (black vs non-black), home oxygen use, gender (female vs male), current smoking (in the past 6 months), underlying medical conditions (diabetes mellitus, asthma chronic obstructive pulmonary disease, chronic heart disease, immunosuppression, chronic liver or kidney disease, asplenia, and other type of disease). Correlations among them were brought in through latent Gaussian distribution. We first simulated two multivariate normal variables, R₁ and R₂, from

$$R_1~MVN\left(\right(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}),(\begin{array}{ccc}\hfill 4\hfill & \hfill 2\hfill & \hfill 2\hfill \\ \hfill 2\hfill & \hfill 3\hfill & \hfill 1\hfill \\ \hfill 2\hfill & \hfill 1\hfill & \hfill 1\hfill \end{array}\left)\right)\mathit{\text{ and }}{R}_2~MVN\left(\right(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}),(\begin{array}{ccc}\hfill 4\hfill & \hfill 2\hfill & \hfill 2\hfill \\ \hfill 2\hfill & \hfill 4\hfill & \hfill 2\hfill \\ \hfill 2\hfill & \hfill 2\hfill & \hfill 4\hfill \end{array}\left)\right).$$

Then we obtained the binary variables (z₂, z₃, z₄) from R₁ by choosing the cutoff values so that their marginal probabilities were 0.29, 0.64, and 0.26, respectively. Similarly, we obtained (z₅, z₆, z₇) from R₂ by choosing the cutoff values so that their marginal probabilities were 0.29, 0.66, and 0.50, respectively. The rest of binary variables, (z₁, z₈, ⋯, z₁₁), were simulated from independent binomial distribution with probabilities of 0.36, 0.32, 0.26, 0.12, and 0.10, respectively. The other two variables were continous variables representing patient age (z₁₂ in year) and the timing of admission relative to the onset of influenza season (z₁₃ in day), with z₁₂ simulated from N(73, 22) and z₁₃ simulated from N(59, 158). The coefficients in the two logistic regression models were β₁ = (−0.001, 0.001, −0.459, −0.001, 0.608, −0.441, −0.358, 0.504, −0.292, −0.201, −0.1, 0.022, −0.005), α₂ = (−0.286, 1.992, 0.918, −0.432, 0.127, −0.833, 0.019, −0.292, −0.113, −0.388, −0.001, −0.045, 0.10). We changed the value for β₀ to control the exposure probability. The intercept, α₀, in the outcome model was set to a value so that the outcome incidence is low, which was ranging from 0.001 to 0.0028 in the simulation.

In step 2, we sampled (without replacement) n₁ subjects with outcome positive and 4n₁ subjects with outcome negative from the cohort generated in step 1.

3.2. Factors Considered

We systematically varied the values of the following three factors to investigate their influence on the performance of the odds ratio estimates.

Strength of Association

The strength of association between the exposure and outcome was measured by the odds ratio, that was exp(α₁). The values of OR were set to 1/3, 1/2.5, 1/2, 1/1.5, and 1 in the simulation.

Number of Cases

The number of cases was controlled by the parameter n₁ in our simulation. We considered 15 to 150 cases with increment of 15, allowing us to evaluate the performance when the number of cases per parameters (NCP) varies from 1 to 10. For the NCPs in PSA, PST, and PSH approaches, we only included the parameters in the outcome model but not the parameters in the PS model. NCP was not a global parameter here. It only applied to the studied outcome models.

Imbalance of Exposure

We modified the value of β₀ to evaluate the performance under perfect balance (50% exposure rate) and moderate imbalance (20% exposure rate).

3.3. Evaluation Criteria

The nine methods described in Section 2 were then used to obtain the regression estimate of the exposure of interest α₁. Analyses were performed using R Statistical Software (version 3.0.1). R package glmnet was used for RgR, RgRNoExp, LASSO, and LASSONoExp, and rms for the rest of methods. The constraint s of the shrinkage approaches was determined by 10-fold cross-validation to minimize the deviance of logistic regression model. This could be performed by using cv.glmnet function in the R package glmnet. We conducted 1000 simulations and used five criteria, including bias, empirical standard error (ESE), square root of mean square error (RMSE), median absolute error (MAE), and empirical coverage probability (CP), to assess the performance of the exposures effect estimator.

Bias measures how far away the estimated effect of the exposure is from the true effect and is defined as Bias=α̂̄₁ − α₁, where α̂̄₁ is the average of the estimates from 1000 simulations and α₁ is the true value. Positive bias values when OR>1 or negative bias when OR<1 indicate an overestimation of the effect of the exposure on the outcome; and negative bias values when OR>1 or positive bias when OR<1 indicate an underestimation.

ESE is the standard error of the parameter estimates from 1000 simulations. It measures the variability of the estimates. Given small bias of the estimates, the smaller the empirical standard error is, the more precise the method is.

RMSE is the square root of the sum of the variance and the squared bias of the estimator, and therefore, combines the information from empirical standard error and bias. Smaller RMSE means better estimator.

The drawback of RMSE is that it is sensitive to the outliers. To overcome this potential problem, we also included MAE, which is the median of the absolute difference between the estimates and the true value. This measurement is useful when the distribution of the estimates is skewed.

CP of 95% confidence interval (CI) is defined as percentage of Monte Carlo simulations with their 95% CI covering the true value. The construction of a 95% CI is straightforward for Logistic, PSA, and PSH approaches. For shrinkage approaches including RgR, RgRNoExp, LASSO, and LASSONoExp, we used nonparametric bootstrap method to construct the bootstrap-based percentile CIs ([31], sections 2.3 and 5.3). The tuning parameter for shrinkage approaches was reestimated in each of the bootstrap samples. We expect CP to be close to 0.95 for a valid method. If the CP is greater than 0.95, the CI is too wide and the method is too conservative, and if the CP is less than 0.95, the CI is too narrow and the method is too liberal.

For the shrinkage approaches, another interesting measurement to report is the effective degree of freedom (EDF), which measures the impact of penalty [32]. When the penalty goes to zero, the EDF will increase to the number of parameters in the model; when the penalty goes to infinity, the EDF will reduce to zero. Zou et al. [33] further showed that the number of nonzero coefficients was an unbiased estimate of EDF for LASSO approach, which was reported for LASSO and LASSONoExp in this paper.

4. Results

4.1. Balanced Exposure

We first evaluated the methods under balanced exposure (about 50% exposure rate). Figure 1–4 plotted the results based on the four criteria mentioned above for OR≤1 as the results for OR>1 were similar aside from Monte Carlo errors. We conducted the simulations using the nine approaches described in the Methods Section but only presented eight of them in the figures because PST approach was closely overlapped with PSA with indistinguishable differences.

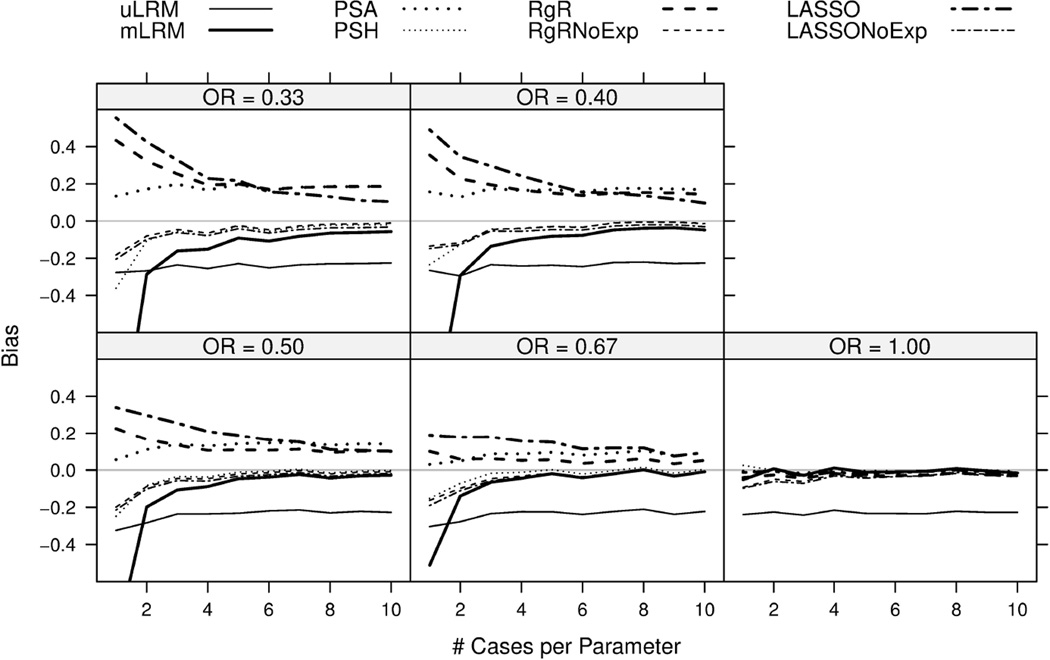
Figure 1.

Biases of the log odds ratio estimates are plotted for eight candidate approaches. The results were based on 1,000 simulations.

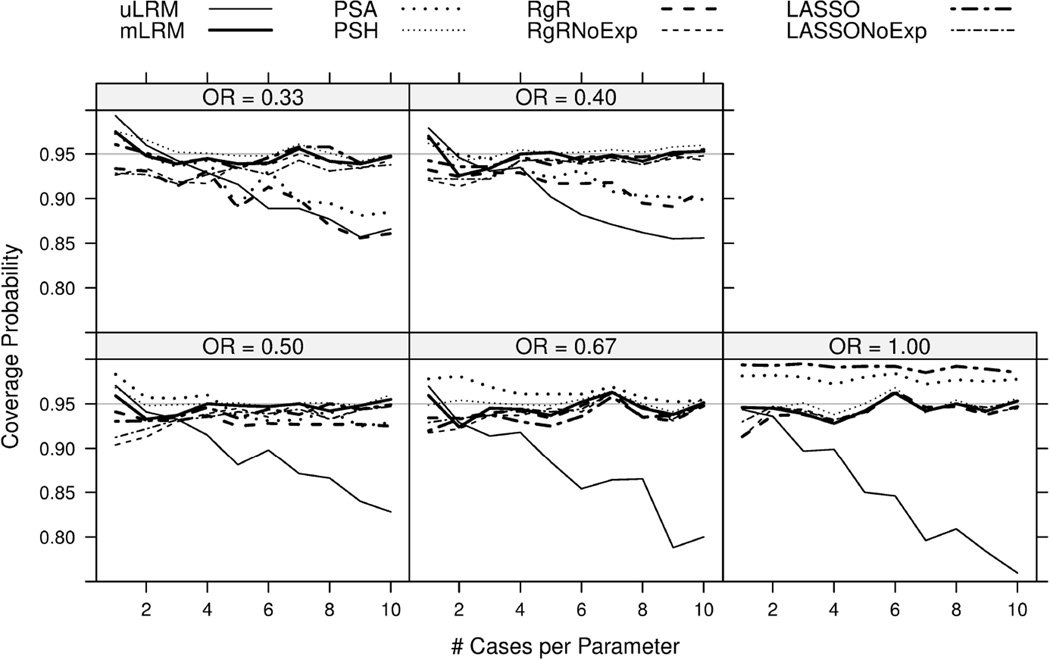
Figure 4.

Coverage probabilities (for 95% confidence intervals) of the log odds ratio estimates were plotted for eight candidate approaches. The results were based on 1,000 simulations.

When calculating the evaluation criteria for each method, we removed the simulations with nonconvergence or collinearity in that particular approach (using the software default criteria in the R package rms), which happened almost only for mLRM when NCP=1. For mLRM with NCP=1, the nonconvergence rate varied from 0% to 4.3% when OR moved from 1 to 1/3 and the collinearity rate remained stable around 13%. The median variance ination factors (VIFs) for different combinations of sample size and odds ratio ranged from 1.08 to 1.87 with their interquantile ranges falling between 1 and 2. The results were similar with stronger association of the exposure with its determinants (interquantile ranges of VIFs were between 3 and 5).

In general, the bias of uLRM was fairly stable for NCPs and ORs, showing asymptotic bias of around −0.3 due to lack of adjusting for confounders. The rest of the seven approaches provided estimates with negligible bias (close to zero) when the null hypothesis was true (OR=1), and their biases decreased when NCP increased or when OR moved closer to 1 (Figure 1). The biases of RgRNoExp and LASSONoExp approaches were the smallest among all the candidate approaches in almost all the scenarios except when OR was closer to null. The methods of mLRM and PSH tended to overestimate α₁, but their biases became smaller when the NCP increased from 1 to 10. Nonetheless, the bias of mLRM was the largest of all candidate approaches when NCP was one, including uLRM. On the other hand, PSA, RgR, and LASSO tended to underestimate the exposure effects and their biases stayed at relative high levels even when the NCP increased to 10. The results of RgR and LASSO were not surprising as they penalized the estimate towards the null and were known to be biased estimates. The non-negligible bias of PSA was likely due to its non-collapsibility.

Similar to Bias, ESEs of the candidate approaches decreased with increasing NCP. The ESEs of mLRM was the highest followed by PSH. The rest of approaches had similar values of ESEs with RgR being the winner in most scenarios. Due to limited space, this figure was included in the supplemental document (Figure S.1).

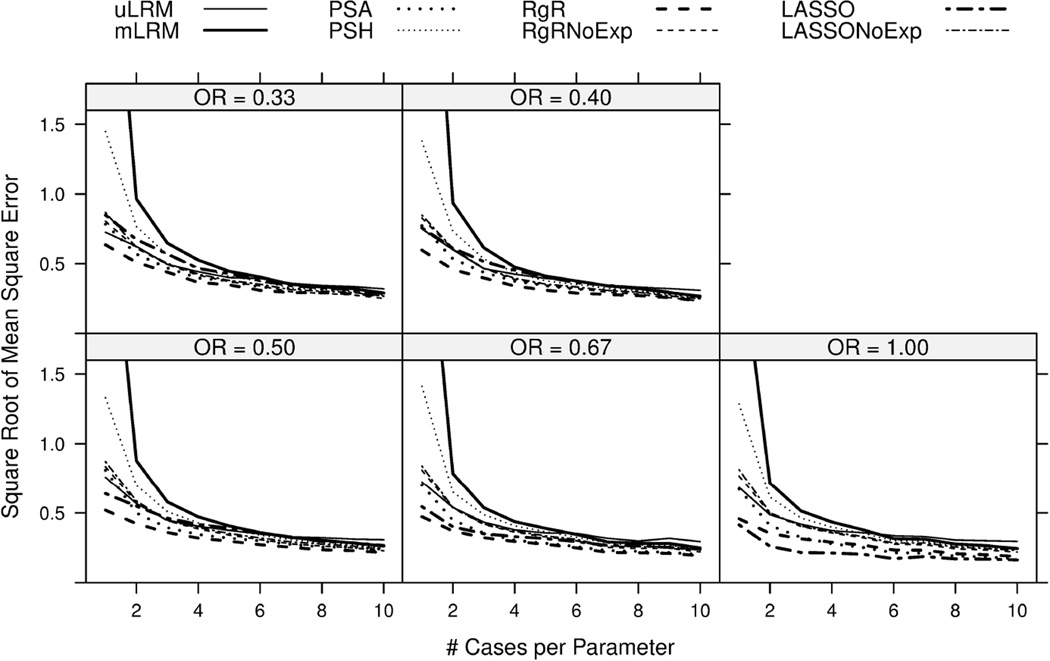
Similar to Bias, the RMSEs of all eight approaches declined with increasing NCP. When NCP was less than 4, mLRM had much larger RMSE values compared to the other approaches. In fact, the RMSEs of mLRM ranged from 2.51 to 4.19 when NCP=1, which were off the chart of Figure 2. PSH had the next largest RMSEs with values falling between mLRM and PSA. For the remainder of approaches, RgR tended to have the smallest RMSE values in all scenarios except when OR=1. The variable selection feature of LASSO led to majority zero estimates of log(OR) and therefore, smaller RMSEs when OR=1. The RMSE of LASSO, however, increased when OR moved away from the null. The RMSEs of the other four approaches, uLRM, PSA, RgRNoExp, and LASSONoExp, were similar and fell between PSH and RgR.

Figure 2.

Square Root of Mean square errors of the log odds ratio estimates were plotted for eight candidate approaches. The results were based on 1,000 simulations.

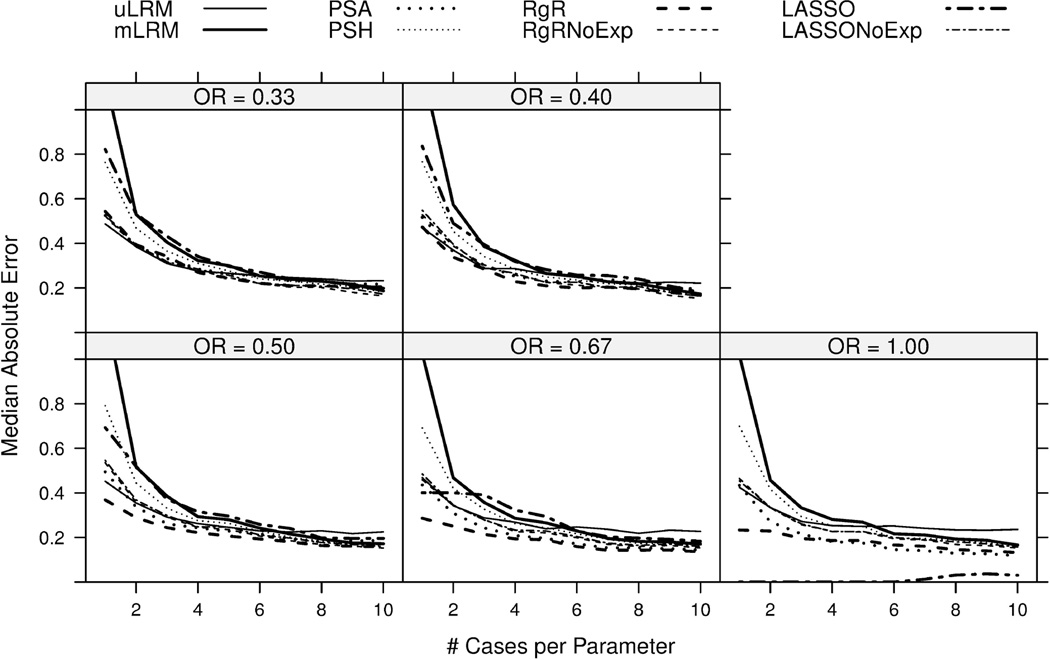
Compared to RMSE, the MAE differences among the candidate approaches were less significant, implying the effect of extreme values on RMSE. On the other hand, the order of the performance of the candidate approaches remained similar. In addition, Figure 3 shows that the MAE of LASSO remained relatively high with increasing NCP when OR=0.33, which was driven by the relatively large bias of LASSO in this setting.

Figure 3.

Median absolute errors of the log odds ratio estimates were plotted for eight candidate approaches. The results were based on 1,000 simulations.

The expected value of the empirical coverage probability of a 95% CI was 0.95. As shown in Figure 4, the CPs of mLRM, PSH, RgRNoExp, and LASSONoExp fluctuated around the nominal level of 0.95. The CIs of uLRM, PSA, RgR, and LASSO were under-covered, especially with increasing NCP and increasing exposure effect (OR away from 1). The under-coverage of PSA was also observed in [9]. RgR may be preferred (due to best RMSE) if its bias even under large NCP was acceptable and coverage of confidence interval was improved.

We also examined EDF for shrinkage approaches. The median EDFs ranged from 13.43 to 13.997 for RgR, from 13.39 to 13.998 for RgRNoExp, from 5 to 11 for LASSO, and from 5 to 11 for LASSONoExp, showing greater impact of penalty on LASSO than on Ridge. In general, the EDF increased with NCP. Note that the EDF calculation did not include intercept.

4.2. Moderate Unbalance Exposure

We also evaluated all methods under moderate exposure imbalance (about 20% exposure rate), for which the nonconvergence became more severe. When NCP=1, the nonconvergence rates for mLRM were 4.3%, 12.6%, 20.4%, 30.6%, and 34.7% for OR values of 1, 1/1.5, 1/2, 1/2.5, and 1/3, respectively. When NCP increased to 2, the nonconvergence rates reduced to 0.2%, 1.3%, 4.2%, 7.7%, and 9.3%, respectively. Unlike balanced exposure, for which the nonconvergence happened almost only for mLRM, under moderate exposure, the nonconvergence happened for PSA and PSH as well, although less severe than mLRM. Collinearity rates for mLRM were similar to balanced exposure scenario. Due to high nonconvergence rate when NCP=1, we excluded the corresponding results from Figure S.2–S.6 as the Monte Carlo samples might be biased. The nonconvergence with low NCP was also discussed in [1]. Due to limited space, the figures presenting the results under this scenario were included in the supplemental document (Figure S.2–S.6).

5. Example: Vaccine Effectiveness Study

All the methods evaluated in this paper were applied to reanalyze our motivating influenza vaccine study [6] and to calculate the adjusted VE for the prevention of medically-attended acute respiratory illness (see [6] for a detailed description of the study). We introduced the study at the beginning of Section 3. All the aforementioned covariates were considered as potential confounders and were included in the mLRM, RgR, RgRNoExp, LASSO, and LASSONoExp. The two continuous covariates, age and admission time, were included in the model as cubic spline functions, which led to 19 parameters in the model including intercept. All the potential confounders were included in the PS models of PSA, PST, and PSH. In addition, the non-overlapping subjects (0 cases and 10 controls) were removed from the PST. For the PSH method, the two covariates with biggest effect size, kidney/liver disease and admission time, were included in the outcome model as well to explain additional heterogeneity. The 95% CIs of all penalized regression approaches were constructed based on 5,000 bootstrap samples. Table 1 provided the regression coefficients of vaccine status and influenza VE estimates in percent, which was (1 − OR) × 100%, together with their 95% CIs. We also included the EDF for the penalized approaches in Table 1. The VIF for this study was 1.94. As the NCP of the mLRM was roughly 1, the mLRM was likely over-parameterized. On the other hand, due to the high vaccine rate, there were only 41 subjects without vaccination leading to potential over-parameterization problem for the PS model as well. Consistent with the results from simulation studies, RgR had narrower CI (width=2.95) than RgRNoExp (width=3.42) for β, although after transforming to VE estimate the CI of RgR (width=0.945) became wider than RgRNoExp (width=0.590) due to non-symmetry of VE’s CI. Based on the results from simulation studies, RgR likely underestimated the VE effect. Unlike simulation results, LASSONoExp had the widest CI (width=6.74) among all the methods for β, followed by LASSO (width=6.65) and mLRM (width=4.14). The method with the narrowest CI was uLRM (width=2.37). If we focused on VE estimate, the estimates and 95% CIs using RgRNoExp and LASSONoExp were similar, which were 79.6% (95% CI: 39.0%–98.0%) and 79.6% (95% CI: 41.7%–99.9%), respectively. They were the two methods with the narrowest CIs for VE estimate. Their EDFs, however, were different, 17.7 for RgRNoExp and 8 for LASSONoExp, highlighting the unique sparcity feature of LASSONoExp and the difference in their final models. The coefficient profile for the coefficient paths using RgR, RgRNoExp, LASSO, and LASSONoExp were provided in the supplemental document (Figure S.7). Compared to the previous published analyses [6], the results here were slightly different because additional covariates were adjusted in this reanalysis.

Table 1.

VE study with 135 patients.

Methods	β (95% CI)	VE (95% CI) (in %)	EDF
uLRM	−1.46 (−2.65,−0.28)	76.8 (24.1, 92.9)	-
mLRM	−2.57 (−4.64,−0.50)	92.4 (39.3, 99.0)	-
PSA	−1.64 (−2.96,−0.32)	80.6 (27.3, 94.8)	-
PST	−1.64 (−2.96,−0.32)	80.6 (27.3, 94.8)	-
PSH	−1.75 (−3.13,−0.37)	82.6 (30.7, 95.6)	-
RgR	−0.46 (−2.95,−0.00)	37.1 (0.3, 94.8)	17.5
RgRNoExp	−1.59 (−3.91, −0.49)	79.6 (39.0, 98.0)	17.7
LASSO	−0.00 (−6.65, 0.00)	0.00 (0.0, 99.9)	1
LASSONoExp	−1.59 (−7.28,−0.54)	79.6 (41.7, 99.9)	8

uLRM: univariable logistic regression model.

mLRM: multivariable logistic regression model.

PSA: propensity score adjustment.

PST: propensity score with trimming.

PSH: propensity score with additional heterogeneity adjustment.

RgR: ridge regression.

RgRNoExp: ridge logistic regression without penalizing exposure variable.

LASSO, least absolute shrinkage and selection operator regression.

LASSONoExp, LASSO logistic regression without penalizing exposure variable.

6. Discussion

There was a vast literature on PS since the seminal paper [7] and by no means were the references provided in this paper complete. Notably, in order to construct the PS, Lee et al. [17] advocated using a machine learning approach of boosted classification and regression trees under conditions of both moderate non-additivity and moderate non-linearity in the PS model; Feng et al. [18] proposed the generalized propensity score method when exposure was multi-level; Austin et al. [12] compared the ability of different PS models to balance measured variables between treated and untreated subjects through a Monte Carlo study; and Austin et al. [19] compared 12 algorithms for matching PS. Note that we included the PS covariate adjustment approach in this paper as one of the comparison approaches because research had advocated its validity in the similar setting [9]. It is possible that better performance can be achieved using propensity score matching or inverse probability weighting as they can avoid modelling the rare outcome. However, the primary goal of this paper was not to compare the performance of various PS-based approaches to estimate the adjusted odds ratios in mLRM as this had been studied and discussed intensively in [13, 14] and their follow-up papers. Our focus was on the validity and performance of the shrinkage or penalized approaches in this setting. The research of the shrinkage approaches had been primarily focused on the variable selection in the high dimensional studies with p >> n, but rarely on the estimation and confidence interval construction in the medical setting when the number of confounders was close to the valid sample size (the number of cases or controls, whichever fewer). We hoped the numerical comparison studies conducted in this paper could shed some light on the potential usage of shrinkage approaches in this setting and motivate further investigation on this matter. In fact, during the revision of this paper, Franklin et al. [34] conducted simulation studies to compare the regularized regression versus the high-dimensional PS in the logistic regression model with large sample size (n=30,000 and number of events=300, 1500, or 3000) and large NCP (ranged from 27 to 136) with focus on OR=1 and on the scenarios that a large set of pseudo confounders were available in the dataset. Their PS methods were, however, based on indicators for propensity score deciles. The noncollapsibility of their propensity score approaches seemed to be less severe and outperformed their regularized approaches based on RMSE in their simulation setups with large sample size and large NCP, although the hybrid method combining PS and LASSONoExp also performed well in their settings. Extending the future comparative studies to include their decile-based propensity score approaches in the low NCP and low sample size scenario is under investigation.

It was also worth mentioning that PS analyses had some additional advantages over multivariable models. By using PS, one might restrict analyses to exposed and unexposed subjects that have similar distributions in the confounders, and thus study the causal effect of exposure. With multivariable models, equality of confounder distributions was only mathematically controlled and this might involve some degree of extrapolation of missing parts of the confounder distribution in one of the exposure groups. Thus, multivariable modeling relied more heavily on correctly specified models.

In addition to ridge and lasso, many other regularization methods were developed and recently reported for variable selection, including, but not limited to, bridge regression [35], smoothly clipped absolute deviation [36], and their extensions such as adaptive lasso [37], group lasso [38], and the elastic net [39]. Future research is needed to investigate the performance of other regularization methods in controlling the unbalance in observational studies.

For the simulation setups considered in this paper, mLRM performed reasonably well when NCP was greater than four. This cutoff number was, however, not a universal rule. For example, in the scenario described by Cepeda et al. [9], they recommended the usage of mLRM when NCP was greater than seven. As for uLRM, its performance based on RMSE was not worse than the competitive methods when NCP was close to 1 due to its small variability. This, however, depended on the amount of confounding. Regarding the method to use in practice, we found RgR, RgRNoExp, and LASSONoExp to be competitive and which method to use depended on the context of application. RgR was the method with the lowest RMSE in almost all the scenarios except when the exposure had null effect (OR=1), for which LASSO was the winner due to its sparsity property. However, two limitations on RgR were found in the simulation studies: (a) the bias was high for low NCP and it didn’t go away when NCP increased to 10; (b) the under-coverage of 95% CI became more severe with increasing NCP when the OR moved away from null effect. RgR sacrificed bias for smaller variability. If the sacrificed bias was acceptable, RgR should be considered for low NCP as it performed the best in the trade-off between bias and variability. On the other hand, RgRNoExp and LASSONoExp sacrificed variability for smaller bias. Their biases quickly became negligible when NCP increased and their coverage probabilities fluctuated around the nominal level. If unbiasedness was important to the application, these two methods were worth considering. Between these two approaches, RgRNoExp was preferred when the effects of confounders were of interest and LASSONoExp should be considered when a parsimonious model was desired. When these two approaches are used in pactice, we recommmend computing and evaluating the EDF, and comparing the effect estimate from these methods with the unadjusted effect estimate. If EDFs were very small (close to 1) then RgNoExp and LASSONoExp might not sufficiently control the confounder and their estimates would go towards unadjusted estimate. In this case, the analyst should be cautious when using ‘NoExp’ methods. Furthermore, for all the shrinkage approaches, we recommended to save the random seed to obtain reproducible results when cross-validation procedure was used to find the optimal penalty parameter. It was also worth emphasizing that unnecessarily over-parameterizing the shrinkage methods was not without cost. Our experience (in addition to the simulation results shown in this paper) showed that unnecessarily expanding the outcome model in the shrinkage methods would increase the standard error estimates of the regression coefficients, widen the CIs, thereby, decreasing the power to detect exposure effects, which was consistent with the results from Franklin et al. [34].

Constructing the CIs of the regression coefficients was still an open problem for shrinkage approaches in mLRM. For practical and illustrative purpose, we used the bootstrap approach to construct the CIs for the shrinkage approaches in this paper following Tibshirani [28]. The validity of nonparametric bootstrap procedure in the shrinkage approaches was in question because bootstrap-based approaches only assessed the variance of the estimates but not the bias, while shrinkage approaches purposely introduced bias to the coefficient estimates to reduce the variance of the estimates [40]. Compared to the regular shrinkage approaches of LASSO and RgR, the modified shrinkage approaches, LASSONoExp and RgRNoExp, could reduce the bias associated with the estimator of the exposure in the clinical setting with NCP≥1, as observed in our simulation studies. The slight under-coverage, although acceptable in our simulation setup (at worst, ~0.91 vs 0.95), of the CIs constructed by nonparametric bootstrap for LASSONoExp and RgRNoExp at NCP=1 might be improved by the residual bootstrap, which had been shown to be consistent in a multiple linear regression model [41]. On the other hand, further development on the route of Lockhart et al. [42] and van de Geer et al. [43] might provide an analytical approach to estimate the standard error and construct the CIs directly without relying on resampling techniques such as bootstrap.

Our simulation study had several limitations. Our results were based on our choice of sample size, number of confounders, and parameter values, which were carried from the motivating study. Secondary, we presented the results using three indexes including OR, NCP, and exposure rate, however, other factors such as total sample size, number of covariates, or amount of confounding might affect the performance of different approaches as well.