Abstract
Interaction between electrons has long been a focused topic in condensed-matter physics since it has led to the discoveries of astonishing phenomena, for example, high-Tc superconductivity and colossal magnetoresistance (CMR) in strongly-correlated materials. In the study of strongly-correlated perovskite oxides, Nb-doped SrTiO3 (Nb:SrTiO3) has been a workhorse not only as a conducting substrate, but also as a host possessing high carrier mobility. In this work, we report the observations of large linear magnetoresistance (LMR) and the metal-to-insulator transition (MIT) induced by magnetic field in heavily-doped Nb:STO (SrNb0.2Ti0.8O3) epitaxial thin films. These phenomena are associated with the interplay between the large classical MR due to high carrier mobility and the electronic localization effect due to strong spin-orbit coupling, implying that heavily Nb-doped Sr(Nb0.2Ti0.8)O3 is promising for the application in spintronic devices.
Recent discoveries of a high mobility (μ) two-dimensional electron gas (2DEG), superconductivity, and ferromagnetism at the interface of SrTiO3 (STO) with other oxides such as LaAlO3 and LaTiO31,2,3,4, have attracted interest in the properties of STO and doped STO. Conducting Nb-doped STO has also been studied as a potential candidate for creating a high-μ 2DEG by using a δ-doped quantum well structure5. Previous studies have been conducted in a limited range of Nb concentration (0 ~ 5 at.%)6,7,8,9,10,11, where μ was observed to be ~22,000 cm2/Vs at 4 K for Nb concentrations of 0.02 at. % and decrease with increasing Nb concentration. In the heavy doping regime above 5 at. %, however, μ barely changes as a function of the Nb concentration contrary to the result of the low Nb concentration11. On the other hand, heavily Nb-doped STO (20 at. % Nb) has been reported to show intriguing properties such as large thermoelectric power12. Therefore, a deeper exploration into the effect of high-concentration doping on the carrier transport is needed to understand the physical properties of Nb-doped STO. In this work, we have investigated the magnetotransport properties of a heavily Nb-doped (~20 at.%) STO (Nb:STO) epitaxial thin film and observed intriguing phenomena, large linear magnetoresistance (LMR) and metal-to-insulator transition (MIT) induced by the magnetic field, which are unprecedented in Nb:STO with low Nb concentration. We also present a few evidences supporting that those phenomena are associated with the interplay between the large classical MR due to high carrier mobility and the localization effect due to strong spin-orbit coupling.
Sr(Nb0.2Ti0.8)O3 thin films are grown on STO (001) substrates by pulsed laser deposition (PLD). The Sr(Nb0.2Ti0.8)O3 polycrystalline target with 20 at.% Nb is prepared by a conventional solid-state reaction technique. During the film growth, the laser power, the laser repetition rate, the substrate temperature, and the oxygen partial pressure are 1.6 J/cm2, 2 Hz, 700 °C, and 1 × 10−5 Torr, respectively. The composition of the grown film is found to be Sr:Ti:Nb = 1:0.79:0.21 using the Rutherford back scattering (RBS) method. We have examined the homogeneity of a film using the scanning electron microscopy with energy dispersive X-ray spectroscopy (SEM/EDX, Supplemental Material S1). For the measurement of electrical properties, platinum is deposited by e-beam evaporation through a shadow mask to form the electrode pattern shown in Fig. 1(b). The longitudinal resistance (Rxx = V23/I14) and Hall resistance (Rxy = V65/I14) are measured with the excitation current of 100 μA using a Source-Measure Unit (Keithley 2612A) and a nano-voltmeter (Keithley 2182). With this setup, the contacts are confirmed to be Ohmic by measuring the two probe resistance (V14/I14). The electrical properties have been investigated as a function of temperature (T) (1.8 K ~ 300 K) and magnetic field (B) to 9 T using a commercial cryogen-free cryostat (CMag Vari-9, Cryomagnetics Inc.).
Figure 1.
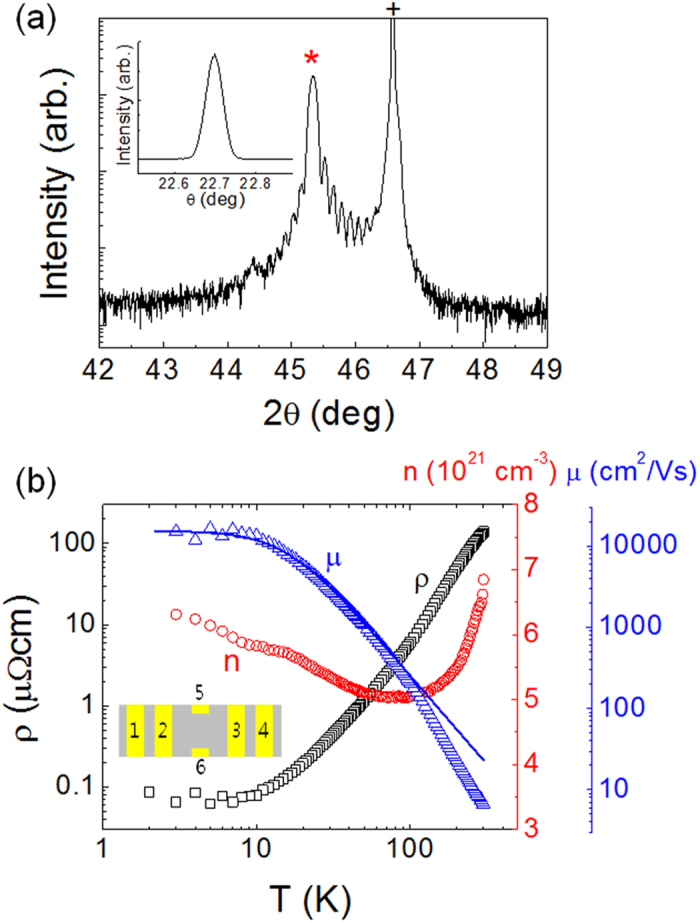
(a) X-ray diffraction θ–2θ scan of a 65 nm thick Sr(Nb0.2Ti0.8)O3 film grown on a STO (100) substrate by PLD. The black cross and red asterisk represent STO and Sr(Nb0.2Ti0.8)O3, respectively. The inset shows the X-ray rocking curve. (b) Resistivity (ρ, black square), carrier density (n, red circle), and the carrier mobility (μ, blue triangle) as a function of T. n was obtained by Hall measurement under ±2 T. The blue solid line is a fitting curve to the Fermi liquid theory, 1/μ(T) = α + βT2ln(1/T), where α and β are constants. The inset shows a schematic illustration of the film (grey) and the electrodes (yellow) for the electrical characterization.
Figure 1(a) shows the X-ray diffraction θ–2θ scan of a 65 nm-thick Sr(Nb0.2Ti0.8)O3 film near (002) peak of SrTiO3, which indicates that the Sr(Nb0.2Ti0.8)O3 films are epitaxial with the c-axis along the surface normal direction without any features of secondary phases or phase segregations. The observed fringe pattern indicates the atomically smooth surface of our samples. From the fringe pattern, the thickness of the film is estimated to be about 65 nm consistent with the nominal thickness. The rocking curve of the (002) peak of a Sr(Nb0.2Ti0.8)O3 film with the full width at half maximum (FWHM) of 0.046° indicates good crystallinity, as shown in the inset.
Figure 1(b) shows the basic transport properties of a 65 nm-thick Sr(Nb0.2Ti0.8)O3 film as a function of T, where the carrier density (n) is obtained by Hall measurement with B of ±2 T. The data displays a few intriguing features which have not been observed in lightly doped Nb:STO. First, note that, despite a huge n (~1021 cm−3), μ is unexpectedly high at low temperature (~14,000 cm2/Vs at 1.8 K) resulting in a remarkably low resistivity (ρ) of about 8 × 10−8 Ωcm at 1.8 K. It is a quite unexpected observation since μ was reported to be 419 cm2/Vs and 316 cm2/Vs for Sr(Nb0.01Ti0.99)O3 and Sr(Nb0.02Ti0.98)O3, respectively11. Therefore, the observed high μ implies that there is a change in the transport mechanism or in the electronic band structure of the heavily-doped Nb:STO films. Below 100 K, the dependence of μ on T fits quite well to the Fermi liquid theory, 1/μ(T) = α + βT2ln(1/T) where α and β are constants13 meaning that Sr(Nb0.2Ti0.8)O3 films are degenerate. The deviation from the fit above 100 K could originate from the contribution of phonon scattering at high temperature14. Or, it might be associated with the phase transition of STO from the tetragonal to the cubic phase above 105 K15,16. This fact might lead to the emergence of multiple electronic bands. Indeed, as will be discussed in the later part, a fingerprint of the existence of multiple types of carriers is shown in the B-dependence of the Hall resistance (Rxy), unveiling one type of carrier having remarkably high μ at low temperature. Therefore, we believe that such a high μ originates from the change in the electronic band structure without ruling out other possibilities, for example, the effect of strain.
Another intriguing feature is shown in the non-monotonic T-dependence of n. While n decreases with lowering T down to 100 K due to the reduction of thermal energy, it shows the opposite behavior below 100 K. This increase in n is associated with the increased dielectric screening due to the drastic increase of the dielectric permittivity of STO. In fact, a similar increase of n has been reported in oxygen vacancy (VO)-doped STO17.
In Fig. 2(a), the magnetoresistance (MR = R(B)/R(0)) a 65 nm-thick is plotted as a function of B at 1.8 K for two different orientations of B. Note that both MR vs. B curves are quite linear irrespective of the orientation although the amplitude of MR is about three-times higher for the case of the perpendicular B. In this work, we have investigated three samples with varying thickness (65 ~ 88 nm) and all investigated samples are shown to reproduce the LMR (Supplemental Material S2). As T increases, the linear dependence of MR turns into the classical quadratic dependence as shown in Fig. 2(b).
Figure 2.
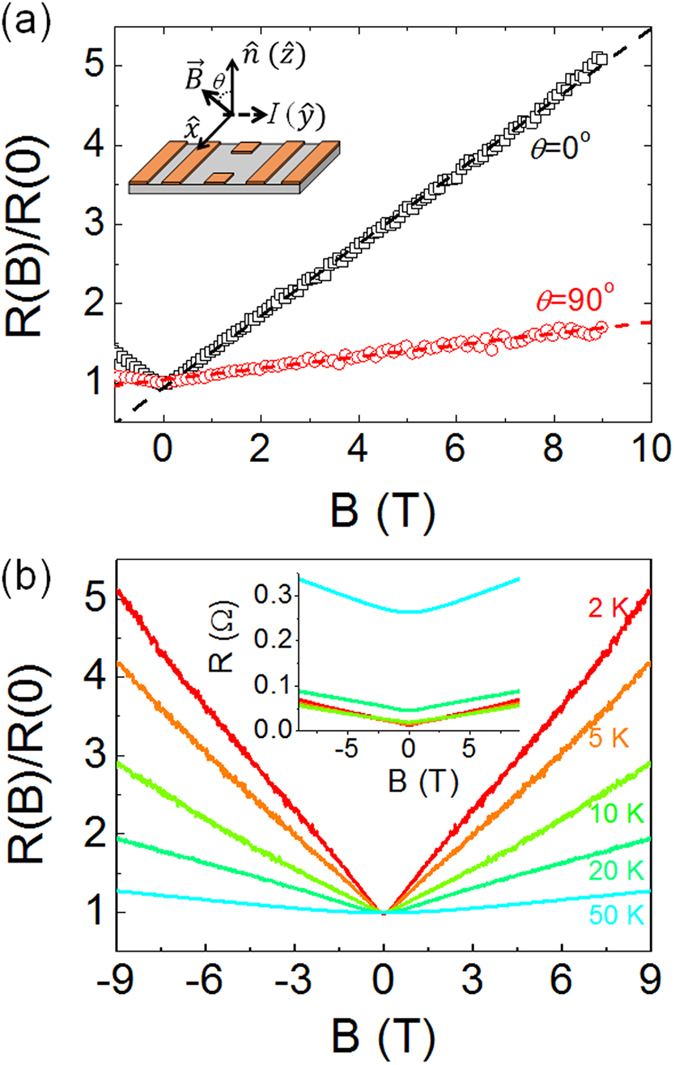
(a) MR a 65 nm-thick Sr(Nb0.2Ti0.8)O3 film as a function of B for B// (black square) and B⊥
(black square) and B⊥ (red circle). Dashed lines represent the linear fitting curves to each data. Inset shows the definition of θ. (b) Temperature dependence of MR for B//
(red circle). Dashed lines represent the linear fitting curves to each data. Inset shows the definition of θ. (b) Temperature dependence of MR for B// . Inset shows the resistance as a function of B at various temperatures.
. Inset shows the resistance as a function of B at various temperatures.
Since the first report of LMR in Bi crystals18, LMR have attracted much interest because MR is expected to be an even function of B owing to symmetry. Nevertheless, LMR has been reported for various materials leading to the development of several theoretical models (for a review, see refs 19,20 and references therein). Recently, the interest has been revived due to the observation of LMR in topological insulators21,22, multilayer epitaxial graphene23, and Dirac semimetals such as Cd3As224,25. I. M. Lifshitz and V. G. Peschanskii explained the LMR using the classical electron trajectories in B when the material has an open Fermi surface26. For materials with a closed Fermi surface, A. A. Abrikosov has developed a quantum mechanical picture for the LMR27. According to his picture, in the quantum limit where the Landau level spacing is much larger than the thermal energy (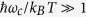 , where
, where 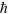 , ωc, and kB are reduced Planck constant (h/2π), cyclotron frequency, and Boltzmann constant, respectively), only the lowest Landau level is occupied by electrons leading to the LMR. This LMR is dubbed as “quantum LMR (QLMR)”. About 30 years later, the LMR was observed in Ag2+δTe and Ag2+δSe under a low B down to 10 Oe and high T up to 300 K, which does not satisfy the quantum limit criterion28. Again, based on his QLMR picture, A. A. Abrikosov also showed that the LMR could be observed at high T with low B under assumptions of (1) a gapless semiconductor with a linear energy vs. momentum (E vs. k) relation and (2) inhomogeneous carrier distribution19,29. As an alternative explanation, M. M. Parish and P. B. Littlewood also showed that the LMR could appear in inhomogeneous materials making the Hall effect involved in the calculation of the longitudinal resistance30,31.
, ωc, and kB are reduced Planck constant (h/2π), cyclotron frequency, and Boltzmann constant, respectively), only the lowest Landau level is occupied by electrons leading to the LMR. This LMR is dubbed as “quantum LMR (QLMR)”. About 30 years later, the LMR was observed in Ag2+δTe and Ag2+δSe under a low B down to 10 Oe and high T up to 300 K, which does not satisfy the quantum limit criterion28. Again, based on his QLMR picture, A. A. Abrikosov also showed that the LMR could be observed at high T with low B under assumptions of (1) a gapless semiconductor with a linear energy vs. momentum (E vs. k) relation and (2) inhomogeneous carrier distribution19,29. As an alternative explanation, M. M. Parish and P. B. Littlewood also showed that the LMR could appear in inhomogeneous materials making the Hall effect involved in the calculation of the longitudinal resistance30,31.
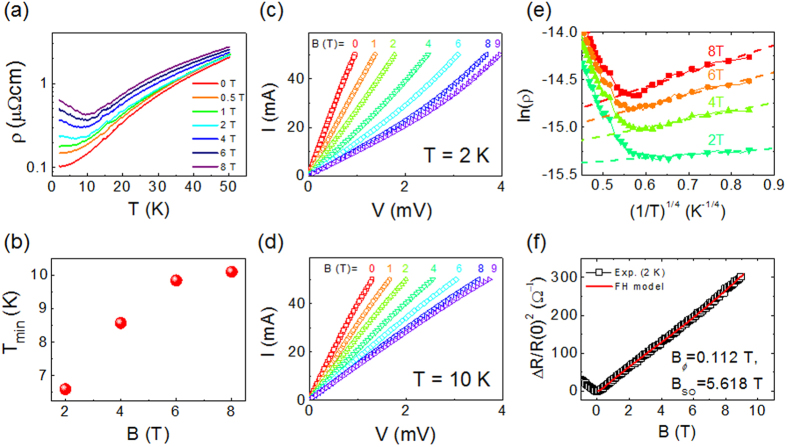
In order to clarify the origin of the LMR in our samples, T-dependence of ρ and Rxy are investigated with varying B. Figure 3(a) shows ρ vs. T curves at various B. Note that, under a sufficiently strong B, ρ(T) shows a metal-insulator transition (MIT) at a certain temperature which increases with B (Fig. 3(b)). The insulating nature under a strong B at low T is also verified by the non-linear current (I)-voltage (V) characteristics at 2 K (Fig. 3(c)) in comparison with the linear I-V curves at 10 K with varying B (Fig. 3(d)). In addition, we have found that, below the MIT temperature, the temperature dependence of the resistivity can be described by 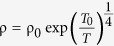 as shown in Fig. 3(e), implying that the carrier transport is dominated by the variable-range hopping (VRH)32. It means that the carriers become localized by the magnetic field, invoking the effect of the weak antilocalization (WAL)33,34,35,36.
as shown in Fig. 3(e), implying that the carrier transport is dominated by the variable-range hopping (VRH)32. It means that the carriers become localized by the magnetic field, invoking the effect of the weak antilocalization (WAL)33,34,35,36.
Figure 3.
(a) Resistivity (ρ) of a 65 nm-thick Sr(Nb0.2Ti0.8)O3 film as a function of temperature (T) with varying magnetic field (B), (b) Temperature at the resistance minimum (Tmin) as a function of B, (c,d) the current (I)-voltage (V) characteristic curve with varying B at 2 K and 10 K, respectively. (e) ln(ρ) vs. (1/T)1/4 curves under various magnetic field. Solid lines are linear fitting to each curve below the Tmin. (f) ΔR/R(0)2 as a function of B at 2 K (replotted from Fig. 2(b)). A red solid line is the fitting curve by Fukuyama-Hoshino model (see the text) with the fitting parameters, Bϕ = 0.112 T and BSO = 5.618 T.
In the three dimensional WAL, MR 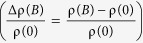 can be described by Fukuyama-Hoshino (FH) model37,38,39 which is expressed as the following equation (Eq. (1)).
can be described by Fukuyama-Hoshino (FH) model37,38,39 which is expressed as the following equation (Eq. (1)).
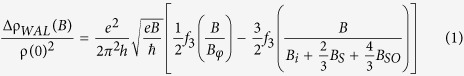 |
where
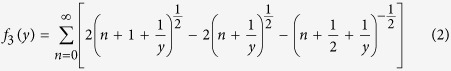 |
In Eq. (1), Bi, BS, and BSO are the characteristic field for inelastic, spin-flip, and spin-orbit scattering, respectively. Bϕ is the characteristic dephasing field given by Bi + 2BS. Assuming that the measured MR is given by a sum of ΔρWAL and the classical MR (Δρorb ~ B2) due to Lorentz effect38, we have fitted the observed MR as shown in Fig. 3(f). Note that the model well describes the observed LMR resulting in an estimation of the fitting parameters, Bϕ = 0.112 T and BSO = 5.618 T. These values are consistent with the result previously obtained in the LaAlO3/SrTiO3 heterojunction in a high carrier density regime induced by the electric field effect40, supporting the assumed model (Δρ = ΔρWAL + Δρorb.) as the origin of the observed LMR.
As another check of the localization by the magnetic field, we have investigated Rxy as a function of B at various temperatures (Fig. 4(a)). Note that the curve is nonlinear at high temperatures (10 K ~ 50 K) in contrast to the linear dependence at low temperatures (below 10 K). The nonlinear Rxy vs. B curve indicates the existence of multiple electron bands. By using the two-band model for ρ and Rxy41, we calculate n and μ of the two bands, (n1, μ1) and (n2, μ2), which are plotted in Fig. 4(b,c), respectively. The curve at 2 K is nearly linear resulting in erroneous values of n2 and μ2, which are reflected by big error bars. Nevertheless, it is apparent that n2 consistently decreases resulting in ~103-fold reduction with lowering T from 50 K to 2 K. On the other hand, n1 increases by about one order with lowering T, leading to an overall reduction of the carrier density (n = n1 + n2). Furthermore, we have investigated the T-dependence of n under high magnetic field (±5 T) as shown in Fig. 4(d). Below 20 K, a drastic reduction of n(T)5T is observed in contrast to the continued increase of n(T)2T, which provides a clear evidence of the carrier localization induced by the magnetic field.
Figure 4.
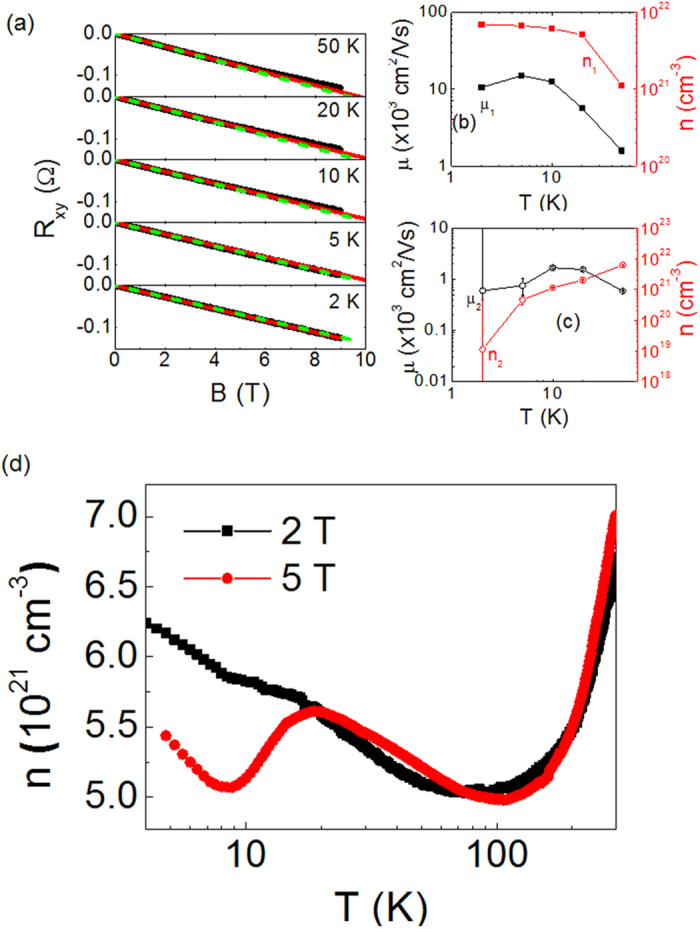
(a) Temperature dependence of Rxy vs. B curve for B// . Black, red solid lines, and green dashed line represent the experimental data, the fitting curve by two-band model, and the linear fitting curve in the range of [0, 2 T], respectively. (b,c) Temperature dependence of carrier density (n) and carrier mobility (μ) of the two bands calculated by fitting to two-band model. Error bars in (c) represent the standard deviation while they are smaller than the size of the symbol in (b). (d) Temperature dependence of n measured with B = ±2 T (black square) and ±5 T (red circle).
. Black, red solid lines, and green dashed line represent the experimental data, the fitting curve by two-band model, and the linear fitting curve in the range of [0, 2 T], respectively. (b,c) Temperature dependence of carrier density (n) and carrier mobility (μ) of the two bands calculated by fitting to two-band model. Error bars in (c) represent the standard deviation while they are smaller than the size of the symbol in (b). (d) Temperature dependence of n measured with B = ±2 T (black square) and ±5 T (red circle).
The resurgence of n(T)5T below 10 K is also intriguing, which might imply that another mechanism or new phase sets in at low temperatures under strong B-field. We have also investigated the magnetic properties to find a drastic increase in the magnetization (M) below 10 K and a little magnetic hysteresis at 5 K (see Supplemental Material S3). It seems to imply that the observed resurgence of n(T)5T below 10 K is associated with a possible emergence of an unprecedented electronic and magnetic phase in the heavily-doped Nb:STO films.
The above results, that are, (1) VRH-dominated transport under strong magnetic field, (2) the MR described by the FH model for the WAL, and (3) decrease in n under strong magnetic field, seem to indicate that the large LMR observed in Sr(Nb0.2Ti0.8)O3 results from the interplay between a large classical MR due to the high carrier mobility and the localization effect due to strong spin-orbit coupling. As other possibilities, the role of inhomogeneity suggested by M. M. Parish and P. B. Littlewood29,30 is ruled out based on the observation of homogeneous distribution of components as confirmed by the SEM/EDX (see Supplemental Material S1). On the other hand, an interpretation in terms of the QLMR model is not ruled out supposing that Sr(Nb0.2Ti0.8)O3 should be a gapless material with a linear energy-momentum relation and have inhomogeneous carrier distribution. According to the QLMR model, the normalized MR,  , is known to approach to a constant value, which depends on the material, in the quantum limit and does not depend on T33. It has been tested and found to be true in our case up to 10 K (Figure S4 in the Supplemental Material). Therefore, we cannot rule out the QLMR although there are many evidences supporting the interplay between the classical MR and the WAL as the origin for the observed large LMR in heavily-doped Sr(Nb0.2Ti0.8)O3.
, is known to approach to a constant value, which depends on the material, in the quantum limit and does not depend on T33. It has been tested and found to be true in our case up to 10 K (Figure S4 in the Supplemental Material). Therefore, we cannot rule out the QLMR although there are many evidences supporting the interplay between the classical MR and the WAL as the origin for the observed large LMR in heavily-doped Sr(Nb0.2Ti0.8)O3.
To summarize, we have observed the non-saturating LMR at low temperatures (below 20 K) and MIT induced by magnetic field in heavily-doped Sr(Nb0.2Ti0.8)O3 epitaxial thin films grown on SrTiO3. In addition, this material is featured by very low electrical resistivity (~8 × 10−8 Ωcm at 1.8 K) and high carrier mobility (~14,000 cm2/Vs at 1.8 K), far exceeding an expectation obtained by an extrapolation from low Nb concentration regime. We propose that the LMR is associated with the interplay between the large classical MR due to high carrier mobility and the localization effect due to strong spin-orbit coupling. Conversely, it means that the investigated Sr(Nb0.2Ti0.8)O3 thin film possesses the high carrier mobility and the strong spin-orbit coupling simultaneously, which imply a long spin diffusion length and an ability to effectively modulate electron’s spin, respectively. Therefore, we believe that Sr(Nb0.2Ti0.8)O3 is a promising channel material for the application in spintronic devices although further exploration is needed into the heavily doped Nb:STO. A study on the dependence on the Nb concentration is ongoing, which will be presented in near future.
Additional Information
How to cite this article: Jin, H. et al. Large linear magnetoresistance in heavily-doped Nb:SrTiO3 epitaxial thin films. Sci. Rep. 6, 34295; doi: 10.1038/srep34295 (2016).
Supplementary Material
Acknowledgments
The authors thank Dr. Satoshi Okamoto for discussions and valuable comments. This work was supported by the Korea Institute of Science and Technology (KIST) through 2E26420 and 2E26370. B.H.P. was supported by the National Research Foundation of Korea (NRF) grants funded by the Korea government (MSIP) (No. 2013R1A3A2042120). S.S.A.S. acknowledges the support of National Science Foundation grant DMR-1454200 for sample synthesis.
Footnotes
Author Contributions H.J. and S.L. conceived the experiment, synthesized the sample by PLD, and performed electrical characterization. K.L., S.-H.B., B.H.P., J.-S.K. and S.S.A.S. contributed to the fabrication of heavily-doped Nb:STO thin films. B.-k.C. and C.K. contributed to the measurement and analysis of magnetotransport properties. S.Y. and B.J.S. contributed to the measurement and analysis of the magnetic properties. H.J., S.S.A.S. and S.L. wrote the manuscript with discussions and improvements from all authors.
References
- Brinkman A. et al. Magnetic effects at the interface between non-magnetic oxides. Nat Mater 6, 493–496, doi: http://www.nature.com/nmat/journal/v6/n7/suppinfo/nmat1931_S1.html (2007). [DOI] [PubMed] [Google Scholar]
- Ohtomo A. & Hwang H. Y. A high-mobility electron gas at the LaAlO3/SrTiO3 heterointerface. Nature 427, 423–426 (2004). [DOI] [PubMed] [Google Scholar]
- Reyren N. et al. Superconducting Interfaces Between Insulating Oxides. Science 317, 1196–1199, 10.1126/science.1146006 (2007). [DOI] [PubMed] [Google Scholar]
- Ohtomo A., Muller D. A., Grazul J. L. & Hwang H. Y. Artificial charge-modulationin atomic-scale perovskite titanate superlattices. Nature 419, 378–380 (2002). [DOI] [PubMed] [Google Scholar]
- Jalan B., Stemmer S., Mack S. & Allen S. J. Two-dimensional electron gas in δ-doped SrTiO3. Physical Review B 82, 081103 (2010). [Google Scholar]
- Frederikse H. P. R. & Hosler W. R. Hall Mobility in SrTiO3. Physical Review 161, 822–827 (1967). [Google Scholar]
- Liu Z. Q. et al. Reversible room-temperature ferromagnetism in Nb-doped SrTiO3 single crystals. Physical Review B 87, 220405 (2013). [Google Scholar]
- Markovich M. et al. Epitaxial growth of Nb-doped SrTiO3 films by pulsed laser deposition. Applied Surface Science 258, 9496–9500, doi: http://dx.doi.org/10.1016/j.apsusc.2012.02.041 (2012). [Google Scholar]
- Takahashi K. S. et al. Electrostatic modulation of the electronic properties of Nb-doped SrTiO3 superconducting films. Applied Physics Letters 84, 1722–1724, doi: http://dx.doi.org/10.1063/1.1667279 (2004). [Google Scholar]
- Zhao T. et al. Highly conductive Nb doped SrTiO3 epitaxial thin films grown by laser molecular beam epitaxy. Journal of Crystal Growth 212, 451–455, doi: http://dx.doi.org/10.1016/S0022-0248(00)00307-9 (2000). [Google Scholar]
- Spinelli A., Torija M. A., Liu C., Jan C. & Leighton C. Electronic transport in doped SrTiO3: Conduction mechanisms and potential applications. Physical Review B 81, 155110 (2010). [Google Scholar]
- Ohta S. et al. Large thermoelectric performance of heavily Nb-doped SrTiO3 epitaxial film at high temperature. Applied Physics Letters 87, 092108, doi: http://dx.doi.org/10.1063/1.2035889 (2005). [Google Scholar]
- Gould H. & Ma S.-k. Low-Temperature Mobility of Heavy Impurities in Fermi Liquids. Physical Review Letters 21, 1379–1382 (1968). [Google Scholar]
- Schoofs F., Egilmez M., Fix T., MacManus-Driscoll J. L. & Blamire M. G. Impact of structural transitions on electron transport at LaAlO3/SrTiO3 heterointerfaces. Applied Physics Letters 100, 081601, doi: http://dx.doi.org/10.1063/1.3687706 (2012). [Google Scholar]
- Lytle F. W. X‐Ray Diffractometry of Low‐Temperature Phase Transformations in Strontium Titanate. Journal of Applied Physics 35, 2212–2215, doi: http://dx.doi.org/10.1063/1.1702820 (1964). [Google Scholar]
- Rimai L. & deMars G. A. Electron Paramagnetic Resonance of Trivalent Gadolinium Ions in Strontium and Barium Titanates. Physical Review 127, 702–710 (1962). [Google Scholar]
- Liu Z. Q. et al. Magnetic-field induced resistivity minimum with in-plane linear magnetoresistance of the Fermi liquid in SrTiO3 single crystals. Physical Review B 85, 155114 (2012). [Google Scholar]
- Kapitza P. The Study of the Specific Resistance of Bismuth Crystals and Its Change in Strong Magnetic Fields and Some Allied Problems. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences 119, 358–443, 10.1098/rspa.1928.0103 (1928). [DOI] [Google Scholar]
- Abrikosov A. A. Quantum linear magnetoresistance. EPL (Europhysics Letters) 49, 789 (2000). [Google Scholar]
- Hu J. & Rosenbaum T. F. Classical and quantum routes to linear magnetoresistance. Nat Mater 7, 697–700 (2008). [DOI] [PubMed] [Google Scholar]
- Wang X., Du Y., Dou S. & Zhang C. Room Temperature Giant and Linear Magnetoresistance in Topological Insulator Bi2Te3 Nanosheets. Physical Review Letters 108, 266806 (2012). [DOI] [PubMed] [Google Scholar]
- Wang W. et al. Large Linear Magnetoresistance and Shubnikov-de Hass Oscillations in Single Crystals of YPdBi Heusler Topological Insulators. Scientific reports 3, 2181, 10.1038/srep02181 http://www.nature.com/articles/srep02181#supplementary-information (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman A. L. et al. Quantum Linear Magnetoresistance in Multilayer Epitaxial Graphene. Nano Letters 10, 3962–3965, 10.1021/nl101797d (2010). [DOI] [PubMed] [Google Scholar]
- Novak M., Sasaki S., Segawa K. & Ando Y. Large linear magnetoresistance in the Dirac semimetal TlBiSSe. Physical Review B 91, 041203 (2015). [Google Scholar]
- He L. P. et al. Quantum Transport Evidence for the Three-Dimensional Dirac Semimetal Phase in Cd3As2. Physical Review Letters 113, 246402 (2014). [DOI] [PubMed] [Google Scholar]
- Lifshitz I. M. & Peschanskii V. G. Galvanomagnetic Characteristics of Metals with Open Fermi Surfaces. Sov. Phys. JETP 8, 875–883 (1959). [Google Scholar]
- Abrikosov A. A. Gal Vanomagnetic Phenomena In Metals In The Quantum Limit. Sov. Phys. JETP 29, 746–753 (1969). [Google Scholar]
- Xu R. et al. Large magnetoresistance in non-magnetic silver chalcogenides. Nature 390, 57–60 (1997). [Google Scholar]
- Abrikosov A. A. Quantum magnetoresistance. Physical Review B 58, 2788–2794 (1998). [Google Scholar]
- Parish M. M. & Littlewood P. B. Non-saturating magnetoresistance in heavily disordered semiconductors. Nature 426, 162–165 (2003). [DOI] [PubMed] [Google Scholar]
- Parish M. M. & Littlewood P. B. Classical magnetotransport of inhomogeneous conductors. Physical Review B 72, 094417 (2005). [Google Scholar]
- Mott N. F. Conduction in non-crystalline materials. Philosophical Magazine 19, 835–852, 10.1080/14786436908216338 (1969). [DOI] [Google Scholar]
- Qu D.-X., Hor Y. S., Xiong J., Cava R. J. & Ong N. P. Quantum Oscillations and Hall Anomaly of Surface States in the Topological Insulator Bi2Te3. Science 329, 821–824, 10.1126/science.1189792 (2010). [DOI] [PubMed] [Google Scholar]
- Xiong J. et al. Quantum oscillations in a topological insulator Bi2Te2Se with large bulk resistivity (). Physica E: Low-dimensional Systems and Nanostructures 44, 917–920, doi: http://dx.doi.org/10.1016/j.physe.2011.09.011 (2012). [Google Scholar]
- Checkelsky J. G. et al. Quantum Interference in Macroscopic Crystals of Nonmetallic Bi2Se3. Physical Review Letters 103, 246601 (2009). [DOI] [PubMed] [Google Scholar]
- Altshuler B. L., Aronov A. G. & Khmelnitsky D. E. Effects of electron-electron collisions with small energy transfers on quantum localisation. Journal of Physics C: Solid State Physics 15, 7367 (1982). [Google Scholar]
- Fukuyama H. & Hoshino K. Effect of Spin-Orbit Interaction on Magnetoresistance in the Weakly Localized Regime of Three-Dimensional Disordered Systems. Journal of the Physical Society of Japan 50, 2131–2132, 10.1143/JPSJ.50.2131 (1981). [DOI] [Google Scholar]
- Hu J., Liu J. Y. & Mao Z. Q. Spin–orbit coupling and weak antilocalization in the thermoelectric material β-K2Bi8Se13. Journal of Physics: Condensed Matter 26, 095801 (2014). [DOI] [PubMed] [Google Scholar]
- Hikami S., Larkin A. I. & Nagaoka Y. Spin-Orbit Interaction and Magnetoresistance in the Two Dimensional Random System. Progress of Theoretical Physics 63, 707–710, 10.1143/ptp.63.707 (1980). [DOI] [Google Scholar]
- Caviglia A. D. et al. Tunable Rashba Spin-Orbit Interaction at Oxide Interfaces. Physical Review Letters 104, 126803 (2010). [DOI] [PubMed] [Google Scholar]
- Ashcroft N. W. & Mermin N. D. Solid state physics 240 (Holt, Rinehart and Winston, 1976). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.