Can we believe the DAGs? A comment on the relationship between causal DAGs and mechanisms

Abstract

Directed acyclic graphs (DAGs) play a large role in the modern approach to causal inference. DAGs describe the relationship between measurements taken at various discrete times including the effect of interventions. The causal mechanisms, on the other hand, would naturally be assumed to be a continuous process operating over time in a cause–effect fashion. How does such immediate causation, that is causation occurring over very short time intervals, relate to DAGs constructed from discrete observations? We introduce a time-continuous model and simulate discrete observations in order to judge the relationship between the DAG and the immediate causal model. We find that there is no clear relationship; indeed the Bayesian network described by the DAG may not relate to the causal model. Typically, discrete observations of a process will obscure the conditional dependencies that are represented in the underlying mechanistic model of the process. It is therefore doubtful whether DAGs are always suited to describe causal relationships unless time is explicitly considered in the model. We relate the issues to mechanistic modeling by using the concept of local (in)dependence. An example using data from the Swiss HIV Cohort Study is presented.

1 Introduction

Causal inference has become a topic of major importance in statistics. There is now a large body of literature on causal modeling in the statistical and epidemiological literature. On the other hand, we see the emergence of fields such as systems biology which aim at understanding biological mechanisms, for example, with the purpose of suggesting useful medical treatments. Here, and in the rest of the paper, “mechanisms” is defined as an explanation of the internal dynamics of a given system using chemical, biological, or physical laws; this is in contrast to a statistical understanding, which “merely” attempt to describe how an exposure is related to a given outcome. Medications are often suggested on the basis of mechanistic reasoning, for example, the angiogenesis inhibitors which inhibit the growth of blood vessels. These have been proposed as a treatment against cancer, depriving the tumor of nutrition. The statistical analysis comes from clinical trials which in this case have been somewhat disappointing although some angiogenesis inhibitors are in use. ¹ The mechanistic thinking can also be seen in other fields, such as social science and economics.

Baron and Kenny² express very well the idea of causal mediation as “the generative mechanism through which the focal independent variable is able to influence the dependent variable of interest.” Causal effects should be expected to be mediated by mechanisms that operate in a continuous manner; that is, there must be some process that ties the cause and the effect together. An example could be the angiogenesis inhibitor mentioned above, or, alternatively, a medication that blocks a receptor whereby it decreases the blood pressure. The expected presence of continuity can be expressed by saying that a true model should be local in time, meaning that changes can take place in any small time interval. This idea of locality might correspond to considering differential equations of a deterministic or stochastic kind. Just like ordinary differential equations play an important role in describing physical systems, stochastic differential equations are important for biology where randomness is more strongly present due to the complexity of biological systems. More broadly, there is a concept of local dependence^3–5 that has been recently much discussed and that seems a possible tool for formulating stochastic mechanisms.

The process describing a mechanistic relationship is likely to be a complex type of process in most cases, but the idea here is that one might learn something from considering a simple process, namely a linear dynamic system. This is a special case of a stochastic differential equation which is a time-local presentation of the process.

When formulating mechanistic or causal models as time-continuous stochastic systems, the issue arises on how this is related to the causality concept based on directed acyclic graphs (DAGs) and counterfactuals. DAGs equipped with probability distributions to define Bayesian networks, describe the relationship between variables measured at various discrete times (the times being usually unspecified in the DAG itself). The arrows connecting the nodes in Bayesian network represent conditional dependencies; nodes that are not connected are conditionally independent (more precisely defined by a Markov property⁶). Pearl⁶ (Definition 1.3.1) defined causal Bayesian networks by specifying rules for the effects of interventions. We shall show, in a highly simplified setting, that the conditional independence relationships between variables in a time-discrete setting do not generally correspond to the relationship at an infinitesimal or system level.

For illustration, we wish to use an example discussed by Cole and Hernán.⁷ Here they give an introduction to the estimation of direct and indirect effects and the difficulties in separating out these effects. They consider a case where aspirin treatment is given to reduce the risk of myocardial infarction, and the issue is to consider to what extent the effect of aspirin is mediated through the level of platelet aggregation which is measured. This is discussed in terms of causal DAGs. However, these DAGs do not represent the process aspects of a variable such as platelet aggregation. It is possible that the whole effect of aspirin is mediated through platelet aggregation, but if one just has limited observation of this process, like the single measurement apparently considered by Cole and Hernán,⁷ one could still estimate a considerable direct effect, also in the absence of confounders. We wish to make the following points for a time-continuous linear dynamic system:

• We assume that a system of differential equations is a mechanistically correct representation of the system (as is often assumed in natural science, e.g. the predator–prey equations). The relationship can be illustrated by a local independence graph as defined below.

• When considering the same system at discrete times, the graph will get additional connections due to coarser observations. Hence, there is less clear correspondence to a causal understanding. Time-discrete systems will tend to fill out with new arrows in the DAG, without this relating to causal connections in a mechanistic sense.

• When considering sampling from the process at discrete times, which is the type of data one may normally have in epidemiology, the conditional independence relationships generated by the sampled variables may have an even less clear relationship to any causal connection, as we shall show in the simulations.

Note that this paper is intended as a commentary on the extensive use of Bayesian networks and DAGs in causal inference. The aim is to show that the use is not unproblematic. This does not mean that causal DAGs represent a useless idea; on the contrary, they can certainly be very suggestive as to the presence of biases as illustrated, for instance, by the examples of Cole and Hernán.⁷ But one should be cautious in their application. Given the extensive and increasing use of ideas such as causal DAGs it is important to be aware of the limitations. We do not formulate detailed alternative models, but give simple examples to illustrate our points.

We are of course aware that criticism of causal models may not be limited to causal DAGs. However DAGs are very popular, not least in epidemiology. They have an immediate appeal by their suggestive graphical structure. We have therefore chosen to focus on causal DAGs in this paper.

It is important to note that causal models are different from statistical models. A model that fits an observational scenario is causal for a hypothetical intervention if a prescribed perturbation of this model would fit the counterfactual situation where this intervention had been carried out. This corresponds to the modularity assumption given, for example, by Pearl.⁶

Causal formulations of stochastic process models are given in two recent papers.^8,9 These formulations are intervention based following the lead of Pearl.⁶

Finally, a note on notation. The term “causal DAG” is used by Hernán and Robins¹⁰ and Dawid.¹¹ We use this throughout, but sometimes also follow Pearl⁶ and say “causal Bayesian network.”

2 Causal DAGs

2.1 The benefits

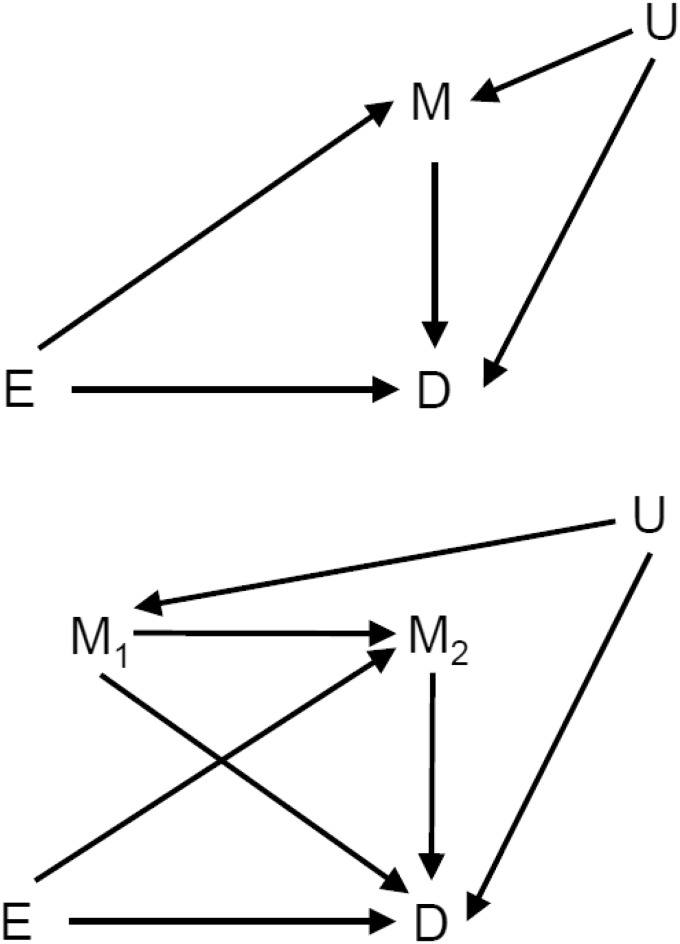
One important use of causal DAGs is to clarify the limitations and possibilities of what can actually be estimated from the data. A classical case is that of estimating direct and indirect effects in the presence of unmeasured confounders as noted, for instance, by Cole and Hernán.⁷ An important piece of knowledge in this area is that direct effects cannot in general be estimated when there is an unmeasured confounder between mediator and outcome. An illustration is given in the upper panel of Figure 1 where E denotes treatment, M is mediator, D is outcome, and U is the unmeasured confounder. An application of the elegant collider and backdoor rules as presented by Pearl⁶ tells us that the direct effect cannot be isolated. However, this may change when more measurements are taken. In the lower panel of Figure 1, there is a DAG showing the situation when the mediator is measured twice and the confounding is only mediated through the initial value of the mediator. In this case, following Pearl’s rules, all effects of the unmeasured confounder U is blocked by conditioning on the variable M₁, and so direct and indirect effects can be estimated.

Figure 1.

Illustration of causal connections in mediation analysis in the face of unmeasured confounders (U).

The upper panel depicts a setup without repeated measures while the lower panel depicts a setup with the mediator being measured twice. In the upper panel, the direct and indirect cannot be estimated separately while this can be done in the lower panel.

The point here is to show that when considering developments over time the picture may be quite different from that shown by a static DAG. The relationship between the underlying system and the actual observations taken may be complex and may vary from case to case. Moreover, the issue of mediation is really a process aspect; when something is “mediated” it is through a process taking place over time. How then can we know that a putative DAG between some measurements of the process is really meaningful in a causal sense?

2.2 The difficulties

A rather critical account of the use of causal DAGs was presented by Greenland.¹² He states that “causal inference from observational data using formal causal models remains a theoretical and largely speculative exercise (albeit often presented without explicit acknowledgement of that fact).” Models, especially those presented in terms of DAGs, are often highly simplified, while realistic models would contain a mass of arrows as indicated in Figure 2 of Greenland’s paper. Greenland’s paper is not entirely critical, but clearly intends to infuse some realism into causal inference.

Figure 2.

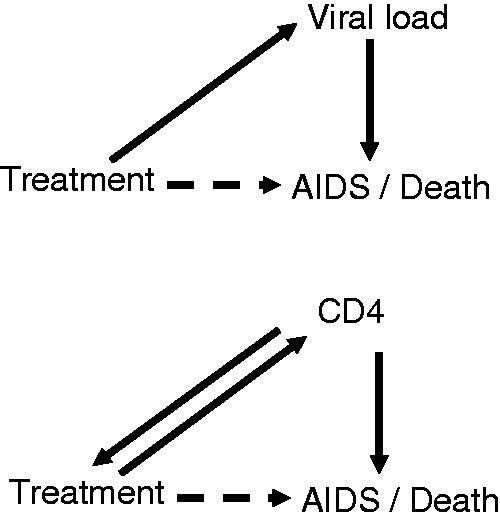
Illustration of local dependence between HAART treatment, viral load or CD4, and AIDS/death.

Full lines indicate direct mechanisms while dashed lines indicate indirect effects operating through other variables. The upper panel shows how the treatment works by influencing (reducing) viral load. The lower panel does the same for CD4 count, also including the issue that start of treatment may depend on CD4 count. HAART: highly active anti-retroviral treatment.

Also, in his paper “Beware of the DAG!” Dawid¹¹ presents a critical attitude toward the DAG as a universal tool for understanding causality. In particular, he stresses the need for prior justification of the DAG.

The aim of the present paper is to bring the discussion further by focusing on the aspect of time. It is rather obvious that causality operates in time, and the moment this aspect is ignored (as it often, but certainly not always, is) the use of “causal DAGs” becomes unclear and problematic. Partly, this concerns the question of what causality can be said to influence. The nodes presented in DAGs are often measurement of some quantities taken at some specific times as well as one or more interventions. However, causal influences and interventions have the main characteristic of producing changes in measured quantities, or producing events (consider e.g. the angiogenesis inhibitors mentioned above which are intended to destroy tumors). And quite often the nodes in the DAGs are neither of these.

In general, DAGs are simplifications of the real relationships that exist. Whether true edges are correctly reflected in the simplified DAGs may be formulated as a question of to what extent the edges are unchanged under marginalization, since a number of potential measurements are necessarily left out. A model is collapsible if relationships are preserved and there is a good deal of theory about this, see for example, Xie and Geng.¹³ However, except for special cases, we would not expect relationships to be preserved.

The definition of a causal Bayesian network as given in Definition 1.3.1 in ref. [6] specifies both distributions and the effect of interventions. Hence, the causal DAG contains both assumptions on causal relationships and on conditional independencies; both these aspects must hold. When applying causal DAGs in practice the epidemiologist, say, must be able, on the basis of usually limited evidence, to specify a DAG that fulfills to a reasonable extent the strong assumptions of both unmeasured and measured variables.

3 Local independence and causality

An important concept which has recently received increasing attention is that of local independence.^3,4,14 Local independence is a concept that looks at how well future values of a process can be predicted by past. The concept focuses on local characteristics such as intensity processes for counting processes and drift coefficients for diffusion processes. The issue is to what extent these local characteristics depend functionally on past observations of processes. One may, for instance, consider a number of counting processes, say N₁(t), N₂(t) and N₃(t) with intensity processes λ₁(t), λ₂(t) and λ₃(t), where the intensity processes are defined as functions of the past.¹⁵ Then, N₃(t) is locally independent of N₁(t) and N₂(t) if λ₃(t) is functionally independent of these two processes. If, say, λ₃(t) is functionally dependent on N₁(t), then N₃(t) is locally dependent on N₁(t). This can be represented in a local independence graph. The concept of local (in)dependence is naturally tied to stochastic differential equations, and we shall return to this below.

There is also a relationship to mechanistic understanding,¹⁶ subject of course to completeness of observations (possible unmeasured confounder processes as usual being a problem). The concept of local independence is just as relevant for complex processes as for simple ones; it represents the natural extension of conditional independence (Bayesian networks) to a dynamic time-continuous framework.^3–5 A general definition is based on martingale theory.

Just as a Bayesian network, local independence is merely a statistical concept, but, in the sense of Pearl⁶ it can be made into a causal concept by specifying the effects of interventions. In fact, the question is whether local characteristics such as intensity processes have a structural interpretation. Let us consider a multivariate counting process. Then intervening on one of the processes shall not have any influence on the functional form of the intensities of the other processes (i.e. how the intensities depend on the sample paths of the processes). The same definition holds for local characteristics in general. For a study of causal models with local independence, see Røysland.⁸

This may be illustrated by using the do operator of Pearl.⁶ Let $\lambda (t;x,\dots )$ be an intensity process which is a function of time and of a number of covariates measured at baseline or at some other time prior to t. One of these covariates is x that could be, say, some treatment one wants to intervene on. Then we will have a causal model with a structural intensity process if

$$\lambda (t;x,\dots )=\lambda (t;\mathrm{do}(x),\dots )$$

where do(x) means that the value of x is determined by an intervention. Note that intensities and local characteristics are merely defined as predictive quantities, so the structural aspect is something that has to be added. This is analogous to the conditional probabilities of Pearl⁶ (Definition 1.2.1).

An illustration of local independence is given in Figure 2 which concerns treatment for HIV positive patients. The upper panel shows how treatment affects the risk of AIDS or death through influencing (reducing) the viral load. In addition, there may possibly be effects that take other paths, indicated by the dashed arrow. This diagram pictures a mechanistic relationship since it is well known that the treatment (denoted HAART) delaying HIV progression works through blocking the reproduction of virus. Note that the figure, although a DAG, is not a causal graph in the sense of, for example, Cole and Hernán⁷ since the nodes are stochastic processes. The influence between the processes is taking place continuously over time: treatment is locally independent on the other two processes, viral load is locally dependent on treatment, while AIDS /death is locally dependent on viral load, and also on treatment if the dashed arrow carries a non-zero influence.

The difference between DAGs and local independence graphs is made even clearer when considering the lower panel of Figure 2 which is no more a DAG, since there are two arrows between treatment and CD4. The CD4 T-cell count is a measure of the functioning of the immune system; this is influenced by treatment but also determines when treatment starts. Hence, we have a feedback system which again has a natural description as a local independence graph. (Note that treatment start would not only depend on CD4 but also on viral load and other relevant factors. However, there is often considerable emphasis on CD4 and that is why we focus on this here.)

Petersen et al.¹⁷ discuss the HIV issue in much detail and present a number of DAGs. It is not clear in their paper whether the nodes in the graphs are to be seen as single measurements or as processes, which would seem more natural. We suggest that when people attempt to draw causal diagrams it is often most natural to think of the nodes as processes and use local independence. That is because it would usually be some mechanistic structure that one is trying to express in the graph.

4 Mechanistic models

An alternative to the intervention-based, or counterfactual approach to causality, is a mechanistic view.¹⁸ One approach to thinking about mechanisms would be to make mathematical models akin to those known from physics, a natural tool being that of differential equations. In fields such as medicine, biology, and social science, differential equations do not have the canonical role that they do in physics, where they may embody deep natural laws, but still they represent a useful way of thinking. One recent example is the modeling of treatment effects on HIV infection presented by Prague et al.¹⁹ where they use differential equations to model the relationship between number of CD4 cells and virus concentrations. An excellent review showing the usefulness of differential equations in biology is given by Perelson.²⁰ A stochastic version will be used below, but first we point out connections to the concept of local (in)dependence.

4.1 A linear dynamic system

As an instructive example we shall consider linear stochastic differential equations; these have the advantage that explicit computations can be made. A simple example of a differential equation model for an output vector X(t) could be a linear system of the following kind

$$\text{d}X(t)=[A(t)(\mu (t)-X(t))+a(t)]\text{d}t+\sigma (t)\text{d}W(t),\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}X(0)=x$$ (1)

The differential equation specifies how the process X(t) changes over a short time interval. The change is dependent on the present value. More specifically, the change of X(t) in a short interval (t, t + dt) is determined by the external input vector a(t), and by internal input from $X(t)-\mu (t)$ through the matrix –A(t). Here, μ(t) is a point of balance such that the process will at any time have a tendency to drift toward this function. Moreover, dW(t) denotes a white noise process that introduces a random disturbance to the development of X(t). (W(t) is a Wiener process; see, e.g. Aalen et al.,¹⁵ for a brief introduction to this process and for a discussion of what the “derivative” dW(t) means in this context.) The matrix σ(t) gives the covariances of the noise process.

Stochastic differential equations have been suggested as models for biological pathways.^21–23 Realistic equations will often be more complex than the simple linear one described in (1), having non-linear components and error coefficient σ dependent on the process X(t). In order to better understand the structure we use the simple linear setting (1) here.

4.2 Example for illustration

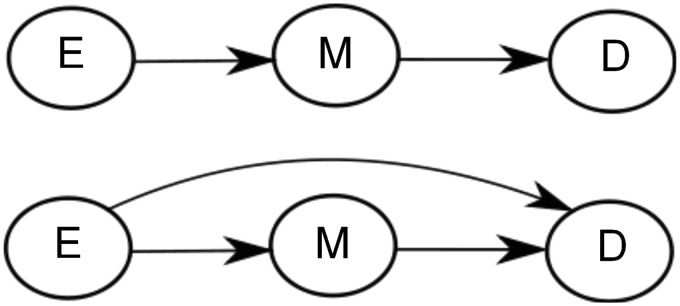
We shall relate the theoretical results of the paper to the following example concerning the relationships among aspirin, blood platelet aggregation, and risk of myocardial infarction. The example is adapted from Cole and Hernán.⁷ In their first DAG, Cole and Hernán assume that the (protective) effect of aspirin is mediated through a lowering of blood platelet aggregation and they describe this by using the DAG: $E\to M\to D,$ where E denotes aspirin treatment, M is the level of platelet aggregation, and D represents myocardial infarction.

Cole and Hernán⁷ describe a situation where the mediator, level of blood platelet aggregation, is measured without error and apparently is supposed to stay at a high or low level throughout the period of observation. We wish to construct a more realistic situation where there is variation over time in the mediator, partly due to real biological variation which will usually be present for biological parameters and partly due to measurement uncertainty. We extend the setup from Cole and Hernán⁷ by introducing processes for the different variables thus capturing their development over time. Let E(t) denote the treatment at time t, M(t) the level of platelet aggregation (measured in aspirin reaction units²⁴), D(t) the log-hazard for myocardial infarction at time t, and X(t) = (E(t),M(t),D(t)). In addition, assume that the system can be represented by a linear stochastic differential equation as (1). To match the values for platelet aggregation²⁴ and number of cases per 50,000 person years reported in Cole and Hernán⁷ we set

$$A=(10050021/1000-1/10001/2),\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}\mu =(0648\log (240/50,000)),\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}a=(E00),\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}x=\mu +(E{e}_1{e}_2)$$ (2)

where E is 0 when randomized to no-treatment and 1 otherwise and e₁ and e₂ are random normal variables corresponding to random individual levels of the blood platelet aggregation and log-risk, respectively. Finally, define the variance of the noise process W_t as σ = diag (0, 100, 1/100). The zeros in the upper right hand corner of the matrix A encodes that there is no causal effect of log-risk on treatment or platelet aggregation and no causal effect of platelet aggregation on treatment. Likewise, the zero in the lower left corner of the matrix A implies that there is no direct causal effect of treatment on log-risk. The positive numbers on the diagonal of A implies that all processes drift toward an equilibrium level when they get perturbed away from this equilibrium value. The signs of the remaining coefficients in the matrix A encode the direction of the effect. Finally, the values in μ are equilibrium values in the absence of treatment, which are chosen to match the observed values.^7,24 Thus, the aspirin process is constantly equal to the randomized treatment assignment, blood platelet aggregation is negatively affected by aspirin, and log-hazard is in turn positively affected by blood platelet aggregation. Note that mechanistically all effects of aspirin on log-hazard is mediated through blood platelet aggregation.

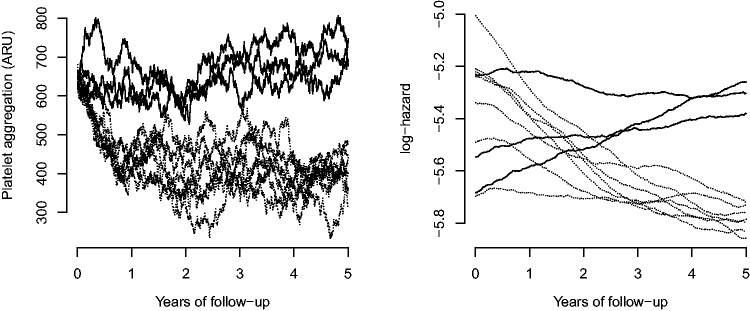
Figure 3 depicts the sample paths for blood platelet aggregation and log-hazard for 10 persons covering 5 years of follow up. It is evident how blood platelet aggregation for persons assigned to aspirin treatment evolves from the pre-treatment level to a new post-treatment level, but also has variation between persons and time points. In addition, we see that blood platelet aggregation varies much faster than log-hazard, which only changes significantly over long time spans. These complete paths would of course never be available to the researcher who would merely observe the process at a few distinct locations.

Figure 3.

Example sample paths for 10 persons.

Dashed lines correspond to people treated with aspirin and ARU is aspirin reaction units.

We do not intend our example to be a comprehensive description of the phenomenon, which would certainly be more complex, but we wish to use it for illustration of the relationship between a model explicitly incorporating time, and one which does not. In the simulation study, in Section 6, it will be explored how the speed with which treatment affects blood platelet aggregation influences the analysis.

4.3 Making graphs for linear systems: Local independence

For linear stochastic differential equations with a constant A there is a very simple interpretation of local (in)dependence. The relationships between components of X(t) may simply be read off the matrix A, such that, for instance, $X_{i(t)}$ is conditionally locally independent of $X_{j(t)}$, given the remaining processes, if A_i,j = 0.¹⁶ Note that local independence graphs need not be acyclic. In the aspirin example, A is defined in equation (2). This matrix A implies, for example, that process 3 (log-hazard) is locally independent of process 1 (treatment), but locally dependent of process 2 (blood platelet aggregation). Thus the influences can be depicted as $E\to M\to D.$

If the differential equation is structural in the sense that changing an element of A does not change the other elements, then the local (in)dependence relationships are causal.

5 Observing linear systems discretely

In most epidemiological studies, measurements are taken at discrete times. Imagine a simple situation where measurements are made at an initial and a final time. We shall then be interested in the change that takes place over this interval. Assume for simplicity that A(t) = A, a(t) = a and μ(t) = μ are constant over time. Then the expected value of the X process at time t is given by

$$\exp (-\mathrm{At})(x-A^{-1}a-\mu )+A^{-1}a+\mu =e^{-\mathrm{tA}}x-C$$

where $C=(e^{-\mathrm{tA}}-I)(A^{-1}a+\mu )$, see equation (6.6) in Karatzas and Shreve,²⁵ and $e^{-\mathrm{tA}}$ denotes a matrix exponential.

In this particular setting, the relationship between the local dynamics and the change over an interval is as the relationship between A and $e^{-\mathrm{tA}}$. In other words, the first of these matrices gives the local dependence relationship measured infinitesimally at a given time while the second matrix gives the corresponding relations over a discrete time interval of length t (where t is large enough for the process to have evolved, i.e. a non-infinitesimal interval). Hence, it is not at all obvious that analysis of finite interval changes gives a sufficient understanding of the dynamic structure. As an example, consider matrix A from the aspirin example and the corresponding matrix $e^{-3A}$ given below.

$$A=(10050021/1000-1/10001/2)$$ (3)

$$\exp (-3A)=(0.05000-21.80.00180-0.09470.0001380.223)$$ (4)

(where the three zeros without decimals are exact in the matrix $e^{-3A}$). The graphical local dependence structures for the time-continuous process corresponding to A and the DAG between X(0) and X(0 + 3) given by $e^{-3A}$, respectively, are shown in Figure 4

Figure 4.

Upper panel: local independence (i.e. immediate causation) graph for the Aspirin Example. Lower panel: corresponding graph when treatment (E), blood platelet aggregation (M), and log hazard (D) are measured sequentially and only once for instance at baseline for E, after 2 years of follow-up for M, and after 5 years for D (i.e. the classical DAG).

It is clear from Figure 4 that if we were only to see the process at two distinct time points, 0 and t, we would conclude that there was a direct effect from treatment to log-hazard. This is in contrast to the true causal structure/mechanistics given by A where all effect of treatment is mediated through blood platelet aggregation. Even though Cole and Hernán⁷ say that this is a simplified example it does represent a common feature when talking about DAGs, namely, that it is often not clear whether one talks about the phenomenon as such, extended over time, or about some measurement taking place at a given time.

In fact, when causal DAGs are justified the arguments given are often of a mechanistic type, and this fits with the time-local viewpoint represented by local independence graphs, but it may not fit with a DAG represented by discrete measurements. We assert that causality is most naturally interpreted at a time-local, infinitesimal level and indeed there are some papers in the causal inference literature which use time-continuous models.^26–28

Although we have only considered an example above, it is clearly a general feature that the local dynamic effects would be “smeared out” when considering a longer time interval. Discretization induces artificial connection that do not represent direct causal influences. If we assume that two different indirect paths are not perfectly balanced and thereby canceling each other (this assumption is in spirit equivalent to the faithfulness assumption) we have the following result: all nodes that can be reached in the local independence graph will be connected by a direct arrow in the time-discrete DAG. A discussion with a sketch of proof is given in the appendix.

We shall go one step further and assume that the observations are measurements of the processes taken at various discrete times, but possibly in a less orderly fashion than above. At a given time, some processes are measured while others may not be, corresponding to the reality of an actual follow-up study. The question is to what extent the causal structure can be derived from analysis of summary data from the processes. This is highly relevant since most real-life analyses are based on data from a few points in time.

So how is the relationship between the actual stochastic processes describing the “true” development over time and the sampled variables that go into the DAG? It follows from the theory of linear systems that measured variables will have a joint normal distribution, so partial correlations that tell us which nodes in the DAGs are actively connected, may be found through inversion of the covariance matrix. The elements of any such covariance matrix may be derived from equation (6.11) in Karatzas and Shreve.²⁵ To illustrate the complexity of the implied covariance matrix we will derive the explicit expression for two time points. Let the observed variables be the values of the process X at times s and t and let the matrices A, a and σ be constant. Let also V(0) be the covariance matrix of X(0). The covariances between the components of X(s) and X(t) may be found in the matrix:

$$\rho (s,t)=\exp (\mathrm{As})(V(0)+{\int }_0^{s\wedge t}\exp (-\mathrm{Au})\sigma {\sigma }^T\exp (-A^{T}u)\text{d}u)\exp (A^{T}t)$$

The covariance matrix of any set of variables measured at different times may be derived by using components from ρ(s,t) for the relevant values of s and t. By inverting this matrix one may further derive the partial correlations characterizing the measured variables. Notice that the conditional independence relationships expressed by d-separation for DAGs implies zero partial correlation; see Section 5.2 of Pearl.⁶

This procedure demonstrates the very complex relationship between the dynamic structure given by A and the covariance between sampled measurements from the process. Hence, one may get a very different impression of the relationship between the various processes depending on whether one knows the true dynamic structure, represented by A, or one just has the empirical results for a few measurements of the process. This is illustrated in the simulations in the next section.

6 Simulations

In this section we illustrate the considerations of the proceeding sections by two simulation studies.

6.1 The aspirin example

Consider again the aspirin example and recall that the local independence (i.e. mechanistic effects) diagram is given in the upper panel of Figure 4.

Assume now that we only make some discrete observations of the process: we observe the randomization (E) the blood platelet aggregation at either time 2.5 or 5 and log-risk at time 5. We have simulated a data set with 1000 observations, and regressed log-risk measured at time 5 jointly on aspirin treatment and blood platelet aggregation (the last measured either at time 2.5 or time 5) using multiple regression. Note that the results of Section 5 guarantee that any discrete set of observations will be normally distributed. In consequence, the non-parametrical and intervention-based definitions of effect of treatment will coincide with the simple association measures obtained by multiple regression. The results are presented in the first rows of Table 1.

Table 1.

Effect estimates from simulated data sets using the causal structure of the aspirin example.

Mediator measured at:	Time 2.5	Time 5
Setup 1 (aspirin example)
Mediator ($*{10}^{-3}$)	0.311 (0.047)	0.411 (0.46)
Exposure ($*{10}^{-3}$)	−352 (11)	−328 (11)
Total effect ($*{10}^{-3}$)	−426 (1.4)	−426 (1.4)
Mediated proportion	17%	23%
Setup 2
Mediator ($*{10}^{-3}$)	1.15 (0.034)	1.11 (0.028)
Exposure ($*{10}^{-3}$)	−126 (6.1)	−75.2 (6.5)
Total effect ($*{10}^{-3}$)	−289 (5.3)	−289 (5.3)
Mediated proportion	56%	74%
Setup 3
Mediator ($*{10}^{-3}$)	1.38 (0.032)	1.26 (0.027)
Exposure ($*{10}^{-3}$)	−76.2 (3.8)	−14.9 (4.6)
Total effect ($*{10}^{-3}$)	−190 (4.7)	−190 (4.7)
Mediated proportion	60%	92%

In setup 1, the parameter values are taken from the aspirin example while setup 2 and 3 have progressively slower speed of treatment effect on mediator. However, the total effect of treatment once treatment has taken full effect is the same in all setups. The table reports estimates from ordinary regression with standard errors in parentheses. The first two rows of each setup are from a joint regression of mediator and treatment on outcome, the third row is the total effect of treatment on outcome, and the fourth row presents the mediated proportion (i.e. how large a proportion of the total effect is mediated through the mediated). In the left column the mediator is measured at time point 2.5 (i.e. midway in the observation window) while in the right column the mediator is measured simultaneously with the outcome (i.e. at time point 5).

From the first row of Table 1 it would appear as if as much as 80% of the total effect of treatment on log-hazard is not mediated through blood platelet aggregation. However, since we know the true causal/mechanistic structure (i.e. matrix A) we know that in fact all effect of aspirin is mediated through blood platelet aggregation.

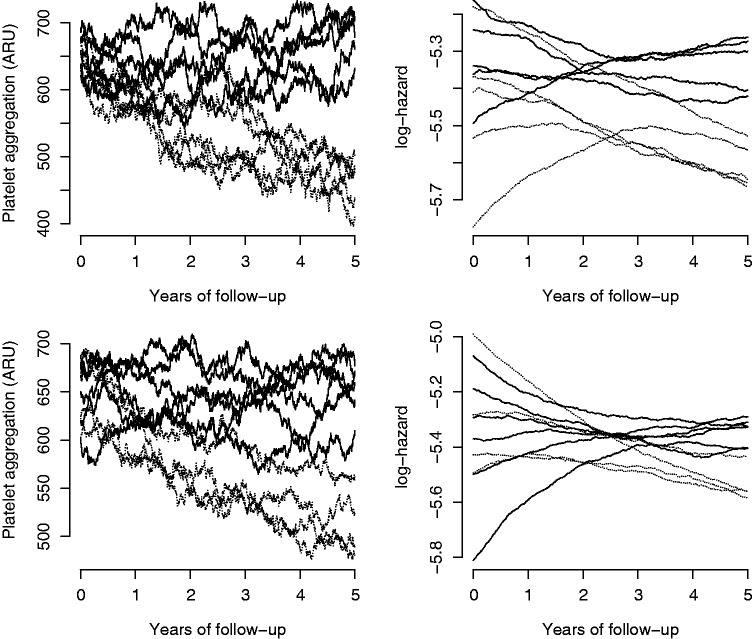
As is evident from Figure 3 the effect of treatment on mediator is very quick in the aspirin example. To explore how different speeds at which treatment affects the mediator can change the conclusions drawn from simple regression analysis we have also conducted two further simulation studies with slower adjustments speeds. These are presented as setups 2 and 3 in Table 1. Figure 5 illustrates possible sample paths from these setups and the A matrices are presented below. In setup 2, most of the effect of treatment on mediator has occurred within 3 years while in setup 3 the effect of treatment on mediator is not even completed at 5 years. All three simulation setups have the same effect of treatment once it has taken full effect, but the time span required for treatment to reach full effect differs.

$$A_{\text{Setup}2}=(100801/300-1/10001/2),\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}{A}_{\text{Setup}3}=(100401/600-1/10001/2)$$ (5)

Figure 5.

Simulated sample paths for 10 persons from either setup 2 (upper panel) or setup 3 (lower panel).

The causal structure is as in the aspirin example, but here the speed at which treatment affect the mediator is progressively slower. Dashed lines correspond to people treated with aspirin and ARU is aspirin reaction units.

By comparing the mediated proportions between setups 1, 2, and 3 from Table 1 it is evident that the slower the speed with which treatment affects the mediator the larger the mediated proportion appears. Likewise, the mediated proportion appears larger when the mediator is measured simultaneously with the outcome; in particular, when treatment only affects the mediator slowly. For all combinations of time of measurement and speed of treatment effect it appears as if there was a direct effect of treatment on outcome in spite of the fact that all of the effect is in fact passed through the mediator.

6.2 A second simulation of a linear system

We shall simulate a slightly more general example of a linear dynamic system. For this purpose we use an Euler scheme⁹; that is, we consider a time-discrete approximation based on using discrete units of length 0.1 over a time interval from 0 to 10. We shall consider a situation where we measure the processes only at certain times, and then consider whether regression analysis of the outcome (final value) on previous measurements would reflect the true underlying relationship between the processes. The linear system is supposed to represent the actual mechanism at work, but as in most practical settings we just have some scattered discrete observations of the processes.

Consider a linear system with matrix

$$A=-(0000100001000010)$$

and with a(t) = 0, μ(t) = 0, and σ(t) equal to the identity matrix. The model would correspond to the following local independence diagram:

$$X_1\to X_2\to X_3\to X_4$$

Assume now that we make the following discrete observations of the process: we observe the process at times 2, 5, and 10. More specifically, we have the following observations: X₁(2), X₂(5), X₃(5), and X₄(10), where the first variable could be a treatment, the next two mediators, and the last one outcome. We have simulated 1000 replications and run a linear regression analysis with X₄(10) as dependent variable and the other three variables as the independent ones. This gives the following regression coefficients with standard errors in parentheses: −3.93 (1.19), 20.93 (0.41), and 4.87 (0.20). Hence, X₂(5) appears to have a much stronger direct effect on the outcome than X₃(5), which does not fit with the mechanistic view given by the continuous time process. Furthermore, X₁(2) yields a negative effect which goes against the local independence diagram, and might presumably lead to a wrong intervention if interpreted as a causal effect.

This example shows that discrete measurements may not show the true underlying dynamic structure. The use of linear regression is equivalent to consider partial correlations which are in this case all non-zero; in fact, the partial correlation of X₁(2) and X₄(10) given the two other variables equals −0.104, and for X₂(5) and X₄(10) the partial correlation is 0.853.

7 Analyzing data from the Swiss HIV Cohort Study

7.1 Statistical analysis

We shall illustrate the ideas here by analyzing data from the Swiss HIV Cohort Study. This is an ongoing multicenter study following up HIV infected adults aged 16 or older.²⁹ The data are organized in monthly intervals, with measures of CD4 cell counts, HIV-1 RNA (viral load – we shall use the brief term RNA here), hemoglobin (HEM), and a number of other clinically relevant measures. Laboratory measurements are collected every 3 months on average.

As an illustration we want to explore how the RNA, CD4, and HEM processes affect each other. We have used data from 1996 to 2003 and only looked at individuals on “highly active anti-retroviral treatment” (HAART), setting the time scale to months since treatment initiation. Data from 717 individuals are included. Maximum observation time is set to 6 years. The RNA, CD4, and HEM are not measured each month, and we used linear interpolation to fill in the gaps.

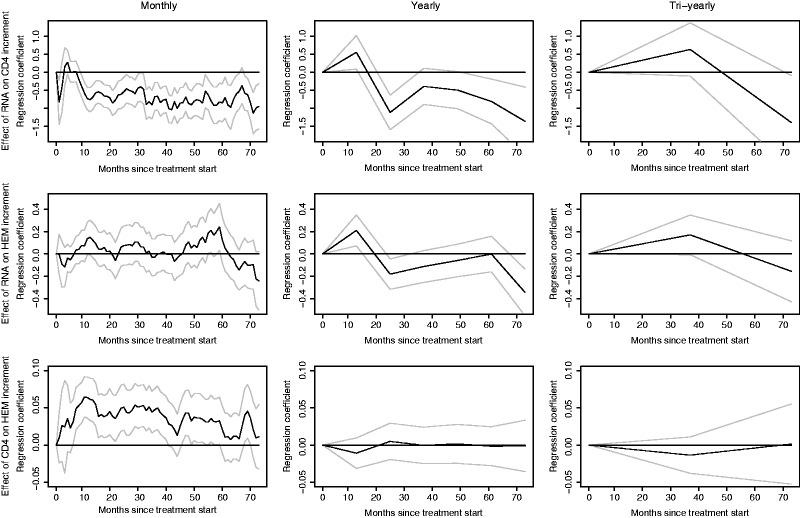
We analyze the relationship between RNA, CD4, and HEM by doing three linear regressions at each time point. We use the increment (the change) of RNA, CD4, and HEM as our three dependent variables and adjust for lagged (i.e. measured at previous time) and baseline values of RNA, CD4, and HEM. The same collection of the independent variables was used in all three regressions. The results of the analyses are given in Table 2. We do not report the effects of the processes on their own increments, since it is the cross-effects we are interested in. Table 2 shows that all cross-effects are non-significant apart from the effect from RNA to CD4 and from CD4 to HEM. Thus, we get a clear direction of how these variables affect each other; that is, RNA to; CD4 to HEM. This confirms the direction which would be expected for individuals on treatment. A part of the results is shown in the first column of Figure 6. The significant effects of RNA on CD4 and from CD4 to HEM are clearly demonstrated while the absence of a direct effect from RNA to HEM is also clear.

Table 2.

Qualitative results of regression analysis of increments on past values of HIV-1 RNA, CD4 count, and hemoglobin.

		Present increment
		RNA	CD4	HEM
Past value	RNA	–	negative	n.s.
	CD4	n.s.	–	positive
	HEM	n.s.	n.s.	–

HEM: hemoglobin. The effects of each process on increments of the other processes are shown. RNA affects CD4, and CD4 affects HEM, but all other effects are non-significant (n.s.).

Figure 6.

Analysis of increments of CD4 and HEM based on repeated regression analyses with lagged and baseline values of RNA, CD4, and HEM as independent variables. Analyses shown for monthly, yearly, and tri-yearly values from left to right.

Next, we reduce the time resolution of the data to see what the effect is. Instead of using monthly data points, we now use yearly or tri-yearly data points (and redefine increments and lagged values correspondingly). The results are given in columns 2 and 3 of Figure 6. From these results we see not only how the picture clearly loses detail as the time resolution gets lower, but also how the effects gets more and more smeared out (see plots for RNA to CD4 and CD4 to HEM). We also see how the direct effect (RNA to HEM), which was non-existing using the fine time-resolution data, seems to appear more, although definitive conclusions cannot be drawn due to estimation uncertainty.

7.2 Discussion of the HIV example

What does this analysis tells us? Firstly, the number of variables included is very limited and we can obviously not expect to get a detailed picture of mechanistic relationships. Nevertheless, it is interesting that the analysis gives the expected direction of the effects between the variables. The treatment is known to strongly reduce the viral load (RNA), which then improves the immune system (CD4). The effect of CD4 on HEM is also well established; patients with low CD4 have low HEM.³⁰ One way in which the pathway indicated (RNA to CD4 to HEM) could plausibly act is via other/opportunistic infections or low-CD4-associated neoplastic diseases which in turn can cause anemia (i.e. the mechanism would extend to e.g. “Virus Load to CD4 to Opportunistic Infection to Hemoglobin”). It should be noted, however, that it is also conceivable that viral RNA (or at least HIV-infected cells) cause directly anemia (i.e. via autoantibodies against erythropoietin). So, direct effects cannot be precluded although statistically they appear unimportant here.

It is also clear that the establishment of a variable (here CD4) as a statistical mediator may have different interpretations. It may be an actual mediator in a biological sense, but it may also conceivably represent other processes that are closely associated.

The medication Zidovudine is known from earlier to have a negative effect on HEM. For some patients, Zidovudine may be a part of their HAART treatment. We do not have information in our data as to which patients have received this treatment, and can therefore not include Zidovudine in our analysis.

Clearly, our analysis is simplified and presented here as an example. Nevertheless, it shows the power of a statistical analysis when data are collected frequently over time. It also shows very clearly that effects are becoming diluted and unclear when there is a low time resolution.

8 Recovering the immediate causal structure

Until now, we have discussed how the mechanistic structure given by local independence graphs and stochastic differential equations is often obscured when we only get to observe the process at a few time points. We will also mention the existence of techniques which allow us to recover the finer mechanistic structure from discrete observations of the process. Efficient estimation of stochastic differential equations (both simple linear models as the ones considered in this paper and highly complex non-linear models) is an active field of research within both pure statistics and mathematical finance; see for instance refs [31, 32] and the many references therein. Note that detailed data may be needed in order to efficiently estimate these models. Such data are also available in a medical setting, for instance, in neuroscience and cardiology (EEG, ECG, and others). One example is the study in Barrett et al.³³

The point of the modeling in this paper is that causal structure has a time-local character, the cause–effect relationship should be thought of as continuous over time. Clearly the possibility of estimating this immediate causal structure, that is causal effects occurring over short time intervals, is much better if the data represent detailed follow-up over time of a number of individuals. Many studies are of this nature, for example, clinical trials where clinical parameters are measured regularly and events of relevance are registered with exact dates. Even though clinical data will not normally be measured continuously, quite frequent measurement will also be very useful for uncovering causal structure. What is meant by “quite frequent” will depend very much on the setting, varying from truly continuous measurements in an EEG or ECG study to, say, a cholesterol measurement every 6 months in a clinical trial for heart disease taking place over many years. In epidemiology, registry data give more or less continuous information of relevance, such as the Norwegian Prescription Database where all prescriptions are registered for each individual. In the Nordic countries, unique personal identification numbers allow the linking of databases and registries to produce detailed life histories for individuals, which can then be analyzed.

When detailed life histories are observed, statistical models which are similar in nature to equation (1) may be written up. If the data are discrete measurements at regular times (e.g. quality of life measurements), then one could use a vector version of Farewell’s linear increments model:

$$\Delta X(t)=A(t)X(t-1)+\varepsilon (t)$$ (6)

where ΔX(t) is the increment $X(t)-X(t-1)$. Dynamic statistical analysis of such models is given by Diggle et al.,³⁴ and Aalen and Gunnes.³⁵ This model was used for estimating the above HIV data. As has been documented in the present paper, we cannot in general expect to get a complete picture when observations are discrete but the closer we are to observing the actual processes over time, the more correct our picture will be.

When events are registered continuously over time, then an additive hazards model^15,36 would be a natural correspondence to equation (1). The hazard rate is then defined by a linear regression model

$$\lambda (t)={\beta }_0(t)+{\beta }_1(t)z_1(t)+\dots +{\beta }_p(t)z_p(t)$$ (7)

Here the coefficients are arbitrarily varying over time, the model is completely non-parametric thereby allowing arbitrary changes in structure. Combining the models (6) and (7) allows the construction of dynamic path models15,37where a series of DAGs can be defined more or less continuously over time, making estimation of immediate structure a more likely possibility.

9 Discussion

There is no doubt that causal DAGs are very useful for understanding various types of biases, such as selection bias and confounding. However, in this article, we have shown that the view of DAGs as a strict representation of causal relationships can be problematic. In particular, we have pointed out that using DAGs for understanding causal connections is entirely dependent on the way measurements are made. If there are just measurements at a few times, then the conditional independence relationships in the data may bear no similarity to the actual causal structure. In addition, we have pointed out that the continuous evolution of most biological processes implies that great care must be exercised when arguing for a specific DAG; in particular, mechanistic arguments can be misleading if the variables in the produced DAG are only measured at specific time points. The (immediate) practical advice of our paper is that the continuous time nature of the world should be remembered when constructing DAGs.

We have demonstrated our points through simulations and by the use of an actual data set. Our simulation of the aspirin example showed that the most correct picture from the DAG was forthcoming when treatment acted slowly on the mediator. This was surprising to us since we had expected that for a fast-acting treatment the relationships should be less obscured. It is possible that uncertainty in the mediator may produce an apparent direct effect and that this, counter-intuitively, is strongest in the fast-acting case. This shows the importance of simulations to teach about how “causal” DAGs may relate to actual mechanisms. The second simulation demonstrates that the partial correlations giving the conditional dependence relationships may have no connection with the actual causal structure.

Finally, the HIV example shows that data collected at relatively brief time intervals can give what presumably would be a reasonably correct picture of the relationships, while more coarse data obscure the results considerably.

In general, the idea that prior causal knowledge can be easily encoded in DAGs is not obviously true. For example, Hernán et al.³⁸ state, “Causal diagrams are a useful way to summarize, clarify, and communicate one’s qualitative beliefs about the causal structure.” But if these diagrams are supposed to be causal Bayesian networks, as suggested by Hernán and Robins,¹⁰ Pearl,⁶ and others, they may not have a simple relationship to any intuitive causal understanding.

Maier et al.³⁹ state, “the directed acyclic graph (DAG) has been shown to be sufficient to represent causal knowledge.” Pearl⁴⁰ states, “To communicate substantive causal knowledge the potential outcome analyst must express causal assumptions as constraints on P (the observational distribution) usually in the form of conditional independence assertions involving counterfactual variables.” But, again, we will assert that conditional independence (with the assumptions about interventions) may not necessarily be a useful way of expressing causality because it depends on the specific measurements that are being made from the process.

The problem is a lack of precision. The discrete observations in a DAG can never fully capture the underlying time-continuous causal processes, and hence conditional independence in a DAG can rarely be identified with causal structures. An example where the time-continuous nature of the involved processes is of particular importance is the technique of instrumental variables,⁴¹ which is being evermore used in epidemiology. In instrumental variables, an auxiliary variable (the instrument), which only affects the outcome thorough its influence on the exposure, is used to overcome unmeasured confounding of the exposure–outcome relationship. However, if the exposure is in fact a process evolving over time the arguments of this paper show that the crucial assumption of the instrument only affecting the outcome through the measured exposure fails since there will be a direct effect of the instrument on the outcome. Thus, estimates obtained by instrumental variables are potentially biased in this case.

In this paper, we have employed a linear stochastic differential equation for the true causal structure. We suggest that epidemiologists should be more clear about the role of time when postulating causal structures in terms of DAGs. In practice, we suggest that epidemiological studies include considerations about a reasonable continuous time model (if the model employed in this paper is too simple) and then examine which estimation techniques are available.

Appendix: How discretization influences direct and indirect effects

Analysis of direct and indirect effects will be an especially delicate matter when observations are subject to a crude discretization of time. Consider a system where the immediate behavior is described by equation (1) of the main text. For simplicity, we shall let A(t) and a(t) be constant, and use the notation X_t for X(t).

Suppose we tried to explain the normalized increments ${\Delta }^{-1}(X_{t+\Delta }-X_t)$ by a linear regression onto the variables X_t and a constant. This would give a matrix and a vector, B and b, such that

$$E[X_{t+\Delta }|X_t]=X_t+\Delta {\mathrm{BX}}_t+\Delta b$$ (8)

On the other hand, equation (6.6) in Karatzas and Shreve²⁵ yields that

$$E[Xt+\Delta |Xt]=e-\Delta AXt+\Delta \sum _{n\ge 0}\frac{(-\Delta )n}{(n+1)!}An(A\mu +a)$$

so B and b would be given by

$$B=-\sum _{n\ge 0}\frac{(-\Delta )n}{(n+1)!}An+1\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}\text{and}\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}b=\sum _{n\ge 0}\frac{(-\Delta )n}{(n+1)!}An(A\mu +a)$$

If the sampling interval Δ is small, then $\sum _{n\ge 0}\frac{(-\Delta )n}{(n+1)!}An$ is approximately equal to the identity matrix I. This means that B and b would also be approximately equal to −A and Aμ +a, so linear regression would indeed resemble the immediate effects from equation (1) of the main text quite well.

If the time resolution is coarse, then the picture becomes totally different, since the difference between B and −A can grow large as Δ increases. Suppose, there exists a path in the local independence graph where the corresponding entries from A are non-zero. Heuristically, most matrices that satisfy $ai,k1ak1,k2\dots akn-1,knakn,j\ne 0$, do also satisfy $〈Amej,ei〉\ne 0$ for some natural number m. It would for instance always be true if A only had non-negative entries. This means that the entry at the i’th row and j’th column of the matrix $\sum _{n\ge 0}\frac{(-\Delta )n}{(n+1)!}An+1$ is non-zero, except possibly for some isolated values of Δ. The entry B_i,j is therefore most likely non-zero. In other words, a naive interpretation of the linear regression from (8) would suggest an effect from $X_t^{(j)}$ on the short-term behavior of the i’th coordinate, even if A_i,j = 0 and there were no such immediate effects.

This illustrates a more general pattern when considering a scenario with instantaneous dynamics. Suppose the dynamical behavior is described in a local independence graph. Any DAG that is compatible with time-discrete observations will in fact be a smeared out version of the local independence graph corresponding to the true mechanisms. A node y in the local independence graph is said to be reachable from x if there is a directed path from x to y. The corresponding time-discrete DAG will have an arrow from x to every node that was reachable in the local independence graph. If the original graph was a DAG, then the time-discrete graph would be its transitive closure. It would therefore be impossible to distinguish between direct and indirect effects, using crude regression methods based on any DAG compatible with sparsely time distributed observations. Clearly, this is mainly a problem for coarse discretization.

Declaration of conflicting interests

The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

Funding

The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: Aalen, Røysland, and Gran were partly supported by the Research Council of Norway contract/grant numbers 191460/V50 and 218368/H20. Røysland was also partly supported by the Norwegian Cancer Society contract/grant number 2197685. The Swiss HIV Cohort Study is supported by the Swiss National Science Foundation (SNF grant #33CS30-134277 and -148522). Kouyos was supported by the Swiss National Science Foundation (SNF grant # PZ00P3-142411).