A Complete Fossil-Calibrated Phylogeny of Seed Plant Families as a Tool for Comparative Analyses: Testing the ‘Time for Speciation’ Hypothesis

Abstract

Explaining the uneven distribution of species richness across the branches of the tree of life has been a major challenge for evolutionary biologists. Advances in phylogenetic reconstruction, allowing the generation of large, well-sampled, phylogenetic trees have provided an opportunity to contrast competing hypotheses. Here, we present a new time-calibrated phylogeny of seed plant families using Bayesian methods and 26 fossil calibrations. While there are various published phylogenetic trees for plants which have a greater density of species sampling, we are still a long way from generating a complete phylogeny for all ~300,000+ plants. Our phylogeny samples all seed plant families and is a useful tool for comparative analyses. We use this new phylogenetic hypothesis to contrast two alternative explanations for differences in species richness among higher taxa: time for speciation versus ecological limits. We calculated net diversification rate for each clade in the phylogeny and assessed the relationship between clade age and species richness. We then fit models of speciation and extinction to individual branches in the tree to identify major rate-shifts. Our data suggest that the majority of lineages are diversifying very slowly while a few lineages, distributed throughout the tree, are diversifying rapidly. Diversification is unrelated to clade age, no matter the age range of the clades being examined, contrary to both the assumption of an unbounded lineage increase through time, and the paradigm of fixed ecological limits. These findings are consistent with the idea that ecology plays a role in diversification, but rather than imposing a fixed limit, it may have variable effects on per lineage diversification rates through time.

Introduction

It is now well recognised that species richness is unevenly distributed across the tree of life and the origin of this variation is the subject of significant debate [1–5]. In seed plants, variation in species richness between sister clades is often large, leading to highly imbalanced phylogenetic topologies [6, 7]. Despite the long history of research on these patterns and an increasingly accurate understanding of the evolutionary history for many taxonomic groups, the mechanisms underlying differences in species richness remain largely undetermined, with possible explanations spanning biological, historical, geographical and neutral processes [8]. A better understanding of the causes of imbalance in species richness across lineages could provide insight into the mechanisms governing the evolution and proliferation of life. Here, we reconstruct a complete phylogenetic tree for all seed plant families, and use this tree to evaluate two alternative explanations for variation in species richness among clades: ‘time for speciation’ versus ‘ecological limits’ [4].

The time for speciation effect [4], whereby older clades, having had more time to diversify, are represented by a larger number of species, implicitly assumes that diversification is unbounded. Under this model, we should therefore expect to see a positive relationship between clade age and the logarithm of species richness, regardless of the range of clade ages [4]. Further, simple calculations of net diversification rate (r) should be able to explain a significant proportion of the variation observed in seed plant diversity. In contrast, the ecological limits model assumes that external factors (ecological limits) restrict clade expansion. According to this alternative model, young clades, which have yet to reach their ecological limits, may show a positive correlation with clade age, but as clades get older and species richness approaches the ecological limit for the clade, the relationship will be lost [9]. In addition, a clade that has reached saturation in species number would appear to have a faster diversification rate when observed at some point in the past than it does now (time [t] is increasing while species number [S] remains constant) despite the fact that its diversification rate during its initial expansion does not change [9].

Large, well sampled phylogenies for species-rich groups allow us to examine variation in evolutionary rates across clades and through time (e.g. amphibians [10], birds [11], mammals [12,13], plants [7,14–17]), and thus provide an opportunity for evaluating macroevolutionary models of diversification. However, the reconstruction of complete, dated, phylogenetic trees for large groups has remained a challenge, and is confounded by poor and uneven sampling of taxa. With advances in molecular sequencing technologies following the development of the polymerase chain reaction (PCR) in the 1980’s, there has been a rapid accumulation of phylogenetic data, but the collection of these data has been largely piecemeal. For some species or clades we have sequences for multiple genes, or even whole genomes, whereas other branches on the tree of life are only sparsely represented (see e.g. [18]). To overcome this data shortfall various heuristics have been developed to assemble large phylogenetic trees [19]. Supertree approaches combine many small but overlapping phylogenies to form a single, more inclusive phylogeny [20,21]. An alternative approach for assembling large phylogenies is to use expert opinion. Phylogenetic hypotheses are constructed using best available knowledge, typically assuming a fixed backbone tree representing the taxonomic relationships among major lineages and including missing taxa as polytomies, and, when possible, manually resolving relationships based on independent phylogenetic hypotheses (see e.g. [22]). In flowering plants, where regional richness might sum to many thousands of species, such approaches are common-place and have been automated in the Phylomatic online tool [23].

Meta-phylogeny reconstruction methods, such as those described above, have obvious utilitarian value, but they also have a number of limitations. Critically, branch length data are typically absent or poorly estimated, confounding studies of evolutionary rates, either in diversification or character evolution. Although it is possible to estimate branching times from topology alone, such approaches must assume, a priori, a particular model of diversification (e.g. [13,24]); hence, estimating evolutionary rates on such trees can be circular (see [25]). When molecular sequence data are available, branch lengths may be estimated directly (e.g. see [7]), and it is possible to derive branch lengths for different genes on different parts of the tree and then calibrate on common nodes if there is sufficient taxonomic overlap in gene coverage and genetic evolution is clock-like [26].

Here, we generate a complete and robustly dated phylogenetic tree for all seed plant families by combining current knowledge on plant family relationships with sequence data on four gene regions with high taxonomic coverage (chloroplast genes rbcL, matK and atpB, and the nuclear ribosomal RNA-encoding gene 18S) and 26 fossil constraints. Our approach complements efforts towards the generation of the comprehensive tree of life [27], but differs in that we additionally provide branch length estimates, a critical parameter for generating and testing phylogenetic hypotheses on evolutionary rates. We use this tree topology and data on the species richness of plant families to map patterns of clade diversification across the phylogeny and contrast predictions of the ‘time for speciation’ versus ‘ecological limits’ models of clade expansion.

Methods

Phylogeny Reconstruction

Phylogeny reconstruction followed a three-step procedure. First, a backbone topology was constructed following the Angiosperm Phylogeny Group III (APG III) classification [28], and missing families placed using best available information. Second, molecular branch lengths were optimized on to the family-level backbone using RAxML v.8.0.0 [29] and four gene regions (rbcL, matK, atpB and 18S rRNA) mined from BOLD (http://www.barcodinglife.com/) and GenBank (http://www.ncbi.nlm.nih.gov/genbank/). Third, the tree was made ultrametric and branch lengths calibrated to millions years using Bayesian analysis in BEAST v.1.8.0 [30]. We did not attempt to reconstruct the phylogeny directly from the raw sequence data because our aim here was not to generate a new hypothesis of seed plant evolutionary relationships, but to take advantage of existing knowledge based on multiple studies using separate lines of evidence, and summarized by experts (i.e. APG III). While current computational tools allow us to rapidly generate phylogenetic hypotheses for many hundreds of taxa, we do not believe such an estimate here would improve on published work that has targeted specific clades and gene regions to maximally resolve phylogenetic relationships (see e.g. [31] for a similar approach to that used here).

The Phylomatic supertree [23] of all plants was downloaded and trimmed to generate a cladogram of all seeded plant families. This topology represents an expert summary of current higher level angiosperm molecular systematics following the APG III [28,32]. We note that, following the initial tree reconstruction described here, APG IV has now been released [33]; however, we retained the APG III backbone so as to be consistent with the taxonomy used to extract family species richness data (see below). This cladogram was enforced as a topological constraint in all subsequent analyses. Three families (Apodanthaceae, Cynomoriaceae and Vahliaceae) were not represented on the megatree and were added manually based on the best available data. Apodanthaceae was added as a polytomy with Anisophyllaceae and Cucurbitaceae [34], Cynomoriaceae was added as a sister to Rosaceae [35], and Vahliaceae was added as a polytomy with lamiids [28].

DNA sequence data were obtained for all 425 seeded plant families accepted by the Plant List v.1.1 (http://www.theplantlist.org/), which is informed by APGIII [28], and the 2001 World Checklist of Conifers [36], to generate a molecular matrix with one sequence per family for each of four genes, rbcL, matK, atpB and 18S rRNA (accession numbers provided in S1 Table). Sequences mined from BOLD and GenBank supplemented the molecular matrix from Bell et al. [37] in order to have all 425 families represented. Sequences for all four genes were available for a majority of families. Sequences were aligned for each gene separately using MUSCLE v.3.8.31 [38] and refined manually using MEGA v.6.05 [39]. The four gene alignments were then concatenated using SeqState v.1.4.1 [40].

Phylogenetic branch lengths were estimated on the Phylomatic cladogram from the molecular matrix by maximum likelihood using RAxML v.8.0.0 [29]. The RAxML output from the original 425 family maximum likelihood tree showed extreme molecular rate variation between 6 families (Apodanthaceae, Balanophoraceae, Corsiaceae, Hydnoraceae, Mitrastemonaceae and Rafflesiaceae) and their closest relatives. These large molecular differences can be explained by the fact that these are mostly parasitic lineages. Parasitism is an alternative evolutionary strategy in some plant families, and may cause the rapid erosion of sequences that may be highly conserved outside of these families [41]. For example, rbcL encodes the long-chain of the enzyme RuBisCO, a key component of carbon fixation, which is highly conserved in photosynthesizing plants, but has been lost or is highly divergent in parasitic plants [42]. Additionally, at least some of these families have been shown to exchange genetic information with their hosts, reducing our ability to infer their relatedness from DNA sequences [43]. Although Corsiaceae is not a parasitic family, but a myco-heterotroph, this alternate evolutionary strategy contributes similarly to the loss of photosynthetic ability and the erosion of genetic sequence information that is highly conserved in the rest of the seeded plants [44]. To reduce bias in branch length estimates, these families were removed and RAxML branch length estimation was executed on the reduced matrix.

Branch lengths were calibrated to millions of years using BEAST v.1.8.0 [30] and 26 fossil calibrations, enforced as minimum age constraints on the appropriate stem or crown nodes, following Bell et al. [37] and Smith et al. [45] (see S2 Table), keeping the branching topology fixed. First, we used PATHd8 [46] to generate a starting tree that satisfied the calibration constraints, and then branch lengths were estimated assuming log-normal priors with means of 5 million years and offset by the fossil date from S2 Table, and with the GTR+I+Γ site substitution model estimated for each of the four genes separately. This site substitution model was determined as the best fit to the data using ModelTest from the phangorn package in R [47]. The analysis in BEAST was run for 325 million generations, sampling every 50,000 generations. Sampling adequacy and model convergence was evaluated by examining parameter effective sample sizes (ESS values) and manually inspecting trace plots in Tracer [48]. We note that new discoveries will tend to push back fossil age estimates, for example, a new fossil age estimate for Nymphaeales [49] suggests the crown group for this clade could be several years older than the age used here; however, by enforcing calibrations as minimal age constraints and setting log-normal priors, our analyses allow for older estimates. A hard maximum age of 350 million years was enforced for the root of the phylogeny, reflecting the oldest reasonable divergence time between gymnosperms and angiosperms [50].

Last, the removed parasitic families were reinserted on the tree by introducing polytomies at the locations from which they were originally excised. These polytomies were then resolved using a BEAST input file generated with PolytomyResolver [51]. This script generates a pseudo-posterior distribution of phylogenies, by constraining the input tree topology and then resolving the introduced polytomies according to a birth-death model. The node heights of the final phylogeny are the median of this distribution, calculated in TreeAnnotator [30].

Diversification Rate Calculations

Species richness estimates for 413 of the 425 seeded plant families were derived from the Plant List v.1.1 (http://www.theplantlist.org/), which reports the number of proposed species which have been accepted as unique species, rejected as synonyms, and have yet to be evaluated by relevant authorities for a given family. Family species richness was then estimated as:

$$S=S_A+\frac{S_A{S}_U}{S_A+S_R},$$

where S_A is the number of officially recognized species in a family, S_R is the number of species names that have been rejected as synonyms from that family and S_U is the number of unevaluated species from that family. In this way we were able to account for the fact that most plant families have not been completely evaluated in terms of species richness. For the remaining twelve families not included in the Plant List, published estimates of family species richness were obtained from the recent literature. Species richness estimates and sources are presented in S3 Table. The total species richness across all families (S_T = 367,831) conforms to current estimates of angiosperm global diversity [52].

We used information on stem age and species richness associated with each clade in the phylogeny to calculate two estimates of diversification rate (r), defined as the difference between the rate of speciation (λ) and the rate of extinction (μ) [8]. Following Magallón & Sanderson [8], we calculated two alternative estimates of diversification rate (r) according to the formula:

$$\widehat{r}=\text{log}\left[S\left(1-\epsilon \right)+\epsilon \right]/t,$$

where ε is the relative extinction rate. The first assumed negligible extinction (ε = 0), and the second assumed a constant relative extinction rate (ε = μ/λ) of 0.9. At relative extinction rates greater than 0.9, it is suggested that speciation and extinction events would have to occur at a rate of more than 1 per million years [8], which is considered unlikely given published estimates of the frequency of these events. Therefore, these two estimates have been argued to represent reasonable upper and lower bounds on each clade’s net diversification rate [8].

We evaluated the time for speciation effect by fitting a linear model to the relationship between log (S) and clade age for adjacent 10 million year time windows, adjusting P-values for multiple tests using the Benjamini-Hochberg correction [53]. Clades over 100 million years in age were excluded from the analysis because the phylogeny becomes relatively node-poor and highly nested at this depth. To avoid the confounding effects of including clades nested within one another in the same subset of the data [4], clades with overlapping taxon sets were identified, and only one of which was included in a given analysis. This procedure was run twice, once removing the younger of the nested clades and then again removing the older of the nested clades. We chose this method rather than attempting to correct for phylogenetic non-independence, for example, by using a phylogenetic regression, because nested clades are by definition less species rich than the encompassing clades.

To evaluate the relationship between diversification rate and clade species richness, we modeled log(S) as a function of the net diversification rate (r) for all clades in the phylogeny.

Last, we identified major shifts in diversification rate across the tree using MEDUSA [54] in the geiger package in R [55], with the phylogeny and species richness estimates for each tip as inputs. MEDUSA first estimates a diversification rate model for the entire tree, and then adds a series of random break-points at which speciation and extinction rates are allowed to change. Alternative models are compared using AIC, with only the best performing break-point being retained. The process is repeated iteratively until the addition of new break-points no longer improves the sample-size corrected Akaike information criterion (AICc).

Results

The 425 family phylogeny is available from the KNB Data Repository (doi:10.5063/F13T9F5P at https://knb.ecoinformatics.org/knb/d1/mn/v2/object/knb.1177.1). The timing of major divergence events align well with established molecular and fossil-based estimates, notably for angiosperms [37,56] and the entirety of the spermatophyte lineage [50].

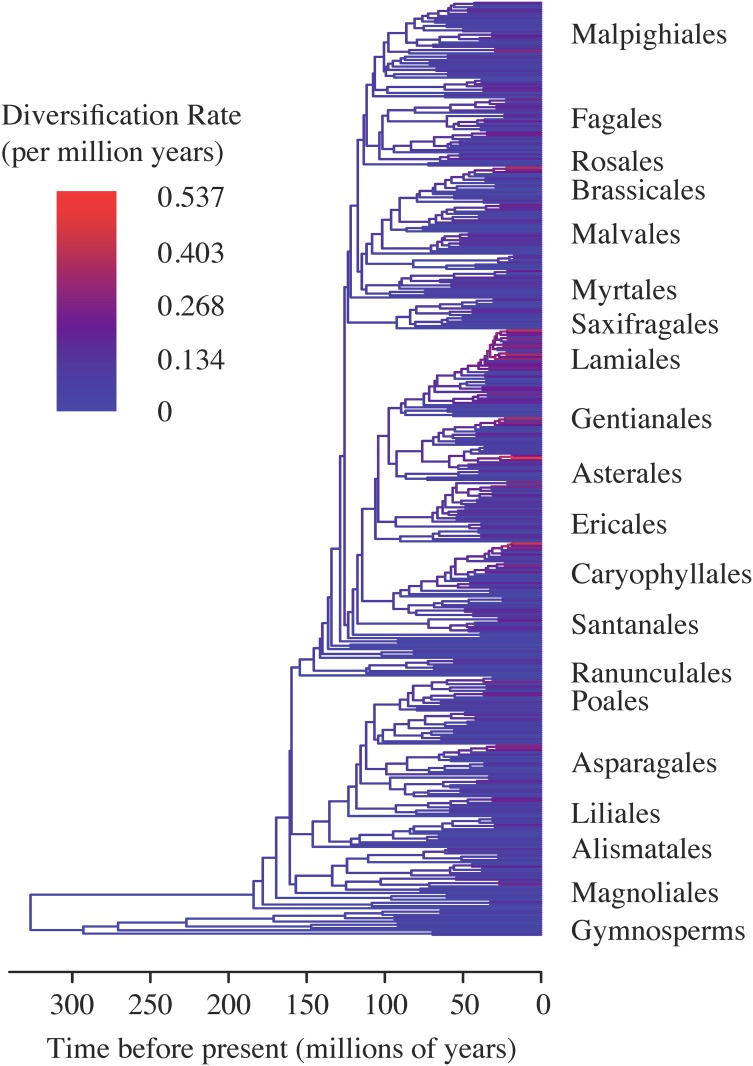
Species richness, total diversification, and diversification rate estimation are reported for all 849 clades of the phylogeny (S4 Table). Absolute diversification (log(S)) ranged from 0 within single-species families to 12.82 for the entire phylogeny, with an average of 5.94. Estimates for net diversification rate varied greatly across the tree (Fig 1), and ranged from 0 to 0.537 per million years with a mean of 0.104 per million years when extinction was assumed to be negligible (ε = 0), and from 0 to 0.414 per million years with a mean of 0.067 per million years under our upper bound of relative extinction rate (ε = 0.9). We note that upper rate estimates should be interpreted cautiously, as they appear as obvious outliers (see also S1 Fig), a point we return to in the Discussion. Although the magnitude of extinction influenced the absolute estimates of diversification rate, changes to the rank order of clades were generally modest, with the rank of 8 of the top 10 fastest diversifying clades being conserved between the two models.

Fig 1. The reconstructed seeded plant phylogeny.

Branches coloured according to the estimated diversification rate (assuming a relative extinction of ε = 0) of each clade following Magallón & Sanderson (2001). Rate estimates vary from 0/million years (blue) to 0.537/million years (red). Selected orders are labeled to aid interpretation.

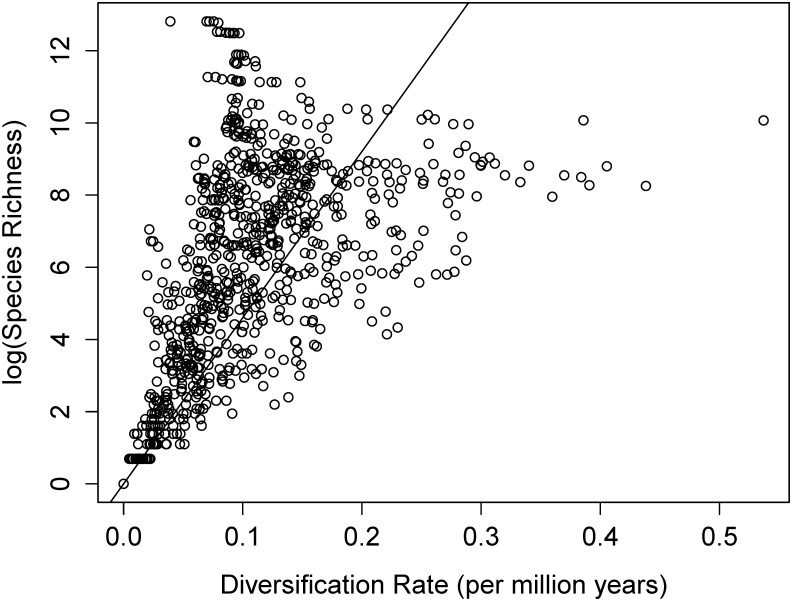
Linear models of ln(S) and clade age within each of the 10 million year time windows are presented in Table 1. None of the models showed any significant relationship (p>0.10) between age and diversification rate after correcting for multiple tests. However, we find a highly significant relationship between log(S) and diversification rate (Fig 2, p<0.0001, R² = 0.77).

Table 1. Linear models of clade age (million years: my) against ln(S) within 10 million year time windows.

Time window: subset younger node removed	Mean clade age (my)	Slope	Adjusted p	R2	Number of included nodes
20–30 my	26.9	0.218	0.477	0.044	48
30–40 my	36.1	-0.120	0.505	0.014	82
40–50 my	45.2	0.178	0.477	0.031	80
50–60 my	56.1	0.126	0.477	0.014	106
60–70 my	65.3	0.231	0.318	0.071	76
70–80 my	74.9	0.189	0.477	0.047	60
80–90 my	85.4	0.194	0.477	0.035	42
90–100 my	94.7	0.231	0.477	0.046	46
Time window: subset older node removed	Mean clade age (my)	Slope	Adjusted p	R2	Number of included nodes
20–30 my	25.2	0.081	0.689	0.009	62
30–40 my	35.0	-0.124	0.477	0.018	94
40–50 my	44.4	-0.041	0.773	0.000	89
50–60 my	55.4	-0.035	0.773	0.001	120
60–70 my	64.1	0.013	0.889	0.000	94
70–80 my	74.4	0.106	0.513	0.016	65
80–90 my	84.3	-0.054	0.773	0.003	52
90–100 my	94.3	0.100	0.717	0.008	51

Fig 2. Logarithm of species richness plotted against net diversification rate (r) across all clades in the phylogeny.

The correlation between log richness and diversification is highly significant (p<0.001, R² = 0.77, from the linear regression).

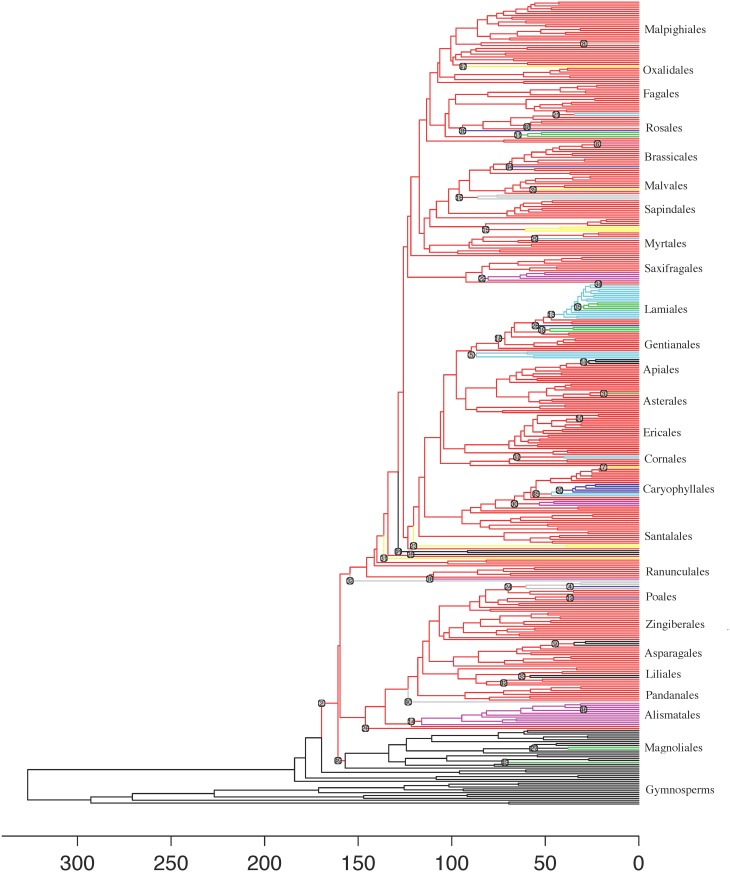
The MEDUSA analysis assigned 49 different models to the phylogeny (Fig 3). Most of these models were of the Yule-process type, with only five of the fitted models including extinction >0 (S5 Table), although these five models cover a majority of the tree (Fig 3). Some of the models fit closely with specific taxonomic orders, including model 13 for Lamiales and model 14 for Alismatales.

Fig 3. Results of the MEDUSA analysis of diversification rate-shifts on the reconstructed spermatophyte phylogeny.

Numbered circles indicate the model number (see S5 Table) that corresponds with the model of diversification that was fit to the immediately descendent clade, with colour shading identifying the descendent lineages fitting to that model of diversification, allowing rate shifts within clades to be easily distinguished. Parameters associated with these models can be found in S5 Table. Horizontal scale bar represents time in millions of years.

Discussion

We present here a new dated phylogenetic tree for spermatophytes that is completely sampled at the family level, and calibrated using molecular and fossil data with Bayesian inference. This phylogeny reflects expert consensus on plant phylogenetic relationships [28,32] along with robustly dated estimates of divergence times, and represents a valuable tool for comparative analysis. While several phylogenetic trees with greater density of sampling have been published recently (e.g. [31,57]), our reconstruction is notable in that it represents a complete sample of all seed plant families. Nonetheless, we note that the phylogenetic placement of Cynomoriaceae, Apodanthaceae and Vahliaceae remain controversial, and the evolutionary hypotheses presented here regarding these families should be used with caution. We used this new dated phylogeny of all seed plant families to contrast two alternative hypotheses for differences in species richness among higher taxa by exploring patterns of diversification across the spermatophyte family tree. Our results support previous analyses, illustrating large variation in diversification rates across spermatophyte lineages [7,15,58,59]. Monospecific families such as Barbeuiaceae, for example, have had similar length of time to diversify as species-rich groups such as Ericaceae.

Diversification rate estimates are sensitive to calibration of divergence times, number of recognized species within higher taxa, and phylogenetic accuracy. For example, the erroneous placement of a species-rich family towards the tips of the phylogeny will inflate diversification rate estimate for that family. This might occur if it is incorrectly placed as sister to an evolutionary distant family, or if branch lengths underestimate true divergence times because, for example, fossils are biased young or molecular rates have slowed. By constraining our analysis to a backbone phylogeny based upon a wealth of expert knowledge, we hope we have reduced impacts of phylogenetic error (but see caveats above). The pitfalls of relying upon a single or secondary calibration have been emphasized elsewhere (e.g. [60]). We attempted to provide robust estimates of divergence times by including multiple fossil calibrations, and taking median estimates from the Bayesian posterior distribution of ages, thus reducing sensitivity to outliers. It would also be possible to run all analyses across the posterior distribution of dated tree topologies, although we did not do this here. While we attempted to minimize error, we note that our higher net diversification rate estimates were greater than have been reported elsewhere for angiosperm taxa (e.g. [8,17]). However, these high rate estimates were associated with just a few lineages, and the vast majority of clades are characterized by rates falling well-with in the spectrum reported by Tank et al. [17] using similar methods on a differently sampled tree.

In our diversification rate analysis, we were interested in contrasting the time for speciation versus the ecological limits hypotheses of clade growth. We found no significant relationship between clade age and ln(S) in any of our 10 million year time windows, suggesting that time (stem clade age) is not an important predictor of species richness, at least for seeded plant clades older than twenty million years. Our results therefore do not support a simple time-for-speciation model, as also suggested by results from Salamin and Davies [61], Magallón and Castillo [15], and Tank et al. [17]. However, neither do we find support for a simplified version of Rabosky’s [9] model of ecological limits, in which we would expect the diversification of younger clades to be positively correlated to time, but older clades to show no relationship as they approach their ecological limits. It is, of course, possible that ecological limits might only be manifest when looking at more recent diversification; for which complete species-level phylogenies might be necessary. Unfortunately, we are still some way off from having a complete phylogeny for all c. 300,000 plant species; however, for species-rich animal clades, such as birds, for which complete phylogenies are now available [11], there is some intriguing evidence for density dependent diversification (e.g. [62,63]), that could be consistent with ecological limits.

Why did we not find strong evidence for either the time for speciation or ecological limits hypotheses? When we explore the fit of alternative diversification models to different clades across the phylogeny, we find that a few models fit to broad taxonomic groupings, such as the core eudicots, monocots and particular orders, but clades at lower levels of organization within these groups can follow models with radically different diversification rates. For example, the core eudicots are generally described by a model with a relatively low diversification rate (r = 0.050) and significant relative extinction (ε = 0.974), but the nested order Lamiales fits a model of much more rapid diversification (r = 0.228). As another example, the hyperdiverse monocot family Poaceae was fit to a model with a diversification rate (r = 0.256) more than eight times as fast as its closest relatives (Ecdeiocoleaceae, Joinvilleaceae and Flagellariaceae, r = 0.038). This pattern of nested radiations also matches to observations by Tank et al. [17], and likely helps explain why there is no strong support for either time or ecological limits in determining clade richness. However, we also note that a few simple models that cover a wide range of taxa can explain the species richness of most families. Much emphasis has been placed on rate variation across the plant tree of life (e.g. [7,8,15,16,17,37]); our results show that much of the spermatophyte family tree can be described by a few models, and are thus perhaps surprising.

The two models fit to the vast majority of the tree (models 1 and 2), have relative extinction values (ε = 0.993 and ε = 0.974, respectively) well above the reasonable upper limit proposed by Magallón and Sanderson [8] of ε = 0.9. A relative extinction rate this high would suggest an unfeasibly rapid turnover of lineages and imply a very large number of species extinctions for which there is no evidence in the fossil record. We suggest, therefore, that these results might indicate that assumptions of constant speciation and extinction rates may be violated. Although a model of non-constant rates could match to the asymptotic approach to an ecological limit, as suggested by Rabosky [9], it could equally result from fluctuating rates caused by changing ecological, environmental or geographic conditions through time [64]. Diversification rate variation might therefore reflect the contingent process of evolutionary diversification [65] whereby lineages with particular traits or key innovations are favoured in some environments or time periods. Thus it is possible that a lineage could originate but remain quite species poor until a changing ecological context allows its expansion sometime in the future. This may have occurred in mammals, for example [12,66]. Under this scenario, species richness is a product of the interaction between the life history traits of the clade and its ecological context [14].

There is a very large literature on seed plant diversification and, in particular the rise to ecological dominance of angiosperms (see recent review by Augusto et al. [67]). While the list of putative key traits associated with increased diversification is large, several have attracted particular attention, and can be grouped into two general classes: those that facilitate reproductive isolation and those that increase evolutionary rates. For example, modes of pollination and dispersal can enhance reproductive isolation through pollinator specificity or isolation by distance following long distance dispersal [68,69]. Growth form or generation time might directly influence evolutionary rates via cell generation times and rates of mitosis [70,71]. However, geographical extent is the best single predictor of clade species richness, with large-ranged clades characterized by higher diversification rates [72,73], although the direction of causation is unclear. In contrast, explanations for the low diversity of gymnosperms have focused on ε rather than S, and it is suggested that present day low richness reflects high extinction rather than low speciation rates [74]. Given this complexity, it may be unsurprising that we do not find strong support for any one hypothesis. Time for speciation is likely important, but clades possessing different key innovations may accumulate species at different rates. The link between clade richness and geographic extent provides some support for ecological limits, but traits, such as mode of dispersal, might also mediate this relationship.

While the MEDUSA analysis implemented here allows rate variation between clades, it fits birth-death models that assume underlying constant speciation and extinction rates within lineages, and Rabosky et al. [5] suggested that it is not appropriate to fit such models when there is no strong relationship between clade age and richness (but see Stadler et al. [75]). Alternative approaches allow more flexible models to be fit, for example, allowing time-dependent or diversity-dependent diversification processes (e.g. BAMM http://bamm-project.org/ [76] and RPANDA [77]), but their performance on higher-level phylogenies at the genus-level or family-level have not yet been well explored. It is possible to use a stochastic polytomy resolver, such as PASTIS [78], to return a set of completely resolved topologies given information on species richness of the terminal taxonomic units sampled in the tree. However, such approaches typically assume a constant birth-death process to resolve and, as a consequence, add bias to diversification rate analyses [25]. Because the MEDUSA algorithm is well suited for exploring diversification rates across higher taxa, it remains perhaps our best current option for describing the diversification of seed plants, but some underlying assumptions may be violated, and it is not yet clear whether rate estimates are thus unreliable. It will be interesting to explore additional methods that allow for more complex diversification models as more detailed phylogenetic trees become available.

Rabosky [9] and Wiens [4] have debated the validity of simple estimates of net diversification rate in explaining the variation in species richness across the tree of life. In Rabosky’s view, since we will observe most clades at their ecological limit of diversification, measures of net diversification rate are misleading because they will decrease over time [9]. Wiens [4] argues that as long as species richness is correlated to diversification rate, these metrics are still relevant to explaining patterns of species diversity. We show here that the two metrics are indeed correlated closely, indicating that, even if the underlying assumptions of these estimates are flawed, a significant proportion of the variation in species richness can be explained by net diversification rate. However, it is important to note that this relationship is to be expected because diversification rate is itself a function of clade species richness, and they are therefore not independent. When richness and clade age are randomized, the correlations are at least as good as the one observed from the data (mean R² of 0.81 over 1000 runs). Consequently, estimates of net diversification rate will always capture some variation in species richness.

While we show diversification rate and species richness are inextricably intertwined, we argue that diversification rate remains an important metric for identifying contemporary clades that are undergoing rapid diversification versus clades that are species rich because they have had long to diversify. In addition, comparisons of relative rates allows us to separate species poor clades that have yet to diversify due to their young age from those which are species poor because they lack key innovations, ecological suitability and/or because of historical contingency.

Supporting Information

S1 Fig. Frequency histogram of clade net diversification rate estimates from Medusa.

(PDF)

S2 Fig. Complete seed plant phylogeny with internal nodes numbered.

(PDF)

S1 Table. Literature citations and/or Genbank accession numbers for DNA sequence data.

(XLSX)

S2 Table. Age constraints used to calibrate the phylogeny.

(PDF)

S3 Table. Species richness estimates for the 425 families in the phylogeny.

(PDF)

S4 Table. Diversification metrics and clade ages of all clades of the seeded plant phylogeny.

(PDF)

S5 Table. Model parameter estimates for the MEDUSA models of diversification.

(PDF)

S6 Table. List of clade members for each internal node of the seeded plant phylogeny.

(CSV)

Data Availability

All sequence data are available from GenBank; accession numbers are provided in S1 Table. The phylogenetic tree is available from the KNB Data Repository (doi:10.5063/F13T9F5P at https://knb.ecoinformatics.org/knb/d1/mn/v2/object/knb.1177.1).

Funding Statement

JD was supported by an NSERC Discovery grant.