Feasibility of Using Linearly Polarized Rotating Birdcage Transmitters and Close-Fitting Receive Arrays in MRI to Reduce SAR in the Vicinity of Deep Brain Simulation Implants

Abstract

Purpose

MRI of patients with deep brain stimulation (DBS) implants is strictly limited due to safety concerns, including high levels of local specific absorption rate (SAR) of radiofrequency (RF) fields near the implant and related RF-induced heating. This study demonstrates the feasibility of using a rotating linearly polarized birdcage transmitter and a 32-channel close-fit receive array to significantly reduce local SAR in MRI of DBS patients.

Methods

Electromagnetic simulations and phantom experiments were performed with generic DBS lead geometries and implantation paths. The technique was based on mechanically rotating a linear birdcage transmitter to align its zero electric-field region with the implant while using a close-fit receive array to significantly increase signal to noise ratio of the images.

Results

It was found that the zero electric-field region of the transmitter is thick enough at 1.5 Tesla to encompass DBS lead trajectories with wire segments that were up to 30 degrees out of plane, as well as leads with looped segments. Moreover, SAR reduction was not sensitive to tissue properties, and insertion of a close-fit 32-channel receive array did not degrade the SAR reduction performance.

Conclusion

The ensemble of rotating linear birdcage and 32-channel close-fit receive array introduces a promising technology for future improvement of imaging in patients with DBS implants.

INTRODUCTION

The symptoms of several disabling and medication-resistant neurological and psychiatric disorders are effectively treated by stimulating structures that are located deeply within the brain using a technique called deep brain stimulation (DBS) (1–4). Deep brain stimulation is a neurosurgical procedure that uses an implantable pulse generator to send electrical pulses via implanted electrodes to specific nuclei in the brain. Despite the general effectiveness of DBS, its underlying mechanisms of action are still unclear and controversial (5–7). In this regard, neuroimaging is extremely useful both for target verification and program optimization, and more importantly, to study treatment-induced changes in functional connectivity of affected brain networks.

When investigating neuromodulatory effects of DBS, neuroimaging studies have largely used either positron emission tomography or single-photon emission computed tomography (8,9). The use of MRI provides additional advantages due to its excellent soft-tissue contrast, noninvasive nature, and the richness of the postprocessing analytical methods that are available to use for functional neuroimaging. One of the major restrictions of present MRI technology for DBS imaging is due to the interaction of MR radiofrequency (RF) fields with the implanted device. Coupling of MR transmitter’s electric field (E-field) with long DBS leads induces electric currents on lead metallic wires. These currents induce additional E-fields into the tissue that surrounds the electrode, leading to extra power absorption that causes excessive heating and potential tissue damage (10–12). Consequently, postoperative MRI of DBS patients is only approved at 1.5 Tesla (T) and is restricted to use pulse sequences with root mean square (rms) of ${\mathrm{B}}_1^{+}$ fields below 2 μT. If a ${\mathrm{B}}_1^{+}$ rms setting is not available on the MRI equipment, the more conservative specific absorption rate (SAR) of less than 0.1 W/kg should be applied (13). These safety restrictions pose limitations on the applicability and quality of postoperative DBS MRI. First, following the low SAR recommendation in clinical settings is problematic because MRI protocols that optimally image DBS leads and subcortical structures tend to have much higher SAR than currently approved (14). Second, the inherently lower signal-to-noise ratio (SNR) at field intensities that are recommended for DBS imaging tend to limit image resolution and compromise the quality of functional MRI (fMRI) data (15).

Besides safety concerns, the interaction of MRI RF fields and DBS electrodes causes image artifact at the location of electrode contacts, which pose serious challenges to the detection of hemorrhagic lesions, electrode displacement, and infections, as well as to studies that investigate functional connectivity of affected brain networks. Resting state fMRI studies that investigate post-surgical neuromodulatory effects of DBS are, for example, very useful to determine how coupling parameters between affected brain regions are different in responsive versus nonresponsive patients. Such studies however, are severely hampered by electrode artifact contamination, which precludes inclusion of DBS target structures into statistical models (16–18).

Attempts to reduce the interaction of MRI fields and conductive implants are very recent and limited to proof-of-concept studies at higher fields (3T). Eryaman et al. and McElcheran et al. proposed to manipulate the E-field distribution of RF transmit coils to generate E-field–free zones in the body, which could be then steered to coincide with the implant to reduce SAR amplification (19–22). These studies, however, only demonstrated the feasibility of SAR reduction for simplified implant geometries that consisted of planar wires. Realistic DBS leads, on the contrary, have wire segments that are 15 to 30 degrees out of plane (23), and in most cases consist of looped segments that are reported to significantly affect SAR (11,24,25). Specific absorption rate reduction techniques, which are based on E-field modification, work by generating region(s) of zero E-field, which contain the whole implant. This is important because even if a portion of implant lies outside of this region, a risk remains for RF currents to be induced in the leads. Yet, there is no study showing the validity of such methodologies in situations with complex implant geometries.

Thus far, studies on implant-friendly coils have been limited to one-channel volume transmit–receive coils. It is well-established that incorporation of close-fit anthropomorphic receive arrays into volume transmitters can significantly increase the SNR even at low field intensities (26–28). Such ensembles can be extremely useful for DBS imaging because they allow the acquiring of high-resolution anatomical and functional images even at currently recommended low SAR labeling of DBS devices. The insertion of receive-only arrays, however, may potentially modify the E-field of the transmitter, as recently demonstrated at higher fields (29), and thus could sabotage the SAR reduction strategy. To date, there is no study that investigates the effect of incorporating receive arrays into implant-friendly transmit coils.

The goal of this study is to investigate the feasibility of eliminating SAR amplification during MRI of DBS patients using a mechanically rotating linearly polarized birdcage transmitter and a 32-channel close-fit receive array. It is known that the longitudinal E-field of a linearly polarized birdcage transmitter has a slab-like region of zero E-field. By mechanically rotating the birdcage, it is possible to steer this null E-region to make it coincide with the DBS implant. We hypothesized that at 1.5T, this strategy allows for low induced currents in the implants and low SAR in the surrounding tissue, even for nonplanar implant geometries. By applying comprehensive electromagnetic simulations and experimental field measurements, we demonstrate that:

1. The null E-region of a rotating linear birdcage transmitter is thick enough at 1.5T to encompass DBS implantation paths with wire segments that are up to 30 degrees out of plane, as well as leads with looped segments. Particularly, both our simulations and experiments showed that for a wide range of DBS implantation paths, it is always possible to find an optimum coil rotation angle that maintains SAR in the tissue around the electrode at levels below background SAR.

2. Insertion of a close-fit 32-channel receive array does not increase the local SAR and does not degrade the SAR reduction performance.

3. The optimum coil rotation angle for SAR minimization can be easily and quickly found at the scanner by monitoring electrode artifact in the ${\mathrm{B}}_1^{+}$ field maps.

4. The SAR reduction strategy is not sensitive to tissue conductivity; in other words, our results are not sensitive to electrical properties of simulated head model.

This contribution provides the groundwork for the application of multichannel close-fit transmit–receive implant-friendly head coils, which will have vast applications in both clinical assessments and research studies involving patients with DBS implants. This technology will be particularly useful for SNR-sensitive applications, such as blood-oxygen-level-dependent fMRI studies that are very limited to perform with birdcage-only head coils.

METHODS

Construction of a Linearly Polarized Rotating Birdcage Transmit Coil

We designed and built a mechanically rotating linearly polarized low-pass birdcage coil on an optically clear, cast acrylic tube with outer diameter of 35.56 cm (14 inch) (84865K218, McMaster-Carr, Elmhurst, IL).

The coil consisted of 16 legs and two end rings laid out of conductive copper tape (13-mm width). Two 11pF capacitors were placed in series in each leg (Series 25, Voltronics Corp., Denville, NJ). At the drive port, a cable balun was implemented in order to suppress common mode currents. PIN diodes (Macom MA4P7446F-1091T, Lowell, MA) were soldered in the end-ring segments in order to detune the birdcage array during signal reception with the 32-channel array coil. A rotating housing that enabled smooth rotation of the coil around its axis without touching the load was designed in computer-aided design (CAD) software and built using a Fortus 360mc 3D printer (Stratasys, Eden Prairie, MN). Supporting Figure S1 shows details of the rotating housing.

A custom-made mold for an anthropomorphic head phantom was made from a numerical head model developed in our lab based on MRI of a healthy volunteer. The same model was used in finite element simulations for SAR calculations. The mold was composed of two equivalent parts (sagittal cut) that could be perfectly sealed together (similar geometry to our previous work (30)). A hole was present at the bottom of the mold to pour a mixture of 4.5% ± 5% liter distilled H₂O, 40.50 g NaCl (purity 98%, Sigma-Aldrich Corp., St. Louis, MO) and 1.2 kg of edible agar powder, which contained 4% sugar (Golden Coin Agar Agar Powder, Capital Food International, Inc., Santa Fe Springs, CA). After the phantom gel was coagulated, its complex permittivity was measured using a network analyzer (ENA series, Agilent Technologies, Santa Clara, CA) with a high-temperature dielectric probe (85070E kit, Agilent Technologies). The measured complex permittivity values were ε_r = 66:34 and σ = 0:49 Sm⁻¹. These values were comparable to electrical properties of the average human head, which was calculated as ε_r = 62:78 and a = 0.45 S/m by taking the volume-weighted average of permittivity and conductivity values of tissue classes given in Figure 1.

FIG. 1.

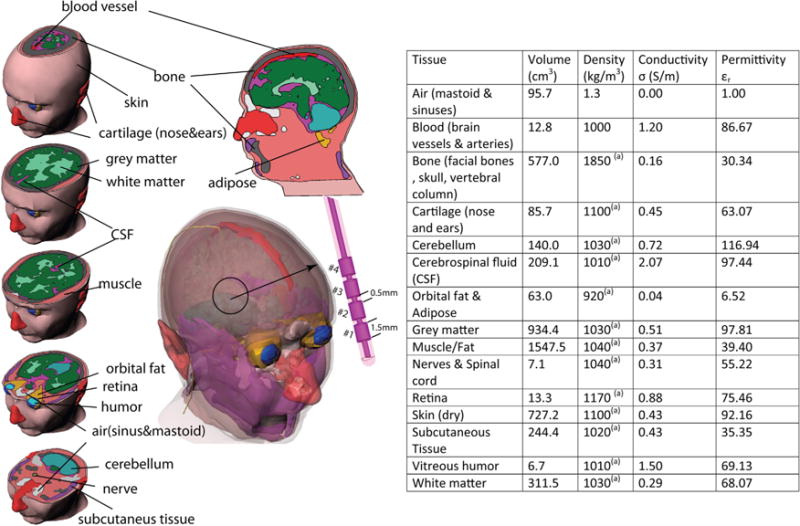
Anatomical structures segmented for the head model with related biophysical properties assigned for this study. ^(a) Ref 52.

32-Channel Close-Fit Receive Array

A close-fit 32-channel receive array with a soccer-ball tiling pattern of overlapping wire loops similar to our previous works (31,32) was modeled and incorporated into the birdcage model for simulations. The array geometry was designed in a CAD software based on an anatomically shaped three-dimensional (3D) surface consisting of a large posterior head neck part and an overlapping anterior head portion. Overlapping loop elements were then exported to the finite element method (FEM) solver for simulations. Receive coils were simulated as closed loops to allow maximum induced currents and maximum potential coupling with transmitter and DBS implant.

Numerical Models and Finite Element Method Simulations

ANSYS HFSS (high-frequency structure simulator) (ANSYS, Inc., Canonsburg, PA) and ANSYS Designer (ANSYS, Inc.) were chosen for a combined FEM-circuit analysis simulation approach because they have been shown to provide an accurate prediction of electromagnetic fields of MRI coils (33,34) and because we have successfully used them in the past to simulate brain stimulators (35). In the first step, the multiport scattering matrix of the birdcage coil in the presence of magnet gradient shield and the head model was calculated with tuning and matching circuit components substituted with equivalent lumped ports. The multiport S-parameter matrix was then exported to ANSYS circuit analyzer (ANSYS, Inc.) for tuning and matching, and the updated port voltage and current values were pushed back to the FEM model to calculate complex magnitudes of the E-field and magnetic field. A detailed description of this procedure can be found in (36).

Birdcage Coil and Head Model

A fine-grained 1 × 1 × 1 mm³ numerical head model based on MRI of a healthy volunteer adult was used for SAR calculations (see Figure 1). Details of MRI data acquisition and anatomical segmentation and postprocessing are given elsewhere (36). The model consisted of 15 different tissue classes with biophysical properties evaluated at 64 MHz (37–39). The birdcage coil was modeled with 16 legs and two end rings constructed from 13-mm copper strips (σ = 5.8 × 10 S/m) and tuned to 64 MHz. The RF gradient shield of the scanner was modeled as an open-ended cylindrical copper sheet. A 50 Ω coaxial cable was designed as the feed and connected to one of the legs over a matching port. For SAR calculations, the input voltage at the feed cable was adjusted to produce a $B_1^{+}=6\mu T$ at the center of the head model. The head model, birdcage coil, and shield were enclosed in a vacuum cylinder terminated with radiation boundary condition. Figure 2 depicts the constructed coil and details of FEM simulation setup.

FIG. 2.

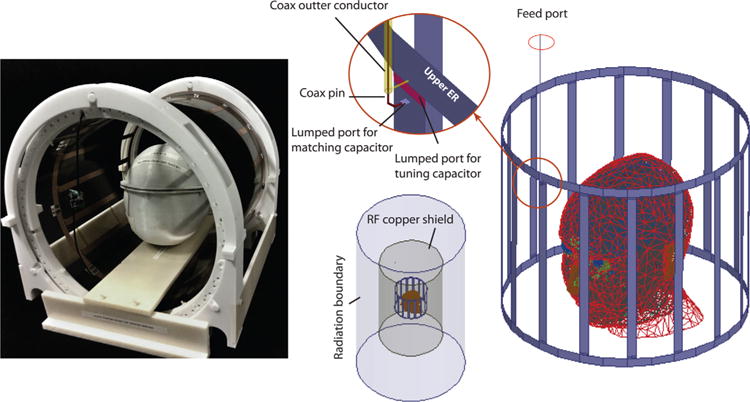
Left: the linearly polarized rotating birdcage and the anthropomorphic head phantom. The coil can be easily rotated by hand and locked in a marked position. Right: Finite element method simulation setup. Linear birdcage was fed with a 46-cm coaxial cable (inner conductor radius Rin = 0.245 mm, shield radius Rout = 0.856 mm, dielectric relative permittivity ε_r = 2:25). Positions of the head model, scanner shield, and tuning/matching ports are illustrated. RF = radiofrequency.

DBS Implant Model

We built a numerical model of DBS lead with four cylindrical electrode contacts, spaced 0.5 mm between each other (as in (40)), connected through a straight solid core, and surrounded by a hollow insulator (41). The lead architecture was developed composed of 14 segments. The first segment included four cylindrical electrodes with outer diameter of 1.27 mm and wall thickness of 150 μm, connected through a solid straight central core (see Figure 3). Electrodes and the core were made of platinum-iridium (σ = 4 × 10⁶ S/m) and were separated by a 150-μm-thick cylindrical insulation made of polyurethane (σ = 10⁻¹⁰s/m, ε_r = 3.5).

FIG. 3.

Left: Typical DBS implantation paths modeled based on conventional subthalamic nucleus DBS surgical approach as laid out in Ref 43. Right: Generic DBS lead model used in the simulations, with spacing of 0.5 mm based on lead model 3389 (Medtronic Inc., Minneapolis, MN). DBS = deep brain stimulation.

Subthalamic nucleus (STN) is one of the most widely targeted brain structures in DBS (42). The location of the STN in the FEM head model was estimated from the MRI data that the model was built from. In a common atlas-based approach, typical anatomical coordinates for the ventral and sensorimotor STN are 11 to 13 mm lateral to the midline, 4 to 5 mm ventral to the intercommisural plane, and 3 to 4 mm posterior to the midcommissural point (43). After the STN was located on the anatomical MRI data, its location in the FEM model was estimated using relative position of the sagittal midplane and ear-to-ear and nose-to-top-of-the-head distances. Different entry points were then selected based on typical angles of approach for the STN target, at ~60 degrees in anterior–posterior direction and 15 and 30 degrees from the sagittal plane respectively (43) (see Figure 3). The first segment of the DBS lead (which included the tip and the electrodes) was located between the STN and the entry point on the skull. The remaining segments of the implant were placed in the head model along the subcutaneous structure, with each wire connected to the previous one along the anterior–posterior direction. The last segment was terminated at the last axial slice of the head model, by the neck. The total length of the lead was ~40 cm.

In many practical cases, to keep the extension connector at the level of cranium and avoid positioning it at the neck, the lead is looped at the top of the head around the surgical burr hole. This configuration has been reported to affect RF-induced heating (11,24). To investigate the effectiveness of SAR reduction strategy on looped implants, we also modeled a ~50 cm lead with its extracranial portion looped twice around the entry point. The rest of the implant path was similar to the model with 15-degree-off sagittal segments.

Simulations: Mesh Settings, Numerical Convergence, and SAR Calculations

ANSYS HFSS (ANSYS, Inc.) was set to follow an adaptive mesh scheme. The algorithm generated an initial tetrahedral mesh with a density automatically decided by the software based on the solution frequency (64 MHz). The adaptive algorithm started by refining the mesh by 30% between each two iterative simulations. At each step, the maximum change in the magnitude of S-parameters, ΔS, was defined as ΔS = Max_ij|S^N_ij–S^N–1_ij|, where i and j covers all matrix entries and N represents the iteration number. The adaptive simulation continued until the threshold of ΔS < 0.01 was reached. All simulations converged after N = 4 adaptive passes. Final mesh statistics (i.e., number of elements per structure; minimum, maximum, and rms of edge lengths) were comparable across simulations. Supporting Table S1 gives mesh statistics for a representative case.

Both 1 g averaged and 10 g averaged SAR were calculated based on Institute of Electrical and Electronics Engineers Standard P1528.4 recommendation (44) using the built-in SAR calculator module in ANSYS HFSS (ANSYS, Inc.). The HFSS calculates local SAR at each mesh point as:

$$\mathit{SAR}=\frac{1}{2\mathrm{\rho }}\mathrm{\sigma }{\Vert E\Vert }^2,$$ [1]

where E is the magnitude of E-field (V/m), ρ is the mass density of the material (kg/m³), and s is the material conductivity (S/m). The averaged SAR is then calculated over a volume that surrounds each mesh point. The volume used in the 1 g or 10 g SAR estimation is determined in each mesh point by a closed surface with a volume such that the sum of the product of each material subvolume by its mass density totals either 1 g or 10 g.

For each implantation path, SAR values were calculated for an input voltage that produced $B_1^{+}=6\mathrm{\mu }T$ at the center of the head and a range of coil rotation angles. For each simulation, the maximum local SAR at electrode location (referred to as MaxSAR) was calculated as the maximum of 1 g or 10 g averaged SAR in a 2 cm × 2 cm × 2 cm cube that encompassed all four contact electrodes. The reference SAR (referred to as RefSAR) was calculated as the maximum of 1 g or 10 g averaged SAR outside of this cube, in an axial plane passing through the distal electrode contact (Figure 4).

FIG. 4.

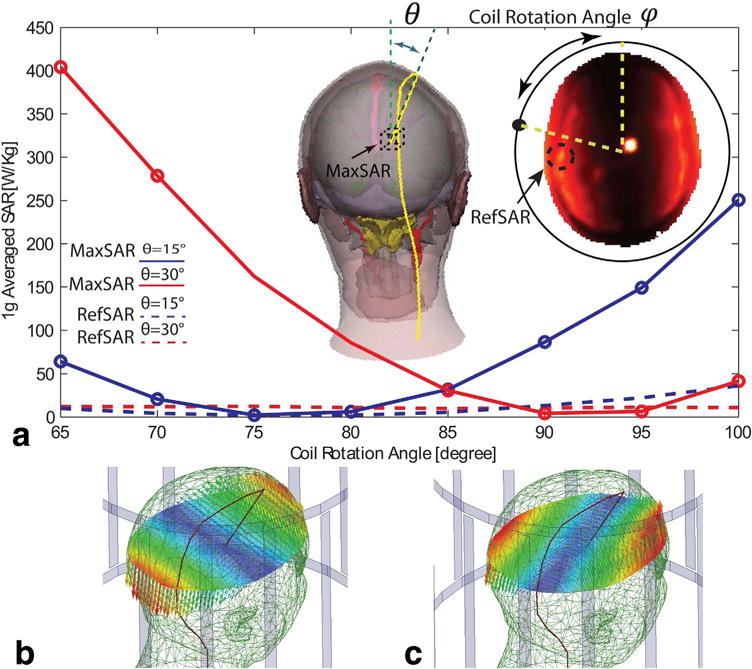
(a) MaxSAR and RefSAR values for 1g-averaged SAR in the heterogeneous head model in presence of DBS implant models with different entry angles. (b)&(c) Electric field of the linear birdcage transmitter with feed in the default position (φ = 0°) and optimum position for SAR reduction. The path of DBS lead is indicated. DBS = deep brain MaxSAR = maximum SAR; RefSAR = reference SAR; SAR = specific absorption rate.

Unwanted temperature rise occurs when the induced currents on DBS leads generate a secondary E-field, which leads to power deposition in the lossy tissue. Thus, the actual value of tissue conductivity affects the magnitude of local SAR, and a range of different conductivity values (~0.04–0.5 S/m) are usually considered in safety assessments (45). To investigate the sensitivity of the SAR reduction strategy to variations in tissue conductivity, we performed a series of simulations with a range of gray matter conductivities from 0.01 to 3 S/m at two coil rotation angles that corresponded to maximum SAR and minimum SAR.

${\mathrm{B}}_1^{+}$ Field Maps: Simulations and Measurements

In all simulations, $B_1^{+}$ maps were calculated as $B_1^{+}=0.5$ (B_1x+jB_1y) (46). Phantom measurements were performed with 18-American wire gauge isolated copper wire. Four implantation paths with wire segments roughly following the 15- to 30-degree sagittal penetration angles were tested. Experimental $B_1^{+}$ field maps were generated using a 3D actual flip-angle imaging (AFI) pulse sequence, which consisted of two identical RF pulses with a nominal flip angle of α followed by two delays TR₁ and TR_2, as described in (47). The ratio between free induction decay signals S₁ and S₂ observed after the corresponding pulses can be expressed as (47):

$$r=\frac{S_2}{S_1}\cong \frac{1+n\cos \mathrm{\alpha }}{n+\cos \mathrm{\alpha }},$$ [2]

where n = TR₂/TR_1. From these signals, the actual flip angle map can be calculated as:

$$\mathrm{\alpha }\cong {\cos }^{-1}\frac{rn-1}{n-r}.$$ [3]

We used TR₁ = 6 ms, TR₂ = 180 ms, and nominal flip angle of 60 degrees. The large dynamic range of n = 30 was chosen to capture abrupt changes of magnetic field in the vicinity of the electrode tip. Actual flip angle maps were then converted to ${\mathrm{B}}_1^{+}$ values using the relationship $B_1^{+}=\mathrm{\alpha }/\mathrm{\gamma }t$, with α being the actual flip angle, γ the gyromagnetic ratio of proton, and t the duration of applied RF pulse (800 μs).

RESULTS

Accuracy of Numerical Simulations

The accuracy of numerical simulations was verified against phantom measurements. Finite element method simulations with a homogenous head model (ε_r = 66.34 and σ = 0:49 S/m) inside the unshielded birdcage coil were performed, and the multiport scattering matrix of the loaded coil (S) was computed. The S matrix was then exported to the circuit analyzer software in which values of tuning and matching capacitors were tuned to obtain the best fit between simulated and measured one-port reflection coefficient S₁₁. Figure 5 gives the result, showing an excellent agreement between simulated and measured curves. As an extra step in model verification, a solid copper shield was incorporated into the FEM model to represent the scanner’s gradient shield. The multiport S matrix of the shielded, loaded coil was computed, and the S₁₁ curve was calculated using the same values of tuning and matching capacitors as obtained in previous step. Figure 5 also shows the simulated and measured S₁₁ curves inside the magnet bore. It can be observed that simulations perfectly predicted the upward shift in the location of the resonance frequency (error < 0.1%) and captured the loading effect of magnet bore (error < 0.4 dB).

FIG. 5.

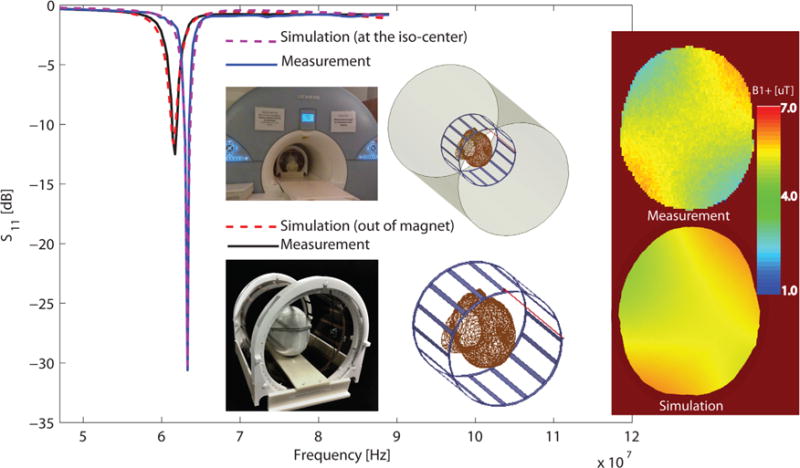
Simulations results versus measurements. Integrated computation pipeline combines finite element method simulations with radiofrequency circuit analysis and includes details of feed model. Simulation show excellent agreement between scattering parameters (S) measured both outside and inside of magnet bore. ${\mathrm{B}}_1^{+}$ maps are simulated and measured on an axial plane at 8 cm from the top of the head.

Finally, ${\mathrm{B}}_1^{+}$ field was measured experimentally and the results were compared with simulated values. A 3D AFI pulse sequence was used to obtain the actual flip angle maps inside the phantom with TR₁ = 6 ms, TR₂ = 48 ms, TE = 2.63 ms, and nominal flip angle of 60 degrees. Note that the pulse sequence parameters for model verification were different from those used for artifact imaging.

Actual flip angle maps were converted to ${\mathrm{B}}_1^{+}$ values using the relationship ${\mathrm{B}}_1^{+}=\mathrm{\theta }/\mathrm{\gamma }\mathrm{t}$, with θ being the actual flip angle, γ the gyromagnetic ration of proton (2.67e8 radT⁻¹s⁻¹), and t the duration of applied RF pulse (800 ms). In the simulations, $B_1^{+}$ maps were obtained by exciting the coax port with the same input voltage as was manually adjusted at the scanner console (~120 V). Figure 5 gives the results of simulated and measured ${\mathrm{B}}_1^{+}$ maps. Simulated fields (mean ± standard deviation 5.1 μT ± 0. 3 μT) overestimated the measurement (mean ± standard deviation 4.0 μT ± 0.5 μT) by almost 20%, which could be attributable to hardware losses that include those in cables and the transmit–receive switch.

Effect of Variation in Deep Brain Stimulation Lead Implantation Path

Figure 4 shows the MaxSAR as the function of coil rotating angle for two realistic implantation paths with entry points at 15 and 30 degrees off the midsagittal place, respectively. It can be observed that for both cases an optimum rotation angle was found, which reduced the MaxSAR to levels below the RefSAR. Details of MaxSAR and RefSAR for both 1 g averaged SAR and 10 g averaged SAR are given in Supporting Table S2 for different coil rotation angles.

Figure 6 shows the simulation results for the case of a 50-cm DBS lead with a two-turn loop around the surgical burr hole compared with the same implantation path without the loop. Details of SAR values for different coil rotation angles are given in Supporting Table S3. It can be observed that presence of the loop significantly increases SAR amplification. However, an optimum coil rotation angle could still be found that reduced the Max-SAR below RefSAR values.

FIG. 6.

MaxSAR and RefSAR values for 1 g-averaged SAR in the heterogeneous head model in presence of a deep brain stimulation implant with 15-degree off-sagittal entry angel. Simulations are performed with and without loops around the surgical burr hole. DBS = deep brain stimulation; MaxSAR = maximum SAR; RefSAR = reference SAR; SAR = specific absorption rate.

Effect of Close-Fit Receive Array

We simulated MaxSAR and RefSAR for the range of all possible coil rotation angles (φ = 0°–180°, Δφ = 5°) with and without the receive helmet. In none of the cases did the presence of the receive array increase the local SAR. Figure 7 gives the 1 g-averaged SAR in terms of coil rotating angle for the case of DBS implant with 15-degree off-sagittal penetration angle with and without the 32-channel receive array. For both cases, the input voltage has been adjusted to produce a $B_1^{+}=6\mathrm{\mu }T$ at the center of the head. The insertion of the receive array degraded coil matching (an effect that was also verified in bench measurements), which implies slight modification of coil E-fields. This affects the E-field because SAR slightly decreased with receive array insertion. Specific absorption rate reduction strategy, however, remained effective, and the same reduction was obtained when the transmitter was rotated to be at the optimum angle. Table 1 gives details of input voltages, scattering parameters, and maximum and reference SAR values for 1 g-averaged SAR.

FIG. 7.

MaxSAR values for 1 g-averaged SAR in the heterogeneous head model in the presence of a deep brain stimulation implant with 15-degree off-sagittal entry angel with and without 32-channel receive array. MaxSAR = maximum specific absorption rate; SAR = specific absorption rate.

Table 1.

MaxSAR, RefSAR, S₁₁, and Stimulating Voltage for Simulations of the DBS Implant with 15° Off-Sagittal Entry Angel, with and Without 32-Channel Helmet Receive Array.

Coil Rotation Angle	MaxSAR (1g) [W/kg]	RefSAR (1g) [W/kg]	S11 [dB]	Input Voltage [V]
DBS Lead with 15° Off-Sagittal Segment, No Receive Array
0°	1200	25	−15	115
65°	64	114	−12	113
70°	21	12	−12	112
75°	2	12	−12	110
80°	6	10	−12	110
85°	32	11	−13	109
90	86	11	−13	108
95°	149	11	−12	108
100°	251	12	−12	107
DBS Lead with 15° Off-Sagittal Segment, 32-Channel Close-Fit Receive Array
0°	844	18	−8	189
65°	28	7	−8	180
70°	8	7	−8	175
75°	2	8	−7	175
80°	6	7	−7	175
85°	22	7	−7	175
90°	55	7	−7	171
95°	90	7	−8	167
100°	142	7	−7	171

Input voltage is adjusted for each rotating angle to produce a ${\mathit{B}}_1^{+}=6\mathit{\mu }\mathit{T}$ in the center of the head.

DBS = deep brain stimulation; MaxSAR = maximum SAR; RefSAR = reference SAR; S₁₁ = one-port reflection coefficient; SAR = specific absorption rate.

Effect of Tissue Conductivity on SAR Reduction Strategy

Figure 8 shows the MaxSAR in the vicinity of electrode contacts and the RefSAR for a range of gray matter conductivities from 0.01 to 3.00 S/m, including very low and very high values to study asymptotic behavior of SAR. Simulations were performed for the lead with 30° off-sagittal penetration angle and the feed in default position (φ = 0°), as well as optimum position for SAR reduction (φ = 90°). It can be observed that for the feed at default position (φ = 0°), which corresponds to the maximum coupling between E-fields and the implant, SAR amplification is a function of gray matter conductivity with a maximum at about σ = 0.89 S/m. Specific absorption rate amplification decreases at very low tissue-resistivity values, as can be predicted from Eq. [1] for very low σ values. Specific absorption rate amplification also drops in highly conductive tissue because the E-field declines with increasing electrical conductivity due to RF losses. On the contrary, the implant is virtually invisible to the coil for the coil at optimum position (σ = 90°). It can be observed from Figure 8 that, in this case, local SAR at the electrode tip is below background SAR for the whole range of tissue conductivities and thus is not sensitive to tissue properties. It is important to note, however, that the values of the maximum SAR and its dependencies on tissue properties change with the implant trajectory and properties of tissues that it passes through. Local changes in tissue conductivity (due to edema or scarring, for example) could lead to different (and potentially higher) SAR values. A more detailed study of effects of model heterogeneity around the lead trajectory is needed to better address this issue.

FIG. 8.

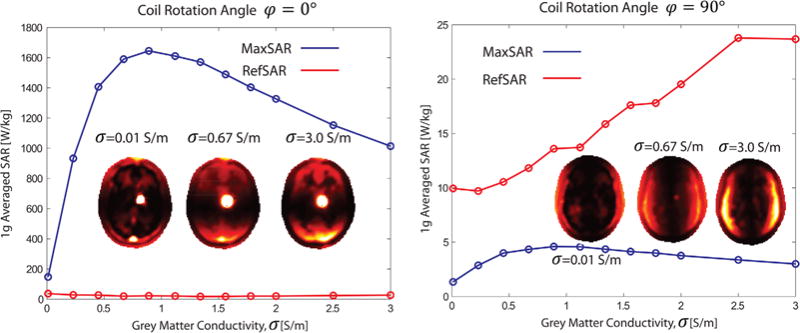
MaxSAR and RefSAR for 1 g averaged SAR inside the inhomogeneous head model for a range of gray matter conductivities. Left: coil in default position (feed up), Right: coil with optimum rotation angle for SAR reduction. MaxSAR=maximum SAR; RefSAR=reference SAR; SAR=specific absorption rate.

${\mathrm{B}}_1^{+}$ Field Maps

To be able to use the outlined SAR reduction technique in clinical settings, it is important to have a marker generated and monitored at the scanner that can predict the optimum coil rotation angle. Because induced currents on the DBS lead, which are responsible for SAR amplification, also produce a transient magnetic field around the wire, which causes artifacts in B₁ field, the visual artifact in B₁ field maps may be used to determine the optimum coil rotation angle (26,48). Figure 9 shows the simulated percentage of change in ${\mathrm{B}}_1^{+}$ field calculated as $100({B_1^{+}}_{\mathrm{Max}}-{{\mathrm{B}}_1^{+}}_{\min }/{{\mathrm{B}}_1^{+}}_{\mathrm{Max}})$ in a 5 mm × 5 mm area around the tip of DBS electrode for different coil rotation angles. It can be observed that, as predicted, the location of minimum ${\mathrm{B}}_1^{+}$ image artifact coincides with the location of minimum SAR. Figure 9 also shows experimental results with implanted wires and actual DBS leads.

FIG. 9.

(a) Simulation results showing visual artifact in ${\mathrm{B}}_1^{+}$ field maps vs. 1g averaged SAR for different coil rotation angles. As predicted, the location of minimum ${\mathrm{B}}_1^{+}$ artifact coincides with the location of minimum SAR amplification. (b) Anthropomorphic head phantom with implants used in artifact measurement. (c)&(d) Several implantation paths with typical subthalamic nucleus deep brain stimulation surgical approach were studied. In all studies, we were able to find an optimum coil rotating angle that significantly reduced the electrode artifact in ${\mathrm{B}}_1^{+}$ field maps. SAR = specific absorption rate.

DISCUSSION

This work represents the feasibility of using an ensemble of a rotating birdcage transmitter and a close-fit receive array to significantly reduce local SAR during MRI of patients with implanted DBS electrodes. The idea of generating and steering electric-field free regions in MR transmit coils to reduce implant heating was recently suggested by Atalar’s group (19,21) and adopted in studies suggesting design of implant-friendly modes in parallel transmit volume coils at 3T (22). In all of these studies, the proof of concept was applied on simple wire representation of DBS leads with segments that all lie on the same plane. To the authors’ knowledge, the only study that has reported on nonplanar (i.e., helical) wire implants is that of Eryaman et al. (21), which concluded that elliptically polarized birdcage transmitters are required to reduce the heating of such leads. Typical DBS implantation paths, however, have wire segments that could be up to 30 degrees out of plane (43). Moreover, in practice the excessive extracranial part of the lead is usually looped around the surgical burr hole. Because the SAR reduction strategy based on generating and steering an E-field—free region works only if the implant can be fully contained in this region, it is crucial to investigate whether technique works in clinically realistic situations. This is important because, even if a portion of the lead remains outside of the zero E-field region, there is a risk that RF currents are induced on the whole lead wire.

In this work, we showed that the null E-region of a rotating linear birdcage transmitter is thick enough at 1.5 T to fully encompass long DBS leads with wire segments that are up to 30 degrees out of plane, as well as leads with looped segments around the entry point to the skull. We simulated DBS implantation path based on conventional STN DBS surgical approach, and for all simulation scenarios we were able to find an optimum coil rotation angle that reduced SAR at the tip of the electrode to levels below the background SAR.

The optimum coil rotation angle, however, depends on DBS lead path and geometry, and thus has to be determined for each individual patient separately. We demonstrated that this can be done for each patient using a $B_1^{+}$ field mapping pulse sequence because the location of minimum visual electrode artifact on $B_1^{+}$ field maps coincides with the location of minimum SAR amplification. In our phantom experiments with both implanted wires and actual DBS electrodes, we were able to find the optimum rotation angle with two to three adjustments using a quick 3D AFI $B_1^{+}$ map sequence (< 2 min). This means that, for each individual patient, it will take less than 6 minutes to adjust the coil at its optimum position prior to the high-resolution anatomical or functional scans. However, it is important to note that typical AFI B1+ map sequences have higher SAR levels compared to current DBS guidelines (0.64–1.6 W/kg). Thus, it is important to develop and use specific pulse sequences that are in compliance with current limits.

CONCLUSION

Thus far, studies that have investigated SAR reduction strategies based on manipulation of transmit coil E-field have used volume transmit–receive coils. Application of close-fit receive arrays is shown to increase the SNR up to fivefold at the level of cortical tissues and up to twofold at the level of deep brain structures that are direct targets of DBS (26–28). This can be particularly useful at lower magnetic field intensities, which are currently recommended for DBS imaging. Receive arrays, however, can potentially change the RF field distribution of the transmitter and are shown to increase local and global SAR of transmitters at higher fields (7 T)(29). This SAR increase is highly sensitive to the geometry and type of the receiver as well as transmit coil, and thus should be investigated for each specific coil system. In our case, the insertion of a 32-channel close-fit helmet array into the rotating birdcage transmitter reduced maximum and reference local SAR at all rotation angles. This means that the ensemble of linear rotating birdcage and 32-channel helmet array can be considered for postoperative DBS imaging at its current SAR labeling (maximum ${\mathrm{B}}_1^{+}$ rms of 2 μT, or total head SAR < 0.1 W/kg according to (13)). Defining a higher safe SAR limit, however, needs a more comprehensive study that accounts for uncertainty budget due to variations in all possible implantation paths, diameter, and location of looped segments, as well as uncertainties due to patient motion inside the coil.

Limitations

It is important to note several limitations of the present work. First of all, we report results of numerical simulation of SAR distribution and have not performed measurements to calculate the associated temperature rises. Although SAR has been routinely used as an indirect quantitative measurement for clinical MRI procedures when conductive implants are present (11,48), some studies have shown that reported whole-body SAR values that lead to the same temperature rise in implants significantly varied across different MRI scanners (49). Moreover, local SAR values do not always directly translate to temperature rise because factors such as thermal conduction and perfusion should be taken into account (50). Consequently, when it comes to patient safety, temperature calculations/measurements should be considered instead of SAR monitoring alone.

Another limitation of the present study is due to simplifications in the numerical models of DBS lead. Although we attempted to include geometrical features of the lead based on available Medtronic (Medtronic Inc., Minneapolis, MN) manuals (40), the realistic lead system defers from the present study in its details. For example, the electrode contacts are usually connected through spiral wires (41) (and not a solid straight core). The effect of including such features on results of numerical modeling remains to be tested.

Finally, although we have shown that in our case the coil rotation angle that generated minimal ${\mathrm{B}}_1^{+}$ artifact coincided with minimum local SAR values, SAR distribution in general is a function of both ${\mathrm{B}}_1^{+}$, ${\mathrm{B}}_1^{-}$, and B_1z fields (51). This warrants a thorough characterization of SAR dependencies on B₁ profile of a particular RF coil to devise a reliable mechanism for quantitative estimation of SAR reduction.

Supplementary Material

Supp Info

Supp. FIG. S1. The birdcage was constructed on an optically clear 14” outer diameter cast acrylic tube. End caps (blue), one with axial holes equally spaced 5 degrees apart, were secured to the birdcage ends. The end caps rested on 4 guide wheels located on the sliding frames, allowing the birdcage to rotate freely. Once the desired rotation has been obtained, a locking pin is inserted into the rotation lock mechanism and through an axial hole, securing the birdcage in the desired position. The entire assembly rest on two guide rails, allowing the birdcage to be moved to facilitate subject access to the array coil.

Supp. Table S1. Mesh statistics for the head model and DBS lead with 15° off-sagittal wire segments. Statistics for leads with 30 off-sagittal segments and looped leads were comparable.

Supp. Table S2. MaxSAR and RefSAR values for different DBS implantation paths and different coil rotation angles. Simulations are performed without the 32-ch receive array. SAR values are nomalized for a ${\mathrm{B}}_1^{+}=6\mathrm{\mu }T$.

Supp. Table S3. MaxSAR and RefSAR for 1g averaged SAR in the inhomogeneous head model in presence of a DBS implant with 15° off-sagittal entry angel, with and without loops around surgical burr hole. Simulations are performed without the 32-ch receive array. SAR values are nomalized for a ${\mathrm{B}}_1^{+}=6\mathrm{\mu }T$.