Mitigation of Partial-Volume Effects in Susceptibility-Based Oxygenation Measurements by Joint Utilization of Magnitude and Phase (JUMP)

Abstract

Purpose

Susceptibility-based blood oxygenation measurements in small vessels of the brain derive from GRE phase, and can provide localized assessment of brain function and pathology. However, when vessel diameter becomes smaller than the acquisition voxel size, partial-volume effects compromise these measurements. In this study, a technique is proposed to improve the reliability of vessel oxygenation estimates in the presence of partial-volume effects.

Methods

Intravoxel susceptibility variations are present when a vessel and parenchyma experience partial-volume effects, modifying the voxel’s GRE phase signal and attenuating the GRE magnitude signal. By Joint Utilization of Magnitude and Phase (JUMP), both vessel susceptibility and voxel partial-volume fraction can be estimated, providing measurements of venous oxygen saturation (Y_v) in straight, nearly-vertical vessels that have improved robustness to partial-volume effects.

Results

JUMP is demonstrated by estimating vessel Y_v in numerical and in vivo experiments. Deviations from ground truth of Y_v measurements in vessels tilted up to 30° from B₀ were reduced by over 50% when using JUMP compared to when using phase-only techniques.

Conclusion

JUMP exploits both magnitude and phase data in GRE imaging to mitigate partial-volume effects in estimation of vessel oxygenation

Introduction

Accurate, quantitative, in vivo measurements of brain oxygenation have many clinical and scientific applications, including identification of penumbra during ischemic injury (1), monitoring of cancer therapy (2), and calculation of the cerebral metabolic rate of oxygen (CMRO₂) (3). Several techniques have been developed to obtain venous oxygen saturation (Y_v) measurements non-invasively using MRI. These include quantitative BOLD (4) and QUIXOTIC (5) for microvasculature measurements; MRI susceptometry (6) and Quantitative Susceptibility Mapping (QSM) (7) for local macrovasculature measurements; and TRUST (8) for global measurements in large, draining veins. In particular, susceptibility-based techniques such as QSM and MRI susceptometry have been used for Y_v assessment in many clinical and pre-clinical studies (9–14), and qualitative Susceptibility-Weighted Imaging (SWI) has found increasing clinical usage to evaluate oxygenation based on vessel contrast (1,15). Susceptibility-based techniques are relatively easy to adopt in the clinic, as they derive from the phase of a gradient-echo acquisition.

Y_v estimation from susceptibility requires the isolation of pure venous blood signal from a vascular structure. Whole-brain Y_v techniques can reliably isolate blood signal from large draining veins, but these do not provide regional Y_v information that would be important for functional or pathological assessment. We are interested measuring Y_v in smaller vessels, as they reflect local physiology. However, studies measuring Y_v in small vessels by MRI susceptometry and QSM suffer from partial-volume effects between veins and parenchyma (11,13,14). This excludes many visible venous voxels from QSM analysis, limiting both the number of data points that can be analyzed for a given blood vessel, and the minimum radius of blood vessels that can be analyzed. In susceptibility-based imaging, it has been observed that partial-volume effects between veins and parenchyma lead to attenuation of the magnitude signal (16), a fact which is exploited in clinical SWI (15). However, a proper treatment of and correction for partial-volume effects in QSM oxygenation measurements is currently lacking.

We propose a novel technique utilizing both the magnitude and phase of the GRE acquisition to mitigate partial-volume effects in Y_v measurements. We call this Joint Utilization of Magnitude and Phase (JUMP). Prior studies utilize only the signal phase (QSM, MRI susceptometry) or signal magnitude (qBOLD, TRUST), for Y_v estimation, and thus only have a single measurement per voxel. This single measurement does not provide enough information to characterize both partial-volume fraction and Y_v. However, the full complex GRE signal provides two measurements from the acquisition – magnitude and phase - which together provide sufficient information to estimate both Y_v and the degree of partial-voluming if a vein can be modeled as a long, straight cylinder.

QSM techniques have employed the GRE magnitude image as a structural prior to aid in solution of the underdetermined dipole inversion problem (7,17). However, these optimization techniques utilize the phase image alone to enforce data consistency, and thus suffer from partial-volume effects. Joint use of the magnitude and phase signals has been applied to GRE data for tractography by calculating the eigenvectors shared by the $R_2^{\ast }$ and susceptibility tensors (18), and to reduce banding artifacts due to B₀ inhomogeneity in balanced steady-state free procession (bSSFP) images (19).

In this work, we describe JUMP and demonstrate its efficacy to estimate venous susceptibility values and Y_v from vessels that are nearly parallel to the main magnetic field. JUMP is compared to traditional MRI susceptometry and QSM-based measurements of Y_v from simulated and in vivo experiments acquired at different image resolutions.

Theory

Oxygen Saturation and Magnetic Susceptibility

Hemoglobin in blood is strongly paramagnetic relative to water when in the deoxygenated state (20). In whole blood, this can be expressed as a relationship between its magnetic susceptibility Δχ and its absolute fractional hemoglobin oxygen saturation, Y_v:

$$\mathrm{\Delta }\chi ={\chi }_{do}·\mathit{Hct}·(1-Y_v)$$ (1)

χ_do is the susceptibility difference between fully oxygenated and fully deoxygenated red blood cells, and is taken to be 0.27 ppm (cgs) (9, 21). The blood hematocrit, Hct, is taken to be 0.38 for females and 0.42 for males (3,22). Our goal is to use MRI signals to measure the susceptibility shift in a vein (relative to water) and quantify its Y_v through the linear relationship in Eq. 1.

Susceptibility-Induced Field Variations

An object with non-zero magnetic susceptibility relative to water (Δχ), when placed in a magnetic field B₀, will generate a spatially-varying magnetic field pattern that can be observed with MRI. For a general vessel with arbitrary orientation and geometry, this field perturbation has a complex relationship with the underlying susceptibility distribution that is determined by the intrinsic dipole imaging kernel.

If a straight blood vessel is modeled as a long parallel cylinder, however, the estimation of susceptibility inside the vein is simplified and Eq. 1 can then be used for Y_v quantification (16). For a long, cylindrical object with susceptibility Δχ oriented with its longitudinal axis at an angle θ to B₀, the induced field inside the cylinder, ΔB_0,cyl, will be:

$$\mathrm{\Delta }{B}_{0,\mathit{cyl}}=\mid B_0\mid ·4\pi \mathrm{\Delta }\chi ·\frac{(3{cos}^2\theta -1)}{6}$$ (2)

The field outside the cylinder, B_out, will be:

$$\mathrm{\Delta }{B}_{0,\mathit{out}}=\mid B_0\mid ·4\pi \mathrm{\Delta }\chi ·\frac{1}{2}{\left(\frac{R}{r}\right)}^{2}cos2\varphi {sin}^2\theta$$ (3)

Here, R is the radius of the cylinder, r is the distance from the cylinder’s axis, and ϕ is the azimuthal angle about the cylinder (23). Since this term is proportional to sin² θ, it is small for small tilt angles θ between the vessel and B₀. For this reason, we will assume that ΔB_0,out = 0, which removes any dependence on the parameters r, R, and ϕ.

Partial-Volume Effects and GRE Signal

Suppose we overlay a grid on an in-plane vessel where the cells represent the voxels of a GRE acquisition (Figure 1a). For small vessels, many voxels/grid cells that intersect the vessel will contain compartments of both vein and parenchyma – i.e. they suffer from partial-volume effects (Figure 1b). Assuming linear phase evolution with time, the phase in each compartment is equal to:

$$\mathrm{\Delta }{\phi }_{\mathit{cyl}/\mathit{out}}=\mathrm{\Delta }{B}_{0,\mathit{cyl}/\mathit{out}}·2\pi \gamma ·TE$$ (4)

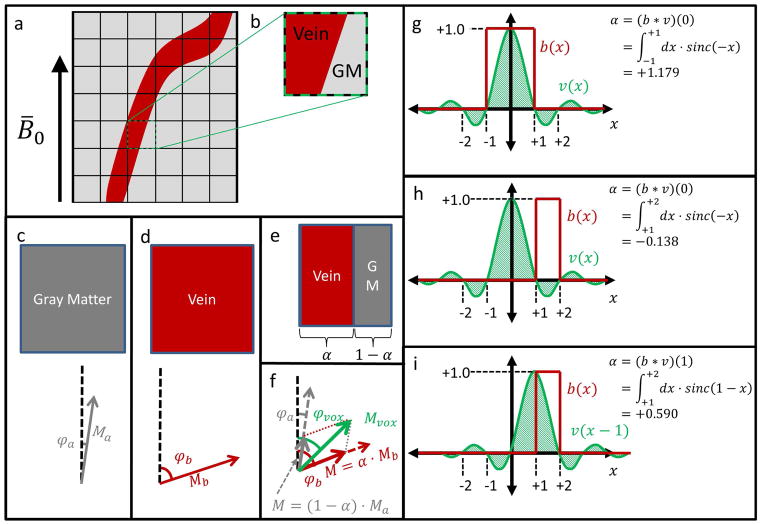
Figure 1.

(a) A small vessel relative to the acquisition voxel size will suffer from partial-volume effects. (b) Such a voxel with partial-volume effects overlays two distinct tissue regions: vein and parenchyma (eg gray matter). (c) A voxel containing entirely gray matter has a complex signal with magnitude M_a and phase φ_a. (d) A voxel containing entirely venous blood has a complex signal with magnitude M_b and phase φ_b. (e) A voxel containing regions of each tissue consists of a fraction α of blood, and a fraction 1 − α of gray matter. (f) The partial-volume voxel signal will be the sum of the signals in (c) and (d) weighted by the fractions in (e). φ_a, φ_b, M_a, M_b, α, φ_vox, and M_vox are defined in Table 1. (g) Simplified 1D example where the vessel binary mask b(x) coincides with the main lobe of the voxel function v(x), and α > 1. (h) 1D example where b(x) coincides with a negative lobe of v(x), and α < 0. In (g) and (h), the different limits of integration represent the different spatial extents of the respective blood vessels. (i) For the same system as in (h), an adjacent voxel has positive α with a larger magnitude.

We can then use a complex signal addition model akin to Dixon methods (24) to describe how the measured complex voxel signal depends on the tissue parameters and the partial-volume fraction α (Figure 1c–1f). For a given voxel, α represents the fraction of that voxel’s signal that originates in the blood vessel compartment, which is not necessarily the physical fraction of the ideal, rectangular voxel that consists of blood. This is because of the sinc spatial voxel function associated with an MRI acquisition, where sinc(x) = sin(πx)/(πx).

As a consequence, α is given by a convolution between a sinc function (representing the voxel) and a shifted rect function (representing blood vessel position). For particular vessel sizes and positions, α can be either larger than 1 or less than 0. This illustrated in two simplified 1D cases in Figure 1g, where α > 1, and 1h, where α < 0. For this study, it was assumed that α ∈ [−0.16, 1.39], as detailed in the Appendix section Partial-Volume Fraction α. Voxels with negative α necessarily have less than 16% signal contribution from blood, and are immediately adjacent to a voxel with larger, positive α, as illustrated in Figure 1i. As a consequence, we do not consider such voxels in the remainder of this work, as we can always use an adjacent voxel with much larger signal.

Using the parameters in Table 1, we find that the measured voxel magnitude and phase are equal to:

$$M_{\mathit{vox}}=\sqrt{{\alpha }^2{M}_b^2+{(1-\alpha )}^2{M}_a^2+2\alpha (1-\alpha )M_a{M}_b\text{cos}({\phi }_b-{\phi }_a)}$$ (5)

$${\phi }_{\mathit{vox}}={\phi }_a+{tan}^{-1}\left[\frac{sin({\phi }_b-{\phi }_a)M_b\alpha }{cos({\phi }_b-{\phi }_a)M_b\alpha +M_a(1-\alpha )}\right]$$ (6)

$${\phi }_b=\mathrm{\Delta }{\phi }_{\mathit{cyl}}(Y_v,\theta ,TE)=2\pi \gamma ·TE·\mid B_0\mid ·4\pi \mathrm{\Delta }\chi ·\frac{(3{cos}^2\theta -1)}{6}$$ (7)

Table 1.

Two-compartment signal model parameters

Parameter	Physical Meaning	Known or Unknown?
α	Fraction of voxel comprised of vein (quantifies partial-volume effects)	Unknown model parameter
Yv	Venous blood oxygenation	Unknown model parameter
φa	Spin phase in parenchyma compartment	Approximated as ≈ 0
φb	Spin phase in blood compartment	Function of Yv and θ
Ma	Parenchyma signal magnitude	Known from signal model
Mb	Blood signal magnitude	Function of Yv
K	Absolute signal intensity scale factor	Known from image
θ	Blood vessel tilt angle relative to B0	Known from image
φvox	Voxel phase in acquired image	Known from image
Mvox	Voxel magnitude in acquired image	Known from image

We assume extravascular magnetic field equals 0. Further, susceptibilities of gray matter, white matter, and CSF are an order of magnitude lower than typical venous blood susceptibilities (25–27) and are comparable to the oxyhemoglobin susceptibility, which is typically ignored (28). Thus, we make the approximation that phase in the parenchyma φ_a = 0.

M_a and M_b are the magnitude signal intensities for parenchyma and venous blood, respectively, for voxels without partial-volume effects. We assume M_a and M_b both undergo monoexponential $T_2^{\ast }$ decay.

For parenchyma:

$$M_a(TE)=K·0.0721·e^{-\raisebox{1ex}{$TE$}\!\left/ \!\raisebox{-1ex}{$66.0ms$}\right.}$$ (8)

And for blood:

$$M_b(TE,Y_v)=K·0.0786·e^{-(TE·R_2^{\ast }(Y_v))}$$ (9)

$$R_2^{\ast }(Y_v)=17.5+39.1·(1-Y_v)+119·{(1-Y_v)}^2$$ (10)

The derivation of Eqs. (8–10) is given in the Supporting Appendix section Tissue GRE Signal Magnitude. The constant K describes the absolute signal intensity, and varies slowly across an image (29). Since our magnitude signal measurements M_vox are in absolute scanner units, we include the absolute signal intensity K as an unknown parameter. K is calculated from a gray matter ROI near each vessel at each TE (Figure 4b). This measurement is potentially affected by CSF contamination (30) and by vascular microstructure variations in gray matter (31). However, these effects are expected to be small in JUMP, and are ignored (see Appendix sections CSF Contamination in Gray Matter Voxels and Gray Matter Magnitude Signal Estimation).

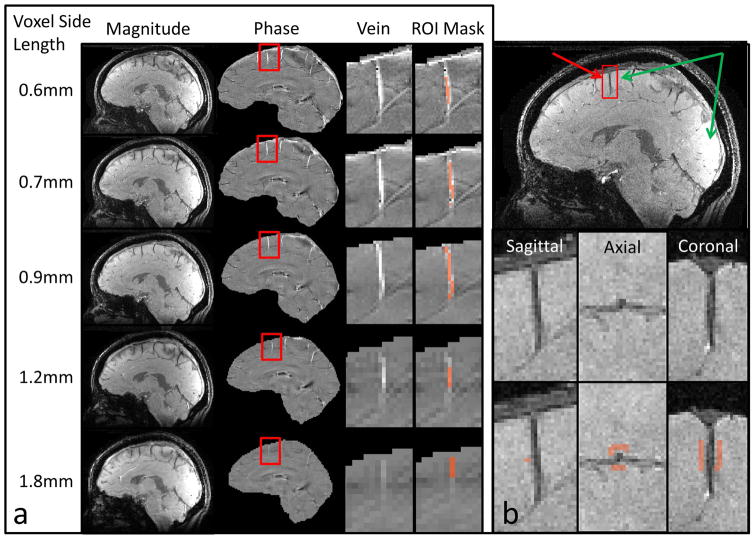
Figure 4.

(a) in vivo data acquired from one subject at all five native resolutions showing: GRE magnitude images; GRE phase images; Close-up of the phase image, centered on highlighted vein; Close-up showing vein ROI mask. (b) GRE magnitude image. Green arrows illustrate the signal variation due to inhomogeneous coil sensitivities. To estimate the background bias field, the signal is averaged over a rectangular gray matter ROI proximal to the vessel of interest.

The calculation of blood phase in the signal model requires knowledge of the vessel tilt angle θ with respect to B₀ (Eq. 7). This angle is determined by fitting the set of voxel coordinates along the centerline of the vein of interest to a line.

Parameter Estimation from Signal Magnitude and Phase

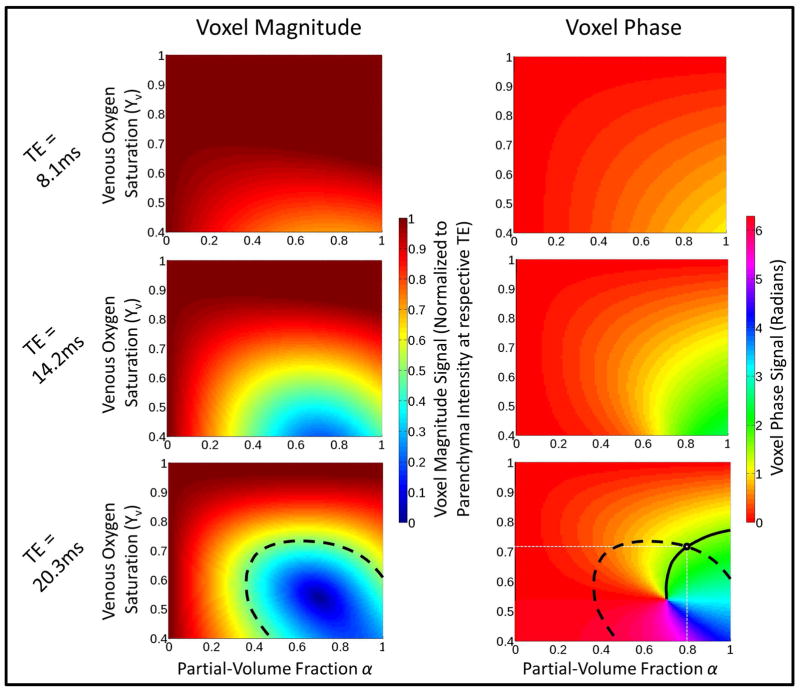
The two-compartment signal model is described by Eqs. 1 and 5–10 and the parameters in Table 1. The goal of JUMP is to calculate Y_v and α for a voxel given M_vox and φ_vox. Figure 2 shows M_vox and φ_vox, for all possible choices of α and Y_v at TE of 8.1ms, 14.2ms, and 20.3ms at θ = 20°. The dashed curves illustrate how a given measurement of M_vox determines a particular contour in (α, Y_v)-space. Likewise, the solid curves show how a measurement of φ_vox specifies a different locus of such points. The intersection of these sets is, in general, a single point (α̂, Ŷ_v), so that a single complex signal measurement (φ_vox, M_vox) provides enough information to determine both the partial-volume fraction and the phase inside the vein. Due to the form of Eqs. 1 and 5–10, there are no analytical expressions for α̂ and Ŷ_v in terms of other parameters. Therefore, we solve for α̂ and Ŷ_v with the following least-squares minimization problem:

$$\underset{\widehat{\alpha },{\widehat{Y}}_v}{min}\left[\sum _i{\Vert {\widehat{M}}_{v,i}(\widehat{\alpha },{\widehat{Y}}_v)·e^{j{\widehat{\phi }}_{v,i}(\widehat{\alpha },{\widehat{Y}}_v)}-M_{v,i}·e^{j{\phi }_{v,i}}\Vert }^2\right]$$ (11)

where the i index indicates the i-th echo time. This minimization problem requires the measured complex signal vectors at each echo time (M_v,i, φ_v,i) to match those predicted by the model (M̂_v,i and φ̂_v,i), and uses the sum of the ℓ₂ norms of the complex residuals as a cost function. The least-squares formulation allows for complex data from multiple echoes to be simultaneously used to solve for α̂ and Ŷ_v. For the solution to Eq. 11 to be physically meaningful, we require: Ŷ_v ∈ [0,1] and α̂ ∈ [−0.163,1.39]. The range of acceptable α̂ derives from the sinc-shaped voxel functions inherent in the MRI acquisitions and the assumption that blood vessels are 1D cylinders. A detailed analysis of α is found in the Supporting Appendix section Partial-Volume Fraction α. Solutions of Eq. 11 that fall on the corners of the Ŷ_v - α̂ range are assumed to be unreliable and are discarded.

Figure 2.

Voxel magnitude intensity and signal phase for different percent hemoglobin oxygen saturation (Y_v) and partial-volume fraction (α) choices at TE of 8.1ms, 14.2ms, and 20.3ms. A voxel magnitude signal of 0.5 at TE=20.3ms is shown with the dashed line. This line illustrates the set of possible (α, Y_v) pairs that correspond this magnitude. Similarly, a phase measurement of 1.5 rad is shown by the solid line, and specifies a different set of possible (α, Y_v) pairs. The intersection of the two curves determines a single possible solution of (α = 0.78, Y_v = 0.715)

It is also possible with JUMP to obtain a single measurement of Ŷ_v for a vessel as opposed to a separate Ŷ_v measurement for each voxel. This is done by modifying the minimization problem in Eq. 11 to minimize the sum of the residuals from all voxels simultaneously while requiring that Ŷ_v be the same for each voxel:

$$\underset{\{{\widehat{\alpha }}_k\},{\widehat{Y}}_v}{min}\left[\sum _k\sum _i{\Vert {\widehat{M}}_{v,i}({\widehat{\alpha }}_k,{\widehat{Y}}_v)·e^{j{\widehat{\phi }}_{v,i}({\widehat{\alpha }}_k,{\widehat{Y}}_v)}-M_{v,ik}·e^{j{\phi }_{v,ik}}\Vert }^2\right]$$ (12)

In this minimization, the sum over i adds the residuals at different TE, and the sum over k adds those from different voxels. {α̂_k} represents the set of partial-volume fractions for all voxels. This approach, which we call Multi-Voxel JUMP (MV-JUMP) reduces the total number of degrees of freedom in the optimization at the cost of ignoring variation in Y_v within a set of voxels.

In all cases, measured voxel phase is the signal phase at a particular value of TE, and not a difference in signal phase between multiple TEs. The distinction is important when partial-volume effects are present, as they cause nonlinear phase signal evolution with TE. This can be seen in Eqs 6 and 7, where blood phase (φ_b) evolves linearly with TE, but the measured voxel phase φ_vox does not linearly depend on φ_b.

Methods

Simulation Experiments – Numerical Vessels

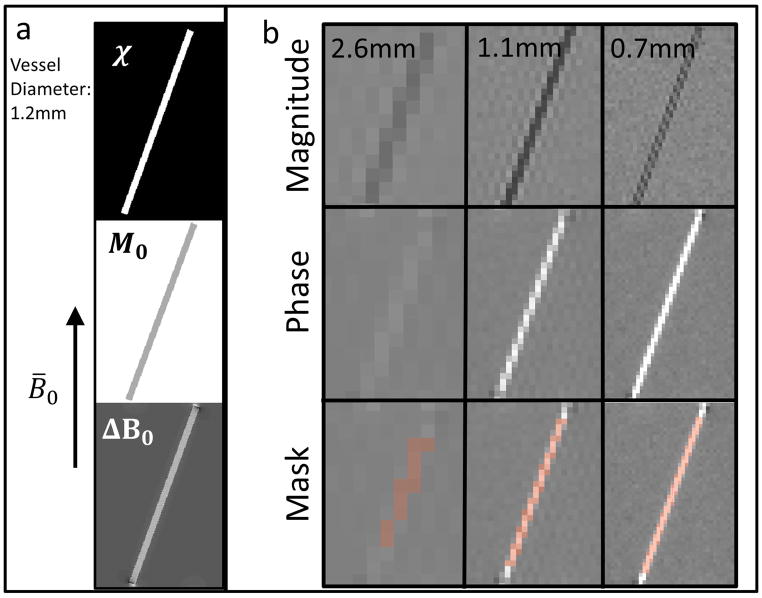
Numerical vessels were created with a physiological range of six susceptibility values corresponding to Y_v values between 0.4 and 0.9, and were placed in a background with susceptibility equal to zero. The numerical vessels had a radius of 1.2mm, and were created at a resolution of 0.12mm isotropic. Vessels with tilt angle relative to B₀ of 0° to 40° were simulated in 10° increments. Vessels with offsets relative to the field of view of 0mm, 0.48mm, and 0.96mm were simulated by shifting the vessel location in the transverse plane. Corresponding magnitude intensity maps for the vessel and surrounding parenchyma were also created using Eqs. (8–10). The susceptibility maps were convolved with the dipole kernel (32,33) to generate ΔB₀ maps. Using the dipole kernel imposes a physically correct model on the system that does not assume the extravascular field, ΔB_0,out, is equal to zero when calculating the magnetic field pattern induced by a susceptibility cylinder. Signal phase maps were then created by scaling the ΔB₀ maps via Eq. 4, assuming echo times (TE) of 8.1ms and 20.3ms and a B₀ field of 2.89T. Using this phase map and the intensity maps, complex signal maps were generated. Complex Gaussian noise was then added such that the SNR of the simulated acquisitions matched the SNR of the in vivo acquisitions obtained in this study with a 32-channel surface coil (SNR = 20 at 0.6mm isotropic voxel size). Figure 3a shows the susceptibility, magnetization, and ΔB₀ map for vessel tilt angle of 20°.

Figure 3.

(a) Susceptibility (χ), magnitude signal (M₀), and field perturbation (ΔB₀) maps used for simulation. (b) Representative simulated acquisitions at 2.6mm, 1.1mm and 0.7mm isotropic voxel size. The magnitude image, phase image, and vessel ROI mask are shown.

Low-resolution acquisitions with 18 voxel sizes between 0.49mm and 6.00mm isotropic were simulated by truncating the high-resolution k-space data to the appropriate size and applying an inverse DFT. Figure 3b shows example simulated low-resolution magnitude and phase images acquired at 2.6mm, 1.1mm, and 0.7mm isotropic voxel sizes. Vessel ROI masks were manually identified from the low-resolution acquisitions and analyzed with the processing pipeline (described below). Example vessel ROI masks are shown in Figure 3b.

For each vessel and acquisition, ground truth α-maps and JUMP-estimated α̂-maps were created. Maps of extravascular magnetic field were also created to analyze the effects of vessel susceptibility on parenchyma field offset.

Simulation Experiments – Retrospective Analysis of in vivo Data

Previously-published in vivo GRE data were analyzed (28). These acquisitions had a native resolution of 0.6 × 0.6 × 0.6mm³, and were numerically cropped in k-space to simulate acquisitions with voxel sizes of 1.2 × 1.2 × 1.2 mm³, 1.8 × 1.8 × 1.8 mm³, and 2.4 × 2.4 × 2.4mm³. A single pial vessel was identified for analysis.

In vivo Experiments

Four subjects (2 male, 2 female) were scanned with IRB approval on a 3T Siemens Trio system. Flow-compensated GRE images were acquired at five resolutions: 0.6 × 0.6 × 0.6 mm³, 0.7 × 0.7 × 0.8mm³, 0.9 × 0.9 × 1.0mm³, 1.2 × 1.2 × 1.5mm³, and 1.8 × 1.8 × 1.8 mm². Sequence parameters for all acquisitions were: TR = 30ms; TE = 8.1ms, 20.3ms; flip angle = 15°; SENSE acceleration factor R=2 × 2; bandwidth = 260Hz/pixel; field of view = 224 × 189 × 144mm³. Acquisition times varied between 10m23s (0.6 × 0.6 × 0.6 mm³) to 1m21s (1.8 × 1.8 × 1.8mm³), and matrix sizes varied from 384 × 324 × 240 to 128 × 108 × 80. Data were acquired with the product 32-channel head coil, and individual coil data were saved for all acquisitions.

Separate low-resolution GRE acquisitions were acquired for coil sensitivity estimation with the following parameters: TR = 4ms; TE = 1.68ms; flip angle = 5°; bandwidth = 1000Hz/pixel; resolution = 1.8 × 3.0 × 3.0mm³; field of view = 224 × 189 × 144mm³; acquisition time (TA) = 16s. Data were acquired with the product 32-channel head coil and with the body coil, and individual coil data were saved. SNR was not explicitly matched between different-resolution acquisitions, and a single average was acquired for each resolution.

Reconstruction and coil data combination was performed with ESPIRiT/SENSE using the Berkeley Advanced Reconstruction Toolbox (34). Brain masks for further analysis were created from the reconstructed magnitude images using FSL BET (35). Phase images were unwrapped with the Robust Unwrap algorithm (36). Background field removal was performed with SHARP (37) using the Fast QSM Magnitude Toolbox (38). Figure 4a shows sagittal sections of representative magnitude and SHARP phase images for all resolutions, respectively.

Processing Pipeline

Data from numerical simulations and in vivo experiments were analyzed with the same pipeline. Unwrapped phase maps with background variations removed were processed with the Fast QSM Magnitude Toolbox to generate L1-regularized susceptibility maps. ROI masks for nearly-vertical veins were then manually identified from susceptibility maps and SHARP phase maps at all resolutions (Figure 4a). To estimate vessel tilt angle, these masks were fit to a line in 3D with least-squares. Baseline magnitude signal intensity was estimated from the average signal in a gray matter ROI adjacent to each vessel (Figure 4b). The ROI consisted of rectangular regions in the axial and coronal planes of at least 6mm and 10mm in length, respectively. The tissue ROI was selected to exclude any voxels that visibly contained large blood vessels. To enable comparisons with other SvO₂ quantification techniques, OEF was estimated in four ways:

1. JUMP was performed to estimate α̂ and Ŷ_v from Eqs 11. The average and variance of Ŷ_v across all voxels in a vessel were obtained,

2. MV-JUMP was performed to estimate α̂ for each voxel and Ŷ_v for the whole vessel from Eq. 12,

3. Y_v was also measured using direct measurement from an L1-regularized QSM map, and

4. Direct measurement from a SHARP phase map using MRI susceptometry (16).

For both JUMP and MV-JUMP, the nonlinear inverse problems in Eqs. 11 and 12 were solved using the MATALB fmincon function with an initial guesses for α̂ and Ŷ_v of 0.4 and 0.6. For JUMP, we imposed the constraints: α̂ ∈ [0.2, 1.3] and Ŷ_v ∈ [0.2, 0.99], and for MV-JUMP, we required that: α̂ ∈ [−0.1, 1.3] and Ŷ_v ∈ [0.2, 0.99]. For the L1-regularized QSM and MRI susceptometry methods, the single voxel with the highest average signal from both TEs within in the vessel ROI was used. Vessel diameter was visually estimated in order to normalize the acquisition voxel sizes to vessel size.

For the numerical and in vivo acquisitions, JUMP and MV-JUMP α̂-maps were created.

Results

Effects of Background Removal on Phase Signal

The effect of the processing pipeline on the underlying vessel phase signal was assessed. In one subject, two vessels were analyzed at three different stages of processing:

1. As raw phase data (unprocessed, wrapped phase)

2. As unwrapped phase data with no background phase removal performed

3. As background-removal-processed (SHARP-processed), unwrapped phase data

Three voxels in each vessel were identified. For each voxel, its phase signals relative to the voxels immediately anterior and immediately posterior were calculated, as illustrated in Supporting Figure S1. The average of these phase signals is assumed to accurately reflect the voxel signal, since it removes zeroth- and first- order variations in background phase across the brain. The processing pipeline, including phase unwrapping and SHARP background removal, introduced less than 0.03% error to the individual voxel signals.

Simulation Experiments – Numerical Vessels

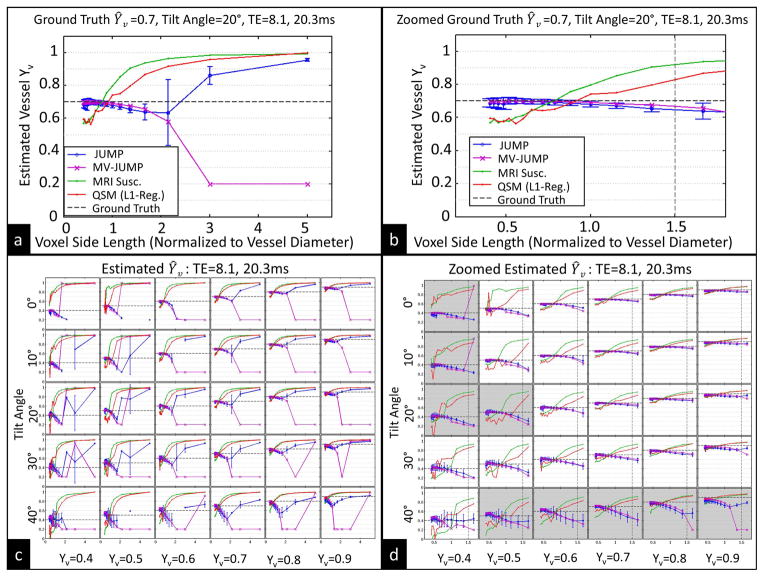
Figure 5a and 5b show the estimated Ŷ_v from a vessel with known Y_v of 0.7 and tilt angle of 20° for different acquisition voxel sizes using all four techniques: JUMP, MV-JUMP, QSM, and MRI susceptometry. The estimated vessel Ŷ_v was always between 0.64 and 0.70 using JUMP, and between 0.66 and 0.70 using MV-JUMP, for voxel sizes up to 2x the vessel diameter. The estimates obtained with QSM and MRI susceptometry were between 0.65 and 0.70 for a voxel size of 0.7x the vessel diameter. Partial volume effects, however, led to overestimation or underestimation of OEF by QSM and MRI susceptibility, depending on acquisition resolution. For all combinations of vessel angle up to 30° and acquisition resolution up to 1.5x vessel diameter, the variation in Ŷ_v across acquisition resolution was, for both JUMP and MV-JUMP, less than half of that obtained with either MRI susceptometry or QSM.

Figure 5.

Numerical vessel simulation results. (a) JUMP, MV-JUMP, MRI susceptometry, and QSM estimates of Ŷ_v for Ground Truth Y_v =0.7, vessel angle=20°, for all resolutions. (b) Same data in (a), zoomed to shown only resolutions with voxel side length under 2x vessel diameter. (c) JUMP and MV-JUMP Ŷ_v estimates for combinations of ground truth Y_v and vessel angle. (d) Same data in (c), zoomed to shown only resolutions with voxel side length under 2x vessel diameter. Vertical dashed line in (b) and (d) represents 1.8mm isotropic voxel size, the largest size used in in vivo experiments.

Figures 5c and 5d show JUMP and MV-JUMP estimates of Ŷ_v from vessels with six different ground truth Y_v values oriented at five different angles to B₀, obtained with TE={8.1ms, 20.3ms}. Each sub-plot shows Ŷ_v estimates obtained with all three techniques for a given choice of ground truth Y_v and vessel angle. Subplots that are shaded in Figure 5d have JUMP Ŷ_v estimates that deviate less than 0.12 from ground truth up for all resolutions up to 1.5x vessel diameter. For acquisition resolutions less than 1.5x the vessel diameter, vessel tilt angles up to 30° from B₀ and true vessel Y_v of 0.6 and greater, the JUMP- and MV-JUMP-estimated Ŷ_v were within 0.10 (absolute oxygenation fraction) of ground truth. For the same acquisition resolutions and vessel tilt angles, and with Y_v down to 0.4, JUMP obtained Ŷ_v estimates that were within 0.12 of ground truth, and MV-JUMP obtained Ŷ_v estimates within 0.19 of ground truth. Under the same conditions, QSM and MRI susceptometry produced Ŷ_v measurements that deviated from ground truth by up to 0.23 and 0.32, respectively, for vessels with Y_v down to 0.6. For vessels with Y_v down to 0.4, the errors were up to 0.47 and 0.54, respectively.

For the case where tilt angle is 20° and Y_v is 0.6, the RMSE across voxel size of JUMP Ŷ_v estimates from ground truth is 0.032, while the RMSE of MV-JUMP Ŷ_v is 0.028, a 13% reduction. When tilt angle is 20° and Y_v is 0.9, the JUMP Ŷ_v RMSE is 0.052 and the MV-JUMP Ŷ_v RMSE is 0.033, a 37% reduction. All RMSEs were calculated for voxels up to 1.5x vessel diameter, and accounted for non-uniform sampling across voxel size.

Supporting figures highlight additional simulations:

1. Supporting Figures S2a and S2b show that Ŷ_v estimates obtained using JUMP and MV-JUMP are similar for vessels situated at different sub-voxel offsets relative to the field of view.

2. Supporting Figures S3a and S3b show corresponding correlation plots between ground truth and JUMP-estimated α̂-maps for each vessel. For Y_v = 0.9, MV-JUMP has 38% lower RMSE than JUMP at a 0.7mm voxel size, and 39% lower at a 1.1mm voxel size. For Y_v = 0.6, MV-JUMP outperforms JUMP by 18% at 0.7mm voxel size, and by 9.2% at 1.1mm voxel size.

3. Supporting Figures S4 and S5 summarize the extravascular magnetic fields produced by the blood vessels. For 0.7mm isotropic voxel size and Y_v = 0.4, a positive phase shift was observed in the parenchyma compartment of voxels immediately above and below the vessel. For a 2.6mm voxel size and Y_v = 0.4, a negative phase shift was observed in the parenchyma compartment of vessel-containing voxels.

4. Supporting Figure S6 summarizes JUMP and MV-JUMP Ŷ_v estimates obtained when assuming gray matter $R_2^{\ast }$ was different from ground truth, and shows that JUMP is robust to 10% variations in gray matter magnitude intensity. Details are described in the Supporting Appendix section Gray Matter Magnitude Signal Estimation.

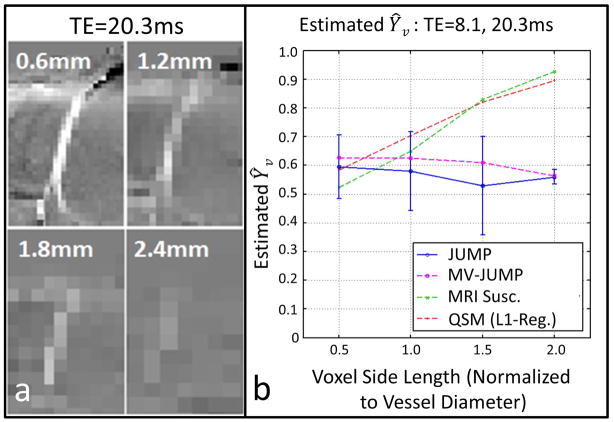
Simulation Experiments – Retrospective Analysis of in vivo Data

A pial vein analyzed by retrospective undersampling of in vivo data is shown in Figure 6. JUMP Ŷ_v-measurements varied between 0.53 and 0.58 and MV-JUMP Ŷ_v measurements varied between 0.56 and 0.63 as voxel size varies. For comparison, QSM and MRI susceptometry measurements varied from 0.52 to 0.96 and 0.58 to 0.95, respectively. Thus, JUMP and MV-JUMP saw smaller variations in Ŷ_v than the other two methods.

Figure 6.

(a) Zoomed view of pial vein measured at four simulated acquisition resolutions (b) Measured Ŷ_v across simulated acquisition voxel size. Curves show measurements obtained with JUMP, MV-JUMP, MRI susceptometry, and QSM.

In vivo Experiments

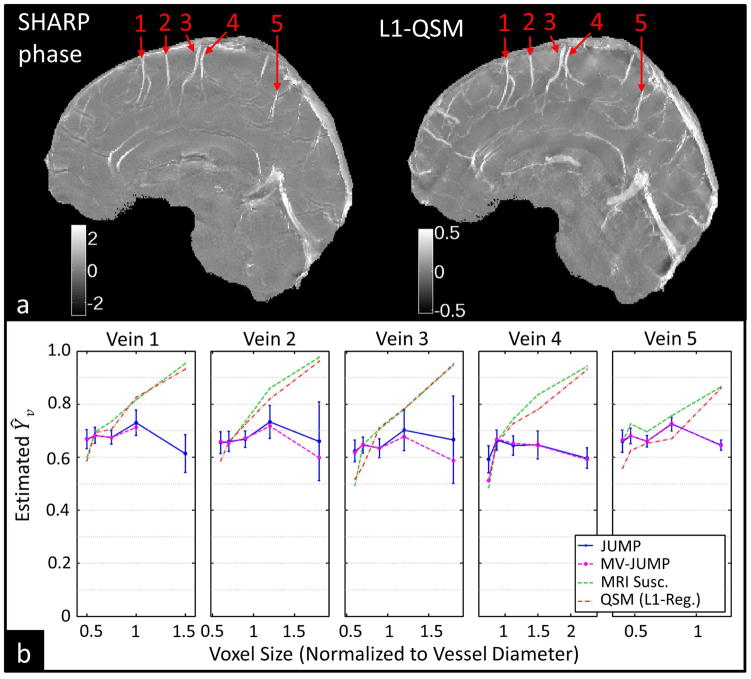
Figure 7a shows representative phase and susceptibility map maximum intensity projections from subject 4. Five veins were identified in the subject, and Ŷ_v was determined by JUMP and MV-JUMP for different voxel sizes (Figure 7b). For voxel dimensions larger than the vessel diameter, direct measurement using QSM and MRI susceptometry yielded Ŷ_v measurements with large errors. Table 2 summarizes individual vessel Ŷ_v measurement ranges for all three techniques. For Subject 4, the range of JUMP Ŷ_v estimates was 62% smaller than that of MRI susceptometry or QSM for all five veins, while for MV-JUMP the range was 61% smaller.

Figure 7.

Ŷ_v results from subject 4 (a) Maximum-intensity projections of SHARP-processed phase images and L1-regularized QSM images showing measured pial veins. (b) Ŷ_v measurements from JUMP, MV-JUMP, MRI susceptometry, and QSM plotted across acquisition resolution for all veins.

Table 2.

Single-vein Ŷ_v results from subject 4; and 5-vein average Ŷ_v from all subjects. Figures appended with an asterisk represent statistics computed from incomplete data.

		JUMP		MV-JUMP		MRI susceptometry		QSM
		Yv Range	ΔYv	Yv Range	ΔYv	Yv Range	ΔYv	Yv Range	ΔYv
Subject 4, Single Vein	Vein 1	0.61 to 0.73	0.12	0.67 to 0.71	0.04*	0.60 to 0.96	0.36	0.59 to 0.93	0.34
	Vein 2	0.66 to 0.73	0.07	0.60 to 0.72	0.12	0.65 to 0.98	0.33	0.59 to 0.96	0.37
	Vein 3	0.62 to 0.70	0.08	0.59 to 0.68	0.09	0.49 to 0.95	0.46	0.52 to 0.95	0.43
	Vein 4	0.59 to 0.66	0.07	0.51 to 0.67	0.16	0.49 to 0.94	0.45	0.52 to 0.93	0.41
	Vein 5	0.65 to 0.72	0.07	0.64 to 0.73	0.09	0.66 to 0.87	0.21	0.56 to 0.86	0.30
All Subjects, 5-vein average	Subject 1	0.52 to 0.62	0.10	0.49 to 0.61	0.12	0.45 to 0.92	0.47	0.54 to 0.89	0.35
	Subject 2	0.50 to 0.74	0.24	0.56 to 0.75	0.19*	0.62 to 0.93	0.31	0.55 to 0.93	0.38
	Subject 3	0.67 to 0.74	0.07	0.67 to 0.75	0.08*	0.54 to 0.89	0.35	0.53 to 0.89	0.36
	Subject 4	0.64 to 0.71	0.07	0.61 to 0.70	0.09*	0.58 to 0.94	0.36	0.55 to 0.93	0.38

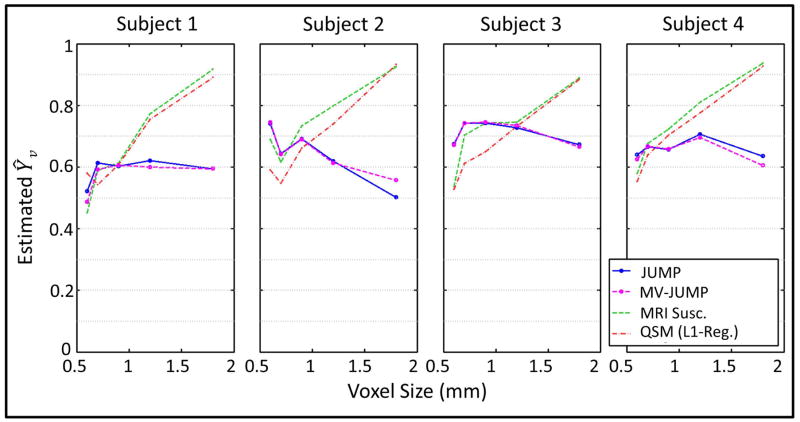
Figure 8 shows average Ŷ_v for each subject (from five pial veins) at all acquisition resolutions. Table 2 summarizes across-vessel Ŷ_v averages for each subject for all three techniques. Excepting subject 2, variation in MRI susceptometry and QSM Ŷ_v measurements across voxel size was more than 2.5x the variation observed with JUMP. For subject 2, the variations with JUMP and MV-JUMP were under 78% that observed with the other two techniques. Note that for some vessels in the four subjects, MV-JUMP did not provide a valid Ŷ_v solution at the lowest acquisition resolution, so those vessel Ŷ_v ranges are for 4 resolutions instead of 5. Statistics that depend on such incomplete data are appended with an asterisk in Table 2.

Figure 8.

5-vessel average Ŷ_v measurements obtained with JUMP and MV-JUMP, shown for all subjects plotted against acquisition resolution.

Discussion

In both simulation and in vivo experiments, JUMP provides Ŷ_v estimates in veins that are robust to changes in acquisition resolution and to partial-volume effects for voxel sizes up to 1.5x to 2x vessel diameter. Ŷ_v measurements obtained with QSM or MRI susceptometry do not account for partial-volume effects, and are highly dependent on acquisition resolution. Thus, JUMP provides greater absolute Ŷ_v measurement accuracy in small vessels. The background removal pipeline did not alter the phase signal of the blood vessels studied. In numerical experiments, neither vessel shift relative to the field of view, nor a 10% error in the presumed parenchyma intensity resulted in significant error.

By obtaining useful measurements from voxels that suffer from vein/parenchyma partial volume behavior, JUMP is able to accurately measure smaller blood vessels than QSM or MRI susceptometry. This fact also allows a greater number of voxels from a single blood vessel to be measured, and removes the need for manual identification of “reliable” voxels. This has two main consequences. The first is the elimination of artificial biases inherent in the manual identification of voxels without partial-voluming. The second is the ability to better quantify measurement uncertainty thanks to the larger number of data points per vessel. Both of these advantages mean that JUMP provides greater objectivity and quantifiable uncertainty in vessel Ŷ_v measurements.

Two techniques, JUMP and MV-JUMP, were proposed and tested. MV-JUMP was observed to have 37% less RMSE in Ŷ_v estimates and 38% less RMSE in α̂ estimates than JUMP in vessels with tilt angle of 20° and Y_v = 0.9.This may be because the MV-JUMP estimation problem has fewer degrees-of-freedom than the JUMP problem, and thus outperforms JUMP for high Y_v/low susceptibility. However, this possibility requires further study. With tilt angle of 20° and Y_v = 0.6, JUMP and MV-JUMP provide closer RMSE in Ŷ_v and α̂ estimates. MV-JUMP required longer computation times for the same set of voxels than did JUMP due to the non-linear computational complexity of the MATLAB fmincon solver. JUMP and MV-JUMP both involve solving optimization problems to minimize the difference between the measured complex signal and the signal predicted from a model. Using the complex signal rather than only the phase means both JUMP and MV-JUMP are less sensitive to phase wrapping.

At voxel sizes smaller than 1x the vessel diameter, partial-volume effects were not expected to be a major problem. However, at these resolutions, MRI susceptometry and QSM sometimes underestimated vessel Ŷ_v in numerical experiments, while JUMP did not show any such trend at smaller voxel sizes (eg. Figure 5a). This Ŷ_v underestimation behavior of phase-only approaches may be a consequence of using only the single most intense voxel from each vessel. Selecting only a single voxel increases the effect of noise on the resulting measurement, since there is no averaging. This effect can be especially pronounced at smaller voxel sizes, where SNR is lower. By averaging across multiple voxels, this source of error is reduced in JUMP. One could likewise average across multiple voxels when using MRI susceptometry or QSM, but this would entail manually identifying voxels that lack partial-volume effects and would reduce the objectivity of the measurement.

In simulation, JUMP was less accurate for Ŷ_v estimates at voxel sizes greater than 2x the vessel diameter. This is a natural consequence of limiting the minimum acceptable α̂ value to 0.2 (i.e. a voxel whose side length is 2x the vessel diameter). For larger voxel sizes, the limit on acceptable α̂ forbids JUMP from obtaining the correct solution. However, even for MV-JUMP, where we limited the minimum acceptable α̂ to −0.1, voxels larger than 2x vessel diameter gave inaccurate Ŷ_v estimates. This suggests that at such low resolutions, there is simply insufficient vessel signal in each voxel to make any accurate phase-based measurement of susceptibility. This error for voxel size greater than 2x vessel diameter may also be due to violation of the 2-compartment model at large voxel sizes.

In subject 2, several vessels could not be visibly identified in the phase image at 1.2mm and 1.8mm isotropic voxel size, which resulted in erroneous vessel Ŷ_v measurements at these resolutions. This explains the large variation in 5-vessel average Ŷ_v across acquisition resolution that was observed in subject 2.

JUMP is currently limited to relatively straight vessels parallel to the main field. In this work, all measured vessels had a tilt angle equal to or less than 30° to B₀. In experiments on numerical vessels, JUMP consistently underestimated Ŷ_v in vessels oriented at 40° away from B₀. Several recent studies have utilized MRI susceptometry as a means of quantifying Ŷ_v in such vertical vessels (3,9–14), and this work would be immediately relevant to such studies. Most vessels, however, do not meet these geometric specifications, and will not benefit from the current implementation of JUMP. The reasons for this dependence on vessel angle are twofold.

First, as vessel angle θ nears 54.7° – the “magic angle” – the intravascular field offset given in Eq. 2 nears zero. Thus, estimation of χ from ΔB₀ becomes an underdetermined problem. Second, as θ nears 90°, the extravascular field perturbations given by Eq. 3 increase, and the approximation that ΔB_0,out = 0 is invalidated. These effects are described in the Supporting Appendix section Effects of Assuming ΔB_0,out = 0 on Estimated Ŷ_v.

Phase images in this study were processed using SHARP, which requires convolution of the brain-masked brain image with a spherical kernel. Since this convolution is not possible near the edge of the brain ROI, the brain mask is eroded by this spherical kernel to remove these unreliable voxels. As is particularly visible in Figure 6a, this reduces the field of view for vessel identification. Future work will examine background phase removal methods that do not suffer from this edge erosion problem.

In addition to obtaining an estimate of vessel oxygenation, JUMP provides estimates of partial-volume fraction for all voxels in an ROI. These estimates were observed to agree closely with the ground truth fractions for vessels tilted at 20° from B₀ (Supporting Figure S3), suggesting that JUMP and MV-JUMP can also obtain sub-voxel estimates of the sizes of structures. This is described further in the Supporting Appendix section Partial-Volume Fraction α.

Conclusion

We have demonstrated a method to obtain better accuracy in Y_v measurements from blood vessels oriented close to B₀. Accurate measurements can be obtained when the voxel size is up to 2x the vessel diameter and partial-volume effects are present. We further demonstrate that this technique can estimate the voxel signal fraction originating from blood.

Supplementary Material

Supp Info

Figure S1: Effects of SHARP on voxel phase. (a) Two vessels (Vessel 1 and Vessel 2) in subject 4 were identified in phase images at the highest acquisition resolution (0.6 × 0.6 × 0.6mm³). (b) and (c) Three three-voxel ROIs were identified in Vessel 1 and in Vessel 2. One ROI for each vessel contained vein voxels (red), one contained parenchyma voxels located immediately anterior to the vessel (blue), and one contained parenchyma voxels located immediately posterior to the vessel (green). For each vessel voxel (red), an “anterior difference” and “posterior difference” were calculated by subtracting the anterior (blue) or posterior (green) voxel phase from the vessel voxel (red) phase. The average of these two differences was taken to be the “vessel phase signal” and was computed for all voxels using (1) unprocessed raw phase images, (2) unwrapped phase images, and (3) unwrapped, SHARP-processed phase images. For the worst-case voxel, the “vessel phase signal” was: from raw phase image, 1.176; from unwrapped phase image, 1.176; and from SHARP phase image, 1.177. The error incurred from applying SHARP was under 0.03%.

Figure S2: Numerical vessel offset simulation results for JUMP and MV-JUMP. Vessels have a diameter of 1.2mm and were simulated with sub-voxel shifts of 0mm, 0.48mm, and 0.96mm. Results are shown across acquisition resolution for vessels with Y_v of 0.4 to 0.9 in 0.1 increments. All vessels have a tilt angle of 20° and data were used with TE of 8.1ms and 20.3ms. (a) Measurements from all acquisition resolutions are shown. (b) Measurements from acquisitions with voxel size under 2x vessel diameter are shown. The x-axes of all subplots show the ratio of voxel side length to vessel diameter.

Figure S3: Ground truth α vs. estimated α̂ correlation. Vessel diameter is 1.2mm and tilt angle is 20°. JUMP and MV-JUMP α̂ results are presented as scatterplots with voxel ground truth α representing an x-coordinate, and estimated α̂ for the same voxel representing the y-coordinate. (a) α - α̂ scatterplot for JUMP α̂ estimates for the vessel at resolutions of 2.6mm, 1.1mm, and 0.7mm. (b) α - α̂ scatterplot for MV-JUMP α̂ estimates for the same vessel at resolutions of 2.6mm, 1.1mm, and 0.7mm. RMSE for voxel α̂ vs. voxel α is shown for several cases. For Y_v =0.9, MV-JUMP has RMSE 38% and 39% lower than JUMP for voxel dimensions of 0.7mm and 1.1mm, respectively. For Y_v =0.6, MV-JUMP has RMSE 18% and 9.2% lower than JUMP for voxel dimensions of 0.7mm and 1.1mm, respectively.

Figure S4: Extravascular parenchyma compartment signal phase. Results are shown for vessels with tilt angle of 20° and diameter of 1.2mm. At smaller voxel sizes and with lower vessel hemoglobin saturations (and thus higher vessel susceptibility), the signal phase shift in the extravascular parenchyma compartment becomes more significant. These results show the average ΔB_0,out (from Eq 3) across the parenchyma compartment of “vessel voxels”.

Figure S5: Extravascular parenchyma compartment signal magnitude. Results are shown for vessels with tilt angle of 20° and diameter of 1.2mm. At intermediate voxel size close to the vessel diameter and with lower vessel hemoglobin saturations (and thus higher vessel susceptibility), extravascular parenchyma compartment magnitude signal is most attenuated. These results summarize the variance in ΔB_0,out, (from Eq 3) across parenchyma compartment of “vessel voxels”, and represent R₂′ decay in this compartment that is caused by vessel susceptibility.

Figure S6: Ŷ_v estimates using different parenchyma $T_2^{\ast }$. JUMP and MV-JUMP estimates of Ŷ_v were obtained using erroneous gray matter $T_2^{\ast }$ values of 49.1ms and 95.5ms, and the correct value of 66.0ms. These Ŷ_v estimates are shown for vessels with tilt angle of 20° and Ŷ_v of 0.5, 0.7 and 0.9, using simulated TE of 8.1ms and 20.3ms.