Abstract
Proteins are often functionally dependent on conformational changes that allow them to sample structural states that are sparsely populated in the absence of a substrate or binding partner. The distribution of such structural microstates is governed by their relative stability, and the kinetics of their interconversion is governed by the magnitude of associated activation barriers. Here, we have explored the interplay among structure, stability, and function of a selected enzyme, adenylate kinase (Adk), by monitoring changes in its enzymatic activity in response to additions of urea. For this purpose we used a 31P NMR assay that was found useful for heterogeneous sample compositions such as presence of urea. It was found that Adk is activated at low urea concentrations whereas higher urea concentrations unfolds and thereby deactivates the enzyme. From a quantitative analysis of chemical shifts, it was found that urea redistributes preexisting structural microstates, stabilizing a substrate-bound open state at the expense of a substrate-bound closed state. Adk is rate-limited by slow opening of substrate binding domains and the urea-dependent redistribution of structural states is consistent with a model where the increased activity results from an increased rate-constant for domain opening. In addition, we also detected a strong correlation between the catalytic free energy and free energy of substrate (ATP) binding, which is also consistent with the catalytic model for Adk. From a general perspective, it appears that urea can be used to modulate conformational equilibria of folded proteins toward more expanded states for cases where a sizeable difference in solvent-accessible surface area exists between the states involved. This effect complements the action of osmolytes, such as trimethylamine N-oxide, that favor more compact protein states.
Introduction
Conformational changes are crucial for the function of numerous proteins, and understanding of the distribution of different folded conformations or structural microstates is essential for understanding their activities. The distributions of these microstates is governed by their relative stabilities, while their dynamic interconversions are controlled by the free energy differences between a stable ground state and transition states separating the structural microstates. Hence, an intricate interplay among structure, stability, and dynamics governs protein function. For example, fine-tuning of domain-domain or intramolecular interactions control activity levels of autoinhibited signaling proteins (1, 2). Similarly, enzymatic activity is often dependent on conformational changes during their reaction cycles, and it has been established for a few enzymes that the dynamic interconversions between structural microstates are rate-limiting for turnover of substrate molecules (3, 4). For instance, the rate of the reaction catalyzed by Escherichia coli adenylate kinase (Adk), is limited by slow reopening of substrate-binding subdomains in the presence of bound nucleotides (5, 6, 7), as illustrated in the following minimal reaction scheme.
| (Scheme 1) |
Here, E refers to Adk, S to substrate, P to product, and superscripts open and closed to Adk in open and closed states (Fig. 1). The rate constant for domain opening, kopen, limits the rate of the overall reaction, such that kcat = kopen.
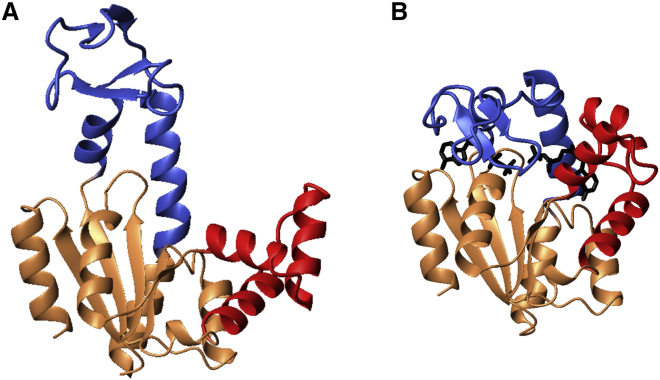
Figure 1.
Structures of the (A) open apo and (B) closed inhibitor-bound states of Adk: PDB: 4AKE (11) and PDB: 1AKE (12), respectively. The ATPlid and AMPbd domains are colored blue and red, respectively, while the CORE subdomain is colored beige.
Adk is a small kinase that catalyzes the reversible, magnesium-dependent interconversion of ATP and AMP into two ADP molecules. The enzyme predominantly populates inactive substrate-free open and active substrate-bound closed conformations (Fig. 1). Adk has a modular structure composed of a CORE domain, responsible for thermodynamic stability (8), and flexible ATP- and AMP-binding domains, respectively denoted ATPlid and AMPbd (Fig. 1). The AMP-binding domain is the substrate-presenting domain, analogous to the peptide-binding segment of protein kinases, which presents the protein substrate to the active site, thereby enabling ATP-mediated phosphorylation (9). Intensive investigation of the interplay between Adk activity and dynamics has, for instance, revealed a kcat-versus-KM compensation where changes in the kcat value result in compensatory changes in KM, so the specificity constant (kcat/KM) remains invariant (10).
It has been observed that common denaturants like urea can increase activities of certain enzymes, including dihydrofolate reductase (13, 14), Adk (15), prostaglandin D synthase (16, 17), and biliverdin-Ixα (18). Various mechanisms for these increases have been proposed, for example removal of inhibition in biliverdin-Ixα (18) and structural reorganization in prostaglandin D synthase (16). Exposure to 1 M urea has been shown to increase activity of Adk by ∼50% (15), putatively due to an increase in conformational flexibility in the active site. To explore the general effects of urea on enzymatic activity collectively indicated by these examples, we have analyzed the urea-dependency of Adk activity in detail, using a 31P NMR kinase assay (19). 31P NMR spectroscopy has previously, for instance, been used to characterize the activity of an ATPase in intact E. coli cells (20), characterization of ATP synthesis in rat hearts (21), and characterization of time-dependent changes in nucleotide concentrations in E. coli cells (22). The results indicate that the urea-induced activation of Adk is primarily mediated by a redistribution of structural microstates. Further, adding urea may provide a way to shift the distribution of the structural states of proteins toward expanded states. This is then possible for cases where a significant difference in solvent-accessible surface (SAS) area exists between the states involved. Hence, urea can be viewed as complementary to agents such as trimethylamine N-oxide (TMAO) that favor more compact states (10).
Materials and Methods
Protein production
Self-inducing plasmids containing wild-type Adk (23) or the I116G Adk variant (24) were transformed into BL21(DE3) cells in the presence of carbenicillin, transferred to liquid cultures and grown overnight. To label the proteins uniformly for use in 15N-NMR applications, all variants were expressed in M9 minimal media with 15NH4Cl (Cambridge Isotopes, Tewksbury, MA) as the sole nitrogen source, and purified following a previously described protocol (5).
Lactate dehydrogenase activity assay
Lactate dehydrogenase (LDH) was purchased from Sigma-Aldrich (St. Louis, MO) and used without further purification. LDH activity was assayed using a spectroscopic assay based on the enzyme’s ability to oxidize NADH to NAD+ while reducing pyruvate to lactate. The rate of reaction was determined by monitoring absorption at 340 nm, at which NADH and NAD+ have molar extinction coefficients of 6220 M−1 cm−1 and approximately zero, respectively.
Circular dichroism analysis of urea effects on Adk stability
Effects of urea on Adk-stability were investigated by measuring circular dichroism (CD) at 220 nm of samples in the presence of urea at various concentrations. Data were acquired using a Model No. 815 spectrometer (JASCO, Oklahoma City, OK). In each case, CD signals were measured for 3 min, to obtain an estimate of the measurement uncertainty of the CD-spectrometer, at 298 K (25°C). A quantity of 20 mM ADP was added to ensure the enzyme was in its active form. The and m values for urea-induced unfolding were determined by fitting Eq. 1, derived from the linear extrapolation method (25), to the observed CD signals:
| (1) |
Here, eN and mN are, respectively, the intercept and slope of the native state baseline; eU and mU are, respectively, the intercept and slope of the unfolded baseline; and Kobs is given by
where R is the gas constant, and T is the absolute temperature.
In all CD experiments, 15 μM of Adk in 5 mM Tris buffer with 10 mM NaCl at pH 7.5 was used.
Before all measurements of stability, binding, and activity, samples were incubated in urea at the selected concentrations for at least 1 h at room temperature.
NMR spectroscopy
Kd values were determined by NMR-monitored ATP titrations. Activities were determined using a real-time 31P-NMR-based assay (19). All NMR experiments were conducted at 298 K (25°C) in 30 mM MOPS buffer with 50 mM of NaCl at pH 7. For activity measurements, the concentration of Adk was varied between 10 nM and 1 μM. The ADP concentration was kept constant at 20 mM and the buffer was supplemented with 10 mM MgCl2 and 0.2 mg/mL BSA. Each activity measurement was repeated three times to gain an estimate of the errors. ATP binding constants were determined using an Adk concentration of 200 μM, and ATP was titrated to 20 mM to approach saturation.
15N-HSQC spectra for Kd determination were recorded using an 850-MHz Avance III HD Bruker spectrometer with a 5-mm HCN cryo probe. 31P NMR spectra for the Adk activity assay were recorded using a 360-MHz DRX spectrometer (Bruker) equipped with a 5-mm BBI probe.
NMR projection analysis
For projection analysis of chemical shifts (26), two vectors in the 1H-15N plane of the HSQC-spectra were defined for each amino acid: a reference vector, A, between the 15N-HSQC signal of Adk bound to the inhibitor Ap5A in water and free Adk in water (see black arrow in Fig. 12 B); and an activity vector, B, between the Ap5A-bound Adk in water and urea. 15N-shifts were scaled by a factor of 0.2, to give the 1H-shift and 15N-shift comparable weight. The projection of vector B on vector A, Bproj (see red dashed arrow in Fig. 12 B), was then calculated, and the activity (X) was defined as
| (2) |
The cosine of angle (θ) between the two vectors was calculated from
| (3) |
Cos(θ) is an indicator of the magnitude of the chemical shifts that are explained by a studied event, and only residues displaying linear behavior are suitable for the analysis, hence only amino acid residues with cos(θ) > 0.9 were included in the projection analysis.
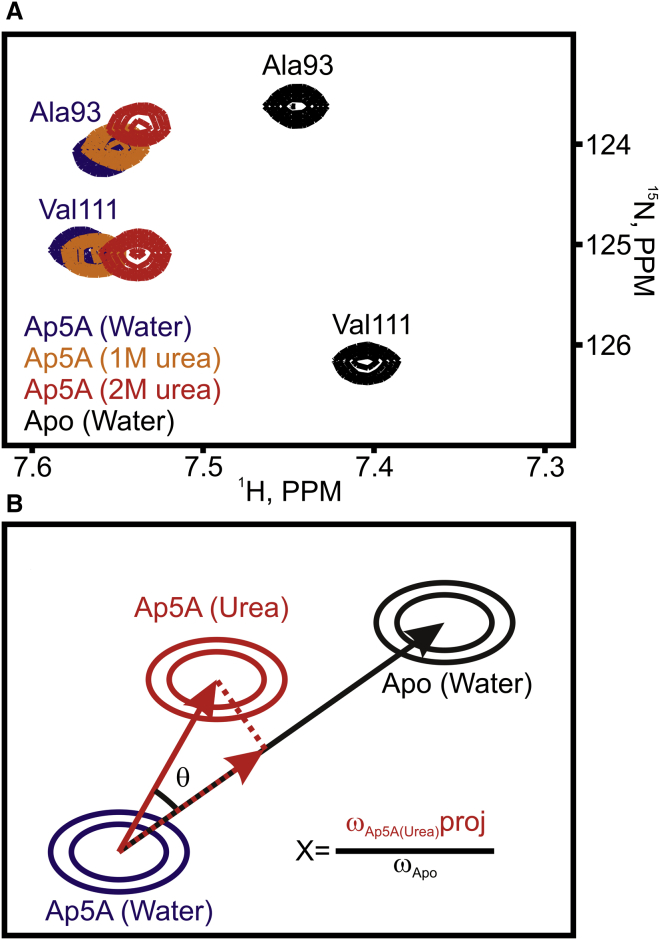
Figure 12.
Urea-induced perturbation of the opening/closing equilibrium in Adk. (A) Changes in 1H-15N-HSQC spectra of Ap5A-bound Adk induced by addition of urea, showing the gradual shift toward the open conformation (Apo). (B) Schematic representation of results of a projection analysis, based on two vectors: the differences in chemical shift between Ap5A-bound Adk in water and in urea (red), and between Ap5A-bound and Apo Adk in water (black). The projection amplitude (X) is defined as the relative magnitude of the projection of the red vector (dashed red line) onto the black vector and is sensitive to the equilibrium constant for the opening and closing reaction. The angle between the two vectors (θ) indicates the contribution of structural noise to the projection analysis. If cos(θ) = 1, the chemical shift of the Ap5A-bound state in urea is on the straight line between those of apo and Ap5A-bound states in water, while if cos(θ) = 0 there is no correlation between the chemical shifts of amino acids in the three states, excluding residues with cos(θ) < 0.9 from the analysis (26).
Results and Discussion
Urea dependency of LDH activity
The expected effect of urea on the activity of an enzyme is that activity scales with the fraction of folded protein. The fraction folded protein has a well-known dependence on denaturant concentration in the limit case of a two-state folding reaction (27). For example, the denaturant-dependency of LDH activity is well described by the product of its intrinsic activity in water and the fraction of folded protein (Eq. 4 and Fig. 2). LDH catalyzes conversion of pyruvate and NADH to lactate and NAD+ (28), which can be quantified by monitoring absorbance at 340 nm (to follow depletion of NADH). Because no coupling enzymes are required, changes in activity in response to changes in urea concentrations can be accurately measured. The analytical function used for the activity assay is
| (4) |
The denaturant-dependency of the fraction of folded protein, pf(D), is obtained from the equilibrium constant of the protein folding reaction (Eq. 5):
| (5) |
Here, the denaturant-dependency of the equilibrium constant for the protein folding reaction, Kfold(D), is given by
| (6) |
where is the standard Gibb’s free energy for folding, mfold is the m value for denaturant-dependent unfolding (27), D is the concentration of denaturant (here urea), R is the gas constant, and T is the absolute temperature.
Figure 2.
Denaturant-dependency of lactic dehydrogenase activity. Model 1 of denaturant effects on enzyme activity (Eqs. 4–6) was fitted to the acquired activity data, yielding and mfold values of 13.7 kJ mol−1 and 7.2 kJ mol−1 M−1, respectively. In model 1, the activity is scaled only with the fraction folded enzyme.
The Vmax of commercially available rabbit (Oryctolagus cuniculus) muscle LDH in the presence of selected concentrations of urea was measured, and found to fit Eqs. 4–6 (denoted “model 1”) well, yielding and mfold values of 13.7 kJ mol−1 and 7.2 kJ mol−1 M−1, respectively (Fig. 2). The analysis gives, in essence, a denaturation profile of LDH, with the enzymatic activity providing quantitative indications of the fraction of folded molecules. Hence, the effect of urea is to effectively decrease the observed LDH activity through deactivation of the enzyme through unfolding.
Effect of urea on Adk activity
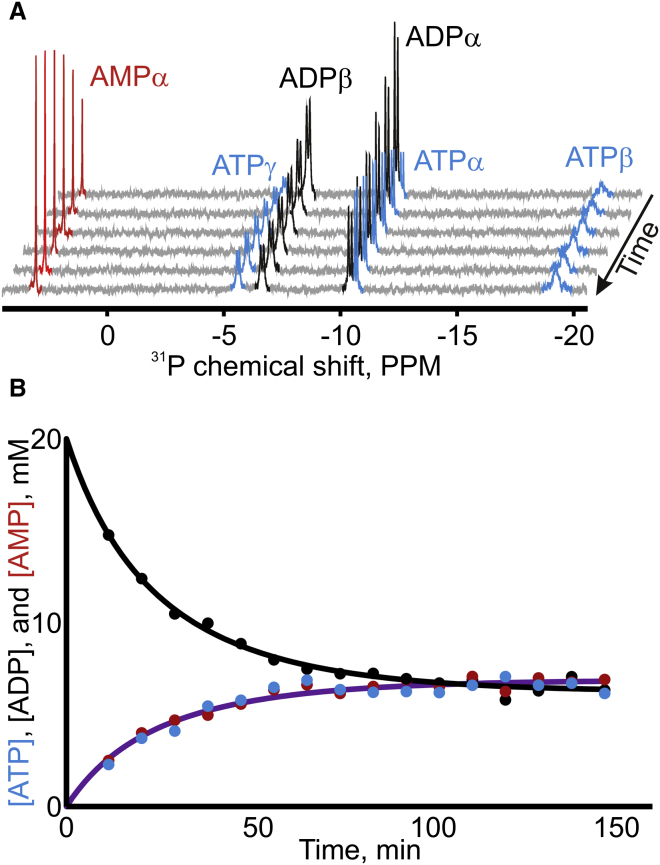
The standard assay for quantifying Adk activity couples production of ADP from ATP and AMP to oxidation of NADH through the activity of LDH and pyruvate kinase (29). However, Adk is significantly more resistant against urea-unfolding than LDH (Fig. 3), so the coupled Adk assay is unsuitable for quantifying the denaturant-dependency of Adk activity. Thus, to measure changes in Adk activity in response to increases in urea concentrations accurately, without using coupling enzymes, we used a real-time 31P NMR assay (19), in which the Adk-dependent depletion of ADP and simultaneous accumulation of ATP and AMP are quantitatively monitored to obtain kcat values (Fig. 4).
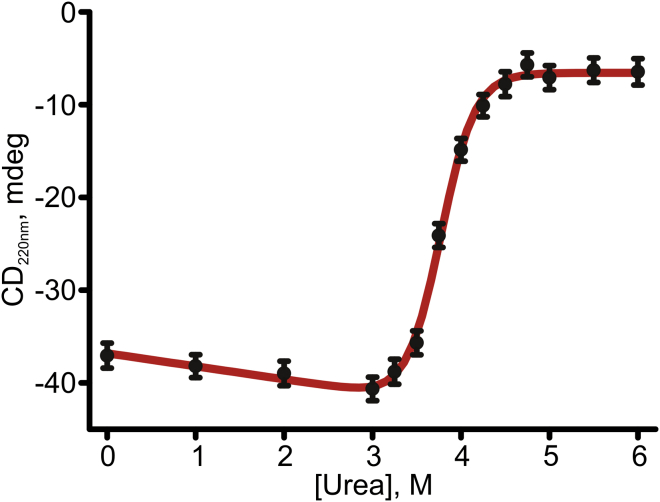
Figure 3.
Equilibrium thermodynamic stability of Adk. Unfolding of Adk by urea was monitored by recording the CD signals at 220 nm at 25°C. The and mfold unfolding parameters obtained by fitting Eq. 1 to the data were 49 kJ mol−1 and 13 kJ mol−1 M−1, respectively, while the determined midpoint of unfolding was at 3.8 M.
Figure 4.
Results of the real-time 31P NMR assay for measuring Adk activity. (A) The assay was initiated by adding Adk to ADP and Mg2+ at fixed concentrations. Depletion of ADP and accumulation of ATP and AMP were followed by recording 31P NMR spectra at indicated time points. Signals corresponding to ATP (blue), ADP (black), and AMP (red) were then integrated to obtain their concentrations at each time point (B). kcat was calculated from the initial turnover rate, obtained by fitting the analytical solution (solid lines) for the rate equation to the observed concentrations (19).
In contrast to the expected decline in catalytic activity with increases in denaturant concentration, as observed for LDH, the activity of Adk increased before declining as urea levels rose. These responses to urea cannot be explained with model 1 (activity scales with fraction folded enzyme), as shown in Fig. 5 (dashed line). To account for this behavior, we introduced a kinetic activation term, as shown in Eq. 7. The activation term is equivalent to the established expressions that account for the denaturant-induced modulation of folding or unfolding rate constants in stopped flow experiments (30). In Eq. 7, and mact, respectively, refer to intrinsic Adk activity in water and the kinetic m value accounting for the urea-dependent activation. In protein folding, the m value is proportional to the difference in SAS area between the folded ground state and transition state for the folding/unfolding process. Because the catalytic rate of Adk is limited by slow opening of the substrate-binding domains in the presence of bound nucleotides (5, 6), the mact value will be proportional to the difference in SAS area between the closed state and the transition state associated with the opening reaction.
| (7) |
However, the activity is also dependent on the fraction of folded Adk molecules (as in model 1) and global urea-induced unfolding of the enzyme will reduce the observed catalytic activity. Thus, a model that includes both global unfolding and urea-dependent activation is required, as shown in Eq. 8 (denoted “model 2”).
| (8) |
Here, is calculated in the same manner as in model 1, Eqs. 5 and 6.
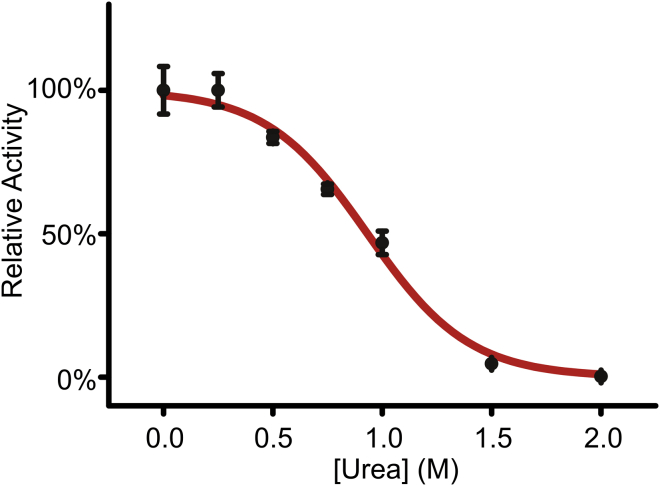
Figure 5.
Urea-dependent activation of Adk. The kcat for Adk catalysis at indicated urea concentrations (and saturating ADP concentrations). The dashed and solid lines, respectively, indicate fits of measured activities to model 1 (in which activity is scaled with global Adk unfolding) and model 2 (in which activity is scaled with global unfolding and a kinetic activation term). The activation m value (mact) and value from the fit to model 2 were 0.51 kJ mol−1 M and 297 s−1, respectively. The error represents the SD from triplicate measurements.
To reduce the degrees of freedom in the following regression analysis, the and mfold values (49 kJ mol−1 and 13 kJ mol−1 M−1, respectively), determined in the Adk unfolding experiment (Fig. 3), were used.
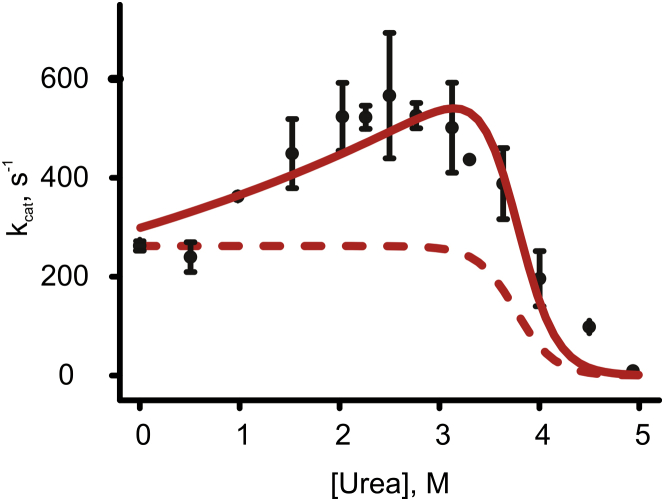
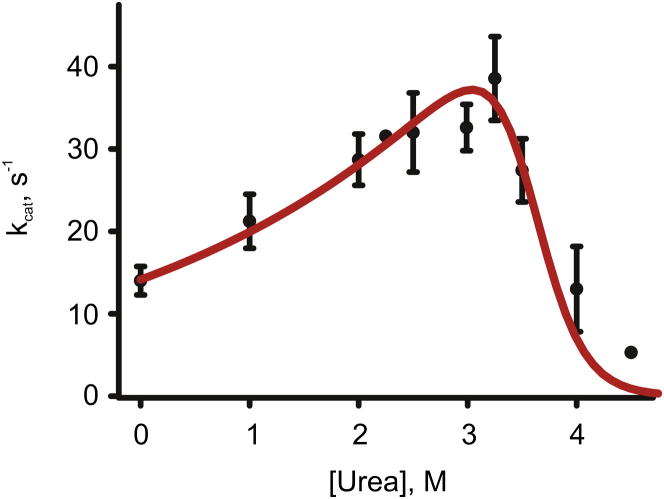
Model 2 provides a significantly better fit to the observed Adk activities than model 1 (Fig. 5), particularly for the urea-induced activation of Adk, although it indicates that the maximum activity is at 3.2 M rather than 2.5 M urea (as observed).
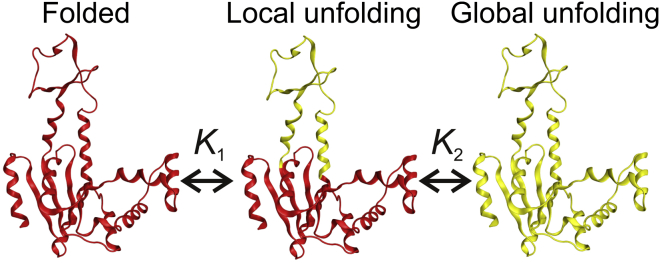
Thus, model 2 must be modified to explain the urea dependency of Adk activity comprehensively. Measurements of the temperature dependency of Ap5A-binding affinity to wild-type and surface-exposed glycine variants (31) of Adk, and the observation that the ATPlid domain can be selectively unfolded by disrupting a local hydrophobic cluster (8), have shown that the ATPlid domain of Adk undergoes a cooperative local unfolding event at temperatures below that of global unfolding. An unfolding scheme that includes the local unfolding event is displayed in Fig. 6. If such a local unfolding would produce an inactive enzyme, a reasonable expansion of model 2 is to include the contribution of the local unfolding event to the fraction of fully folded Adk molecules (pf). This can be done using the partition function (Q) derived from the folding model illustrated in Fig. 6 with the folded state set as a reference state, according to
| (9) |
From the partition function it follows that the fraction of folded molecules is equal to
| (10) |
where , while and mlocal are, respectively, the stability and unfolding m values corresponding to local unfolding of the ATPlid domain. This analytical expression of pf can now be used together with the urea activation term (Eq. 7) to formulate a refined model of the urea-dependency of Adk activity, denoted “model 3”:
| (11) |
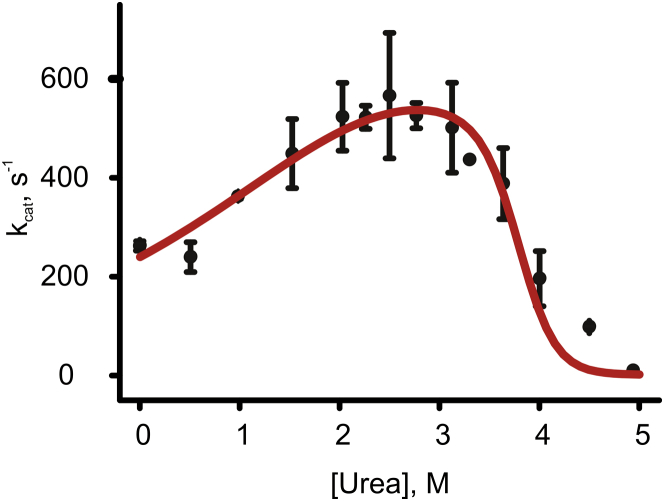
Model 3 provides a significantly improved fit compared to model 2. The improvement of the fit is statistically significant at the 95% level as judged by an F-test, and the most prominent difference is that model 3 can account for the complete urea dependency including an accurate indication of the urea concentration at which Adk activity is at its maximum. Fitting model 3 to the observed kcat values for Adk (Fig. 7) yields an activation term mact of 1.2 kJ mol−1 M−1, of 253 s−1 and local and mlocal unfolding terms of 7.4 kJ mol−1 and 2.5 kJ mol−1 M−1. The global unfolding parameters were again taken from the values obtained from CD spectroscopy (49 kJ mol−1 and 13 kJ mol−1 M−1 for and mfold, respectively).
Figure 6.
Model for local and global unfolding of Adk. Segments undergoing unfolding are colored yellow. The local event comprises unfolding of the ATPlid domain: residues 109–165 (31). The equilibrium constants of the local (K1) and global (K2) events in the direction of unfolding are indicated.
Figure 7.
Fit of model 3 (red line) to measured Adk activities at indicated urea concentrations. Model 3 (Eqs. 9–11) includes contributions from global and local unfolding, and a kinetic activation term. The error represents the SD from triplicate measurements.
A mutation unfolding the ATP lid abolishes the local deactivation term
In a regular protein unfolding experiment (yielding a curve such as shown in Fig. 3), the mfold value obtained is proportional to the difference in SAS area between the folded and unfolded states, which in turn is proportional to the number of amino acid residues in the protein (32). As described above, the local unfolding event that modulates the urea-dependency of Adk activity by reducing the number of fully folded Adk molecules is governed by a local stability term and a denaturant-dependency term (mlocal). According to the unfolding model presented in Fig. 6, mlocal reflects the denaturant-dependency of local unfolding of the ATPlid domain. The m-values obtained for global and local unfolding are 13 and 2.5 kJ mol−1 M−1, respectively, suggesting that the local unfolding event involves 40 residues. This number was calculated by multiplying the ratio of the m-values (0.19) by the number of amino acid residues (214) in Adk. This estimate agrees reasonably well with a previous finding that 57 residues (109–165) unfold locally in response to a temperature perturbation (31).
A strategy to test the validity of the estimated size of the segment that undergoes local unfolding is to quantify the denaturant-dependency of kcat for an Adk variant with a destabilized ATPlid domain. A variant that meets this condition should theoretically have an attenuated contribution to kcat from local unfolding of the domain. One such variant is the I116G variant (24), which has the ATPlid domain destabilized through perturbation of a hydrophobic cluster that is essential for its structural integrity (8). Stability, activity, and substrate binding affinity parameters have previously been characterized for this variant. The global stability parameters of I116G were determined with CD spectroscopy and corresponds to and mDN values of 42 kJ mol−1 and 12 kJ mol−1 M−1, respectively. Although this variant has substantially lower activity than the wild-type enzyme, model 2 for the denaturant-dependency of its activity provided a satisfactory fit to the kcat values determined with the 31P NMR assay (Fig. 8). Furthermore, model 3 (which includes local unfolding) does not provide a significantly improved fit, according to an F-test. Hence, the denaturant-dependency of I116G activity can be adequately modeled with terms describing activation and global unfolding. The indications that the local unfolding event included in model 3 does not occur in a variant with a destabilized ATPlid supports the fundamental aspects of model 3 used for analysis of the wild-type enzyme.
Figure 8.
Activity of the Adk mutant I116G as a function of urea concentration. The red line shows the fit of model 2 (which includes global unfolding terms and the urea-dependent kinetic activation term) to the measured activities. Fitted activity in water and urea activation (mact) terms were 14 s−1 and 0.85 kJ mol−1 M−1, respectively. The and mfold unfolding parameters, obtained from a CD-monitored unfolding experiment, were 42 kJ mol−1 and 12 kJ mol−1 M−1, respectively. The error represents the SD from triplicate measurements.
Adenylate kinase kcat versus Kd compensation
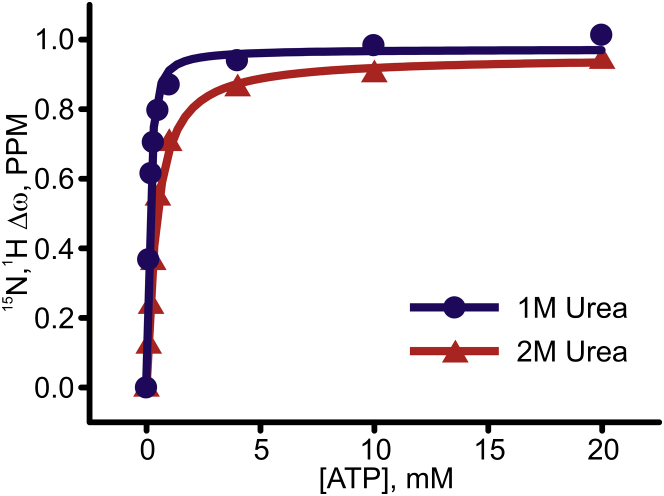
We have previously discovered a kcat-versus-KM compensation phenomenon in Adk catalysis (10), i.e., changes in Adk that alter kcat have compensatory effects on KM, so the specificity constant (kcat/KM) remains constant. In the case of Adk, the compensatory effect is dependent on the limitation of catalytic activity by opening of substrate-binding domains (kcat = kopen in Scheme 1) in the presence of bound nucleotides (5). The coupling between kcat and KM then arises because KM is also dependent on kopen in the coupled substrate-binding equilibrium (Scheme 1). These observations indicate an energetic coupling between Adk substrate-binding affinity and activity. In this study we investigated this coupling in detail by comparing kcat values with binding affinities (Kd values) obtained for wild-type Adk in water and at 1 and 2 M urea, and for the I116G Adk variant in water. The Kd values for ATP-binding to wild-type and I116G Adk in water are reportedly 50 and 0.78 μM, respectively (24, 33), and Kd values for ATP binding to Adk in 1 and 2 M urea determined here from NMR titrations were 61 and 365 μM, respectively (Fig. 9). The kcat values at 1 and 2 M urea for the wild-type enzyme were obtained from the fit with model 3 (Fig. 7) and normalized with respect to the fraction of folded Adk to generate the intrinsic kcat at these urea concentrations.
Figure 9.
ATP binding affinities of Adk in 1 and 2 M urea. 1H-15N HSQC spectra were acquired for Adk at increasing ATP concentrations in 1 and 2 M urea (blue and red, respectively). The Kd values obtained were 61 ± 10 and 365 ± 40 μM, respectively. The compounded chemical shift changes were calculated from (∣ΔωH∣+∣ΔωN∣∗ 0.2). The solid lines indicate fitted binding isotherms.
The difference in energy between the bound-closed state and the open apo state can be calculated from the binding affinity:
| (12) |
where is the Kd for ATP binding to Adk in water (50 μM).
Following transition state theory, the difference between the ground state and the transition state for the rate-limiting step can be calculated from the kcat:
| (13) |
where is the kcat value of Adk in water (262 s−1).
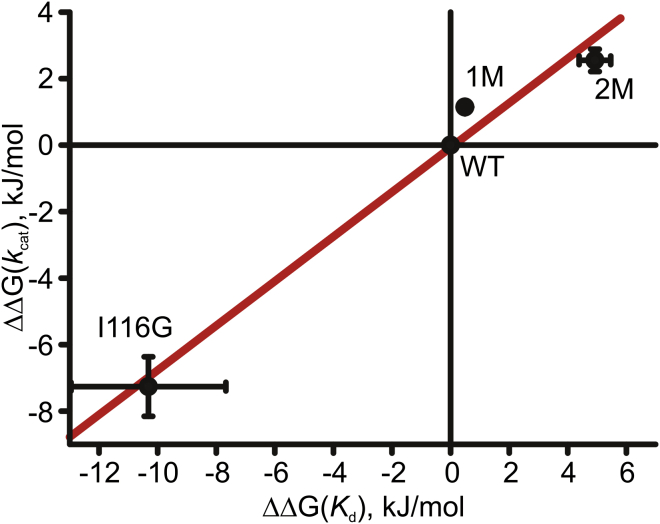
There exists a striking correlation between the obtained and values, corroborating the notion of an energetic coupling between ligand binding affinity and catalytic turnover (Fig. 10). Qualitatively, this indicates that the catalytic rate constant is negatively correlated with the ATP-binding affinity. Linear regression yields a slope of 0.69, indicating that although kcat and Kd are energetically coupled, the coupling is not 1:1. From a physical perspective, this result indicates that other aspects of Adk catalysis dampen the effect of binding affinity on the reaction rate, possibly via modulation of the energy of the transition state separating open and closed structures in the presence of bound substrate. This interpretation is based on the conclusion that the rate of Adk catalysis is limited by the free energy barrier for opening of the closed transition state in the presence of bound substrate (5, 6). Nevertheless, the analysis provides experimental evidence of energetic coupling between Adk activity and ligand-binding affinity.
Figure 10.
Energetic coupling between kcat and Kd in Adk catalysis. is displayed versus values, calculated as described in the text for wild-type Adk in water (WT), 1 M urea (1 M) and 2 M urea (2 M), and the Adk variant I116G in water (I116G). The fitted straight line, displayed in red, has a slope of 0.69.
Urea shifts the conformational equilibrium of Ap5A-bound Adk toward the open conformation
Urea is generally expected to have more impact on proteins in expanded states, e.g., unfolded globular proteins, for example the unfolded state of a globular protein interacts more favorably with urea compared to the more compact native state (27, 32). Thus, urea would be expected to interact more readily with open substrate-free Adk than with closed, Ap5A-bound Adk, and induce more substantial chemical shifts in Adk in the substrate-free state in a chemical shift perturbation experiment. We tested this hypothesis by following the chemical shift perturbations of both open and closed Adk in response to increasing amounts of urea. In contrast to expectations, larger urea-induced chemical shift changes were observed for the closed state (Fig. 11, A and B). This suggests that urea interacts more readily with the more compact closed state than with the more expanded open state. A possible reason for this deviation from urea’s general patterns of interactions is provided when the chemical shifts of the closed Ap5A bound state are plotted as a function of urea concentration and benchmarked against the chemical shift of apo Adk in water (Fig. 12 A). The chemical shifts show a striking linear relationship, as addition of urea to the Ap5A-bound protein gradually moves the chemical shifts toward those of the apo state. Binding of nucleotides to Adk is dependent on a coupled equilibrium (Scheme 1), involving an initial binding event followed by large-scale conformational changes in both the ATPlid and AMPbd domains. The binding model involves an intermediate with bound nucleotide and the substrate-binding domains in open conformations. This intermediate has previously been enriched and characterized with NMR spectroscopy (6). The transition of the intermediate into the closed state occurs with a significant burial of SAS area. Conversely, there is an increase in the SAS in the reverse direction, i.e., from the closed state to the intermediate. The most probable explanation of the large chemical shift perturbations in the Ap5A-bound state is that urea shifts the open/closed equilibrium toward the open and more expanded state, and the resulting chemical shift changes then report on the perturbed open/closed equilibrium.
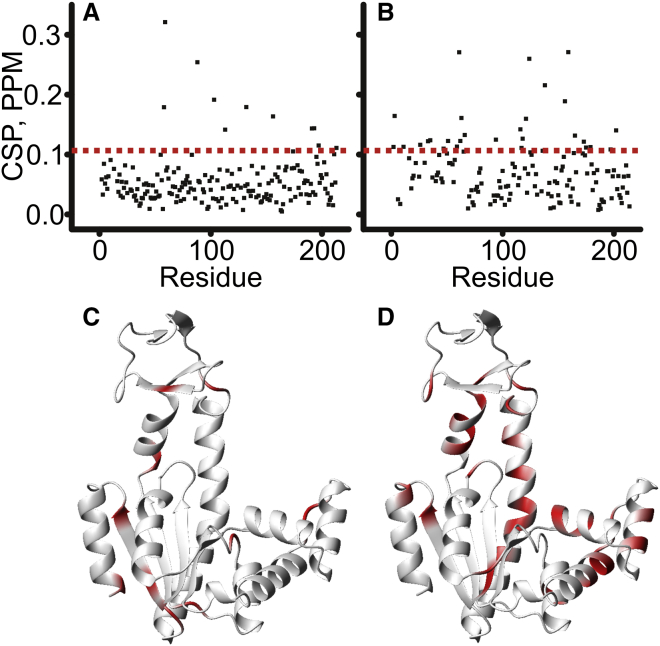
Figure 11.
Urea-dependent chemical shift perturbations in Adk in the apo state (A) and bound to Ap5A (B) between 0 and 2.5 M urea. The compounded 1H and 15N chemical shift changes were calculated from (∣ΔωH∣+∣ΔωN∣∗0.2). (C and D) Structural display of the amino acid residues with chemical shift perturbations larger than 1 SD above the average (indicated by the dotted line in A and B) are colored in red for Apo Adk (C) and Ap5A-bound Adk (D). Both data sets are visualized on the open (Apo) structure (11) for clarity.
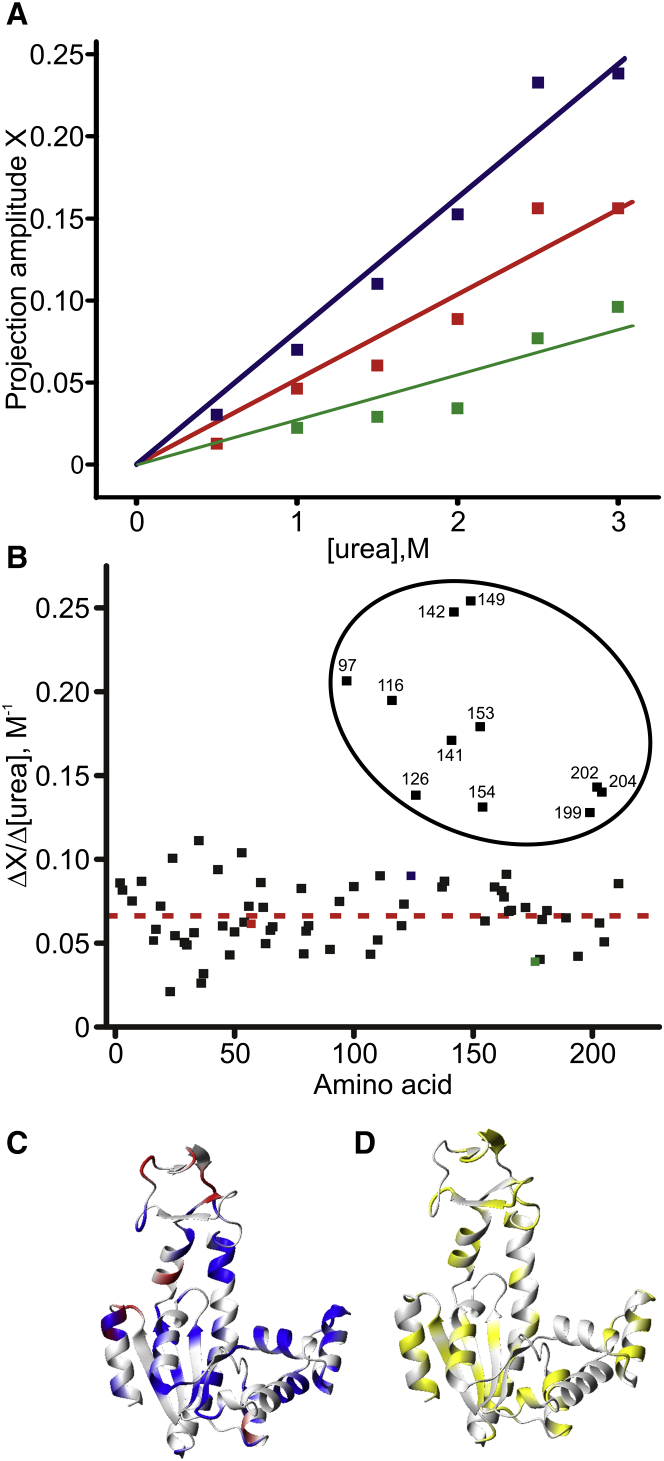
This effect was analyzed quantitatively by projection analysis (Fig. 12 B), in which the Ap5A-bound state was compared to the apo state at selected urea concentrations, using Ap5A-bound Adk in water as the reference. The reference Ap5A-bound state in water was treated as fully closed and corresponding to the x-ray structure in complex with Ap5A (PDB: 1AKE) (12), while the apo reference state was approximated with the open state observed in PDB: 4AKE (11). It should be noted that these reference states only provide approximations to fully open and closed states, because opening/closing dynamics occur in both the apo (34) and Ap5A-bound states (35). As shown by the three representative examples in Fig. 13 A, a linear relationship between the projection amplitudes (X) and urea concentration was observed. The slope of this linear relationship is a direct measure of the shift of each amino acid residue toward the open conformation induced by a given increase in urea concentration. Displaying the resulting slopes against the primary sequence (Fig. 13 B) for global analysis of the urea effect revealed an average shift toward the open state of 6.6 ± 1.9% per molar increase in urea concentration. In addition, a cluster of outlying residues with a significantly stronger urea response (equivalent to at least 3 SDs) in the order of 20% per molar increase was observed. Of the 214 amino acid residues in Adk, 144 were assigned in sufficient numbers of urea concentrations for the regression analysis described in Fig. 13 A. Of these residues, 13 displayed too-small chemical shifts to be used reliably in the projection analysis, leaving 131 amino acid residues for the analysis. Of these 131 amino acid residues, 72 had a cos(θ) larger than 0.9, indicating that their behavior in response to increased urea concentrations was dominated by the shift toward the open state. Residues with lower cos(θ) do not follow the general trend with linear shifts, and it is likely that the data from these residues is dominated by structural noise and/or local processes other than global domain opening and closing. From hydrogen exchange studies, it is well known that urea can affect both global and local processes (36), and the chemical shift data presented here appear to be consistent with this notion.
Figure 13.
(A) Illustrative projection amplitudes (X) for three amino acid residues (57, red; 124, blue; and 176, green). The slope of the projection amplitude as a function of the urea concentration is used as a measure of the ability of urea to shift the conformation of Adk toward the open state. Errors were estimated based on the errors in the determination of the chemical shifts. All errors were <0.004, which is smaller than the size of the markers in (A). (B) The slope (calculated from the regression analysis in (A) for each amino acid considered in the projection analysis plotted against the primary sequence. The mean slope was 0.066 ± 0.019 M−1. For the encircled residues, the effect of urea was stronger (>3 SD more than the average). These highly effected residues clustered in the ATP lid and close to the binding site of the ATP base. They are colored red on the structure of Adk in the open state (C) (PDB: 4AKE), while residues that cluster around the average slope are colored blue. (D) Amino acid residues that have a cos(θ) value <0.9 are colored yellow. These residues were not included in the analysis.
Taken together, the data indicate that the opening event induced by urea is at least a two-step process, where initial local opening at lower urea concentrations is centered on the top of the ATPlid. Further, urea appears to stabilize the substrate-bound open state (corresponding to the intermediate discussed above) at the expense of the substrate-bound closed state. This shift of equilibrium of the substrate-bound Adk toward the open state by urea explains the reduced binding affinity for ATP (Fig. 9) because the binding affinity is dependent on the magnitude of the equilibrium constant for domain opening/closing (Scheme 1). Also the increased activity can be accounted for if the shift of the equilibrium is predominantly dependent on an increased rate-constant of domain opening. The effects of urea addition are opposite to those of the osmolyte TMAO, which shifts the conformational equilibrium toward the closed state, with an accompanying reduction in activity and increase in binding affinity (10).
Conclusions
Protein function is dependent on an intricate interplay among protein structure, stability, and dynamics where stability refers to the difference in free energy between the structural microstates that are dynamically sampled (37). Protein folding dynamics can be perturbed by addition of chaotropic denaturants such as urea and guanidinium hydrochloride, which stabilize the states in a dynamic ensemble with the largest SAS areas (unfolded states in protein folding reactions). Our detailed investigation into the interplay among the structure, stability, dynamics, and catalysis of Adk shows that denaturants can also modulate the distribution of structural microstates within a folded structural basin. Using a 31P NMR-based enzymology assay, we have conclusively shown that Adk can be activated by addition of urea, and resolved the underlying mechanism. The rate of the Adk-catalyzed reaction is limited by the reopening of substrate-binding domains in the presence of bound nucleotide (5, 6) (Scheme 1), and urea addition stabilizes the more expanded open and bound state at the expense of the closed and bound state. A model that connects the activity data with the redistribution of structural states is a scenario where the structural redistribution is primarily dependent on an increased rate-constant for domain opening. However, from the equilibrium data presented here, it cannot be excluded that urea also affects the rate-constant for domain closing. In fact, a decreased rate-constant for domain closing would also result in a structural redistribution favoring the open substrate-bound state. However, modulation of only the rate-constant for domain closing cannot explain the increased Adk activity and the results collectively points toward that urea predominantly affects the rate-constant for domain opening. This interpretation is qualitatively in agreement with that urea generally has a larger effect on the unfolding rate constant compared to the refolding rate-constant in protein folding studies (30). Urea activation of other enzymes has also been observed—including dihydrofolate reductase (13, 14), prostaglandin D synthase (16, 17), and biliverdin-Ixα (18). Possibly, the increased activities in these other enzymes are also mediated by a redistribution of existing structural states. In practical terms, it appears that urea (and other denaturants) can be used to manipulate conformational dynamics in a controlled manner. This is possible for proteins where a significant difference in SAS area exists between the structural states involved. Urea has opposite effects on these dynamics to those of osmolytes like TMAO, which favor the closed and more compact state of Adk at the expense of the open, more expanded state (10, 38). Previous studies involving the combined use of TMAO and urea has shown that the apparent on-rate for formation of a Michaelis complex in LDH was increased and decreased in presence of low amounts of urea and TMAO, respectively. These effects in LDH were attributed to the propensity of urea to favor expanded structural states while TMAO favors compact states (39). In a detailed NMR spin relaxation study it was shown that picosecond-nanosecond fluctuations of the protein ribonuclease A were increased by addition of the denaturant guanidine hydrochloride (40). This effect could be reversed by addition of TMAO, illustrating that the fast timescale motions were quenched by the osmolyte. Finally, in a NMR-based study of hydrogen exchange kinetics, it was shown for ribonuclease A that one subset of residues displayed increased exchange kinetics in presence of urea, while the same residues displayed decreased exchange kinetics in presence of TMAO (41). It thus seems that the effects of Urea and TMAO are to predominantly favor expanded and compact protein states, respectively. Detailed analysis of the urea-dependent activation revealed that Adk can populate states with a locally disordered ATPlid domain, in accordance with a previous finding (31). This observation is also consistent with reports that the ATPlid and AMPbd domains can fold and unfold independently of unfolding of the CORE domain (8, 24). In addition, we detected a strong inverse correlation between the free energy of the Adk catalytic rate (kcat), and the free energy for substrate binding (Kd) in accordance with our previous observation of a kcat versus KM compensation effect (10). Similar covariation of kcat and KM has been observed previously in cold-adaptation of lactate-dehydrogenase A4 (A4-LDH). It was shown that A4-LDH isolated from organisms living in colder habitats have increased Kcat and KM values compared to A4-LDH isolated from organisms living in warmer habitats (42). Further Kcat-versus-KM compensation has been observed for the oxidative DNA repair enzyme AlkB (43). Taken together, our results provide a detailed illustration of the complex interplay among structure, stability, and catalysis of Adk, and demonstrate that urea can be used to manipulate conformational dynamics of proteins in a controlled manner.
Author Contributions
P.R. and M.W.-W. designed the experiments; P.R. executed the experiments; P.R. and M.W.-W. analyzed the data; and P.R. and M.W.-W. wrote the article.
Acknowledgments
This work was financially supported by the Swedish Research Council (grant no. 621-2013-5954) to M.W.-W.
The NMR experiments were conducted at NMR4life, and we thank the Wallenberg and Kempe foundations for supporting this infrastructure.
Editor: H. Jane Dyson.
References
- 1.Cho J.-H., Muralidharan V., Palmer A.G., 3rd Tuning protein autoinhibition by domain destabilization. Nat. Struct. Mol. Biol. 2011;18:550–555. doi: 10.1038/nsmb.2039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Panchal S.C., Kaiser D.A., Rosen M.K. A conserved amphipathic helix in WASP/Scar proteins is essential for activation of Arp2/3 complex. Nat. Struct. Biol. 2003;10:591–598. doi: 10.1038/nsb952. [DOI] [PubMed] [Google Scholar]
- 3.Beach H., Cole R., Loria J.P. Conservation of mus-ms enzyme motions in the apo- and substrate-mimicked state. J. Am. Chem. Soc. 2005;127:9167–9176. doi: 10.1021/ja0514949. [DOI] [PubMed] [Google Scholar]
- 4.Boehr D.D., McElheny D., Wright P.E. The dynamic energy landscape of dihydrofolate reductase catalysis. Science. 2006;313:1638–1642. doi: 10.1126/science.1130258. [DOI] [PubMed] [Google Scholar]
- 5.Wolf-Watz M., Thai V., Kern D. Linkage between dynamics and catalysis in a thermophilic-mesophilic enzyme pair. Nat. Struct. Mol. Biol. 2004;11:945–949. doi: 10.1038/nsmb821. [DOI] [PubMed] [Google Scholar]
- 6.Kovermann M., Ådén J., Wolf-Watz M. Structural basis for catalytically restrictive dynamics of a high-energy enzyme state. Nat. Commun. 2015;6:7644. doi: 10.1038/ncomms8644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hanson J.A., Duderstadt K., Yang H. Illuminating the mechanistic roles of enzyme conformational dynamics. Proc. Natl. Acad. Sci. USA. 2007;104:18055–18060. doi: 10.1073/pnas.0708600104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Rundqvist L., Adén J., Wolf-Watz M. Noncooperative folding of subdomains in adenylate kinase. Biochemistry. 2009;48:1911–1927. doi: 10.1021/bi8018042. [DOI] [PubMed] [Google Scholar]
- 9.Huse M., Kuriyan J. The conformational plasticity of protein kinases. Cell. 2002;109:275–282. doi: 10.1016/s0092-8674(02)00741-9. [DOI] [PubMed] [Google Scholar]
- 10.Ådén J., Verma A., Wolf-Watz M. Modulation of a pre-existing conformational equilibrium tunes adenylate kinase activity. J. Am. Chem. Soc. 2012;134:16562–16570. doi: 10.1021/ja3032482. [DOI] [PubMed] [Google Scholar]
- 11.Müller C.W., Schlauderer G.J., Schulz G.E. Adenylate kinase motions during catalysis: an energetic counterweight balancing substrate binding. Structure. 1996;4:147–156. doi: 10.1016/s0969-2126(96)00018-4. [DOI] [PubMed] [Google Scholar]
- 12.Müller C.W., Schulz G.E. Structure of the complex between adenylate kinase from Escherichia coli and the inhibitor Ap5A refined at 1.9 Å resolution. A model for a catalytic transition state. J. Mol. Biol. 1992;224:159–177. doi: 10.1016/0022-2836(92)90582-5. [DOI] [PubMed] [Google Scholar]
- 13.Fan Y.-X., Ju M., Tsou C.-l. Activation of chicken liver dihydrofolate reductase in concentrated urea solutions. Biochim. Biophys. Acta. 1995;1252:151–157. doi: 10.1016/0167-4838(95)00125-e. [DOI] [PubMed] [Google Scholar]
- 14.Fan Y.X., Ju M., Tsou C.L. Activation of chicken liver dihydrofolate reductase by urea and guanidine hydrochloride is accompanied by conformational change at the active site. Biochem. J. 1996;315:97–102. doi: 10.1042/bj3150097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Zhang H.-J., Sheng X.-R., Zhou J.-M. Activation of adenylate kinase by denaturants is due to the increasing conformational flexibility at its active sites. Biochem. Biophys. Res. Commun. 1997;238:382–386. doi: 10.1006/bbrc.1997.7301. [DOI] [PubMed] [Google Scholar]
- 16.Inui T., Ohkubo T., Hayaishi O. Enhancement of lipocalin-type prostaglandin D synthase enzyme activity by guanidine hydrochloride. Biochem. Biophys. Res. Commun. 1999;266:641–646. doi: 10.1006/bbrc.1999.1881. [DOI] [PubMed] [Google Scholar]
- 17.Inui T., Ohkubo T., Urade Y. Characterization of the unfolding process of lipocalin-type prostaglandin D synthase. J. Biol. Chem. 2003;278:2845–2852. doi: 10.1074/jbc.M209934200. [DOI] [PubMed] [Google Scholar]
- 18.Franklin E., Mantle T., Dunne A. Activation of human biliverdin-IXα reductase by urea: generation of kinetically distinct forms during the unfolding pathway. Biochim. Biophys. Acta. 2013;1834:2573–2578. doi: 10.1016/j.bbapap.2013.09.009. [DOI] [PubMed] [Google Scholar]
- 19.Rogne P., Sparrman T., Wolf-Watz M. Real-time 31P NMR investigation on the catalytic behavior of the enzyme adenylate kinase in the matrix of a switchable ionic liquid. ChemSusChem. 2015;8:3764–3768. doi: 10.1002/cssc.201501104. [DOI] [PubMed] [Google Scholar]
- 20.Brown T.R., Uğurbil K., Shulman R.G. 31P nuclear magnetic resonance measurements of ATPase kinetics in aerobic Escherichia coli cells. Proc. Natl. Acad. Sci. USA. 1977;74:5551–5553. doi: 10.1073/pnas.74.12.5551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kingsley-Hickman P.B., Sako E.Y., Uğurbil K. 31P NMR studies of ATP synthesis and hydrolysis kinetics in the intact myocardium. Biochemistry. 1987;26:7501–7510. doi: 10.1021/bi00397a045. [DOI] [PubMed] [Google Scholar]
- 22.Ugurbil K., Rottenberg H., Shulman R.G. 31P nuclear magnetic resonance studies of bioenergetics and glycolysis in anaerobic Escherichia coli cells. Proc. Natl. Acad. Sci. USA. 1978;75:2244–2248. doi: 10.1073/pnas.75.5.2244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Reinstein J., Brune M., Wittinghofer A. Mutations in the nucleotide binding loop of adenylate kinase of Escherichia coli. Biochemistry. 1988;27:4712–4720. doi: 10.1021/bi00413a020. [DOI] [PubMed] [Google Scholar]
- 24.Olsson U., Wolf-Watz M. Overlap between folding and functional energy landscapes for adenylate kinase conformational change. Nat. Commun. 2010;1:111. doi: 10.1038/ncomms1106. [DOI] [PubMed] [Google Scholar]
- 25.Tanford C. Isothermal unfolding of globular proteins in aqueous urea solutions. J. Am. Chem. Soc. 1964;86:2050–2059. [Google Scholar]
- 26.Selvaratnam R., VanSchouwen B., Melacini G. The projection analysis of NMR chemical shifts reveals extended EPAC autoinhibition determinants. Biophys. J. 2012;102:630–639. doi: 10.1016/j.bpj.2011.12.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Santoro M.M., Bolen D.W. Unfolding free energy changes determined by the linear extrapolation method. 1. Unfolding of phenylmethanesulfonyl alpha-chymotrypsin using different denaturants. Biochemistry. 1988;27:8063–8068. doi: 10.1021/bi00421a014. [DOI] [PubMed] [Google Scholar]
- 28.Schwert G.W., Takenaka Y. Lactic dehydrogenase. III. Mechanism of the reaction. J. Biol. Chem. 1956;223:157–170. [PubMed] [Google Scholar]
- 29.Rhoads D.G., Lowenstein J.M. Initial velocity and equilibrium kinetics of myokinase. J. Biol. Chem. 1968;243:3963–3972. [PubMed] [Google Scholar]
- 30.Fersht A.R. W.H. Freeman; New York: 1999. Structure and Mechanism in Protein Science. [Google Scholar]
- 31.Schrank T.P., Bolen D.W., Hilser V.J. Rational modulation of conformational fluctuations in adenylate kinase reveals a local unfolding mechanism for allostery and functional adaptation in proteins. Proc. Natl. Acad. Sci. USA. 2009;106:16984–16989. doi: 10.1073/pnas.0906510106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Myers J.K., Pace C.N., Scholtz J.M. Denaturant m values and heat capacity changes: relation to changes in accessible surface areas of protein unfolding. Protein Sci. 1995;4:2138–2148. doi: 10.1002/pro.5560041020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Adén J., Wolf-Watz M. NMR identification of transient complexes critical to adenylate kinase catalysis. J. Am. Chem. Soc. 2007;129:14003–14012. doi: 10.1021/ja075055g. [DOI] [PubMed] [Google Scholar]
- 34.Esteban-Martín S., Fenwick R.B., Salvatella X. Correlated inter-domain motions in adenylate kinase. PLOS Comput. Biol. 2014;10:e1003721. doi: 10.1371/journal.pcbi.1003721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Henzler-Wildman K.A., Thai V., Kern D. Intrinsic motions along an enzymatic reaction trajectory. Nature. 2007;450:838–844. doi: 10.1038/nature06410. [DOI] [PubMed] [Google Scholar]
- 36.Bai Y., Sosnick T.R., Englander S.W. Protein folding intermediates: native-state hydrogen exchange. Science. 1995;269:192–197. doi: 10.1126/science.7618079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kovermann M., Rogne P., Wolf-Watz M. Protein dynamics and function from solution state NMR spectroscopy. Q. Rev. Biophys. 2016;49:e6. doi: 10.1017/S0033583516000019. [DOI] [PubMed] [Google Scholar]
- 38.Nagarajan S., Amir D., Haas E. Modulation of functionally significant conformational equilibria in adenylate kinase by high concentrations of trimethylamine oxide attributed to volume exclusion. Biophys. J. 2011;100:2991–2999. doi: 10.1016/j.bpj.2011.03.065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Qiu L., Gulotta M., Callender R. Lactate dehydrogenase undergoes a substantial structural change to bind its substrate. Biophys. J. 2007;93:1677–1686. doi: 10.1529/biophysj.107.109397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Doan-Nguyen V., Loria J.P. The effects of cosolutes on protein dynamics: the reversal of denaturant-induced protein fluctuations by trimethylamine N-oxide. Protein Sci. 2007;16:20–29. doi: 10.1110/ps.062393707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Qu Y., Bolen D.W. Hydrogen exchange kinetics of RNase A and the urea:TMAO paradigm. Biochemistry. 2003;42:5837–5849. doi: 10.1021/bi0206457. [DOI] [PubMed] [Google Scholar]
- 42.Fields P.A., Somero G.N. Hot spots in cold adaptation: localized increases in conformational flexibility in lactate dehydrogenase A4 orthologs of Antarctic notothenioid fishes. Proc. Natl. Acad. Sci. USA. 1998;95:11476–11481. doi: 10.1073/pnas.95.19.11476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Yu B., Hunt J.F. Enzymological and structural studies of the mechanism of promiscuous substrate recognition by the oxidative DNA repair enzyme AlkB. Proc. Natl. Acad. Sci. USA. 2009;106:14315–14320. doi: 10.1073/pnas.0812938106. [DOI] [PMC free article] [PubMed] [Google Scholar]