Skip to main content
PMC home page
Acta Crystallographica Section D: Structural Biology logoLink to Acta Crystallographica Section D: Structural Biology
. 2016 Sep 20;72(Pt 10):1137–1148. doi: 10.1107/S2059798316013541

PRISM-EM: template interface-based modelling of multi-protein complexes guided by cryo-electron microscopy density maps

Guray Kuzu a,‡, Ozlem Keskin a,b,*, Ruth Nussinov c,d, Attila Gursoy e,*
PMCID: PMC5053140  PMID: 27710935

A new approach is reported to computationally generate plausible structural models using a procedure that combines crystallographic structures and density maps obtained from three-dimensional electron microscopy.

Keywords: multimolecular protein complexes, modelling protein assemblies, PRISM-EM, three-dimensional electron microscopy, protein structure prediction

Abstract

The structures of protein assemblies are important for elucidating cellular processes at the molecular level. Three-dimensional electron microscopy (3DEM) is a powerful method to identify the structures of assemblies, especially those that are challenging to study by crystallography. Here, a new approach, PRISM-EM, is reported to computationally generate plausible structural models using a procedure that combines crystallographic structures and density maps obtained from 3DEM. The predictions are validated against seven available structurally different crystallographic complexes. The models display mean deviations in the backbone of <5 Å. PRISM-EM was further tested on different benchmark sets; the accuracy was evaluated with respect to the structure of the complex, and the correlation with EM density maps and interface predictions were evaluated and compared with those obtained using other methods. PRISM-EM was then used to predict the structure of the ternary complex of the HIV-1 envelope glycoprotein trimer, the ligand CD4 and the neutralizing protein m36.

1. Introduction  

In the cell, proteins typically associate into multimolecular assemblies. Protein structures are solved at the atomic scale using nuclear magnetic resonance (NMR) spectroscopy (Wüthrich, 1990 ▸) and X-ray crystallography (Pennisi, 1998 ▸; Allen et al., 2009 ▸) and stored in the Protein Data Bank (PDB; Berman et al., 2002 ▸). However, these experimental techniques are often limited when applied to large protein assemblies. Other techniques, such as small-angle X-ray scattering (SAXS; Pelikan et al., 2009 ▸) and fluorescence resonance energy transfer (FRET; Raicu & Singh, 2013 ▸) have historically provided data for these large assemblies, albeit at low resolution. More recently, three-dimensional electron microscopy (3DEM), including approaches using cryo-electron microscopy and cryo-electron tomography, have begun to provide information on structures of protein complexes at increasingly high resolutions (Carragher et al., 2004 ▸; Orlova & Saibil, 2011 ▸; Rachel et al., 1986 ▸; Kühlbrandt, 2014 ▸; Hashem et al., 2013 ▸; Zhang et al., 2010 ▸). 3DEM data (at high and low resolution) can be usefully merged with crystallographic information using computational tools to model the structures of complex biological assemblies, maximizing resolution and biological relevance.

Computational methods can exploit and complement 3DEM data in at least two ways: (i) by fitting assembly subunits into 3DEM density maps to form the complex structure and (ii) by selecting structures from docked solutions that fit into the density maps. In the former, computational methods, such as ADP_EM (Garzón et al., 2007 ▸), Foldhunter (Jiang et al., 2001 ▸), URO/UROX (Navaza et al., 2002 ▸; Siebert & Navaza, 2009 ▸), DockEM (Roseman, 2000 ▸), EMfit (Rossmann, 2000 ▸; Rossmann et al., 2001 ▸) and Situs (Wriggers et al., 1999 ▸), perform an exhaustive search to fit protein structures into 3DEM density maps. Situs is also capable of flexible docking (Rusu et al., 2008 ▸). FRM (Kovacs et al., 2003 ▸) and gEMfitter (Hoang et al., 2013 ▸) use a fast Fourier transform to fit structures into the density maps, Gorgon (Baker et al., 2011 ▸) considers secondary-structure matching, and 3SOM (Ceulemans & Russell, 2004 ▸) is based on surface-overlap maximization. Some other methods carry out segmentation of 3DEM density maps using different approaches, such as level sets (VolRover; Baker et al., 2006 ▸), elastic networks (hENM; Burger et al., 2011 ▸), watershed (Volkmann, 2002 ▸) and watershed/scale-space filtering (Segger; Pintilie et al., 2010 ▸; Pintilie & Chiu, 2012 ▸). After the segmentation process, subunits can be docked individually. Other tools such as MultiFit (Lasker et al., 2009 ▸; Tjioe et al., 2011 ▸), GMFit (Kawabata, 2008 ▸) and ATTRACT-EM (de Vries & Zacharias, 2012 ▸) go a step further and perform multiple docking. They fit multiple protein structures simultaneously based on molecular-docking and molecular-fitting approaches; ATTRACT-EM also refines the models after docking structures into the density map. Another important tool is UCSF Chimera (Pettersen et al., 2004 ▸), which is used for interactive visualization and analysis of molecular structures and related data, including density maps. Structures can be fitted into density maps automatically. Chimera has plug-in versions of MultiFit and Segger. Although powerful, methods for docking protein structures into 3DEM density maps can provide models with false-positive protein–protein interfaces unless filtered, for example by removing those with steric clashes.

The second way is to exploit 3DEM density maps to select structures among docking solutions. In this approach, one can use computational docking methods (Pierce et al., 2005 ▸; Schneidman-Duhovny et al., 2005a ▸,b ▸; Karaca et al., 2010 ▸; Inbar et al., 2005 ▸; Kuzu et al., 2014 ▸) to first construct a large number of protein-assembly models by exploiting existing high-resolution structural information from X-ray crystallography and NMR spectroscopy. Using this as a basis set, it is possible to use lower resolution 3DEM density maps to evaluate, rank and select the best models that are both structurally plausible and consistent with the experimental density maps. Recently, the use of HADDOCK with cryo-EM data (van Zundert et al., 2015 ▸) has been introduced. Besides cryo-EM, additional information such as mutagenesis and hydroxyl radical footprinting data are utilized to construct structures of complexes with correct interfaces. A general method which does not require any additional information would be helpful in constructing protein assemblies in cases where such data are unavailable. In an earlier effort to address this problem, we presented a method to construct protein assemblies starting from binary interactions (Kuzu et al., 2014 ▸). There, only PDB structures (and models if the PDB structures were unavailable) were exploited in the construction, and the model of the complex was obtained based on the predicted interfaces. 3DEM density maps were not used. The output was a set of solutions. As a test, we checked whether a model that fitted into the 3DEM density map was in our solution set. The model most similar to the PDB structure of the assembly was found to be consistent with the 3DEM density map.

Here, we develop a method that models the multimolecular complex by exploiting 3DEM density maps. It adds protein units one by one, at each step checking quantitatively whether the structures fit any part of the 3DEM density map. In this method, at each step structures that do not fit into the 3DEM density map are eliminated, avoiding conformations other than those that the 3DEM data cover, and thus saving computational time. Binary interactions are predicted by using interface motifs that recur at protein interfaces (Tsai et al., 1996 ▸, 1997 ▸; Keskin & Nussinov, 2005 ▸; Keskin et al., 2008 ▸, 2016 ▸). PRISM is based on these principles and considers recurring motifs in protein interfaces (Tuncbag et al., 2011 ▸; Baspinar et al., 2014 ▸; Ogmen et al., 2005 ▸; Aytuna et al., 2005 ▸). In modelling protein assemblies. such predictions complement the 3DEM data. Below, we describe our algorithm PRISM-EM. We illustrate its usage with the example of a HIV-1 envelope glycoprotein trimer complexed with the antibody 17b. We present its performance on benchmark data sets and compare our results with those obtained using other methods. Finally, we propose a model for the HIV-1 envelope glycoprotein trimer complexed with soluble CD4 and the neutralizing protein m36, a complex that has been analyzed by cryo-electron tomography at ∼20 Å resolution, but for which an atomic resolution structure is currently unavailable.

2. Materials and methods  

We construct protein assemblies based on binary protein interactions predicted by PRISM (Tuncbag et al., 2011 ▸; Baspinar et al., 2014 ▸; Ogmen et al., 2005 ▸; Aytuna et al., 2005 ▸). The complete predicted assemblies are those docked into the 3DEM density map in the final step. The prediction of binary interactions, the construction of protein assemblies using 3DEM density maps, case studies and the benchmark data set are detailed below.

2.1. Pairwise protein-interaction prediction using PRISM  

PRISM (PRotein Interactions by Structural Matching) is a template-based method which predicts interactions and their structural models between query proteins (the target set). The template set of PRISM is the structurally nonredundant set of known protein interfaces. The query proteins constitute the target set. The logic of PRISM is as follows: if a protein has a similar surface to one side of a known protein interface, and another protein has a similar surface to the other side of that interface, then PRISM considers a possible interaction between these two proteins using the known interface as the template. Procedure-wise, the surfaces of proteins in the target set are first extracted (step 1 in Fig. 1 ▸). They are then structurally aligned with the interfaces in the template set using the MultiProt tool (Shatsky et al., 2002 ▸; step 2 in Fig. 1 ▸). PRISM makes use of the top three conformations for each target protein–template alignment, which results in nine candidate structures for the prediction of a binary interaction based on a template interface. Thirdly, the candidate interactions are filtered by eliminating the sterically clashing proteins. PRISM then checks if the matched residues from both sides are in contact with each other and at least one residue matches a hot spot in the template interface (step 3 in Fig. 1 ▸). Fourthly, the energy score of the candidate interactions is calculated using FiberDock (Mashiach et al., 2010 ▸; step 4 in Fig. 1 ▸). FiberDock mainly reorients side chains and slightly reorients the backbones of the proteins and calculates the energy. The binding energy score (BES) threshold was chosen as −10 as in our previous studies (Kuzu et al., 2013 ▸, 2014 ▸; Kar et al., 2012 ▸).

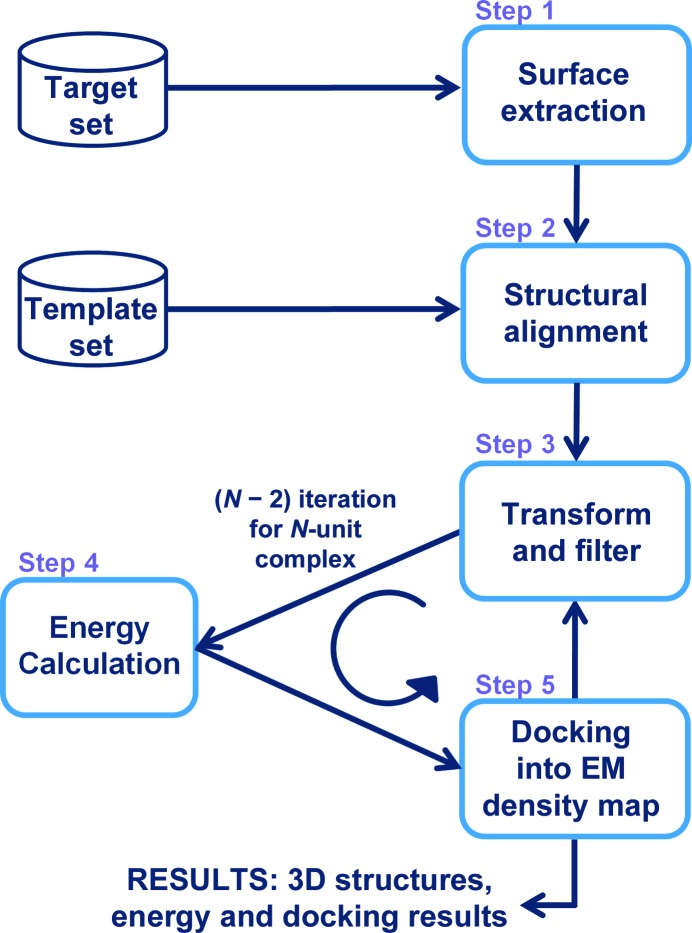
Figure 1.

Figure 1

Open in a new tab

Flowchart of assembly construction using a 3DEM density map. Step 1: the surfaces of the target proteins are extracted. Step 2: the surfaces of the target proteins are aligned onto the template interfaces of the known interactions. Step 3: target proteins are transformed next to each other with regard to the template interfaces they match; candidate interactions are filtered with regard to hot-spot matches and clashes. Step 4: flexible refinement and energy calculation are performed. Interactions with favourable energies pass this step. Step 5: structures are docked into the 3DEM density map and checked whether they fit. N − 2 iterations are performed through steps 3–5 to construct N-subunit assemblies. The end result consists of assembly structures together with their energies and docked 3DEM density maps. PRISM predicts binary interaction through steps 1–4. It gives the structures of the interactions and their energies as the result.

2.2. Constructing protein assemblies based on EM density maps  

In the fifth step, after PRISM has predicted binary interactions, assemblies are constructed based on these inter­actions. Subcomplexes are docked into the 3DEM density map using the Situs tool (Wriggers et al., 1999 ▸) and scored according to their fit (step 5 in Fig. 1 ▸). Structures that can fit into the 3DEM density map pass this step.

N-unit complexes (N-mers) are constructed in N − 2 iterations of the last two steps of PRISM and are docked into the 3DEM density map (steps 3–5 in Fig. 1 ▸). In each iteration, one protein is added (step 3) to the subcomplex obtained in the previous step according to the predicted binary inter­actions; clashes in the new subcomplexes are identified and their energies are calculated (step 4), and subcomplexes are then docked into the 3DEM density map (step 5). Those that fit into the density map are passed to the next iteration. The best subcomplexes (dimers, trimers) are not necessarily the best N-mer; therefore, all possible combinations obtained by adding a protein to a subcomplex of the previous round are considered. If a binary interaction could not be predicted in the initial step, the complex could still be modelled based on other binary interactions. Structures are filtered with respect to clashes (step 3), energy scores (step 4) and 3DEM density map fits (step 5). At the end, the method gives the number of N-unit complexes that fit into the 3DEM density map. The complex with the best (lowest) Situs score is selected as the best model; Situs gives a score of the r.m.s.d. between the codebook vectors created for the density map and the structure, where codebook vectors are the vector positions of a coarse-grained representation of three-dimensional data. Here, we select one structure as the solution according to how the structures fit into the density map.

To run the script, the user needs to enter the inputs: a list of pairs of proteins between which interactions are searched for, a template list, the set of proteins in the complex, the 3DEM density map and the approximate number of residues in the density map. The first two are the inputs of PRISM. The script (available at http://prism.ccbb.ku.edu.tr/prismem) is run as <script> <pair_list> <template_list> <job_id> <set_of_proteins> <3DEM_data> <size_of_the_density_map>.

As an example, the following were used for the construction of 3cre, the first case in our set.

  • Pair list: 3crf B–2co1 A, 3crf B–2co1 B, 2co1 A–2co1 B.

  • Template list: default set + 2cnz AB.

  • Job ID: defined by the user.

  • Set of proteins: 3crf B, 2co1 A, 2co1 B.

  • 3DEM data: EMDB ID 1494.

  • Size of the density map (approximate in residues): 286.

  • python prismEM.py pair_list template_list 1 3crfB.pdb,2co1A.pdb,2co1B.pdb EMDB_1494.map 286.

The complex is constructed for the given set of proteins; if the user gives an incomplete list of proteins as input, the method will provide the ‘best’ subcomplex fit into the density map; if the list includes more than the density map covers, after the best fitted structure is obtained, another protein is added in the following step and the construction process is then terminated since larger structures will not fit well into the density map. [As an example, we also run our method for the first case of the MultiFit set, PDB entry 7cat, with an additional monomer (a third monomer) and an extra other protein (1urz A, a different protein from another case of the set) to obtain a tetramer; it terminated after the dimers since no further good fitting into the density map could be obtained.] The approximate number of residues present in the density map is needed for docking via Situs; this information is used to compare the volume of structures and the density map, therefore it tolerates an approximate number.

2.3. Case studies and the benchmark data set  

We illustrate the construction of models of antibody-bound HIV-1 envelope glycoprotein as a representative example. Where available, atomic resolution protein structural models are taken from the PDB (Berman et al., 2002 ▸) and 3DEM density maps are taken from the EMDataBank (EMDB; Lawson et al., 2011 ▸). In the first example (HIV gp120–CD4–17b complex) the structure of the assembly is available in the PDB; in the second example (HIV protein gp120–CD4–m36) the structure of the antibody complex is unknown. Here, we use the modelling tool I-TASSER (Roy et al., 2010 ▸; Zhang, 2008 ▸). Structures are modelled with templates (with 100% sequence similarity) to mimic cases where crystallographic structures were not available. We use the best model (based on the I-TASSER score) in our predictions (Supplementary Table S1; PDB files of the models are available in the Supporting Information). Chimera v.1.6.2 (Pettersen et al., 2004 ▸) is used to calculate the correlation between high-resolution and low-resolution data. The backbone r.m.s.d. (heavy atoms N, Cα, C, O) of all residues is calculated. We compare the atomic positions of interface predictions with the atomic positions of the experimental PDB interface. The IS-score evaluates side-chain contact similarity in addition to geometric similarity (Gao & Skolnick, 2011 ▸); we consider IS-scores lower than 0.12 as ‘incorrect’ predictions, IS-scores between 0.12 and 0.17 as ‘acceptable’ and IS-scores higher than 0.17 as ‘correct’, as indicated in the original study.

We have prepared a benchmark data set to test our method (Table 1 ▸). We searched the PDB entries and selected representative complexes for which an experimental density map was available, rather than creating artificial volume data using a prediction tool. The benchmark data set covers seven assemblies from three to eight subunits encompassing 19–521 residues in a single subunit and 286–4168 residues in total in the complex. The data set includes symmetric/asymmetric and homo/hetero complexes. The proteins have 1.4–26.7% sequence similarity (based on the Needleman–Wunsch algorithm, BLOSUM62) and 0.7–15.3% sequence identity to proteins in other complexes. They cover the main SCOP (Structural Classification of Proteins) classes (Lo Conte et al., 2000 ▸): all-alpha proteins (all-α), all-beta proteins (all-β), alpha and beta proteins (α+β) and alpha–beta proteins (α/β), which were found using the Superfamily 1.75 server (de Lima Morais et al., 2011 ▸). For proteins that lack a SCOP classification, the SCOP class was determined from homologues of the proteins. 3DEM density maps have resolutions of 6–23 Å. The conformational changes of the proteins during binding are given in Supplementary Table S2. We constructed assemblies starting from unbound (crystal or I-TASSER-modelled) structures of the proteins whose binary interactions can be predicted by PRISM. For comparison purposes, we also run MultiFit (Lasker et al., 2010 ▸; Tjioe et al., 2011 ▸) and a combined Chimera–Segger method (Pettersen et al., 2004 ▸; Pintilie et al., 2010 ▸; Pintilie & Chiu, 2012 ▸; fitting structures into segments). We fitted structures using MultiFit with symmetric or non­symmetric modes and obtained up to ten models for each case. For models that are not similar to the PDB structure, we selected the first model as the solution. In Chimera, ‘segment map’ and ‘fit to segments’ functions are available to obtain a structural model for multimers by using Segger. We first segmented the density map; if we obtained the desired segments then we docked the structures using the ’fit to segments’ option of Chimera.

Table 1. Benchmark data set.

Assembly EMDB ID EM resolution (Å) PDB code No. of subunit residues No. of assembly residues Structure SCOP class of chains
Saf pilus type A 1494 17 3cre 19, 123, 144 286 Heterocomplex, asymmetric All-β
ParM filament 1980 7.2 4a6j 320 960 Homocomplex, asymmetric α/β
Biomphalaria glabrata acetylcholine-binding protein type 1 2055 6 4aod 205 1025 Homocomplex, symmetric All-β
Antibody VRC-PG04 in complex with HIV-1 gp120 2427 23 3se9 208, 228, 353 789 Heterocomplex, asymmetric All-β, α+β
Lidless Mm-cpn in the open state 5140 8 3iyf 521 4168 Homocomplex, symmetric All-α, α+β, α/β
Conjugal transfer protein TrwB 5505 20 1e9r 437 2622 Homocomplex, symmetric α/β
Circadian clock protein KaiC 5672 16 3dvl 519 3114 Homocomplex, symmetric α/β
Open in a new tab

We also tested our method on the MultiFit benchmark set. However, we discarded some cases from the set. In our study, interfaces are defined as regions consisting of residues that are at a distance of less than the summation of their van der Waals distances plus 0.5 Å, and PRISM works for interfaces which have at least ten residues. The interfaces are not large enough in some cases according to our criteria: the RecA protein (PDB entry 2rec) and nitrite reductase (PDB entry 1nic). Nitrite reductase (PDB entry 1nic) is given as a monomer in the PDB; we tried to obtain a trimeric form using crystal symmetry, but the interfaces were not sufficiently large. We included the methane monooxygenase enzyme (PDB entry 1mty) and the GroEL chaperone (PDB entry 1gru) in the benchmark set. EMDB ID 1046 was used for the density map of the GroEL chaperone, and the other density maps were created using Situs, as described by Lasker et al. (2010 ▸). We ran MultiFit with default parameters and specified the resolution of the density map.

We tested the dimers (7cat AB and 1gte AB) in the MultiFit set to measure the computational time. The predictions were completed in 1942 and 5790 s, respectively. 7cat AB has 1012 residues and 1gte AB has 2050 residues. The predictions were performed with a template interface; in each prediction process, 18 structures were predicted and two structures were docked with Situs. If the docking into 3DEM step was omitted, the predictions were computed in 832 and 4987 s. The prediction of the interfaces was responsible for this computational cost. The process would be faster without the interface predictions, as in MultiFit. Docking the same structures with MultiFit took 177 and 292 s, respectively.

Furthermore, we tested PRISM-EM on the HADDOCK-EM benchmark set, which is a subset of the ZDOCK benchmark set 4.0 (Hwang et al., 2010 ▸). We created the density maps of the complexes at 10 Å, using the molmap function in Chimera, following the procedure introduced in the HADDOCK-EM study, and model complexes using our default template set. We report the i.r.m.s.d. (interface r.m.s.d., interface residues were determined with a cutoff of 10 Å) of the predictions as in the HADDOCK-EM study.

3. Results  

We first illustrate the results of PRISM-EM for the construction of assemblies of the HIV-1 Env trimer complexed with a portion of the ectodomain of the human transmembrane receptor CD4 (sCD4) and the Fab fragment of the antibody 17b. The structure of the gp120–CD4–17b complex is available in the PDB (PDB entry 1gc1). We then tested PRISM-EM on a benchmark data set of various assemblies. We constructed the assemblies and evaluated our predictions with respect to the PDB structures and 3DEM density maps. We also tested MultiFit (Lasker et al., 2010 ▸; Tjioe et al., 2011 ▸) and Chimera–Segger (fitting structures into segments obtained by Segger; Pintilie et al., 2010 ▸; Pintilie & Chiu, 2012 ▸) on our benchmark set, and compared the results. Moreover, we tested the method on the MultiFit and HADDOCK-EM benchmark sets. Finally, we constructed a complex for which a structure was not available in the PDB: HIV protein complexed with CD4 and the antibody m36.

3.1. Case study 1: HIV protein gp120–CD4–antibody 17b complex  

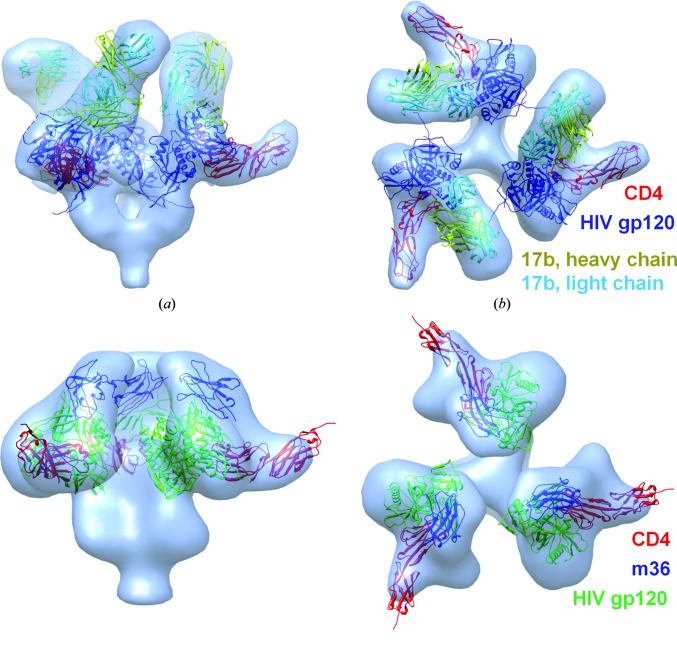
The PDB structure 1gc1 has four chains and shows the interaction of HIV gp120 with sCD4 and the heavy and light chains of the Fab fragment of the antibody 17b. The 3DEM density map of this assembly is available in the EMDB (ID 5020). We constructed the assembly using the PDB structures 3jwo A (HIV gp120), 3cd4 A (sCD4) and 1rz8 AB (17b). 3jwo contains the interaction of HIV gp120 with another antibody (48d), 3cd4 is the unbound form of sCD4 (which includes the two most membrane-distal domains of the CD4 ectodomain), and 1rz8 includes the Fab fragment heavy and light chains of the antibody 17b. The model with the best fit has a Situs score of 1.07 Å, an i.r.m.s.d. of 3.85 Å and an r.m.s.d. of 5.70 Å. The correlation calculated by Chimera is 0.91. The IS-scores of the interfaces (gp120–CD4, gp120–17b heavy chain and 17b heavy chain–17b light chain) are 0.71, 0.19 and 0.53, respectively, which are greater than 0.17 and indicate the interfaces to be ‘correct’. Figs. 2 ▸(a) and 2 ▸(b) present the best model fitted into the density map.

Figure 2.

Figure 2

Open in a new tab

HIV interactions. The best models of HIV gp120–CD4–17b [side (a) and top (b) views] and HIV gp120–CD4–m36 [side (c) and top (d) views] are shown as fitted into their 3DEM density maps (EMDB IDs 5020 and 5554, respectively). In (a) and (b), HIV gp120 is shown in blue, CD4 in red, the heavy chain of 17b in yellow and the light chain of 17b in cyan. In (c) and (d), HIV gp120 is shown in green, CD4 in red and m36 in blue. Three symmetric complexes are created using Chimera based on the symmetry of the density maps.

3.2. Benchmark data set  

We tested our method on a benchmark data set including various proteins (Table 1 ▸) in a similar way as in the construction of HIV-1 envelope glycoprotein models. We constructed assemblies starting from unbound structures of the proteins, if available, or from modelled structures. We used our default template set (Tuncbag et al., 2008 ▸) and manually included specific interactions for some cases (Table 2 ▸); 2cnz AB is the interaction of Saf pilus complexed with Saf pilus peptide, 3iku HJ is the dimer interface of the ParM filament, 3ngb GH is the interface of HIV gp120 and the antibody VRC01, and 3kfk CD is the dimer interface of a chaperonin. These additional interfaces are now available in our most recent template set (Cukuroglu et al., 2014 ▸). We selected the model with the lowest Situs score as the best model. Table 2 ▸ and Fig. 3 ▸ show the results. We compared our predictions with the PDB structures and present docking results with Situs scores and correlations.

Table 2. Assembly-construction results of the benchmark data set.

The EMDB IDs of the density maps and the number of subunits of the complexes are given. PDB structures or models obtained by modelling were used as target structures. The fifth column shows the Situs score of docking the PDB structure into the density map. The sixth column gives the r.m.s.d.s of the models and the seventh column shows the IS-score of interfaces in the model structures evaluated with respect to the PDB structures. The eighth and ninth columns present the results of docking the model structures into the density maps: the Situs score and the correlation calculated by Chimera, respectively.

EMDB ID Predicted structure Target structures Template set PDB structure, Situs result (Å) Model, r.m.s.d. (Å) Model, IS-score Model, Situs result (Å) Model, correlation
1494 Trimer 3crf B, 2co1 AB Default set + 2cnz AB 1.16 4.92 0.80–0.83 1.36 0.79
1980 Trimer 2zhc A Default set + 3iku HJ 6.16 3.83 0.14–0.21 4.17 0.59
1980 Tetramer 2zhc A Default set + 3iku HJ 6.16 4.16 0.12–0.20 7.38 0.51
2055 Pentamer 4aod A model Default set 2.22 2.16 0.33–0.38 1.95 0.89
2427 Trimer 4lsp G, 3se9 H model, 3se9 L model Default set + 3ngb GH 1.78 4.64 0.14–0.33 2.01 0.84
5140 Octamer 3iyf A model Default set + 3kfk CD 2.35 7.35 0.24–0.37 2.95 0.78
5505 Hexamer 1e9r A model Default set 3.04 2.44 0.67–0.71 1.07 0.84
5672 Hexamer 3dvl A model Default set 1.53 1.86 0.41–0.51 4.50 0.96
Open in a new tab

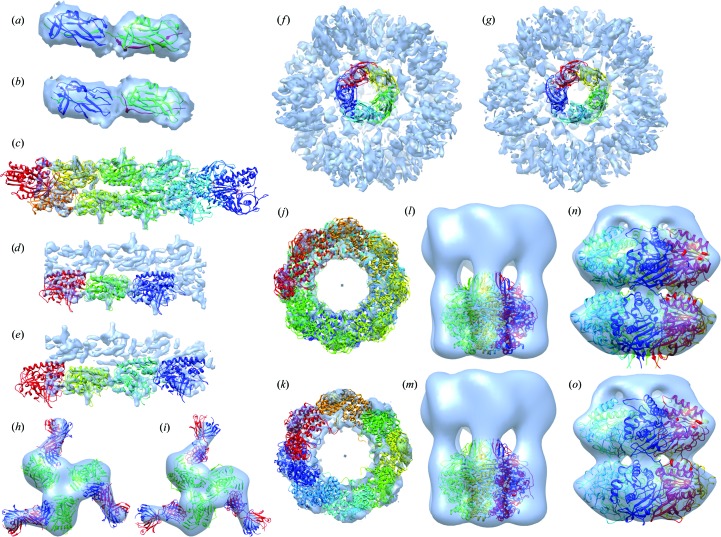
Figure 3.

Figure 3

Open in a new tab

Benchmark assemblies. The PDB structures and the best models fitted into EM density maps are shown. Each chain is shown in different colours. (a, b) Case 1: Saf pilus type A. PDB entry 3cre (a) and the model (b) are fitted into EMDB ID 1494. (c–e) Case 2: ParM filament. PDB entry 4a6j (c), trimer model (d) and tetramer model (e) are fitted into EMDB ID 1980. (f, g) Case 3: acetylcholine-binding protein type 1. PDB entry 4aod (f) and the model (g) are fitted into EMDB ID 2055; the EM density map level was decreased to 1.80 to obtain an image with the Chimera fit. (h, i) Case 4: VRC-PG04 in complex with HIV-1 gp120. PDB entry 3se9 (h) and the model (i) are fitted into EMDB ID 2427; three complexes are created using Chimera based on the symmetry of the density map. (j, k) Case 5: lidless Mm-cpn. PDB entry 3iyf (j) and the model (k) are fitted into EMDB ID 5140. (l, m) Case 6: conjugal transfer protein TrwB. PDB entry 1e9r (l) and the model (m) are fitted into EMDB ID 5505; the EM density map level was decreased to 0.6 to obtain a distinctive image of the density map. (n, o) Case 7: circadian clock protein KaiC. PDB entry 3dvl (n) and the model (o) are fitted into EMDB ID 5672; the 3DEM density map level was decreased to 0.1 to obtain a distinctive image of the density map.

Our models have r.m.s.d. values of 1.86–7.35 Å when compared with the PDB structures, Situs scores of 1.07–7.38 Å and correlations of 0.51–0.96 when docked into density maps. Our results have an r.m.s.d. of less than 5 Å, excluding the result for Lidless Mm-cpn (PDB entry 3iyf and EMDB ID 5140), and we obtained correlations close to or higher than 0.8, excluding the result for the ParM filament (PDB entry 4a6j, EMDB ID 1980; the inadequate results are explained below). We evaluated each interface in our assemblies using the IS-score. 28 interfaces were evaluated as ‘correct’, four interfaces as ‘acceptable’ and none as ‘incorrect’ (all IS-scores are given in Table 3 ▸). Two interfaces (one interface of 1e9r and 3iyf) could not be obtained owing to imperfect cyclic models.

Table 3. Evaluation of the interfaces predicted by our method.

Model interfaces are evaluated with respect to the PDB structures: IS-score < 0.12, ‘incorrect’; 0.12 < IS-score < 0.17, ‘acceptable’; 0.17 < IS-score, ‘correct’.

PDB code PDB, interface Model Model, interface IS-score Result
3cre AB 3cre model AB 0.83 Correct
BC BC 0.80 Correct
4a6j AC 4a6j trimer model AB 0.21 Correct
BC 0.14 Acceptable
4a6j tetramer model AB 0.14 Acceptable
BC 0.20 Correct
CD 0.12 Acceptable
4aod AB 4aod model AB 0.38 Correct
BC 0.34 Correct
CD 0.38 Correct
DE 0.33 Correct
EA 0.35 Correct
3se9 GH 3se9 model GH 0.14 Acceptable
HL HL 0.33 Correct
3iyf AB 3iyf model AH 0.24 Correct
HG — —
GD 0.37 Correct
DF 0.27 Correct
FE 0.33 Correct
EC 0.26 Correct
CB 0.37 Correct
BA 0.28 Correct
1e9r AB 1e9r model AB 0.70 Correct
BC 0.69 Correct
CD 0.71 Correct
DE 0.71 Correct
EF 0.67 Correct
FA — —
3dvl AB 3dvl model AB 0.41 Correct
BC 0.42 Correct
CD 0.39 Correct
DE 0.46 Correct
EF 0.51 Correct
FA 0.41 Correct
1gc1 GH 1gc1 model GB 0.1925 Correct
HL BA 0.5326 Correct
GC GC 0.7067 Correct
GC m36 model AC 0.7701 Correct
Open in a new tab

We investigated the cases for which we could not obtain good results. The ParM filament density map, EMDB ID 1980, shows two stripes. Each covers three complete and one partial subunit. We modelled the trimer structure starting from the unbound form 2zhc. The correlation of our trimer model (Fig. 3 ▸ d) is 0.59, which is quite low; but the Situs score is 4.17 Å and the r.m.s.d. compared with the PDB structure, 4a6j, is 3.83 Å, which are relatively acceptable results. Based on the trimer model, we obtained a tetramer model. The tetramer model is larger than the density map (Fig. 3 ▸ e) and docking into the density map was not very successful, as expected, with a correlation of 0.59 and Situs score of 7.38 Å. However, our model is similar to the PDB structure; the r.m.s.d. is 4.16 Å and docking the PDB structure into the density map gave similar results. The Situs score is 6.16 Å, which is close to the Situs score of our tetramer model (7.38 Å). Here, our models have similar correlation and fitting results to the PDB structure.

In another case, we modelled the open state of lidless Mm-cpn (PDB entry 3iyf and EMDB ID 5140) and obtained an octamer model (Fig. 3 ▸ k) which does not have a perfect cyclic structure (IS-scores are given in Table 3 ▸). It has an r.m.s.d. of 7.35 Å. However, when we docked our model and the PDB structure into the density map, we obtained very similar Situs scores of 2.95 and 2.35 Å, respectively. This indicates that our model can fit into the density map as does the PDB structure. For this case, we also used our method without docking into the 3DEM density map. One of the models that we obtained is similar to the PDB structure, 3kfe, which is the closed form of the complex (Supplementary Fig. S2). This shows that starting with the same protein we could achieve a solution space of different conformations and with the help of the density map we could identify the ‘correct’ one.

Another case where we could not have a perfect cyclic model is the conjugal transfer protein TrwB (PDB entry 1e9r, EMDB ID 5505; IS-scores are given in Table 3 ▸). However, we obtained a hexamer model very similar to the PDB structure, 1e9r, and the r.m.s.d. is 2.44 Å. Docking into the density map also resulted in favourable results, with a Situs score of 1.07 Å and a correlation of 0.84. The templates used in modelling complexes and the sequence identity between the complex and template proteins are given in Supplementary Tables S4 and S5, respectively.

Protein-complex structures could also be predicted by using Situs only. Multiple proteins can be docked simultaneously into the density map using the collage function of Situs. However, it is more suitable for the refinement of previously docked structures. This is why using Situs directly to model multimolecular complexes is likely to lead to clashes. The results for Saf pilus type A (PDB entry 3cre) are given in Supplementary Table S3.

We also tested MultiFit and fitting structures into segments obtained by Segger using our benchmark data set. The models obtained using these methods are shown in Supplementary Fig. S3. MultiFit could not model the pentamer of acetyl­choline-binding protein type 1 (PDB entry 3iyf, EMDB ID 5140), the octamer of lidless Mm-cpn (PDB entry 3iyf, EMDB ID 5140) and the tetramer of the ParM filament (PDB entry 4a6j, EMDB ID 1980). It could successfully predict the hexamer of the circadian clock protein KaiC (PDB entry 3dvl, EMDB ID 5672) and only one interface in the trimer of the ParM filament with regard to the IS-score (IS-scores are given in Supplementary Table S6). When we used Segger, we could obtain the desired segments only for the pentamer of acetyl­choline-binding protein type 1 and the octamer of lidless Mm-cpn in the open state. We could also obtain the desired number of segments for the ParM filament, the conjugal transfer protein TrwB and the circadian clock protein KaiC, but segmentation was not obtained properly (segmentation results are given in Supplementary Fig. S1). Only two interfaces of lidless Mm-cpn were evaluated as ‘correct’ with respect to the IS-score (IS-scores are given in Supplementary Table S7). We also found the correlation and calculated the r.m.s.d. values compared with the PDB structures for the models that we could obtain (Table 4 ▸). Comparing the performance of our method with others, we obtain 28 ‘correct’ and four ‘acceptable’ interface predictions, and could not model two interfaces (there is no interface or insufficient contacting residues of two proteins). For the five assembly models that MultiFit could provide, seven ‘correct’ and ten ‘incorrect’ interfaces were obtained, and one interface could not be modelled. Fitting structures into segments obtained by Segger could predict the models of two assemblies, and provided two ‘correct’ and five ‘incorrect’ interface predictions; six interfaces could not be modelled. If we consider that a successful prediction of an assembly is obtained when all subunits are connected by predicted interfaces, which are labelled as ‘correct’ or ‘acceptable’, we could successfully construct all eight assemblies; however, MultiFit could successfully predict only one of them and fitting structures into segments obtained by Segger could construct none. Correlation results are similar, but compared with the PDB structures our r.m.s.d. results are lower than the results of the other two methods.

Table 4. Assembly-construction results of three methods in our benchmark set.

A comparison of the performance of our method, MultiFit and fitting structures into segments obtained by Segger is shown. Correlation is calculated using Chimera. IS-score gives the evaluation of interfaces predicted with respect to the PDB structures, and the r.m.s.d. of models is also shown. If MultiFit could not predict a structure or Segger could not segment the density map properly, the result is shown as ‘—’.

    Our method MultiFit Fitting structures into segments obtained by Segger
EMDB ID PDB code Correlation IS-score results R.m.s.d. (Å) Correlation IS-score results R.m.s.d. (Å) Correlation IS-score results R.m.s.d. (Å)
1494 3cre 0.79 2 correct 4.92 0.76 2 incorrect 22.46 —
1980 4a6j 0.59 1 correct, 1 acceptable 3.83 0.68 1 correct, 1 incorrect 3.20 —
1980 4a6j 0.51 1 correct, 2 acceptable 4.16 — —
2055 4aod 0.89 5 correct 2.16 — 0.85 5 incorrect 5.07
2427 3se9 0.84 1 correct, 1 acceptable 4.64 0.84 1 incorrect, 1 no interface 16.14 —
5140 3iyf 0.78 7 correct, 1 no interface 7.35 — 0.86 2 correct, 6 no interface 30.31
5505 1e9r 0.84 5 correct, 1 no interface 2.44 0.91 6 incorrect 27.40 —
5672 3dvl 0.96 6 correct 1.86 0.79 6 correct 2.34 —
Open in a new tab

Moreover, we tested PRISM-EM on the MultiFit benchmark set and evaluated our performance (Table 5 ▸). We also reconstructed these assemblies using MultiFit with Chimera to calculate the r.m.s.d. and correlation values. The r.m.s.d. values that we calculated are very similar to the values given in the MultiFit paper (Tjioe et al., 2011 ▸). In assembly construction, we could obtain better results compared with the performance of MultiFit (correlation, 0.81–0.98; r.m.s.d., 0.90–4.62 Å); the correlation values of our models are between 0.91 and 0.99, equal or higher than the correlation of MultiFit results, and the r.m.s.d. values are between 0.50 and 1.68 Å, lower than the MultiFit results in each case. We also evaluated the interfaces of the models via IS-scores (Supplementary Table S8). Based on IS-scores, we could obtain more ‘correct’ predicted interfaces than MultiFit. We predicted all 51 interfaces as ‘correct’ and MultiFit had 33 ‘correct’, one ‘acceptable’ and five ‘incorrect’ interface predictions (12 interfaces could not be predicted). Based on predicting all interfaces as ‘correct’ and/or ‘acceptable’, we could successfully construct all eight assemblies; however, MultiFit could successfully predict five of them (PDB entries 1qu9, 1urz, 1mty, 1oel and 1gru). The correlations and r.m.s.d.s are calculated for each subunit and are given in Supplementary Tables S9 and S10.

Table 5. Assembly-construction results in the MultiFit benchmark set.

The performances of MultiFit and our method are given. The number of subunits in the complexes is given. The r.m.s.d. of models with respect to the PDB structures and the correlations calculated using Chimera are shown.

    MultiFit Our method
PDB code Structure R.m.s.d. (Å) I.r.m.s.d. (Å) Correlation R.m.s.d. (Å) I.r.m.s.d. (Å) Correlation
7cat Dimer 4.13 4.55 0.92 0.36 1.24 0.91
1gte Dimer 3.28 4.96 0.92 0.56 1.05 0.92
1qu9 Trimer 0.90 1.69 0.98 0.50 1.25 0.98
1urz Trimer 0.98 1.58 0.98 0.74 1.76 0.98
1z5s Tetramer 4.62 4.29 0.86 1.68 2.10 0.97
1e6v Hexamer 2.88 7.28 0.93 0.70 1.26 0.99
1mty Hexamer 2.08 3.42 0.98 0.81 1.38 0.99
1tyq Heptamer 3.31 8.90 0.85 1.31 2.23 0.98
1oel Heptamer 2.40 3.99 0.97 1.03 2.36 0.98
1gru Heptamer 3.36 6.1 0.81 1.15 1.58 0.98
Open in a new tab

Furthermore, we tested PRISM-EM on the HADDOCK-EM benchmark set. Among 17 cases, PRISM-EM could predict models for nine cases with i.r.m.s.d. ≤ 4 Å by docking query structures (Table 6 ▸, third column). In our previous study (Kuzu et al., 2013 ▸), we showed that exploiting alternative conformations of the query proteins resulted in improved predictions. We considered structures with 95% sequence similarity as alternative conformations to the query proteins (as indicated in our previous study, this introduces an ensemble of conformations), and tested our method on the docking set, but this time also considering alternative conformations of the query proteins, which resulted in 12 predictions with i.r.m.s.d. ≤ 4 Å (Table 6 ▸, fourth column; Supplementary Table S5). In addition, when we used also bound structure information in our predictions, we had 15 predictions with i.r.m.s.d. ≤ 4 Å. We could not obtain a model for two cases, PDB entries 1ahw and 4cpa; however, the energy-calculation tool FiberDock could not find any bio­logically favourable energy between chains of the bound structure of PDB entry 1ahw. van Zundert et al. (2015 ▸) reported that HADDOCK-EM could predict 13 of them successfully (i.r.m.s.d. ≤ 4 Å). For easy cases, they obtained smaller i.r.m.s.d. values; we are using MultiProt, a heuristic tool in the alignment of the query protein and the templates, and the search stops when an alignment with less than 2 Å is obtained; the backbone of the structure is then slightly oriented in the flexible refinement step. Therefore, predictions with less than 2 Å are sufficient for our method. However, for medium and difficult cases we could obtain better results in some cases (for three out of seven cases, PDB entries 1bgx, 1m10 and 1bkd, without using bound data and for all seven cases using bound data), and they succeeded in the others (four out of seven cases; PDB entries 1r6q, 1acb, 1jk9 and 1jmo). PRISM is a rigid-body docking tool and we considered protein flexibility by including conformational ensembles where available. Docking structures onto template interfaces may not give a ‘perfect’ prediction; however, it works relatively well for difficult cases.

Table 6. The performance of our method in the HADDOCK-EM set.

The performance of our method on the HADDOCK-EM set, where cases were selected from the ZDOCK benchmark set, is given. Models were compared with the PDB structures and results are presented with i.r.m.s.d. values.

    I.r.m.s.d. (Å)
    Our method  
Complex Difficulty Docking query proteins Docking query proteins and their alternatives Using bound structure data HADDOCK-EM
1avx Easy 4.89 1.88 1.88 0.96
2oul Easy 1.63 1.38 1.38 0.66
1ay7 Easy 1.95 1.74 1.38 0.72
4cpa Easy       1.44
1ahw Easy       1.04
7cei Easy 1.78 1.26 1.26 1.01
2oob Easy 3.96 1.13 1.13 1.06
2fd6 Easy 2.68 1.88 1.88 1.62
1ak4 Easy 2.61 2.52 2.52 1.93
1b6c Easy 3.21 3.27 2.23 2.71
1bgx Medium 29.16 1.72 1.10 6.29
1r6q Medium 5.56 4.89 1.33 1.83
1m10 Medium 3.63 1.52 1.52 4.47
1acb Medium 3.03 3.44 1.58 2.86
1jk9 Hard 5.63 5.75 1.27 2.83
1bkd Hard 13.62 1.69 1.08 4.37
1jmo Hard 13.28 11.64 2.37 4.51
Open in a new tab

3.3. Case study 2: HIV protein gp120–membrane protein CD4–antibody m36 complex  

Lastly, we tested PRISM-EM construction of an assembly for which the structure is not available in the PDB. Here, we showed that exploiting EM and high-resolution PDB data together could be used to provide a plausible model of the structure. EMDB ID 5554 presents the assembly of HIV gp120 protein complexed with sCD4 and the engineered domain antibody (dAb) m36. Unlike HIV-1 gp120 and sCD4, the structure of m36 is unknown. We first modelled the structure of m36 using I-TASSER. We constructed assemblies using the PDB structures 4dku A (HIV gp120), 1gc1 C (sCD4) and the m36 model that I-TASSER created. Here, we used different PDB structures of HIV gp120 and CD4 rather than those we used in the construction of HIV gp120–CD4–17b; PDB entry 4dku is the dimer of HIV gp120 and PDB entry 1gc1 shows the interaction of HIV gp120–CD4–17b. We modelled the trimer structures; the best assembly model has a Situs score of 3.01 Å and a Chimera correlation of 0.89. Figs. 2 ▸(c) and 2 ▸(d) present the best model fitted into the density map. The HIV gp120–CD4 interface has an IS-score of 0.77, which indicates the interface to be ‘correct’. Since the HIV gp120–m36 interface is unknown, we could not calculate an IS-score for this interface. The dAb m36 in our model is placed in the same direction and in the same space in the density map suggested in the original 3DEM analysis of this complex (Meyerson et al., 2013 ▸), where the density map could not be fitted reliably owing to the absence of a PDB structure or a model.

4. Discussion  

EM density maps combined with atomic details from the PDB data help in obtaining more accurate structures for protein complexes. Here, we present a method, PRISM-EM, that constructs protein assemblies based on PDB data and selects structures based on 3DEM density maps. PRISM-EM can produce a number of solutions with 3DEM data, pointing to a preferred solution model among these.

In the first case study (the HIV-1 Env–sCD4–17b complex), we constructed the assembly using PDB structures. However, the knowledge-based method has limitations and the PDB information is incomplete. Some structures lack a domain or a part of the protein and thus the modelled structures are error-prone. Constructing assemblies of incomplete proteins is more difficult than predicting their binary interactions. Binary interactions of incomplete structures can be predicted successfully if the missing parts do not cover the binding site. In contrast, a protein in a complex can interact with more than one protein and it is more likely that the missing part is a segment that includes one of its binding sites. It is also possible that the segment obstructs a binding site or creates steric hindrance with the protein partners.

We tested our method on a benchmark data set that covers proteins with a varying number of chains, residues and SCOP classes, representing a small subset of all proteins. We especially selected symmetrical cyclic structures for the benchmark data set. Symmetrical cyclic proteins are challenging for PRISM-EM, which constructs assemblies based on binary interactions and is not optimized for symmetrical structures. During the addition of the final protein, more than one interface needs to be considered and a small error in binary predictions may hamper the completion of the cyclic structure. In two of four cyclic cases (EMDB IDs 5140 and 5505), we could not obtain perfect cyclic structures. However, comparing with the PDB structures or docking into the density maps suggested that these are acceptable predictions. Some methods, such as MultiFit, handle symmetric structures differently from asymmetric structures. They can treat cyclic structures accordingly and provide models with a proper cyclic shape. However, this may bias interface predictions by preferring subunits with a certain angle, as in the case of EMDB ID 5505. Its model has a better cyclic shape compared with our model, yet the interfaces are ‘incorrect’ with respect to the IS-score. On the other hand, Segger could not perform the segmentation properly for complexes that include buried (EMDB ID 1494) or entwined (EMDB ID 2427) subunits. It could predict correct segments in two cases: EMDB IDs 2055 and 5140. However, the interfaces obtained after docking proteins into the segments were ‘incorrect’ with respect to the IS-score. Methods whose priority is to dock proteins into the density map may create models with high correlation with the density map; however, they may also give false-positive predictions of protein–protein interfaces, ending up with clashes of the residues, and are more likely to lead to un­favourable structures of assemblies. PRISM-EM depends on interface-based structure predictions and docking the complex into the 3DEM density map, which is likely to be more robust. We have shown that the accuracy of our interface predictions is high and combining it with an exhaustive-search docking method led us to obtain accurate predictions of protein-assembly structures. The interface prediction increases the computational time compared with tools such as MultiFit; however, this computational cost is balanced by the ‘correct’ knowledge-based interfaces in the models.

PRISM-EM also gives good predictions for the MultiFit benchmark set. The density maps were specific and biased for the PDB structures in this set, since they were created from PDB structures using Situs (except for one case: PDB entry 1gru, EMDB ID 1046). Density maps can be huge and represent large structures, as in our benchmark set. Docking structures into larger 3DEM density maps is even more challenging. Using MultiFit in Chimera, we had initial errors in some cases; running MultiFit failed. The errors may be owing to the starting positions of the protein structures with respect to the density map. Better models could be obtained with a different orientation of the structures with respect to the density maps. Our method does not work for complexes with small interfaces (less than ten residues at the interface, as in the example of PDB entry 2rec in the MultiFit benchmark set); MultiFit does not depend on the size of the interface and could construct such complexes.

In the last case study, we tested the method on an assembly for which the structure has been analyzed by cryo-electron tomography at ∼20 Å resolution but where an atomic resolution model is not yet available in the PDB. Constructing assemblies starting from (homology) models suggests that PRISM-EM can perform satisfactorily if the structures of proteins are unknown (even though modelling structures is error-prone). The model could not be obtained using either the PDB or EM data alone.

PRISM-EM is composed of three successive prediction steps: prediction of protein structures (if necessary), prediction of protein interactions and docking structures into EM density maps. Each step can be error-prone. However, we should note that if a proper template is not present for the modelling, we cannot obtain a proper structure. Each of the tools that we use (I-TASSER, PRISM and Situs) also has its shortcomings, and using them in tandem increases the likelihood of error even more. Another limitation comes from the rigid-body treatment of the structures. Exploiting alternative conformations available in the PDB may include a certain extent of protein flexibility (Kuzu et al., 2014 ▸, 2013 ▸), which however is limited by the richness of the PDB. Conformational changes upon binding and allostery may affect the final structures of the assemblies. Despite these limitations, there are obvious advantages in using both X-ray and 3DEM information simultaneously. Exploiting only the PDB structures might provide possible assemblies, yet it would be unclear which one is the ‘best’ solution. On the other hand, exploiting only the EM data would indicate the shape of the complex, but verification on the atomic scale would be needed. One also needs to consider that the prediction success also depends on the quality of the experimental data used, crystal structures and/or 3DEM information. The models are obtained based on these data, and the accuracy of predicting the native structure cannot surpass the accuracy of the experimental data used in the prediction. This method may not be appropriate for cases in which sub-optimal solutions are more accurate. One might need to consider other models obtained in the final step, instead of the top model, especially when low quality of data is used. Here, the method provides the ‘best’ answer with respect to the data used in the prediction, and the accuracy of the solution should be considered along with the quality of the data.

Here, we present a multimolecular complex-prediction method which constructs models based on predictions of complexes and 3DEM information. We were unsuccessful in some of the predictions, but obtained good models in most cases. The accuracy of the predictions rests on the accuracy in interface predictions. We also showed that our method works well with divergent real experimental 3DEM data, indicating that our method can be used for real problems. The model for the structure of HIV gp120–CD4–m36, which is consistent with the experimental result, further supports its usefulness.

Supplementary Material

Supplementary Tables and Figures.. DOI: 10.1107/S2059798316013541/kw5127sup1.pdf

d-72-01137-sup1.pdf (515.9KB, pdf)
Click here for additional data file. (4.2MB, zip)

PDB files of the models. DOI: 10.1107/S2059798316013541/kw5127sup2.zip

Click here for additional data file. (51.7KB, gz)

PRISM-EM scripts.. DOI: 10.1107/S2059798316013541/kw5127sup4.gz

Acknowledgments

We thank Drs Sriram Subramaniam, Erin E. H. Tran and Lesley A. Earl for guidance relating to the incorporation of the 3DEM information and for critical reading of this manuscript, insight and discussions. GK was supported by a TUBITAK (The Scientific and Technological Research Council of Turkey) fellowship. This work was supported by TUBITAK Research Grant No. 114M196. It was also funded in whole or in part with Federal funds from the National Cancer Institute, National Institutes of Health under contract HHSN261200800001E. The content of this publication does not necessarily reflect the views or policies of the Department of Health and Human Services, nor does mention of trade names, commercial products or organizations imply endorsement by the US Government. This research was supported (in part) by the Intramural Research Program of the NIH, National Cancer Institute, Center for Cancer Research.

References

  1. Allen, J. P., Seng, C. & Larson, C. (2009). Photosynth. Res. 102, 231–240. [DOI] [PubMed]
  2. Aytuna, A. S., Gursoy, A. & Keskin, O. (2005). Bioinformatics, 21, 2850–2855. [DOI] [PubMed]
  3. Baker, M. L., Abeysinghe, S. S., Schuh, S., Coleman, R. A., Abrams, A., Marsh, M. P., Hryc, C. F., Ruths, T., Chiu, W. & Ju, T. (2011). J. Struct. Biol. 174, 360–373. [DOI] [PMC free article] [PubMed]
  4. Baker, M. L., Yu, Z., Chiu, W. & Bajaj, C. (2006). J. Struct. Biol. 156, 432–441. [DOI] [PubMed]
  5. Baspinar, A., Cukuroglu, E., Nussinov, R., Keskin, O. & Gursoy, A. (2014). Nucleic Acids Res. 42, W285–W289. [DOI] [PMC free article] [PubMed]
  6. Berman, H. M. et al. (2002). Acta Cryst. D58, 899–907. [DOI] [PubMed]
  7. Burger, V., Bahar, I. & Chennubhotla, C. (2011). Biophys. J. 100, 534a.
  8. Carragher, B., Fellmann, D., Guerra, F., Milligan, R. A., Mouche, F., Pulokas, J., Sheehan, B., Quispe, J., Suloway, C., Zhu, Y. & Potter, C. S. (2004). J. Synchrotron Rad. 11, 83–85. [DOI] [PubMed]
  9. Ceulemans, H. & Russell, R. B. (2004). J. Mol. Biol. 338, 783–793. [DOI] [PubMed]
  10. Cukuroglu, E., Gursoy, A., Nussinov, R. & Keskin, O. (2014). PLoS One, 9, e86738. [DOI] [PMC free article] [PubMed]
  11. Gao, M. & Skolnick, J. (2011). Proteins, 79, 1623–1634. [DOI] [PMC free article] [PubMed]
  12. Garzón, J. I., Kovacs, J., Abagyan, R. & Chacón, P. (2007). Bioinformatics, 23, 427–433. [DOI] [PubMed]
  13. Hashem, Y., des Georges, A., Fu, J., Buss, S. N., Jossinet, F., Jobe, A., Zhang, Q., Liao, H. Y., Grassucci, R. A., Bajaj, C., Westhof, E., Madison-Antenucci, S. & Frank, J. (2013). Nature (London), 494, 385–389. [DOI] [PMC free article] [PubMed]
  14. Hoang, T. V., Cavin, X. & Ritchie, D. W. (2013). J. Struct. Biol. 184, 348–354. [DOI] [PubMed]
  15. Hwang, H., Vreven, T., Janin, J. & Weng, Z. (2010). Proteins, 78, 3111–3114. [DOI] [PMC free article] [PubMed]
  16. Inbar, Y., Benyamini, H., Nussinov, R. & Wolfson, H. J. (2005). J. Mol. Biol. 349, 435–447. [DOI] [PubMed]
  17. Jiang, W., Baker, M. L., Ludtke, S. J. & Chiu, W. (2001). J. Mol. Biol. 308, 1033–1044. [DOI] [PubMed]
  18. Kar, G., Keskin, O., Nussinov, R. & Gursoy, A. (2012). J. Proteome Res. 11, 1196–1207. [DOI] [PMC free article] [PubMed]
  19. Karaca, E., Melquiond, A. S. J., de Vries, S. J., Kastritis, P. L. & Bonvin, A. M. J. J. (2010). Mol. Cell. Proteomics, 9, 1784–1794. [DOI] [PMC free article] [PubMed]
  20. Kawabata, T. (2008). Biophys. J. 95, 4643–4658. [DOI] [PMC free article] [PubMed]
  21. Keskin, O., Gursoy, A., Ma, B. & Nussinov, R. (2008). Chem. Rev. 108, 1225–1244. [DOI] [PubMed]
  22. Keskin, O. & Nussinov, R. (2005). Protein Eng. Des. Sel. 18, 11–24. [DOI] [PubMed]
  23. Keskin, O., Tuncbag, N. & Gursoy, A. (2016). Chem. Rev. 116, 4884–4909. [DOI] [PubMed]
  24. Kovacs, J. A., Chacón, P., Cong, Y., Metwally, E. & Wriggers, W. (2003). Acta Cryst. D59, 1371–1376. [DOI] [PubMed]
  25. Kühlbrandt, W. (2014). eLife, 3, e03678. [DOI] [PMC free article] [PubMed]
  26. Kuzu, G., Gursoy, A., Nussinov, R. & Keskin, O. (2013). J. Proteome Res. 12, 2641–2653. [DOI] [PMC free article] [PubMed]
  27. Kuzu, G., Keskin, O., Nussinov, R. & Gursoy, A. (2014). Mol. Cell. Proteomics, 13, 887–896. [DOI] [PMC free article] [PubMed]
  28. Lasker, K., Sali, A. & Wolfson, H. J. (2010). Proteins, 78, 3205–3211. [DOI] [PMC free article] [PubMed]
  29. Lasker, K., Topf, M., Sali, A. & Wolfson, H. J. (2009). J. Mol. Biol. 388, 180–194. [DOI] [PMC free article] [PubMed]
  30. Lawson, C. L. et al. (2011). Nucleic Acids Res. 39, D456–D464. [DOI] [PMC free article] [PubMed]
  31. Lima Morais, D. A. de, Fang, H., Rackham, O. J. L., Wilson, D., Pethica, R., Chothia, C. & Gough, J. (2011). Nucleic Acids Res. 39, D427–D434. [DOI] [PMC free article] [PubMed]
  32. Lo Conte, L., Ailey, B., Hubbard, T. J., Brenner, S. E., Murzin, A. G. & Chothia, C. (2000). Nucleic Acids Res. 28, 257–259. [DOI] [PMC free article] [PubMed]
  33. Mashiach, E., Schneidman-Duhovny, D., Peri, A., Shavit, Y., Nussinov, R. & Wolfson, H. J. (2010). Proteins, 78, 3197–3204. [DOI] [PMC free article] [PubMed]
  34. Meyerson, J. R., Tran, E. E. H., Kuybeda, O., Chen, W., Dimitrov, D. S., Gorlani, A., Verrips, T., Lifson, J. D. & Subramaniam, S. (2013). Proc. Natl Acad. Sci. USA, 110, 513–518. [DOI] [PMC free article] [PubMed]
  35. Navaza, J., Lepault, J., Rey, F. A., Álvarez-Rúa, C. & Borge, J. (2002). Acta Cryst. D58, 1820–1825. [DOI] [PubMed]
  36. Ogmen, U., Keskin, O., Aytuna, A. S., Nussinov, R. & Gursoy, A. (2005). Nucleic Acids Res. 33, W331–W336. [DOI] [PMC free article] [PubMed]
  37. Orlova, E. V. & Saibil, H. R. (2011). Chem. Rev. 111, 7710–7748. [DOI] [PMC free article] [PubMed]
  38. Pelikan, M., Hura, G. L. & Hammel, M. (2009). Gen. Physiol. Biophys. 28, 174–189. [DOI] [PMC free article] [PubMed]
  39. Pennisi, E. (1998). Science, 279, 978–979. [DOI] [PubMed]
  40. Pettersen, E. F., Goddard, T. D., Huang, C. C., Couch, G. S., Greenblatt, D. M., Meng, E. C. & Ferrin, T. E. (2004). J. Comput. Chem. 25, 1605–1612. [DOI] [PubMed]
  41. Pierce, B., Tong, W. & Weng, Z. (2005). Bioinformatics, 21, 1472–1478. [DOI] [PubMed]
  42. Pintilie, G. & Chiu, W. (2012). Biopolymers, 97, 742–760. [DOI] [PMC free article] [PubMed]
  43. Pintilie, G. D., Zhang, J., Goddard, T. D., Chiu, W. & Gossard, D. C. (2010). J. Struct. Biol. 170, 427–438. [DOI] [PMC free article] [PubMed]
  44. Rachel, R., Jakubowski, U. & Baumeister, W. (1986). J. Microsc. 141, 179–191.
  45. Raicu, V. & Singh, D. R. (2013). Biophys. J. 105, 1937–1945. [DOI] [PMC free article] [PubMed]
  46. Roseman, A. M. (2000). Acta Cryst. D56, 1332–1340. [DOI] [PubMed]
  47. Rossmann, M. G. (2000). Acta Cryst. D56, 1341–1349. [DOI] [PubMed]
  48. Rossmann, M. G., Bernal, R. & Pletnev, S. V. (2001). J. Struct. Biol. 136, 190–200. [DOI] [PubMed]
  49. Roy, A., Kucukural, A. & Zhang, Y. (2010). Nature Protoc. 5, 725–738. [DOI] [PMC free article] [PubMed]
  50. Rusu, M., Birmanns, S. & Wriggers, W. (2008). Bioinformatics, 24, 2460–2466. [DOI] [PMC free article] [PubMed]
  51. Schneidman-Duhovny, D., Inbar, Y., Nussinov, R. & Wolfson, H. J. (2005a). Proteins, 60, 224–231. [DOI] [PubMed]
  52. Schneidman-Duhovny, D., Inbar, Y., Nussinov, R. & Wolfson, H. J. (2005b). Nucleic Acids Res. 33, W363–W367. [DOI] [PMC free article] [PubMed]
  53. Shatsky, M., Nussinov, R. & Wolfson, H. J. (2002). Algorithms in Bioinformatics, edited by R. Guigó & D. Gusfield, pp. 235–250. Berlin, Heidelberg: Springer.
  54. Siebert, X. & Navaza, J. (2009). Acta Cryst. D65, 651–658. [DOI] [PMC free article] [PubMed]
  55. Tjioe, E., Lasker, K., Webb, B., Wolfson, H. J. & Sali, A. (2011). Nucleic Acids Res. 39, W167–W170. [DOI] [PMC free article] [PubMed]
  56. Tsai, C.-J., Lin, S. L., Wolfson, H. J. & Nussinov, R. (1996). Crit. Rev. Biochem. Mol. Biol. 31, 127–152. [DOI] [PubMed]
  57. Tsai, C.-J., Xu, D. & Nussinov, R. (1997). Protein Sci. 6, 1793–1805. [DOI] [PMC free article] [PubMed]
  58. Tuncbag, N., Gursoy, A., Guney, E., Nussinov, R. & Keskin, O. (2008). J. Mol. Biol. 381, 785–802. [DOI] [PMC free article] [PubMed]
  59. Tuncbag, N., Gursoy, A., Nussinov, R. & Keskin, O. (2011). Nature Protoc. 6, 1341–1354. [DOI] [PMC free article] [PubMed]
  60. Volkmann, N. (2002). J. Struct. Biol. 138, 123–129. [DOI] [PubMed]
  61. Vries, S. J. de & Zacharias, M. (2012). PLoS One, 7, e49733. [DOI] [PMC free article] [PubMed]
  62. Wriggers, W., Milligan, R. A. & McCammon, J. A. (1999). J. Struct. Biol. 125, 185–195. [DOI] [PubMed]
  63. Wüthrich, K. (1990). J. Biol. Chem. 265, 22059–22062. [PubMed]
  64. Zhang, Y. (2008). BMC Bioinformatics, 9, 40. [DOI] [PMC free article] [PubMed]
  65. Zhang, J., Baker, M. L., Schröder, G. F., Douglas, N. R., Reissmann, S., Jakana, J., Dougherty, M., Fu, C. J., Levitt, M., Ludtke, S. J., Frydman, J. & Chiu, W. (2010). Nature (London), 463, 379–383. [DOI] [PMC free article] [PubMed]
  66. Zundert, G. C. P. van, Melquiond, A. S. J. & Bonvin, A. M. J. J. (2015). Structure, 23, 949–960. [DOI] [PubMed]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Tables and Figures.. DOI: 10.1107/S2059798316013541/kw5127sup1.pdf

d-72-01137-sup1.pdf (515.9KB, pdf)
Click here for additional data file. (4.2MB, zip)

PDB files of the models. DOI: 10.1107/S2059798316013541/kw5127sup2.zip

Click here for additional data file. (51.7KB, gz)

PRISM-EM scripts.. DOI: 10.1107/S2059798316013541/kw5127sup4.gz

Articles from Acta Crystallographica. Section D, Structural Biology are provided here courtesy of International Union of Crystallography

RESOURCES