Abstract
Longitudinal neuroimaging analysis of the dynamic brain development in infants has received increasing attention recently. Many studies expect a complete longitudinal dataset in order to accurately chart the brain developmental trajectories. However, in practice, a large portion of subjects in longitudinal studies often have missing data at certain time points, due to various reasons such as the absence of scan or poor image quality. To make better use of these incomplete longitudinal data, in this paper, we propose a novel machine learning‐based method to estimate the subject‐specific, vertex‐wise cortical morphological attributes at the missing time points in longitudinal infant studies. Specifically, we develop a customized regression forest, named dynamically assembled regression forest (DARF), as the core regression tool. DARF ensures the spatial smoothness of the estimated maps for vertex‐wise cortical morphological attributes and also greatly reduces the computational cost. By employing a pairwise estimation followed by a joint refinement, our method is able to fully exploit the available information from both subjects with complete scans and subjects with missing scans for estimation of the missing cortical attribute maps. The proposed method has been applied to estimating the dynamic cortical thickness maps at missing time points in an incomplete longitudinal infant dataset, which includes 31 healthy infant subjects, each having up to five time points in the first postnatal year. The experimental results indicate that our proposed framework can accurately estimate the subject‐specific vertex‐wise cortical thickness maps at missing time points, with the average error less than 0.23 mm. Hum Brain Mapp 37:4129–4147, 2016. © 2016 Wiley Periodicals, Inc.
Keywords: missing data completion, longitudinal study, cortical surface, cortical thickness, early brain development
Abbreviations
- CRF
Conventional regression forest
- DARF
Dynamically assembled regression forest
- FA
Fractional anisotropy
- MAE
Mean absolute error
- MEM
Mixed effect model
- NMSE
Normalized mean squared error
- PR
Polynomial regression
- SLR
Sparse linear regression
INTRODUCTION
In recent years, with the advance of pediatric MR imaging acquisition and post‐processing techniques, longitudinal neuroimaging analysis of the early postnatal brain development, which can uniquely capture both subject‐specific and population‐averaged developmental trajectories, has received increasing attention [Almli et al., 2007; Fan et al., 2011; Gilmore et al., 2012; Kaukola et al., 2009; Li et al., 2013, 2014b; Meng et al., 2014; Nie et al., 2014; Schumann et al., 2010; Shi et al., 2010]. During the early postnatal stage, the human cerebral cortex develops extremely dynamically, with the surface area increasing 80% and the cortical thickness increasing 40% in the first postnatal year [Li et al., 2013; Lyall et al., 2015]. Charting longitudinal cortical developmental trajectories in this early postnatal period can help better understand the relationship between normal structural and functional development of the cerebral cortex [Awate et al., 2010; Dubois et al., 2008; Gilmore et al., 2007; Schnack et al., 2014], and also provide fundamental references for understanding of many neurodevelopmental disorders that are likely the outcomes of abnormal brain development during this period [Gilmore et al., 2012; Lyall et al., 2015].
To accurately study the dynamic early brain development, many studies expect using subjects with complete longitudinal scans. However, in practice, missing data at certain time points are unavoidable in longitudinal studies due to various reasons, such as subject's absence from the scheduled scan or poor imaging quality of the scan. On one hand, directly using the incomplete data would introduce biases and consequently reduce precision and power in statistical analysis. For example, when constructing spatial‐temporal infant cortical surface atlases [Li et al., 2014c], each time point will have a different number of subjects because of missing data. As a result, different biases could be introduced to different time points, thus leading to low accuracy and longitudinal inconsistency for subsequent analysis, especially for those time points with limited number of scans. Another example is that, in longitudinal study of the spatial distribution of deep sulcal landmarks on infant cortical surfaces [Meng et al., 2014], each involved subject needs to be scanned at all time points for consistent and unbiased comparison across ages. Due to missing data, different subjects are scanned at different time points, thus leading to biased and inconsistent comparison. On the other hand, discarding subjects with missing time point(s) is a terrible waste of the useful information in these subjects and also the considerable cost for data acquisition. Hence, accurate estimation of information at missing time points plays an important role in longitudinal analysis of early brain development.
A common strategy to handle missing data is to replace the missing data by the weighted average over the most representative subset of existing data (e.g., k‐nearest neighbors) [Ching et al., 2010; Troyanskaya et al., 2001; Tsiporkova and Boeva, 2007], but the effectiveness of this strategy often decreases with the increase of the portion of missing data. For recovering a large portion of missing data, several methods based on low‐rank matrix completion were proposed [Cai et al., 2010; Cand and Tao, 2010; Candès and Recht, 2009; Liu et al., 2013], but these methods work well only if the missing data are distributed randomly and uniformly. Unfortunately, in neuroimaging study, the missing data are usually distributed in blocks and not uniformly [Li et al., 2014f; Thung et al., 2014; Yuan et al., 2012]. For example, the missing data can be the entire image, rather than some independent pixels or clinical scores, thus the methods based on low‐rank matrix completion can no longer work properly. Recently, multi‐source feature learning methods [Yuan et al., 2012] and deep convolutional neural networks [Li et al., 2014f] were proposed to estimate information of missing imaging modalities based on the available modalities, and the estimated modalities were demonstrated to help diagnose neurodegenerative diseases. To deal with the missing modalities in the application of disease diagnosis, another alternative method is to first select the most discriminative features extracted from the available modalities and then estimate only those most discriminative features in the missing modalities [Thung et al., 2014]. However, the estimation of missing vertex‐wise cortical morphological maps in this paper has specific characteristics. First, many longitudinal analysis needs information of morphological measurements at every vertex on the cortical surface, rather than just a simple mean value in each region. For example, to extract deep sulcal landmarks from the infant cortex [Meng et al., 2014], the whole cortical morphological map containing the depth values for all vertices of the cortical surface is needed. Second, cortical surfaces are usually represented by triangular meshes, rather than by 3D volumes. Thus, the ways used to extract features as employed in the image‐based methods [Li et al., 2014f; Yuan et al., 2012] are not naturally extendable to extraction of features from cortical surfaces. Therefore, the existing image‐based methods [Li et al., 2014f; Thung et al., 2014; Yuan et al., 2012] cannot be directly applied to our task of estimating missing vertex‐wise morphological maps on the dynamic developing cortical surfaces.
In this paper, we propose a novel learning‐based framework for subject‐specific estimation of the vertex‐wise map for cortical morphological attributes at missing time point(s) in the longitudinal infant brain studies. Of note, this is challenged by the extremely dynamic and regionally heterogeneous growth of the infant cortex and also by the considerable inter‐subject variability of cortical morphology and developmental patterns. Technically, we leverage the regression forest [Breiman, 2001] as our core regression tool to estimate cortical morphological attributes at each vertex of the cortical surface. However, using a single conventional regression forest (CRF) to estimate vertex‐wise cortical morphological attributes of the entire surface is not suitable. Because the cortical morphological attributes and their developments in infants are highly regionally heterogeneous, using a single CRF cannot precisely estimate values at vertex level. An intuitive way to solve this problem is to partition the whole cortical surface into a set of small regions of interest (ROIs), and then train a local regression forest for each ROI. However, this will lead to spatially unsmooth estimation results around the boundaries of neighboring ROIs. This is because cortical attributes of vertices in the two sides of a ROI boundary are estimated using two different regression forests that are trained independently with different training samples. Intuitively, increasing the overlapping area among ROIs or training a complete regression forest at each vertex could produce smoother estimation results, but it unexpectedly increases the computational cost. Based on our experiments, to make the estimation results as smooth as the real data, more than 90% area of a ROI needs to be overlapped with its neighboring ROIs. Unfortunately, such a large portion of overlap requires a large number of ROIs in order to cover the whole cortex, and thus leads to huge computational workload, since a respective set of individual trees need to be trained for each ROI. Taking account all these issues, we propose a novel dynamically assembled regression forest (DARF). Specifically, by first training one decision tree for each vertex in the training stage and then locally grouping decision trees of neighboring vertices as forests in the testing stage, DARF is able to produce the spatially smooth regression results and meanwhile also save a lot of computational cost.
In general, for estimating the vertex‐wise cortical attributes maps at missing time point(s), our method includes two major stages. In the first stage, in order to use as many training subjects as possible, the missing data (e.g., vertex‐wise cortical attributes maps) at each missing time point of each subject is estimated multiple times with each time based on the available data at each existing time point independently, and then these estimated results at each missing time of each subject are averaged as an initial estimation. In the second stage, to better use longitudinal information, the missing data at each time point of each subject is refined based on both real data and the initially estimated missing data at all other time points jointly. We have validated our missing data estimation method on an incomplete longitudinal dataset of infants for the estimation of vertex‐wise map of cortical thickness, which is an important morphological measure for the cerebral cortex and also correlates with both normal development and neurodevelopmental disorders [Lyall et al., 2015]. The experimental results show that our method achieves high accurate estimations, with the average vertex‐wise error of less than 0.23 mm. It is worth mentioning that, among all the cortical attributes, cortical thickness is relatively more difficult to estimate, as it is quite variable in terms of both spatial distribution and dynamic longitudinal development across individuals. Of note, our method is very generic and not limited to only estimating cortical thickness, as it can also be extended to estimate other morphological attributes, such as sulcal depth, surface area, cortical folding, and local cortical gyrification [Li et al., 2014e].
DATASET AND IMAGE PROCESSING
Subjects and MR Image Acquisition
This study was approved by the Institutional Review Board of the University of North Carolina (UNC) School of Medicine. The UNC hospitals recruited healthy pregnant mothers during their second trimesters of pregnancy. There was no abnormal fetal ultrasound, congenital anomaly, metabolic disease or focal lesion in the infants in the study cohort. For each infant, informed consents were obtained from both parents. All infants were scanned during natural sleep with no sedation used. During each scan, the heart rate and oxygen saturation of the infant were monitored by a physician or a nurse using a pulse oximeter.
For each infant, MRI scans were scheduled at every 3 months in the first year of life, every 6 months in the second year of life, and every 12 months in the third year of life. At each scheduled scan, T1‐, T2‐, and diffusion‐weighted MR images were acquired by a Siemens 3T head‐only MR scanner with a 32 channel head coil. T1‐weighted images (144 sagittal slices) were acquired with the imaging parameters: TR = 1,900 ms, TE = 4.38 ms, flip angle = 7, acquisition matrix = 256 × 192, and voxel resolution = 1 × 1 × 1 mm3. T2‐weighted images (64 axial slices) were acquired with the imaging parameters: TR/TE = 7,380/119 ms, flip angle = 150, acquisition matrix = 256 × 128, and voxel resolution = 1.25 × 1.25 × 1.95 mm3. Diffusion‐weighted images (DWI) (60 axial slices) were acquired with the parameters: TR/TE = 7,680/82 ms, acquisition matrix = 128 × 96, voxel resolution = 2 × 2 × 2 mm3, 42 non‐collinear diffusion gradients, and diffusion weighting b = 1,000 s/mm2. More information on image acquisition can be found in Li et al. [2014a]; Nie et al. [2012]; Wang et al. [2012].
The whole longitudinal dataset is illustrated in Figure 1, where each black block denotes the missing data at a respective time point for a certain subject. It can be seen that this dataset contained a large portion (≈25.7%) of missing data. In this paper, only a subset (enclosed by the red rectangle in Fig. 1) of all the data is used, because we need a sufficient amount of real data as the ground truth to evaluate our proposed method. In the selected subset, 31 healthy infants were scanned at five time points, i.e., 1, 3, 6, 9, and 12 months of age; 16 infants have complete 5 scans, 10 infants have one missing scan, and 5 infants have two missing scans.
Figure 1.
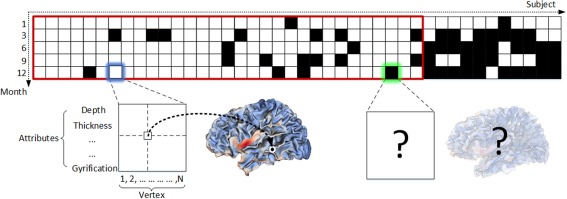
Illustration of the longitudinal infant dataset used in our study. Each block indicates the cortical morphological attributes of all vertices of the entire cortical surface for a specific subject (column) at a specific time point (row). The black blocks indicate the missing data at the respective time point. The blocks enclosed by the red rectangle indicate the dataset used in this paper. [Color figure can be viewed at http://wileyonlinelibrary.com.]
Cortical Surface Reconstruction and Registration
All infant MR images were processed by using an infant‐specific computational pipeline for cortical surface based analysis, which has been extensively verified on over 500 infant MRI scans [Li et al., 2013; Li et al., 2015b; Li et al., 2014c; Lyall et al., 2015]. Of note, our infant‐specific computational pipeline was inspired by many existing work for cortical surface analysis of adults [Dale et al., 1999; Fischl and Dale, 2000; Fischl et al., 1999b; Han et al., 2004; Kim et al., 2005; Liu et al., 2008; MacDonald et al., 2000; Mangin et al., 2004; Shattuck and Leahy, 2002; Shi et al., 2013; Thompson and Toga, 1996; Van Essen et al., 2001]. First, distortion correction of DWI has been performed and the respective fractional anisotropy (FA) images were then computed. T2 images were first linearly aligned to their respective T1 images using normalized mutual information. Then, FA images were linearly aligned to the warped T2 images. To ensure the quality of alignment, the aligned T1, T2, and FA images were visually inspected. Second, for each set of aligned T1, T2, and FA images, skull stripping was performed using a learning‐based method [Shi et al., 2012], and then brain stem and cerebellum were removed by propagation of their respective masks from the atlas images to the subject images using an in‐house developed registration method. Third, intensity inhomogeneity was corrected by N3 [Sled et al., 1998]. Fourth, all longitudinal images of the same infant were rigidly aligned. Fifth, an infant‐specific 4D level‐set method was used to segment brain tissues by leveraging longitudinal information and complementary multimodal information in T1, T2 and FA images [Wang et al., 2014a, 2014b]. Finally, non‐cortical structures were filled, and each brain was separated into left and right hemispheres.
For cortical surface reconstruction, we used a deformable surface method to reconstruct the topologically correct and geometrically accurate cortical surfaces for each hemisphere [Li et al., 2012]. Specifically, topology correction was first performed for the white matter of each hemisphere. Then, the topology‐corrected white matter was tessellated as a triangulated surface mesh. Finally, a deformable surface method was applied to deform the shape of triangulated surface mesh while keeping its initial topology and also spatially adaptive smoothness, to reconstruct the inner and outer cortical surfaces [Li et al., 2014a]. To prevent surface meshes from self‐intersection, in each step of the surface deformation, a fast triangle–triangle intersection detection method was also performed at each vertex in the local region. Once any triangle–triangle intersection was detected, the deformation was reduced to a location without such intersection [Li et al., 2014a]. Cortical thickness of each vertex was then computed as the mean of the minimum distances from inner to outer surfaces and also from outer to inner surfaces [Li et al., 2015a; Li et al., 2014a] as in FreeSurfer [Fischl, 2012]. The sulcal depth of each vertex was defined as the shortest distance from the vertex to the cerebral hull surface, and was computed using the method in Li et al. [2014b].
For cortical surface registration, all inner cortical surfaces were first mapped onto a spherical surface by minimizing the metric distortion [Fischl et al., 1999a] using FreeSurfer [Fischl, 2012]. The intra‐subject registration was then performed to unbiasedly align all longitudinal cortical surfaces of the same infant together, using a group‐wise surface registration method, namely Spherical Demons [Yeo et al., 2010]. The inter‐subject registration was then performed by group‐wise registration of the mean cortical surfaces of all different infants, using Spherical Demons again. Finally, each cortical surface was resampled to the same mesh tessellation on the spherical space based on the registration results, and thus the vertex‐wise correspondences of all cortical surfaces of different infants were established [Li et al., 2014d]. More details on both intra‐subject and inter‐subject surface registrations can be found in Li et al. [2014c].
Methods
In this section, we first introduce our regression model, named dynamically assembled random forest (DARF), and then describe how to use this method for subject‐specific estimation of missing vertex‐wise cortical morphological attributes at missing time point(s) for an incomplete longitudinal infant dataset.
Regression Model
Training and testing a decision tree
In the training stage, given a set of training samples , where and are respectively the d‐dimensional feature vector and the scalar target value of the i‐th training sample, each binary decision tree is independently trained by recursively finding a series of optimal partitions of the training samples. Specifically, at the root node, the training samples are optimally partitioned into two subsets by maximizing the following objective function:
| (1) |
where is the set of training samples at the current node; and are respectively the subsets of in the left child node and the right child node after partition; is a metric that estimates the consistency of training samples in terms of regression target. Mathematically, is defined as:
| (2) |
where is the covariance matrix, and is the matrix trace. The partition is determined by two factors and . For the ‐th sample in the training set, if the ‐th feature in the feature vector is less than the threshold , the sample is dispatched to the left child node; otherwise, it is dispatched to the right child node. To maximize the objective function Eq. (1), all dimensions of the feature vector are tested one after another with a certain number of thresholds, which are selected randomly between the minimum and maximum feature values of training samples, and the pair ( and ) with the largest objective value is selected as the optimal parameters and stored in the root node. The partition continues recursively for the subset of training samples in the left and right child nodes, until reaching any of the following two terminal criteria: (1) the tree reaches the specified maximum depth, and (2) the amount of training samples in a node falls below the specified minimum number. For each leaf node, where the partition stops, the target values of all training samples falling into this leaf node are averaged as the regression result and stored in this leaf node.
In the testing stage, for each individual decision tree, the testing sample goes from the root node to a leaf node according to the results of binary tests in the non‐leaf nodes, and the output is the regression result stored in the leaf node.
Dynamically assembled regression forest (DARF)
In the training stage, an individual binary decision tree is independently trained at each vertex on the resampled spherical surface. Specifically, as shown in Figure 2a, for a given vertex, all its nearby vertices in a specified neighborhood (the red region) are used together as training samples. For each training sample, we have a feature vector and a scalar target . The feature vector consists of a set of features (see the next section) extracted from the local cortical attribute maps at the input time points, and the scalar target is the attribute value at the target time point. In the testing stage, to estimate the cortical attribute at a given vertex , as shown in Figure 2b, all trained nearby individual trees in a specified neighborhood (i.e., the green region) are grouped together to form a forest , where is a specified threshold. Then, features of the given vertex is computed and fed to each tree in the forest to estimate the cortical attribute at the corresponding vertex of target time point. Finally, the regression results from all the trees in the forest are averaged as the final estimation.
Figure 2.
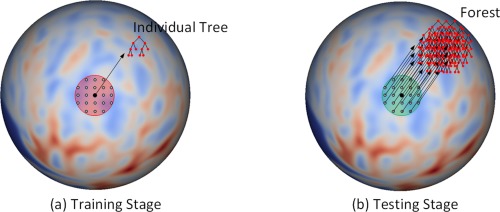
Training stage (a) and testing stage (b). (a) The red region is the neighborhood, where all the vertices on the spherical space are used as training samples. (b) The green region is the neighborhood, where all the individual trees are combined together to form a forest in the testing stage. Note that the red and green regions in (a) and (b) could have different sizes. [Color figure can be viewed at http://wileyonlinelibrary.com.]
Feature computation on spherical surface
For each vertex , its feature vector includes two types of features: local features and context features. Local features provide local information at each vertex, while context features provide rich neighboring information. In our current implementation for estimating cortical thickness at missing time point(s), the local features include cortical thickness and sulcal depth, and the context features include a number of Haar‐like features of cortical thickness and sulcal depth. Herein, Haar‐like features provide two types of context information: (1) the mean attribute of a small cortical region, and (2) the difference between mean attributes of two small regions. Next, we introduce how to compute Haar‐like features on a spherical surface.
As shown in Figure 3, given a vertex on the resampled spherical surface, its neighbor is locally projected to the tangential plane, where a local 2D coordinate system is built at the center of vertex . Two blocks and are randomly selected in the neighborhood , and their sizes and are also chosen randomly in the interval , where , , , and are the user‐defined parameters. Letting denote the set consisting of all the vertices in block and also denote the set consisting of all the vertices in block , then the Haar‐like feature at vertex can be mathematically formulated as:
| (3) |
where is the value of cortical morphological attribute (i.e., cortical thickness or sulcal depth) at position ; and is a random coefficient that can only be 0 or 1. In the case of , Haar‐like feature is the mean value of cortical morphological attributes within the block . In the case of , Haar‐like feature is the difference between the mean values of cortical attributes within block and block .
Figure 3.
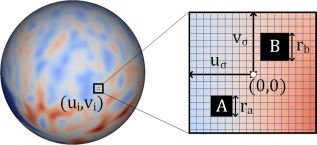
Computation of Haar‐like features on a resampled spherical surface atlas. The horizontal and vertical lines in the rectangular patch denote for latitude and longitude directions, respectively. The blocks A and B are the two randomly selected regions. The value of Haar‐like feature is defined as 1) the mean value of the cortical attributes in the block A, or 2) the mean value of the cortical attributes in the block A subtracting that in the block B. [Color figure can be viewed at http://wileyonlinelibrary.com.]
Estimation of Missing Cortical Thickness Map
As shown in Figure 1, in our longitudinal dataset for early brain development study, many time points are missing due to various reasons. Intuitively, to maximize the capability of estimating missing data, we expect using as much available information as possible to train the regression model (i.e., DARF). Specifically, by increasing the number of subjects for training, the regression model can better learn the large diversity among individuals; and by engaging more time points in training process, the regression model can better capture the longitudinal information of cortex development. Unfortunately, due to the data incompleteness, increasing the number of training subjects and engaging more time points are conflicting with each other. For example, as shown in Figure 1, to estimate the missing data at 6 months, we can use at most 28 subjects to train the regression model, since only 28 infants have real data at both 1 and 6 months. Consequently, only one time point (i.e., at 1‐month‐old) is taken account into the training process. In another way, we can engage at most four time points in the training process, but only 16 infants have real data at all five time‐points and can be used as training subjects. To eliminate this confliction and fully use the available information, we propose a two‐stage missing data completion method. Figure 4 shows the overview of the proposed method, containing the stages of (1) pairwise estimation and (2) joint refinement.
Figure 4.
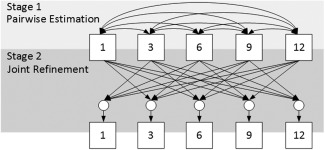
Overview of the proposed method for estimation of missing data. The box with number stands for the data at the corresponding time point. The directed edges represent the processes of estimation of the missing data at the target time points (as pointed by the arrowhead) based on the data at the available time points (at the tail side). In Stage 1, the edges are bidirectional, which means that the estimation is performed twice by exchanging between the input and the output time points. The circles in Stage 2 denote the use of multiple time points jointly.
In Stage 1, to use as many subjects as possible for training, the data (i.e., cortical thickness) of each subject at each missing time point is estimated based on the existing data at each of other time points independently, and then these independent estimations are averaged together to obtain an initial estimation. For example, to obtain the initial estimations at 6 months, we will first use all the subjects with available data at both 1‐month‐old and 6‐months‐old as training subjects to train a set of decision trees, by taking the data at 6‐months‐old as the regression target while the data at 1‐month‐old as the inputs. After training, for the subjects with available data at 1‐month‐old but without data at 6‐months‐old, these decision trees are dynamically/locally assembled as forests to estimate the missing data at 6‐months‐old. Similarly, we can also obtain the estimations of missing data at 6‐months‐old, respectively, using the existing data at each of the 3‐, 9‐, and 12‐months‐old. In this way, the available data at all other time points can contribute to the estimation of the data at 6‐months‐old. Finally, we average all the estimations contributed from different time points together as the initial estimation. Similarly, for the missing data at each of 1‐, 3‐, 9‐, and 12‐months‐old, the same process can be performed to obtain their own initial estimations. After Stage 1, the missing data of all subjects at all time points will be approximately recovered, thus providing a pseudo‐complete longitudinal dataset.
In Stage 2, to take advantage of the longitudinal information and also to make the estimation temporally consistent, the data at each missing time point is further refined based on the data at all other time points jointly. For example, to obtain the final estimation of the missing data at 6‐months‐old, we use all subjects with real data at 6‐months‐old as the training subjects to train a set of decision trees, by taking the data at 6‐months‐old as the regression target and the data at 1‐, 3‐, 9‐, and 12‐months‐old as the inputs. After training, for each subject with missing data at 6‐months‐old, the trained decision trees can be dynamically/locally assembled as forests to estimate the missing data. Note that we do not require each training/testing subject to have real data at 1‐, 3‐, 9‐, and 12‐months‐old, since we already recovered them in Stage 1 for all subjects with missing data at any time point. Similarly, for the missing data at other time points, the same process can be conducted to obtain their final estimations. It is worth noting that, using the above two stages (Stage 1 and Stage 2), our method leverages information from all time points of all available training subjects for the missing data estimation.
Quantitative Evaluation
To quantitatively evaluate the estimation results, we employed three metrics: normalized mean squared error (NMSE) [Faramarzi et al., 2013], mean absolute error (MAE), and MRE (mean relative error). These metrics are respectively computed as follows:
| (4) |
| (5) |
| (6) |
where and are respectively the ground truth and estimated result, and is the number of vertices.
RESULTS
To evaluate our proposed missing data estimation method, we tested the method by recovering cortical thickness maps at five missing time points. Specifically, from the incomplete dataset (Fig. 1), we selected 16 subjects with complete data at all five time points as the reference subjects. Then, we manually selected one of these 16 subjects, deleted its data at a certain time point, and put it back to the dataset. The deleted data was then recovered using our missing data estimation method. After recovering the missing data, we compared the recovered result with the real data. This experiment was repeated for each of those 16 subjects at each of five time points.
Figure 5 shows the error map of our proposed method at each stage for estimation of missing cortical thickness at 9‐months‐old on a randomly selected infant. Figure 6 further shows the averaged errors for all reference subjects in each step of estimation. From these two figures, we can see that using the data at 6‐ or 12‐months‐old as inputs to estimate the cortical thickness at 9‐months‐old is better than using the data at 1‐ or 3‐months‐old. A possible explanation is that the cortical thickness at 9‐months‐old is more similar to that at 6‐ and 12‐months‐old than to that at 1‐ and 3‐months‐old. Figure 6 also shows that the result of joint refinement is generally better than all the results in the previous stage (Stage 1), indicating the effectiveness of joint refinement stage (Stage 2). Figure 7 illustrates the average estimation errors of vertex‐wise cortical thickness at all five time points. We found that the estimation precision is region‐specific, with high precision in the unimodal cortex while relatively low precision in the high‐order association cortex. A possible explanation is that the unimodal cortex may have less variable cortical thickness patterns across individuals than the high‐order association cortex during infancy. Hence, our method can better capture patterns of the unimodal cortex than those of the high‐order association cortex, thus producing more accurate prediction in the unimodal cortex. Note that, among all time points, the estimations were relatively less accurate at around 6 months of age. The reason is that, during this development stage, the cortex develops exceptionally rapid [Li et al., 2014a] and the image contrast is also extremely low. All of the above observations are further proved by the quantitative evaluation given in Tables 1, 2, 3. From these tables, we can further conclude that our method is able to effectively recover the missing cortical thickness, with the average absolute error of less than 0.23 mm and the average relative error of less than 9.24%. Moreover, we also performed paired t‐test to statistically compare between results of pairwise estimation and joint refinement. All p‐values are much less than 0.01, indicating that the performance improvement by the joint refinement over the pairwise estimation (reported in Tables 1, 2, 3) is statistically significant. The estimation error by our method is about 10% of cortical thickness. Considering that the MRI resolution is 1mm and the average cortical thickness is around 2 mm in infants, our estimation error is just around 0.2 mm, which is much less than the resolution of a half voxel. Meanwhile, around 96.5%, 95.2%, 85.3%, 91.4%, and 92.0% vertices on the cortical surface have the absolute errors less than 0.5mm (half voxel) for 1st, 3rd, 6th, 9th, and 12th month, respectively. These results indicate that our prediction is accurate and acceptable. We further computed the estimation errors in each of 36 ROIs. Figure 8 shows both the MAE and the mean relative error in each of 36 ROIs for estimation of the missing cortical thickness at 9‐months‐old. We can see that, in all ROIs, the use of joint refinement led to obvious improvements over the use of only the pairwise estimation. Figure 9 shows error measures in each ROI for estimation the missing cortical thickness at all five time points. We can see that the joint refinement consistently improved the result of the pairwise estimation in some challenging ROIs, such as caudal anterior‐cingulate cortex (ROI 3), cuneus cortex (ROI 6), lateral orbitofrontal cortex (ROI 13), middle temporal gyrus (ROI 16), pars orbitalis (ROI 20), pericalcarine cortex (ROI 22), posterior‐cingulate cortex (ROI 24), and superior frontal gyrus (ROI 29).
Figure 5.
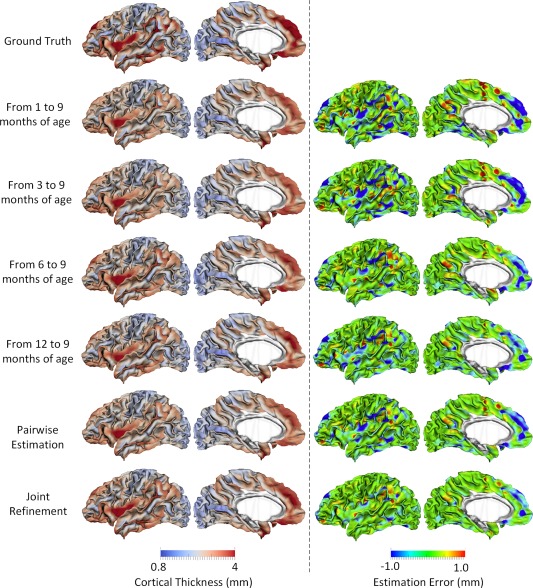
Estimations of the vertex‐wise missing cortical thickness at 9‐months‐old for a randomly selected infant. The first two columns show the maps of ground truth and the estimation of cortical thickness at each step. The last two columns show the maps of estimation errors at each step. [Color figure can be viewed at http://wileyonlinelibrary.com.]
Figure 6.
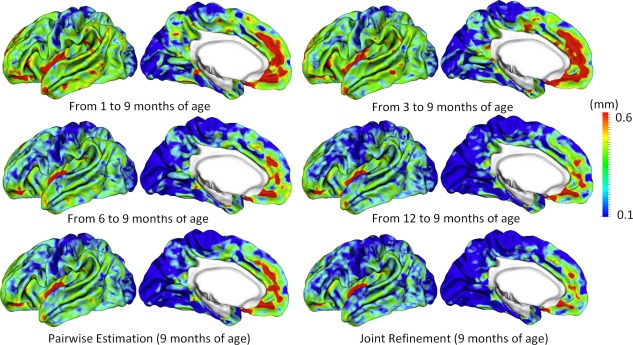
Vertex‐wise average estimation errors (mm) of missing cortical thickness at 9‐months‐old for all subjects at each step of estimation. [Color figure can be viewed at http://wileyonlinelibrary.com.]
Figure 7.
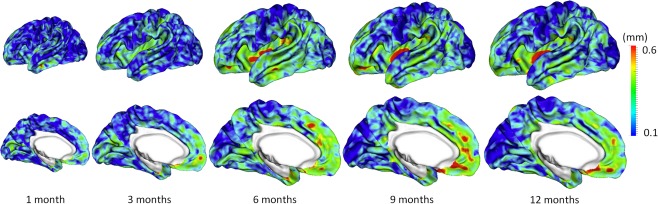
Vertex‐wise average estimation errors (mm) of missing cortical thickness at five time points for all subjects by using the proposed method. [Color figure can be viewed at http://wileyonlinelibrary.com.]
Table 1.
Quantitative measures of estimation results for the missing cortical thickness by NMSE
| NMSE | Baseline time points (months) | PE | JR | P‐value | |||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 6 | 9 | 12 | |||||
| Target time points (months) | 1 | – | 0.0129 ± 0.0022 | 0.0153 ± 0.0028 | 0.0156 ± 0.0024 | 0.0147 ± 0.0025 | 0.0128 ± 0.0022 | 0.0117 ± 0.0019 | 9 × 10−4 |
| 3 | 0.0163 ± 0.0032 | – | 0.0187 ± 0.0035 | 0.0186 ± 0.0039 | 0.0175 ± 0.0035 | 0.0157 ± 0.0035 | 0.0140 ± 0.0032 | 6 × 10−6 | |
| 6 | 0.0231 ± 0.0037 | 0.0221 ± 0.0049 | – | 0.0157 ± 0.0049 | 0.0158 ± 0.0035 | 0.0155 ± 0.0040 | 0.0139 ± 0.0030 | 1 × 10−3 | |
| 9 | 0.0220 ± 0.0023 | 0.0211 ± 0.0025 | 0.0155 ± 0.0025 | – | 0.0133 ± 0.0015 | 0.0147 ± 0.0019 | 0.0121 ± 0.0021 | 2 × 10−3 | |
| 12 | 0.0191 ± 0.0024 | 0.0182 ± 0.0021 | 0.0139 ± 0.0021 | 0.0124 ± 0.0022 | – | 0.0128 ± 0.0018 | 0.0107 ± 0.0019 | 7 × 10−8 | |
PE and JR respectively stand for two stages of pairwise estimation and joint refinement.
Table 2.
Quantitative measures of estimation results for the missing cortical thickness by MAE
| MAE (mm) | Input time points (months) | PE | JR | P‐value | |||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 6 | 9 | 12 | |||||
| Target time points (months) | 1 | – | 0.176 ± 0.015 | 0.195 ± 0.014 | 0.198 0.017 | 0.192 ± 0.016 | 0.179 ± 0.015 | 0.168 ± 0.013 | 5 × 10−4 |
| 3 | 0.209 ± 0.026 | – | 0.230 ± 0.027 | 0.231 ± 0.029 | 0.222 ± 0.026 | 0.209 ± 0.027 | 0.193 ± 0.025 | 8 × 10−6 | |
| 6 | 0.307 ± 0.035 | 0.306 ± 0.046 | – | 0.252 ± 0.043 | 0.252 ± 0.040 | 0.264 ± 0.041 | 0.233 ± 0.034 | 2 × 10−4 | |
| 9 | 0.326 ± 0.027 | 0.317 ± 0.025 | 0.264 ± 0.023 | – | 0.241 ± 0.016 | 0.261 ± 0.021 | 0.224 ± 0.016 | 5 × 10−8 | |
| 12 | 0.308 ± 0.025 | 0.301 ± 0.021 | 0.253 ± 0.022 | 0.232 ± 0.017 | – | 0.245 ± 0.019 | 0.215 ± 0.016 | 7 × 10−11 | |
Table 3.
Quantitative measures of estimation results for the missing cortical thickness by mean relative error (MRE).
| MRE (%) | Input time points (months) | PE | JR | P‐value | |||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 6 | 9 | 12 | |||||
| Target time points (months) | 1 | – | 8.75 ± 0.75 | 9.71 ± 0.84 | 9.92 ± 1.01 | 9.65 ± 1.01 | 8.93 ± 0.95 | 8.32 ± 0.69 | 3 × 10−4 |
| 3 | 9.94 ± 1.14 | – | 11.05 ± 1.49 | 11.07 ± 1.34 | 10.90 ± 1.39 | 10.02 ± 1.33 | 9.23 ± 1.25 | 6 × 10−7 | |
| 6 | 12.25 ± 0.67 | 11.99 ± 0.82 | – | 9.81 ± 0.77 | 9.83 ± 0.70 | 9.92 ± 0.74 | 9.08 ± 0.79 | 6 × 10−6 | |
| 9 | 11.91 ± 0.62 | 11.64 ± 0.69 | 9.54 ± 0.85 | – | 8.72 ± 0.33 | 9.51 ± 0.56 | 8.14 ± 0.51 | 3 × 10−9 | |
| 12 | 11.33 ± 0.59 | 11.08 ± 0.52 | 9.25 ± 0.67 | 8.43 ± 0.52 | – | 9.04 ± 0.55 | 7.81 ± 0.52 | 9 × 10−12 | |
PE and JR respectively stand for two stages of pairwise estimation and joint refinement.
Figure 8.
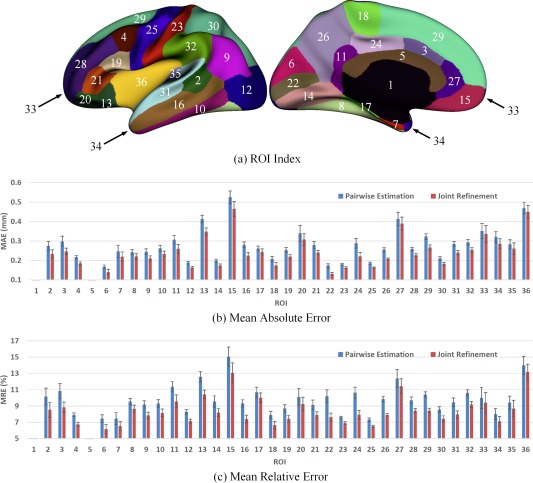
Error measures in 36 ROIs for estimation of missing cortical thickness at 9‐months‐old. ROIs 1 and 5 are excluded as there is no definition of cortical thickness for these two regions. [Color figure can be viewed at http://wileyonlinelibrary.com.]
Figure 9.
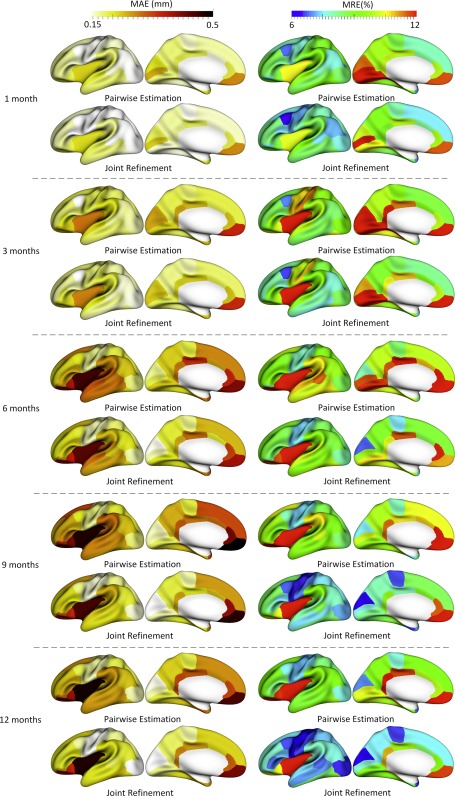
The accuracy of each step in estimating the missing cortical thickness at 1‐, 3‐, 6‐, 9‐ and 12‐months‐old in 36 ROIs. [Color figure can be viewed at http://wileyonlinelibrary.com.]
To demonstrate the advantages of DARF, we compared it with other four representative methods, including mixed effect model (MEM) in FreeSurfer [Bernal‐Rusiel et al., 2013], polynomial regression (PR), CRF, and sparse linear regression (SLR). MEM, which explicitly models fixed effects and random effects, is a powerful method for analyzing longitudinal neuroimaging [Bernal‐Rusiel et al., 2013]. In our comparison experiments, MEM assumes that the development of cortical thickness increases with age (fixed effect) during the first year, while each subject has individual variant due to personal reasons (random effect), such as genetic and environmental influences. PR method assumes that the development of cortical thickness at each vertex has a two‐order polynomial relationship with age. CRF trains a single forest for the entire surface with the spherical location of each vertex as additional features (in addition to the Haar‐like features). SLR is an effective method for high‐dimensional data analysis [Tibshirani, 1996], which can extract the most “useful” features from a high‐dimensional feature representation by setting zero coefficients for irrelevant features. Specifically, given a target vector and the feature matrix , SLR method finds the optimal coefficients by solving Eq. (7) below, with the constraint that the number of non‐zero elements in is no more than .
| (7) |
where and were optimally set to 12 and 0.001 respectively in our experiments based on a grid search, which was performed on a subset of the training data.
Figure 10 provides a comparison among MEM, PR, CRF, SLR and DARF for estimation of vertex‐wise cortical thickness at 9‐months‐old for a representative subject. As we can see, DARF estimated cortical thickness map more precisely than other four methods. Figure 10 also shows that the error map of CRF is very spotty compared with the error maps of other methods, which indicates that the estimation result of CRF is not as smooth as the real cortical thickness map. Table 4 reports the complete quantitative evaluation for five methods based on leave‐one‐out cross‐validation. It shows that DARF outperforms all other methods. An interesting observation is that PR performs much worse at the first and last time points, but it does relatively better at the intermediate time points. This means that when using a quadratic curve to fit the development trajectory of cortical thickness, it is relatively difficult to precisely estimate the two ends of the curve. We further performed paired t‐test between our method and all other methods, and obtained all p‐values less than 0.001, demonstrating the significant advantage of our method.
Figure 10.
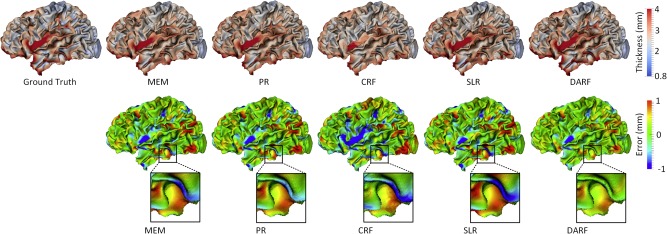
Estimation of the vertex‐wise cortical thickness map (mm) of a randomly selected infant at 9 months of age by five different methods. The first row shows the ground truth and the estimation of cortical thickness map. The second row shows the estimation error maps (mm). [Color figure can be viewed at http://wileyonlinelibrary.com.]
Table 4.
Quantitative evaluation of the performance of cortical thickness estimation by using MEM, PR, CRF, SLR and DARF
| Metric | Method | 1 month | 3 months | 6 months | 9 months | 12 months |
|---|---|---|---|---|---|---|
| NMSE | MEM | 0.0177 ± 0.0023 | 0.0244 ± 0.0175 | 0.0185 ± 0.0033 | 0.0156 ± 0.0012 | 0.0154 ± 0.0010 |
| PR | 0.2321 ± 0.0506 | 0.0389 ± 0.0100 | 0.0223 ± 0.0053 | 0.0142 ± 0.0027 | 0.0888 ± 0.0171 | |
| CRF | 0.0165 ± 0.0035 | 0.0188 ± 0.0031 | 0.0285 ± 0.0051 | 0.0189 ± 0.0031 | 0.0163 ± 0.0023 | |
| SLR | 0.0139 ± 0.0037 | 0.0161 ± 0.0039 | 0.0183 ± 0.0044 | 0.0153 ± 0.0034 | 0.0154 ± 0.0042 | |
| DARF | 0.0117 ± 0.0019 | 0.0140 ± 0.0032 | 0.0139 ± 0.0030 | 0.0121 ± 0.0021 | 0.0107 ± 0.0019 | |
| MAE (mm) | MEM | 0.215 ± 0.016 | 0.269 ± 0.049 | 0.264 ± 0.035 | 0.270 ± 0.015 | 0.258 ± 0.020 |
| PR | 0.764 ± 0.091 | 0.328 ± 0.043 | 0.295 ± 0.044 | 0.245 ± 0.024 | 0.634 ± 0.072 | |
| CRF | 0.181 ± 0.023 | 0.224 ± 0.028 | 0.330 ± 0.041 | 0.306 ± 0.024 | 0.204 ± 0.027 | |
| SLR | 0.175 ± 0.023 | 0.205 ± 0.027 | 0.263 ± 0.038 | 0.268 ± 0.026 | 0.259 ± 0.026 | |
| DARF | 0.168 ± 0.013 | 0.193 ± 0.025 | 0.233 ± 0.034 | 0.224 ± 0.016 | 0.215 ± 0.016 | |
| MRE (%) | MEM | 12.25 ± 0.73 | 13.68 ± 0.44 | 11.05 ± 0.98 | 10.46 ± 0.45 | 10.68 ± 0.33 |
| PR | 37.17 ± 0.048 | 15.96 ± 2.30 | 11.12 ± 1.05 | 8.5 ± 0.67 | 22.52 ± 2.42 | |
| CRF | 9.23 ± 0.91 | 11.51 ± 1.73 | 12.63 ± 1.25 | 11.65 ± 0.95 | 11.42 ± 0.76 | |
| SLR | 9.05 ± 0.83 | 10.05 ± 1.52 | 11.01 ± 1.12 | 10.44 ± 0.98 | 10.69 ± 0.77 | |
| DARF | 8.32 ± 0.69 | 9.23 ± 1.25 | 9.08 ± 0.79 | 8.14 ± 0.51 | 7.81 ± 0.52 |
DISCUSSION
Parameter Selection and Robustness
The performance of the proposed method can be affected by several parameters, e.g., maximal depth of trees and the neighborhood size for computing Haar‐like features. We chose these parameters by searching their optimal values based on leave‐one‐out cross‐validation on the training data, which could effectively prevent DARF from over‐fitting the training data. Specifically, to search the optimal value for the maximal depth of trees, we fixed all other parameters, and then tried all possible values from 10 to 120 with each 10 increment. As shown in Figure 11a, when the maximal depth is less than 60, the accuracy is improved with increase of the maximal depth; but when the maximal depth is larger than 60, the accuracy is relatively steady. Therefore, we chose 70 as the maximal depth of trees. Figure 11b shows the relationship between the minimal sample number in each leaf node and the MAE. It can be seen that the MAE fluctuates slightly when the number is less than 8; however, when the number is larger than 10, the error starts increasing. This is because increasing samples in each leaf node could make more training samples with different target values fall into the same leaf node and thus lead to more rough regression results. Accordingly, we chose three as the minimal sample number in each leaf node in all our experiments. For the Haar‐like features, four parameters , , , and , as shown in Figure 3, controls their computations. In our experiments, we simply set , as there is no specific reason to treat them differently. Assuming the radius of the spherical surface is 100, when and are in , the highest accuracy can be achieved (Fig. 11c). The main reason is that, when and are too small, less neighboring information could be effectively encoded by the Haar‐like features; however, when and are too large, Haar‐like features might fail to precisely describe local information. Thus, we chose for and . For , which is the lower bound for the size of a Haar‐like feature block, we simply set it 0, which means that the minimal region described by a Haar‐like feature could be of the size of a single vertex. For , which is the upper bound for the size of a Haar‐like feature block, we tested the value from to . As shown in Figure 11d, the best accuracy can be achieved when is in the range of . When is larger than , the estimation error increases with the increase of . In our experiments, we chose for . Figure 11e shows how the estimation error changes with the number of Haar‐like features. It can be seen that, when the number of Haar‐like features is larger than 500, further increasing does not benefit much. In fact, increasing the number of Haar‐like features will lead to high computational cost. Thus, we chose 500 as the number of Haar‐like features in all our experiments. In the training process, to maximize the objective function Eq. (1), all dimensions of the feature vector were tested one after another. For each dimension, a certain number of thresholds was selected randomly between the minimum and maximum feature values of all training samples, as suggested in Criminisi et al. [2012]. We tested different sample numbers for selecting threshold . As shown in Figure 11f, increasing the number of sampled thresholds could improve the accuracy. But, when the sample number is larger than 10, the accuracy could no longer be improved if further increasing the sample number. Moreover, larger sample number could also cause high computational overhead. Thus, we chose 20 in our experiments. In summary, we can see from Figure 11 that all the parameters are selected in a relatively stable range, which means that the slight adjustment of parameters will not affect the estimation accuracy, indicating robustness of our method to the parameter configuration.
Figure 11.
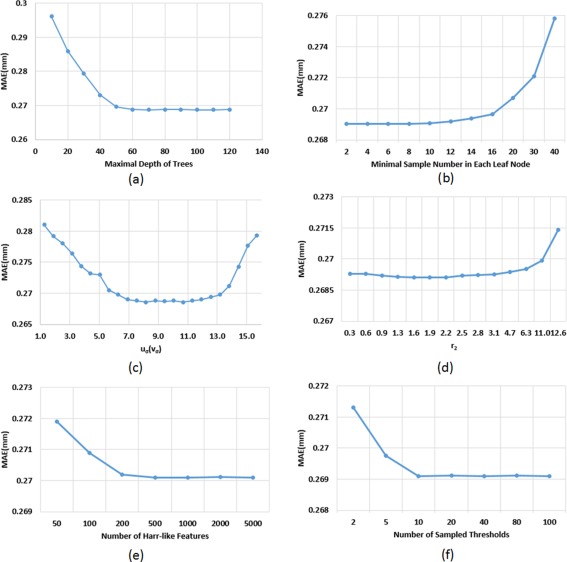
The influence of 6 parameters to the estimation accuracy (mm). [Color figure can be viewed at http://wileyonlinelibrary.com.]
Smoothness
DARF can obtain very smooth estimations because of the following two reasons. First, DARFs of neighboring vertices are very similar, as they share a large number of same decision trees. Second, features of neighboring vertices are also similar. Thus, by feeding the similar DARFs with the similar input features, the outputs at neighboring vertices generally have small differences, and thus the estimated cortical attributes for the whole surface are smooth.
Computational Cost
To achieve the similar smooth estimation results, DARF significantly saves the computational cost, compared to CRF with highly‐overlapped ROIs. For example, if the number of ROIs is , the total number of trees we need to train for CRF is , where is the number of trees in each forest. Based on our experiments, a well‐trained forest needs approximately 100 decision trees. Besides, in order to make the estimation as smooth as the real data, needs to be close to , where is the number of vertices on the spherical surface. So the total number of decision trees for the whole surface is about . If using DARF, the total number of trees to train is , since we need to train only one decision tree at each vertex. As a result, DARF reduces the computational cost by approximately 20 times.
Performance on Large Portion of Missing Data
We randomly removed some existing data, and tested the proposed method with different portions of missing data. Of note, the original missing data in our dataset (enclosed by the red rectangle in Fig. 1) is 12%. By randomly removing some existing data the entire dataset, we can get the datasets with 13%, 20%, 40%, and 60% missing data, respectively. From Figure 12, we can see that the estimation errors increase with the portion of missing data increasing. However, even the missing data reaches 40%, the proposed method is still able to produce the average estimation error to less than 0.23 mm. Note that, like most machine learning methods, the estimation precision of DARF depends on the quantity and quality of training data. As long as we have enough quality training data, DARF is able to estimate the missing data precisely. Figure 12 also shows that joint refinement consistently improves the result of pairwise estimation.
Figure 12.
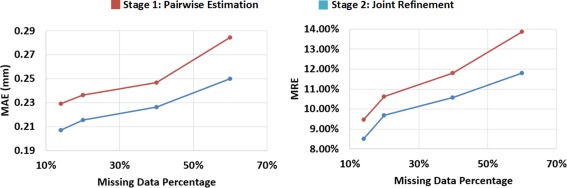
Relationship between estimation errors and the portions of missing data. [Color figure can be viewed at http://wileyonlinelibrary.com.]
Estimation of Abnormal Cortical Attribute Maps
Our current study focuses on the normal early brain development. Note that the abnormal cortical attribute map could have much larger variability across subjects/diseases than the normal ones, thus needing larger‐scale datasets to train our estimation model for effectively covering all the possibilities. If training DARF by the normal subjects and then directly using it to estimate the abnormal cortical attributes, the estimation results may not reflect the true abnormal development. However, this can indirectly benefit the detection of abnormal brain development. For example, given a new subject, we can first estimate its cortical attribute maps using DARF, which has been trained by the normal subjects. Then, the estimated maps can be compared with the real maps. If their difference is significantly larger than the estimation errors reported in Table 2, this may indicate an abnormal brain development in this subject. Moreover, for a certain disease, if DARF could be trained by subjects with this disease, the estimation accuracy would likely be better than the results estimated by DARF that is trained with a general dataset.
Potential Applications
After recovering the missing cortical attribute maps in a longitudinal dataset by our method, the “completed” dataset could be used for studying early brain development. For example, the recovered dataset can be used to better build longitudinal cortical surface atlases. Note that, before recovering the missing data, building such atlases could introduce different biases for different time points since the atlas at each time point is constructed by a different number of subjects. While, after recovering the missing data, the atlases at all time points can be constructed based on the same subjects, thus introducing less bias and leading to more accurate and longitudinally consistent atlases. Another application example is that the recovered dataset can be used to carry out less biased and longitudinally more consistent groupwise comparisons of cortical attributes across ages, since each pair of ages will have the same subjects. Also, the recovered dataset can be used for more accurate modeling of early brain developmental trajectories.
CONCLUSION
There are two major contributions in this paper. First, we proposed a DARF. By independently training one decision tree at each vertex on the spherical surface and also dynamically grouping trees in the local neighborhood as a forest, the smoothness of regression results can be guaranteed, and also the computational cost can be largely reduced, compared with using the CRFs with highly‐overlapped ROIs. Second, we proposed a novel two‐stage method to recover the missing data of vertex‐wise cortical morphological attributes in an incomplete longitudinal dataset. The proposed method can effectively exploit all available information in the incomplete dataset to help estimate the missing information. Specifically, in the stage of pairwise estimation, as many training subjects as possible are used in the training process, thus better learning the huge diversity among subjects by the regression model; in the stage of joint refinement, all time points are taken into account simultaneously, thus better capturing longitudinal information. Our proposed missing data estimation method has been extensively tested on an incomplete dataset with 31 infants, each having up to five time points in the first postnatal year, and obtained promising performance for estimation of the cortical thickness maps. In our future work, we will test our method for estimation of other cortical morphological attributes, such as sulcal depth, surface area, cortical folding, and cortical local gyrification.
Contributor Information
Gang Li, Email: dgshen@med.unc.edu.
Dinggang Shen, Email: gang_li@med.unc.edu.
REFERENCES
- Almli CR, Rivkin MJ, McKinstry RC, Brain Development Cooperative, G. (2007): The NIH MRI study of normal brain development (Objective‐2): newborns, infants, toddlers, and preschoolers. NeuroImage 35:308–325. [DOI] [PubMed] [Google Scholar]
- Awate SP, Yushkevich PA, Song Z, Licht DJ, Gee JC (2010): Cerebral cortical folding analysis with multivariate modeling and testing: Studies on gender differences and neonatal development. Neuroimage 53:450–459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernal‐Rusiel JL, Greve DN, Reuter M, Fischl B, Sabuncu MR, Alzheimer's Disease Neuroimaging I (2013): Statistical analysis of longitudinal neuroimage data with linear mixed effects models. NeuroImage 66:249–260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breiman L (2001): Machine Learning 45:5–32. Random Forests. [Google Scholar]
- Cai JF, Cand EJ, Shen Z (2010): A singular value thresholding algorithm for matrix completion. SIAM J Optimization 20:1956–1982. [Google Scholar]
- Cand EJ, Tao T (2010): The power of convex relaxation: near‐optimal matrix completion. IEEE Trans. Inf. Theor 56:2053–2080. [Google Scholar]
- Candès E, Recht B (2009): Exact matrix completion via convex optimization. Found Comput Math 9:717–772. [Google Scholar]
- Ching WK, Li L, Tsing NK, Tai CW, Ng TW, Wong AS, Cheng KW (2010): A weighted local least squares imputation method for missing value estimation in microarray gene expression data. Int J Data Mining Bioinform 4:331–347. [DOI] [PubMed] [Google Scholar]
- Criminisi A, Shotton J, Konukoglu E (2012): Decision forests: A unified framework for classification, regression, density estimation, manifold learning and semi‐supervised learning. Found Trends Comput Graph Vis 7:81–227. [Google Scholar]
- Dale AM, Fischl B, Sereno MI (1999): Cortical surface‐based analysis. I. Segmentation and surface reconstruction. NeuroImage 9:179–194. [DOI] [PubMed] [Google Scholar]
- Dubois J, Benders M, Borradori‐Tolsa C, Cachia A, Lazeyras F, Ha‐Vinh Leuchter R, Sizonenko SV, Warfield SK, Mangin JF, Huppi PS (2008): Primary cortical folding in the human newborn: an early marker of later functional development. Brain 131:2028–2041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan Y, Shi F, Smith JK, Lin W, Gilmore JH, Shen D (2011): Brain anatomical networks in early human brain development. NeuroImage 54:1862–1871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faramarzi E, Rajan D, Christensen MP (2013): Unified blind method for multi‐image super‐resolution and single/multi‐image blur deconvolution. IEEE Trans Image Process 22:2101–2114. [DOI] [PubMed] [Google Scholar]
- Fischl B (2012): FreeSurfer. NeuroImage 62:774–781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, Dale AM (2000): Measuring the thickness of the human cerebral cortex from magnetic resonance images. Proc Natl Acad Sci U S A 97:11050–11055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, Sereno MI, Dale AM (1999a): Cortical surface‐based analysis. II: Inflation, flattening, and a surface‐based coordinate system. NeuroImage 9:195–207. [DOI] [PubMed] [Google Scholar]
- Fischl B, Sereno MI, Tootell RB, Dale AM (1999b): High‐resolution intersubject averaging and a coordinate system for the cortical surface. Hum Brain Mapp 8:272–284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilmore JH, Lin W, Prastawa MW, Looney CB, Vetsa YS, Knickmeyer RC, Evans DD, Smith JK, Hamer RM, Lieberman JA, Gerig G (2007): Regional gray matter growth, sexual dimorphism, and cerebral asymmetry in the neonatal brain. J Neurosci 27:1255–1260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilmore JH, Shi F, Woolson SL, Knickmeyer RC, Short SJ, Lin W, Zhu H, Hamer RM, Styner M, Shen D (2012): Longitudinal development of cortical and subcortical gray matter from birth to 2 years. Cereb Cortex 22:2478–2485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han X, Pham DL, Tosun D, Rettmann ME, Xu CY, Prince JL (2004): CRUISE: Cortical reconstruction using implicit surface evolution. NeuroImage 23:997–1012. [DOI] [PubMed] [Google Scholar]
- Kaukola T, Kapellou O, Laroche S, Counsell SJ, Dyet LE, Allsop JM, Edwards AD (2009): Severity of perinatal illness and cerebral cortical growth in preterm infants. Acta Paediatr 98:990–995. [DOI] [PubMed] [Google Scholar]
- Kim JS, Singh V, Lee JK, Lerch J, Ad‐Dab'bagh Y, MacDonald D, Lee JM, Kim SI, Evans AC (2005): Automated 3‐D extraction and evaluation of the inner and outer cortical surfaces using a Laplacian map and partial volume effect classification. NeuroImage 27:210–221. [DOI] [PubMed] [Google Scholar]
- Li G, Lin W, Gilmore JH, Shen D (2015a): Spatial patterns, longitudinal development, and hemispheric asymmetries of cortical thickness in infants from birth to 2 years of age. J Neurosci 35:9150–9162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li G, Nie J, Wang L, Shi F, Gilmore JH, Lin W, Shen D (2014a): Measuring the dynamic longitudinal cortex development in infants by reconstruction of temporally consistent cortical surfaces. NeuroImage 90:266–279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li G, Nie J, Wang L, Shi F, Lin W, Gilmore JH, Shen D (2013): Mapping region‐specific longitudinal cortical surface expansion from birth to 2 years of age. Cerebral Cortex 23:2724–2733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li G, Nie J, Wang L, Shi F, Lyall AE, Lin W, Gilmore JH, Shen D (2014b): Mapping longitudinal hemispheric structural asymmetries of the human cerebral cortex from birth to 2 years of age. Cerebral Cortex 24:1289–1300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li G, Nie J, Wu G, Wang Y, Shen D, Alzheimer's Disease Neuroimaging I (2012): Consistent reconstruction of cortical surfaces from longitudinal brain MR images. NeuroImage 59:3805–3820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li G, Wang L, Shi F, Gilmore JH, Lin W, Shen D (2015b): Construction of 4D high‐definition cortical surface atlases of infants: Methods and applications. Med Image Analysis 25:22–36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li G, Wang L, Shi F, Lin W, Shen D (2014c): Constructing 4D infant cortical surface atlases based on dynamic developmental trajectories of the cortex. Medical image computing and computer‐assisted intervention : MICCAI. International Conference on Medical Image Computing and Computer‐Assisted Intervention, 17:89–96. [DOI] [PMC free article] [PubMed]
- Li G, Wang L, Shi F, Lin W, Shen D (2014d): Simultaneous and consistent labeling of longitudinal dynamic developing cortical surfaces in infants. Med Image Analysis 18:1274–1289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li G, Wang L, Shi F, Lyall AE, Lin W, Gilmore JH, Shen D (2014e): Mapping longitudinal development of local cortical gyrification in infants from birth to 2 years of age. J Neurosci 34:4228–4238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li R, Zhang W, Suk HI, Wang L, Li J, Shen D, Ji S. (2014f) Deep learning based imaging data completion for improved brain disease diagnosis. Medical image computing and computer‐assisted intervention: MICCAI.. International Conference on Medical Image Computing and Computer‐Assisted Intervention, 17:305–312. [DOI] [PMC free article] [PubMed]
- Liu J, Musialski P, Wonka P, Ye J (2013): Tensor completion for estimating missing values in visual data. IEEE Trans Pattern Analysis Machine Intell 35:208–220. [DOI] [PubMed] [Google Scholar]
- Liu T, Nie J, Tarokh A, Guo L, Wong ST (2008): Reconstruction of central cortical surface from brain MRI images: method and application. NeuroImage 40:991–1002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyall AE, Shi F, Geng X, Woolson S, Li G, Wang L, Hamer RM, Shen D, Gilmore JH. (2015) Dynamic development of regional cortical thickness and surface area in early childhood. Cerebral cortex 25, 2204–2212 [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacDonald D, Kabani N, Avis D, Evans AC (2000): Automated 3‐D extraction of inner and outer surfaces of cerebral cortex from MRI. NeuroImage 12:340–356. [DOI] [PubMed] [Google Scholar]
- Mangin JF, Riviere D, Cachia A, Duchesnay E, Cointepas Y, Papadopoulos‐Orfanos D, Scifo P, Ochiai T, Brunelle F, Regis J (2004): A framework to study the cortical folding patterns. NeuroImage 23:S129–S138. [DOI] [PubMed] [Google Scholar]
- Meng Y, Li G, Lin W, Gilmore JH, Shen D (2014): Spatial distribution and longitudinal development of deep cortical sulcal landmarks in infants. NeuroImage 100:206–218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nie J, Li G, Wang L, Gilmore JH, Lin W, Shen D (2012): A computational growth model for measuring dynamic cortical development in the first year of life. Cerebral Cortex 22:2272–2284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nie J, Li G, Wang L, Shi F, Lin W, Gilmore JH, Shen D (2014): Longitudinal development of cortical thickness, folding, and fiber density networks in the first 2 years of life. Hum Brain Mapp 35:3726–3737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schnack, H.G. , van Haren, N.E. , Brouwer, R.M. , Evans, A. , Durston, S. , Boomsma, D.I. , Kahn, R.S. , Hulshoff Pol, H.E. (2014) Changes in thickness and surface area of the human cortex and their relationship with intelligence. Cerebral cortex 25:1608–1617. [DOI] [PubMed] [Google Scholar]
- Schumann CM, Bloss CS, Barnes CC, Wideman GM, Carper RA, Akshoomoff N, Pierce K, Hagler D, Schork N, Lord C, Courchesne E (2010): Longitudinal magnetic resonance imaging study of cortical development through early childhood in autism. J Neurosci 30:4419–4427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shattuck DW, Leahy RM (2002): BrainSuite: an automated cortical surface identification tool. Med Image Analysis 6:129–142. [DOI] [PubMed] [Google Scholar]
- Shi F, Fan Y, Tang S, Gilmore JH, Lin W, Shen D (2010): Neonatal brain image segmentation in longitudinal MRI studies. NeuroImage 49:391–400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi F, Wang L, Dai Y, Gilmore JH, Lin W, Shen D (2012): LABEL: pediatric brain extraction using learning‐based meta‐algorithm. NeuroImage 62:1975–1986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi Y, Lai R, Toga AW, Alzheimer's Disease Neuroimaging I (2013): Cortical surface reconstruction via unified Reeb analysis of geometric and topological outliers in magnetic resonance images. IEEE Trans Med Imaging 32:511–530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sled JG, Zijdenbos AP, Evans AC (1998): A nonparametric method for automatic correction of intensity nonuniformity in MRI data. IEEE Trans Med Imaging 17:87–97. [DOI] [PubMed] [Google Scholar]
- Thompson P, Toga AW (1996): A surface‐based technique for warping three‐dimensional images of the brain. IEEE Trans Med Imaging 15:402–417. [DOI] [PubMed] [Google Scholar]
- Thung KH, Wee CY, Yap PT, Shen D, Alzheimer's Disease Neuroimaging I (2014): Neurodegenerative disease diagnosis using incomplete multi‐modality data via matrix shrinkage and completion. NeuroImage 91:386–400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tibshirani R (1996): Regression shrinkage and selection via the Lasso. J Roy Stat Soc B Met 58:267–288. [Google Scholar]
- Troyanskaya O, Cantor M, Sherlock G, Brown P, Hastie T, Tibshirani R, Botstein D, Altman RB (2001): Missing value estimation methods for DNA microarrays. Bioinformatics 17:520–525. [DOI] [PubMed] [Google Scholar]
- Tsiporkova E, Boeva V (2007): Two‐pass imputation algorithm for missing value estimation in gene expression time series. J Bioinform Comput Biol 5:1005–1022. [DOI] [PubMed] [Google Scholar]
- Van Essen DC, Drury HA, Dickson J, Harwell J, Hanlon D, Anderson CH (2001): An integrated software suite for surface‐based analyses of cerebral cortex. J Am Med Inform Assoc 8:443–459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Shi F, Gao Y, Li G, Gilmore JH, Lin W, Shen D (2014a): Integration of sparse multi‐modality representation and anatomical constraint for isointense infant brain MR image segmentation. NeuroImage 89:152–164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Shi F, Li G, Gao Y, Lin W, Gilmore JH, Shen D (2014b): Segmentation of neonatal brain MR images using patch‐driven level sets. NeuroImage 84:141–158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Shi F, Yap PT, Gilmore JH, Lin W, Shen D (2012): 4D multi‐modality tissue segmentation of serial infant images. PLoS One 7:e44596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeo BT, Sabuncu MR, Vercauteren T, Ayache N, Fischl B, Golland P (2010): Spherical demons: fast diffeomorphic landmark‐free surface registration. IEEE Trans Med Imaging 29:650–668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan L, Wang Y, Thompson PM, Narayan VA, Ye J, Alzheimer's Disease Neuroimaging I (2012): Multi‐source feature learning for joint analysis of incomplete multiple heterogeneous neuroimaging data. NeuroImage 61:622–632. [DOI] [PMC free article] [PubMed] [Google Scholar]


