Non-symbolic approximate arithmetic training improves math performance in preschoolers

Abstract

Math proficiency in early school age is an important predictor of later academic achievement. Thus, an important goal for society should be to improve math readiness in pre-school age children, especially in low-income children who typically arrive in kindergarten with less mathematical competency than their higher-income peers. The majority of existing research-based math intervention programs target symbolic, verbal number concepts in young children. However, very little attention has been paid to the preverbal, intuitive ability to approximately represent numerical quantity, which is hypothesized to be an important foundation for full-fledged mathematical thinking. Here, we test the hypothesis that repeated engagement of non-symbolic approximate addition and subtraction of large array of items results in improved math skills in very young children, an idea that stems from our previous studies in adults. Three to five year-old children showed selective improvements in math skills after multiple days of playing a tablet-based non-symbolic approximate arithmetic game compared to children who played a memory game. These findings, collectively with our previous reports, suggest that mental manipulation of approximate numerosities provides an important tool for improving math readiness, even in preschoolers who have yet to master the meaning of number words.

Introduction

Mathematical competence in early school years is a powerful predictor of later academic success not only in math but also in other domains such as reading (Aubrey, Godfrey, & Dahl, 2006; Duncan et al., 2007; Geary, Hoard, Nugent, & Bailey, 2013; Jordan, Glutting, & Ramineni, 2010; Jordan, Kaplan, Locuniak, & Ramineni, 2007; Jordan, Kaplan, Ramineni, & Locuniak, 2009; Martin, Cirino, Sharp, & Barnes, 2014). Unfortunately, however, many children especially from low-income families start kindergarten with minimal competencies in math (Jordan et al., 2007; Jordan, Kaplan, Nabors Oláh, & Locuniak, 2006; Klibanoff, Levine, Huttenlocher, Vasilyeva, & Hedges, 2006; Starkey, Klein, & Wakeley, 2004). Thus, enhancing mathematical competence in pre-school years is an important societal challenge.

The traditional approach to enhancing mathematical achievement in young children is to target skills foundational to mathematics, including domain-specific abilities such as counting skills and domain-general abilities such as working memory (Baroody, Eiland, & Thompson, 2009; Bryant et al., 2011; Chard et al., 2008; Clements & Sarama, 2007; Dyson, Jordan, & Glutting, 2013; Fuchs et al., 2005; Ramani & Siegler, 2008; Siegler & Ramani, 2009; Starkey et al., 2004). Many of these programs are curriculum-based and focus on enhancing specific foundational mathematical knowledge in everyday activities to improve children's mathematical competence. In particular, almost all of these programs focus on symbolic number concepts such as counting and number facts as well as arithmetic operations with numerical symbols. These intervention programs have started to show great successes in increasing children's mathematical knowledge at young ages (Clements & Sarama, 2011). Nonetheless, there are some limitations to the approaches that currently dominate the landscape. First, many of these programs require a large investment of teacher training and must be implemented over a full academic year. Relatedly, because the teachers are given a great deal of additional training to implement the intervention curricula, it is often difficult to find a fair control group. Another limitation from the standpoint of cognitive science is that most interventions are very heterogeneous, often consisting of multiple different tasks or skills. While such large-scale interventions may be a very effective strategy for improving mathematical ability, it is difficult to pinpoint which aspects of the curriculum are most effective.

Here we take an alternative approach and ask whether training aimed at children's preverbal number sense could be an effective way to improve math readiness. Children come into the world with a preverbal number sense that allows an approximate sense of quantity (Dehaene, 1999; Gallistel & Gelman, 1992). This system has been termed the approximate number system (ANS) and has been shown to present in newborn infants (Izard, Sann, Spelke, & Streri, 2009; Xu & Spelke, 2000), to operate in adults from cultures without symbolic counting systems (Gordon, 2004; Pica, Lemer, Izard, & Dehaene, 2004), and to be present in a wide range of nonhuman animals (Agrillo, Cohen Kadosh, & Dowker, 2014; Beran, Perdue, & Evans, 2015). Furthermore, the system increases in precision with age and is found across the lifespan (Halberda & Feigenson, 2008; Halberda, Ly, Wilmer, Naiman, & Germine, 2012).

Despite the profound differences between a symbolic representation of number, which allows the representation of number with extreme precision, and approximate non-symbolic representations, which are noisy and follow Weber's Law, recent studies have uncovered a correlation between individual ANS acuity and symbolic math ability (e.g., Gilmore, McCarthy, & Spelke, 2010; Halberda, Mazzocco, & Feigenson, 2008; Libertus, Feigenson, & Halberda, 2011; Mazzocco, Feigenson, & Halberda, 2011) but see (Fuhs & McNeil, 2013; Gobel, Watson, Lervag, & Hulme, 2014; Inglis, Attridge, Batchelor, & Gilmore, 2011; Kolkman, Kroesbergen, & Leseman, 2013; Nosworthy, Bugden, Archibald, Evans, & Ansari, 2013; Sasanguie, Gobel, Moll, Smets, & Reynvoet, 2013; Tibber et al., 2013; Wei, Yuan, Chen, & Zhou, 2012). We use the term symbolic math to refer to any learned mathematical concepts and knowledge including identifying symbols, number words, using the count list and solving arithmetic problems based on number words or numerals. This correlation between ANS and symbolic math indicates that approximate numerical abilities may be foundational for learned math skills and therefore suggests an alternative approach to improving math readiness. However, given the correlational nature of the findings, alternative possibilities are plentiful (e.g., see Gilmore et al., 2013; Lyons & Beilock, 2011; Piazza, Pica, Izard, Spelke, & Dehaene, 2013). To investigate the causal nature of the relationship our previous research asked whether repeated training on an approximate arithmetic task, which requires addition and subtraction of non-symbolic numerical quantities, would selectively improve mental arithmetic skills in college students (Park & Brannon, 2013, 2014). In these experiments, adult participants first received a set of pretests, which included a symbolic arithmetic test, among others. Participants were then randomly assigned into cognitive training groups. In each study, the experimental training group spent six to ten daily sessions engaged in approximate non-symbolic arithmetic, while control groups underwent others types of cognitive training such as visual short-term memory or numerosity comparison training. We found participants who were engaged in the non-symbolic approximate arithmetic training, and only those participants, showed improvement in symbolic arithmetic skills. Given that numerosity comparison and short-term memory training did not yield significant benefit in symbolic arithmetic performance, we concluded that mental manipulation of nonverbal numerical quantity was the critical factor driving improvements in math skills. Consistent with our findings, another research group found that first graders briefly exposed to similar preverbal number sense tasks performed better than peers in a subsequent symbolic arithmetic test (Hyde, Khanum, & Spelke, 2014). Collectively, these recent findings suggest that engaging the preverbal number sense via approximate arithmetic may be an effective way to improve mathematical ability throughout the lifespan.

Here, we test this possibility by asking whether approximate arithmetic training benefits preschoolers' math abilities. Local preschoolers, largely from low-income families, first received a battery of pretests that assessed their math, vocabulary, verbal short-term memory, and executive function. Children were then pseudorandomly assigned to one of two groups: the first group played a tablet-based game that required adding and subtracting arrays of icons, and the second group played a tablet-based game that required remembering the location of pairs of pictures. Then, we assessed the effectiveness of the two cognitive training programs by comparing pre- and posttest scores for each of the test measures. From this study design, we aimed to evaluate how approximate arithmetic— presumably the process of mental manipulation of numerical quantity—could benefit very young children at the verge of the introduction to formal math education and often with minimal symbolic math knowledge. This study was meant as an important first step to test the effectiveness of approximate arithmetic training in preschool children with no formal math education and as a springboard for a larger scale math intervention study.

Methods

Participants

Participants were recruited from local preschools that were largely composed of children funded by a state-funded preschool program. This program provides assistance to children from families whose gross income is at or below 75% of the state median income level. We intentionally focused on children of low-income families since they represent the greatest need for improving early mathematical competence. A total of 109 preschoolers across four schools initially enrolled in the study.

Children must have completed pre- and posttest sessions and all ten training sessions to be included in the final analysis. Out of 109 total children six children didn't meet these requirements and thus were excluded. Four were from the math group and two from the memory group (see Procedure below). One of the children finished the training phase but was unable to perform the posttests because she moved to a different school. The remaining five children completed only one to six training sessions because they moved to a different school (2), because of extended absence due to illness (1) or family travel (1), or because of unwillingness to play the game (1). The final sample included 103 preschoolers ranging in age from 3.94 to 5.56 years (mean of 4.87 and standard deviation of 0.40 years; 53 boys). Most children were from low-income families who qualified for state-funded preschool, while 24 of the children were from middle-income families enrolled in classrooms in the same preschools. Tests were administered in Spanish by a native Spanish speaker for 16 of the bilingual children who appeared to be more comfortable speaking in Spanish.

Parents gave written consent for their children to participate in the study. Children were compensated with stickers and small toys throughout the study and with a math themed storybook and a building toy at the completion of the study. Additionally, each participating classroom received an educational toy of the teacher's choice. All procedures were approved by Duke's University Institutional Review Board.

Procedure

The study consisted of three phases: pretest, training, and posttest. Pre- and posttests were conducted individually for each child in a small room at each preschool location. Pretests were administered over two sessions of approximately 25 to 35 minutes each. In Session 1, the children completed the TEMA-3 (Test of Early Mathematical Achievement, 3^rd Edition), a standardized test for assessing mathematical achievement. In Session 2, the children completed a receptive vocabulary assessment PPVT-4 (Peabody Picture Vocabulary Test, 4^th Edition), a short-term memory task, and two executive function tasks (Stroop interference and card sorting) in that order. Posttests were administered the same way, except children were assessed on different versions of the same tests. All five assessments had two versions (e.g., versions A and B). The order of the versions (pre- vs. post-test) was counterbalanced across children.

After completing the pretests, children in a given classroom were pseudorandomly assigned to either the approximate-arithmetic group or picture-memory group with a constraint to minimize differences in age, sex, TEMA and PPVT pretest scores between the two groups. To be specific, all children in the given classroom were randomly assigned into two groups, and this random assignment was done 10,000 times. In each of the 10,000 repetitions, a t-test was performed on age, sex, TEMA, and PPVT pretest scores, and the average p-values for age and sex was recorded only when both TEMA and PPVT p-values were larger than 0.95. Then, the random grouping that yielded the largest average p-value (of age and sex) was selected as the final group assignment. The randomization process was done by the first author who never directly interacted with the children.

The training phase, which consisted of ten 12-minute sessions, was conducted in small groups of two to four children. The ten daily sessions were typically spread out over two to three weeks. Children wore headphones to prevent auditory interference while listening to verbal instructions. During the training phase, the approximate-arithmetic group completed an adaptive tablet-based game (using iPad, Apple Inc.) requiring children to approximately add and subtract large arrays of icons. The picture-memory group completed an adaptive tablet-based card-matching game where children flipped and matched pairs of cards. The training phase was followed by posttests. The logistics of the project prevented us from relying solely on experimenters who were blind to the child's experimental group assignment. However 17 of the children were blind-tested. It took approximately one month to complete the study in each classroom.

Approximate-arithmetic training

The approximate-arithmetic group training game (Figure 1A) was modeled after the approximate arithmetic training task used in previous studies with adults (Park & Brannon, 2013, 2014). On each trial, children viewed an animation of addition or subtraction with two arrays containing discrete objects (e.g. paintbrushes, palm trees, and many more categories). Children were asked to help a fictitious character, Max, choose the right answer.

Figure 1.

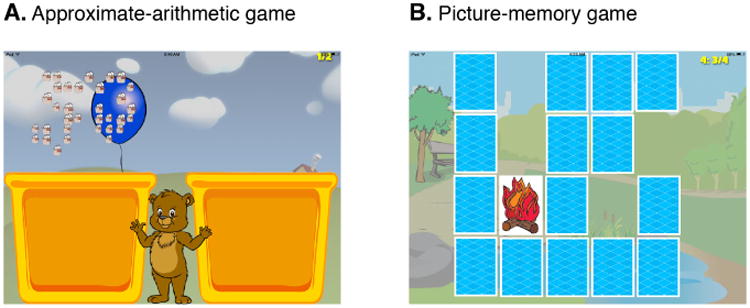
Screen shots of the two training games.

Trials followed one of four different structures: addition compare, addition match, subtraction compare, or subtraction match. On all trials children were first asked to “touch the red balloon” at which point the balloon popped and an array of items dropped into an opaque bucket with a verbal remark, “Look, some [items] are going in to the box.” In the addition trials, the blue balloon then popped spontaneously and a second array of homogeneous items dropped into the opaque bucket with a verbal remark, “More [items] are going in to the box.” In the subtraction trials, after the contents of the red balloon dropped into the opaque bucket a bird spontaneously popped out of the blue balloon and took a subset of the items away and off the screen with a verbal remark, “Some [items] are taken away.” In both cases, children were instructed to imagine the total number of items in the opaque bucket. On addition-compare trials and subtraction-compare trials, a second visible array was shown on the right side of the opaque bucket, and children were verbally instructed to “touch the one that has more” after the addition or subtraction event was complete. This second array contained a number of items that differed by a specific ratio (or a difference in a log₂-scale) to the correct sum or difference (either larger or smaller than the correct answer). On addition-match and subtract-match trials, two additional arrays were shown on the right side of the screen. Here, children were verbally asked to “touch the one that shows Max how many he has.” One of these two arrays contained the correct sum or difference that matched the contents of the opaque bucket, and the other contained a number that differed by a specific ratio (either larger or smaller than the correct answer).

Stimuli remained on the screen until a response was made. When children made a correct response, they heard one of the following responses: “nice job,” “you are correct,” or “yes, that's right!” randomly chosen. After an incorrect response, they heard “nope,” “try again,” or “not quite” randomly chosen. The four trial-types were presented in blocks of 10 trials and the order of the blocks was fixed from addition-compare, subtraction-compare, addition-match, to subtraction-match. This order continued throughout the training. For example, if a child played five blocks in one session ending with addition-compare, her next session started from subtraction-compare. Children on average played a total of 40 blocks (roughly 4 blocks per session) throughout the experiment.

The number of items in each array ranged from 4 to 80. On about 87% of the trials, the number of objects in the two arrays representing the operands ranged from 4 to 16 items in the addition conditions and from 12 to 40 in the subtraction conditions. This design yielded correct answers ranging from 12 to 20 in both the addition and subtraction conditions. This narrow number range for the correct answers was necessary as we started the game with the log²-difference of 2 (4:1 ratio), and the maximum number of objects that could fit into the container was limited to 80 due to the screen size of an iPad. Nevertheless, because all the correct answers were within this range, it would be technically possible for subjects to learn the structure of the problems and answer just based on the final array presented without actually adding or subtracting the first two arrays, especially when the log²-difference level is high. In order to minimize the use of such a strategy, we incorporated another problem structure on the remaining 13% of the trials. On these trials, the addition and subtraction problems were designed so that the correct answer ranged widely from 4 to 56 items, although this problem structure limited the alternative choices (e.g., if the correct answer was 4 and the log²-difference was 2, then the alternative option was always 16 and was never 1; if the correct answer was 56 and the log₂-difference was 2, then the alternative option was always 14 and was never 224).

Difficulty was manipulated separately for each trial type by varying the numerical difference between the correct and incorrect answers on a log scale, beginning with a log difference of 2 for the easiest level (e.g. 12 vs. 48 items). Following a typical psychophysical adaptive staircase procedure, the log₂-difference level increased by one of the values randomly chosen from [0.08, 0.09, 0.10, 0.11, 0.12] when the average accuracy of a block of ten trials was equal or less than 65%, and the level decreased by one of the values randomly chosen from [0.13, 0.14, 0.15, 0.16, 0.17] when the average accuracy was equal or greater than 80% (Park & Brannon, 2013, 2014). After every 2 blocks (i.e., 20 trials), children were shown a short classic children's cartoon (45-60s) that was designed to maintain interest and motivation.

Picture-memory training

Children in the picture-memory group played an iPad game, which began with a virtual set of faced-down cards (Figure 1B). Children were verbally instructed to “flip the cards over to make a pair.” Touching a card resulted in it flipping over to reveal an icon that remained visible until a second card was touched. If the icons matched, both cards disappeared from the board with a sweeping bell tone. In contrast, if the two icons did not match, the two cards both returned to their original faced-down position without a sound. The game was comprised of 7 different difficulty levels based on the number of cards presented: 2×2, 3×2, 4×3, 5×4, 6×5, 7×6, and 8×7 cards. The difficulty level for each child was set each day such that they would play easier levels before progressing to more difficult levels on that day. For the majority of the children, levels 2×2 and 3×2 were very easy and for all children levels 7×6 and 8×7 were very difficult, therefore almost all children played trials set at levels 4×3, 5×4, and 6×5 daily. Note that picture-memory training was thus not adaptive in the sense of the approximate-arithmetic game; however, the progression of difficulty levels within each day allowed children to be challenged and engaged without becoming too frustrated and discouraged. Children were shown the same 45-60 second video cartoon clip as in the approximate-arithmetic group after about every four minutes of game play to maintain children's interest in completing the session.

Math assessment

We measured symbolic mathematical ability with the Third Edition of the Test of Early Mathematics Achievement (TEMA-3; Ginsburg & Baroody, 2003). This test, which is designed for children of ages 3 years 0 months to 8 years 11 months, assesses formal (e.g., numeral literacy) and informal mathematics abilities (e.g., relative magnitude). Examples of questions primarily targeted for ages 4 and 5 include asking the child to verbally count from 1 to 10, to hold up 4 fingers, to state which number (word) comes after a single-digit number, to choose the numerically larger of the two Arabic numbers, and to solve simple single-digit addition and subtraction word problems. For Spanish-speaking students, directions were given in Spanish and answers in either English or Spanish were acceptable. Raw scores were obtained from all children and scores were converted to a normalized score based on each child's age at the time of enrollment to this study, with a standard score of 100. It should be noted that while TEMA-3 includes a very small number of nonverbal math problems (e.g., asking a child to reproduce a set of items to match based on number), the majority of the problems are symbolic and verbal in nature and none of the problems require nonverbal estimation or addition and subtraction of large values.

Reliability measures for the TEMA-3 are known to be relatively high ranging from 0.82 to 0.97 across different types of reliability coefficients, according to the examiner's manual. In addition to these published measures, our pre- to posttest design allowed a unique opportunity to assess the correlation between pre- and posttest TEMA measures across children within each training group, which serves as a proxy for a test-retest reliability measure. The correlation coefficients were r=0.85 and r=0.94 in the approximate-arithmetic group and the picture-memory group respectively (see Fig. 4), suggesting reasonably high reliability of the TEMA scores.

Figure 4.

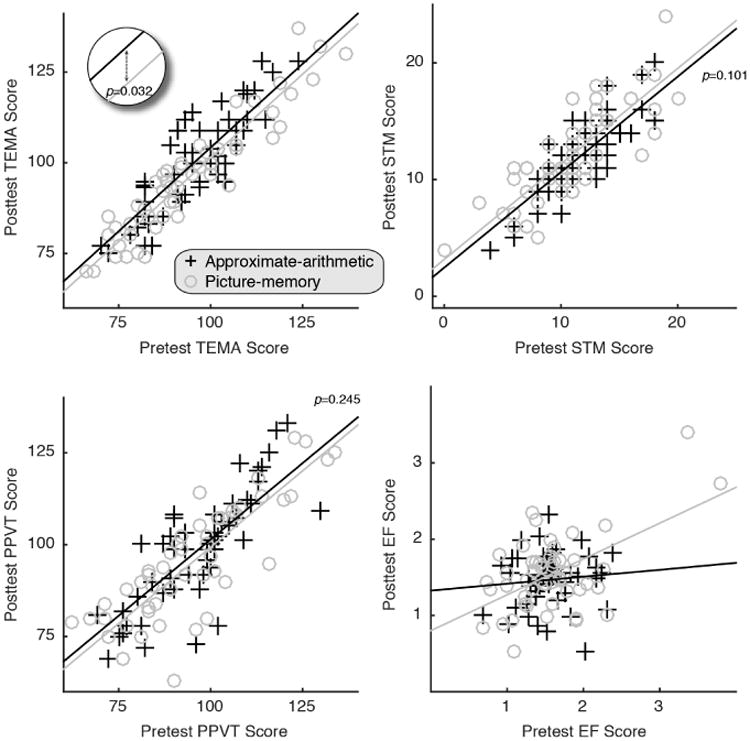
Results of the ANCOVA/regression-based approach to assess the treatment effects in TEMA, PPVT, STM, and EF measures.

Vocabulary assessment

Children's receptive vocabulary was assessed using the Fourth Edition of the Peabody Picture Vocabulary Test (PPVT-4; Dunn & Dunn, 1997). The test is designed for children as young as 2.5 years old. On each trial, the experimenter presented four pictures, spoke one word, and asked the child to select which of the pictures that word described. For Spanish-speaking students, the word was spoken in both English and Spanish. Raw scores were obtained from all children and converted to a normalized scale with a standard score of 100, based on each child's age at the time of enrollment in this study.

Published reliability measures of PPVT are very high ranging from 0.88 to 0.95 across different types of reliability coefficients, according to the examiner's manual. As in the case of TEMA, we assessed the correlation between pre- and posttest PPVT measures across children within each training group in order to get a rough estimate of the reliability of the measures in our sample. The correlation coefficients were r=0.80 and r=0.83 for the approximate-arithmetic group and the picture-memory group respectively, also suggesting a reasonable reliability of the PPVT scores (see Fig. 4).

Short-term memory assessment

A letter-span task was used to assess children's verbal short-term memory (STM). On each trial, the experimenter asked the child to repeat a string of letters in the correct order. Children were tested with up to 6 different string-lengths starting with 2-item sequences and progressively increasing up to 7-item sequences. Children were given a total of 5 trials at each string length, and the testing was terminated when the participant erred on 3 or more of the 5 trials. Only 13 letters of the alphabet were used, and different letters for Spanish and English speakers were used to ensure that all letters were monosyllabic. Similar sounding letters such as M & N, D & B, or P & T in English were excluded. Total number of correctly repeated strings was used as the final dependent measure. The correlation between pre- and posttest STM measures across children within each training group were r=0.83 and r=0.82 in the approximate-arithmetic group and the picture-memory group, respectively, indicating reasonable reliability (see Fig. 4).

Stroop interference test

A measure of children's executive function (EF) was constructed from two tasks: Stroop interference test and a card sorting test. First, a variant of the Stroop-like “day-night” task (Gerstadt, Hong, & Diamond, 1994) was used to probe inhibitory control, a component of executive function. “Day-night” was replaced with “red-blue” because pilot testing on an independent group of preschoolers revealed that children often responded inconsistently to the original images (e.g., by saying “moon” in place of “night”). This test consisted of 16 congruent and 16 incongruent trials. For children who did not know the color names (6 children), we conducted the same Stroop interference task with “cat and dog” instead of “red and blue.”

On congruent trials the experimenter presented a red or blue square (alternatively a cat or a dog) and the child was asked to label the card as red or blue (alternatively, cat or dog). Children were required to answer correctly on four practice trials before starting the 16 congruent trials successively. Children were then told that they would play a “silly version” of the game, the incongruent trials, in which they would name the opposite of each card—for example, say “red” for a blue card. Children practiced this silly version until they correctly answered four practice trials, and were then given 16 incongruent trials successively.

An audio recording was made for later analysis of accuracy and reaction time. The experimenter said the word “go” every time a card was turned over in order to mark the moment each card became visible to the child. Reaction time for each trial was measured from the beginning of the experimenter's word “go” to the beginning of the child's response. Self-correction was ignored and only the first response was evaluated (e.g., “red… no, blue” to a red card in the opposite trial would be marked as incorrect). Two card orders were created so that children received different versions for pre- and posttests. The order of the versions administered was counterbalanced across participants.

Performance was assessed by a composite score in which the number of correct responses on incongruent trials was divided by the number of correct responses on congruent trials. A composite score of 1 represents equal performance between the congruent and the incongruent trials. Composite scores less than 1 represent a decrement in performance in the incongruent trials. A second analysis incorporated reaction time. The number of correctly responded incongruent trials was divided by the median reaction time of all the incongruent trials, and the same measure was computed from the congruent trials. The ratio between the two measures served as the composite score. The overall results from this analysis were qualitatively identical to the original analysis (i.e., gain score difference between the two experimental groups did not show a reliable difference, t(97)=-0.373, p=0.710), and therefore we report the results from the original analysis.

Unlike the other pre- and posttest measures described so far, this measure yielded poor reliability. To be specific, the correlation coefficients between pre- and posttest measures were r=-0.08 and r=0.56 in the approximate-arithmetic group and the picture-memory group, respectively (see Fig. 4).

Card sorting test

A variant of the Standard Dimensional Change Card Sort task (Zelazo, Frye, & Rapus, 1996) was used to probe executive function. Two versions (Version A with bird/fish and Version B with plane/ship) were created to avoid administering the same task for both pretest and post-test, and the order of the versions was counterbalanced across participants. Each version consisted of a set of 10 cards that could be sorted according to two rules: color (rule 1: white/black) and shape (rule 2: bird/fish or plane/ship, depending on the version). In Version A, there were 5 white cards and 5 black cards, which could be divided into 6 bird cards and 4 fish cards. In Version B, there were 6 white cards and 4 black cards, which could be divided into 5 planes and 5 ships.

Two boxes were labeled with a target card (e.g., one box with a white bird and one box with a black fish) that had to be matched according to the rule of each trial (e.g., color for rule 1). Children first watched the experimenter sort 3 cards into boxes according to rule 1 (color) and then were asked to sort 10 additional cards as quickly as possible. The experimenter then demonstrated sorting 3 cards according to rule 2 (shape) and asked to sort the same 10 cards according to the new rule. Accuracy and time spent to complete each trial were recorded.

A composite score was computed by dividing the number of correctly sorted cards according to rule 2 by the number of correctly sorted cards according to rule 1. The gain scores (posttest composite score minus pretest composite score) in this test resulted in a large variation, indicating potential outliers. Accordingly, we removed extreme outliers that were 2.5 times the interquartile range from the first and the third quartiles. This procedure resulted in five outliers, one from the approximate-arithmetic group and four from the picture-memory group. We performed a second analysis taking the total time spent sorting into account (by dividing the number of correctly sorted cards by the total time spent in each rule), and the results did not differ qualitatively from our initial analysis (i.e., gain score difference between the two experimental groups did not show a reliable difference, t(99)=-0.214, p=0.831).

Similar to the Stroop interference test, the card-sorting test also yielded poor reliability. The correlation coefficients between pre- and posttest measures were r=0.11 and r=0.39 for the approximate-arithmetic group and the picture-memory group, respectively (see Fig. 4). A summarized measure of EF, the sum of Stroop interference and card sorting scores, did not improve the reliability by much (r=0.10 and r=0.51). Note that questionable reliability in the EF tasks makes it difficult to interpret any changes from pre to post test as a function of training.

Results

We first report the performance progression in the two experimental games. Children who played the approximate-arithmetic game showed consistent decrease in the log-difference level (Figure 2A), as indicated by a negative slope of the linear fit for each individual child's log-difference level (t(50)=-20.391, p<0.001). This monotonic decrease in the log-difference level could reflect the progression of the threshold of the adaptive staircase procedure used in this game rather than children's improved performance in approximate arithmetic (Lindskog & Winman, 2016). To test whether there is direct evidence for performance improvement in this adaptive training design, we adopted a novel analytic technique that quantified the trend in accuracy under comparable difficulty levels across time (Park & Brannon, 2016). In each participant, the accuracy measure from the median log-difference level (from 45^th to 55^th percentile) across all blocks was regressed on time (session). The slope of this regression model was non-significantly positive (slope=0.0183, t(11)=0.673, p=0.515), suggesting that there is no direct evidence for improvement in approximate arithmetic performance over the training sessions. However, as elaborated in Park & Brannon (2016), the treatment effect of cognitive training does not hinge upon evidence of observable performance improvement in the training task because the effect of treatment is through improvement, facilitation, strengthening, or growth of the unobservable cognitive element that drives the transfer of skills between training and test tasks. Children who received the picture-memory game showed significant reduction in time to completion (Figure 2B), particularly in more difficult conditions perhaps due to a floor effect in the easiest condition (Level 3: linear effect, t(51)=-1.593, p=0.117; Level 4: linear effect, t(49)=-2.719, p=0.009; Level 5: linear effect, t(32)=-3.905, p<0.001). Overall, results from both of these training tasks suggest that young children were capable of performing the tasks consistently over the course of the experiment.

Figure 2.

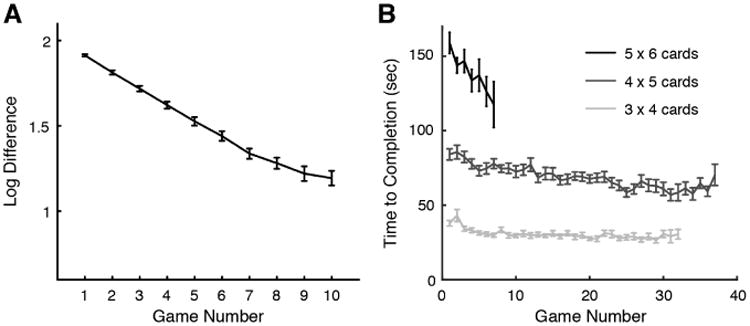
Progression of the dependent measure over the course of training on the approximate-arithmetic group (A) and the picture-memory game (B). A Game represents one set of 40 trials in the approximate-arithmetic game, and the corresponding log-difference values indicate the log₂-difference value at the end of each Game. A Game in the picture-memory game represents one round of n-by-n card game. Error bars represent the standard error of the mean.

The critical analyses central to our research question were the comparisons of the pre- to posttest scores on the TEMA, PPVT, STM, and EF assessments in the two experimental groups. In Table 1, we report the pre- and posttest scores along with subject demographics in each group. Our pseudorandom group assignment assured that there was little difference in the TEMA (t(101)=0.311, p=0.756) and PPVT (t(101)=0.508, p=0.613) pretest scores between the two groups. Pretest scores in short-term memory (STM) (t(101)=1.289, p=0.200), Stroop interference (t(97)=-0.647, p=0.519), and card sorting (t(99)=0.184, p=0.854) also showed few group differences.

Table 1.

Mean (standard deviation) pre- and posttest scores sorted by the two training groups.

	Age (years)	Sex (# Boys)	TEMA		PPVT		STM		Stroop Interference		Card Sorting
			Pre	Post	Pre	Post	Pre	Post	Pre	Post	Pre	Post
Approximate-arithmetic group (N=51)	4.9 (0.4)	26	95.5 (12.1)	100.1 (14.1)	96.6 (13.6)	98.6 (15.4)	11.8 (3.2)	12.1 (3.3)	0.60 (0.23)	0.64 (0.24)	0.95 (0.36)	0.83 (0.28)
Picture-memory group (N=52)	4.9 (0.4)	27	94.6 (17.2)	96.4 (16.3)	95.1 (16.8)	95.2 (15.9)	10.8 (4.3)	12.0 (4.2)	0.63 (0.23)	0.69 (0.23)	0.94 (0.42)	0.83 (0.36)

The effects of approximate-arithmetic and picture-memory training on pre- to posttest changes were evaluated first using the gain score approach then using the ANCOVA/regression-based approach.

Standardized gain scores were computed by taking the difference between each of the post- and pretest measures and dividing this value by the standard deviation of the pretest measures. The gain scores for the two training groups were compared using two-sample t-tests (Figure 3). Among all the pre- and posttest measures, TEMA gain scores were found to be significantly greater in the approximate-arithmetic group (gain score of 4.549) compared to the picture-memory group (gain score of 1.789) (Cohen's d=0.414 computed with a pooled standard deviation of 6.670, t(101)=2.100, p=0.038), and STM gain scores were found to be significantly greater in the picture-memory group compared to the approximate-arithmetic group (t(101)=-1.990, p=0.049). There were no group differences in the gain scores in the PPVT (t(101)=0.991, p=0.324) or in the EF measures (t(95)=-0.477, p=0.635).

Figure 3.

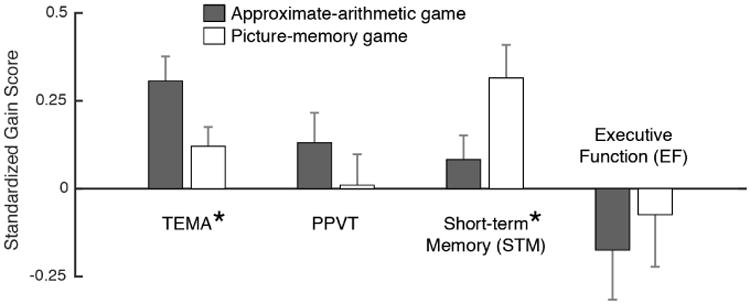
The mean standardized gain scores of multiple assessments. Error bars indicate the standard error of the mean. * p < 0.05.

While the gain score results (Figure 3) provide a preliminary view on the effects of cognitive training (i.e., treatment) on pre- to posttest change, particularly in TEMA and STM, gain score approach is not without its weaknesses—for example, it does not adequately take into consideration potential individual differences in the pretest scores and is likely to have large statistical noise especially if the measures are not reliable. Thus, an ANCOVA/regression-based approach was performed in which posttest scores were predicted by categorical group membership (approximate-arithmetic versus picture-memory) with the pretest scores entered as a covariate. The interaction between group and pretest was initially modeled but was then dropped if it did not reach significance at p<0.1. Note that, in such cases, the beta estimate associated with group membership represents the point estimate of the treatment effects if divided by 15, which is the assumed population standard deviation of the normed TEMA and PPVT scores. The interaction was dropped in the model for TEMA, PPVT, and STM, while it was retained in the model for EF.

There was a significant treatment effect in TEMA scores (β=2.83, η_p²=0.045, F(1,100)=4.73, p=0.032) (Figure 4). This pattern held when only the blind-tested children were analyzed (β=7.40, η_p²=0.283, F(1,14)=5.54, p=0.034). More central to the aim of this study, we performed the same analysis only with children from low-income families. In these children, TEMA scores improved from 93.3 to 98.7 in the approximate-arithmetic group and from 93.2 to 95.5 in the picture-memory group, which resulted in a significant treatment effect, with somewhat larger effects size than when all children were included (β=3.21, η_p²=0.056, F(1,76)=4.49, p=0.037). We also performed the same analysis separately on younger and older age groups split by the median age (4.9 years). There was a significant treatment effect in younger children (β=4.09, η_p²=0.091, F(1,48)=4.83, p=0.033) but not in older children (β=1.22, η_p²=0.010, F(1,48)=0.49, p=0.485). Finally, the treatment effect on TEMA remained significant when all the pretest measure (PPVT, STM, and EF) scores were included as covariates (β=2.70, t(92)=2.02, p=0.046).

The same ANCOVA/regression-based approach was performed in PPVT and STM scores (Figure 4). The treatment effect in PPVT was not significant although the effect size in terms of beta coefficient was moderate (β=2.11, η_p²=0.013, F(1,100)=1.37, p=0.245). The treatment effects in STM was not significant unlike the gain score results (β=-0.70, η_p²=0.027, F(1,100)=2.73, p=0.101), which suggests that significant group differences in the STM gain scores was perhaps due to added noise and/or idiosyncratic individual differences in the pretest measures. There were no treatment effects on EF scores (β=-0.07, η_p²=0.007, F(1,94)=0.66, p=0.419) while the interaction was significant (β=0.38, t(93)=2.09, p=0.040). Collective, the ANCOVA/regression-based results (as well as the gain score results) indicate that playing the approximate-arithmetic group game compared to playing the picture-memory game selectively improved TEMA scores, and no other measures showed a significant improvement.

One unexpected finding was that the approximate-arithmetic game appeared to yield a non-significant but small benefit in PPVT performance (β=2.11). In the approximate-arithmetic game the objects are repeatedly named on each trial (e.g., “Look, some donkeys are going in to the box” and “More donkeys are going in to the box”). In contrast, there was no verbal labeling of the items in the picture-memory game. Repeated labeling of object identity in the verbal instructions of the approximate arithmetic game, therefore, may have enhanced children's name labeling skills which is central to PPVT. At a more concrete level we also considered the possibility that items labeled in the approximate-arithmetic game were actually tested in the PPVT. For instance, a child who initially does not know what a donkey is may have learned what it looks like and what it is called by playing the approximate-arithmetic game, thereby resulting in improved PPVT score when the child is asked to find a “donkey” at posttest. In fact, there were five words on each of the two PPVT versions that appeared in the approximate-arithmetic game. An important question is, then, to what extent these five words contributed to the PPVT scores. We used the following approach to quantify this contribution. First, the contribution of the five words (that appeared in the approximate-arithmetic game) in each child's posttest PPVT score was computed by taking the total number of words tested and got correct (0-5) ¹ divided by his/her raw PPVT score. Across children, this value (let's call it k) ranged from 0 to 0.1739 with a median of 0.0147. Then, each child's normed posttest PPVT score was adjusted to remove the contribution of those words by multiplying 1–k to the posttest score. Finally, an ANCOVA was used to test the treatment effect of experimental group on this adjusted posttest score with the pretest score as a covariate. The treatment effect was smaller in effect size (β=2.01, η_p²=0.009, F(1,100)=0.936, p=0.336) than the treatment effect of the original analysis without removing the contribution of the five words (β=2.11, η_p²=0.013, F(1,100)=1.37, p=0.245). These results are consistent with the idea that verbal labeling in the approximate-arithmetic game may have influenced the posttest PPVT scores more positively than in the picture-memory game.

One may wonder whether there exist any ANS-based problems in TEMA and that improved TEMA after approximate arithmetic training may have been driven by improvement solely in those ANS-based problems. It should be noted that almost all the TEMA problems are symbolic (i.e., language-based) as they involve counting, enumeration, and numerals, and only one problem (“Perception of More,” which is akin to a non-symbolic numerosity comparison task) is potentially ANS-based. Thus, it is unlikely that the main treatment effect in TEMA is driven by that single problem. We nevertheless provide an empirical support to this argument as follows. Given that the TEMA is a heterogeneous assay of number knowledge we quantified itemized gain scores for each participant for each item, and computed the mean gain scores for each problem item (from problem number 1 to problem number 32) across all children in the approximate-arithmetic group². Following the primary finding, these gain scores were significantly different from zero (t(31)=5.503, p<0.001, d=0.949). The same analysis done in the picture-memory group resulted in a significant gain score but with much smaller effect size (t(31)=2.078, p=0.046, d=0.358). Indeed, the itemized gain scores were greater in the approximate-arithmetic group than in the picture-memory group (t(31)=2.497, p=0.018). Now, this statistic was computed again after excluding the gain score from that one ANS-based problem, and the gain score remained highly significant in the approximate-arithmetic group (t(30)=5.452, p<0.001, d=0.955). The same analysis performed in the picture-memory group again resulted in much smaller effect size (t(30)=1.944, p=0.061, d=0.340), which was comparatively smaller than the effect of approximate-arithmetic group (t(30)=2.580, p=0.015).

Discussion

Although humans are uniquely capable of symbolic mathematics, we share with other animals an intuitive ability to estimate, compare, and manipulate large numbers of items without counting that is present in human infancy before symbolic math skills are acquired (Dehaene, 1999). A growing body of research suggests that the preverbal number sense that supports approximate non-symbolic number representations is fundamentally related to full-fledged math abilities, particularly in children (Fazio, Bailey, Thompson, & Siegler, 2014; Gilmore et al., 2010; Halberda et al., 2008; Libertus et al., 2011; Mazzocco et al., 2011). However, the nature of this relationship and its developmental trajectory are being queried by many research groups and proposals have been made that attribute the correlation between ANS and math to tertiary mediating factors. Thus, research approaches that directly test the causal relationship between them are sorely needed. To that end, our previous studies demonstrated that repeated training on approximate arithmetic, one form of intuitive number sense, improves mental arithmetic skills in adults (Park & Brannon, 2013, 2014). Importantly, similar training tasks designed to enhance approximate comparison or matching, visuo-spatial short-term memory, or a numeral order judgment did not show such an effect (Park & Brannon, 2014). From these previous findings, we proposed that numerical quantity manipulation in the mental workspace may be a common cognitive denominator to both non-symbolic approximate arithmetic and (symbolic) mental arithmetic, and that facilitation of this common denominator via approximate arithmetic training may drive effective cognitive processing for solving mental arithmetic problems (Park & Brannon, 2014).

The goal of the present study was to test the effectiveness of approximate arithmetic training in young children with minimal knowledge in math. Testing such an effect in young children is critical for both theoretical and practical reasons. Theoretically, it allows more in-depth assessment of the causal link between approximate arithmetic and acquired mathematical skills. Because these young children have yet to receive formal math education, especially symbolic addition and subtraction, and also because TEMA largely tests elementary concepts of number and counting at this age, finding a positive relationship between approximate arithmetic training and TEMA improvement would suggest a deeper connection between approximate arithmetic training and math performance. Practically, approximate arithmetic training could benefit children with minimal background in math, in many cases from low-income families, allowing them to catch up with their math skills as early as possible.

The results of the present study demonstrate that repeated training in nonverbal quantity manipulation yields selective improvements in math ability in preschool children. The TEMA measures young children's formal and informal math abilities broadly including numeral literacy, number facts, enumeration, and counting. Our analyses suggest that the effect of approximate arithmetic training was not selective to a particular type of early math problem—in particular, mental arithmetic—and instead suggest that there is a deep cognitive overlap between nonverbal quantity manipulation and learned math in general. Future research could attempt to isolate the mechanism by which approximate arithmetic training benefits learned mathematics by more systematically sampling different types of math skills pre and post approximate arithmetic training.

An important question is whether the current results can be explained by placebo effects whereby participants in the approximate-arithmetic group training group expected to improve in mathematics (e.g., see Boot, Simons, Stothart, & Stutts, 2013). While the present study did not specifically test for a placebo effect, our previous work with adult participants makes that interpretation unlikely. Specifically, adults trained with a) an approximate number comparison and approximate numerical matching task or b) a numeral ordering task, showed negligible benefits in math improvement (Park & Brannon, 2013, 2014). In fact, a recent study directly probed whether children's expectations about their own subsequent symbolic arithmetic performance differed as a function of different types of cognitive training tasks. The study reports that six- to eight-year-old children did not show differences in their expectation between training that involved non-symbolic numerical quantity and training that did not involve numerical quantity (Dillon, Pires, Hyde, & Spelke, 2015).

While our study provides an important first step that suggests targeting approximate arithmetic in preschoolers could be an effective tool for improving math readiness, an important caveat is that assessing the feasibility and effectiveness of approximate arithmetic training in educational settings will require a much larger scale study with complete random assignment and experimenter-blind testing. Future research should compare approximate arithmetic training to other conditions that receive other types of math training designed to directly improve the targeted skills (e.g., teaching concepts and knowledge covered in TEMA to improve TEMA). Similarly, future research should assess whether there are dose-dependent effects of the training and the longevity of the benefits for math. Finally, another important caveat to early educational interventions in general is that the effectiveness of such interventions diminishes over time, potentially suggesting that later academic success is primarily driven by stable underlying characteristics related to learning (e.g., domain-general cognitive abilities, motivation, socioeconomic status) rather than by prior knowledge (Bailey, Watts, Littlefield, & Geary, 2014). Thus, from a practical point of view, an important future goal is to find ways not only to boost mathematical knowledge and skills but also to positively influence other latent sources of learning.

In sum, these findings provide additional evidence for a causal link between approximate non-symbolic numerical abilities and learned mathematics and may hold important practical implications for math education in pre-school aged children. Most existing research-based math intervention programs for early childhood focus directly on the skills that are targets for improvements (e.g., providing counting activities to improve counting abilities, but see Siegler & Ramani, 2009) (for review see Clements & Sarama, 2011). While these existing approaches are very valuable, our approach suggests that including training that taps deeper cognitive links may open new promising avenues for math intervention. In particular, a major advantage of approximate arithmetic training is that it can be used with very young children before they have mastered the meaning of number words and symbols, thus providing opportunities to develop maximally effective ways of closing the achievement gap before kindergarten.

Highlights.

• Preschoolers underwent a pre- and posttest cognitive training experiment.

• Experimental group children played a non-symbolic approximate arithmetic game.

• Control group children played a picture memory game.

• Symbolic math and other cognitive skills were assessed before and after the games.

• Experimental, compared to control, group selectively improved in symbolic math.