Comparative Analysis of Transcription Start Sites Using Mutual Information

Abstract

The transcription start site (TSS) region shows greater variability compared with other promoter elements. We are interested to search for its variability by using information content as a measure. We note in this study that the variability is significant in the block of 5 nucleotides (nt) surrounding the TSS region compared with the block of 15 nt. This suggests that the actual region that may be involved is in the range of 5–10 nt in size. For Escherichia coli, we note that the information content from dinucleotide substitution matrices clearly shows a better discrimination, suggesting the presence of some correlations. However, for human this effect is much less, and for mouse it is practically absent. We can conclude that the presence of short-range correlations within the TSS region is species-dependent and is not universal. We further observe that there are other variable regions in the mitochondrial control element apart from TSS. It is also noted that effective comparisons can only be made on blocks, while single nucleotide comparisons do not give us any detectable signals.

Introduction

The clustered bacterial genes (operons) that encode proteins are necessary to perform coordinated functions, such as biosynthesis of amino acids. The RNA transcribed from prokaryotic operons is polycistronic. There are a number of key features to the promoter region that give it the ability to provide a signal for transcription initiation. Two signal regions are located approximately 10 bp or 32 bp upstream of the transcription start site (TSS). Each sequence of the two regions consists of 6 bp. For an ideal promoter, the sequence is TTGACA for the –35 region and TATAAT for the –10 region. In prokaryotes, all three RNA classes (mRNA, tRNA, and rRNA) are synthesized by a single polymerase that consists of 2α, 1β, 1β′ subunits and a σ factor. However, in eukaryotes the non-coding sequences that do not code for proteins make up a major part of the genome. Protein coding genes contain exons, introns, and promoters. Specific DNA sequence regions within the promoter region (like TATA-box, CCAAT-box, and GC-box) exhibit similarities in both prokaryotes and eukaryotes. The core promoter region (which can extend ~35 bp upstream from TSS) usually has the TATA-box (30%–50% of promoters) and the TSS region that are not conserved. Each of these core promoter elements is found in some but not in all core promoters. Therefore, it appears that there are no universal core promoters. Eukaryotic system uses three different RNA polymerases, I, II, and III. In eukaryotes, RNA polymerase-II is involved in mRNA synthesis. A reliable identification of the core promoter region by RNA polymerase-II prior to transcription initiation is mandatory for the proper initiation and regulation of mRNA synthesis (1). Accurate and efficient transcription from the core promoter requires the polymerase along with general transcription factors (TFIIA, TFIIB, TFIID, TFIIF, and TFIIH).

In the mitochondrial genome, the presence of rRNA, tRNA, and protein coding genes do not leave any space for promoters comparable to those found in eukaryotic nuclear or bacterial genomes. The transcription is carried out all around the circle, and a polycistronic RNA is produced (2). The primary transcript is cleaved afterwards, releasing individual rRNA, tRNA, and mRNA. The mitochondrial DNA (mtDNA) molecule encodes 37 genes for 2 rRNAs, 22 tRNAs, and 13 polypeptides. All of these 13 polypeptides are components of the oxidative phosphorylation system (3). Initiation of transcription at mitochondrial promoters in mammalian cells requires the simultaneous presence of a monomeric mitochondrial RNA polymerase, mitochondrial transcription factor A, and either transcription factor B1 or B2. The mtDNA strands are classified as heavy (H) or light (L) based on the GC content of each strand. The non-coding region (control region/D-loop) of approximately 1.1 kb is located between the tRNA^Phe and tRNA^Pro genes. This region contains the origin of replication for the heavy strand (O_H), the transcription promoters (light and heavy strand promoters, LSP and HSP, respectively), and other regulatory elements for the mtDNA expression. The length of the mtDNA control region varies a lot among animal taxa. In vertebrates it ranges from 200 bp to nearly 4,000 bp. Sometimes there are tandem repeats in the D-loop (most commonly at the beginning/end). In some cases there are also other structures (such as stem loop) that can increase the size. The human mitochondrial genome gives three different RNA transcripts from three different points (H₁, H₂, and L) (4). The most frequently used point of TSS is H₁, which is located 16 nucleotides (nt) upstream of the tRNA^Phe gene. Replication of mammalian mtDNA is linked with and dependent on mitochondrial transcription.

The identification of promoter elements in DNA by computational methods directly depends on the statistical analysis of consensus sequences as overrepresented regions. But in the case of TSS, the region is not overrepresented by any consensus sequences. One way of tackling such problem is to analyze the sequence carefully using scores in the substitution matrices, which can identify patterns that are not clearly visible. The elements of these substitution matrices are explicitly calculated from the target and expected frequencies of aligned nucleotides. The information in these matrices depends on quantification approaches like evolutionary models, structural properties, and chemical properties of aligned sequences. There are several well-known substitution matrices used in the scoring algorithms, including Point Accepted Mutation (PAM; ref. 5., 6.), BLOck SUbstitution Matrix (BLOSUM; ref. 7), Gonnet matrix (8), and DNA identity matrix. In the present study, we considered both neighbor-independent and neighbor-dependent nucleotide substitutions in our computations. Neighbor-independent and neighbor-dependent substitution matrices have been used to describe the non-coding sequences 9., 10. like core promoter regions (11) and transcription factor binding sites 12., 13., 14.. There are several attempts to study TSS with the help of nucleotide frequencies 15., 16. and the DNA weight matrix methods 17., 18., but it is poorly understood due to the lack of proper signals in TSS. Mutual information has been used to identify the co-evolving functional residues in protein sequences (19) and the gene mapping of complex diseases in population based case-control studies (20). Along with the Fourier technique, mutual information is used to identify homologous DNA sequences (21). Information content of whole genomes has been studied against random sequences, and it shows that complete genomes have much greater information content than that in random sequences (22). In the present study, we analyzed the promoters and mitochondrial control regions of human, mouse, and Escherichia coli by calculating the information content of the TSS regions.

Information theory

The concept of entropy is very important in information theory. It is characterized by the quantity of a random process’s uncertainty. If the entropy of the source is less than the capacity of the channel, then the asymptotically error free communication can be achieved (23). The entropy of a discrete random variable X with a probability mass function p(x) is defined by:

$$H(X)=-{\sum }_{x}p(x){\log }_{2}p(x)$$

The joint entropy of two discrete random variables X and Y with probability mass functions p(x) and p(y), respectively, is defined by:

$$H(X,Y)=-{\sum }_{x,y}p(x,y){\log }_{2}p(x,y)$$

Conditional entropy H(X|Y) is the entropy of a random variable X, given another random variable Y, which is defined by:

$$H(X|Y)=-{\sum }_{x,y}p(x,y){\log }_{2}p(x|y)$$

These entropies have the following relationship:

$$\begin{array}{l}H(X|Y)=H(X,Y)-H(Y)\\ H(X,Y)=H(Y,X)\\ H(X|Y)\ne H(Y|X)\end{array}$$

[equality is obtained if and only if H(X) = H(Y)]

The relative entropy D(p||q) is a measure of the distance between two distributions. The relative entropy (or Kullback Leibler distance) between two probability mass functions p(x) and q(x) is defined as $D(p\parallel q)=\sum p(x){\log }_2\frac{p(x)}{q(x)}$. The relative entropy is always non-negative and is zero if and only if p = q. However, it is not a true distance between distributions since it is not symmetric and does not satisfy the triangle inequality (24).

The reduction in uncertainty X due to the knowledge of random variable Y is called the mutual information. For two random variables X and Υ, this reduction is:

$$\begin{array}{l}I(X;Y)=H(X)-H(X|Y)\\ I(X;Y)=H(Y)-H(Y|X)\\ I(X;Y)=H(X)+H(Y)-H(X,Y)\\ I(X;Y)={\sum }_{x,y}p(x,y){\log }_2\frac{p(x,y)}{p(x)p(y)}\end{array}$$

where p(x, y) is the joint probability mass function, p(x) and p(y) are marginal probability mass functions of x and y, respectively, and I(X; Y) is a measure of the dependence between the two random variables. It is symmetric in X and Y and is always non-negative.

Results

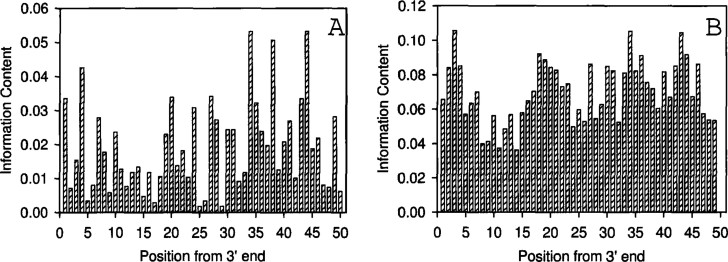
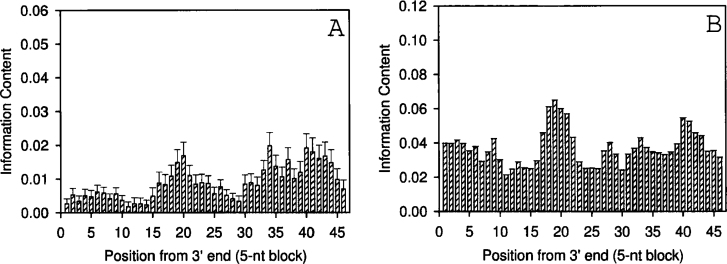
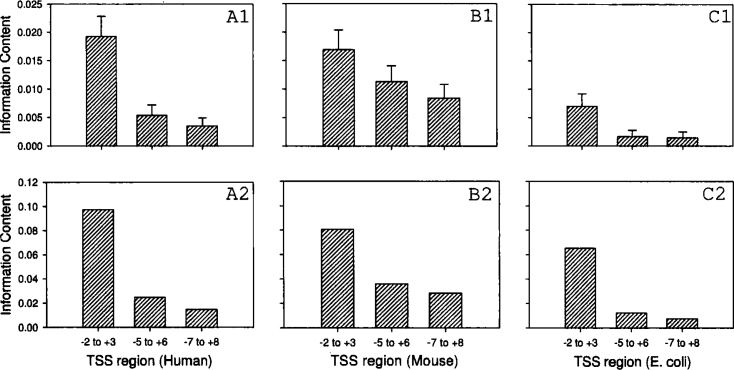
We constructed substitution matrices with mono and dinucleotide substitutions using multiple aligned TSS regions of human, mouse, and E. coli, as well as the mitochondrial control element, and calculated the average mutual information content (in bits). The information content of the mitochondrial genome near the control element as a function of the position is shown in Figure 1. In Figure 1A, the information content is computed based on a neighbor-independent substitution (4×4) matrix, while in Figure 1B a neighbor-dependent substitution (16×16) matrix is used. The average information content of the mitochondrial genome near the control element is computed as a 5-nt overlapping block (Figure 2). The 240 sequences used here are from the 3′ end of the control element, which contains the potential promoter region. The information content of the TSS regions of human, mouse, and E. coli as a function of the block size is shown in Figure 3. Histograms shown in A1, B1, and C1 (top row; for human, mouse, and E. coli, respectively) represent the information content determined by using the neighbor-independent substitution matrix. Similarly, A2, B2, and C2 (bottom row; for human, mouse, and E. coli, respectively) represent the information content by using the neighbor-dependent substitution matrix. In each graph the bars represent the information content for blocks of 5 (–2 to +3), 11 (−5 to +6), and 15 (−7 to +8) nt, respectively. The positions are with reference to TSS that represents +1. The standard errors are plotted in Fig. 2, Fig. 3 (but the error bars for the 16×16 matrices cannot be seen as they are too small, since there are 256 data points on which the variance and standard errors are computed).

Fig. 1.

The information content of the mitochondrial genome near the control element as a function of the position. A. Computation by using the neighbor-independent substitution (4×4) matrix. B. Computation by using the neighbor-dependent substitution (16×16) matrix. The 240 sequences used here are from the 3’ end of the control element, which contains the potential promoter region.

Fig. 2.

The information content of the mitochondrial genome near the control element computed as an average for a 5-nt overlapping block. A. Computation by using the neighbor-independent substitution (4×4) matrix. B. Computation by using the neighbor-dependent substitution (16×16) matrix. The 240 sequences used here are from the 3’ end of the control element, which contains the potential promoter region. The error bars in Panel Β are too small to be seen in the plot.

Fig. 3.

The average information content of the TSS regions of human, mouse, and E. coli as a function of the block size. Histograms shown in A1, B1, and C1 (top row) represent the information content determined by using the neighbor-independent matrix. Similarly, A2, B2, and C2 (bottom row) represent the information content by using the neighbor-dependent matrix. In each graph the bars represent the information content for blocks of 5 (–2 to +3), 11 (–5 to +6), and 15 (–7 to +8) nt, respectively. The positions are with reference to TSS that represents +1. The error bars in A2, B2, and C2 are too small to be seen in the plot.

Discussion

Analysis of transcriptional regulatory regions in DNA is very important to understand the mechanisms governing gene expression and its regulation. It is well known that the TSS region shows greater variability compared with the other promoter elements, and we are interested to search these variable regions by using information content. In this study we observed that the variability is significant in the 5-nt block surrounding the TSS region, but with a greater block size (for example, 15 nt) the variability is not significant. This suggests that the actual region that may be involved is in the range of 5–10 nt in size, which is apparent from the histograms in Figure 3. We are also interested to find out whether there are any short-range correlations within the nucleotides in the TSS region. For E. coli, we observed that the information content decreases significantly as we go from a block size of 5 to 11 to 15 nt (Figure 3C). We consider this significant as the information content is logarithmically related to the probability. Comparatively speaking, for human this effect is much less (Figure 3A), and for mouse it is practically absent (Figure 3B), because although the information content for human and mouse decreases, the contents for block sizes of 11 and 15 nt are still significant (suggesting considerable randomness). This fact decreases the discrimination power of the information content as a tool to identify the TSS region. However, the numbers presented here must be treated as a trend rather than absolute quantities. We can perhaps safely conclude that the presence of short-range correlations within the TSS region is species-dependent and is not universal. We must, however, note that we have considered only three species and further studies need to be conducted to establish any clear conclusions in this regard.

We further note that there are other variable regions in the mitochondrial control element apart from TSS. In Figure 2, a prominent peak appears around 17–22 nt (for both dependent and independent cases), but a similar peak is also found near 38–43 nt, which is known not containing TSS. However, this region may also be as interesting as other important variable regions. Effective comparisons can only be made on blocks, while single nucleotide comparisons (Figure 1) do not give us any detectable signals. The high recombination rate in the mitochondrial control region may not alter the overall nature of the TSS region. These results imply a similar regulatory structure in almost all organisms that has been conserved during evolution due to functional constraints.

Finally, we know that there are well-established tools to locate conserved regions in DNA, but looking for variability is also important. We have found that information content may be useful to study the variable regions in genome in an efficient manner. For example, we can locate the TSS region (and other variable regions) by using this approach.

Materials and Methods

Sequence data

The promoter sequences of human (25), mouse (25), E. coli (26), and mitochondria (Entrez genome; http://www.ncbi.nlm.nih.gov/genome) were obtained from different databases (Table 1). The mitochondrial sequences here included are not more than 1,021 bp (excluding sequences that contain tandem repeats and stem loops). The sequences from the Eukaryotic Promoter Database (EPD) are representative sets of not closely related sequences.

Table 1.

The Number of Promoter Sequences from Corresponding Databases

Organism	No. of Sequences	Database
Human	1,789	EPD
Mouse	118	EPD
E. coli	472	PromEC
Mitochondria (chordate)	240	Entrez genome (NCBI)

Blocks of TSS

For our computational purposes, we divided the TSS regions of human, mouse, and E. coli into overlapping blocks of 5 (−2 to +3), 11 (−5 to +6), and 15 (−7 to +8) nt, respectively (with reference to TSS that represents +1). In the case of the mitochondrial genome, a sliding window of 5-nt block from the 3′ end of the control element was used.

DNA substitution matrices

For the meaningful comparison of DNA sequences, the information about the similarity of the bases must be derived in a contextual fashion. The coding regions and non-coding regions must be compared using a substitution matrix specifically designed for this purpose. A substitution matrix constructed for the coding regions may perform poorly for the non-coding sequences and vice versa. For this reason, we constructed a set of substitution matrices and calculated the average mutual information content of the TSS regions that are non-coding ones. The single nucleotide substitution matrix is a 4×4 matrix and lacks any neighbor preferences. In other words, adjacent bases are considered independent. In dinucleotide substitutions, two bases are taken together, which correspond to a nearest neighbor preference. As we are considering a pair, it forms a 16×16 matrix. These matrices include adjacent pair preferences explicitly. Mononucleotide substitutions in multiple aligned sequences give neighbor-independent nucleotide substitution matrices. The substitutions of nucleotides are calculated in each column of the block and the summed results of all columns are stored in a 4×4 matrix. The total number of nucleotide pairs [observed or target frequency, q(ij)] in a given block is [ws(s–1)]/2, and the total number of nucleotides [expected frequency, p(i)} in the block is ws, where s is the number of nucleotides in the given position and w is the block length. The resulting 4×4 matrix is used to calculate the “log-odds” and is given by $s(ij)={\log }_2\frac{q(ij)}{p(i)p(j)}$ 27., 28.. Dinucleotide substitutions in multiple sequence alignments give neighbor-dependent substitution matrices. The total number of dinucleotide pairs [observed or target frequency, q(ij, kl)] in a given block is [(w–1)s(s–1)]/2, and the total number of dinucleotides [expected frequency, p(ij)] is given by (w–1)s, where s is the number of sequences and w is the block length. The resulting 16×16 matrix is used to calculate the “log-odds” and is given by $s(ij,kl)={\log }_2\frac{q(ij,kl)}{p(ij)p(kl)}$.

Information content of DNA

Information content is calculated from the mono and dinucleotide substitution matrices of multiple aligned sequences. The average mutual information content (H) is the relative entropy of the target and background pair frequencies, and is used as a measure of the average amount of information (in bits) available per nucleotide pair (28). The average mutual information content in a given block of neighbor-independent and neighbor-dependent substitution matrices is given by $H={\sum }_{ij}q(ij)s(ij)$ and $H={\sum }_{(ij,kl)}q(ij,kl)s(ij,kl)$, respectively. We assessed the reliability of our computations by performing a simple error analysis of the results. That is, we considered the elements of the information content matrix H_ij[q(ij) s(ij)] as the elements of our data and computed the standard error of the 16 (or 256 in the case of pair preferences) elements using standard techniques. The standard errors are plotted in graphs along with the histograms.

Authors’ contributions

DAR carried out the programming and the analysis, and drafted the manuscript. CKM supervised the study and participated in its discussions. Both authors read and approved the final manuscript.

Competing interests

The authors have declared that no competing interests exist.