Abstract
Novel microarray technologies such as the AB1700 platform from Applied Biosystems promise significant increases in the signal dynamic range and a higher sensitivity for weakly expressed transcripts. We have compared a representative set of AB1700 data with a similarly representative Affymetrix HG-U133A dataset. The AB1700 design extends the signal dynamic detection range at the lower bound by one order of magnitude. The lognormal signal distribution profiles of these high-sensitivity data need to be represented by two independent distributions. The additional second distribution covers those transcripts that would have gone undetected using the Affymetrix technology. The signal-dependent variance distribution in the AB1700 data is a non-trivial function of signal intensity, describable using a composite function. The drastically different structure of these high-sensitivity transcriptome profiles requires adaptation or even redevelopment of the standard microarray analysis methods. Based on the statistical properties, we have derived a signal variance distribution model for AB1700 data that is necessary for such development. Interestingly, the dual lognormal distribution observed in the AB1700 data reflects two fundamentally different biologic mechanisms of transcription initiation.
Key words: transcriptome, microarray analysis, signal/variance distribution, distribution modeling, parameter approximation, stochastic transcription initiation
Introduction
Since its first appearance, microarray technology has seen constant improvements, especially with respect to transcript coverage. The sequencing of ever more genomes and high-throughput identification of transcripts and their variants have spurred this development. At present there exist two kinds of major complementary designs for gene expression microarrays, one is based on the use of partial or entire cDNA probes, the other is based on oligonucleotide probes. While both designs have their proper advantages and disadvantages, making their utility situation-dependent, the design of oligonucleotide arrays usually is less cumbersome and can be achieved from sequence knowledge alone. For most applications it seems that oligonucleotide arrays are thus more robust and more often used than cDNA arrays. Accordingly, a majority of commercial microarray platforms with high-genome coverage are based on oligonucleotide design. It is a known fact that the optimal oligonucleotide length for best sensitivity and specificity ratios in transcriptome studies is in the range of 60 mers 1., 2., 3.. However, due to historical reasons, high production costs, and accuracy issues, current oligonucleotide-based technologies (such as Affymetrix) use shorter probe sequences and rather rely on the use of multiple probes against a single transcript. Generally, current cDNA and oligonucleotide microarray technologies use fluorescence intensity measurements for quantification of spot intensities. Signal intensities thereby display simple lognormal distributions, which is in tune with theoretical biologic models.
Meanwhile, next-generation microarray technologies are being developed and starting to find applications in academic and private researches. Recently Applied Biosystems has released its AB1700 gene expression array platform (http://www.appliedbiosystems.com), which breaks the two customs mentioned above. AB1700 microarrays are 60-mer oligonucleotide arrays where chemiluminescence is used for sample detection. The manufacturer suggests that these novel design features in conjunction with advanced surface chemistry lead to a significant increase in sensitivity and accuracy of the transcriptome assays performed on the AB1700 platform. This view seems to be shared by researchers already using the technology (http://marketing.appliedbiosystems.com/iscience_v3/v1i3_discuss_foltz.asp) (4); however, to our knowledge, currently no systematic independent assessment is publicly available.
We hence report here on the systematic comparison of a representative set of fifty heterogeneous AB1700 Human Genome Survey (HGS) V1.0 arrays with a similarly representative set of fifty Affymetrix Human Genome U133A (HG-U133A) V2.0 arrays. We specifically investigated the signal dynamic range, sensitivity, signal distribution, and signal variance distribution for both datasets. We thereby achieved several observations with fundamental impact on data analysis and biologic interpretation.
Results and Discussion
Comparison of AB1700 and Affymetrix datasets
Signal dynamic range
In order to characterize the novel AB1700 platform and to analyze the general quality and properties of the microarray data generated using this system, we analyzed a collection of fifty individual and highly heterogeneous arrays generated on two different AB1700 machines (see Materials and Methods). The AB1700 data were processed by the AB1700 Expression Array System Software V1.1.1 (http://www.appliedbiosystems.com), and all the selected arrays individually passed all quality controls set forward by the AB1700 analysis software. Probes with set flags equal to or greater than 212 were removed from the dataset as suggested by the manufacturer.
We furthermore decided to directly compare the obtained characteristics of the AB1700 data with fifty individual and similarly heterogeneous Affymetrix HG-U133A arrays from two previous studies 2., 5.. First we thought to obtain an indication of the dynamic range for signals generated by both datasets. To this end, we calculated 98% and 95% signal intervals on logarithmic scale for the total 100 arrays, and then the average logarithmic signal range for each dataset, respectively [note that hereinafter “logarithm” will refer to the natural logarithm (ln) unless otherwise stated]. The results are summarized in Table 1, and the entire collected measures are contained in the Supporting Online Material (“00DynRange.pdf”). The reason for the restriction on 98% and 95% signal intervals is to circumvent the outliers biasing the measurement. Contending that both the Affymetrix and the AB1700 datasets are representative, we observed a signal range difference of 1.92 (6.28 vs. 8.20 for 98% signal interval) and 1.99 (5.20 vs. 7.19 for 95% signal interval) logarithmic units, respectively (Table 1). Thus on average the signal dynamic range of the AB1700 data is about two logarithmic units larger (corresponding to an increase by ∼34.5%) than that of the Affymetrix data. This result corresponds to roughly one order of magnitude on the absolute signal scale. We also performed these calculations for the AB1700 data with a signal-to-noise ratio S/N>3 (Table 1). This condition reduces the number of considered probes by roughly 48%; however, the estimated signal range still exceeds the one covered by the unfiltered Affymetrix data by 19% (note that S/N filtering cannot be achieved with the Affymetrix data in their published form). Therefore, it can be concluded that the AB1700 data provide a significantly extended (by ∼34.5%) signal dynamic range when compared with the Affymetrix data.
Table 1.
Dynamic Range Estimation and Comparison of Affymetrix and AB1700 Datasets
| Dataset | Averages over 98% signal interval |
Averages over 95% signal interval |
||||
|---|---|---|---|---|---|---|
| No. of probes | Signal range (ln) | Variance | No. of probes | Signal range (ln) | Variance | |
| Affymetrix HG-U133A 2.0 50× | 22,288 | 6.28 | 0.63 | 21,606 | 5.20 | 0.51 |
| AB1700 HGS 1.0 50× | 33,928 | 8.20 | 0.80 | 32,889 | 7.19 | 0.76 |
| AB1700 HGS 1.0 50× (S/N>3) | 17,718 | 7.18 | 0.79 | 17,176 | 6.45 | 0.85 |
Lognormal signal distribution
We next compared the signal distributions over the dynamic range for both datasets. Histograms of median normalized [ln(Median)=0] logarithmic signals were plotted for the fifty Affymetrix HG-U133A (Figure 1A, left panel) and the fifty AB1700 HGS arrays (Figure 1B, left panel), respectively. The resulting lognormal signal distributions are strikingly different. This difference can be further demonstrated by approximation of the data with a single three-parameter (3p) lognormal distribution function (single distribution; middle panels in Figure 1A and 1B) or two independent superposed 3p lognormal distribution functions (mixture distribution; right panels in Figure 1A and 1B). The parameters for these model functions were estimated using the expectation maximization (EM) algorithm (http://www.cs.duke.edu/courses/spring04/cps196.1/handouts/EM/tomasiEM.pdf) (6) and the orthogonalized gradient method (OGM) (7). While the single lognormal distribution function well approximates the Affymetrix data 8., 9., 10., 11., 12. and the mixture distribution model only slightly increases their descriptive accuracy, for the AB1700 data, however, the single distribution model quite obviously fails to represent the original data. The mixture distribution model, on the other hand, much better captures the particular signal distribution observed in the AB1700 HGS arrays.
Fig. 1.
Lognormal signal distributions of Affymetrix HG-U133A (A) and AB1700 HGS (B) datasets. Histograms of normalized lognormal signal distributions and their approximations through standard lognormal model and the mixture model are shown, respectively. Left panel: a histogram view of the original data; Middle panel: the fifty corresponding approximations by a single lognormal distribution; Right panel: the corresponding approximations by two independent lognormal distributions. All the displayed data are median and surface normalized such that ln(Median)=0.
To better illustrate this difference, we co-plotted the logarithmic signal histograms with both the single model and the mixture model for three randomly selected individual arrays from each dataset (Figure 2). For the three Affymetrix HG-U133A arrays, the two models in general perfectly superpose, whereas for the three AB1700 HGS arrays this is not the case. In order to quantify these differences, we calculated the likelihood estimates for three different lognormal signal distribution models. That is, besides the two models mentioned above, we added a model composed of two individual 3p lognormal distributions, where the parameter x0 for only one of the functions was allowed to diverge from zero while the x0 of the second function was kept at zero in order to include all the data in the estimation (See Materials and Methods). The averaged results are summarized in Table 2, and the entire set of likelihood estimates is contained in the Supporting Online Material (“01SignalDist.pdf”). Note that all the information referred to as “likelihood” is in fact the natural logarithm of the likelihood (ln L), that is, for a set of values and a probability density function f(x),
Fig. 2.
Lognormal signal distributions of three Affymetrix HG-U133A arrays (A) and three AB1700 HGS (B) arrays. Black curve: original data; Blue curve: standard lognormal model; Red curve: mixture model. Note that for the Affymetrix data the standard lognormal model and the mixture model are basically identical and superpose, which is in stark contrast to the AB1700 data. What is perceived as significant deviation of the actual data from the models in part needs to be attributed to the binning and mean calculation for displaying the data as histograms.
Table 2.
Likelihood Estimates for Three Lognormal Signal Distribution Models
| Dataset | Mean likelihood (L) estimates for signal distributions |
|||||
|---|---|---|---|---|---|---|
| L (single) | L (dual) | L (dual, x0) | Single/Dual | Single/(Dual, x0) | Gain | |
| Affymetrix HG-U133A 2.0 50× | −34394.71 | −34170.27 | −34050.21 | 1.0069 | 1.0104 | 1.04% |
| AB1700 HGS 1.0 50× | −85885.00 | −80233.11 | −79468.81 | 1.0699 | 1.0802 | 8.02% |
According to the averaged likelihood estimate ratios of the single vs. dual (Single/Dual) and the single vs. dual with diverging x0 [Single/(Dual, x0)], the gain in descriptive accuracy for the Affymetrix data averages around 0.7% by the dual lognormal distribution and averages around 1% by the dual lognormal x0 distribution, while for the AB1700 data the average gain is around 7% and 8%, respectively (Table 2). Thus very significant increases in descriptive accuracy are observed for the latter dataset when two independent lognormal distributions are modeled (note that an absolute comparison of the likelihood estimates between the two datasets is not possible). In addition, by ever increasing the number of lognormal distributions used to approximate a single experimental distribution, the error of the estimation is ever decreasing. Therefore, only the magnitude of relative increase of descriptive power reflects whether or not the addition of another distribution is reasonably required to accurately capture the main characteristics of the distribution under study. An increase in one percent thereby would not warrant the assumption of two independent superimposed distributions; hence, the Affymetrix data studied here are sufficiently well approximated using a single lognormal distribution. In this context, it is worthy to note that the lognormal signal distribution for Affymetrix data has been studied before and the same conclusion has been reached 8., 9., 10., 11., 12.. However, for AB1700 data a mixture of two independent distributions is required for data approximation. This requirement also implies the presence of two different mechanisms leading to such a mixture distribution.
Origin of the dual signal distribution in AB1700 data
In principal, the superposed signal distributions described above could result either from biophysical, technical, or physiological mechanisms. Biophysical properties, such as fundamentally different probe sample hybridization kinetics, can be ruled out as the subpopulation of signals belonging with high probability to either one distribution is not constant. For instance, a probe specific signal in one experiment will be part of the first distribution while in another biologic condition will be part of the second distribution (Table 3). Since neither the probe structure nor the biophysical properties of the sample have changed (only relative sample quantity is significantly different), differences in the biophysical properties of the molecules are not at the basis of this complex signal distribution in AB1700 data. Similarly, a technical origin for this composite signal distribution can be excluded using the same observation. For instance, differences in surface properties, camera aperture and so on would either always affect the same probes or randomly any probe. In the former case, indeed two individual distributions could result; however, they would always be composed of the same probes as the spot position is invariant from one assay to another. In the latter case, only a single distribution would result with changed characteristic parameters.
Table 3.
Probes Switching Between the Two Signal Distributions in AB1700 data*
| Probe ID | ln(Signal) |
|
|---|---|---|
| HGS1-01 | HGS1-09 | |
| 117345 | 1.89 | −0.86 |
| 125410 | 3.04 | −0.31 |
| 125730 | 2.22 | −0.60 |
| 156007 | 3.65 | −1.94 |
| 171526 | 2.02 | −0.34 |
| 198055 | 1.78 | −0.67 |
| 219524 | 2.37 | −1.87 |
| 235141 | 2.07 | −0.98 |
| 104215 | −1.47 | 3.04 |
| 104795 | −0.98 | 1.72 |
| 112730 | −1.75 | 1.66 |
| 124726 | −0.64 | 2.30 |
| 144329 | −2.25 | 4.74 |
| 207163 | −1.87 | 2.30 |
| 218004 | −0.50 | 1.85 |
| 218266 | −1.75 | 1.68 |
Examples of 16 selected probes where a shift between the signal sub-distributions has occurred with a probability superior to 0.95. Such shifts were observed in both directions (upper eight vs. lower eight probes).
We therefore postulated that the characteristics of the signal distribution as observed with the AB1700 platform are the results of two independent biologic mechanisms at work. This postulation immediately poses the question of why such a composite signal distribution is not observed with Affymetrix or other microarray technologies 8., 9., 10., 11., 12.. We reasoned that the second distribution might have gone undetected by such technologies and that only the increase in signal dynamic range for the AB1700 platform, which we reported here (Table 1), allows detection of this second group of signals. This in turn implies that either one of the two sub-distributions measured by AB1700 falls outside of the signal dynamic range of Affymetrix or similar microarray platforms. We therefore thought to superpose the signal distributions from both datasets and directly compare them.
Significantly increased sensitivity of the AB1700 platform
In order to superposition the signal distributions of both datasets on a single scale, we first calculated the weighted average logarithmic signal intensities of thirteen housekeeping genes (Table 4) (13) over the entire collection of fifty arrays for each dataset. We then determined the average difference in logarithmic signal intensities for these thirteen housekeeping genes between the two datasets (Table 5). We reasoned that the selected housekeeping genes, according to their definition (13), should show relative invariance over the fifty arrays, and given the representative nature of both datasets, albeit not identical, this average should be directly comparable between the two datasets. Thus the difference between the averages over the averaged logarithmic signal intensities for the housekeeping genes should provide for a relative factor by which the signal distributions of both datasets are offset. From the calculation (Table 5) we estimated the relative offset of the AB1700 data vs. the Affymetrix data to be 2.20 on the logarithmic scale, with a variance of 1.01 when both datasets are median normalized [ln(Median)=0]. In consequence, the average signal density curve of the AB1700 data needs to be shifted by 2.20 units towards lower logarithmic signal relative to the averaged Affymetrix curve. Figure 3 shows the resulting histogram plots taking account of this offset.
Table 4.
The Thirteen Housekeeping Genes Selected for Estimation
| No. | GenBank ID | Transcript |
|---|---|---|
| 1 | NM_001101 | hs actin, beta (ACTB) |
| 2 | NM_000034 | hs aldolase A, fructose-bisphosphate (ALDOA) |
| 3 | NM_002046 | hs glyceraldehyde-3-phosphate dehydrogenase (GAPD) |
| 4 | NM_000291 | hs phosphoglycerate kinase 1 (PGK1) |
| 5 | NM_005566 | hs lactate dehydrogenase A (LDHA) |
| 6 | NM_002954 | hs ribosomal protein S27a (RPS27A) |
| 7 | NM_000981 | hs ribosomal protein L19 (RPL19) |
| 8 | NM_000975 | hs ribosomal protein L11 (RPL11) |
| 9 | NM_007363 | hs non-POU domain containing, octamer-binding (NONO) |
| 10 | NM_004309 | hs Rho GDP dissociation inhibitor (GDI) alpha (ARHGDIA) |
| 11 | NM_000994 | hs ribosomal protein L32 (RPL32) |
| 12 | NM_022551 | hs ribosomal protein S18 (RPS18) |
| 13 | NM_007355 | hs heat shock 90kDa protein 1, beta (HSPCB) |
Table 5.
Estimation of the Relative Signal Intensities of Thirteen Housekeeping Genes for Both Datasets
| No. | Affymetrix HG-U133A 2.0 |
AB1700 HGS 1.0 |
ln(Signal) difference |
||||||
|---|---|---|---|---|---|---|---|---|---|
| Probe ID | Merge signal | Variance | ln(Signal) | Probe ID | Merge signal | Variance | ln(Signal) | ||
| 1 | 213867_x_at | 132.47 | 0.31 | 4.89 | 138921 | 122.64 | 1.80 | 4.81 | −0.08 |
| 2 | 200966_x_at | 26.79 | 0.82 | 3.29 | 120590 | 125.52 | 0.78 | 4.83 | 1.54 |
| 3 | 212581_x_at | 88.83 | 0.51 | 4.49 | 175324 | 390.73 | 0.31 | 5.97 | 1.48 |
| 4 | 200737_at | 3.00 | 0.46 | 1.10 | 138964 | 98.80 | 0.66 | 4.59 | 3.49 |
| 5 | 200650_s_at | 14.48 | 0.41 | 2.67 | 120739 | 315.16 | 0.52 | 5.75 | 3.08 |
| 6 | 200017_at | 26.35 | 0.59 | 3.27 | 132198 | 305.72 | 0.47 | 5.72 | 2.45 |
| 7 | 200029_at | 17.93 | 0.30 | 2.89 | 133819 | 245.38 | 0.52 | 5.50 | 2.61 |
| 8 | 200010_at | 14.83 | 0.63 | 2.70 | 222435 | 105.55 | 0.68 | 4.66 | 1.96 |
| 9 | 200057_s_at | 9.00 | 0.58 | 2.20 | 139072 | 77.61 | 0.71 | 4.35 | 2.15 |
| 10 | 201167_x_at | 1.24 | 0.40 | 0.22 | 211134 | 4.96 | 1.16 | 1.60 | 1.38 |
| 11 | 200674_s_at | 27.36 | 0.17 | 3.31 | 223821 | 312.28 | 0.39 | 5.74 | 2.43 |
| 12 | 201049_s_at | 37.74 | 0.51 | 3.63 | 162103 | 349.19 | 0.61 | 5.86 | 2.23 |
| 13 | 214359_s_at | 5.84 | 0.69 | 1.76 | 197185 | 267.60 | 0.47 | 5.59 | 3.83 |
| mean | 31.22 | 0.49 | 2.80 | mean | 209.32 | 0.70 | 5.00 | 2.20±1.01 | |
Fig. 3.
Superposition of the averaged signal distribution histograms for the Affymetrix and the AB1700 datasets. Black solid curve: the Affymetrix histogram with ln(Median)=0; Black broken curve: the AB1700 histogram with ln(Median)=0; Grey solid curve: the AB1700 histogram with ln(Median)=−2.20. The relative shift of the AB1700 histogram (grey solid) vs. the Affymetrix histogram (black solid) corresponds to the average difference (2.20) in the logarithmic signal intensity between both datasets.
Rather than setting the surface areas for both datasets to the same constant, they could also have been scaled to the total number of probes considered (HGS V1.0 average: 34,600, HG-U133A V2.0 average: 22,743); however, we feel that for the purpose of comparing the signal dynamic ranges and their relative positioning, identical surface areas are more appropriate. It can easily be appreciated from Figure 3 that the AB1700 signal range covers an area to the lower signal end that is not covered by Affymetrix, indicating a significant increase in sensitivity. Indeed almost the entire gain in signal dynamic range (Table 1) falls within this region, lending strong support to the contention that the combined use of 60-mer oligonucleotides as probes and an altered surface chemistry in conjunction with chemiluminescence indeed increases significantly the sensitivity of the technology. It is also interesting to note that, over the fifty individual arrays, the averaged Affymetrix histogram displays a shoulder towards the lower signal range (Figure 3). Albeit this shoulder is not sufficiently pronounced to result in significantly altered likelihood estimates when comparing the three different signal distribution models, it seems to be reminiscent of the second distribution we detected using the HGS V1.0 data. Moreover, the points where the second order derivatives of both distributions change sign seem to coincide at ln(Signal)=∼−0.75 in the Affymetrix histogram, lending further support to the hypothesis that the second distribution clearly observed with AB1700 is also weakly detectable in the Affymetrix data. Taken together, these observations show a significantly increased sensitivity of the AB1700 platform, which allows faithful detection of a second signal distribution towards the low end of the covered signal dynamic range.
Stochastic transcription initiation explains the observed signal distributions
As mentioned above, the second signal distribution of the AB1700 data is of biologic origin and not detectable using lower sensitivity technology such as the Affymetrix platform, albeit the shoulder in the corresponding averaged signal histogram for the latter technology could already be an indication towards its existence. Since a single biologic mechanism will engender only a single lognormal distribution 8., 9., 10., 11., 12., the presence of a composite signal distribution in these microarray data implies two fundamentally distinct biologic mechanisms at work. Recently, it has been shown possible to demonstrate stochastic transcription initiation in prokaryotes and also to gather evidence for such a phenomenon in eukaryotes 14., 15.. These observations have rapidly spurred interest in the theoretical biology community, leading to the proposition of several models 16., 17., 18., 19., 20., 21.. At least in eukaryotic organisms several levels of stochasticity should be distinct. The absolute rate of transcription of a single gene shows elements of stochasticity 15., 16., 17., 19., but there also seems good indication of random start site selection and transcription initiation in absence of a specific regulatory signal 19., 22.. The latter phenomenon leads to the low level expression of the randomly activated target genes (19). The mechanisms involved are arguably, albeit highly likely, distinct. Transcriptional regulators, such as transcription or enhancer factors, seem to be dispensable for random initiation of transcription, whereas they are required for regulated transcription initiation 22., 23.. We hence speculate that the two lognormal signal distributions detected using the AB1700 platform correspond to stochastic start site selection on the one hand and regulated transcription initiation on the other hand. The fact that the second signal distribution is observed for low signal intensities lends further credibility to our hypothesis. It will be indeed very interesting to achieve experimental verification of this assumption using different technologies, as this would mark the first time that stochasticity in start site selection has been observed using a whole-genome analysis method such as microarray technology, and hence would allow in the future a systematic, genome-wide simultaneous assessment of this phenomenon. This challenge is currently not met by existing methods, and its overcoming would result in major breakthroughs in the comprehension of the different mechanisms leading to transcription initiation and regulation on a genome-wide scale. For instance, questions relating to the origin and maintenance of robustness of gene transcriptional programs during cellular differentiation need thorough investigation in light of the recently discovered existence of stochasticity at several levels during the transcription process.
Properties of AB1700 data
Signal variance distribution
The particularity of the AB1700 platform to determine signal intensity using chemiluminescence and in parallel probe/spot integrity using fluorescence-labeled controls allows quality estimation of the measured signal. Therefore, even for single-measurement arrays, a probe specific pseudo-variance estimate can be obtained. We were interested in investigating the properties of the signal variance distribution, especially after having made the above discussed observations concerning the composite signal distribution. To this end, we calculated the mean logarithmic normalized variance distribution as a function of the logarithmic signal (see Materials and Methods for the procedure and the Supporting Online Material “05Pseudocode.pdf” for the algorithmic implementation). The resulting graphs for the fifty individual AB1700 arrays as well as the mean of all the fifty individual curves are displayed in Figure 4A. The underlying variance distribution function is monotonous but far from trivial. We therefore also plotted the mean normalized variance distribution (Figure 4B) and the mean de-normalized variance distribution (Figure 4C), respectively. Note that for all three plots the distributions are median normalized such that ln(SignalMedian)=0. Furthermore, the plots are discontinued below ln(Signal)=−2 since the contributing number of probes for individual bins used for histogram calculation becomes too small for robust mean estimation. Specifically, in Figure 4C the particularities of the variance distribution for the AB1700 data become fully graspable. As one would expect for well behaved data, the mean normalized variance is a linear function of the logarithmic signal intensities for ln(Signal)<−1 and also for ln(Signal)>2 (Figure 4C). In the intervening interval, however, the variances do not follow this law. While we cannot give a formal explanation for the observed phenomenon, we note that ln(Signal)=1.34 and ln(Signal)=2.20 correspond to the two maxima of the averaged individual contributing signal distributions for normalized AB1700 data with ln(SignalMean)=0 (Fig. 1, Fig. 2, Fig. 3). Therefore, the nonlinear variance progression occurs between the two maxima, with the interval between them corresponding to the fusion region of both signal distributions. This observation further sustains the presence of two individual contributing signal distributions, since in this case nonlinear behavior per se is expected to occur. We can to the contrary only speculate as to the particular nature of the nonlinearity over the fusion interval: stochastic start site selection will result in proportionally larger variances over individual transcript numbers when averaged over many individual cells than regulated transcription initiation. Therefore, the linear de-normalized variance progression through the lower signal distribution will be parallel shifted towards higher absolute variances when compared to the variance progression through the other signal distribution. Such a parallel shift would lead in the zone where both distributions combine to a progression curve highly similar to the one observed here. Again, if our hypothesis of two fundamentally different molecular mechanisms leading to the composite data structure could be independently confirmed using different technologies such as quantitative PCR on individual cells, the nonlinear variance progression would also find satisfactory biologic explanation.
Fig. 4.
Distribution of the estimated probe signal variances for the fifty AB1700 arrays (grey curves) and their mean (black curve). A. Mean logarithmic variance vs. logarithmic signal. B. Mean variance vs. logarithmic signal. C. De-normalized (absolute) variance vs. logarithmic signal.
A signal variance distribution model (Neonex) for AB1700 data
The drastically different structure of AB1700 transcriptome profiles requires adaptation or even redevelopment of the standard microarray analysis methods. Based on the statistical properties we analyzed above, we derived a signal variance distribution model, which is the necessary basis for such development. The bimodal signal distribution has been sufficiently discussed. The mean-variance progression, however, can be best approximated in mean-normalized variance over logarithmic signal space (Figure 4B). In order to do so, we have used two independent functions:
| (1) |
| (2) |
which are connected at some point x0
| (3) |
where the two conditions f1(x0) = f2(x0) = y0 and must hold to preserve continuity and differentiability of the resulting function. Two additional conditions are introduced to preserve shape and validity: 0 < y0 < 1 and . For the definition of f(x), the parameters y0 and are necessary and sufficient and, respecting the two latter conditions, always valid. The single function parameters (x0, k, m, c) can be readily calculated as following:
| (4) |
| (5) |
| (6) |
| (7) |
To preserve smooth differentiability for any order, the two independent functions were initially “faded” by a sigmoid with the center at x0, which later showed to be unnecessary when using the gradient method for approximation (see Materials and Methods as well as the Supporting Online Material “05Pseudocode.pdf” and “06Formulae.pdf”).
Three additional parameters, namely yscl, yoff, and xoff, were introduced for vertical scaling, vertical shift, and horizontal shift, respectively, yielding the five-parameter function:
| (8) |
Since Equation 1 has been proposed and used by us as an error function for inter-array transcriptome profile normalization, which was dubbed as the NeONORM function (24), we thereby dub the five-parameter function (Equation 8) as Neonex for it is composed of the NeONORM function and a negative exponential function. A schematic presentation of how the Neonex function can be obtained by combining (1), (2) is shown in Figure 5A. The Neonex function has a sigmoidal shape, asymptotically approaching 1 at negative infinity and 0 at positive infinity. To show applicability, we first manually fitted the Neonex function to the average normalized variance over logarithmic signal curve (Figure 5B). Next, by using the EM algorithm (see Materials and Methods and the Supporting Online Material “05Pseudocode.pdf”), we estimated the five free Neonex parameters for each of the fifty AB1700 arrays (see the Supporting Online Material “03NeonexVar.pdf” for the entire parameter collection). The resulting Neonex curves were then plotted together with a Neonex curve calculated from the averages of each of the five parameters (Figure 6A), which should be compared to Figure 4B (original data). Finally, in Figure 6B, we co-plotted the original data’s average mean-variance curve (black) together with the averaged Neonex curve over all fifty arrays (red) and the Neonex curve calculated from the averaged individual parameter estimates (blue). It can be seen that all the three curves sufficiently well superpose. Therefore, it can be concluded that the Neonex function satisfactorily describes the normalized mean-variance progression over logarithmic signal for the AB1700 data and can be used for parameter estimation with the EM algorithm (Supporting Online Material “06Formulae.pdf”), representing a robust model for AB1700 originating average signal variances.
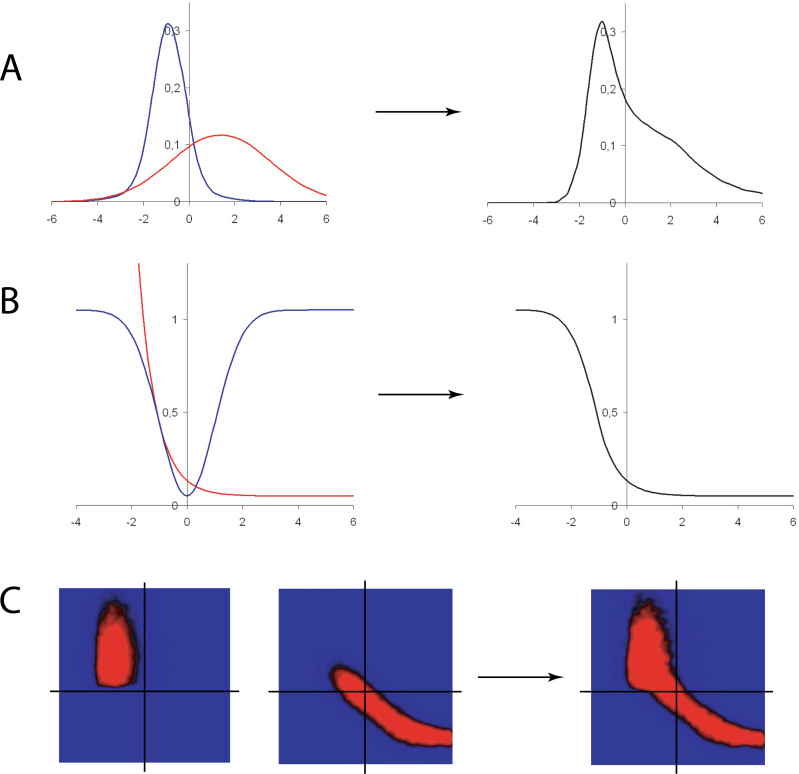
Fig. 5.
A. Schematic presentation of the two individual contributing functions, NeONORM (blue curve) and the negative exponential function (black curve), as well as the resulting composite Neonex function (red curve). The NeONORM function and the negative exponential function are fused at the unique point where both first order derivatives are equal, corresponding to identical slopes. B. The Neonex function (red curve) was manually fitted to the average of the mean variance vs. logarithmic signal curve (black curve) for the fifty AB1700 arrays in Figure 4B.
Fig. 6.
Neonex-based estimates for the signal variance distributions of the AB1700 data. A. Ten free parameters of the Neonex function were estimated for each of the fifty individual AB1700 arrays (Supporting Online Material “04AllParam.pdf”). The resulting scaled Neonex approximates (grey curves) as well as the Neonex function using the averaged parameters from the fifty individual estimations (red curve) are depicted. B. Superposition of the average of the mean variance vs. logarithmic signal curve for the fifty AB1700 arrays (black curve), the mean of the fifty individual Neonex estimates (blue curve), and the Neonex function scaled using the averaged parameters from the fifty individual estimations (red curve).
The signal variance for a given signal is lognormal distributed in AB1700 data
In order to assess how the number of over 34,000 probe signal and signal variance measures distribute over the signal range, we analyzed the variance over the signal variance distribution within the fifty AB1700 arrays. The signal-dependent variance distribution is, as would be expected for well behaved data, in the limit of sufficiently large and overlapping bins, for every ln(Signal) a lognormal distribution, with the estimated Neonex curve being parallel to the continuum of logarithmic means over the entire logarithmic signal range (Supporting Online Material “04AllParam.pdf”). Using this information, the approximate probability density functions over the signal range can be generated and used to calculate 3D density plots of the data (see Materials and Methods and the Supporting Online Material “05PseudoCode.pdf”). The 3D density plots capture well the variance over the signal distribution properties we discussed above. By taking all the three factors together, namely the signal distribution (Figure 7A), the mean logarithmic variance (Figure 7B), and the signal-dependent variance, a composite eighteen-parameter model for the AB1700 HGS V1.0 data was developed (Figure 7C), which well illustrates the properties of these high-sensitivity next-generation transcriptome profiles.
Fig. 7.
Schematic presentation of the composite structure model for the AB1700 HGS V1.0 data. A. The signal distribution of the AB1700 data is modeled in logarithmic space using two independent lognormal distributions with divergent x0, which are then combined. B. The signal variance distribution is approximated in logarithmic space using the composite Neonex function. C. The variance over the signal variance distribution and the local density of the data is modeled for each signal distribution individually. The signal-dependent variance is lognormal distributed in both sub-populations. Both individual distributions are combined using a sigmoid blending function to result in the final signal-dependent variance distribution. A total of eighteen free parameters are used to model the signal, the signal variance, and the variance of signal variance distributions (Supporting Online Material “04AllParam.pdf”). These parameters can be derived from original microarray experiments as shown in Materials and Methods.
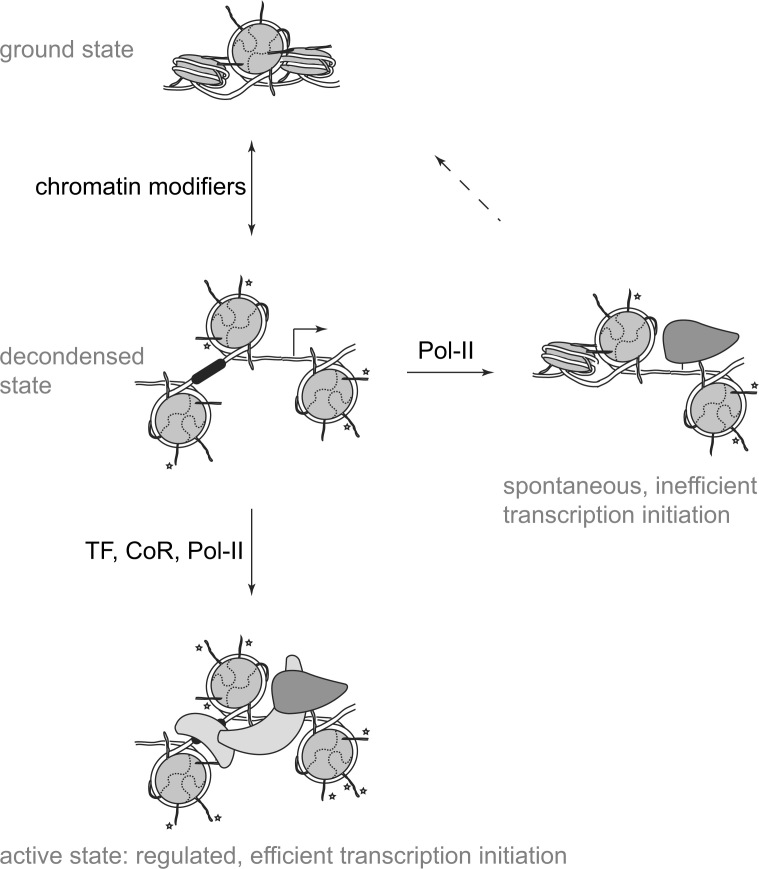
A chromatin-dynamics model potentially explains the observed dual distribution in AB1700 data
A chromatin-transcription model (Figure 8) explaining the dual lognormal signal distribution observed in high-sensitivity transcriptome profiles was derived from our previous works 22., 23. and the literature (19). The chromatin code hypothesis predicts stochastic chromatin “breathing” (a hypercycle of modification and de-modification by chromatin modifiers, where the modified nucleosomal array decondenses and subsequently allows DNA access by transcription factors) (23). The underlying DNA-coded regulatory element (black box in “de-condensed state”) as well as transcription start sites (arrow) thereby become randomly exposed through this mechanism. Provided that the accessible DNA contains a bona fide transcription start site, the holo-RNA pol-II would spontaneously initiate transcription, leading to the production of complete or abortive mRNA. In the absence of specific coregulators, the stochastically initiated transcription will be on average of low efficiency, and hence the average signal intensity for genes transcribed stochastically will be significantly lower than the one for regulated transcription initiation events. This explains the positioning of the resulting distribution at the low end of the signal scale. Furthermore, when averaged over a population over 106 individual cells (as is true for transcriptome microarray experiments), this stochastic distribution will display relative larger signal variances compared with the regulated transcription initiated through a combination of transcription factors (TF), coregulators (CoR), and pol-II holoenzymes (Pol-II).
Fig. 8.
A chromatin-based model for the biologic interpretation of the observed dual lognormal signal distribution in the AB1700 data.
Significant implications
Significant implications for statistical data analysis
We have evidenced here a fundamentally distinct data structure of the high-sensitivity AB1700 microarray data. In stark contrast to other lower sensitivity technologies, the main difference is that the signal distribution of AB1700 data is composed of two individual distributions. Furthermore, through the combined use of fluorescence probe/spot integrity estimation with chemiluminescence sample quantification, AB1700 data possess signal variance estimates. While these are rather pseudo-variances, they provide additional probe specific information that can be valorized during statistical analysis. The signal variance distribution is even more complex than the signal distribution itself, and also reflects two independent signal distributions covering the effective signal range.
The implications for biologic analysis and comprehension of the fundamental mechanisms of gene regulation on a genome-wide scale have been sufficiently discussed; however, the particularities of the AB1700 data also have major implications for statistical analysis, generating novel and unmet challenges and possibilities. Currently most analysis methods for microarray data are firmly based on the null-hypothesis of a single lognormal signal distribution 8., 9., 10., 11., 12.. In particular, nonlinear normalization techniques, false discovery rate approaches, and quantile-based analysis, will fail to operate in the expected manner on AB1700 data if they do not take into account the presence of a second, independent, and parametrically different signal distribution. A widely employed method of intra- and inter-array normalization is the LOWESS algorithm and its derivatives 25., 26., 27.. LOWESS for instance will, if not modified to operate independently on both individual signal distributions present in AB1700 data, mix the local derivation of errors, which is used to calculate smoothing weights, from both distributions and hence lead to a biased result. Similarly, many other currently used methods, such as principal component analysis, Bayesian hierarchical clustering, two component clustering, were developed or adapted for microarray analysis on the underlying hypothesis of a single lognormal signal distribution 28., 29., 30., 31., 32., 33., 34..
At present, we cannot quantify the impact of the alternate data structure of AB1700 on the performance of such methods; however, it seems very clear that a possible impact at least will have to be considered and carefully studied. This is even more necessary since the existence of a single lognormal signal distribution is not only explicitly implied in such methods cited above, but has been thought to be true throughout the entire history of microarray analysis tool development 28., 29., 30., 31., 32., 33., 34.. To our knowledge, there exists no formal way of assessing the potential implications that the fundamentally altered AB1700 data structure might have on these analysis methods. Therefore, we strongly recommend to take the features we reported here into consideration when analyzing AB1700 data. We firmly believe that in this context the composite data structure model we described will be a very helpful tool for the re-evaluation, adaptation, or even redevelopment of microarray analysis methods. For example, using the approximate probability density functions adapted here, the complex signal distribution can be decomposed in order to analyze each underlying lognormal signal distribution independently. On this basis it should be possible to derive LOWESS methods that operate on both signal distributions with adaptive sensitivity. Furthermore, not only statistical misinterpretation of the data needs to be avoided, but also great interest should be taken to fully benefit from the increased specificity, sensitivity, and dynamic range of AB1700 data. Simple operations, such as merging/averaging of technical and biological replicates, have already benefitted from being able to individually weight any probe signal by its variance. Similarly, composite and true variance estimates can be calculated from the unique combination of signal and signal-variance estimates present in individual data files. This can lead to significantly reduced number of required technical and biological replicates to reach preset significance thresholds, or in turn allow to better estimate whether those thresholds can possibly be met and at what experimental costs. Better statistical and process control of large-scale studies where hundreds or thousands of individual experiments are conducted will also be achieved.
Significant implications for biologic interpretation
Having access to high-sensitivity measurements will also have a significant impact on the study of the fundamental processes of genome-wide transcription regulation. The potential for analyzing the particular class of stochastic processes involved in start site selection have been discussed; however, one should also expect that determination of composite multilayer signatures for diagnostic and prognostic studies will be more readily achieved (35). Here, in combination with other genome-wide technologies such as systematic chromatin immunoprecipitations, it might be possible to derive signatures composed of direct target genes, which certainly would better represent the regulatory signal under study. Similarly, the high-sensitivity nature of the data, especially the presence of a second signal distribution that covers almost half of the probes on the HGS V1.0 arrays, might provide for an internal reference or control, and, if fully exploited, might lead in combination with sequence-specific physical models of the hybridization between probe and target (36) to the development of absolute transcript level estimates. This in turn would overcome the current limitation of microarray experiments with respect to absolute quantification (37). Such achieved microarray experimentation might gain the same level of reproducibility and applicability as quantitative PCR in biomedical and medical research and treatment. While such perspectives are long-term goals, we feel that the novel design of upcoming next-generation technologies such as AB1700 will have a significant impact on the different research areas utilizing transcriptome profiling. Exciting new opportunities seem to come to reach.
Conclusion
In this study we have presented a thorough analysis of the data structure and features of a next-generation microarray technology AB1700 with comparison to those widely used existing approaches. We have evidenced significant increases in the overall signal dynamic range and sensitivity of the AB1700 data. A second independent lognormal signal distribution at the low end of the signal range has been described, which on average represents almost half of the present probes on the AB1700 arrays. Thus not only thousands of weakly expressed additional transcripts can be detected using this technology, but also direct conclusions might be drawn as to the fundamental mechanisms of gene regulation. Since a composite signal distribution has not been reported before for microarray data, its presence has fundamental implications for data analysis and biologic interpretation. After excluding biophysical or technical explanations for this dual distribution, as evidenced here, an essentially different biologic mechanism leading to the second distribution inevitably has to exist. We have presented here such a biologic model based on the hypothesis that random chromatin “breathing” could lead to the observed random initiation of transcription (Figure 8). The observations we made are likely to spur future research into the fundamental principles of gene regulation, and already today lends further support to the observations concerning the stochasticity of random target gene start site selection (19). A composite eighteen-parameter model for the AB1700 HGS V1.0 data has also been developed. This model takes account of the signal, the signal variance, and the variance over the signal variance distribution, and therefore can accurately describe the global features of AB1700 data. Using this AB1700 data structure model, new avenues for microarray data quality control could be explored. Moreover, the particularity of the AB1700 data warrants re-evaluation, adaptation, and redevelopment of statistical analysis methods, since existing approaches explicitly or implicitly rely on a single lognormal signal distribution hypothesis. Again, the existence of a sound model for these data structures will prove important. Finally, as we believe, this study will help inspire new statistical approaches in microarray analysis as to fully exploit the enhanced signal dynamic range and sensitivity of this next-generation technology, hopefully leading to an even increased usefulness of transcriptome studies in the biological and biomedical arenas.
Materials and Methods
Affymetrix HG-U133A V2.0 dataset
All the experimental data referred to as Affymetrix HG-U133A V2.0 were obtained from the NCBI Gene Expression Omnibus database (38). We used the microarray experiments from two different experimental studies 2., 5.. The majority of experiments was originated from the study (5) that contains the transcriptome profiles of 48 different human tissues, hence representing a heterogeneous and representative set for human transcriptome profiles. The experiments from the other study (2) were included to detect/avoid any machine dependent bias.
AB1700 HGS V1.0 dataset
All the experimental data referred to as AB1700 HGS V1.0 (Applied Biosystems, Foster City, USA; ProdNo: 4337467) used in this study were generated on two different AB1700 transcriptome platforms (http://www.appliedbiosystems.com), one of which is installed in our laboratory (ProdNo: 4338036). These arrays contain probes for 29,918 validated human genes (http://docs.appliedbiosystems.com/pebiodocs/00114084.pdf). The individual arrays were selected from a pool of transcriptome profiles belonging to several independent ongoing projects in order to be similarly representative as the Affymetrix dataset. The data distribute to three different human cells lines and additionally six different human tissues, which were generated either with or without amplification. The dataset thereby is representative for the ensemble of data that we have so far generated and analyzed.
RNA extraction
RNA extraction was performed using the Qiagen RNeasy method according to the manufacturer’s recommendations (Qiagen, Chatsworth, USA; ProdNo: 75144). Quality and quantity of the isolated total RNA was determined using an Agilent Bioanalyzer 2100 (Agilent, Palo Alto, USA) as well as standard spectro-photometry.
RNA labeling, hybridization, and detection
RNA amplification, labeling, hybridization, and detection were performed following the protocols supplied by Applied Biosystems together with the corresponding kits. An amount of 15–20 μg of total RNA sample was subjected to Chemiluminescence RT Labeling (Applied Biosystems, ProdNo: 4339628); alternatively, an amount of 2 μg of total RNA was subjected to RT-IVT amplification and labeling (Applied Biosystems, ProdNo: 4339628). The labeled cDNAs or cRNAs were then hybridized and detected according to the supplied protocols (Applied Biosystems, ProdNo: 4346875).
Data preprocessing and primary analysis
Applied Biosystems Expression Array System Software V1.1.1 (ProdNo: 4364137) was used to acquire the chemiluminescence and fluorescence images and primary data analysis. Briefly, the primary analysis consists of the following individual operations: (1) Image correction; (2) Global and local background correction; (3) Feature normalization; (4) Spatial normalization; (5) Global normalization. Note that we renormalized the resulting data according to the median once more after having removed probes for which the software has set flags equal to or greater than 212, indicating compromised or failed measurements (as recommended by Applied Biosystems). This secondary normalization is implemented in the ace.map suite that we developed (39).
Parameter estimation models
Signal distribution model
The probability density distribution of the signals is estimated using two lognormal distributions. Each lognormal distribution has three free parameters: x0 (low end constraint), m (mean), and s (variance). Additionally, a relative weight parameter is estimated, which reflects the relative contribution of each lognormal distribution to the combined distribution. This parameter is composed of two individual weights, f1 and f2, where f1+f2=1. Since the lognormal distribution is constraint by x0 at the lower end (all measures <x0 have a probability density of zero), and the model is supposed to consider all signal values (for all signal values Si ≥ 0), the x0,1 of the first sub-distribution is set to x0,1=0. The remaining six parameters are estimated using the EM algorithm. Indeed the EM algorithm keys the x0,2 of the second sub-distribution such that x0,2,i prevails with the higher maximum likelihood.
Variance distribution model
The variance distribution is estimated using a mixture of two lognormal distributions just as that for the signal distribution. However, the parameters of the contributing distributions as well as the relative contribution of either distribution are a function of logarithmic signal. Specifically, the first lognormal distribution describes only high variances (>0.34, x0,1=0.34), and parameters m1 and s1 are estimated as constant functions (hence remain unchanged over logarithmic signal). The second distribution essentially describes the small variances (x0,2=0), and parameters m2 and s2 are approximated as sigmoid functions over logarithmic signal. The yoff (Y-axis offset) parameters of the sigmoids thereby are estimated ab initio using those variances corresponding to large logarithmic signals (lnSi > 4.0), and remain constant during further parameter estimation.
The composite probability density function over logarithmic signal gives an a priori probability:
where θn (n= 1 or 2) represents the individual distribution that a non-specified variance value, corresponding to a defined logarithmic signal Si, is attributed to the first or the second distribution. The measure
as a function of logarithmic signal is constrained using a two-parameter sigmoid.
The estimation process is embedded into individual EM steps. Every EM step thereby re-estimates all the parameters over the weighted sample data (logarithmic signal and logarithmic variance) in the previous step. In our case, for every data point i [ln(Signali) | ln(Variance0.0i)] and [ln(Signali) | ln(Variance0.34i)] (hereinafter [Si|Vi]), the weights w1,i and w2,i are calculated, which correspond to the combined probabilities:
These combined probabilities p(θ1,2 | [Si|Vi]) are the product of the a priori probability p(θn|Si), and hence the mixture function, and also the probability that is determined over the lognormal probability density function at position Vi with the parameters for the corresponding Si. The weights are being used for the calculation of weighted mean and weighted variance for the first lognormal distribution [m1(Si) and s1(Si)]. They are also being used by the gradient method-based parameter estimation as factors for calculating the cumulative error (which is being minimized) for the second lognormal distribution. After each EM estimation step, the mixture function is reestimated using the new weights w1,i. The EM algorithm terminates either after a preset number of steps is reached (negative abortion), or if the likelihood increase between two EM steps falls below a preset convergence threshold (positive abortion).
Neonex function parameter reduction
The Neonex function needs five parameters to be completely specified as described above. However, a four-parameter Neonex function, where the yoff parameter is pre-calculated and unchanged during gradient method parameter optimization, was frequently employed. It is preferred to a direct five parameter estimation process because yoff can be directly calculated from the variances belonging to the very high signals and the gradient method works more efficient with fewer parameters.
Authors’ contributions
SN has made the initial observation of a mixture lognormal signal distribution in the AB1700 data, and has significantly participated in the mathematical formulation of the Neonex function, the statistical data analysis, and the algorithmic implementation of all the methods described here. GB has significantly participated in the algorithmic implementation of the methods. FXP has significantly contributed to the data analysis and the development of biologic models for interpretation. AB has significantly participated in the mathematical formulation of the Neonex function, the statistical data analysis and biologic interpretation, as well as manuscript preparation. AB has designed and coordinated this study, and has selected the experimental data. All authors read and approved the final manuscript.
Competing interests
The authors have declared that no competing interests exist.
Acknowledgements
The authors thank their collaborators Drs. B. Bell, J. Elion, M. Müller-Trutwein, L. Rogge, C. Zennaro, and their coworkers for sharing unpublished data as well as their continuous support and encouragement throughout this study. All members of the systems epigenomics group are thanked for stimulating discussions. This work was supported by the European Hematology Association—José Carreras Foundation, the Institut des Hautes Etudes Scientifiques, the Institut de Recherches Interdisciplinaires, the Centre National de la Recherche Scientifique (CNRS), the Institut National de la Santé Et de la Recherche Médicale (INSERM), the Région Nord, and the French Ministry of Research through the “Complexité du Vivant—Action STICS-Santé” program (all to AB).
Supporting Online Material
References
- 1.Hughes T.R. Expression profiling using microarrays fabricated by an ink-jet oligonucleotide synthesizer. Nat. Biotechnol. 2001;19:342–347. doi: 10.1038/86730. [DOI] [PubMed] [Google Scholar]
- 2.Castle J. Optimization of oligonucleotide arrays and RNA amplification protocols for analysis of transcript structure and alternative splicing. Genome Biol. 2003;4:R66. doi: 10.1186/gb-2003-4-10-r66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Jordan R. Performance and bioinformatics evaluation of overlapping variable length oligonucleotide probes used in spotted microarrays. Trans. Integr. Biomed. Inform. Enabl. Technol. Symp. 2004;1:15–24. [Google Scholar]
- 4.Stefano G.B. Regulation of various genes in human leukocytes acutely exposed to morphine: expression microarray analysis. Med. Sci. Monit. 2005;11:MS35–MS42. [PubMed] [Google Scholar]
- 5.Su A.I. A gene atlas of the mouse and human protein-encoding transcriptomes. Proc. Natl. Acad. Sci. USA. 2004;101:6062–6067. doi: 10.1073/pnas.0400782101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bilmes J.A. University of California; Berkley, USA: 1998. A gentle tutorial of the EM algorithm and its appliaction to parameter estimation for Gaussian mixture and hidden Markov models. Technical report, ICSI TR-97-021. [Google Scholar]
- 7.Shewchuk J.R. Carnegie Mellon University; Pittsburgh, USA: 1994. An introduction to the conjugate gradient method without the agonizing pain. Technical report, CS-94-125. [Google Scholar]
- 8.Konishi T. Three-parameter lognormal distribution ubiquitously found in cDNA microarray data and its application to parametric data treatment. BMC Bioinformatics. 2004;5:5. doi: 10.1186/1471-2105-5-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Broberg P. Ranking genes with respect to differential expression. Genome Biol. 2002;3 doi: 10.1186/gb-2002-3-9-preprint0007. preprint 0007. [DOI] [PubMed] [Google Scholar]
- 10.Dean N., Raftery A.E. Normal uniform mixture differential gene expression detection for cDNA microarrays. BMC Bioinformatics. 2005;6:173. doi: 10.1186/1471-2105-6-173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wit E., McClure J. Statistical adjustment of signal censoring in gene expression experiments. Bioinformatics. 2003;19:1055–1060. doi: 10.1093/bioinformatics/btg003. [DOI] [PubMed] [Google Scholar]
- 12.Arita M. Scale-freeness and biologic networks. J. Biochem. (Tokyo) 2005;138:1–4. doi: 10.1093/jb/mvi094. [DOI] [PubMed] [Google Scholar]
- 13.Eisenberg E., Levanon E.Y. Human housekeeping genes are compact. Trends Genet. 2003;19:362–365. doi: 10.1016/S0168-9525(03)00140-9. [DOI] [PubMed] [Google Scholar]
- 14.Elowitz M.B. Stochastic gene expression in a single cell. Science. 2002;297:1183–1186. doi: 10.1126/science.1070919. [DOI] [PubMed] [Google Scholar]
- 15.Blake W.J. Noise in eukaryotic gene expression. Nature. 2003;422:633–637. doi: 10.1038/nature01546. [DOI] [PubMed] [Google Scholar]
- 16.Raser J.M., O’Shea E.K. Control of stochasticity in eukaryotic gene expression. Science. 2004;304:1811–1814. doi: 10.1126/science.1098641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kurakin A. Self-organization vs Watchmaker: stochastic gene expression and cell differentiation. Dev. Genes Evol. 2005;215:46–52. doi: 10.1007/s00427-004-0448-7. [DOI] [PubMed] [Google Scholar]
- 18.Lipniacki T. Transcriptional stochasticity in gene expression. J. Theor. Biol. 2006;238:348–367. doi: 10.1016/j.jtbi.2005.05.032. [DOI] [PubMed] [Google Scholar]
- 19.Kaern M. Stochasticity in gene expression: from theories to phenotypes. Nat. Rev. Genet. 2005;6:451–464. doi: 10.1038/nrg1615. [DOI] [PubMed] [Google Scholar]
- 20.Meng T.C. Modeling and simulation of biological systems with stochasticity. In Silico Biol. 2004;4:293–309. [PubMed] [Google Scholar]
- 21.Dasika M.S. DEMSIM: a discrete event based mechanistic simulation platform for gene expression and regulation dynamics. J. Theor. Biol. 2005;232:55–69. doi: 10.1016/j.jtbi.2004.07.020. [DOI] [PubMed] [Google Scholar]
- 22.Benecke A. Genomic plasticity and information processing by transcription coregulators. Complexus. 2003;1:65–76. [Google Scholar]
- 23.Benecke A. Chromatin code, local non-equilibrium dynamics, and the emergence of transcription regulatory programs. Eur. Phys. J. E (Soft Matter) 2006;19:353–366. doi: 10.1140/epje/i2005-10068-8. [DOI] [PubMed] [Google Scholar]
- 24.Noth S. Normalization using weighted negative second order exponential error functions (NeONORM) provides robustness against asymmetries in comparative transcriptome profiles and avoids false calls. Genomics Proteomics Bioinformatics. 2006;4:90–109. doi: 10.1016/S1672-0229(06)60021-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Cleveland W.S. Robust locally weighted regression and smoothing scatterplots. J. Amer. Statist. Assoc. 1979;74:829–836. [Google Scholar]
- 26.Cleveland W.S., Devlin S. Locally weighted regression: an approach to regression analysis by local fitting. J. Amer. Statist. Assoc. 1988;83:596–610. [Google Scholar]
- 27.Berger J.A. Optimized LOWESS normalization parameter selection for DNA microarray data. BMC Bioinformatics. 2004;5:194. doi: 10.1186/1471-2105-5-194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Leung Y.F., Cavalieri D. Fundamentals of cDNA microarray data analysis. Trends Genet. 2003;19:649–659. doi: 10.1016/j.tig.2003.09.015. [DOI] [PubMed] [Google Scholar]
- 29.Nguyen D.V. DNA microarray experiments: biological and technological aspects. Biometrics. 2002;58:701–717. doi: 10.1111/j.0006-341x.2002.00701.x. [DOI] [PubMed] [Google Scholar]
- 30.Lipschutz R.J. High density synthetic oligonucleotide arrays. Nat. Genet. 1999;21:20–24. doi: 10.1038/4447. [DOI] [PubMed] [Google Scholar]
- 31.Kerr M.K. Analysis of variance for gene expression microarray data. J. Comput. Biol. 2000;7:819–837. doi: 10.1089/10665270050514954. [DOI] [PubMed] [Google Scholar]
- 32.Martin D.E. Rank Difference Analysis of Microarrays (RDAM), a novel approach to statistical analysis of microarray expression profiling data. BMC Bioinformatics. 2004;5:148. doi: 10.1186/1471-2105-5-148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Pan W. A comparative review of statistical methods for discovering differentially expressed genes in replicated microarray experiments. Bioinformatics. 2002;18:546–554. doi: 10.1093/bioinformatics/18.4.546. [DOI] [PubMed] [Google Scholar]
- 34.Khan J. Classification and diagnostic prediction of cancers using gene expression profiling and artificial neural networks. Nat. Med. 2001;7:673–679. doi: 10.1038/89044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ein-Dor L. Outcome signature genes in breast cancer: is there a unique set? Bioinformatics. 2005;21:171–178. doi: 10.1093/bioinformatics/bth469. [DOI] [PubMed] [Google Scholar]
- 36.Carlon E., Heim T. Thermodynamics of RNA/DNA hybridization in high density oligonucleotide microarrays. Physica A. 2006;362:433–449. [Google Scholar]
- 37.Irizarry R.A. Multiple-laboratory comparison of microarray platforms. Nat. Methods. 2005;2:345–350. doi: 10.1038/nmeth756. [DOI] [PubMed] [Google Scholar]
- 38.Barrett T. NCBI GEO: mining millions of expression profiles—database and tools. Nucleic Acids Res. 2005;33:D562–D566. doi: 10.1093/nar/gki022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Noth S., Benecke A. Avoiding inconsistencies over time and tracking difficulties in Applied Biosystems AB1700™/Panther™ probe-to-gene annotations. BMC Bioinformatics. 2005;6:307. doi: 10.1186/1471-2105-6-307. [DOI] [PMC free article] [PubMed] [Google Scholar]