Optimal Allocation of Replicates for Measurement Evaluation Studies

Abstract

Optimal experimental design is important for the efficient use of modern high-throughput technologies such as microarrays and proteomics. Multiple factors including the reliability of measurement system, which itself must be estimated from prior experimental work, could influence design decisions. In this study, we describe how the optimal number of replicate measures (technical replicates) for each biological sample (biological replicate) can be determined. Different allocations of biological and technical replicates were evaluated by minimizing the variance of the ratio of technical variance (measurement error) to the total variance (sum of sampling error and measurement error). We demonstrate that if the number of biological replicates and the number of technical replicates per biological sample are variable, while the total number of available measures is fixed, then the optimal allocation of replicates for measurement evaluation experiments requires two technical replicates for each biological replicate. Therefore, it is recommended to use two technical replicates for each biological replicate if the goal is to evaluate the reproducibility of measurements.

Introduction

Optimal experimental design ensures that experiments are cost-effective, internally valid, and statistically powerful. Optimal design has particular importance for modern high-throughput technologies, such as microarrays or proteomics, because it can considerably increase the efficiency of experiments (1). In this context, it is useful to distinguish between two broad categories of experiments. We use the term “Type A” experiments to refer to the experiments conducted to address specific biological questions such as “What genes are differentially expressed or what proteins are differentially accumulated in tissue X among mice exposed versus not exposed to stimulus Y?” We use the term “Type B” experiments to refer to the experiments that are meant to evaluate aspects of the measurement technology and answer questions such as “What is the reliability of our gene expression or proteomics measurements under such-and-such conditions?” The results of Type B studies that estimate measurement reliability are often important in helping us design optimal Type A studies.

A number of experimental layouts such as loop and common reference have been proposed, and general recommendations have been given such as necessity of proper randomization, replication, and blocking 2., 3., 4.. However, while great efforts were directed toward the design for Type A studies, little attention has been given to the design for Type B experiments where the reproducibility [the terms “reliability” and “reproducibility” are often used interchangeably (5)] of measurements is assessed. Here, we address the problem of finding an optimal allocation of biological and technical replicates for such measurement evaluation studies. We provide an analytical solution based on the assumption that the total number of available measurements is fixed while biological and technical error terms are independent and normally distributed. The correctness of our analytical result is illustrated by simulations.

Results and Discussion

Accurate information about measurement reliability (or its complement, the degree of unreliability) is often important for the design and interpretation of Type A experiments addressing specific biological questions (for example, detecting differences in gene expression levels or protein amounts between two or more conditions). Therefore, Type B experiments are needed to assess measurement reliability. While a number of experiments addressing the reproducibility of microarray and proteomics studies have been conducted 6., 7., 8., 9., 10., 11., 12., optimal design could have made such an experiment more cost-effective. For example, the stability of measurements for evaluation of two kinds of hybridization standards was analyzed using five replicates without rationalization for the number of replicates used (13). Here, we find an optimal design for Type B experiments using an analytical approach and simulations.

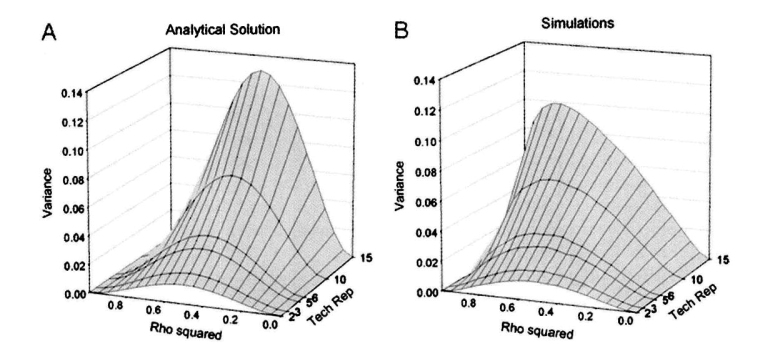
Briefly, we consider a scenario in which the total number of available measurements is fixed, but the number of biological replicates and the number of technical replicates are variable. Biological replicates are independent biological samples, such as rats or mice, or cell lines that have been separately subjected to biological treatments. Technical replicates are repeated measures of one biological sample. We define an allocation of replicates as optimal if it minimizes the variance of the ratio of technical sample variance to the total sample variance. By minimizing the variance of this ratio, we will be able to make more precise estimates of reliability defined as a ratio of a biological variance to the total variance. The results are presented in Figure 1. The variance of the ratio of technical variance to the total variance was minimal when the number of technical replicates per biological replicate equals to 2 and increased as the number of technical replicates increases. This is true for all levels of proportion of biological variance in total variance ρ². Simulations were used to illustrate our analytical results. Slight differences in the shape of the plots were probably due to the fact that the approximate formulas were used in the analytical solution.

Fig. 1.

The optimal number of technical replicates for measurement evaluation experiments. The graphs show the dependence of the variance of the ratio of technical variance to the total variance (Variance) on the number of technical replicates (Tech Rep) and the relative contribution of the biological variability [Rho squared (ρ²)]. The total number of available measurements (M) is fixed in both cases as M = 30. A. Visualization of the analytical solution. B. Results of 10,000 times of simulations.

Real microarray or proteomics data are affected by multiple factors that cause variation in observed values. The choice of platform (such as cDNA arrays vs. Affymetrix), image processing algorithm (such as MAS 5.0 vs. RMA), as well as normalization and transformation techniques has a significant impact on results. Sources of variation and their magnitudes are determined experimentally and vary for different experimental systems. For example, relative contribution of biological variation ranges from ~20% to ~80% of total variation 6., 7., 10., 11.. Yet, it is an important factor for experimental design, such as the planning of mRNA pooling in microarray experiments (14) and the determination of a sample size 11., 13.. Our analysis uses certain assumptions to make the solution easily analytically tractable. In this study, we assume that there are two sources of variation: biological variation, which is a combination of all biological factors, and technical variation, which is a combination of all technical factors. Although this assumption is a simplification, we believe that it is reasonable and allows us to construct a realistic model.

We use a normality assumption to take advantage of approximate formulas of sample variance. While our conclusions do not depend critically on this assumption, it simplifies derivations and setup of simulations. The distribution of data remains a controversial topic in high dimensional biology. Distribution often depends on experimental system 9., 15., 16.. For example, two- or three-modal distributions are not uncommon for tumor samples and may reflect underlying genetic polymorphism (17). In most cases, it is hard to reliably determine characteristics of the distribution due to small sample sizes. Hoyle et al. (15) found in their analysis of multiple microarray datasets that distribution of spot intensities could be approximated by log-normal distribution. Giles and Kipling (16) used 59 Affymetrix GeneChips to test the normality of expression data and found that the majority of probe sets showed a high correlation with normality, with the exception of low-expressed genes. Similarly, in an experiment involving 56 independent arrays, Novak et al. (9) found that the distribution of data processed with Affymetrix GeneChip Analysis software was very close to normal. Thus, our normality assumption is quite reasonable and can be further relaxed in future studies. In cases where the distributions of experimental data are clearly non-normal, a number of normalization and transformation methods exist to remedy the situation (18).

Decisions about the number of replicates are often influenced by available funds. Currently, in many cases, technical costs such as price of microarrays plus the cost of their processing (for example, labeling and hybridization) are significantly higher than the cost of biological samples such as mice. However, certain biological samples can be very expensive (for example, brain tumors), but it is unlikely that they will be used for evaluation of technology.

It is also noteworthy that neither the methods nor the results of our study require microarray or other high-throughput data. Our major finding—that the optimal number of technical replicates equals to two in designing studies to estimate measurement reliability—holds for any ratio of technical to biological variance. Thus our result applies not only to the microarray context that inspired it, but also to other contexts. Additionally, our model may appear to apply only to one-channel microarrays. Yet on two-channel microarrays, our conclusions will also hold as long as we have a single value per gene per array—it could be a direct measure of intensity for single-channel arrays or a ratio (or log) difference of two measures for two-channel systems.

Based on results of this study, we give the following recommendations: use a sufficient number of samples; use appropriate normalization and transformation techniques if necessary to hold the normality assumption. It should be pointed out that our conclusion that the optimal number of technical replicates is two only applies to Type B studies to determine measurement reliability and has no direct bearing on the optimal number of technical replicates in Type A studies.

In summary, in this study we demonstrate that if the number of biological replicates and the number of technical replicates are variable, while the total number of available measurements is fixed, then the optimal allocation of replicates for measurement evaluation experiments requires two technical replicates for each biological replicate. Therefore, when investigators design measurement evaluation studies, we advocate that they use only two technical replicates for each biological replicate.

Materials and Methods

Sources of variation

The multiple factors influencing measurements in microarray and proteomics experiments could be divided into two major categories: biological variation and technical variation (1). Biological variation is caused by deviation of mRNA and protein levels within cells and among individuals 6., 7.. We consider the situation where biological variation is not the major focus of studies, but rather a sampling error in traditional definition. Sample preparation, labeling, hybridization, and other factors can contribute to technical variation, which is essentially a measurement error 8., 9., 10., 11., 12.. A common way to represent an observed value (X) is a combination of its “true” value (θ) and a measurement error (σ): X = θ + σ (19). We model an observed value X_i (for example, an expression level of a particular gene or an amount of a particular protein in a particular experiment after appropriate preprocessing techniques such as normalization or transformation have been applied) as a combination of its expected value (θ), a deviation (“error term”) due to true biological variation (${\sigma }_{Bio}^2$), and a deviation (“error term”) due to technical variation (${\sigma }_{Tech}^2$), that is: $X_i=\theta +{\sigma }_{Bio}^2+{\sigma }_{Tech}^2$. We assume that the biological variance is a combination of errors coming from different biological sources and the technical variance is the sum of errors from various technical sources. We define $s_{Bio}^2$ and $s_{Tech}^2$ to be estimates of ${\sigma }_{Bio}^2$ and ${\sigma }_{Tech}^2$ respectively. We further assume that both biological and technical error terms are normally distributed: $s_{Bio}\sim N\left(0,{\sigma }_{Bio}^2\right)$ and $s_{Tech}\sim N\left(0,{\sigma }_{Tech}^2\right)$. Thus, the biological variance of a sample is $s_{Bio}^2$, and the technical variance of a sample is $s_{Tech}^2$. We assume that biological population variance and technical population variance are independent $\left({\sigma }_{Bio}^2\perp {\sigma }_{Tech}^2\right)$ perhaps after suitable transformation (18), and the total population variance is the sum of biological and technical variance $\left({\sigma }_{Tot}^2={\sigma }_{Bio}^2+{\sigma }_{Tech}^2\right)$. Assuming that there are only two sources of variation in measurement X_i, with biological and technical error terms that are independent, then the total variance in a sample is the sum of biological and technical sample variance:

$$s_{Tot}^2=s_{Bio}^2+s_{Tech}^2$$ (1)

Reliability

Reliability is generally defined as the ratio of a “true” variation to the total variation in a set of measurements. We define the reliability, ρ², as a proportion of a biological variation in the total variation, that is, as a ratio of biological population variance to the total population variance: ${\rho }^2=\frac{{\sigma }_{Bio}^2}{{\sigma }_{Bio}^2+{\sigma }_{Tech}^2}$. Note that our definition of reliability is essentially the intraclass correlation coefficient 18., 20.. The biological population variance can be expressed as a function of the technical population variance and ρ²:

$${\sigma }_{Bio}^2=\frac{{\rho }^2}{1-{\rho }^2}{\sigma }_{Tech}^2$$ (2)

The estimate of reliability in a sample is:

$${\rho }^2=\frac{s_{Bio}^2}{s_{Bio}^2+s_{Tech}^2}=1-\frac{s_{Tech}^2}{s_{Bio}^2+s_{Tech}^2}$$

Definition of the problem

Let the total number of measurements (we define a “measurement” as the observation of a single quantitative variable on a single case) affordable in a measurement evaluation study be M, the number of biological replicates utilized be N, and the number of technical replicates per biological replicate be K, thus M = KN. We define a biological replicate as a biological sample, such as a rat or a tumor sample. The technical replicates are repeated measures of the same biological sample, for example, labeling and hybridization in a microarray experiment. We only consider the case of balanced design where the number of technical replicates for each biological replicate is the same. Under the assumption of the independence of biological variation and technical variation, we can estimate the biological sample variance and the technical sample variance separately. Though the ratio of technical population variance to the total population variance is a constant, the ratio of technical sample variance estimate to the total sample variance estimate, $R=\frac{s_{Tech}^2}{s_{Tot}^2}$, is a random variable whose variance depends on the sample size. The variance of the ratio R may vary as a function of the number of technical replicates. We evaluate different ways to allocate technical replicates with respect to the efficiency of an estimate of the ratio of the variance of technical replicates to the total variance. By minimizing the variance of R, we will be able to better estimate reliability in a sample, and thus better estimate reliability in a population, ρ². Therefore, we define the problem of finding an optimal allocation of technical replicates for measurement evaluation experiments as follows: For a fixed M, what value of K minimizes the variance of R? In the following, we provide details of analytical solution to the problem and illustrate our findings using a simulation experiment. Both approaches clearly show that the optimal value (K) of the number of technical replicates equals to 2.

Variance of the ratio R

We utilize an approximate formula for variance of the ratio of two random variables X and Y (21):

$$Var\left(\frac{X}{Y}\right)\approx {\left(\frac{E\left(X\right)}{E\left(Y\right)}\right)}^2\left[\frac{Var\left(X\right)}{{\left(E\left(X\right)\right)}^2}+\frac{Var\left(Y\right)}{{\left(E\left(Y\right)\right)}^2}-2\frac{Cov\left(X,Y\right)}{E\left(X\right)E\left(Y\right)}\right]$$ (3)

where E(X) and E(Y) is the expected value of X and Y, respectively, Var(X) and Var(Y) is the variance of X and Y, respectively, and Cov(X, Y) is the covariance of X and Y. Equation 3 does not make assumptions about distributions of X and Y. In our case, Equation 3 can be written as:

$$Var\left(R\right)=Var\left(\frac{s_{Tech}^2}{s_{Tot}^2}\right)\approx {\left(\frac{E\left(s_{Tech}^2\right)}{E\left(s_{Tot}^2\right)}\right)}^2\left[\frac{Var\left(s_{Tech}^2\right)}{{\left(E\left(s_{Tech}^2\right)\right)}^2}+\frac{Var\left(s_{Tot}^2\right)}{{\left(E\left(s_{Tot}^2\right)\right)}^2}-2\frac{Cov\left(s_{Tech}^2,s_{Tot}^2\right)}{E\left(s_{Tot}^2\right)E\left(s_{Tech}^2\right)}\right]$$ (4)

As we assume the independence of biological and technical sample variance, $s_{Bio}^2\perp s_{Tech}^2$, the covariance can be expressed in variance terms:

$$Cov\left(s_{Tech}^2,s_{Tot}^2\right)=Cov\left(s_{Tech}^2,\left[s_{Bio}^2+s_{Tech}^2\right]\right)=Cov\left(s_{Tech}^2,s_{Bio}^2\right)+Cov\left(s_{Tech}^2,s_{Tech}^2\right)=Var\left(s_{Tech}^2\right)$$ (5)

Equation 4 can be modified as follows (see details of derivation in the appendix):

$$Var\left(R\right)=Var\left(\frac{s_{Tech}^2}{s_{Tot}^2}\right)\approx \frac{Var\left(s_{Tech}^2\right){\left(E\left(s_{Bio}^2\right)\right)}^2+Var\left(s_{Bio}^2\right){\left(E\left(s_{Tech}^2\right)\right)}^2}{{\left(E\left(s_{Tech}^2\right)+E\left(s_{Bio}^2\right)\right)}^4}$$ (6)

We assume that both biological and technical error terms are normally distributed, $s_{Bio}^2\sim N\left(0,{\sigma }_{Bio}^2\right)$ and $s_{Tech}^2\sim N\left(0,{\sigma }_{Tech}^2\right)$. By the law of large numbers, the sample variance will converge to the population variance, thus the expected values of sample variance are those of population variance:

$$E\left(s_{Bio}^2\right)={\sigma }_{Bio}^2$$ (7)

$$E\left(s_{Tech}^2\right)={\sigma }_{Tech}^2$$ (8)

An approximate formula for the variance of a sample variance of a random variable X is as follows: $Var\left(Var\left(X\right)\right)\approx \left({\mu }_4-{\mu }_2^2\right)/S$, where μ₄ is the fourth moment and μ₂ is the second moment of X, and S is the sample size (22). In the case of a normally distributed variable X ~ N(0, σ²), the variance of sample variance is: Var(Var(X)) ≈ (2σ⁴)/S, where σ⁴ is the square of the population variance of X (22). Note that the following adjusted formula gives an unbiased estimate:

$$Var\left(Var\left(X\right)\right)\approx \frac{2}{S-1}{\sigma }^4$$ (9)

Thus, the approximate variance for estimates of the biological variance and the technical variance respectively is:

$$Var\left(s_{Bio}^2\right)\approx \frac{2}{N-1}{\left({\sigma }_{Bio}^2\right)}^2$$ (10)

$$Var\left(s_{Tech}^2\right)\approx \frac{2}{M-1}{\left({\sigma }_{Tech}^2\right)}^2$$ (11)

By substituting (7), (8), (10), (11) into Equation 6, we obtain a formula for Var(R) in terms of biological and technical population variance as well as the numbers of biological and technical replicates (see details of derivation in the appendix):

$$Var\left(R\right)\approx \frac{2{\left({\sigma }_{Tech}^2\right)}^2{\left({\sigma }_{Bio}^2\right)}^2}{{\left({\sigma }_{Bio}^2+{\sigma }_{Tech}^2\right)}^4}\left(\frac{1}{M-1}+\frac{1}{N-1}\right)$$ (12)

Finally, by substituting Equation 2 into Equation 12, we obtain a formula for the variance of the ratio of technical sample variance to the total sample variance (see details of derivation in the appendix):

$$Var\left(R\right)\approx 2{\rho }^4{\left(1-{\rho }^2\right)}^2\left(\frac{1}{M-1}+\frac{1}{N-1}\right)$$ (13)

Simulations

To illustrate our analytical solution, we performed simulations using the following algorithm:

1. Sample random number B_i of K, i = 1 to K, from a standard normal distribution B_i ~ N(0, 1). To represent “true” or biological variation, multiply each of the numbers by ρ, where ρ² is the ratio of biological population variance to the total population variance (see above).

2. For each of the number B_i, sample random number T_ij of N, j = 1 to N, from a standard normal distribution T_ij ~ N(0, 1). To represent technical variation, multiply each of the numbers by $\sqrt{1-{\rho }^2}$.

3. Thus, the observed value of measurements is $X_{ij}=B_i\rho +T_{ij}\sqrt{1-{\rho }^2}$.

4. Compute the variance of all T_ij numbers (“technical sample variance”) and B_i numbers (“total biological variance”).

5. Compute the ratio $R=\frac{Var\left(T_{ij}\right)}{Var\left(B_i\right)+Var\left(T_{ij}\right)}$.

6. Repeat Steps 1 to 5 for desired number of times (for example, 10,000).

7. Compute the variance Var(R) of the 10,000 ratios from Step 6.

Repeat Steps 1 to 7 for different N and K (given that M = KN is fixed), and for different levels of ρ² ranging from 0 to 1.

Authors’ contributions

SOZ performed the analysis and the simulation study. KK, AAB, and GPP contributed to discussion. DBA conceived and supervised the project. All authors contributed to the writing. The final manuscript has been read and approved by all authors.

Competing interests

The authors have declared that no competing interests exist.

Appendix

1. Derivation of Equation 6:

$\begin{array}{lll}Var\left(R\right)\hfill & =\hfill & Var\left(\frac{s_{Tech}^2}{s_{Tot}^2}\right)\approx {\left(\frac{E\left(s_{Tech}^2\right)}{E\left(s_{Tot}^2\right)}\right)}^2\left[\frac{Var\left(s_{Tech}^2\right)}{{\left(E\left(s_{Tech}^2\right)\right)}^2}+\frac{Var\left(s_{Tot}^2\right)}{{\left(E\left(s_{Tot}^2\right)\right)}^2}-2\frac{Var\left(s_{Tech}^2\right)}{E\left(s_{Tot}^2\right)E\left(s_{Tech}^2\right)}\right]\hfill \\ \hfill & =\hfill & {\left(\frac{E\left(s_{Tech}^2\right)}{E\left(s_{Tech}^2\right)+E\left(s_{Bio}^2\right)}\right)}^2\left[\frac{Var\left(s_{Tech}^2\right)}{{\left(E\left(s_{Tech}^2\right)\right)}^2}+\frac{Var\left(s_{Tech}^2+s_{Bio}^2\right)}{{\left(E\left(s_{Tech}^2\right)+E\left(s_{Bio}^2\right)\right)}^2}-2\frac{Var\left(s_{Tech}^2\right)}{\left(E\left(s_{Tech}^2\right)+E\left(s_{Bio}^2\right)\right)E\left(s_{Tech}^2\right)}\right]\hfill \\ \hfill & =\hfill & {\left(\frac{E\left(s_{Tech}^2\right)}{E\left(s_{Tech}^2\right)+E\left(s_{Bio}^2\right)}\right)}^2\left[\begin{array}{l}\frac{Var\left(s_{Tech}^2\right){\left(E\left(s_{Tech}^2\right)+E\left(s_{Bio}^2\right)\right)}^2+Var\left(s_{Tech}^2+s_{Bio}^2\right){\left(E\left(s_{Tech}^2\right)\right)}^2}{{\left(E\left(s_{Tech}^2\right)+E\left(s_{Bio}^2\right)\right)}^2{\left(E\left(s_{Tech}^2\right)\right)}^2}-\\ \frac{2Var\left(s_{Tech}^2\right)\left(E\left(s_{Tech}^2\right)+E\left(s_{Bio}^2\right)\right)E\left(s_{Tech}^2\right)}{{\left(E\left(s_{Tech}^2\right)+E\left(s_{Bio}^2\right)\right)}^2{\left(E\left(s_{Tech}^2\right)\right)}^2}\end{array}\right]\hfill \\ \hfill & =\hfill & \frac{1}{{\left(E\left(s_{Tech}^2\right)+E\left(s_{Bio}^2\right)\right)}^4}\left[\begin{array}{l}Var\left(s_{Tech}^2\right)\left({\left(E\left(s_{Tech}^2\right)\right)}^2+2E\left(s_{Tech}^2\right)E\left(s_{Bio}^2\right)+{\left(E\left(s_{Bio}^2\right)\right)}^2\right)+\\ Var\left(s_{Tech}^2\right){\left(E\left(s_{Tech}^2\right)\right)}^2+Var\left(s_{Bio}^2\right){\left(E\left(s_{Tech}^2\right)\right)}^2-\\ 2Var\left(s_{Tech}^2\right){\left(E\left(s_{Tech}^2\right)\right)}^2-2Var\left(s_{Tech}^2\right)E\left(s_{Bio}^2\right)E\left(s_{Tech}^2\right)\end{array}\right]\hfill \\ \hfill & =\hfill & \frac{1}{{\left(E\left(s_{Tech}^2\right)+E\left(s_{Bio}^2\right)\right)}^4}\left[Var\left(s_{Tech}^2\right){\left(E\left(s_{Bio}^2\right)\right)}^2+Var\left(s_{Bio}^2\right){\left(E\left(s_{Tech}^2\right)\right)}^2\right]\hfill \end{array}$

2. Derivation of Equation 12:

$$\begin{array}{lll}Var\left(R\right)\hfill & \approx \hfill & \frac{1}{{\left(E\left(s_{Tech}^2\right)+E\left(s_{Bio}^2\right)\right)}^4}\left[Var\left(s_{Tech}^2\right){\left(E\left(s_{Bio}^2\right)\right)}^2+Var\left(s_{Bio}^2\right){\left(E\left(s_{Tech}^2\right)\right)}^2\right]\hfill \\ \hfill & =\hfill & \frac{1}{{\left({\sigma }_{Bio}^2+{\sigma }_{Tech}^2\right)}^4}\left[\frac{2}{M-1}{\left({\sigma }_{Tech}^2\right)}^2{\left({\sigma }_{Bio}^2\right)}^2+\frac{2}{N-1}{\left({\sigma }_{Bio}^2\right)}^2{\left({\sigma }_{Tech}^2\right)}^2\right]\hfill \\ \hfill & =\hfill & \frac{2{\left({\sigma }_{Tech}^2\right)}^2{\left({\sigma }_{Bio}^2\right)}^2}{{\left({\sigma }_{Bio}^2+{\sigma }_{Tech}^2\right)}^4}\left(\frac{1}{M-1}+\frac{1}{N-1}\right)\hfill \end{array}$$

3. Derivation of Equation 13:

$$\begin{array}{lll}Var\left(R\right)\hfill & \approx \hfill & \frac{2{\left({\sigma }_{Tech}^2\right)}^2{\left({\sigma }_{Bio}^2\right)}^2}{{\left({\sigma }_{Bio}^2+{\sigma }_{Tech}^2\right)}^4}\left(\frac{1}{M-1}+\frac{1}{N-1}\right)\hfill \\ \hfill & =\hfill & \frac{2{\left(\frac{{\rho }^2}{1-{\rho }^2}{\sigma }_{Tech}^2\right)}^2{\left({\sigma }_{Tech}^2\right)}^2}{{\left(\frac{{\rho }^2}{1-{\rho }^2}{\sigma }_{Tech}^2+{\sigma }_{Tech}^2\right)}^4}\left(\frac{1}{M-1}+\frac{1}{N-1}\right)\hfill \\ \hfill & =\hfill & \frac{2{\left({\sigma }_{Tech}^2\right)}^4\frac{{\rho }^4}{{\left(1-{\rho }^2\right)}^2}}{{\left({\sigma }_{Tech}^2\right)}^4{\left[\frac{{\rho }^2+\left(1-{\rho }^2\right)}{1-{\rho }^2}\right]}^4}\left(\frac{1}{M-1}+\frac{1}{N-1}\right)\hfill \\ \hfill & =\hfill & 2{\rho }^4{\left(1-{\rho }^2\right)}^2\left(\frac{1}{M-1}+\frac{1}{N-1}\right)\hfill \end{array}$$