MOF: An R Function to Detect Outlier Microarray

Abstract

We developed an R function named “microarray outlier filter” (MOF) to assist in the identification of failed arrays. In sorting a group of similar arrays by the likelihood of failure, two statistical indices were employed: the correlation coefficient and the percentage of outlier spots. MOF can be used to monitor the quality of microarray data for both trouble shooting, and to eliminate bad datasets from downstream analysis. The function is freely avaliable at http://www.wriwindber.org/applications/mof/.

Introduction

DNA microarray analysis has gained widespread application and a wide variety of methods have been developed to analyze the large and complex datasets generated by this technology (1). Due to the sheer volume of data, and the high number of sources of potential error, quality control and quality assurance (QC/QA) are critical to microarray experiments (2). Since error may be the result of many factors at multiple steps, a number of QC/QA measures have been proposed to monitor specific sources of error. Most of these methods focus on individual spots or spots within a single array (3). Other methods monitor an individual array as a whole during the experimental process using classification methods (4) or by comparison of the statistical features of an array with the same statistical features based on historical data (5). Here we report an R function (www.rproject.org) named microarray outlier filter (MOF), which was designed to screen outliers at the whole array level by using the arrays from the current experiment and those from the historical archive that meet defined criteria. Our lab now routinely applies this software to the QA of our microarray experiments (6). MOF is freely avaliable at http://www.wriwindber.org/applications/mof/.

Resource Description

Capabilities

In essence, MOF examines the consistency of arrays in a large scale experiment (multiple arrays). Arrays, as a whole, are inspected to reveal those arrays that are obviously different from most others. These few “abnormal” arrays are most likely failed arrays that may contain unreliable data. This analysis is based on two assumptions: first, that all samples are similar in gene expression profile (that is, technical or biological replicates) and that they have been subjected to the same experimental procedure (in principle, the results should be similar between arrays since expression levels should be uniform for the majority of the probes); second, that data from most of the arrays are of good quality, resulting in only a few unusual arrays being labeled as potentially failed ones. Otherwise, it is possible for a systematic experimental error to result in the few good arrays being suspected as failures because they are identified as “abnormal” by MOF. Note that historical arrays satisfying these two criteria can be included to generate a larger dataset for analysis of the outliers.

MOF employs two statistical indices for array comparison. One index is the percentage of outlier spots on an array. An outlier data point is defined in the context of all the data points for the same specific probe, across all the arrays. The resistant z-score is used to tag an outlier data point, which is defined as:

$$z_i=\frac{X_i-\tilde{X}}{\tilde{s}}$$

where $\tilde{X}$ and $\tilde{s}$ are the median and median absolute deviation values, respectively, for each probe across all arrays. This statistical index is chosen because of its resistance to outliers (7). A data point is designated as an outlier if its resistant z-score falls outside a preset threshold, which may be 3, 4 or 5 in our experience. The percentage of outliers among all data points in consideration from an array is used as an indicator of the quality of the array. This is based on our observation that an outlier array, which is largely different from the majority of comparable arrays in its gene expression profile, tends to have more data points distributed at extremes. An unusually high percentage of outlier spots on an array signals a failed array. The other statistical index is the Pearson correlation coefficient, expressed as:

$$r=\frac{{\displaystyle {\sum }_{i=1}^k}(X_i-\overline{X})(Y_i-\overline{Y})}{(n-1)S_x{S}_y}$$

where X and Y are two variables of the signal intensities from the two arrays, n is the number of probes included, $\overline{X}$ and $\overline{Y}$ stand for means, S_x and S_y stand for standard deviations of two variables, respectively. The correlation coefficient between two arrays is computed by a function provided in the R package. Each array is represented by a collection of data points in the same order of probes. Thus, the correlation coefficient reflects the similarity of the two arrays in regard to the expression levels for all the probes collectively. If an array displays apparently low correlation or even reverse correlation to many other arrays, it is flagged as an unusual array merit closer review for failure.

Therefore, MOF can be used to assist in the detection of potentially failed arrays. As an R function, MOF is a ready-to-use tool for listing the arrays by the possibility of failure. The lists give the user a better opportunity to identify potentially failed arrays quickly. It does not mean that there must be failed arrays in each batch of arrays. Thus it is very important for the user to further verify that the outlier arrays are actually failed arrays by other means, such as scatter plots, clustering, etc., starting from the worst outlier arrays. In our experience, the two lists determined by the MOF indices often show the same “unusual” arrays, thus confirming each other. However, since these two indices do not reflect exactly the same properties of the data, they may detect different abnormalities in the arrays and thus complement each other. Again, additional validation is critical to identify the truly failed arrays and the underlying causes.

Implementation and developer resources

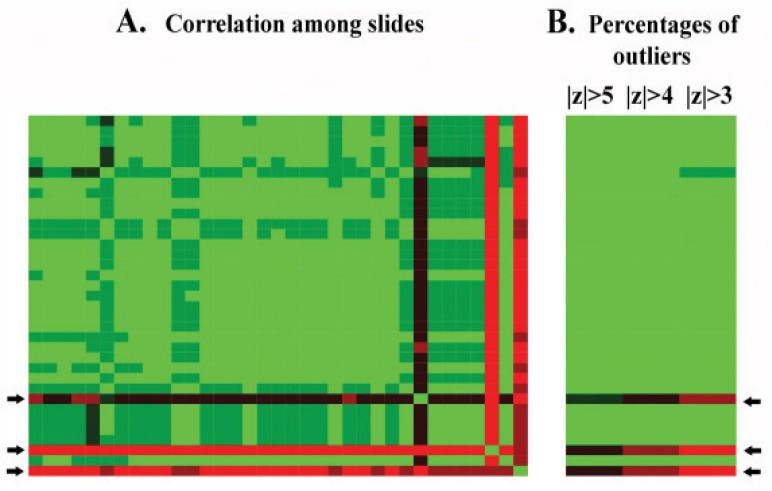
MOF is implemented as an R function. The input text file is a matrix containing preprocessed microarray data with rows as probes and columns as arrays. For maximum reliability, data points with expression levels close to the background or within the scanner saturation range should be discarded. The output is three text files and two heat maps. In the first text file, two lists of arrays are ordered according to the average correlation coefficient to the rest of the arrays and percentage of outlier spots, respectively. A correlation coefficient table containing the correlation coefficients for all pairs of arrays is found in the second text file. A heat map is generated to provide a general visualization of this table (Figure 1A) as a guide for the utilization of the data for additional detailed analysis. Similarly, percentages of outlier spots for all the arrays are also given as a table in a text file and a corresponding heat map (Figure 1B).

Fig. 1.

Heat maps showing correlation among arrays (A) and percentages of outliers on the arrays (B). Green color stands for high correlation and low percentage of outliers while red color represents the opposite. Black refers to the middle range between green and red. The color scale is different between analyses depending on the range of values represented by the colors. In this heat map, the correlation coefficient spans from 0.18 to 0.98, and the lowest and highest percentages of outlier spots are 0 and 42%, respectively. The arrays are arranged in the same vertical order on both heat maps, and panel A has the same horizontal and vertical order. Thresholds of 3, 4, and 5 are used in panel B for the resistant z-score to determine outlier data points. These results are from 35 arrays of the UHR RNA sample. The UHR sample was used as the control in experiments and was expected to produce highly consistent data. However, both correlation coefficient and percentage of outlier spots suggested the same 3 arrays (indicated by arrows) as outlier arrays.

Empirical Demonstration

Using MOF requires setting proper thresholds for the two statistics to flag problematic arrays. In our practice we set the cut-offs at 0.8, 3, and 6% for Pearson correlation coefficient, z-value, and the outlier percentage, respectively. Then, common arrays on the two lists reported by MOF satisfying the thresholds respectively can be considered primary candidates of problematic arrays. Another way to set the threshold is to take the top 15%–20% worst arrays as indexed in the two lists, and then identify common arrays. We would like to caution that the user needs to adjust the threshold based on their experience and the available resources.

For reference, we report here two scenarios in using MOF, illustrated with experimental data generated by our core facility. In one scenario, a couple of problematic arrays are so different from the rest of the arrays that the two statistics effectively singled them out. For example, we have a dataset composed of 35 arrays using the universal human reference (UHR) RNA sample (Stratagene, La Jolla, USA), both indices flagged the same 3 arrays as outlier arrays (Figure 1). Each of the 3 arrays had a distinctly lower average correlation coefficient and higher percentage of outlier spots than other arrays. In details, Pearson correlation coefficients were 0.22, 0.30, and 0.49 for the top 3 arrays, and >0.76 for the rest; taking |z|=3, the same 3 arrays contained outliers of 28%–42%, with the fourth showing 11% and the rest showing 5% or less. Two of these three arrays were confirmed by the laboratory as failed experiments with reasons identified.

In another scenario, there is a lack of outstanding problematic arrays and on the two lists reported by MOF the statistical index changes relatively smoothly, from low to high for Pearson correlation coefficient or from high to low for z-score reported outlier percentages. Our recommended thresholds work for this scenario as well. For example, in a dataset composed of 185 arrays of human blood samples (30 controls and 155 patients with breast disease), following the thresholds we have about 30 arrays from either reported list to work on. 12 arrays were common in the top 30 arrays on both lists and were later verified to have obvious problems by scatter plots.

Discussion

MOF has been successfully applied to our in-house microarray data as a routine QA measure (6). However, users should note that in order to apply MOF to any microarray datasets, the two assumptions mentioned above must be met. In our practice, when applying MOF to a mouse dataset from different tissue types, tissue specific clusters were generated apparently due to the differences in gene expression profiles between tissue types. In such a case, the first of the two assumptions was not satisfied and thus MOF was not applicable.

As an additional note, the percentage of outliers changes when using different z-scores. Selecting different z-scores may make some arrays to stand out with apparently higher percentages of outlier data points. Therefore, the relative level of percentage of outliers is a more meaningful characteristic for judgment than the absolute value itself. The same reasoning also applies when using the Pearson correlation coefficient. Users are encouraged to identify more realistic cut-offs in their specific settings using our thresholds as guidance. Although a minimal of three arrays is required for correlation coefficient to pick out an outlier array, we recommend that MOF should be used on datasets comprised of ten or more arrays. The procedure also works well for over a hundred arrays in our microarray experiments. Historical data obtained with the same technology on the same tissue type can be used in the analysis to increase the normal array base.

Authors’ contributions

SY developed the method, performed data analyses and drafted the manuscript. XG programmed the graphics presentation part of MOF and assisted in manuscript preparation. HH initiated and supervised the project, and co-drafted the manuscript. All authors read and approved the final manuscript.

Competing interests

The authors have declared that no competing interests exist.