Abstract
Composition vector trees (CVTrees) are inferred from whole-genome data by an alignment-free and parameter-free method. The agreement of these trees with the corresponding taxonomy provides an objective justification of the inferred phylogeny. In this work, we show the stability and self-consistency of CVTrees by performing bootstrap and jackknife re-sampling tests adapted to this alignment-free approach. Our ultimate goal is to advocate the viewpoint that time-consuming statistical re-sampling tests can be avoided at all in using this alignment-free approach. Agreement with taxonomy should be taken as a major criterion to estimate prokaryotic phylogenetic trees.
Key words: composition vector, phylogeny, topological distance, bootstrap, jackknife, CVTree
Introduction
Composition vector (CV) trees are inferred from whole-genome data by using an alignment-free and parameter-free method (1), implemented as a web server entitled CVTree 2, 3. The CV method has been successfully applied to infer phylogeny of viruses 4, 5, bacteria 1, 6, 7, chloroplast (8) and fungi (9). In all cases, the majority of branchings in the CVTrees agree well with the biologists’ classification at all taxonomic ranks from phyla down to species while a few disagreements remain. They indicate strongly on possible taxonomic revisions debated by microbiologists since a long time ago (7). This overall agreement serves as a major and objective justification of the CVTrees.
However, traditionally phylogenetic trees obtained using various methods are subject to statistical re-sampling tests such as bootstrap or jackknife (10). In fact, due to the limited size of sampling space, most researchers could not afford to do jackknife tests and had to be content with bootstrap type tests. Nonetheless, even successful passing of these tests merely shows stability and self-consistency of the inferred trees with respect to certain variations in the original dataset. Objective judgment of the meaningfulness of trees must rely on arguments beyond trees themselves, say, by direct comparison with the efforts of many generations of taxonomists as ideally phylogeny and taxonomy should agree with each other. However, several anonymous referees of our previous publications and a few users of the CVTree web server 2, 3 have repeatedly raised the questions of statistical support of the CVTrees. Correspondingly, we have shown a few bootstrap results in Qi et al. (1) and Wang et al. (9) without giving details. In these papers, we described the method of our bootstrap, jackknife and anti-jackknife (see below) tests of CVTrees. We showed the results on the examples of virus, bacteria and fungi. Since full-fledged bootstrap/jackknife tests are extremely time-consuming and soon come the epoch of inferring phylogeny for thousands of species in not-too-distant future, our ultimate goal is to advocate the viewpoint that one may give up routine statistical re-sampling tests for the robust and stable CV method, and rely on direct comparison of phylogeny with taxonomy to justify the inferred trees.
In the CV approach, each organism is represented by a composition vector made of K-peptide counts obtained from the organism’s proteome. The K-value controls the resolution of the method. A subtraction procedure based on (K−2)-th order Markov prediction is introduced to suppress effect of neutral mutations and to highlight the shaping role of natural selection (1). The most suitable K-values depend on the overall size of the proteome of the group of organisms under study. Our previous work has shown that the “best” Ks are 4 and 5 for viruses, 5 and 6 for prokaryotes, 6 and 7 for fungi. We will see that bootstrap tests provide another angle to look at these K-values.
Thus our justification of CVTrees goes in two steps. First, we show that the CVTrees based on whole proteomes (to be called the original CVTrees hereafter) are robust, and the branchings agree well with the corresponding taxonomy. This has been done in our previous studies 1, 5, 6, 7, 8, 9. Second, in this paper, trees obtained by bootstrap or jackknife re-sampling of the datasets are compared to the original CVTrees at the same K in terms of topological distances between them. As CVTrees are calculated by Neighbor-Joining algorithm (11), which is a robust and quartet-based method (12), our strategy reminds what adopted by Rzhetsky and Nei (13) in estimating minimal-evolution trees by comparison with the corresponding NJ-tree. We make emphasis on topology, i.e., branching schemes, of the trees as they are directly related to taxonomy.
Method
As CV method does not use sequence alignment, statistical re-sampling cannot be carried out in the usual way of random choice of nucleotide or amino acid sites with replacement. Instead, we pick up proteins at random from the pool of all proteins in the genome of an organism. We used four datasets of protein sequences encoded in the genome:
-
1.
A collection of 124 double-strand DNA (dsDNA) virus genomes as studied and listed in Gao and Qi (5), denoted as “Virus 124” in Figure 1, Figure 2.
-
2.
A collection of 16 archaea, 87 bacteria, and 6 eukarya genomes, denoted as “Prokaryote 109” in Figure 1, Figure 2. This 109-genome dataset was used in Qi et al. (1) and served as a touchstone for many further studies.
-
3.
A collection of 41 archaea, 401 bacteria, and 8 eukarya genomes, denoted as “Prokaryote 450” in Figure 1, Figure 2. The list of these 450 genomes may be fetched from the authors’ webpage (http://www.itp.ac.cn/~hao/450list.pdf).
-
4.
A collection of 82 fungal genomes plus 3 eukarya as outgroups. This dataset was used in Wang et al. (9) and denoted as “Fungi 85” in Figure 1, Figure 2.
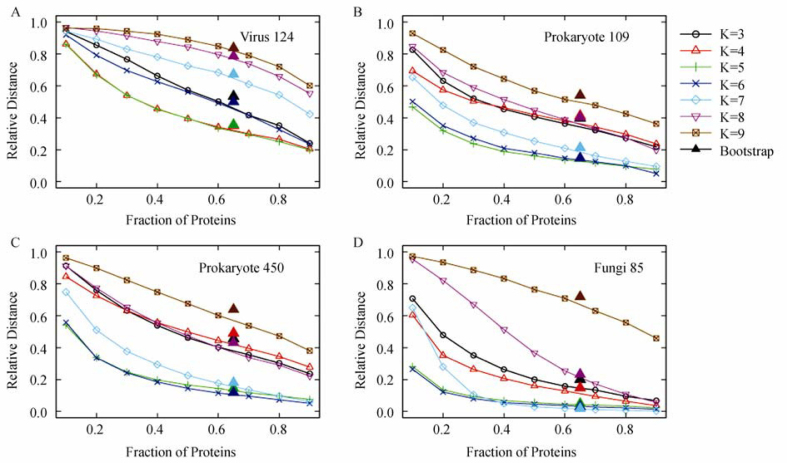
Figure 1.
Summary of jackknife tests for the four datasets. A. “Virus 124” dataset. B. “Prokaryote 109” dataset. C. “Prokaryote 450” dataset. D. “Fungi 85” dataset. Solid triangles drawn near fraction of proteins 0.6321 show the results of bootstrap tests at different K-values as represented by the same color used for the jackknife tests.
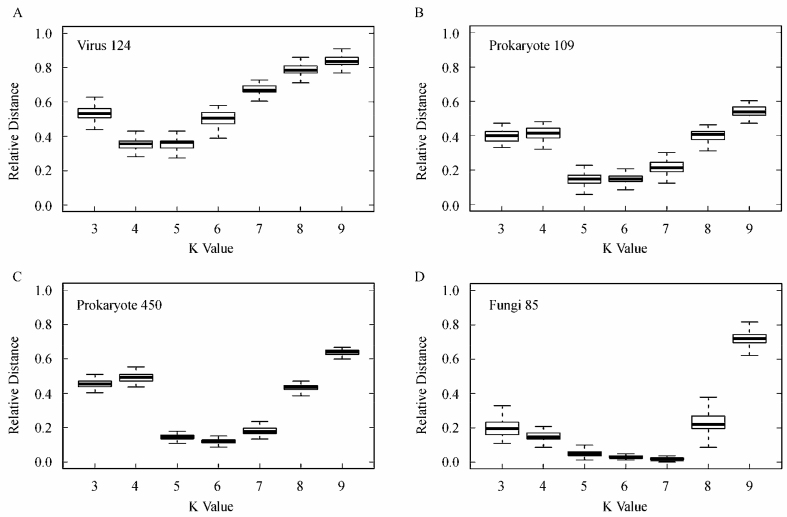
Figure 2.
Distribution of bootstrap results for “Virus 124” (A), “Prokaryote 109” (B), “Prokaryote 450” (C), and “Fungi 85” (D) datasets. At each K-value shown are the median, the 25% and 75% margin, and the minimal and maximal distance.
On each of these datasets, jackknife and bootstrap tests are performed in the following way. In the CV method, a species is represented by a composition vector made of overlapping K-residues, designated as “K-peptides” hereafter, from all proteins in the genome. To do jackknife tests, we first take randomly 90% of proteins from the whole protein pool. This is done for all species and a CVTree is constructed by carrying out the crucial “subtraction procedure” (1). The topological distance between this tree and the original CVTree inferred from the whole protein pool is calculated. This re-sampling is performed 100 times and the average topological distance between these 100 trees and the original 100% CVTree at the same K is taken. Then the protein fraction is decreased to 80%, 70%, …, 10% and the average topological distance at a given K is plotted against the protein fraction (Figure 1).
Suppose a species’ genome contains M protein products. In order to do bootstrap tests, the same number M proteins are drawn at random from the pool. The drawing is done with replacement, i.e., some proteins may be drawn repeatedly and some others may be skipped at all. The topological distance between a bootstrap tree and the original CVTree with the same K is calculated. Again the average topological distance of 100 bootstrap trees is retained as the final result (see the discussion of Figure 2 below).
In doing a bootstrap test, the probability that a designated protein is drawn at the first try is 1/M; the probability of its being skipped is 1−/M. The probability of its being dropped at M tries is (1−1/M)M and the probability of being drawn is 1−(1−1/M)M. At the limit of very big M, the latter goes to 1−1/e ≈ 0.63212, where e=2.71828 is the base of natural logarithm. This means that in performing a bootstrap test, though M proteins are drawn from the pool on average, only 63.21% of the protein assortment is kept. Therefore, we superimpose the results of bootstrap tests for various K conditionally against protein fraction 0.6321 in Figure 1 of jackknife tests.
We used the topological distance to measure the difference between phylogenetic trees. The definition of topological distance could be found in the previous literature 14, 15. An unrooted tree with N terminal leaves has N−3 internal edges. Cutting any of these internal edges defines a split of the set of leaves into two subsets. To measure the distance between two trees constructed for the same set of leaves, we compare the two lists of split-trees obtained by cutting each of the N−3 internal edges. If the two lists are identical up to reordering, the two trees have the same topology and the topological distance dT=0. In general, the topological distance is defined as (16):
The factor 2 was introduced to incorporate more general cases of multi-furcating nodes (CV method yields only bifurcating trees). Therefore, if the two trees have entirely different topologies, the topological distance between them reaches the maximal value dT = 2×(N−3). We have written a program to implement the definition of topological distance. In fact, we adopt a relative topological distance by dividing the calculated dT by its maximal possible value 2×(N−3), thus the factor 2 drops out and the relative distance varies between 0 and 1.
Results and Discussion
Jackknife results for the four datasets are shown in Figure 1. We first consider the bottom figure for the “Fungi 85” dataset. When more than 60% proteins are used for the K=6 and 7 jackknife trees, it yields results comparatively close to the original CVTree at the same K-value. In fact, at protein fraction 0.9, the average result of K=7 tree appears to be closest to the original CVTree.
For prokaryotes we show the results for two datasets with 109 and 450 genomes, respectively. The two figures bear great similarity at more than threefold differences of the number of genomes. Therefore, it is natural to expect that similar behavior holds for even greater datasets. For both datasets, the lowest K=5 and 6 curves yield results closest to the original CVTrees.
The topmost figure shows jackknife results for viruses. As the overall size of virus proteomes is much smaller, these trees differ more in their topological distance from the original CVTrees. Yet at K=4 and 5 for not-too-small protein fractions, the trees are reasonably close to the original CVTrees as discussed in Gao and Qi (5), displaying significant agreement with present understanding of the virus classification.
There are variations of jackknife tests, for example, by checking the resulted trees when dropping out one species at a time. Conversely, one may add a few genomes, chosen at random, to see the effect of dataset getting larger and larger. We call this an anti-jackknife test. We have published prokaryotic CVTrees for 84 genomes in Hao and Qi, 2003 (17), 109 genomes in Qi et al. (1), 145 genomes in Hao and Qi, 2004 (18), 222 genomes in Gao et al., 2006 (19), 440 genomes in Gao et al., 2007 (6), and 892 genomes in Li et al. (7). Our most recent CVTrees were obtained for 1,173 genomes (unpublished). The quality of CVTrees in the sense of agreement with taxonomy has kept improving. Viewed retrospectively, the CV method has successfully endured the anti-jackknife tests. Besides the well-known fact that, in general, broader sampling improves phylogenetic trees, CVTrees have demonstrated significant robustness with expanding datasets.
As we explained before, triangles superimposed at protein fraction 0.6321 in Figure 1 show bootstrap results at K-values represented by the same color as the jackknife curves. In fact, each triangle gives the average topological distance from 100 bootstrap tests. The distributions of the 100 bootstrap tests at each K-value are shown in Figure 2, which was actually produced by using graphic tools in the R Package (20). Against each K-value, the median, the 25% and 75% range, and the minimal and maximal values are drawn.
It is interesting to note that Figure 2 provides another angle to look at the “best” K-values for different organism groups. It is appropriate to reproduce in more details the order-of-magnitude estimate for the “best” K-values, given in our recent paper (7). Suppose that the frequency of appearance of all amino acids is the same, e.g., 1/20. Then the probability of encountering a designated K-peptide is 20−K. Let L be the total number of amino acids in the collection of proteins of an organism, the expected number of such K-peptide is L/(20)K. In order for a K-peptide to bear species-specificity, this number should be less than what expected for a random sequence, i.e., L/(20)K≪1 or, after taking logarithm of base 10, logL < K(1+log2). On the other hand, the subtraction procedure in CV method requires that the number of (K−2)-peptide should not be too few: L/(20)(K−2)>1, i.e., logL > (K−2)(1+log2). Putting together these inequalities, we get
In an order-of-magnitude discussion, we may take the total number L of amino acids in an organisms’ proteome to be 105, 106, and 107 for viruses, prokaryotes, and fungi, respectively. Thus we get
3.8 < K < 5.8 (for viruses)
4.6 < K < 6.6 (for prokaryotes)
5.4 < K < 7.4 (for fungi)
yielding K=4 and 5 for viruses, 5 and 6 for prokaryotes, and 6 and 7 for fungi, agreeing with what is seen clearly in Figure 2.
The use of whole-genome data is both a merit and a demerit of the CV method, as the number of whole genomes, though growing rapidly, is always limited. However, our jackknife and bootstrap tests show that suffice it to have a substantial part of proteins of each organism, the major branchings in the trees will justify the corresponding taxonomy and vice versa.
Authors’ contributions
GZ and ZX collected data and performed most of the calculations. HY implemented the Penny-Hendy algorithm for calculating topological distance between trees. BH designed the whole work and performed the analysis. GZ and BH wrote the manuscript. All authors read and approved the final manuscript.
Competing interests
The authors have declared that no competing interests exist.
Acknowledgements
This work was partially supported by the National Basic Research Program of China (the 973 Program, Grant No. 2007CB814800) and the Shanghai Leading Academic Discipline Project (Grant No. B111). Most of the number-crunching calculations were performed at Shanghai Supercomputer Center of China and on a Linux cluster at ITP, CAS, in Beijing.
References
- 1.Qi J. Whole proteome prokaryote phylogeny without sequence alignment: a K-string composition approach. J. Mol. Evol. 2004;58:1–11. doi: 10.1007/s00239-003-2493-7. [DOI] [PubMed] [Google Scholar]
- 2.Qi J. CVTree: a phylogenetic tree reconstruction tool based on whole genomes. Nucleic Acids Res. 2004;32:W45–W47. doi: 10.1093/nar/gkh362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Xu Z., Hao B. CVTree update: a newly designed phylogenetic study platform using composition vectors and whole genomes. Nucleic Acids Res. 2009;37:W174–W178. doi: 10.1093/nar/gkp278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Gao L. Molecular phylogeny of coronaviruses including human SARS-CoV. Chin. Sci. Bull. 2003;48:1170–1174. doi: 10.1007/BF03183929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Gao L., Qi J. Whole genome molecular phylogeny of large dsDNA viruses using composition vector method. BMC Evol. Biol. 2007;7:41. doi: 10.1186/1471-2148-7-41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Gao L. Prokaryote phylogeny meets taxonomy: an exhaustive comparison of composition vector trees with systematic bacteriology. Sci. China C Life Sci. 2007;50:587–599. doi: 10.1007/s11427-007-0084-3. [DOI] [PubMed] [Google Scholar]
- 7.Li Q. Composition vector approach to whole-genome-based prokaryotic phylogeny: success and foundations. J. Biotechnol. 2010;149:115–119. doi: 10.1016/j.jbiotec.2009.12.015. [DOI] [PubMed] [Google Scholar]
- 8.Chu K.H. Origin and phylogeny of chloroplasts revealed by a simple correlation analysis of complete genomes. Mol. Biol. Evol. 2004;21:200–206. doi: 10.1093/molbev/msh002. [DOI] [PubMed] [Google Scholar]
- 9.Wang H. A fungal phylogeny based on 82 complete genomes using the composition vector method. BMC Evol. Biol. 2009;9:195. doi: 10.1186/1471-2148-9-195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Felsenstein J. Inferring Phylogenies. Sinauer; Sunderland, USA: 2004. [Google Scholar]
- 11.Saitou N., Nei M. The neighbor-joining method: a new method for reconstructing phylogenetic trees. Mol. Biol. Evol. 1987;4:406–425. doi: 10.1093/oxfordjournals.molbev.a040454. [DOI] [PubMed] [Google Scholar]
- 12.Mihaescu R. Why neighbor-joining works? Algorithmica. 2009;54:1–24. [Google Scholar]
- 13.Rzhetsky A., Nei M. A simple method for estimating and testing minimum-evolution trees. Mol. Biol. Evol. 1992;9:945–967. [Google Scholar]
- 14.Robinson D.F., Foulds L.R. Comparison of phylogenetic trees. Math. Biosci. 1981;53:131–147. [Google Scholar]
- 15.Penny D. The use of tree comparison metrics. Syst. Zool. 1985;34:75–82. [Google Scholar]
- 16.Nei M., Kumar S. Molecular Evolution and Phylogenetics. Oxford University Press; New York, USA: 2000. [Google Scholar]
- 17.Hao B., Qi J. Vertical heredity vs. horizontal gene transfer: a challenge to bacterial classification. J. Sys. Sci. Complex. 2003;16:307–314. [Google Scholar]
- 18.Hao B., Qi J. Prokaryote phylogeny without sequence alignment: from avoidance signature to composition distance. J. Bioinform. Comput. Biol. 2004;2:1–19. doi: 10.1142/s0219720004000442. [DOI] [PubMed] [Google Scholar]
- 19.Gao L. Simple Markov subtraction essentially improves prokaryote phylogeny. AAPPS Bull. 2006;16:3–7. [Google Scholar]
- 20.R Development Core Team . R Foundation for Statistical Computing; Vienna, Austria: 2008. R: A Language and Environment for Statistical Computing. [Google Scholar]