A Modified Ant Colony Optimization Algorithm for Tumor Marker Gene Selection

Abstract

Microarray data are often extremely asymmetric in dimensionality, such as thousands or even tens of thousands of genes but only a few hundreds of samples or less. Such extreme asymmetry between the dimensionality of genes and samples can lead to inaccurate diagnosis of disease in clinic. Therefore, it has been shown that selecting a small set of marker genes can lead to improved classification accuracy. In this paper, a simple modified ant colony optimization (ACO) algorithm is proposed to select tumor-related marker genes, and support vector machine (SVM) is used as classifier to evaluate the performance of the extracted gene subset. Experimental results on several benchmark tumor microarray datasets showed that the proposed approach produces better recognition with fewer marker genes than many other methods. It has been demonstrated that the modified ACO is a useful tool for selecting marker genes and mining high dimension data.

Introduction

The advent of DNA microarray technology has provided the ability to measure the expression levels of thousands of genes simultaneously in a single experiment and made it possible to provide diagnosis for disease, especially for tumor, at molecular level ^{1., 2.}. However, classification based on microarray data is very different from previous classification problems in that the number of genes (typically tens of thousands) greatly exceeds the number of samples (typically a few hundreds or less), resulting in the known problem of “curse of dimensionality” and over-fitting of the training data (3). It is thus important for successful disease diagnosis to select a small number of discriminative genes from thousands of genes (4). The benefits gained from gene selection in microarray data analysis are not only the better classification accuracy, but also the decrease of the cost in a clinical setting (5) and interpretability of genetic nature of the disease for biologists (6). Therefore, marker gene selection plays a crucial role in developing a successful disease diagnostic system based on microarray data.

In recent years, various marker gene selection methods have been proposed. Most of them have been proven helpful for improving predictive accuracy of disease and providing useful information for biologists and medical experts. All of these marker gene selection methods may be grouped into two teams: filter, which is also called gene ranking approach; and wrapper, which is also entitled as gene subset selection approach (7). In filter approach, each gene is evaluated individually and assigned a score reflecting its correlation with the class according to certain criteria. Genes are then ranked by their scores and some top-ranked ones are selected. These filter approaches have been based on t-statistics (1), χ²-statistics (8), informative gain ^{9., 10.}, signal-noise ratio (11), Pearson correlation coefficient (12) and combination of several feature filtering algorithms ^{4., 13.}. In the wrapper approach (14), a search is conducted in the space of genes, evaluating the goodness of each found gene subset by the estimation of the accuracy percentage of the specific classifier to be used, training the classifier only with the found genes. Compared with the filter approach, the wrapper approach may obtain one gene subset with better classification performance but more computational cost. Some wrapper-based approaches have been provided and widely applied in bioinformatics, such as GA (15), PSO (16) and SFS (17). Although these approaches have obtained excellent performance in gene expression data analysis, some congenital drawbacks still puzzle themselves such as excessive computational cost of GA and local optimum of PSO. Therefore, a simple modified ant colony optimization (ACO) algorithm is proposed in the present paper to search the optimum marker gene subset.

ACO algorithm is biologically inspired from the behavior of colonies of real ants, and in particular how they forage for food. Since the idea of ACO was proposed by Colorni et al. in 1991 (17), it has been successfully applied to solve various discrete combinatorial optimization problems, such as TSP (17), telecommunication networks (18), data mining (19) and protein folding (20). In this paper, we made some simple modifications based on conventional ACO algorithm to make it more suitable for marker gene subset search. Support vector machine (SVM) is selected as classifier or evaluator in our study. SVM has been found useful in handling classification tasks in the case of the high dimensionality and small-sample data (21). The proposed approach was applied in several well-known tumor microarray datasets and the experiment results showed excellent prediction performance.

Method

Modified ant colony optimization algorithm for marker gene selection

The ACO algorithm developed by Colorni et al. in 1991 (17) has been proven effective in many discrete combinatorial optimization problems ^{18., 19., 20.}. Since marker gene selection may be regarded as one of the discrete combinatorial optimization problems, we have reasons to believe that ACO will perform outstandingly in the aspect of marker gene subset selection.

To apply ACO effectively to select subset of marker genes, a simple modified ACO algorithm is proposed. As indicated in Figure 1, the procedure of marker gene selection may be regarded as the procedure of foraging for food of ant. In the process of moving from nest to food, ant will pass each gene in candidate gene subset. From one gene to next gene, two pathways may be selected: pathway 1 represents that the next gene will be selected and pathway 0 denotes that the next gene will be filtered. At last, when ant arrives at the food, some genes are extracted and put into the marker gene subset, the others are filtered. A binary set {1, 0, 0, 1, 0, 1} means the 1st, 4th and 6th genes have been selected to construct the marker gene subset. Then the selected feature subset will be evaluated according to the fitness function; the higher fitness value is got, the better feature subset may be obtained. Ants cooperate with each other by intensity of pheromone left in every pathway for searching the optimum feature subset.

Figure 1.

The feature selection procedure of modified ACO algorithm. 1 represents that the corresponding gene will be selected, 0 represents that the corresponding gene will not be selected.

In our modified ACO algorithm, many ants synchronously search pathways from nest to the food. They select pathways according to the quantities of pheromone left in different pathways. The more pheromone is left, the higher probability of the corresponding pathway is selected. We compute the probability of selecting a pathway as below:

$$p_{ij}=\frac{{\tau }_{ij}}{{\displaystyle {\sum }_j^k}{\tau }_{ij}}$$ (1)

where i represents the i^th gene, j may be assigned as 1 or 0 to denote whether the corresponding gene has been selected or not, while τ_ij is pheromone intensity of the i^th gene in the j^th pathway, k is the possible value of pathway j (0 or 1), and p_ij is the probability of the i^th gene selecting the j^th pathway. When an ant arrives at the food, the corresponding feature subset will be evaluated by fitness function as below:

$$fitness=\frac{Acc}{1+\lambda n}$$ (2)

where Acc is the predictive accuracy of the feature subset, n is the number of marker genes in the feature subset, and λ is the weight denoting the importance of the number of marker genes. When one iteration is finished, the pheromone in all of the pathways will be updated. The update formula is described as below:

$${\tau }_{ij}\left(t+1\right)=\left(1-\rho \right){\tau }_{ij}\left(t\right)+\mathrm{\Delta }{\tau }_{ij}$$ (3)

where ρ is the evaporation of pheromone trails, and Δτ_ij is the incremental pheromone of several excellent pathways. In this paper, we add pheromone in the pathways of the best 10% ants after each cycle and store these pathways in a set S. Δτ_ij is defined as below:

$$\mathrm{\Delta }{\tau }_{ij}=\{\begin{array}{l}{\mathrm{fitness}}^a,{\mathrm{pathway}}_{ij}\in S\hfill \\ 0,{\mathrm{pathway}}_{ij}\notin S\hfill \end{array}$$ (4)

In formula 4, parameter a controls the quantity of increased pheromone. When one cycle is finished, the pheromone of some pathways will be intensified and the others will be weakened, so that those excellent pathways will have more chances to be selected in next cycle. With the convergence of ACO algorithm, all of the ants are inclined to select the same pathway. At last, the best solution will be returned.

Considering that the modified ACO algorithm is inclined to sink into local optimization, we also profit from the idea of Stützle and Hoos (22) to set the upper and lower boundary of pheromone in each pathway and to name the improved ACO algorithm as MMACO (Max-Min ant colony optimization), which may be easier to maintain the trade-off between intensification and diversification.

Support vector machine

SVM introduced by Vapnik (23) is a valuable tool for solving pattern recognition and classification problem. Compared with traditional classification methods, SVM possesses prominent advantages such as high generalization capability, absence of local minima, and suitability for small-sample dataset. Given a dataset $S=\left\{\left(x_i,y_i\right)|x_i\in R^d,y_i\in \left\{-1,+1\right\},i=1,\dots N\right\}$, where x_i is a d-dimension sample, y_i is the corresponding class label, and N is the number of samples, the discriminant function of SVM can be described as below:

$$g\left(x\right)=\mathrm{sgn}(\sum _{i=1}^{sv}{\alpha }_i{y}_{i}K\left(x,x_i\right)+b)$$ (5)

In formula 5, sv is the number of support vectors, α_i is lagrange multiplier, b is the bias of optimum classification hyperplane, while K(x, x_i) denotes the kernel function. In this paper, we have finished our experiments with radial basis function (RBF):

$$K\left(x_i,x_j\right)=\exp \{-\frac{{\left|x_i-x_j\right|}^2}{2{\sigma }^2}\}$$ (6)

A complete description of SVM theory for pattern recognition is given by Vapnik in reference (23).

Marker gene selection algorithm based on modified ACO and SVM

In this study, we combine modified ACO and SVM as a novel wrapper marker gene selection approach to extract the marker gene subset as described below:

• Step 1.

  Initialize pheromone of all pathways.

• Step 2.

  Each ant randomly searches a pathway from nest to food using formula 1 to construct some feature subsets.

• Step 3.

  Calculate the fitness of every feature subset obtained in step 2 by SVM. The best one will be compared with the optimum solution obtained in the previous searches. If the new solution is better, the optimum solution will be updated.

• Step 4.

  If the terminative condition is satisfied, the best result will be returned, otherwise the pheromone of all pathways will be updated, then go back to step 2 and continue to run.

An intuitionistic flow chart of marker gene selection algorithm based on ACO and SVM is presented in Figure 2.

Figure 2.

The flow chart of marker gene selection algorithm based on modified ACO and SVM.

Evaluation

Dataset and experimental settings

We firstly used the colon tumor dataset as an example to evaluate performance of the proposed approach in detail. The colon dataset contains 62 samples collected from colon cancer patients. Among them, 40 tumor biopsies are from tumors (labelled as “negative”) and 22 normal biopsies (labelled as “positive”) are from healthy parts of the colons of the same patients. Two thousand out of around 6,500 genes were selected based on the confidence in the measured expression levels. The raw data are publicly available at http://sdmc.lit.org.sg/GEDatasets/Datasets and more information can be found in Alon et al. (2).

All of the algorithms (including the modified ACO algorithm and MMACO algorithm proposed in this paper and GA algorithm used for performance comparison) in the experiments were written in MATLAB 7.0 (MathWorks Inc., Natick, USA), and S. Gunn’s SVM toolbox (http://www.isis.ecs.soton.ac.uk/resources/svminfo/) was used to implement SVM algorithm. We ran the algorithm on a personal computer (Intel Pentium D processor/dual core 2.66 GHz/512 M RAM). Experimental initial parameters are given in Table 1.

Table 1.

Parameters used for experiments

Common parameters for ACO		Value
ant_n	population size	50
NC	the number of iterations	50
a	the weight factor of updating pheromone	5
dispose	evaporation of pheromone trails	0.2
λ	the weight factor of the number of marker genes	0.005
ph(i, 0)	the initial pheromone of pathway 0	1.0
ph(i, 1)	the initial pheromone of pathway 1	1.0
Common parameters for MMACO
phmin	the lower boundary of pheromone	0.3
phmax	the upper boundary of pheromone	1.5
Common parameters for SVM
σ	the parameter of RBF kernel function	5
C	the penalty factor	500

Additionally, in this study we conducted leave-one-out cross-validation (LOOCV) for comparing with the other people’s work. In LOOCV, one of all samples is evaluated as testing data while the others are used as training data. After each sample is used as testing data for once, the predictive accuracy will be got by the ratio between the number of the correctly classified samples and the number of total samples in the dataset.

Experimental results

Firstly, in order to alleviate the burden of computation and accelerate the speed of convergence, 100 top-ranked informative genes were selected by signal-noise ratio estimation approach (1). Then the modified ACO/SVM algorithm was applied to search a more excellent marker gene subset on these 100 genes. The LOOCV classification accuracy of the 100 top-ranked informative genes on colon tumor dataset was tested and a recognition rate of 87.1% was got.

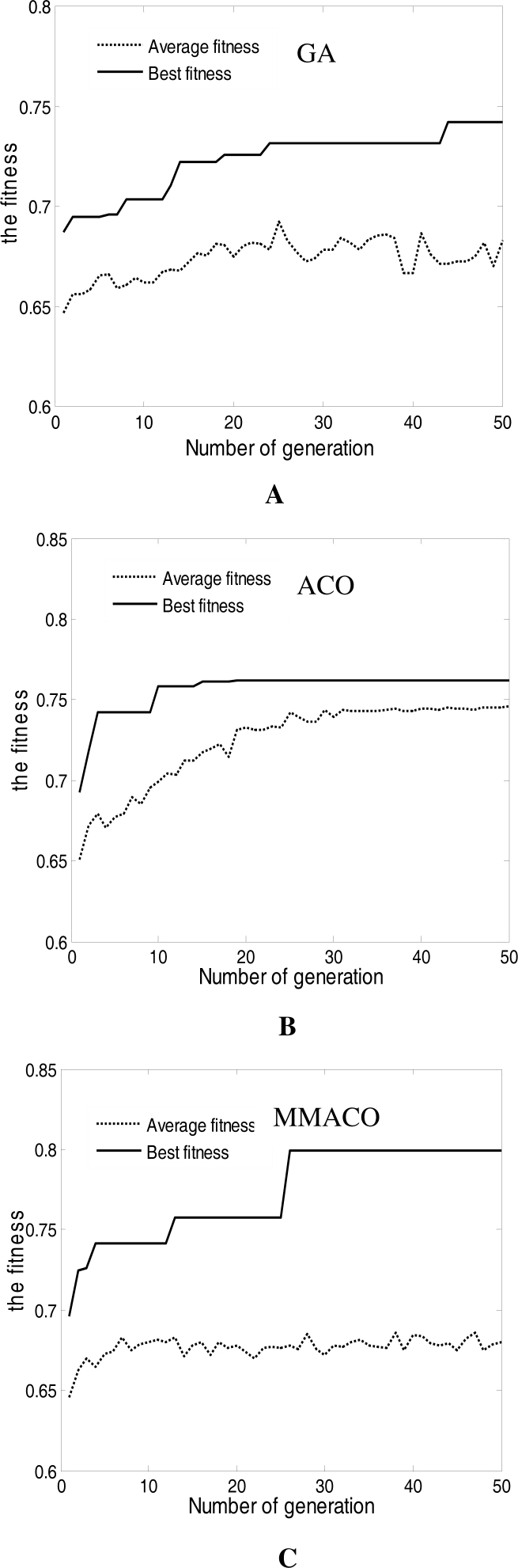
Then we compared the modified ACO algorithm and MMACO algorithm proposed in this paper with the most popular wrapper marker gene selection algorithm—GA algorithm, combined with SVM classifier. The parameters of GA followed Peng et al. (24): crossover operator is 1.0 and mutation operator is 0.006, while the other parameters referred to Table 1. The variational curves of GA, ACO and MMACO are described in Figure 3.

Figure 3.

Variational curves of fitness for GA (A), ACO (B) and MMACO (C).

Figure 3 indicates that the convergence speed of GA is slower compared with ACO and MMACO. Until the 43rd cycle, it can only find a not excellent enough solution (classification accuracy: 88.7%, number of marker genes: 39). The reason may be that cross and mutation operation slow down the convergence speed of GA. In contrast, ACO algorithm proposed in this paper may rapidly converge to a relatively excellent solution (classification accuracy: 90.3%, number of marker genes: 37) in the 15th cycle. Unfortunately, the marker gene subset obtained by ACO is only a local optimum solution due to rapid increase of pheromone in some pathways. It is not difficult to find that average fitness maintains an increased trend despite there are some fluctuations in Figure 3B. MMACO seems to effectively settle this problem by maintaining the trade-off between intensification and diversification. Figure 3C indicates that new better solutions can be found constantly by MMACO until the 28th cycle (classification accuracy: 91.9%, number of marker genes: 30), while the average fitness has no obvious increase or decrease, which means that MMACO is better than modified ACO.

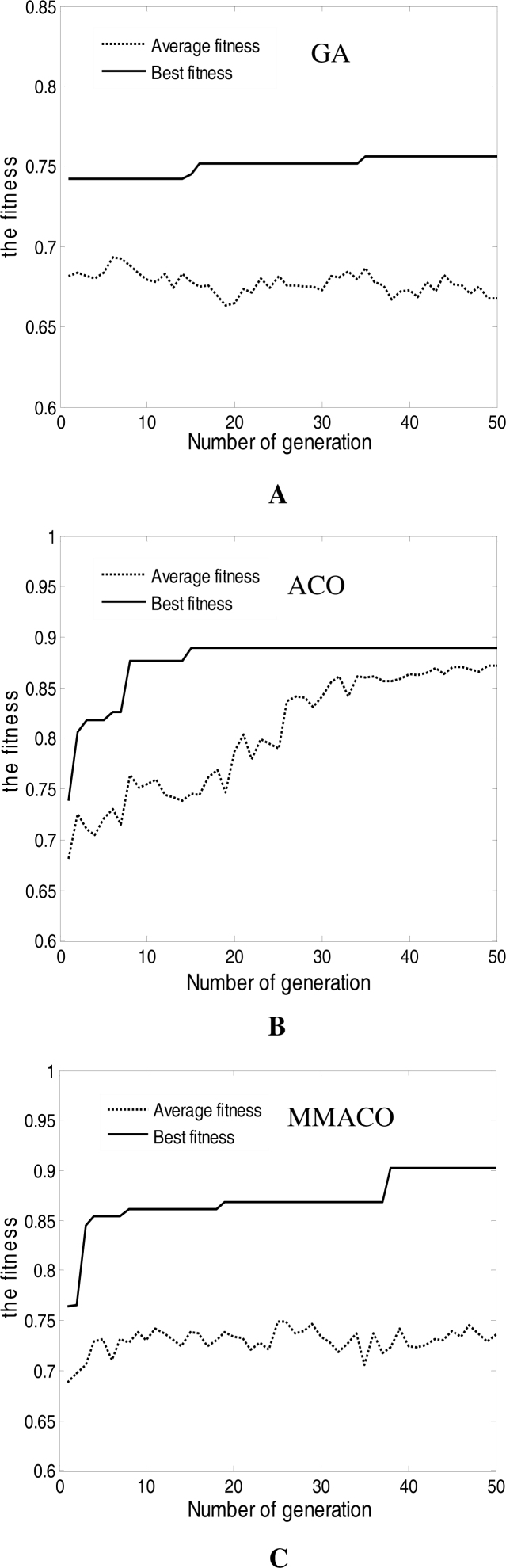
To further reduce the number of marker genes and improve the classification accuracy, we assigned different initial pheromone for pathway 0 and 1 in ACO and MMACO (1.0 for pathway 0 and 0.5 for pathway 1) and different probability for initial binary characters in GA (the probability of 0 is as twice as that of 1). The experimental results are shown in Figure 4. From Figure 4, it is not difficult to gain a fact that the performance of all of the three algorithms have obvious promotion: GA converged in the 35th cycle with 90.3% classification accuracy and 35 marker genes; ACO converged in the 15th cycle with 90.3% classification accuracy but only 3 marker genes; while MMACO converged in the 38th cycle but acquired the best classification accuracy 95.2% with 11 informative genes. When we compared the marker genes obtained in two groups of experiments, we found that most marker genes in the second group of experiments have also appeared in the first one. That means many redundant genes, which existed in the first group of experiments, have been filtered in the latter one.

Figure 4.

Variational curves of fitness for GA (A), ACO (B) and MMACO (C) based on different initial pheromone for pathway 0 and 1 in ACO and MMACO (1.0 for pathway 0 and 0.5 for pathway 1) and different probability for initial binary characters in GA (the probability of 0 is as twice as that of 1).

To evaluate the stability of the algorithms proposed in this paper, we randomly ran GA, ACO and MMACO based on the parameters in the second group of experiments for 30 times, respectively. Experimental results show that the stability of MMACO is the best in all of the three algorithms. For MMACO, classification accuracy of 95.2% appeared 27 times and accuracy of 93.5% occurred 3 times. While in 30 runs of ACO, the highest classification accuracy was 93.5% (11 times), the lowest was 88.7% (2 times), accuracy of 90.3% and 91.9% appeared 14 times and 3 times, respectively. The stability of GA is better than ACO but worse than MMACO: predictive accuracy of 90.3%, 88.7% and 91.9% occurred 22 times, 5 times and 3 times, respectively. However, ACO has averagely extracted less marker genes than GA and MMACO (7.5: 28.4: 10.8).

In 90 random runs above, the times of each gene appearing in marker gene subset were counted and the emergence times of Gene 1423 [J02854: Myosin regulatory light chain 2, smooth muscle isoform (human); contains element TAR1 repetitive element] was most (71 times). Gene 1772 [H08393: Collagen α² (XI) chain (human)], which has been found closely related with colon tumor by other researchers ^{6., 25.}, occupied the second place (63 times). Besides these genes, genes 765, 515, 625, 1067, 1406, 992, 241 and 780 also have been found being correlated with colon tumor in this paper. The detailed information and description of top 10 marker genes are listed in Table 2. We expect these findings may provide useful information for biologists and medical experts.

Table 2.

Detailed description of top 10 marker genes extracted by GA, ACO and MMACO

Rank	Gene ID	Accession No.	Times	Description
1	1423	J02854	71	Myosin regulatory light chain 2, smooth muscle isoform (human); contains element TAR1 repetitive element
2	1772	H08393	63	Collagen α2(XI) chain (H. sapiens)
3	765	M76378	55	Human cysteine-rich protein (CRP) gene, exons 5 and 6
4	515	T56604	50	Tubulin β chain (Haliotis discus)
5	625	X12671	49	Human gene for heterogeneous nuclear ribonucleoprotein (hnRNP) core protein A1
6	1067	T70062	45	Human nuclear factor NF45 mRNA, complete cds
7	1406	U26312	44	Human heterochromatin protein HP1Hs-γ mRNA, partial cds
8	992	X12466	41	Human mRNA for snRNP E protein
9	241	M36981	41	Human putative NDP kinase (nm23-H2S) mRNA, complete cds
10	780	H40095	39	Macrophage migration inhibitory factor (human)

Furthermore, to verify the applicability and generality of the proposed methods, we have conducted additional experiments on other four popular tumor microarray datasets, including two binary-class datasets and two multi-class datasets ^{1., 26., 27., 28.} as shown in Table 3 in detail (parameters referred to the second group of experiments). As to multi-class datasets, one-versus-rest support vector machine (OVR-SVM) was used to classify for samples. At first, top 100 genes were extracted, and then the average classification accuracy and size of selected marker genes of 30 independent running for the proposed methods were compared with several other marker gene selection and classification methods ^{24., 29., 30., 31., 32.} as listed in Table 4.

Table 3.

Other benchmark tumor microarray datasets

Dataset	Quantity			Reference
	Genes	Samples	Classes
Leukemia	7,129	72	2	Golub et al. (1)
DLBCL	4,026	47	2	Alizadeh et al. (26)
NCI60	5,726	60	9	Stuanton et al. (27)
Brain	5,920	90	5	Pomeroy et al. (28)

Table 4.

Related works on five datasets

Method	LOOCV predictive accuracy (Size of selected marker genes)
	Colon	Leukemia	DLBCL	NCI60	Brain
ACO/SVM	91.5%±1.5% (7.5)	100% (8.6)	100% (7.2)	82.4%±1.9% (8.8)	90.7%±1.9% (7.9)
MMACO/SVM	95.0%±0.3% (10.8)	100% (6.3)	100% (5.7)	84.2%±1.8% (12.6)	91.0%±1.4% (8.1)
SNR (top-ranked 100)/SVM	87.1% (100)	97.2% (100)	95.7% (100)	71.7% (100)	84.4% (100)
GA/SVM (24)	90.2%±0.5% (28.4)	100% (17.6)	100% (15.4)	80.7%±2.2% (23.6)	88.9%±1.6% (25.1)
SVM (29)	90.3% (2,000)	94.1% (500)	–	–	–
Bagboost (30)	83.9% (200)	95.9% (200)	98.4% (200)	–	76.1% (200)
SWKC (31)	88.4% (15.0)	98.2% (14.2)	99.3% (14.1)	75.2% (32.5)	81.9% (41.5)
OVR-SVM (32)	–	–	–	65.2% (5,726)	91.7% (5,920)

From Table 4, it can be seen that our proposed ACO/SVM and MMACO/SVM algorithms may select a smaller feature subset with better LOOCV classification accuracy than many other methods in almost all datasets. Therefore, our proposed algorithms are more effective for marker gene subset selection and pattern classification.

Conclusion

Marker gene selection plays a crucial role in developing a successful disease diagnostic system based on microarray data. In the present work, a simple modified ACO algorithm is proposed and combined with SVM for mining tumor-related marker genes. The experimental results running on several benchmark tumor microarray datasets have demonstrated that the proposed approach may extract better marker gene subset than many other methods and the modified ACO algorithm is a useful tool for selecting marker genes.

Authors’ contributions

HY designed and implemented the algorithm, conducted experiments and drafted the manuscript. GG and HL conceived the idea of using this approach and assisted with manuscript preparation. JS and JZ collected the dataset and conducted data analysis. All authors read and approved the final manuscript.

Competing interests

The authors have declared that no competing interests exist.