Significant Deviations in the Configurations of Homologous Tandem Repeats in Prokaryotic Genomes

Abstract

We explored the possibilities of whole-genome duplication (WGD) in prokaryotic species, where we performed statistical analyses of the configurations of the central angles between homologous tandem repeats (TRs) on the circular chromosomes. At first, we detected TRs on their chromosomes and identified equivalent tandem repeat pairs (ETRPs); here, an ETRP is defined as a pair of tandem repeats sequentially similar to each other. Then we carried out statistical analyses of the central angle distributions of the detected ETRPs on each circular chromosome by way of comparisons between the detected distributions and those generated by null models. In the analyses, we estimated a P value by a simulation using the Kullback–Leibler divergence as a distance measure between two distributions. As a result, the central angle distributions for 8 out of the 203 prokaryotic species showed statistically significant deviations (P<0.05). In particular, we found out the characteristic feature of one round of WGD in Photorhabdus luminescens genome and that of two rounds of WGD in Escherichia coli K12.

Introduction

Whole-genome duplication (WGD) is an event that the whole genome of a species is duplicated by way of polyploidization (1). Because the number of genes in the genome is doubled immediately after WGD, the diversity of the genome can be drastically increased by WGD. Therefore, it has been claimed by many researchers of genomics that WGD is one of the major driving forces behind the evolution of eukaryotic genomes. So far, many positive results of studies of WGD have been reported for several kinds of eukaryotic species, for instance, yeast 2., 3., 4., Arabidopsis 5., 6., 7., vertebrates 8., 9., 10., 11., and a ciliate (12). In most of these studies, evidence of WGD was extracted by the methods using the relationships among homologous genes, such as phylogenetic trees, dot-matrix plots, and distributions of synonymous substitutions per synonymous site 13., 14..

Therefore, it is natural to postulate that WGD has also played an important role in evolution of prokaryotic genomes. As for prokaryotic species, however, only a few studies of WGD have been carried out: Wallace and Morowitz (15) argued WGD of prokaryotic species from the point of view of their genome sizes; Riley et al. (16) analyzed the locations of functionally related genes in Escherichia coli and showed a tendency for the genes to lie approximately 90° or 180° apart from one another on the circular genetic map; Kunisawa and Otsuka (17) searched for periodicity of chromosomal locations of the homologous genes in E. coli genome and found a 7-min quasiperiodic gene distribution, which was interpreted as relics of multiple WGDs (Here, “min” means a traditional unit to measure the distance between two points on a circular chromosome of bacterial species, which corresponds to 3.6°). However, because these studies had been carried out before the sequencing of E. coli genome was completed, the information retrieved from the genome data might be insufficient.

Recently, Sugaya et al. (18) investigated the causes of the large genome size of Anabaena sp. PCC7120 and claimed that WGD is most responsible for the large genome size among some possibilities. In addition, one of us (Mizuta) and colleagues analyzed 44 prokaryotic genomes based on a different methodology from the other studies; they identified equivalent tandem repeat pairs (ETRPs) on the chromosomes and examined the central angle distributions of ETRPs (19). They found out distinctive patterns in the distributions and suggested the existence of WGD for some species including E. coli K12. In that study, however, the central angle distributions were not statistically analyzed, and the suggestion was derived from qualitative discussions. Accordingly, in this study, we further analyzed the central angle distributions of ETRPs statistically and sought significant signs of WGD in an extensive collection of prokaryotic species.

Results and Discussion

Significant deviations in the central angle distributions

We searched for tandem repeats (TRs) in all the genomes analyzed and identified ETRPs within each genome according to the procedures described in Materials and Methods. The number of the detected TRs ranges from 6 (Buchnera aphidicola str. Sg) to 959 (Bradyrhizobium japonicum USDA 110). As for the ETRPs, some genomes have no ETRPs, and Bacteroides thetaiotaomicron VPI-5482 has the maximum of 743 ETRPs (Table S1). Because a statistical test on a small dataset would not be reliable, we selected genomes that have 100 or more ETRPs. As a result, 33 genomes remained for further analyses.

We performed the following three statistical tests on the central angle distributions of the detected ETRPs for the 33 genomes: (1) a statistical test using the Kullback–Leibler (K–L) divergence as a distance measure in fixed locus model (FLM) (see Materials and Methods for the details of the null models), (2) the chi-square test in FLM, and (3) the Kolmogorov–Smirnov (K–S) test in non-fixed locus model (NLM). In addition, each test was performed with the full dataset and the subset in which the data below 10° were excluded (see next section), respectively.

Table S2 lists the resultant statistics. Eight genomes have P values <0.05 in the test based on the K–L divergence with the full dataset (the top eight in Table S2), which shows that the central angle distributions of ETRPs for the eight genomes are significantly deviated from those obtained from the null models at 95% confidence level.

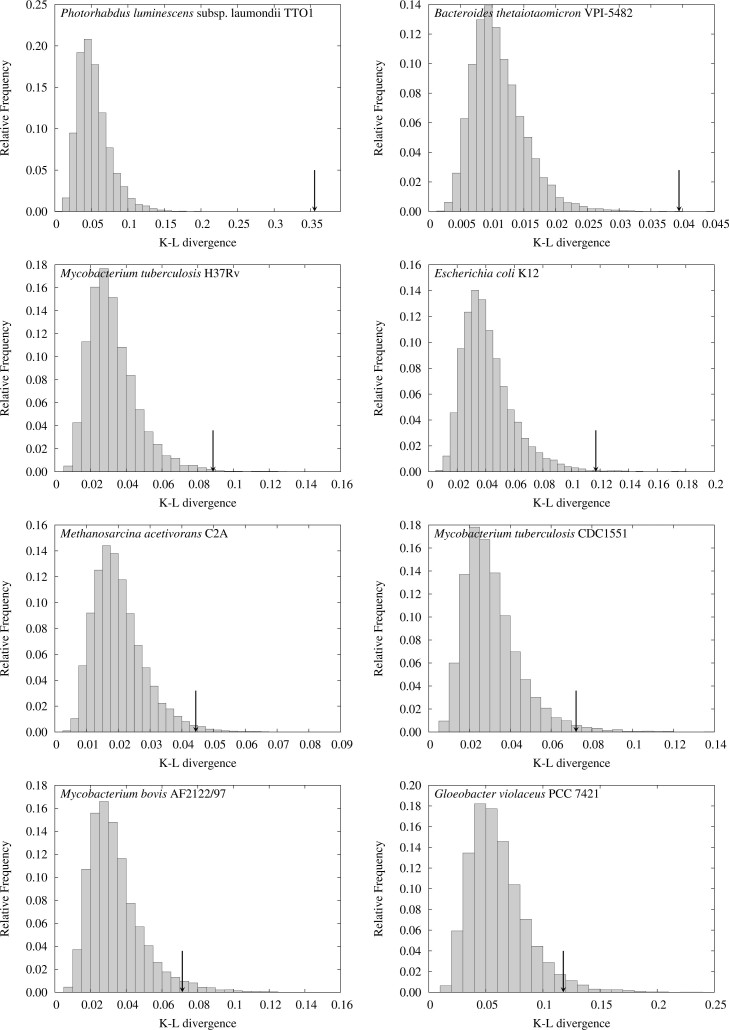
Figure 1 shows the comparisons between the central angle distributions of the detected ETRPs and those obtained from FLM for the eight genomes. The distributions of their K–L divergences of 10,000 random samples in FLM are shown in Figure 2 (The corresponding figures of Figure 1, Figure 2 for the 33 genomes are shown in Figures S1 and S2, respectively).

Figure 1.

Comparisons between the central angle distributions of the detected ETRPs (histograms) and those in FLM (lines) for the eight genomes that have 100 or more ETRPs.

Figure 2.

Distributions of the K–L divergence of 10,000 random samples in FLM for the eight genomes that have 100 or more ETRPs. Each down arrow indicates the observed K–L divergence. The P value is calculated by the proportion of the shaded area on the right hand side of the arrow.

As can be seen in Table S2, there is no serious contradiction among the results of the three tests. In particular, there seems to be a good correlation between the results of the two tests performed in FLM. Therefore, we proceed with our arguments based on the results of the test using the K–L divergence.

Peaks below 10°

A very long TR composed of four or more copies is possibly detected as two separate TRs, which, in turn, are often identified as an ETRP. In addition, some ETRPs might be composed of tandemly duplicated TRs. The central angles of most of such ETRPs seem to fall below 10°. Actually, in the central angle distributions for some species the peaks below 10° are impressive. Because the origins of those ETRPs are independent of WGD or other genome duplications of large scale, they can be noisy backgrounds for the analyses in this study. Therefore, we further analyzed the central angle distributions of ETRPs excluding the data below 10°. As a result, the P values of the four genomes with lowest significance in the eight, Methanosarcina acetivorans C2A, Mycobacterium tuberculosis CDC1551, Mycobacterium bovis AF2122/97, and Gloeobacter violaceus PCC 7421, exceeded 0.05. This observation shows that the small P values for M. tuberculosis CDC1551 and M. bovis seem to be ascribed to the peaks below 10°, although they have distinctive configurations even in the range of >10° (see Figure 1). However, we cannot extract decisive reasons at present why the revised P value for M. tuberculosis H37Rv is still smaller than 0.05, even though it is a close relative of M. tuberculosis CDC1551 and M. bovis, and the distributions for the three genomes look very similar to each other.

In the rest of this study, we concentrate our arguments on Photorhabdus luminescens subsp. laumondii TTO1 and E. coli K12 due to the following reasons: P. luminescens has the most striking result, that is, the P value in FLM equals to 0; E. coli K12 is one of the most frequently studied bacterial genomes and, moreover, the signs of WGD have been indicated by some authors as mentioned before 16., 17..

Rise near 180° for P. luminescens

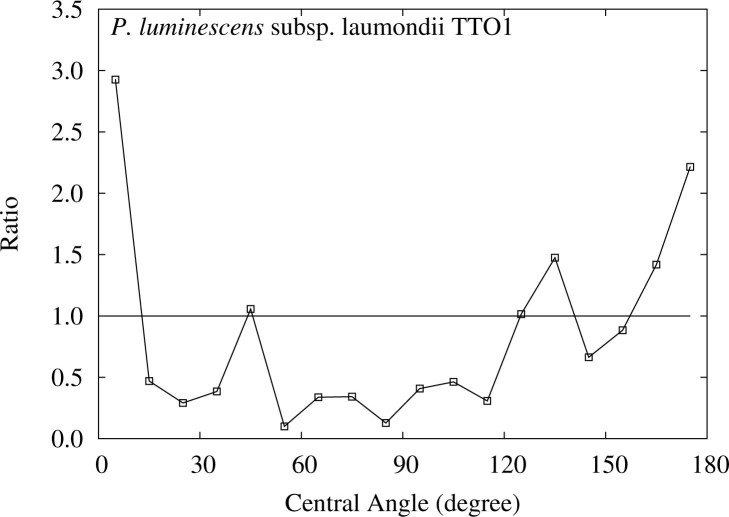
In Figure 1, we can recognize a rise near 180° for P. luminescens as well as the peak below 10°. To see the discrepancies more clearly between the observed distributions and those obtained in FLM, we plot their ratios for each central angle in Figure 3, where the two gaps, below 10° and near 180°, emerge more explicitly.

Figure 3.

Ratios of the frequencies of the central angle of the detected ETRPs to those in FLM for P. luminescens. The area above 1.0 indicates the excess of the observed frequency.

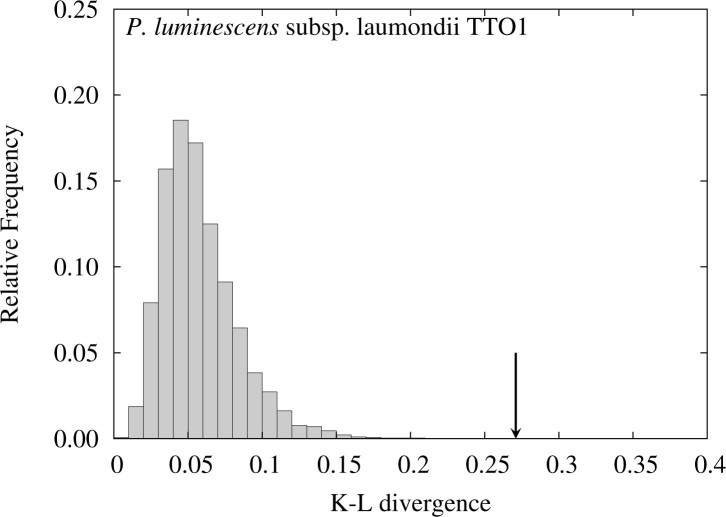
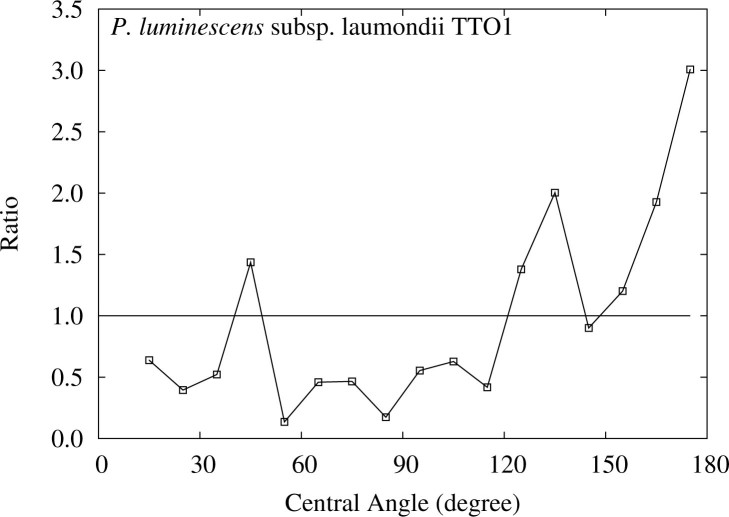
Figure 4 depicts the distribution of the K–L divergence for the subset excluding the data below 10°, and Figure 5 shows the ratios of the relative frequencies for each central angle between the detected ETRPs and those obtained in FLM for the subset. Although the observed K–L divergence decreases from 0.355 for the full set to 0.271 for the subset, the P value still remains 0. This observation shows that the small P value for P. luminescens is due largely to the rise near 180°, which is one of the characteristic features of one round (1R) of WGD (see Materials and Methods).

Figure 4.

Distribution of the K–L divergence in FLM for P. luminescens, with the dataset from which the data below 10° are excluded. A down arrow indicates the observed K–L divergence. The P value is calculated by the proportion of the shaded area on the right hand side of the arrow.

Figure 5.

Ratios of the frequencies of the central angle of the detected ETRPs to those in FLM for P. luminescens, with the dataset from which the data below 10° are excluded. The area above 1.0 indicates the excess of the observed frequency.

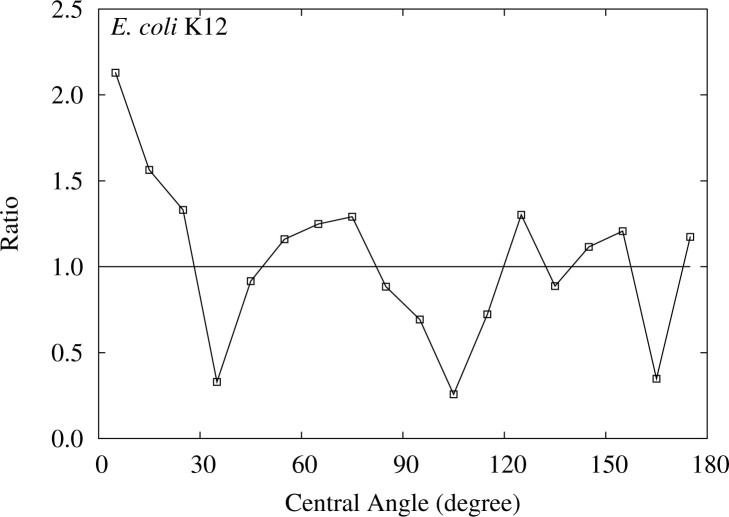
Multiple peaks for E. coli K12

Figure 6 shows the ratios of the relative frequencies for each central angle between the detected ETRPs and those obtained in FLM for E. coli K12. The P value is calculated to be 0.0048 (see Table S2), which shows the significance at 99% confidence level of the deviation. The observed K–L divergence decreases from 0.117 for the full set to 0.101 for the subset excluding the data below 10°, and, accordingly, the calculated P value increases to 0.0115 for the subset (graphs are not shown because the changes are very small), though the significance of the deviation still keeps a 95% confidence level.

Figure 6.

Ratios of the frequencies of the central angle of the detected ETRPs to those in FLM for E. coli K12. The area above 1.0 indicates the excess of the observed frequency.

We can recognize peaks around 0°, 70°, and 140° in Figure 6. A couple of peaks in a central angle distribution of ETRPs around 90° and 180° is a characteristic feature of two rounds (2R) of WGD (see Materials and Methods). The positions of the observed peaks are slightly smaller than those characteristic values. However, because the differences are systematic to some extent, the discrepancy can be understood on the assumption that a foreign body of a certain length had been inserted into E. coli K12 genome during some events in the course of the evolution of E. coli K12 after 2R WGD. Actually, in E. coli K12 genome, a dissimilar region from the rest can be recognized between 45° and 90° (19). If the foreign region is evidently identified, further analyses of the central angle distribution of the ETRPs will reveal more explicitly the relics of WGDs in E. coli K12 genome; these studies are now being advanced.

Fourier analyses of E. coli K12 and P. luminescens genomes

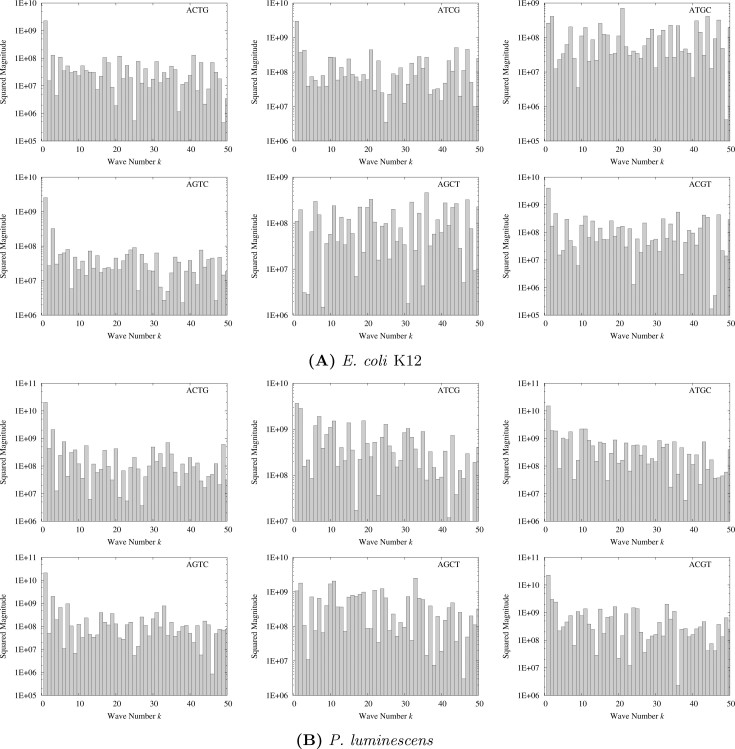
Each genome sequence of E. coli K12 and P. luminescens is converted to a numeric function, f(n), where n is a location on the genome, according to the procedure described in Materials and Methods, and the Discrete Fourier Transform (DFT) is applied to f(n). Figure 7 shows the calculated power spectra for the whole range of wave number k except for k = 0 (k = 0 is corresponding to the direct current component and has no meaning in this study). In Figure 7, we can definitely recognize peaks at k ~ N/3 and 2N/3, where N is the genome size, originated from the three-nucleotide periodicity of the coding regions 20., 21., 22..

Figure 7.

Power spectra of the DFT for E. coli K12 (A) and P. luminescens (B) genomes. The string described on the upper right corner of each diagram denotes the variation of the numeric assignment (see Materials and Methods). The data for the direct current (k = 0) are excluded.

1R and 2R WGDs might have provoked peaks at k = 2 and k = 4 on the power spectra, respectively. To observe the low-frequency regions of the spectra in detail, those regions for 1 ≤ k ≤ 50 are extracted from Figure 7 and depicted in Figure 8. Here, the magnitudes for the numeric assignment AGTC, AGCT, and ACGT are computed by Equation 1 from those of ACTG, ATCG, and ATGC, respectively. The peaks at k = 1, which are observed throughout the diagrams, indicate the asymmetric structure in the leading and lagging strands of bacterial circular genomes revealed by the analyses of GC-skew (23). Compared with the average value over the whole regions of k, which is estimated to be < 10⁸ (see Figure 7), the squared magnitudes in the low-frequency regions are higher by about one or more orders of magnitude. Although the peaks specific for k = 2 and k = 4 are not definitely recognized, these high values in the low-frequency regions indicate large-scale periodicities in the genomes and are not inconsistent with the existence of the 1R and 2R WGDs.

Figure 8.

Power spectra of the DFT in the low-frequency regions (1 ≤ k ≤ 50) extracted from Figure 7. The spectra for numeric assignment AGTC, AGCT, and ACGT are derived from those for ACTG, ATCG, and ATGC, respectively, by Equation 1 in Materials and Methods.

Furthermore, we simulated the mutational randomization processes after WGD events according to the following procedure to investigate their influences on the Fourier spectra. At first, we prepare a random sequence consisting of four letters, A, T, G, C, of 10,000 letters long, configuring the GC content to be 60% in the first half and 40% in the last one to incorporate the asymmetric feature of bacterial genomes. Next, we duplicate the sequence once and twice to realize 1R and 2R WGDs, respectively. After the duplications, we induce mutational processes by replacing the nucleotides at the positions randomly selected on the sequences by certain ratios ranging from 1% to 30% of the sequence length. Lastly, in order to simulate insertion of a foreign sequence, we insert a uniformly distributed random sequence fragment in a length of 20% of each duplicated sequence into the point of a quarter from the origin of the sequence.

Figure S3 shows the Fourier spectra of the artificial sequences generated by the above mentioned procedures with assignment ATGC (see Materials and Methods). We can recognize that large low-frequency spectra survive even after 30% of mutations of the sequences in both cases, one- and two-fold duplications. It is worth noting that the shifts of the peaks in the low-frequency regions in the two-fold duplication case are partly due to the insertion of the randomly generated sequence, in which the peaks are observed at k = 4 without the insertion.

Conclusion

In this study, we explored the possibilities of WGD in prokaryotic species by statistical analyses of the central angle distributions of ETRPs. We obtained statistically significant deviations in the distributions for 8 species out of 203 analyzed by a statistical test based on the K–L divergence in FLM.

Although the deviations do not immediately prove the existence of WGD in prokaryotic species, it is possible that they are consequences of WGD. The central angle distribution of ETRPs for P. luminescens genome shows a peak near 180°, which is a characteristic feature of 1R WGD. On the other hand, E. coli K12 genome has a couple of peaks around 70° and 140°, which is possibly explained by 2R WGD with the assumption that a foreign body had been inserted into E. coli K12 genome in the course of its evolution after the 2R WGD. Furthermore, because 1R and 2R WGDs might have introduced low-frequency periodicities into the genomes, we applied Fourier analyses to the genomes. Although the results do not determinately indicate the 1R or 2R WGDs, the squared magnitudes of the Fourier components are extremely high in the low-frequency regions, which are thus not inconsistent with the WGDs.

So far, many positive results of the studies of WGD in eukaryotic species have been reported. As for prokaryotic species, however, only a few studies of WGD have been conducted. We hope the findings in this study advance the studies of WGD in prokaryotic species hereafter.

Materials and Methods

Genome sequences

The genome sequences of prokaryotic species analyzed in this study were downloaded from GenBank (http://www.ncbi.nlm.nih.gov/). We selected completely sequenced genomes that have a single circular chromosome. In all, 203 prokaryotic genomes—84 proteobacteria, 56 firmicutes, 44 other bacteria, and 19 archaea—were obtained (Table S3). Although some genomes have plasmid DNA sequences, we used only chromosomal ones.

Tandem repeats

A tandem repeat (TR) in DNA is defined as a set of two or more copies of a certain pattern of nucleotides that are adjacently located on a chromosome. A very short example is GCACGCAC, which has two copies of a nucleotide pattern GCAC, though the length of a TR generally ranges from dozens to several thousand of base pairs. Because some TRs in the human genome are known to be related to serious diseases (24), they are of considerable importance and interest from the point of view of medical science. In this study, we use TRs as genetic markers to explore the evolution of bacterial genomes, because TRs, if they are located in the intergenic regions of chromosomes, are thought to be free from the natural selection, and they are thus expected to preserve some kinds of traces of genome evolution.

We detect TRs by Tandem Repeats Finder (TRF) (25) with the following parameter values: Match = 2 (matching weight), Mismatch = 3 (mismatching penalty), Delta = 5 (indel penalty), PM = 80 (match probability), PI = 10 (indel probability), Minscore = 50 (minimum alignment score to report), and Maxperiod = 2000 (maximum period size to report). These values are chosen after some trials so that long TRs can be detected as many as possible.

Equivalent tandem repeat pairs

After excluding noisy sequences (see next section), we conduct all-against-all pairwise alignments on the detected TRs and extract TRs similar in sequence pattern with each other in each genome. For this purpose, we use SSEARCH in sequence analysis tool FASTA (http://fasta.bioch.virginia.edu/fasta_www2/fasta_list2.shtml) with the default parameter values and a threshold E value = 10⁻³. Here, E value means the expected number of TRs that will be detected as similar TRs to the query TR by chance in the dataset.

One more criterion is adopted for identification of an ETRP. Because SSEARCH performs local alignment by the method based on the Smith–Waterman algorithm (26), only a part of each sequence is devoted for alignment. The proportion in length of a TR that contributes to the alignment is defined as an overlap. Because the similarity between two TRs with a too small overlap would lose the meaning in this study, a pair of TRs that has an overlap of more than 50% to the longer TR is defined as an ETRP. Note that the equivalence relationship between TRs defined in this manner is a many-to-many relationship.

The central angle of an ETRP is measured in the range of 0° to 180°, which is defined by

$$\frac{\min \left\{\left|c_1-c_2\right|,L-\left|c_1-c_2\right|\right\}}{L}\times {360}^{\circ }$$

where c₁ and c₂ are the center positions on a chromosome of the two TRs belonging to the ETRP, and L is the length of the chromosome.

Excluding potential sources of noise

There are two potential sources of noise in analyzing genomes based on sequence similarity: low-complexity sequences and mobile genetic elements. Low-complexity sequences are those comprised of only a few types of nucleotides such as AAATAAAATAAT. Even if two low-complexity sequences are completely independent, they easily happen to be similar in a sequence pattern with each other. The complexity of a sequence can be measured by entropy H defined by H = −∑_X={A,C,G,T} f_X log₂ f_X, where f_X is the fraction of nucleotide X in the sequence (0 ≤ f_X ≤ 1, ∑_X={A,C,G,T} f_X = 1). H takes the maximum value 2.0 when all f_X′s are equal to 0.25 and the minimum 0 when one f_X equals to 1.0 (and the others equal to 0). We exclude TRs of entropy H < 1.9 from our dataset and take highly complex TRs into consideration to ensure the validity of the equivalence relationship between TRs of an ETRP.

Mobile genetic elements, on the other hand, are genes that move from one position to another on a chromosome or between chromosomes by way of such as transposition. Since the destination of the movement is arbitrary, the central angle of an ETRP will randomly change if one or both members of the ETRP overlap with mobile genetic elements. We exclude TRs that overlap with the known mobile genetic elements from our dataset according to the annotations in the genome data files of GenBank.

Characteristic features of WGD on a circular chromosome

WGD is an event that the whole genome of a species is duplicated. If WGD had occurred once on a prokaryotic genome having a circular chromosome in the course of its evolution, where the event is described as one round (1R) of WGD, each copy of TRs is located on the opposite side of the chromosome to the original TR. In this case, the original TR and its copy are expected to be observed as an ETRP, the central angle of which measures 180° (Figure 9A). If WGD had occurred twice, where the event is described as two rounds (2R) of WGD, ETRPs with a central angle of 90° besides 180° will be observed (Figure 9B). Therefore, a peak in the central angle distribution of ETRPs around 180° indicates 1R WGD, and a couple of peaks around 90° and 180° indicate 2R WGD. Note that, because in this study the central angle of an ETRP is measured between 0° and 180°, an angle θ > 180° corresponds to 360° − θ.

Figure 9.

Schematic view of the positions of TRs under 1R WGD (A) and 2R WGD (B). The curved solid lines are the original segments of the chromosomes, and the curved dotted lines are the duplicated segments. The copied TRs will be detected on the corresponding positions on the duplicated segments.

Two random models

What we analyze in this study are not the positional distributions or the frequencies in number of TRs, but the central angle distributions of ETRPs. In this case, the primary objects of the analyses are not the TRs themselves but the relative locations of the TRs belonging to ETRPs. We, therefore, start from a presupposition of the existence of TRs, the number of which equals to that of the detected TRs, and the equivalence relationships among them, instead of simulating production of TRs and ETRPs considering the basic processes such as inversion, deletion, and insertion of foreign DNA. The simulation, indeed, would require many undetermined free parameters like the occurrence rates of the basic processes, and it would be hard to analyze the simulation results clearly.

Based on the above postulate, we construct the following two random models and compare the central angle distributions of the detected ETRPs to the distributions randomly generated in the models.

Non-fixed locus model

If TRs are generated on a circular chromosome at random, the positional distribution of the TRs becomes continuous and uniform. In addition, if a TR homologous to another TR is generated on the chromosome by chance without any constraint, the central angle between the TRs will be arbitrary. The first random model stands on this observation, in which the central angle distribution is continuous and uniform. We call this simplest model a non-fixed locus model (NLM).

Fixed locus model

If there are regions on a chromosome where TRs are likely to be generated for some reasons, the central angle distribution of ETRPs is not necessarily uniform even though the equivalence relationships among the TRs are randomly assigned. In reality, the positional distributions of the detected TRs are not uniform (Figure S4). In that situation, the number of ETRPs with the central angle between two peaks of the positional distribution of TRs is expected to be larger than the others.

Because it is quite troublesome to make a distribution of the central angles by probabilistic modeling incorporating the above non-uniformity, we make a distribution by a simulation for each genome as follows. Firstly, the loci of TRs are fixed on a chromosome in accordance with those of the detected TRs. Next, the positional order of the TRs is shuffled at random preserving the equivalence relationships among them, and after that the central angles of the ETRPs are measured. The shuffling is repeated N = 10,000 times, and the relative frequency of the central angles for the i^th bin of the n^th iteration $q_i^{\left(n\right)}$ (1 ≤ i ≤ K, 1 ≤ n ≤ N) and the averaged frequencies over N iterations $\begin{array}{l}{\overline{q}}_i=1/N{\displaystyle {\sum }_{n=1}^N}{q}_i^{\left(n\right)}\end{array}$ are calculated. The central angle distribution of ETRPs for the n^th iteration $Q^{\left(n\right)}\equiv \left(q_1^{\left(n\right)},\dots ,q_K^{\left(n\right)}\right)$ and the averaged distribution $\overline{Q}\equiv \left({\overline{q}}_1,\dots ,{\overline{q}}_K\right)$ are also defined for a statistical analysis (see next section). Here, the number of bins K = 18 is chosen, and the width of each bin is 10°. We call this model a fixed locus model (FLM), in contrast to NLM.

Although FLM is thought to be more conservative and therefore more acceptable than NLM, we take both models into account for confirmation.

Statistical analyses of central angle distributions

Kolmogorov–Smirnov test in NLM

When two samples of data are both continuous, the Kolmogorov–Smirnov (K–S) test is applied to test whether or not the two samples are drawn from the same distribution function. Strictly speaking, the central angles of ETRPs are not continuous because the positions of TRs are expressed by the sites of the nucleotides on a chromosome they stand on, which are indeed integers. However, the positions of TRs and, thus, the central angles of ETRPs can be assumed to be continuous due to the large genome sizes. In addition, the distribution function in NLM is continuous. Therefore, we perform the K–S test for the statistical analyses of the central angle distributions of the detected ETRPs in NLM (the K–S test is performed with the statistical package R version 2.5.1) (27).

A statistical test based on the Kullback–Leibler divergence in FLM

In FLM, the central angles of ETRPs are definitely discrete because they are restricted to the central angles calculated from the loci fixed to those of the detected TRs; let m be the number of the detected TRs, then the maximum number of the possible central angles is _mC₂ = m(m−1)/2. If we would apply the K–S test in FLM, we had better regard the whole samples of 10,000 iterations as a single dataset, in which many equal values, called ties, are included. In that situation the valid P value of the K–S test could not be obtained. Therefore, another test method is required for FLM.

The chi-square test is commonly used to test binned data. It is, however, based on a theoretical assumption that the chi-square probability function is an incomplete gamma function. Because the situation is rather specific and distinct in FLM, the grounds of the assumption are not necessarily evident. Accordingly, we intend to test the data by a simulation to get rid of ambiguities introduced by a theoretical assumption as much as possible, though the chi-square test is also applied for confirmation.

The Kullback–Leibler (K–L) divergence between two probability distributions A = (a₁, …, a_K) and B = (b₁, …, b_K) is defined by

$$D_{KL}\left(A\parallel B\right)=\sum _{i=1}^K{a}_i\log \frac{a_i}{b_i}$$

Because it satisfies D_KL(A ∥ B) = 0 if and only if a_i = b_i for all 1 ≤ i ≤ K, otherwise D_KL(A ∥ B) > 0, it is used as a distance measure between two probability distributions. Let P = (p₁,…, p_K) be the central angle distribution of the detected ETRPs, where p_i is the fraction of the detected ETRPs in the i^th bin $\left({\sum }_{i=1}^K{p}_i=1\right)$, then the K–L divergence between P and $\overline{Q}$, $D_{KL}\left(P\parallel \overline{Q}\right)$, is calculated for each genome. After N iterations of shuffling, we can get a distribution of the K–L divergence between Q⁽ⁿ⁾ and $\overline{Q}$, $D_{KL}\left(Q^{(n)}\parallel \overline{Q}\right)$, for each genome, then we calculate the P value by the proportion of Q⁽ⁿ⁾ among N that satisfies $D_{KL}\left(Q^{(n)}\parallel \overline{Q}\right)\ge D_{KL}\left(P\parallel \overline{Q}\right)$.

Fourier analysis of genome sequences

Fourier analyses are generally used for studying periodicities in various data. Since WGDs might have introduced some large-scale periodicities in the genome sequences, the Discrete Fourier Transform (DFT) is applied to them to investigate the periodicities. The DFT of a numerical sequence f(n) that is converted from a genome sequence is defined by

$$F(k)=\sum _{n=0}^{N-1}f(n)e^{-i\frac{2\pi nk}{N}},k=0,1,\dots ,N-1$$

where n is a location on the genome, N is the genome length, and k is a wave number in the frequency domain.

There are several ways of numeric conversion of a DNA sequence 28., 29., 30.. In most of them a DNA sequence is separately converted to four numerical sequences, f_A(n), f_T(n), f_G(n), and f_C(n), where f_X(n) = 1 if the corresponding nucleotide X(=A, T, G, or C) exists at location n on the sequence and otherwise f_X(n) = 0, and the results of their DFT, F_A(k), F_T(k), F_G(k), and F_C(k), are combined afterward by S(k) = |F_A(k)|² + |F_T(k)|² + |F_G(k)|² + |F_C(k)|², which is used for the subsequent analyses. In this study, however, the four types of nucleotide are concurrently converted to four complex numbers 1, −1, i, and −i, respectively, to incorporate the correlation between the locations of the nucleotides. For example, when 1, −1, i, and −i are assigned to A, T, G, and C, respectively, a sequence AATGCCT is converted to f (·) = (1, 1, −1, i, −i, −i, −1).

Now let the numeric assignment be denoted by a string of four nucleotides lined up counterclockwise from the real axis of the complex plane. In this manner, the assignment of the above example is expressed by AGTC. Here, we consider two attributes derived from the definition of DFT. One is that the cyclic permutation of an assignment (i.e., AGTC → CAGT) is corresponding to a π/2 rotation of f(n) on the complex plane, where the magnitude of DFT, |F(k)|, is invariant under the transformation. And the other is that the flip on the imaginary axis of an assignment (i.e., AGTC → ACTG) is corresponding to taking the complex conjugate of f(n) (i.e., f(n) → f*(n)), of which the DFT is represented by

$$\tilde{F}(k)\equiv \sum _{n=0}^{N-1}{f}^{*}(n)e^{-i\frac{2\pi nk}{N}}=F^{*}(N-k),k=0,1,\dots ,N-1.$$ (1)

Hence the independent power spectra are given by three assignments, for instance, ATGC, ATCG, and ACTG, and the power spectra based on the other assignments are obtained from them.

Authors’ contributions

SH developed the method, collected the datasets, conducted data analyses, and drafted the manuscript. SM supervised the project, participated in data analyses, co-wrote the manuscript, and prepared the graphics. Both authors read and approved the final manuscript.

Competing interests

The authors have declared that no competing interests exist.

Supporting Online Material

Figures S1–S4 and Tables S1–S3

DOI: 10.1016/S1672-0229(08)60046-7