Sequence Signatures of Nucleosome Positioning in Caenorhabditis elegans

Abstract

Our recent investigation in the protist Trichomonas vaginalis suggested a DNA sequence periodicity with a unit length of 120.9 nt, which represents a sequence signature for nucleosome positioning. We now extended our observation in higher eukaryotes and identified a similar periodicity of 175 nt in length in Caenorhabditis elegans. In the process of defining the sequence compositional characteristics, we found that the 10.5-nt periodicity, the sequence signature of DNA double helix, may not be sufficient for cross-nucleosome positioning but provides essential guiding rails to facilitate positioning. We further dissected nucleosome-protected sequences and identified a strong positive purine (AG) gradient from the 5′-end to the 3′-end, and also learnt that the nucleosome-enriched regions are GC-rich as compared to the nucleosome-free sequences as purine content is positively correlated with GC content. Sequence characterization allowed us to develop a hidden Markov model (HMM) algorithm for decoding nucleosome positioning computationally, and based on a set of training data from the fifth chromosome of C. elegans, our algorithm predicted 60%-70% of the well-positioned nucleosomes, which is 15%-20% higher than random positioning. We concluded that nucleosomes are not randomly positioned on DNA sequences and yet bind to different genome regions with variable stability, well-positioned nucleosomes leave sequence signatures on DNA, and statistical positioning of nucleosomes across genome can be decoded computationally based on these sequence signatures.

Introduction

Eukaryotic genomes are organized into nucleosome arrays that are further packaged into high-order chromosomal structures. Each nucleosome is constructed with two copies of the four histone proteins, H2A, H2B, H3 and H4, to form a disk-shaped histone octamer (1). A stretch of approximately 147 bp DNA wraps in 1.67 left-handed turns around the histone octamer to form a nucleosome 2, 3, 4, 5, 6. Adjacent nucleosomes are connected by a linker sequence, and the length of the linkers varies from approximately 10 to 100 bp among different organisms 7, 8. The spatial accessibility of nucleosome-protected sequences differs dramatically from that of their nucleosome-free counterparts (9), so that nucleosome positioning and distribution may affect DNA-related cellular processes such as DNA replication, repair, transcription, and recombination (10), and therefore related to gene expression regulation and local mutation rate. For instance, it was discovered that nucleosome assembly on the human c-fos promoter interferes with transcription factor binding (11), and DNA damage in the nucleosome core is refractory to be repaired by excision nucleases (12).

A long-standing interest for molecular biologists is whether nucleosomes are randomly positioned along the DNA double helix. Early theories suggested that nucleosomes are stochastically distributed around fixed boundaries that comprise nucleosome-free regions 13, 14. For example, transcription factor binding sequences in the promoter region may form intrinsic barriers for nucleosome positioning, resulting in a ~200 bp nucleosome-free region upstream of the transcription start site, but nucleosomes are appropriately positioned with regularity following these barriers along transcripts 15, 16, 17, 18, 19, 20, 21, 22. Sequence signatures or DNA compositional characteristics, especially nucleotide-protected sequences, may also influence the interaction between DNA and the histone octamer in terms of binding affinity or stability of the complex. For example, a 10.5-nt sequence periodicity has long been suggested to be a genomic signal for nucleosome positioning 23, 24, 25, 26, 27, and in vitro experiments indicated that the interruption of this periodicity may reduce nucleosome affinity (28). Furthermore, it was revealed that long CCG triplet repeats prevent nucleosome binding 29, 30, and long-range correlation in genomic sequences strongly affects nucleosome positioning (31).

Recently, Segal and colleagues developed a position-specific scoring matrix (PSSM) algorithm to predict nucleosome positioning based on the 10.5-nt sequence periodicity (28). Using a set of nucleosome-binding sequences isolated from yeast as training data, they calculated dinucleotide frequencies after aligning all the sequences at the center of nucleosomes, and observed the 10.5-nt dinucleotide periodicity that forms a theoretical basis for their nucleosome-DNA interaction model. The PSSM algorithm predicts 54% of well-positioned nucleosomes within a 35-bp vicinity of their correct positions. Very recently, Weng and his colleagues developed another algorithm based on the average frequencies of k-mers (k=1 to 6) between DNA fragments with highest and lowest affinity to nucleosomes, and this method applied a support vector machine (SVM) algorithm to distinguish nucleosome-forming from nucleosome-inhibiting sequences (32). They predicted 50% of well-positioned nucleosomes within a 40-bp vicinity of the correct positions and concluded that only a subset of these nucleosomes possesses intrinsic sequence signals.

Although it has been widely recognized that the 10.5-nt periodicity is associated with nucleosome positioning, how it relates to genomic signals of nucleosome positioning remains elusive as this periodicity also exists in prokaryotic DNA where nucleosomes are largely absent 33, 34, 35, 36. We have previously defined a nucleotide periodicity in a length of 120.9 nt in Trichomonas vaginalis (37) and confirmed that this periodicity is a genomic signal for nucleosome positioning. In current study, we validate this conclusion in a multicellular eukaryote, Caenorhabditis elegans, and explore novel genomic sequence signatures for nucleosome positioning. Based on these signatures, we develop a hidden Markov model (HMM) algorithm to predict nucleosome positioning utilizing empirical data.

Results

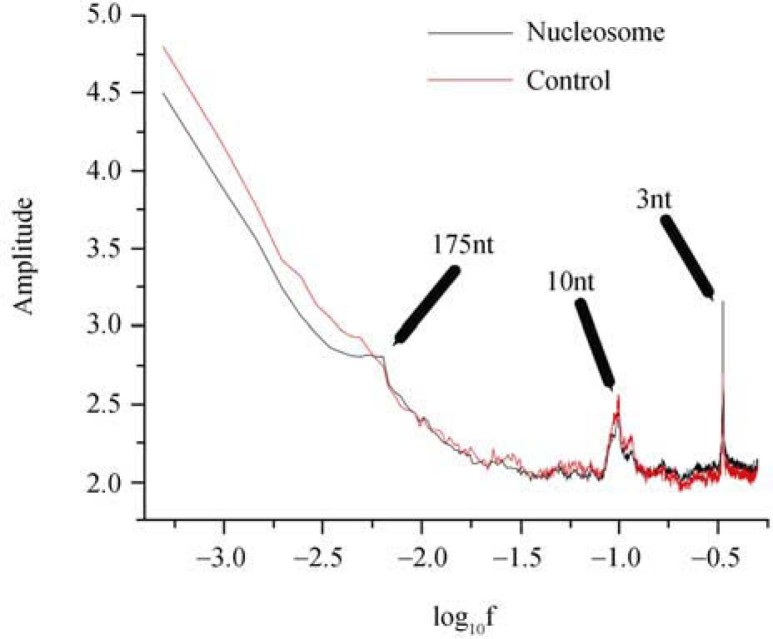
Power spectrum analysis reveals a unique 175-nt periodicity

We defined 15,274 nucleosome-binding regions (8.4 Mb in total length) and 7,194 control regions (3.7 Mb in total length) based on the information of primary experimental data (see Materials and Methods). When applying power spectrum analysis to the nucleosome and control data, we observed not only two previously defined periodicities, the 3-nt and 10.5-nt periodicities (although it is 10.2 nt in this work we still use the universal unit length of 10.5 nt in our discussions), in both datasets, but also a unique 175-nt periodicity only in the nucleosome data (Figure 1). Since the 3-nt periodicity is a characteristic of protein-coding sequence reflecting the repetitive unit of codon triplets, the stronger 3-nt periodicity observed in nucleosome data suggests that protein-coding sequences are enriched in nucleosome-binding regions. There is little difference for the 10.5-nt periodicity between the nucleosome and control data since this periodicity is a manifestation of the DNA double-helix structure. However, the 175-nt periodicity is a novel observation, as we have recently discovered two other periodicities, 120.9 nt and 165 nt in unit length, in T. vaginalis and Saccharomyces cerevisiae, respectively (37).

Figure 1.

Power spectrum analysis on nucleosome and control data. We observe three periodicities in lengths of 3 nt, 10.5 nt, and 175 nt among nucleosome data. The 3-nt periodicity appears obscure in control data, whereas the 10.5-nt periodicity remains obvious. The 175-nt periodicity is unique to nucleosome data and is almost absent in control data.

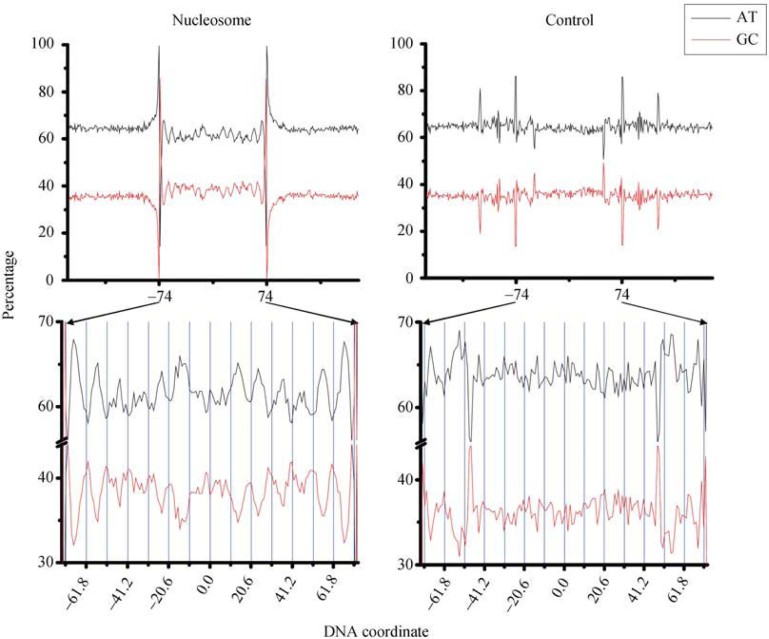
The nucleosome association of 10.5-nt periodicity

To further investigate how the 10.5-nt periodicity is associated with nucleosome positioning, we aligned nucleosome-protected and control sequences according to the nucleosome position to decipher the contribution of each nucleotide and their combinations (Figure 2). Despite the fact that the 10.5-nt periodicity is observed in both the nucleosome and control data in our power spectrum analysis, our nucleotide composition analysis showed striking differences between the two datasets. A/T and G/C contribute differently to the 10.5-nt periodicity in the nucleosome data and fall into two complementary phases. In addition, the GC content of nucleosome-protected sequences is slightly higher than the genome average (38% vs. 35%).

Figure 2.

GC- and AT-contents plotted as a function of nucleotide position. Nucleosome-protected sequences are centered at 0.0. The portions between -74 to 74 (148 nt) are enlarged below the plots. The 10.5-nt periodicity is more pronounced in nucleosome data, whereas it becomes noisy in the control. When we limit the length of nucleosome-protected sequences to 148 nt, the 10.5-nt periodicity is most distinct albeit shorter or longer sequence lengths give similar results.

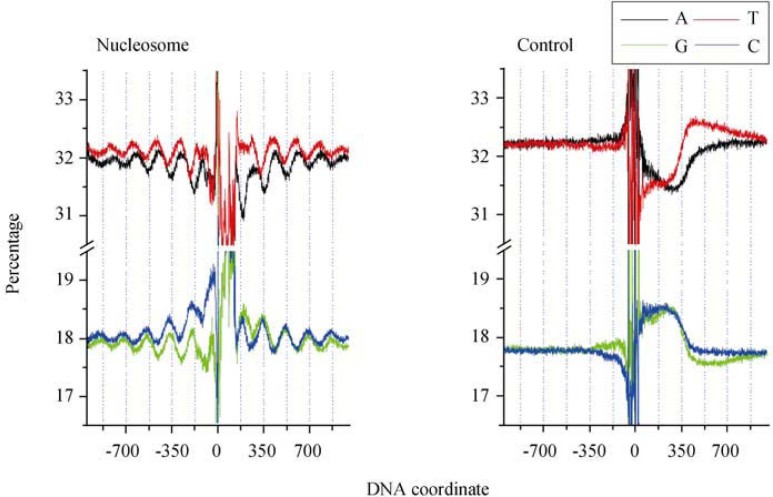
175-nt periodicity and nucleosome positioning

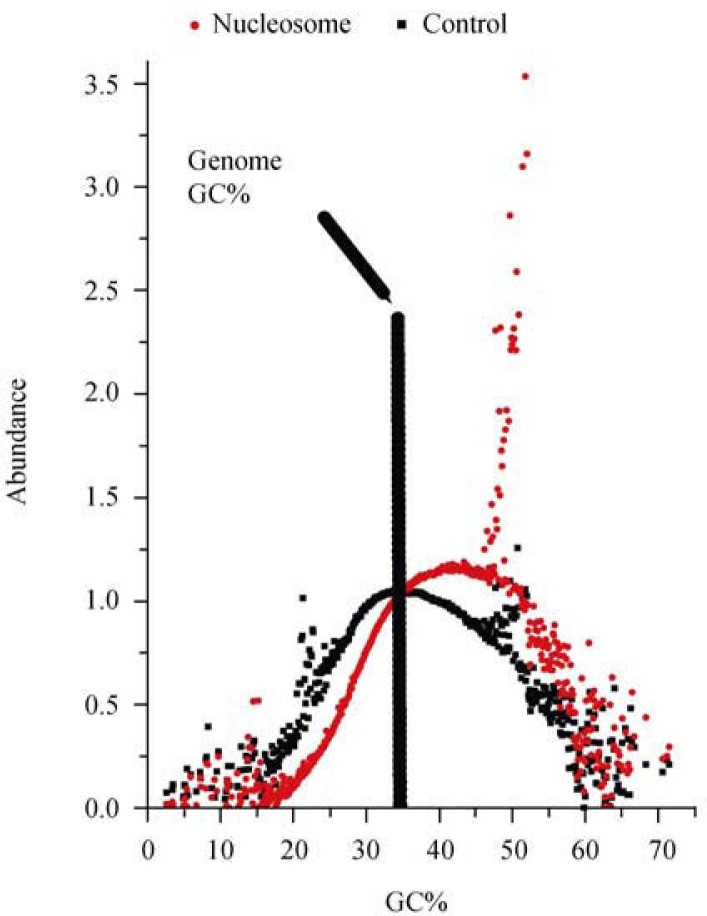
To confirm the nucleosome association of the 175-nt periodicity in the nucleosome data, we defined the 5′-ends of nucleosome-protected (1.61 Mb) and control (1.54 Mb) sequences, and extracted 1-kb flanking sequences to calculate nucleotide frequencies (Figure 3). Similar to our power spectrum analysis, we observed the 175-nt periodicity in nucleosome data, which is absent in the control data. The size of the 175-nt periodicity in C. elegans is contributed by both nucleosome-protected and linker sequences as compared to the 120.9-nt periodicity in T. vaginalis, where both nucleosome-protected and linker sequences are believed to be shorter. In the 175-nt periodicity, the four nucleotides are also partitioned into two complementary phases, with G and C in the same phase, while A and T share the reverse phase. We also find that the four nucleotides are used with different frequencies in nucleosome-protected sequences, and the most frequently used nucleotide is T, followed by A, C, and G. We can also observe that nucleosome-protected sequences are GC-richer than the linker. We analyze nucleosome abundance relevant to genomic GC content calculated in a 2-kb window with a step length of 100 bp for the entire C. elegans genome; the data are calculated for read abundance and sorted based on GC content (Figure 4). The nucleosome distribution is clearly biased toward high GC content.

Figure 3.

Nucleotide frequencies plotted as a function of nucleotide position around 5′-ends of nucleosome-protected sequences. The 175-nt periodicity is present in nucleosome data but absent in the control.

Figure 4.

The nucleosome abundance as a function of GC content among nucleosome-protected sequences. We calculate GC content in 2,000-nt window with a step length of 100 nt. The dashed line indicates the genome average GC content (35%). The distribution of nucleosome-protected sequences shifts toward high GC content. The data points distributed above the curves may represent repetitive reads that are mapped to unique sites of the reference genome.

Purine- and pyrimidine-content gradients in nucleosome-protected sequences

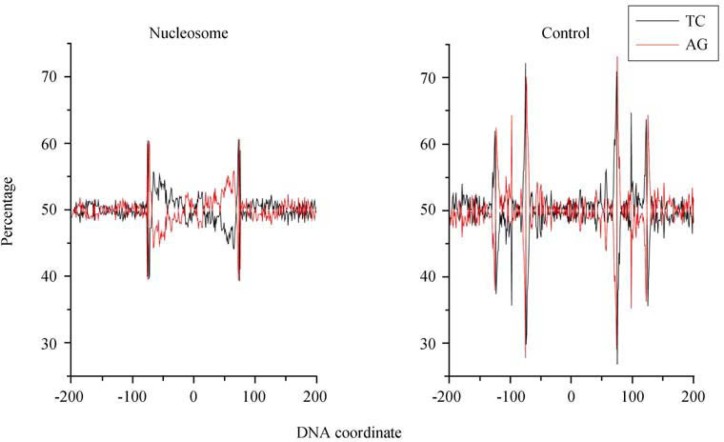
According to the Chargaff’s rules 38, 39, 40, 41, there is a balance between purine and pyrimidine contents in a genome, and the number of A plus G is equal or close to that of T plus C, so that both purine and pyrimidine contents are approximately 50%. However, the Chargaff’s rules may not be followed in a local context. For example, our previous investigation demonstrated a strong asymmetric purine content in a group of low-GC, Gram-positive bacteria (Firmicutes) (42). To examine whether there is a local purine content bias, we plotted the purine content relevant to nucleosome-protected sequences (Figure 5). A positive gradient for the purine content is clearly present starting from the 5′-end of nucleosome-protected sequences; the purine content is 40% at the 5′-end and increases to nearly 60% at the 3′-end.

Figure 5.

Purine (AG) and pyrimidine (TC) contents plotted as a function of nucleotide position around the center of nucleosome-protected sequences. We observe a positive gradient in purine content and a negative gradient in pyrimidine content in nucleosome data. When we limit the length of nucleosome-protected sequence to 148 nt, the gradients are most distinct.

HMM algorithm for the prediction of nucleosome positioning

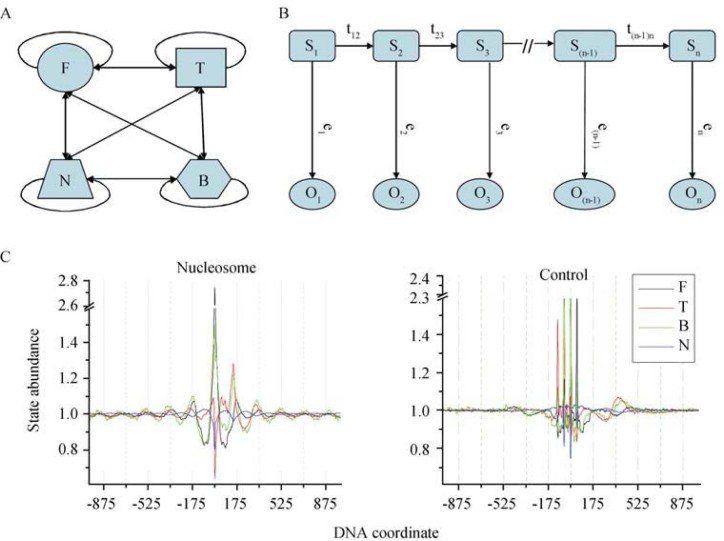
The analysis of sequence signatures observed among nucleosome-protected sequences allows us to develop an algorithm for the prediction of nucleosome positioning. This algorithm considers both the 10.5-nt and 175-nt periodicities as well as the purine gradient in nucleosome-protected sequences. Since the 175-nt periodicity appears to be 165 nt in length in budding yeast and 120.9 nt in T. vaginalis genome (37), and the 10.5-nt periodicity is close to 11 nt in prokaryotes while close to 10 nt in higher eukaryotes 33, 36, a de novo universal prediction seems not applicable to a genome without species-specific training data. Recently, nucleosome-protected sequences are profiled in large scale based on both microarray and sequencing technologies 15, 16, 17, 18, 20, 21, 22. Based on the sequence signature, we defined a profile HMM for multiple sequence alignment (43), and developed an algorithm to predict nucleosome-binding sequences, using the end information of nucleosome positions as hidden states of HMM (Figure 6A and B). We fit each nucleotide into four states: 5′-end (F), 3′-end (T), both ends (5′-end and 3′-end) (B), and non-end states (N), as nucleotide composition appears different at the two ends (5′ and 3′) of the nucleosome-protected sequences. Each of the four states presents individual frequency pattern over the length of nucleosome-protected sequences (Figure 6C). The abundance of F state reaches its peaks at the junction of the 5′-end of nucleosome-protected sequences and the 3′-end of the linker DNA, whereas the T state reaches its maxima at the junction of the 3′-end of the nucleosome-protected sequences and the 5′-end of the linker DNA. The B state has its highest abundance at the two abovementioned junctions and the N state is most abundant around the center of the nucleosome-protected sequences. State transitions occur in the four states with two options: to itself or to any other states but with a limitation that the transitions happen only from one nucleotide position to the next. The emission state of a hidden state can be any of the four nucleotides. To take the advantage of the position-specific information of DNA sequences, our HMM algorithm was applied in such a way that both transition and emission possibilities are position-sensitive.

Figure 6.

A hidden Markov model (HMM) for nucleosome-DNA interaction. A. Hidden states. Each nucleotide in the sequences has four possibilities to be at the ends of nucleosome-protected sequence: 5′-end (F), 3′-end (T), 5′/3′-end (B), and no-end (N), which correspond to four hidden sates, F, T, B, and N of the HMM. The transitions among four states happen between any two states aside from self transitions. B. Profile HMM. State (S) transition happens only from each nucleotide position (1, 2, 3 … n−2, n−1) to the next nucleotide position (2, 3, 4 … n−1, n) along a DNA sequence. The observation (O) for each state can be any of the four nucleotides. To make use of position-specific information, transition possibilities (t) and emission possibilities (e) are calculated for each nucleotide position independently. C. Abundance of the four HMM states around the 5′-ends of nucleosome-protected sequences. All four states coincide with the 175-nt periodicity in nucleosome data.

Genome-wide prediction of nucleosome positions

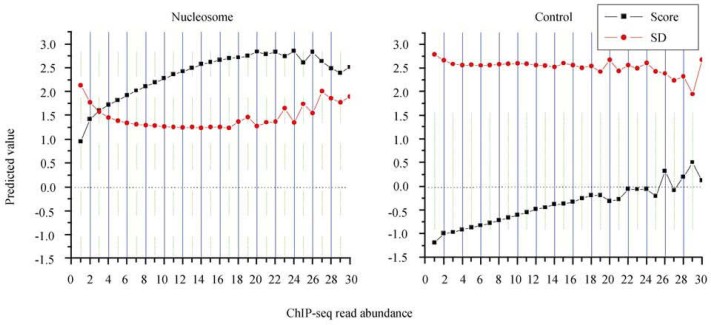
We identified the ends of nucleosome-protected sequences across C. elegans genome from the experimental data (see Materials and Methods) and extracted DNA segments around 5′-ends of the nucleosome-protected sequences from −100 bp to +250 bp. As a result, each fragment covers two units of the 175-nt periodicity. Using these sequence segments from chromosome 5 (~20 Mb) as a training dataset, we have tested the HMM algorithm on the rest of the chromosomes (~80 Mb). Each sequence segment yields a prediction score. When the score is above zero, the segment fits the model better than a random sequence; the higher a score, the greater possibility that a sequence is nucleosome-binding. To estimate the performance of our algorithm, we evaluated nucleosome-binding possibility or “affinity” based on the coverage of sequencing reads at the end of nucleosome-protected sequences from empirical data (Figure 7). The algorithm yields better scores and lesser standard deviations for sequences with higher nucleosome-binding affinity. All sequence segments categorized based on nucleosome-binding affinity have prediction scores above 1.0; it suggests that the average possibility of these segments to bind a nucleosome is at least 10 fold higher than a random sequence. When using the DNA segments from control data as a test set, we obtained an average prediction score below zero and a standard deviation approximately 0.7 fold higher than the nucleosome-protected sequences.

Figure 7.

Prediction of nucleosome positioning based on the HMM algorithm. We first use nucleosome-protected sequences from the fifth chromosome (the largest, ~20 Mb) as a training set to obtain frequencies of state transition and emission (see Figure 6B). We then apply the HMM algorithm on the nucleosome-protected sequences from the rest five chromosomes. Each nucleosome-protected sequence is assigned a prediction score based on the HMM algorithm. A score above zero indicates that the corresponding sequence has a tendency to be nucleosome-associated, whereas a minus score suggests nucleosome-free. We group the sequences based on ChIP-seq read abundance and calculate the average prediction score as well as its standard deviation (SD). Note that average prediction scores for the nucleosome-protected sequence groups are all above zero, as opposed to minus scores for the control. Prediction scores are proportional to read abundance.

Then we predicted nucleosome-binding possibility for the entire C. elegans genome with our HMM algorithm (Table 1), yielding 477,728 possible sequences on the positive strand, which is over 2% higher than those produced from empirical data. When assuming that each nucleosome covers 175 bp DNA sequence, we have predicted nucleosome-binding sequences that cover more than 80% of the genome. To estimate the accuracy of our predictions, we compared the predicted nucleosome positions to experimentally defined ones. The algorithm performs better for sequences that form stable nucleosomes (high affinity). For nucleosome positions with low affinity, the algorithm yields a result that 48% of the nucleosome positions are predicted correctly within a 50-bp vicinity of the empirically defined locations. For nucleosome positions with highest affinity, the algorithm correctly predicts 60%-70% of the nucleosome positions within a 50-nt vicinity of the empirically defined locations. We estimated that the prediction accuracy of our algorithm for well-positioned nucleosomes is 15%-20% better than that for random placement.

Table 1.

Prediction of nucleosome positions across the whole genome

Nucleosome stability*1	Nuclosome			Control
	Pred*2	Expt*3	Percent (%)	Pred	Expt	Percent (%)
1	13,231	27,314	48	10,362	20,530	50
2	15,693	31,619	50	12,598	24,707	51
3	22,556	44,658	51	24,161	47,892	50
4	29,751	57,084	52	31,833	63,507	50
5	33,150	62,478	53	32,340	64,320	50
6	32,257	59,332	54	27,577	55,379	50
7	28,034	50,079	56	22,279	44,459	50
8	22,110	39,008	57	16,936	34,138	50
9	16,436	28,383	58	12,934	25,744	50
10	11,837	20,363	58	9,426	19,026	50
11	8,512	14,165	60	6,896	13,998	49
12	6,007	9,958	60	5,192	10,522	49
13	4,222	6,864	62	3,693	7,498	49
14	2,882	4,629	62	2,798	5,600	50
15	2,068	3,258	63	2,089	4,156	50
16	1,379	2,221	62	1,519	3,116	49
17	1,006	1,618	62	1,113	2,260	49
18	733	1,135	65	878	1,754	50
19	516	791	65	640	1,315	49
20	378	594	64	479	1,046	46
21	316	471	67	382	748	51
22	184	298	62	339	607	56
23	122	196	62	260	498	52
24	122	188	65	182	372	49
25	64	119	54	143	285	50
26	54	83	65	105	216	49
27	54	72	75	83	169	49
28	36	60	60	62	129	48
29	38	52	73	45	105	43
30	20	37	54	47	86	55
Total	253,938	467,478	54	227,543	454,505	50
Random	47,273,688	100,265,350	47

^*1Nucleosome stability (ChIP-seq read abundance) deduced from experimental data.

^*2The number of nucleosome positions deduced from the experimental data and predicted correctly within a 50-nt range.

^*3The number of nucleosome positions inferred from experimental data.

Discussion

The 10.5-nt periodicity and nucleosome positioning

It was suggested that the 10.5-nt periodicity is a genomic code for nucleosome positioning 27, 44. Segal and colleagues carried out an in vitro base-substitution interference experiment to test this hypothesis and demonstrated that this sequence signal influences the affinity between DNA and histone octamer (28). However, it only suggests that “good” sequences are necessary for better affinity, but it does not prove either a sequence context or the 10.5-nt periodicity is sufficient for nucleosome positioning, as both eukaryotic and prokaryotic DNA have the 10.5-nt periodicity 33, 36, and the latter does not possess nucleosome organization (45). Our results also demonstrate that the 10.5-nt periodicity is present in both the nucleosome and control data, whereas the 3-nt and the 175-nt periodicities appear much stronger in the nucleosome data. The 3-nt periodicity is attributable to protein-coding sequences that are often abundant with well-positioned nucleosomes, and appears more pronounced in the nucleosome data as opposed to the control data. We believe that the 10.5-nt and the 175-nt periodicities together provide a guiding rail for nucleosome positioning in different scales, respectively, since the former is always in-phase with nucleosomes and the latter shows a compositional (purine) gradient in the nucleosome-protected sequences. Therefore, interference with the 10.5-nt periodicity may increase free energy of nucleosome-DNA binding thus decreases the stability or affinity of nucleosome-DNA complexes. Only drastic disruptions of the 175-nt periodicity may imply nucleosome-free regions.

Nucleosome positioning signals: codes or signatures?

If a sequence signature or code does exist in a DNA sequence, we should be able to define it by analyzing nucleosome-protected sequences acquired experimentally, especially the high-affinity fraction that can be determined based on either sequence coverage or chemical dynamics. In other words, any sequence or nucleotide compositional patterns discovered in the nucleosome-protected sequences should serve as candidate signatures or codes. What we found from these sequences are multifaceted. First, the size of nucleosome-protected sequences varies among different eukaryotes, such as 175 nt in C. elegans, 120.9 nt in T. vaginalis, and 165 nt in S. cerevisiae; it is governed by two factors, the physical size of the linker and nucleosome-binding sequences. The molecular mechanism that leads to this type of sequence periodicity is differential damage-repair frequencies between nucleosome-protected and linker sequences. Second, there is an obvious positive purine gradient along nucleosome-protected sequence; it could be a collective effect of sequence evolution constrained by DNA-histone octamer interaction and local mutation biases. Finally, we found that the nucleosome-protected sequences are somewhat GC-rich. The GC-richness may be a result of the purine content increase in the nucleosome-protected sequences and positioning in the boundary of introns and exons since exons are known to be both GC- and purine-rich (data not shown).

Computational prediction of nucleosome positioning

Regardless whether there are codes for nucleosome positioning or not, the prediction of possible nucleosome-protected sequences based on their sequence signatures is of importance for gene regulation studies, especially when the prediction is actually testable experimentally. As genome sequences diverge over time, nucleosome binding stability or affinity for a given sequence also varies all the time. Therefore, prediction algorithms should perform better on high-affinity sequences and may not be useful among low-affinity sequences for predicting nucleosome positioning and binding. Since sequencing technology advances in a fast pace in the past few years, there are chances to acquire enough data to define nucleosome-binding sequences experimentally.

Materials and Methods

Primary data

We downloaded genome sequences and experimental data from the January 2007 assembly of C. elegans in the UCSC database (http://genome.ucsc.edu/). The experimental data, including nucleosome data and control data, are from a large-scale sequencing experiment and generated as short reads (SOLiD Analyzer, Applied Biosystems) (22). The nucleosome data were generated from DNA fragments isolated from micrococcal nuclease-digested nuclear lysates. The control data came from lightly digested genomic DNA in a size range of 400-850 bp.

Defining nucleosome position from raw sequencing reads

To identify nucleosome positions, we calculate read coverage for each nucleotide position based on a 20-nt Parzen window and define 5′-end position of nucleosome based on the highest read coverage at the center of 200-nt sequence segment. If a pair of 5′-end positions is located on opposite strands within 100-200 nt, the sequence between the two positions is defined as nucleosome-protected. If a sequence segment contains more than three nucleosomes and the distance between the 5′-ends of two neighboring nucleosomes does not exceed 200 nt, we classify the sequence as nucleosome-binding region.

Power spectrum analysis

Power spectrum analysis is a popular method for detecting periodicity in numerical sequences, and we have applied it to DNA sequence analysis previously (37). To do so, we translate each sample sequence into a numerical sequence x_k. When nucleotide A is present at position k, x_k=0; similarly, when T, G or C is present, x_k=1, 2 or 3. Resultant numerical sequences are subsequently joined into one sequence and split into 2N-nt fragments (N=1024). To accelerate calculation, we used Fast Fourier Transform algorithm to compute power spectrum for each fragment. For a sequence x_k of length 2N (N is a positive integer), its power spectrum is expressed as:

$$S(f_j)=\left|{\displaystyle \sum _{k=1}^{2N}}{x}_k\exp {(-2\pi ik{f}_j)}^2\right|$$

where i² = −1, and f_j = j/2N (j=0, 1, …, N).

HMM algorithm

Using the empirical data from large-scale sequencing, we constructed an HMM that defines the interaction between DNA and histone octamer. We use a dynamic programming method, forward algorithm, to calculate the probability of a target DNA sequence that binds nucleosome.

Authors’ contributions

KC collected the datasets, conducted data analyses, and prepared the manuscript. LW, MY, JL, and CX participated the analyses. HS and JY supervised the project and revised the manuscript. All authors read and approved the final manuscript.

Competing interests

The authors have declared that no competing interests exist.