Mining Functional Gene Modules Linked with Rheumatoid Arthritis Using a SNP-SNP Network

Abstract

The identification of functional gene modules that are derived from integration of information from different types of networks is a powerful strategy for interpreting the etiology of complex diseases such as rheumatoid arthritis (RA). Genetic variants are known to increase the risk of developing RA. Here, a novel method, the construction of a genetic network, was used to mine functional gene modules linked with RA. A polymorphism interaction analysis (PIA) algorithm was used to obtain cooperating single nucleotide polymorphisms (SNPs) that contribute to RA disease. The acquired SNP pairs were used to construct a SNP-SNP network. Sub-networks defined by hub SNPs were then extracted and turned into gene modules by mapping SNPs to genes using dbSNP database. We performed Gene Ontology (GO) analysis on each gene module, and some GO terms enriched in the gene modules can be used to investigate clustered gene function for better understanding RA pathogenesis. This method was applied to the Genetic Analysis Workshop 15 (GAW 15) RA dataset. The results show that genes involved in functional gene modules, such as CD160 (rs744877) and RUNX1 (rs2051179), are especially relevant to RA, which is supported by previous reports. Furthermore, the 43 SNPs involved in the identified gene modules were found to be the best classifiers when used as variables for sample classification.

Introduction

It is well-recognized that complex diseases are caused by multiple gene-gene interactions, in which each gene may have a small effect on disease development, rather than by single gene defects (1). As high-density single nucleotide polymorphism (SNP) arrays and subsequent genome-wide association studies (GWAS) were developed, the study of complex diseases has become of widespread interest for researchers. Traditional methods of genetic analysis are often weak when applied to some complex diseases, which are most likely to be both genetically multifactorial and phenotypically heterogeneous. It is therefore suggested that the study of complex diseases should not be restricted to single gene identification, but should focus on gene interaction studies. Recently, there have been several studies exploring gene-gene interactions in different ways 2, 3, 4, 5.

Furthermore, more and more evidence shows that investigating gene-gene interactions may lead to the development of a functional network and functional modules (6). Iossifov et al. (7) predicted pathways or networks of interacting genes that contribute to common heritable disorders by combining standard genetic linkage formalism with whole-genome molecular interaction data. Similarly, Wang et al. (8) demonstrated pathway-based approaches, which jointly considered multiple contributing factors in the same pathway. In addition, Franke et al. (9) developed a functional human gene network that integrated information on genes and the functional relationships between genes based on multiple databases. They used the network to identify important candidate genes from numerous loci on the basis of their functional interactions and reduced the cost of pinpointing true disease genes in the analyses of disorders. In summary, molecular networks can be obtained from many levels including co-expression (10), co-regulation (11) or protein-protein interactions (6). Depending on the different networks, a variety of methods have been suggested for the mining of useful functional information, such as clustering genes that show high correlation coefficients between gene expression profiles 12, 13, identifying functional modules based on the structure of transcriptional regulation (14), or predicting functional modules encoded in a microbial genome (15). With the rapid development of GWAS, the construction methods of molecular networks provided us with a potential strategy for obtaining a network at the genetic level by using predicted interactions between SNPs. Networks like this may show special features due to the genetic component and may aid in the explanation of complex diseases. Accordingly, by introducing disease information into such a network and further analyzing functional gene modules, we can learn more about the functional characteristics of disease etiology.

As we know, rheumatoid arthritis (RA) is a chronic disease that leads to inflammation of the joints and surrounding tissues. Recent studies have indicated that genetic factors play important roles in the increased risk of developing RA. In the present study, we present a novel method for mining functional gene modules linked with RA. First, we carried out the Haseman-Elston (H-E) test (16) and Random Forest (RF) algorithm (17) to screen out disease-related SNPs from a whole-genome dataset. Secondly, candidate SNPs shared by the H-E test and RF algorithm were used to construct the SNP-SNP network with polymorphism interaction analysis (PIA) algorithm (18), which was developed as a new method to identify the synergistic contribution of SNPs to diseases. Then, sub-networks were extracted by analyzing the structure of the SNP-SNP network. Further, using the dbSNP database, all of sub-networks were mapped onto gene modules. We used a permutation-based procedure to evaluate the significance of associated SNP pairs. For the five gene modules we discovered, Gene Ontology (GO) analysis indicated that genes within a common module were likely to be enriched on some RA-related GO terms. Furthermore, the 43 SNPs involved in the identified gene modules, were found to be the best classifiers when used as variables for sample classification. Finally, we compared the results of our method to existing tools including GRAIL (19) and GSEA-SNP (20) to evaluate the similarity and novelty of our results.

Results

Construction of RA-specific SNP-SNP network

In this study, we defined a total score for each SNP-SNP pair as described in the Materials and Methods section. We found when we kept the top 1,000 SNP pairs obtained using each of seven scores involved in PIA, only a small number of overlapping SNP pairs were found. However, it is interesting to note that using the aforementioned total score, we acquired the maximum number of overlapping SNP pairs with all of seven measures involved in PIA. Therefore, total score was a more reasonable measure for evaluating cooperating SNP pairs contributing to disease. As a result, we used total score to evaluate the interaction strength of each SNP-SNP pair (Table S1).

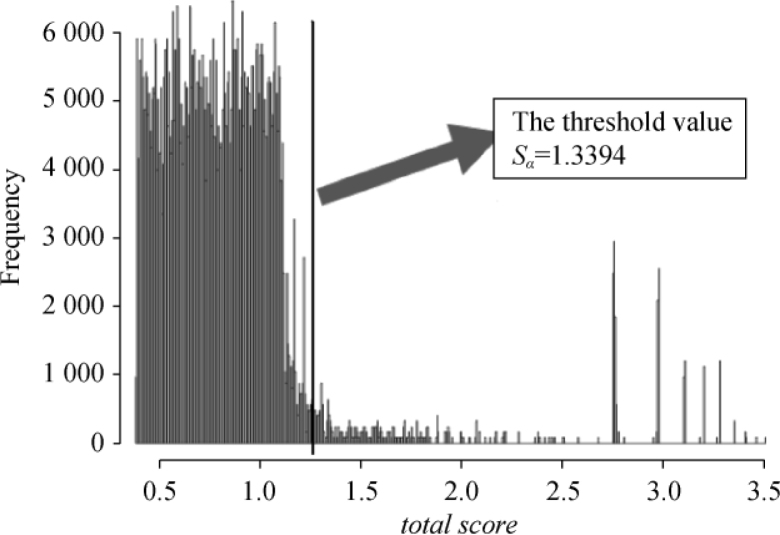
According to our permutation test as described in the Materials and Methods section, the empirical distribution of total scores was formed from 1,000,000 scores, and a threshold value of total score (S_α = 1.3394) was considered as a cut-off value at a significance level (P=0.05) to screen out SNP pairs (Figure 1). Among the top 1,000 SNP pairs acquired with the original dataset, we found that the total scores of the top 100 SNP pairs were all greater than the threshold value. We used these significant SNP pairs to construct a SNP-SNP network specific to RA. This network contains 110 SNPs and 100 edges, where an edge indicated a SNP pair. The total scores and their corresponding P-values for the top 100 SNP pairs are shown in Table S2. The SNP-SNP network shown in Figure S1 was generated with MAVisto software (21).

Figure 1.

The empirical distribution of total scores. By permuting sample labels 1,000 times, the PIA algorithm is performed repeatedly for 1,000 new datasets. The empirical distribution of total scores is formed from all above results. The threshold value of 1.3394 corresponds to a significance level of 0.045.

Identification of functional gene modules

According to our rule for extracting hub SNP, five hub SNPs with a degree greater than 5 were extracted: rs1424903 (degree=18, P=1.5×10⁻¹³), rs744877 (degree=9, P=2.3×10⁻⁵), rs164466 (degree=5, P=0.010), rs1004531 (degree=5, P=0.010) and rs759382 (degree=5, P=0.010). Then, five sub-networks defined by hub SNPs were extracted. To mine functional gene modules and high risk genes linked with RA, we mapped the SNPs onto genes using a dbSNP database. We calculated the distances of all SNPs to the splice variants of their nearest genes along chromosomes. The highest frequency occurs in the range from 0 to 4,000 base pairs. This result closely agrees with previous reports, in which SNPs that are >500 kb away from any gene are not considered because most enhancers and repressors are <500 kb away from genes, and most linkage disequilibrium blocks are <500 kb (8). This mapping method allowed us to identify genes implicated by SNPs of sub-networks to obtain gene-gene interaction modules. As a result, 59 genes associated with RA were identified from 110 SNPs involved in the SNP-SNP network. A total of 12 genes were associated with 19 SNPs in the rs1424903-related gene module. The rs744877 (CD160)-related gene module contained seven genes associated with 10 SNPs. five genes corresponding to six SNPs were included in the rs1004531 (TNFAIP8)—related gene module. The rs164466-related and rs759382 (SLC9A4)-related gene modules each contained two genes corresponding to six SNPs.

We identified 59 genes involved in the SNP-SNP network as the background set, and genes involved in 5 gene modules as the test sets. Using a significance level of 0.05, most enrichment results were found in the rs1424903-related and rs744877-related gene modules. At a significance level of 0.1, two enrichment GO terms occurred in the rs1004531-related gene module: GO: 0005515 (P=0.08591) and GO: 0005886 (P=0.0702). However, no distinct enrichment phenomena were seen in other gene modules owing to their low number of genes. Those gene modules with significant GO terms were considered functional gene modules relevant to RA. Two gene modules particularly enriched in GO terms (the rs1424903-related and rs744877-related gene modules) are shown in Table 1. In addition, the enrichment results for five gene modules are shown in the heat map generated by Cytoscape software (22) in Figure S2.

Table 1.

Enriched GO terms with P<0.1 in the rs1424903-related and rs744877-related gene modules

Gene module	Category	GO term	P	n#	m#	Description
rs1424903-related	MF	GO:0005515	0.0550	16	5	Protein-binding
		GO:0003700	0.0523	5	2	Transcriptional activator activity
		GO:0008270	0.0461	8	3	Zinc ion-binding
		GO:0005524	0.0729	9	3	ATP-binding
	BP	GO:0006355	0.0461	8	3	Regulation of transcription
	CC	GO:0005634	0.0729	9	3	Nucleus
		GO:0005622	0.0461	8	3	Intracellular
		GO:0005737	0.0360	11	4	Cytoplasm
		GO:0016021	0.0729	9	3	Integral to membrane
		GO:0005886	0.0919	6	2	Plasma membrane
rs744877-related	MF	GO:0005524	0.0401	9	2	ATP-binding
	BP	GO:0007165	0.0182	7	2	Signal transduction
	CC	GO:0016021	0.0401	9	2	Integral to membrane
		GO:0005886	0.0109	6	2	Plasma membrane

Note: n#, Number of genes contained in a category counted using 59 background genes. m#, Number of genes contained in a category counted using 12 genes and 6 genes for the rs1424903-related and rs744877-related gene modules, respectively. MF stands for Molecular Function; BP and CC stand for Biological Process and Cellular Component, respectively. Enriched GO terms with P<0.05 are in bold.

We found that SNPs [rs2051179 (RUNX1), rs164466, rs1424903, rs744877 (CD160) and rs759382 (SLC9A4)] involved in functional gene modules were previously identified as susceptibility loci in a study using ensemble decision trees (4) and another study using the BGTA algorithm (14). As shown by “Molecular Function” in Table 1, the rs1424903-related gene module was relevant to protein binding (GO: 0005515). Kristensen has previously reported that there seems to be a qualitative rather than a quantitative change in ³H-imipramine binding in patients with RA (23). As shown by the dimension “Biological Process”, a significant GO term was regulation of transcription (GO: 0006355). Redlich et al. have previously found that overexpression of Ets-1 in RA synovial tissue may be due to tumor necrosis factor-alpha (TNF-α) and interleukin 1 (IL-1). Therefore, they suggested that Ets-1 may be an important transcription factor in the cytokine-mediated inflammatory pathway and destructive cascade characteristic of RA (24). Aud and Peng also investigated whether transcription factors have important roles in the pathogenesis of inflammatory arthritis, and they have proposed several targets for anti-inflammatory therapies to modulate transcription factor activity (25). Based on the dimension “Cellular Component”, there is also evidence to support the significance of cytoplasm (GO: 0005737). Anti-neutrophil cytoplasm antibodies (ANCA) occur occasionally in RA, but their incidence and clinical significance are unknown. Savige et al. demonstrated that ANCA may be associated with systemic vasculitis, and there is an incomplete correlation between indirect immunofluorescence patterns and antibody specificity in enzyme-linked immunosorbent assay (ELISA) systems (26).

For the rs744877-related gene module, four significant GO terms were found. As shown by “Molecular Function”, GO: 0005524 (ATP binding) was related to the inflammatory response (27). Schimitz et al. (28) demonstrated that the ATP-binding cassette (ABC) transporter, ABCA1, was induced during differentiation of human monocytes into macrophages, and there was a dual regulatory function for ABCA1 in macrophage lipid metabolism and inflammation. As shown by ′Biological Process′, the significance of GO: 0007165 (signal transduction) is also supported by previous studies. Extracellular signals are transduced intracellularly via multiple pathways, resulting in alterations in the transcription and translation of specific proteins. Some of these signaling pathways result in the production of proteins, including cytokines and matrix metalloproteinases, which are implicated in the pathogenesis of RA (29).

Further analysis revealed more valuable information in the functional gene modules. Among the 12 genes included in the rs1424903-related gene module, zinc-finger protein 238 (ZNF238) is attached to zinc-finger proteins that can regulate the human immunodeficiency virus type 1 (HIV-1) long terminal repeat (LTR) (30). In the rs744877-related gene module, hub gene CD160 is a potential RA association gene. The CD160 receptor represents a unique triggering surface molecule that is expressed by cytotoxic NK cells, participates in the inflammatory response and determines the type of subsequent specific immunity (31).

In addition, it is interesting to observe two links among five hub SNPs. One pair was rs164466-rs1004531 (TNFAIP8), and the other was rs1424903–rs759382 (SLC9A4). This may suggest that functional gene modules cooperate to affect RA and highlight the need for further study.

Comparison with GRAIL

We also sought to compare our method with another SNP analytical tool, GRAIL. In the GRAIL program, we took all query regions involved in the whole network as the input to GRAIL. Interestingly, common gene cliques were found between gene groups acquired with GRAIL and the functional gene modules identified with our methods (Table 2). For example, MYH9, CTSB, ELOVL6 and PHACTR1 in the rs1424903-related gene module were also included in the gene group obtained with GRAIL (P_text=0.0026). GRAIL and our study are two methods based on different paths for mining gene groups associated with disease. GRAIL can extract similar genes from all query regions that the user is attempting to evaluate. Compared to those gene groups acquired by GRAIL, functional gene modules linked with RA identified using our method are more conservative and represent higher risk because these modules are prioritized layer by layer, and include gene-gene interactions associated with disease.

Table 2.

The comparison between gene modules identified by our method and similar genes acquired with GRAIL

Gene modules identified by our method			Similar genes acquired with GRAIL
Gene module (sub-network)	Genes included in gene module	Pmodulea	Similar genes	Ptextb
rs1424903-related	ZNF238, NDEL1, GMDS, RUNX1, MYH9, ELOVL6, CTSB, PHACTR1, BHMT2, SLC9A4, LOC339977, ANKH	1.5E-13	PRKCB1, PLEK, IQGAP2, MYH9, ELOVL6, CTSB, PHACTR1	0.0026
rs744877 (CD160)-related	CD160, C21orf34, LHFP, GRPEL2, CNTN4, CSNK2A2, WDR62	2.3E-5	CTSB, CASP6, PRKCB1, GRPEL2, CNTN4, CSNK2A2 BTBD9, CASP6, CSNK2A2,	0.0131
rs1004531 (TNFAIP8)-related	TNFAIP8, PLAU, RIMS1, C10orf55, ELF1	0.010	ELF1, TNFATP8, RIMS1, PLAU MYH9, NLRP7,	0.0249
rs164466-related	TNFAIP8, MTMR9	0.010	CSNK2A2, ELOVL6, PRKCB1	0.0038
rs759382 (SLC9A4)-related	SLC9A4, C21orf34	0.010

^aP_module indicates the probability of a hub SNP with >t connections (t is the degree of the hub) in a random network.

^bP_text is the text-based similarity metric based on GRAIL. Similar genes with P_text<0.01 by GRAIL analysis are shown. Genes underlined represent common genes shared by two gene sets, which are gene modules identified by our method and genes acquired with GRAIL.

Comparison with Gene Set Enrichment Analysis-SNP (GSEA-SNP) on five sub-networks defined by hub SNPs

GSEA-SNP programs were performed for five sub-networks. An enrichment score (ES) was computed for each sub-network. Using a permutation test, we obtained the threshold value of ES at a significance level of 0.05 for each sub-network (Figure S3). Those sub-networks with P<0.05 were extracted as enrichment sub-networks associated with disease. The results showed that three sub-networks were significant: the rs1424903-related (P=0.0020), rs164466-related (P=0.0020) and rs759382-related sub-networks (P<0.0001) (Table 3). It is worth noting that the rs1424903-related gene module was also the functional gene module with the most significant GO terms, which indicated that elucidation of the relationship between genes within this module may facilitate interpretation of disease etiology. Furthermore, for each of five sub-networks, we applied GO enrichment analysis to its 1,000 random matched SNP sets. For sub-networks with hubs rs1424903, rs744977, rs164466, rs1004531 and rs759382, each matched set consisted of 19, 10, 6, 6 and 6 SNPs, respectively, randomly selected from a total of 702 candidate SNPs. We found that the frequency of random sub-networks including at least a significant GO term was 2.3%, 1.9%, 0.0%, 0.2% and 0.1%, respectively. This result therefore suggests that a more obvious GO enrichment effect is present in our extracted sub-networks than in matched SNP sets selected by chance.

Table 3.

GSEA-SNP results for five sub-networks defined by hub SNPs

Sub-network	Number of SNPs/genes		ES	Number of significant SNPs by x2-test (P<0.05)	P	FDR	ES threshold values
	SNPs	Genes
rs1424903-related	19	12	0.6672	9	0.0020	<0.001	0.5807
rs744877-related	10	7	0.5652	3	0.2398	0.002	0.6566
rs164466-related	6	2	0.8032	4	0.0020	0.002	0.7455
rs1004531-related	6	5	0.7493	3	0.0551	0.031	0.7618
rs759382-related	6	2	0.8903	4	0.0000	0.066	0.7180

Note: FDR, false discovery rate.

Comparison of classification performances

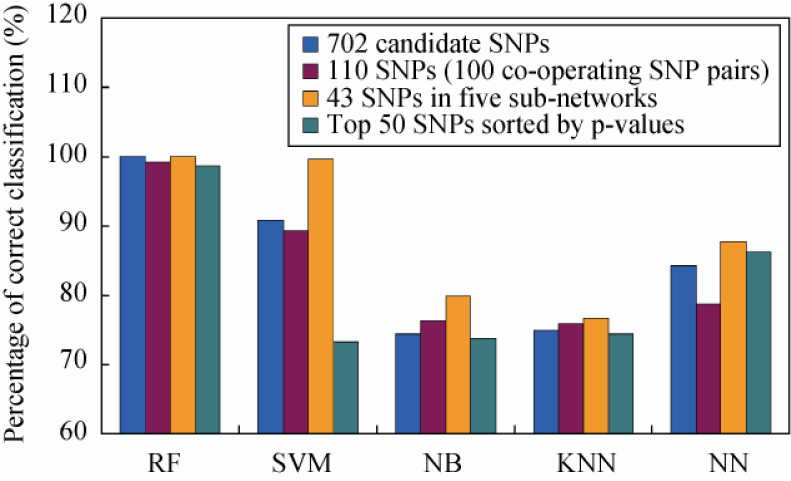
Four SNP groups described in the Materials and Methods section were used to validate the classification performances of risk SNPs identified with our method. These included 43 SNPs involved in five sub-networks (modules), 702 candidate SNPs, 110 SNPs involved in 100 co-operating SNP pairs and the top 50 SNPs sorted by P-values with genotype-based chi-square tests. Logically, the SNP group with 43 SNPs might be a better classifier than the other SNP groups when they are taken as variables to classify samples. Here, five classifiers were used: naïve Bayes (32), k-Nearest Neighbor (kNN) (33), Neural Network (34), Support Vector Machine (SVM) (35) and Random Forests. We used 5-fold cross-validation to assess the classification accuracy rate of these different machine-learning methods. We set k at 3 in the kNN program and took the radial basis function (RBF) as the kernel function in the SVM program. In the Random Forests program, 5,000 trees were constructed. As we expected, five classifiers all showed that the SNP group with 43 SNPs was more powerful than other SNP groups when used as predictor variables for sample classification (Figure 2). This result supports our hypothesis and indicates that mining functional gene modules by constructing a SNP-SNP network is likely to provide an effective approach to map disease loci (genes) linked with RA.

Figure 2.

Comparison of classification performance of four SNP groups using five classifiers. The four SNP groups are: 43 SNPs included in five sub-networks (modules, brown), 702 candidate SNPs identified in the GWA study (blue), 110 SNPs involved in 100 co-operating SNP pairs (red) and the top 50 SNPs sorted by P-values with chi-square tests (green). The five classifiers are naïve Bayes (NB), k-Nearest Neighbor (kNN), Neural Network (NN), Support Vector Machine (SVM) and Random Forest (RF).

Discussion

In this paper, we present a novel method for mining functional gene modules based on a genetic factor (SNPs) to study RA. In contrast to mining gene modules by correlating protein interaction networks and gene expression patterns, we constructed a SNP-SNP network and extracted sub-networks with hub SNPs to mine functional gene modules associated with RA. We found that the best classifier was based on 43 SNPs involved in the gene modules. Moreover, we identified some risk genes associated with RA, many of which were confirmed by previous studies.

Given the constructed SNP-SNP network, it is interesting to note that the strongest SNP-SNP interactions appeared in the functional gene modules. For instance, rs744877*rs1033109 (total score=3.4124, P=0.00022) in the rs1424903-related gene module and rs1424903*rs2077889 (total score=2.9736, P=0.0106) in the rs744877-related gene module. As validation of our strategy, we ranked SNPs according to the sum of their frequency in the top 100 SNP pairs using seven scoring measures, and the top 15 SNPs were designated as feature SNPs associated with RA in our analysis (Table S3). In other words, these feature SNPs appeared most frequently in the top 100 scoring SNP pairs using seven scoring metrics. Interestingly, five hub SNPs, rs164466, rs1424903, rs744877 (CD160), rs1004531 (TNFAIP8) and rs759382 (SLC9A4), were also included in these feature SNPs. Specifically, rs1424903, rs164466 and rs744877 (CD160) ranked the top three with the highest frequencies. Furthermore, among 98 SNPs (P<0.05) identified by the chi-square test out of 702 genome-wide candidate SNPs, 9 (47.4%), 3 (30.0%), 4 (66.7%), 3 (50.0%) and 4 (66.7%) significant SNPs are found in rs1424903-related, rs744877-related, rs164466-related, rs1004531-related and rs759382-related gene modules, respectively. The most significant SNPs, rs164466 (P=0.000126), rs1424903 (P=0.000453) and rs744877 (P=0.000566), were the top three feature SNPs and also hub SNPs of three sub-networks. These results suggest that the functional gene modules discovered by our method are more likely to be associated with RA.

To further analyze the functional gene modules discovered by our method, we performed functional enrichment analysis for the 702 candidate SNPs identified in the GWA study and the whole network (the top 100 cooperating SNP pairs) based on Gene Ontology. Two GO terms (GO: 0005524 and GO: 0006355) were found to be enriched in the functional gene modules, the candidate SNPs and the whole network. Five GO terms (GO: 0005515, GO: 0005524, GO: 0006355, GO: 0005622 and GO: 0016021) were enriched in both the functional gene modules and the whole network. Interestingly, some significant GO terms, such as GO: 0005737 (0.0304) enriched in the rs1424903-related gene module and GO: 0007165 (0.0172) enriched in the rs744877-related gene module, were not enriched in the whole network. This indicates that RA may be more closely associated with the genes concentrated in the gene modules than with the genes involved in the whole network.

Although our study presents a new approach for researchers to study RA and extends the combination of genetic factors and their biological network to explain the mechanisms in pathogenesis, it should be pointed out that our interaction analysis does not take into account pedigree data. In order to identify the synergistic effect between SNPs, we constructed an independent sample by converting the family-based data into a case-control dataset. As such, this process might result in the inflation (or reduction) of type I error rates, so we should be cautious when interpreting the results. In addition, in this process, some samples are excluded, and the minor effect between SNPs was ignored. Further work is needed to identify the minor effect between SNPs by handling family-based data.

It is noteworthy that we did not implement PIA analysis for the whole-genome data, and instead performed the first stage screening for candidate SNPs with the H-E test and RF algorithm to overcome computational complexity. In addition, since the PIA algorithm cannot deal with pedigree-induced residual correlation structure, we did not perform interaction analysis directly using SNPs identified by the H-E test. However, it is of interest to note that 338 risk SNPs (P<0.05) identified by the traditional chi-square test were largely included in the 2,200 SNPs extracted by the RF algorithm. Also, there are still 702 overlapping SNPs (31.9%) shared by the H-E test and RF algorithm although methodological differences are unavoidable. It is therefore suggested that the shared candidate SNPs should show stronger association signals with disease than other SNPs. Indeed, we performed interaction analysis with all of the 2200 SNPs identified by RF, and found that those important hub SNPs, such as rs744877 and rs1004531, were not identified. Therefore, using H-E or RF alone may not be good enough for constructing a SNP-SNP network.

Moreover, it is pointed out that the testing dataset used in this work is relatively small, which might result in insufficient efficacy. Indeed, we also considered using larger datasets to validate our method. Another whole-genome dataset, Wellcome Trust Case Control Consortium (WTCCC) data, has provided us with a chance to address this issue. Preliminary analysis using our new method is encouraging in that we find CD160, TNFAIP8 and PTPN22 are also important hub genes. Further comprehensive investigation will be warranted for future studies. On the other hand, because the genetic network is a complex network with complicated biological and genetic mechanisms, it remains a challenging task to interpret genetic factors in the context of known functional relationships. Chromosome and pathway-based techniques can be introduced into this framework for a better understanding of the mechanisms of disease.

Materials and Methods

Data source

We used the North American Rheumatoid Arthritis Consortium (NARAC) data provided by the Genetic Analysis Workshop 15 (GAW15) Problem 2 (http://www.gaworkshop.org), which included 746 multiplex Caucasian RA families scanned with SNPs. About 5,744 genome-wide SNPs were genotyped using the Illumina system in all families including 66 families from Katherine Siminovitch, a collaborator in Canada (36). After removing those individuals with unclear diagnoses or SNP markers that were not genotyped successfully, a total of 1,989 individuals (1,640 affected vs. 349 unaffected) and 5,407 SNP markers from 22 autosomes were included in the final analysis. In our analyzed dataset, there was no individual with >10% missing SNP genotypes and no SNP with >5% missing genotypes.

Identification of candidate SNPs associated with disease

To overcome the computational complexity of analyzing interactions among all 5,407 SNPs, we performed a first stage screening for candidate SNPs. The rationale behind this first stage screening is that those markers with high-dimension interaction information will show, at a minimum, modest association with RA. Therefore, we will not lose many informative markers if we set a less stringent threshold of association effect in the first stage selection. Considering the structure of pedigree data, we used the H-E regression-based linkage test (16) to identify the non-random association due to genetic linkage between two genomic loci. However, the possible inaccurate Identity by Descent (IBD) computation error included in the H-E analysis may give a false result. Accordingly, to overcome any false positive error caused by an individual analysis, the RF program (17), a nonparametric tree-based predictive model, which has been recommended as a pre-screening tool for large scale association studies, was also applied to implement the same screen progress. Therefore, the shared candidate SNPs should show more association signals with disease than other SNPs despite methodological differences. In the present study, shared candidate SNPs will be used for further interaction analysis.

Identification of SNPs associated with disease by H-E linkage test

We used the H-E linkage test for the pedigree data of 746 families. The SIBPAL program of S.A.G.E.5.4.2 (http://genepi.cwru.edu/) was used to calculate IBD by multipoint consideration. The H-E linkage test was performed separately for pairs with 0, 1 or 2 affected family members (no sib in a sibling pair is affected, only one is affected and both are affected, respectively) as tests for linkage. A total of 1,551 SNPs with P<0.05 were filtered from the whole 5,407 SNPs. To avoid the possible loss of the true positives, we did not perform a multiple-test correction for the number of SNPs evaluated. Instead, we employed another program (RF) to control the Type I error rate. Therefore, SNPs identified by the H-E test can be taken as an indicator for roughly rating relative importance of the candidate SNPs.

Identification of SNPs associated with disease by RF

In order to apply the RF program, we selected one unaffected individual randomly from each of 272 different families, and these 272 unaffected individuals were used as our control group. For 474 families from which an individual was not recruited to the control group, we sampled one individual per family at random, and these 474 affected individuals were taken as the case group. We used the randomForest package in R-2.5.1 (http://www.r-project.org/) to identify risk SNPs covering each of chromosomes respectively from the whole genome of 5,407 SNPs with our constructed case-control dataset. For each chromosome, 5,000 trees were constructed and the out-of-bag (OOB) data, approximately one-third of the observations, were then used to estimate the prediction accuracy. We found that the accuracy of the OOB prediction on 22 chromosomes were all higher than 65%. For this purpose, we used Mean Decrease Gini (MDG) of the RF algorithm to measure the risk level of a SNP. The higher the MDG is, the further the degree of impurity arising from category can be reduced by a SNP. Therefore, high MDG suggests an important SNP. We ranked SNPs in terms of their MDG, and filtered the top 100 SNPs for each chromosome. Accordingly, 2,200 SNPs were extracted as candidate SNPs.

Finally, a total of 702 candidate SNPs shared by the H-E test and RF algorithm were used for further interaction analysis.

Selection of cooperating SNP pairs contributing to disease

In this analysis, we defined a total score for each SNP-SNP pair. The formula was as follows:

$$\mathit{total\; score}=\log ({\displaystyle \sum _{i=1}^7}{\mathit{score}}_i)$$

where score1-score7 were seven scoring metrics included in the PIA algorithm and the definition of these metrics have been described previously (18). According to the definition of these scoring metrics in PIA, higher scores reflect stronger cooperation between SNPs for contributing to a disease.

In the PIA algorithm, SNPs were recoded as 0, 1 or 2 when they were homozygous for the reference allele, heterozygous, or homozygous for the alternate allele, respectively. For each SNP pair, the total score defined in our analysis was used to indicate its extent of interaction.

Permutation of sample labels for calculating interaction threshold value

To identify risk SNP combinations, a permutation test (13) was performed. First, sample labels were permuted 1,000 times and 1,000 new datasets were generated. In the following step, each dataset was repeatedly analyzed by the PIA algorithm and the total scores of the top 1,000 SNP pairs were reserved. Accordingly, the empirical distribution of total scores was formed from 1,000,000 results, and a threshold value was considered as a cut-off value at a significance level (P=0.05) to screen out SNP pairs. Finally, among the top 1,000 SNP pairs obtained from the original dataset, a pair-wise synergistic SNP was considered significant if its total score was greater than this threshold value. All significant synergistic SNP pairs contributing to disease were used to construct a disease-specific SNP-SNP network. In this network, the nodes represent SNPs, and links between SNPs represent their cooperating relationship contributing to disease.

Identification of hub SNPs

It is well-known that a relatively small number of hub nodes (genes or SNPs) play important roles in most cellular networks. As a network measure, degree has frequently been used to measure the importance of a hub node (37). To obtain significant hub nodes, we assumed that the degree of nodes followed a Poisson distribution in a random network. To determine whether a node is considered a hub node, a formula was used to compute its probability of degree of equal or larger than t. The formula is as follows (38):

$$\begin{array}{c}P\left(x>t\right)=1-P\left(x\le t\right)=1-{\displaystyle \sum _{k=0}^t}{\lambda }^k{e}^{-\lambda }/k!\\ \left(\lambda =n{P}_1,P_1=m/C_n^2\right),\end{array}$$

where n is the number of nodes and m is the number of interacting SNP pairs in our constructed disease-specific SNP network. We considered a SNP with >5 connections in a random network (P=0.010) as a rare event under the null hypothesis that n nodes (SNPs) were connected randomly. The probability of this rare event was taken as a threshold, and a SNP was considered a hub SNP when its P value was smaller than this threshold.

Mining of disease-related gene functional modules

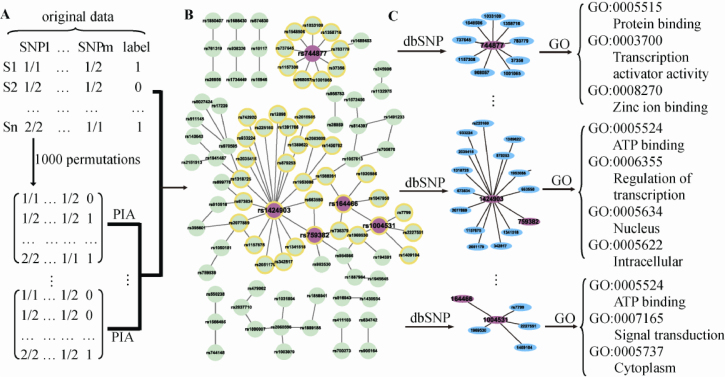
We extracted sub-networks defined by hub SNPs from our SNP–SNP network; that is, we considered a group of SNPs linked directly to a hub SNP as a sub-network in which the hub SNP was also included. Then, sub-networks were turned into gene-gene interaction modules by mapping SNPs to genes using dbSNP database. We used the following rule for mapping SNPs onto genes: a gene is associated with a SNP if this SNP is located within this gene or untranslated regions of this gene. SNPs that mapped onto multiple genes were assigned to a single gene according to the following hierarchy: coding>intronic>5′ UTR>3′ UTR>5′ upstream>3′ upstream. This strategy can avoid issues with weight inflation induced by genes having different numbers of SNPs (39). Genes involved in the constructed primary network were also obtained by the same method. All genes involved in the constructed network were defined as the background gene set G_b, and genes in each gene module were defined as the test gene set G_t for functional enrichment analysis based on GO. A hypergeometric distribution and Onto-express web tools (http://vortex.cs.wayne.edu/ontoexpress) were used to generate P-values (40). In the present study, only those GO terms (and their parents) whose number of annotated genes were more than two for each gene module were considered. We did not perform the multiple test correction for GO terms because the number of genes involved in the network was not large, and the multiple test correction might lead to a loss of true-positive results. A nominal significance level of 0.1 was set in our analysis, and a GO term with a significance level of 0.05 was considered to be particularly enriched in the gene module. The gene modules with significant GO terms were considered as functional gene modules associated with RA. Our work flowchart is shown in Figure 3.

Figure 3.

The flow chart for mining functional gene modules associated with RA via constructing a SNP-SNP network by the PIA algorithm. A. Constructing a SNP-SNP network with the top 100 SNP pairs whose total scores are higher than the threshold. B. Extracting sub-networks involved in hub SNPs whose degree is more than 5. C. Mapping SNPs onto genes using a dbSNP database and performing GO enrichment analysis of gene modules obtained from sub-networks. A gene module is considered a functional gene module in which at least one significant GO term is included.

Comparing with two other SNP anlaysis tools GRAIL and GSEA-SNP

For validation, we compared our method with two other SNP analysis tools, GRAIL and Gene Set Enrichment Analysis-SNP (GSEA-SNP). GRAIL was developed recently to look for similarities in the published scientific text among genes associated with complex disease. In the GSEA-SNP process, an enrichment score (ES) was computed for each sub-network. By permutation tests, we can obtain the threshold value of ES at a significance level of 0.05 for each sub-network. Those sub-networks with P<0.05 were extracted as enrichment sub-networks associated with disease.

Comparison of classification performances

To further validate risk SNPs identified with our method, four SNP groups were defined in the present study: SNPs included in sub-networks (modules), candidate SNPs, SNPs involved in co-operating SNP pairs and the top 50 SNPs sorted by P-values with genotype-based chi-square tests using independent samples constructed. We attempt to find whether SNPs involved in gene modules can perform better than those of SNPs when used as variables to make risk prediction of disease outcome.

Authors’ contributions

LH defined the research theme, designed methods and experiments, conducted the data analyses, interpreted the results and drafted the manuscript. HL co-worked on the interpretation and discussion of the results. HL, DL, LL and ZL revised the manuscript. All authors read and approved the final manuscript.

Competing interests

The authors have no competing interests to declare.

Supplementary Material

Tables S1-S3; Figures S1-S3

DOI: 10.1016/S1672-0229(11)60030-2